3.1. Motion Response
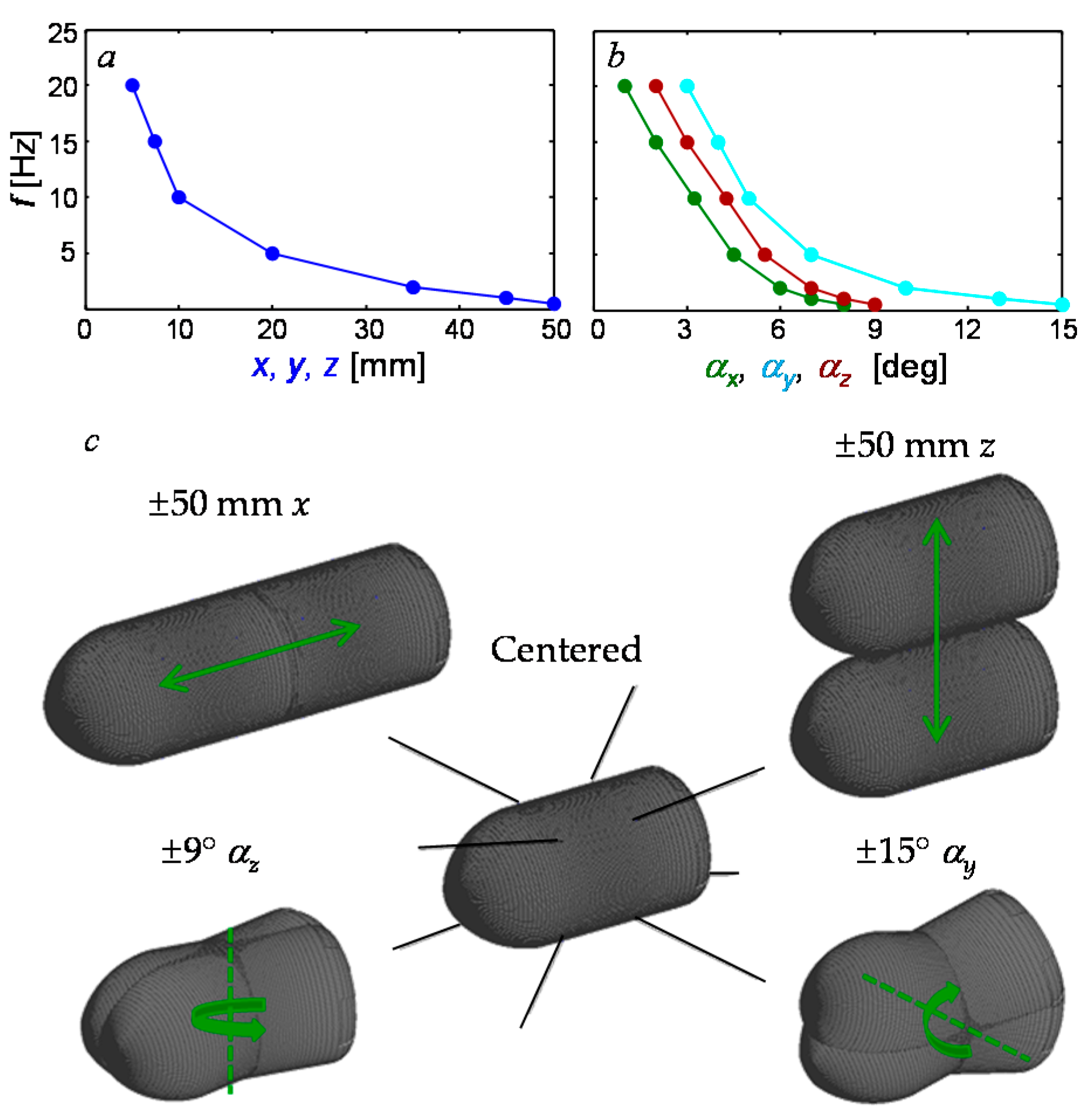
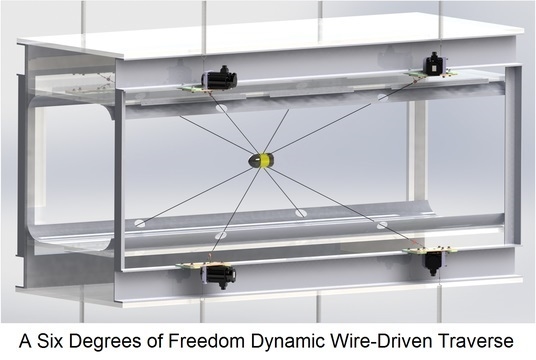
The system dynamic performance is characterized in terms of displacement range and frequency of sinusoidal commands, and is depicted in
Figure 7. Although the mounting points of the wires on the motors and the model determine the ideal maximum range of motion with limitless tension and unbreakable wires, this range diminishes for a fixed maximum tension. This range is also frequency dependent and diminishes with higher frequencies as the wires have to support an accelerating model with a larger inertial force. Therefore, the current controller is tested with a range of frequencies and the maximum range of motion in all six degrees of freedom is measured with a maximum wire tension of 110 N, and the results are shown for translations and rotations, in
Figure 7a,b, respectively. This frequency response is dependent on all of the aforementioned geometric and controls parameters and can be further optimized by modifying these parameters, if necessary. The measured displacement amplitude that is realized is 50 mm in translation (
x,
y, and
z), and rotations of 8°
, 15°
, and 9°
at a frequency,
f = 0.5 Hz, and decreases to 5 mm (
x,
y, and
z), 1°
, 3°
, and 2°
at
f = 20 Hz. Four of these motions are visualized in
Figure 7c, with streamwise (x) translation, vertical (z) translation, pitch (
), and yaw (
).
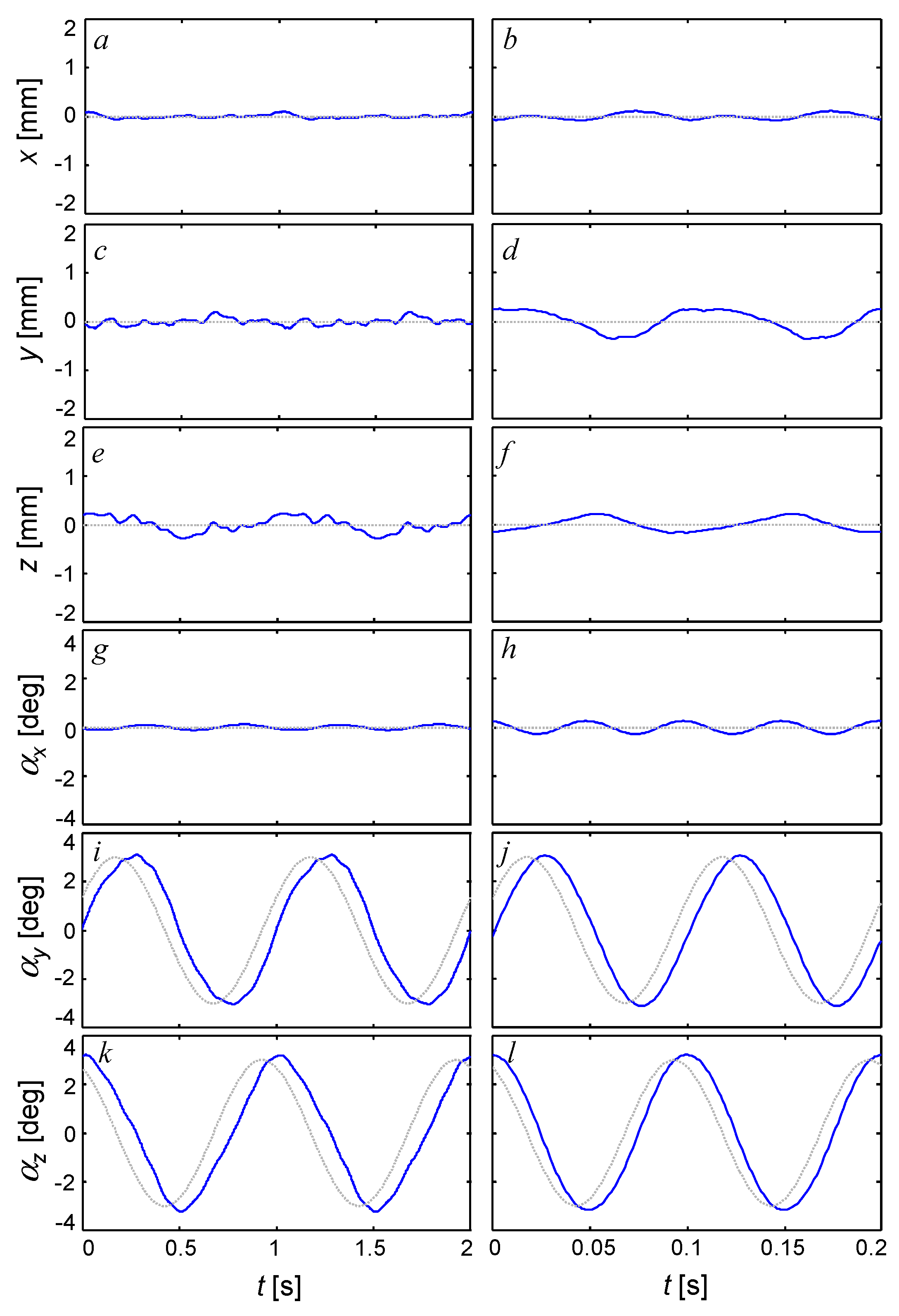
To test the control authority of the traverse for 6-DOF motion tracking, a combination of rotations is commanded (pitch and yaw out of phase) and the instantaneous measurement is shown in
Figure 8 with streamwise translation
x (
Figure 8a,b), cross stream translation
y (
Figure 8c,d), vertical translation
z (
Figure 8e,f), roll
(
Figure 8g,h), pitch
(
Figure 8i,j), and yaw
(
Figure 8k,l), respectively. The commanded signal is a 3° amplitude sinusoidal pitch and sinusoidal yaw, 90° out of phase with each other. This same motion is executed with a representative “low” frequency of 1 Hz in
Figure 8a,c,e,g,i,k along with a “high” frequency of 10 Hz in
Figure 8b,d,f,h,j,l. Both of these motions are executed with wind tunnel flow (
ReD = 2.3 × 10
5) to demonstrate the disturbance rejection of the controller. The time resolved path captured by the motion analysis system is shown in blue while the commanded signal is shown in dotted gray. These data show significant agreement between the commanded and measured signals in terms of peak-peak magnitude (within 5% at 1 Hz in
Figure 8i,k and 7% at 10 Hz in
Figure 8j,l), with a phase lag of 40° at 1 Hz and 30° at 10 Hz. The realized deviations in the four other degrees of freedom that are not commanded are small: within 0.5° in roll (
Figure 8g,h), and within 0.3 mm in all translations (
Figure 8a–f). As mentioned in
Section 2.2, the errors in the motion measurements for this data set (which is the same as for the motions in
Section 3.2 and
Section 3.3) are calculated using the motion analysis system calibration error output (0.45 mm per marker on average), yielding errors of 0.18 mm in translation and 0.02° in rotation. It is noted that these instantaneous traces are measured 10 s after the traverse is activated after the transient response of the traverse has settled. The measurements that are shown in
Figure 8 can also be used as feedback to the triggering lines for flow diagnostics (e.g., particle image velocimetry (PIV)) and/or flow control, and therefore as long as the flow control is a function of the measured DOF the phase lag between the commanded and measured trajectory is inconsequential for the considered harmonic motions. In this section, the wind speed is fixed at 40 m/s and it is noted that the traverse controller treats the external aerodynamic forces on the model as disturbances to be rejected with PID control. Keeping fixed PID coefficients, the phase lag of the commanded and realized responses would increase with increasing wind speed, as the disturbance force grows, but in the present investigations, the PID parameters are pre-adjusted for a given
ReD and can be further tuned with a change in the wind speed.
3.2. Force Response
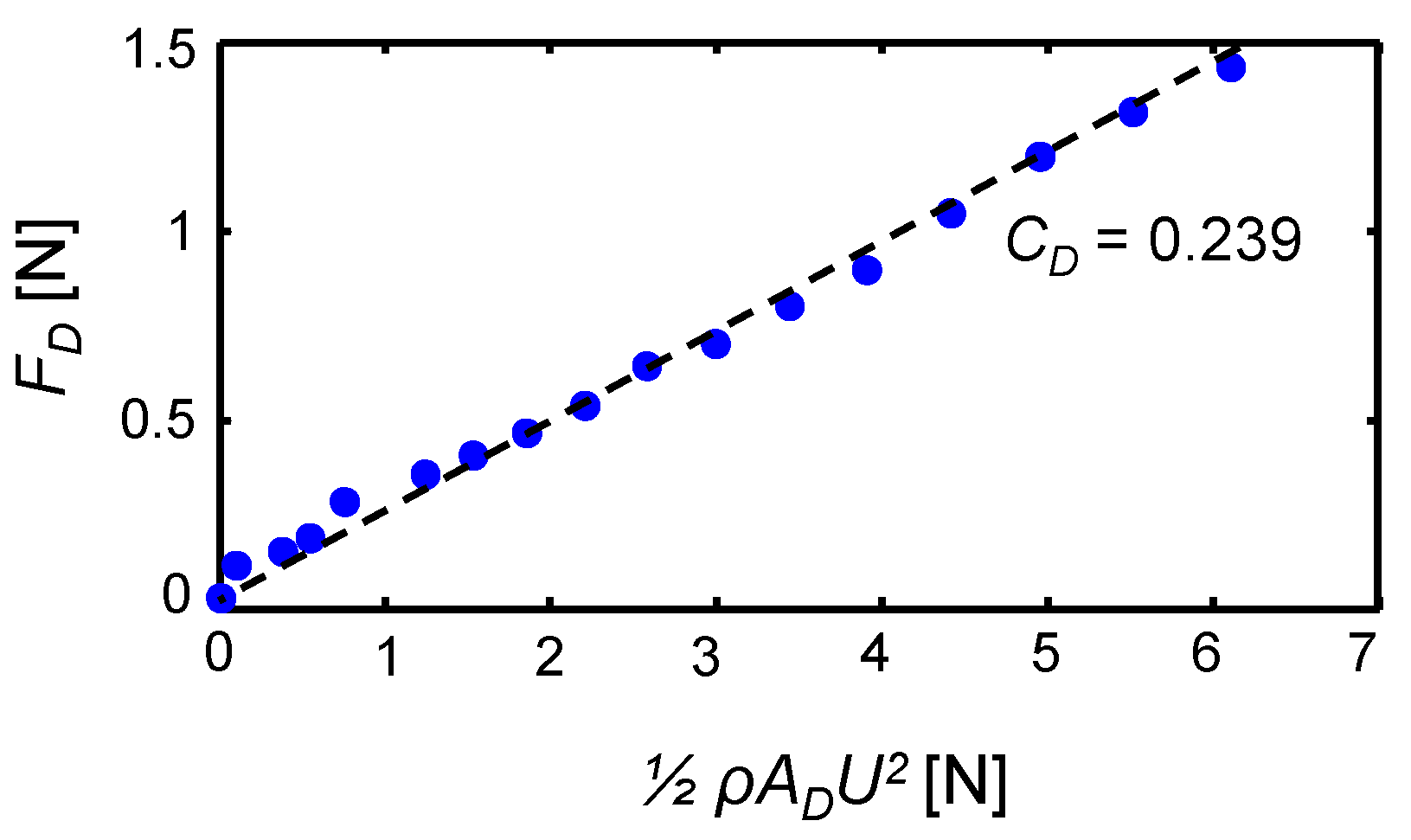
The second analysis that is implemented on the traverse is a validation of the force and moment measurements. Initially, the drag force on the stationary centered model (
FD) is measured over a range of wind tunnel speeds,
U0, of up to 40 m/s (0 <
ReD < 2.3 × 10
5), and these data are presented in
Figure 9a. The measured drag coefficient is
CD = 0.239, which is shown in a dotted line, and is in good agreement with the expected drag coefficient of
CD = 0.25 (for a similar ogive model with a sharp aft end, see Hoerner [
15]). For this stationary centered model, all other forces are nominally zero, and are omitted for brevity. It is noted that for all of the forces presented in this section the force balance method shown in
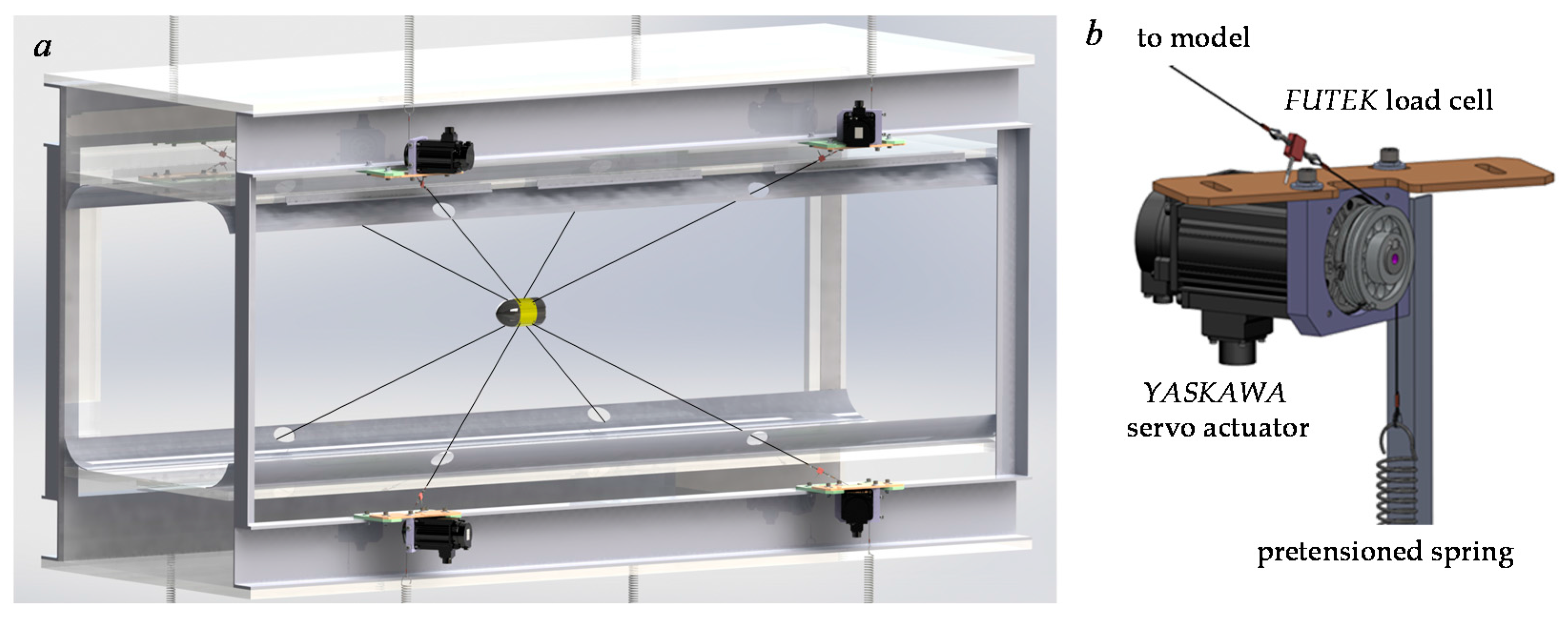
Figure 6 (see
Section 2.5) is applied: the combination of the inertial and gravitational forces is measured first from the model executing the prescribed motion command without wind in the tunnel, and the aerodynamic force on each wire is calculated assuming the wires are cylinders with pure form drag (
CD = 1.25). The drag on each of these wires is normal to the wire and, in general motion, projects components in all six of the measured forces and moments in the system. For
Figure 9, the gravitational force measured (model, wires, and load cells) is a constant, there is no inertial force, and the estimated aerodynamic forces on the wires add up to a pure drag force. These forces are subtracted off of the raw measured forces, which yields the aerodynamic drag force that is used to calculate the model
CD. When the model is set in motion, the projected gravitational moment changes with time as the location of the center of gravity varies, and the inertial force and aerodynamic forces on the wires also change with time. All of these time-varying forces are predicted (inertia and gravity effects are estimated from a commensurate measurement without wind) and subtracted from the raw measurement in order to yield the estimated aerodynamic forces. In addition, for the remainder of this paper the aerodynamic moments are measured relative to the center of the model wires at 0.54
L from the nose. It should be also noted that the wires do not only affect aerodynamic measurements, but also present additional sources of vorticity in the flow. However, increased levels of the flow fluctuations behind the wires do not appear to alter the dominant body wake dynamics, and the coupling between the two is deemed insignificant (see Lambert
et al. [
14]).
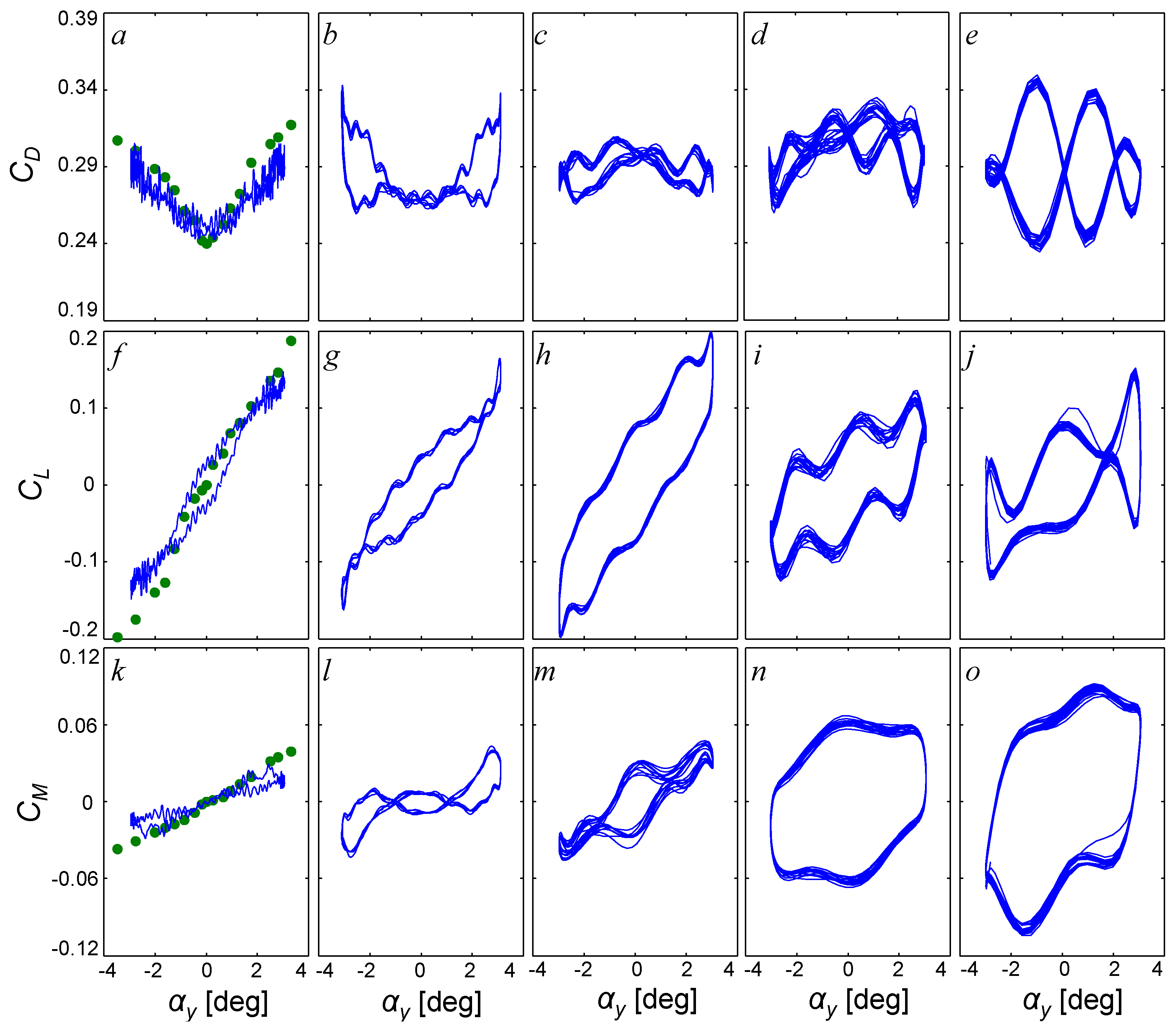
Once the force on a centered stationary model is characterized, three canonical motions are investigated: dynamic pitch, plunge, and streamwise displacement. The first motion presented in
Figure 10 is dynamic
= ±3° (±0.052 radians) amplitude, simple harmonic pitching. This motion is quantified by the drag and lift force coefficients
as well as the pitching moment coefficient
, and for the rest of this force investigation, the free stream is set to
U0 = 40 m/s (
ReD = 2.3 × 10
5). For these flow conditions, the measured side force and roll and yaw moments are negligible in all three of these canonical motions, and they are omitted for brevity.
Figure 10a–e show
CD,
Figure 10f–j show
CL, and
Figure 10k–o show
CM with the pitching angle,
.
Figure 10a,f,k show the a quasi-steady response at
f = 1 Hz, (or a reduced frequency of
= 0.013), and the increased frequency to 5 Hz (
k = 0.065,
Figure 10b,g,l), 10 Hz (
k = 0.130,
Figure 10c,h,m), 15 Hz (
k = 0.194,
Figure 10d,i,n), and 20 Hz (
k = 0.259,
Figure 10e,j,o). For reference, the values of the
CD,
CL, and
CM for a static model at varying fixed angles of attack with the same geometry [
14] are superimposed in
Figure 10a,f,k. The baseline
CD vs. presented in
Figure 10a has a quadratic shape with a minimum of
CD = 0.24 at
= 0 and a change in magnitude of around 25% (0.24 to 0.3). As frequency is increased, the quadratic functionality in the drag with angle becomes broken and the cycle average drag increases to 0.3 at 15 Hz (
Figure 10b–d), and then reduces to 0.28 at 20 Hz (
Figure 10e). It is noted that the shedding frequency of this model is expected to be around 100 Hz (
StD =
fD/
U0 was measured to be ~0.2, for a similar axisymmetric body [
16]), and the high frequency variations in
CD (as well as
CL and
CM) that are not present in the quasi-steady results are at frequencies of harmonics of the model motion near this shedding frequency. The baseline steady
CL vs. presented in
Figure 10f is quasi-linear with a slight hysteresis and a lift slope of
CL/
~0.05/°. Upon increasing the pitching frequency to 10 Hz (
Figure 10g,h), the hysteresis in the lift coefficient increases while the average lift slope remains similar, and at higher frequencies this slope diminishes to 0.03/° and 0.025/° at 15 and 20 Hz, respectively (see
Figure 10i,j). The tendency of the
CL (and
CM) hysteresis to increase with frequency is attributed to unsteady effects of the flow (the magnitude of the wake’s response time remains roughly similar as the model cycle time decreases). The quasi-steady
CM is shown in
Figure 10k, with an increasing slope C
M/
with frequency from 0.01/° at 1 Hz to 0.025/° at 20 Hz, with a large increase in the hysteresis of the response at higher frequencies (
Figure 10l–o). It is noted that this “average slope” is defined as the slope of a linear fit through the dataset and does not take in account variations due to the hysteresis. In addition, having a positive average slope of
CM with
implies that the model is unstable in pitch (the moment increases with an increase in the pitching angle), as expected.
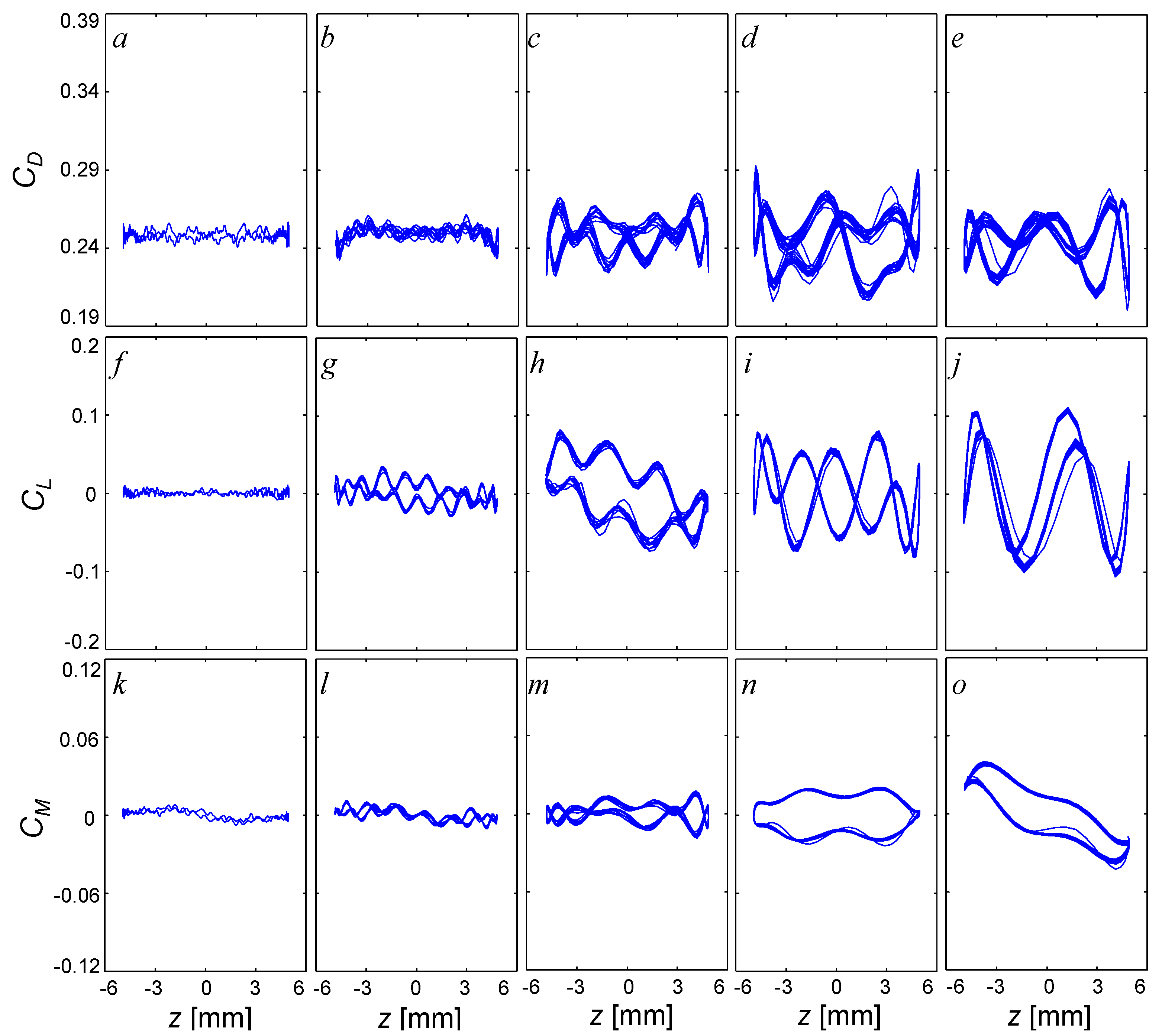
The second motion investigated is dynamic
z = ±5 mm (z/
D = ±0.056) amplitude simple harmonic plunging, shown in
Figure 11.
Figure 11a–e show
CD,
Figure 11f–j show
CL, and
Figure 11k–o show
CM with the plunging coordinate,
z, analogous to
Figure 10, with the same flow conditions, frequencies, and timing. As the motion increases in frequency, the time averaged
CD stays around the same at 0.24, with the introduction of a higher frequency fluctuation (varying in magnitude from 0.01 to 0.08 in
Figure 11a–e) attributed to the wake instability. The quasi-steady
CL is approximately invariant (
Figure 11f), but has the introduction of a small negative slope at higher frequencies (
CL/
z = 0.015/° at 10 Hz, 0.01/° at 15 Hz, and 0.015/° at 20 Hz) in addition to a large higher frequency fluctuation (also attributed to shedding). This negative average slope of
CL with
z implies that the model is stable in plunge, as the aerodynamic force opposes the plunging direction. The quasi-steady
CM has slight variations, shown in
Figure 11k, with negligible slope throughout its frequency, until the plunging frequency is 20 Hz, with the introduction of a
CM/
z slope. This may be due to small deviations between the commanded zero pitching angle of the model and the realized pitching angle, as the pitching moment is very sensitive to pitching angle at this large unsteady frequency (compare
Figure 10o and
Figure 11o).
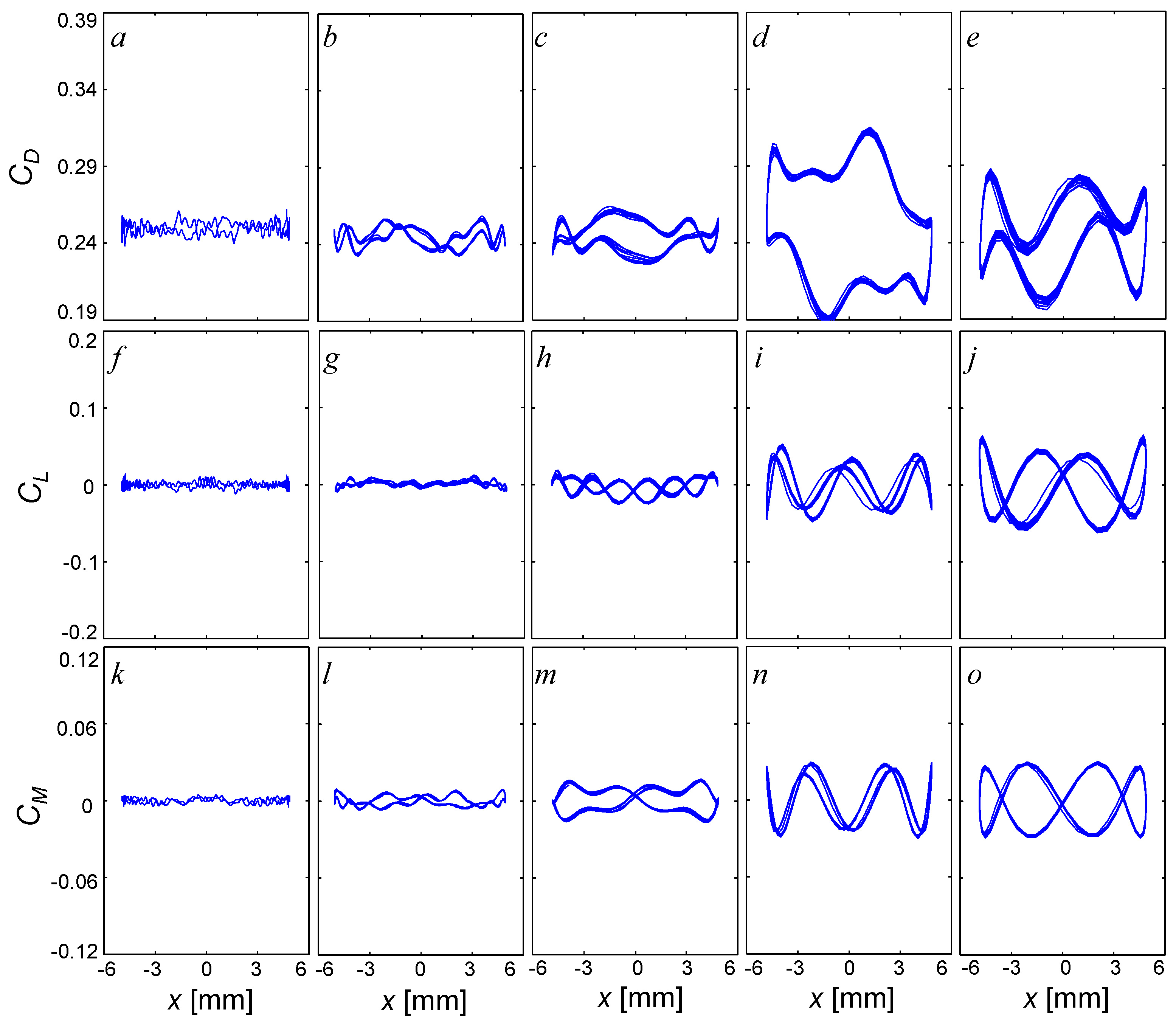
The third and last canonical motion is dynamic
x = ±5 mm (
x/
L = ±0.030) amplitude simple harmonic streamwise displacement, shown in
Figure 12.
CD (
Figure 12a–e),
CL (
Figure 12f–j), and
CM (
Figure 12k–o) are presented with the same frequencies, timing, and conditions as
Figure 10 and
Figure 11, for completion. For this motion, it is noted that both the motion and the freestream velocity are in the same direction, so the predominant changes occur in
CD, while the changes to
CL and
CM are attributed only to phase locking to the instability in the wake, and are approximately symmetric with zero time averaged values (
Figure 12f–o). The time averaged value of the drag retains a value of approximately 0.24, with a growth in hysteresis at 10 Hz (
Figure 12c), which maximizes at 15 Hz (
Figure 12d), and then decreases at 20 Hz (
Figure 12e). It is noted that for most of these drag measurements the average slope of the drag is zero, with the exception of 15 Hz where there is a slight slope of
CD/
x of −0.01/° which suggests this motion is neutrally stable (the aerodynamic drag is roughly invariant to changes in streamwise coordinate throughout most frequencies). This can be expected as this motion can be analyzed as a fluctuation of the freestream with a value of 2π
fx = ±0.0314 to 0.628 m/s, which should not induce large fluctuations in the steady drag coefficient, and the only induced effects are expected to be induced in the unsteady aerodynamics regime.
3.3. Wake Response
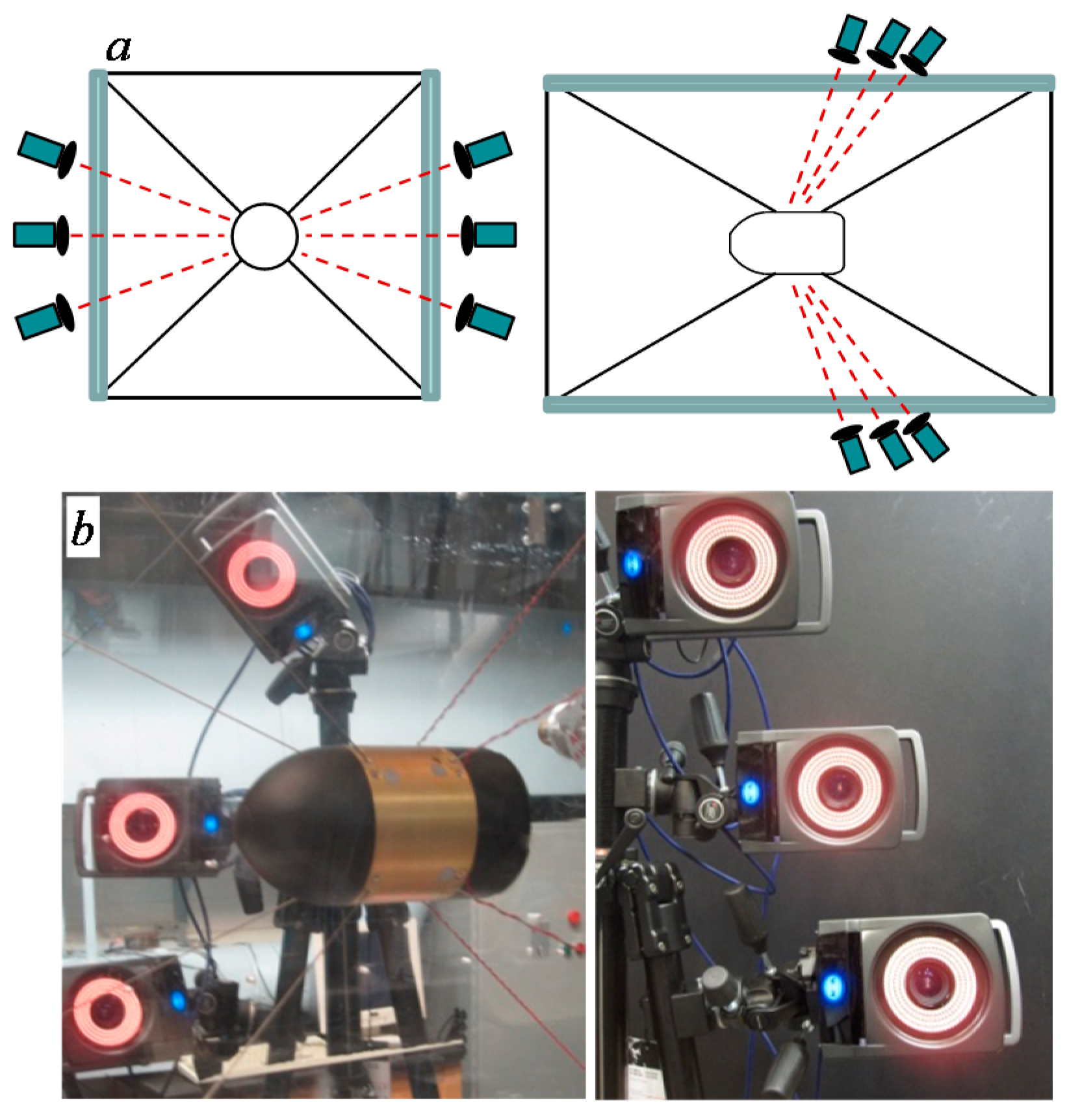
In order to understand the flow mechanisms that result in forces measured on the moving body mounted in this traverse, it is necessary to be able to measure or estimate the wake response around the moving model. The wake response can be measured relative to the real time states of the model as the traverse controller outputs an analog trigger to external devices at either fixed time or fixed trajectory offsets. This triggering system is used to trigger an external
LaVision particle image velocimetry (PIV) system to capture instantaneous images of the wake at the aft end of the model in an interrogation region of 1.6
D × 1.2
D (3.2
R × 2.4
R) in a vertical region along the centerline of the model.
Figure 13 shows six phase-averaged flow fields (each based on 300 individual realizations) for the
= ±3° (
Figure 13a,d,g,j,m,p),
z = ±5 mm (
Figure 13b,e,h,k,n,q), and
x = ±5 mm (
Figure 13c,f,i,l,o,r), with velocity field vectors overlaid on a raster plot of the cross-stream vorticity, ζ, at
ReD = 2.3 × 10
5 (
U0 = 40 m/s). The frequency of these motions are chosen to represent unsteady wake dynamics at 20 Hz (
τ = 0.05 s), and the phases shown are equally spaced in time,
t, throughout the cycles at:
t/
τ = 0 (
Figure 13a–c), 0.167 (
Figure 13d–f), 0.333 (
Figure 13g–i), 0.500 (
Figure 13j–l), 0.667 (
Figure 13m–o), and 0.833 (
Figure 13p–r). For reference, the aft end of the model is superimposed on this data and shown in gray. The wake behind this model has three primary regions of interest: (i) the shear layer with the largest vorticity concentration; (ii) the inner wake with a reversed flow and smaller concentration of vorticity, which is bound by the wake stagnation point; and (iii) the boundary layer along the aft end of the body, which clearly indicates the time-resolved stagnation point on the body. For
= ±3° pitch (
Figure 13a,d,g,j,m,p), the chosen time scale leads to an unsteady flow response, where the wake development time scale is on the same order of the model motion. This leads to the wake response being out of phase with the model (note the wake is approximately centered between
Figure 13a,d, and
Figure 13j,m, respectively, implying an approximate phase lag of the wake response of about 30°) which is also commensurate with the hysteresis measured previously in
CL vs. and
CM vs. (
Figure 10e,j,o). For
z = ±5 mm plunge (
Figure 13b,e,h,k,n,q), the wake response looks similar to pitching with a smaller deflection and a different phase lag (an easy way to observe this effect is to compare the development of the stagnation point on the model in
Figure 13b,e,h,k,n,q to
Figure 13a,d,g,j,m,p). For
x = ±5 mm streamwise displacement (
Figure 13c,f,i,l,o,r), the wake seems approximately unchanged and translates with the model with an addition of small fluctuations in the vorticity in the reversed flow region of the inner wake. In addition to
Figure 13, videos are provided with the manuscript that depict the
= ±3° pitch (
Video S1),
z = ±5 mm plunge (
Video S2), and
x = ±5 mm streamwise displacement (
Video S3) wake dynamics at
f = 20 Hz (see
Supplementary Materials). These results show that the present dynamic traverse is capable of effecting high frequency harmonic motions of the attached model, as well as resolving both the induced aerodynamic forces on a model and the corresponding wake response.