Enhancing Urban Air Mobility Scheduling Through Declarative Reasoning and Stakeholder Modeling
Abstract
1. Introduction
2. Related Work
2.1. UAM Scheduling: Challenges and Domain-Specific Approaches
2.2. Resource-Constrained Scheduling: MILP and Heuristics
2.2.1. RCPSP and MILP Formulations
2.2.2. Heuristic and Metaheuristic Approaches
2.3. Declarative Approaches: Answer Set Programming (ASP) in Scheduling
2.4. Stakeholder-Centric Scheduling
3. Preliminaries
3.1. Scenario I: Vertiport Operations as an RCPSP
- Full Turnaround Sequence: Arrival → Landing → Passenger Disembarkation → Battery Charging → Passenger Embarkation → Pre-flight Checks → Departure. This is a sequence of the general operations that a vehicle drops off passengers, proceeds to required maintenance (like charging), boards new passengers, and then departs. Resources like landing pads, gates or stands, and charging stations are utilized sequentially.
- Quick Drop-off Sequence: Arrival → Landing → Passenger Disembarkation → (Minimal Checks or Preparation) → Departure. This might be used for repositioning flights or short hops where extensive ground services like charging are not immediately required.
- Cargo Operations Sequence: Arrival → Landing → Cargo Unloading → Cargo Loading → Pre-flight Checks → Departure. This is for transporting cargo. Instead of passenger-related jobs, it handles cargo-related jobs.
- Charging-Focused Sequence: Arrival → Landing → Battery Charging → Pre-flight Checks → Departure. This sequence is only for eVTOL to visit the vertiport for charging without handling passengers or cargo.
3.2. RCPSP
- J: a set of jobs ,
- R: a set of resources,
- S: a list of the order in which the tasks in the jobs will be executed,
- T represents the planning horizon, which is a list of potential completion time steps for jobs,
- : the time required to complete job j,
- The formula represents the required unit of resource r to complete job j, and
- : the capacity of resource r.
- task(A) signifies that A is a task to be scheduled.
- step(I) denotes that I is a discrete time step within the planning horizon.
- The predicate start(A,I) means task A is assigned to begin at time step I.
- dur(A,D) indicates that task A has a processing duration of D time steps.
- Resource requirements are specified by rsreq(A,R,AM), meaning task A requires AM units of resource R.
- The predicate assigned_res(TS,A,R,AM1) is used to track that AM1 units of resource R are assigned to task A at time step TS.
- sum_assigned_res(TS,R,AM) is to calculate the total amount AM of resource R to be assigned at time step TS. This includes all active tasks at this time step.
- limit(R,L) specifies that resource R has a maximum capacity of L units.
- psrel(P,S) is a precedence relation. It means that task P must complete before task S starts.
- Finally, etask(A) identifies A as an end task (specifically, the tail dummy task in this context) whose start time is part of the objective function.
- Equation (8) ensures that every task A is assigned exactly one start time I from the available time steps. The construct 1 {…} 1 is an ASP choice rule, guaranteeing one successful assignment.
- Equation (10) calculates the total resource usage. For a given time step TS and resource R, the component of the rule sums (#sum) all amounts AM1 of that resource assigned to any task A (via assigned_res(TS,A,R,AM1)). The result is unified with AM.
- Equation (12) is the objective function. It instructs the ASP solver to find a schedule that minimizes the value I, where I is the start time of the tail dummy task (identified by estart(I), which is derived from start(A,I), etask(A)). Hence, minimizing the start time of this final dummy task effectively minimizes the overall project makespan.
3.3. Multiple Schedules
3.4. Requirements
3.4.1. [Req1] Requirement 1: Punctuality
3.4.2. [Req2] Requirement 2: Boarding of Additional Seats
3.4.3. [Req3] Requirement 3: Managing Delivery Delays
4. Problem Formulation
4.1. Problem Statement
- Input: Instances and requirements
- Output: A set of start times and a solution of requirements
- Process: Calculate a schedule for under the consideration of where .
4.2. Solution Overview
5. Proposed Solution
5.1. Listings of Requirements
5.1.1. Solution for Req1
5.1.2. Solution for Req2
5.1.3. Basic Solution for Req3
5.2. Combining Listings with Procedural Codes
| Algorithm 1: RCPSP-REQ-ASP |
 |
| Algorithm 2: RCPSP-REQ-ASP-ITER |
 |
6. Experiments and Discussions
6.1. Experiments
6.1.1. Toy Example
6.1.2. Numerical Experiments
6.2. Discussions
6.2.1. Performance Issue
6.2.2. What We Have Not Covered Here
- LP Relaxation: Our approach to RCPSP is focused on MILP, not linear programming. This is because our MILP formulation in Section 3.2 was to clearly introduce discrete and countable resource management through integer programming. We can narrow down the possible result sets for a specific RCPSP case. This can be performed by heuristically performing LP relaxation. We can also establish lower bounds [38,76,77,78,79]. However, we chose MILP to obtain an exact solution. Choosing MILP let us easily transition to the ASP formulation, and this allowed for a simpler representation of the requirements.
- Graph-Based Algorithmic Approach: This scheduling problem differs from a simple pathfinding problem in that it does not involve navigating a physical environment. Decisions made in one job plan by the RCPSP will impact other job plans. This approach is quite similar to cooperative pathfinding [49]. Since this perspective is relatively new in research, we need more scenarios and simulation results. This will help us apply this problem and approach in practice.
6.2.3. Future Directions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASP | Answer set programming |
| ATC | Air Traffic Control |
| CDM | Collaborative decision making |
| DE | Differential evolution |
| eVTOL | electric vertical takeoff and landing |
| GA | Genetic algorithm |
| MILP | Mixed-integer linear programming |
| MPF-JSS | Multi-resource partial-order flexible job-shop scheduling |
| PSO | Particle swarm optimization |
| RCPSP | Resource-constrained project scheduling problem |
| UAM | Urban air mobility |
| UATM | UAM Air Traffic Management |
| CDCL | Conflict-driven clause learning |
| SAT | boolean SATisfiability problem |
References
- Patterson, M.D.; Antcliff, K.; Kohlman, L.W. A Proposed Approach to Studying Urban Air Mobility Missions Including an Initial Exploration of Mission Requirements. In Proceedings of the AHS International 74th Annual Forum and Technology Display, Phoenix, AZ, USA, 15–17 May 2018. [Google Scholar] [CrossRef]
- Arafat, M.Y.; Pan, S. Urban Air Mobility Communications and Networking: Recent Advances, Techniques, and Challenges. Drones 2024, 8, 702. [Google Scholar] [CrossRef]
- Hui, K.Y.; Nguyen, C.H.; Lui, G.N.; Liem, R.P. AirTrafficSim: An Open-Source Web-Based Air Traffic Simulation Platform. J. Open Source Softw. 2023, 8, 4916. [Google Scholar] [CrossRef]
- Al–Rubaye, S.; Tsourdos, A.; Namuduri, K. Advanced Air Mobility Operation and Infrastructure for Sustainable Connected eVTOL Vehicle. Drones 2023, 7, 319. [Google Scholar] [CrossRef]
- Wild, G. Urban Aviation: The Future Aerospace Transportation System for Intercity and Intracity Mobility. Urban Sci. 2024, 8, 218. [Google Scholar] [CrossRef]
- Thipphavong, D.P.; Apaza, R.D.; Barmore, B.; Battiste, V.; Burian, B.K.; Dao, Q.; Feary, M.; Go, S.; Goodrich, K.H.; Homola, J.; et al. Urban Air Mobility Airspace Integration Concepts and Considerations. In Proceedings of the 18th AIAA Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar] [CrossRef]
- Hoffmann, R.; Pereira, D.P.; Nishimura, H. Security Viewpoint and Resilient Performance in the Urban Air Mobility Operation. IEEE Open J. Syst. Eng. 2023, 1, 123–138. [Google Scholar] [CrossRef]
- Gutjahr, W.J. Bi-Objective Multi-Mode Project Scheduling Under Risk Aversion. Eur. J. Oper. Res. 2015, 246, 421–434. [Google Scholar] [CrossRef]
- Fahmy, A. Optimization Algorithms in Project Scheduling. In Optimization Algorithms-Methods and Applications; IntechOpen: London, UK, 2016. [Google Scholar] [CrossRef]
- Koné, O.; Artigues, C.; Lopez, P.; Mongeau, M. Comparison of Mixed Integer Linear Programming Models for the Resource-Constrained Project Scheduling Problem with Consumption and Production of Resources. Flex. Serv. Manuf. J. 2012, 25, 25–47. [Google Scholar] [CrossRef]
- Rabbani, M.; Arjmand, A.; Saffar, M.M.; Jalali, M.S. Application of Three Meta-Heuristic Algorithms for Maximizing the Net Present Value of a Resource-Constrained Project Scheduling Problem with Respect to Delay Penalties. Int. J. Appl. Ind. Eng. 2016, 3, 1–15. [Google Scholar] [CrossRef]
- Gebser, M.; Schaub, T. Modeling and Language Extensions. AI Mag. 2016, 37, 33–44. [Google Scholar] [CrossRef]
- Fuscà, D.; Germano, S.; Zangari, J.; Anastasio, M.; Calimeri, F.; Perri, S. A Framework for Easing the Development of Applications Embedding Answer Set Programming. In Proceedings of the 18th International Symposium on Principles and Practice of Declarative Programming (PPDP), Edinburgh, UK, 5–7 September 2016. [Google Scholar] [CrossRef]
- Egly, U.; Gaggl, S.A.; Woltran, S. Answer-Set Programming Encodings for Argumentation Frameworks. Argum. Comput. 2010, 1, 147–177. [Google Scholar] [CrossRef]
- Kaufmann, B.; Leone, N.; Perri, S.; Schaub, T. Grounding and Solving in Answer Set Programming. AI Mag. 2016, 37, 25–32. [Google Scholar] [CrossRef]
- Kim, J.; Kim, K. Agent 3, change your route: Possible conversation between a human manager and UAM Air Traffic Management (UATM). In Proceedings of the Robotics: Science and Systems (RSS) workshop on Articulate Robots: Utilizing Language for Robot Learning, Daegu, Republic of Korea, 10–14 July 2023. [Google Scholar] [CrossRef]
- Kim, J.; Kim, K. Dialogue Possibilities between a Human Supervisor and UAM Air Traffic Management: Route Alteration. Adv. Artif. Intell. Mach. Learn. (AAIML) 2023, 3, 1352–1368. [Google Scholar] [CrossRef]
- Woo, S.; Kim, J.; Kim, K. We, Vertiport 6, are temporarily closed: Interactional Ontological Methods for Changing the Destination. In Proceedings of the IEEE RO-MAN (RO-MAN 2023) Workshop on Ontologies for Autonomous Robotics (RobOntics), Busan, Republic of Korea, 28–31 August 2023. [Google Scholar] [CrossRef]
- Kim, J.; Kim, K. Designing Reactive Route Change Rules with Human Factors in Mind: A UATM System Perspective. In Proceedings of the International Congress on Information and Communication Technology, London, UK, 19–22 February 2024; pp. 323–338. [Google Scholar] [CrossRef]
- Prakasha, P.S.; Papantoni, V.; Nagel, B.; Brand, U.; Vogt, T.; Naeem, N.; Ratei, P.; Villacis, S.P. Urban Air Mobility Vehicle and Fleet-Level Life-Cycle Assessment Using a System-of-Systems Approach. In Proceedings of the AIAA AVIATION 2021 FORUM, Virtual Event, 2–6 August 2021. [Google Scholar] [CrossRef]
- Goodrich, K.H.; Barmore, B. Exploratory Analysis of the Airspace Throughput and Sensitivities of an Urban Air Mobility System. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar] [CrossRef]
- Kotwicz Herniczek, M.T.; German, B. Impact of Airspace Restrictions on Urban Air Mobility Airport Shuttle Service Route Feasibility. Transp. Res. Rec. J. Transp. Res. Board 2022, 2676, 689–706. [Google Scholar] [CrossRef]
- Vascik, P.D.; Hansman, R.J. Evaluating the Interoperability of Urban Air Mobility Systems and Airports. Transp. Res. Rec. J. Transp. Res. Board 2021, 2675, 1–14. [Google Scholar] [CrossRef]
- Vascik, P.D.; Hansman, R.J. Scaling Constraints for Urban Air Mobility Operations: Air Traffic Control, Ground Infrastructure, and Noise. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar] [CrossRef]
- Dai, W.; Low, K.H. Conflict-Free Trajectory Planning for Urban Air Mobility Based on an Airspace-Resource-Centric Approach. In Proceedings of the AIAA Aviation 2022 Forum, Chicago, IL, USA & Virtual, 27 June–1 July 2022. [Google Scholar] [CrossRef]
- Edwards, T.; Verma, S.; Keeler, J. Exploring Human Factors Issues for Urban Air Mobility Operations. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Seifi, A.; Ponnambalam, K.; Kudiakova, A.; Aultman-Hall, L. An Optimization Model for Flight Rescheduling from an Airport’s Centralized Perspective for Better Management of Demand and Capacity Utilization. Computation 2024, 12, 98. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, M.L.; Chen, P.C.; Xie, J.; Zuo, H. An Integrative Approach with Sequential Game to Real-Time Gate Assignment Under CDM Mechanism. Math. Probl. Eng. 2014, 2014, 143501. [Google Scholar] [CrossRef]
- Straubinger, A.; Rothfeld, R.; Shamiyeh, M.; Büchter, K.D.; Kaiser, J.; Plötner, K. An Overview of Current Research and Developments in Urban Air Mobility–Setting the Scene for UAM Introduction. J. Air Transp. Manag. 2020, 87, 101852. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, K.; Qu, X. Urban Air Mobility (UAM) and Ground Transportation Integration: A Survey. Front. Eng. Manag. 2024, 11, 734–758. [Google Scholar] [CrossRef]
- Cohen, A.; Shaheen, S.; Farrar, E. Urban Air Mobility: History, Ecosystem, Market Potential, and Challenges. IEEE Trans. Intell. Transp. Syst. 2021, 22, 6074–6087. [Google Scholar] [CrossRef]
- Ale-Ahmad, H.; Mahmassani, H.S. Factors Affecting Demand Consolidation in Urban Air Taxi Operation. Transp. Res. Rec. J. Transp. Res. Board 2022, 2677, 76–92. [Google Scholar] [CrossRef]
- Hearn, T.A.; Kotwicz Herniczek, M.T.; German, B. Conceptual Framework for Dynamic Optimal Airspace Configuration for Urban Air Mobility. J. Air Transp. 2023, 31, 68–82. [Google Scholar] [CrossRef]
- Huang, C.; Petrunin, I.; Tsourdos, A. Strategic Conflict Management for Performance-Based Urban Air Mobility Operations with Multi-Agent Reinforcement Learning. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Dubrovnik, Croatia, 21–24 June 2022; pp. 442–451. [Google Scholar] [CrossRef]
- Ko, J.; Ahn, J. On-Demand Urban Air Mobility Scheduling with Operational Considerations. J. Aerosp. Inf. Syst. 2025, 22, 401–411. [Google Scholar] [CrossRef]
- Alharbi, A.; Petrunin, I.; Panagiotakopoulos, D. Assuring Safe and Efficient Operation of UAV Using Explainable Machine Learning. Drones 2023, 7, 327. [Google Scholar] [CrossRef]
- Koné, O.; Artigues, C.; Lopez, P.; Mongeau, M. Event-Based MILP Models for Resource-Constrained Project Scheduling Problems. Comput. Oper. Res. 2011, 38, 3–13. [Google Scholar] [CrossRef]
- Araujo, J.A.S.; Santos, H.G.; Gendron, B.; Jena, S.D.; de Brito, S.S.; Souza, D.S. Strong Bounds for Resource Constrained Project Scheduling: Preprocessing and Cutting Planes. Comput. Oper. Res. 2020, 113, 104782. [Google Scholar] [CrossRef]
- Pérez Armas, L.F.; Creemers, S.; Deleplanque, S. Solving the resource constrained project scheduling problem with quantum annealing. Sci. Rep. 2024, 14, 16784. [Google Scholar] [CrossRef]
- Merkle, D.; Middendorf, M.; Schmeck, H. Ant Colony Optimization for Resource-Constrained Project Scheduling. IEEE Trans. Evol. Comput. 2002, 6, 333–346. [Google Scholar] [CrossRef]
- Fu, N.; Lau, H.C.; Varakantham, P.; Xiao, F. Robust Local Search for Solving RCPSP/max with Durational Uncertainty. J. Artif. Intell. Res. 2012, 43, 43–86. [Google Scholar] [CrossRef]
- Wang, H.; Li, T.; Lin, D. Efficient Genetic Algorithm for Resource-Constrained Project Scheduling Problem. Trans. Tianjin Univ. 2010, 16, 376–382. [Google Scholar] [CrossRef]
- Klimek, M. A Genetic Algorithm for the Project Scheduling with the Resource Constraints. Ann. Univ. Mariae-Curie-Sklodowska Sect. AI–Inform. 2010, 10, 117–130. [Google Scholar] [CrossRef]
- Kadam, S.; Mane, S.U. A Genetic-Local Search Algorithm Approach for Resource Constrained Project Scheduling Problem. In Proceedings of the 2015 International Conference on Computing Communication Control and Automation, Pune, India, 26–27 February 2015. [Google Scholar] [CrossRef]
- Eshraghi, A. A New Approach for Solving Resource Constrained Project Scheduling Problems Using Differential Evolution Algorithm. Int. J. Ind. Eng. Comput. 2016, 7, 205–216. [Google Scholar] [CrossRef]
- Zhang, L.; Luo, Y.; Zhang, Y. Hybrid Particle Swarm and Differential Evolution Algorithm for Solving Multimode Resource-Constrained Project Scheduling Problem. J. Control Sci. Eng. 2015, 2015, 923791. [Google Scholar] [CrossRef]
- Wang, J.; Liu, W.R. Forward-Backward Improvement for Genetic Algorithm Based Optimization of Resource Constrained Scheduling Problem. In Proceedings of the 2nd International Conference on Advances in Management Engineering and Information Technology (AMEIT 2017), Shanghai, China, 23–24 April 2017. [Google Scholar] [CrossRef]
- Debels, D.; Reyck, B.D.; Leus, R.; Vanhoucke, M. A Hybrid Scatter Search/Electromagnetism Meta-Heuristic for Project Scheduling. Eur. J. Oper. Res. 2006, 169, 638–653. [Google Scholar] [CrossRef]
- Homberger, J. A Multi-agent System for the Decentralized Resource-constrained Multi-project Scheduling Problem. Int. Trans. Oper. Res. 2007, 14, 565–589. [Google Scholar] [CrossRef]
- El-Kholany, M.M.S.; Gebser, M.; Schekotihin, K. Problem Decomposition and Multi-Shot ASP Solving for Job-Shop Scheduling. Theory Pract. Log. Program. 2022, 22, 623–639. [Google Scholar] [CrossRef]
- Francescutto, G.; Schekotihin, K.; El-Kholany, M.M.S. Solving a Multi-Resource Partial-Ordering Flexible Variant of the Job-Shop Scheduling Problem with Hybrid ASP. In Proceedings of the European Conference on Logics in Artificial Intelligence, Virtual Event, 17–20 May 2021. [Google Scholar] [CrossRef]
- Chintabathina, S. Planning and Scheduling in Hybrid Domains Using Answer Set Programming. In Proceedings of the 28th International Conference on Logic Programming (ICLP 2012): Workshop on Answer Set Programming and Other Computing Paradigms (ASPOCP 2012), Budapest, Hungary, 4–8 September 2012. [Google Scholar] [CrossRef]
- Dahlem, M.; Bhagyanath, A.; Schneider, K. Optimal Scheduling for Exposed Datapath Architectures with Buffered Processing Units by ASP. Theory Pract. Log. Program. 2018, 18, 438–451. [Google Scholar] [CrossRef]
- Kaveh, A.; Khanzadi, M.; Alipour, M.; Naraki, M.R. CBO and CSS Algorithms for Resource Allocation and Time-Cost Trade-Off. Period. Polytech. Civ. Eng. 2015, 59, 361–371. [Google Scholar] [CrossRef]
- Golab, A.; Gooya, E.S.; Falou, A.A.; Cabon, M. Review of Conventional Metaheuristic Techniques for Resource-Constrained Project Scheduling Problem. J. Proj. Manag. 2022, 7, 95–110. [Google Scholar] [CrossRef]
- Hartmann, S. A Self-adapting Genetic Algorithm for Project Scheduling Under Resource Constraints. Nav. Res. Logist. (NRL) 2002, 49, 433–448. [Google Scholar] [CrossRef]
- Katsavounis, S. Scheduling Multiple Concurrent Projects Using Shared Resources with Allocation Costs and Technical Constraints. In Proceedings of the 2008 3rd International Conference on Information and Communication Technologies: From Theory to Applications, Damascus, Syria, 7–11 April 2008. [Google Scholar] [CrossRef]
- Leyman, P.; Vanhoucke, M. A New Scheduling Technique for the Resource–constrained Project Scheduling Problem with Discounted Cash Flows. Int. J. Prod. Res. 2014, 53, 2771–2786. [Google Scholar] [CrossRef]
- Kellenbrink, C.; Helber, S. Scheduling Resource-Constrained Projects with a Flexible Project Structure. Eur. J. Oper. Res. 2015, 246, 379–391. [Google Scholar] [CrossRef]
- Zahid, T.; Agha, M.H.; Warsi, S.S.; Ghafoor, U. Redefining Critical Tasks for Responsive and Resilient Scheduling-an Intelligent Fuzzy Heuristic Approach. IEEE Access 2021, 9, 145513–145521. [Google Scholar] [CrossRef]
- Chand, S.; Rajesh, K.; Chandra, R. MAP-Elites Based Hyper-Heuristic for the Resource Constrained Project Scheduling Problem. arXiv 2022, arXiv:2204.11162. [Google Scholar] [CrossRef]
- Watanabe, K.; Fainekos, G.; Hoxha, B.; Lahijanian, M.; Okamoto, H.; Sankaranarayanan, S. Optimal Planning for Timed Partial Order Specifications. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation, Yokohama, Japan, 13–17 May 2024; pp. 17093–17099. [Google Scholar] [CrossRef]
- Durfee, E.H.; Lesser, V.R. Negotiating task decomposition and allocation using partial global planning. In Distributed Artificial Intelligence; Huhns, M., Gasser, L., Eds.; Morgan Kaufmann: San Mateo, CA, USA, 1989; Volume 2, pp. 229–243. [Google Scholar] [CrossRef]
- Wu, J.; Xu, X.; Zhang, P.; Liu, C. A Novel Multi-Agent Reinforcement Learning Approach for Job Scheduling in Grid Computing. Future Gener. Comput. Syst. 2011, 27, 430–439. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Rousis, A.O.; Bourazeri, A. Trust & Fair Resource Allocation in Community Energy Systems. IEEE Access 2024, 12, 11157–11169. [Google Scholar] [CrossRef]
- Clement, B.J.; Barrett, A. Continual Coordination Through Shared Activities. In Proceedings of the Second International Joint Conference on Autonomous Agents and Multiagent Systems, Melbourne, Australia, 14–18 July 2003. [Google Scholar] [CrossRef]
- Wooldridge, M. An Introduction to MultiAgent Systems, 2nd ed.; Wiley Publishing: Hoboken, NJ, USA, 2009. [Google Scholar]
- Adhau, S.; Mittal, M.; Mittal, A. A Multi-Agent System for Distributed Multi-Project Scheduling: An Auction-Based Negotiation Approach. Eng. Appl. Artif. Intell. 2012, 25, 1738–1751. [Google Scholar] [CrossRef]
- Pritsker, A.A.B.; Waiters, L.J.; Wolfe, P.M. Multiproject Scheduling with Limited Resources: A Zero-One Programming Approach. Manag. Sci. 1969, 16, 93–108. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Complexity Results for Multiprocessor Scheduling under Resource Constraints. SIAM J. Comput. 1975, 4, 397–411. [Google Scholar] [CrossRef]
- Ferraris, P.; Lee, J.; Lifschitz, V. Stable Models and Circumscription. Artif. Intell. 2011, 175, 236–263. [Google Scholar] [CrossRef]
- Lefèvre, C.; Béatrix, C.; Stéphan, I.; Garcia, L. ASPeRiX, a First-Order Forward Chaining Approach for Answer Set Computing. Theory Pract. Log. Program. 2017, 17, 266–310. [Google Scholar] [CrossRef]
- Modaresi, S.; Kılınç, M.R.; Vielma, J.P. Intersection Cuts for Nonlinear Integer Programming: Convexification Techniques for Structured Sets. Math. Program. 2015, 155, 575–611. [Google Scholar] [CrossRef]
- Xia, W.; Vera, J.C.; Zuluaga, L.F. Globally Solving Nonconvex Quadratic Programs via Linear Integer Programming Techniques. INFORMS J. Comput. 2020, 32, 40–56. [Google Scholar] [CrossRef]
- García-Mata, C.L.; Burtseva, L.; Werner, F. Scheduling of Automated Wet-Etch Stations with One Robot in Semiconductor Manufacturing via Constraint Answer Set Programming. Processes 2024, 12, 1315. [Google Scholar] [CrossRef]
- Mingozzi, A.; Maniezzo, V.; Ricciardelli, S.; Bianco, L. An Exact Algorithm for the Resource-Constrained Project Scheduling Problem Based on a New Mathematical Formulation. Manag. Sci. 1998, 44, 714–729. [Google Scholar] [CrossRef]
- Baptiste, P.; Demassey, S. Tight LP Bounds for Resource Constrained Project Scheduling. Or Spectrum 2004, 26, 251–262. [Google Scholar] [CrossRef]
- Bianco, L.; Caramia, M. A New Lower Bound for the Resource-Constrained Project Scheduling Problem with Generalized Precedence Relations. Comput. Oper. Res. 2011, 38, 14–20. [Google Scholar] [CrossRef]
- Demassey, S.; Artigues, C.; Michelon, P. Constraint-Propagation-Based Cutting Planes: An Application to the Resource-Constrained Project Scheduling Problem. INFORMS J. Comput. 2005, 17, 52–65. [Google Scholar] [CrossRef]
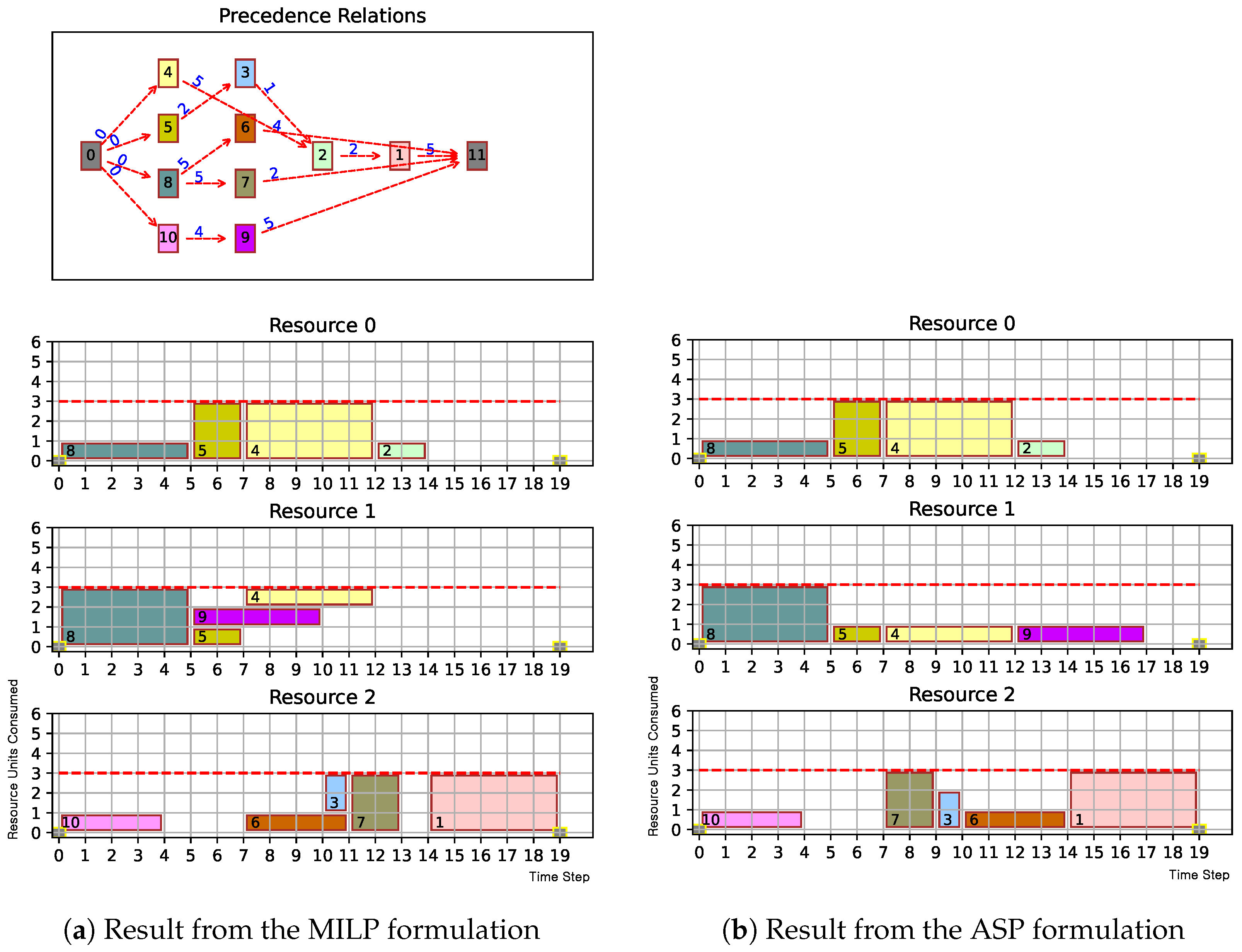

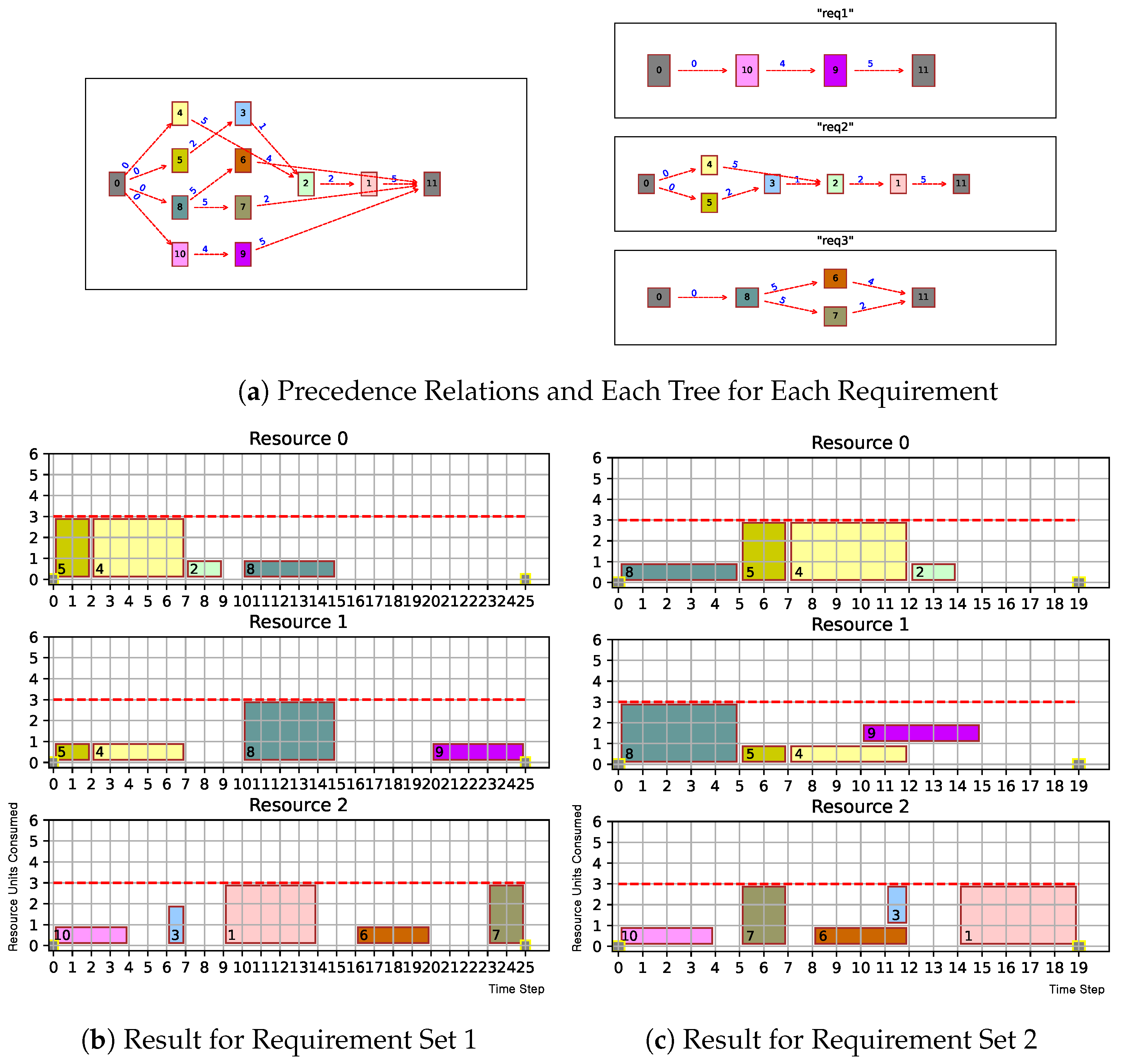
| Job | Duration | Resources Required | Successors | ||
|---|---|---|---|---|---|
| Resource 0 | Resource 1 | Resource 2 | |||
| 1 | 5 | 3 | |||
| 2 | 2 | 1 | 1 | ||
| 3 | 1 | 2 | 2 | ||
| 4 | 5 | 3 | 1 | 2 | |
| 5 | 2 | 3 | 1 | 3 | |
| 6 | 4 | 1 | |||
| 7 | 2 | 3 | |||
| 8 | 5 | 1 | 3 | ||
| 9 | 5 | 1 | 6, 7 | ||
| 10 | 4 | 1 | 9 | ||
| Function | MILP | ASP | Description |
|---|---|---|---|
| Objective | Equation (2) | Equation (12) | It minimizes the start time of the tail dummy. |
| Constraints | Equations (3) and (6) | Equation (7) | Each task should be assigned only once. |
| Equation (4) | Equations (9)–(11) | The required resources for each task should be allocated for the duration from its beginning, and the sum of all allocated resources at every time step should not exceed the limit. | |
| Equation (5) | Equation (8) | Every pair of tasks in the precedence relationship should follow the order. |
| Set 1 | Set 2 | |
|---|---|---|
| Aux. facts for | The set is {“tx1”, “tx2”, “tx3”}. owner(“req1”, “tx3”), owner(“req2”, “tx1”), owner(“req3”, “tx2”), tree(“tx3”, 9..10), tree(“tx1”, 1..5), tree(“tx2”, 6..8). | |
| Aux. facts for | deadline(“tx3”, 25), preferable_range(“tx1”, 1, 2), text_extension(0, “tx2”, 5), delay_range(0..5). | deadline(“tx3”, 15), preferable_range(“tx1”, 2, 3), text_extension(0, “tx2”, 4), delay_range(0..4). |
| Additional facts | delay_margin(0, 0). | |
| punctual_candidate(9, 20), deadline_met(“tx3”). | punctual_candidate(9, 10), deadline_met(“tx3”). | |
| excessed(4, 1), excessed(5, 1), excess_in_total(0, 2). | excessed(4, 1), excessed(5, 1), excess_in_total(0, 2). | |
| actual_delay(0, 4). | actual_delay(0, 1). | |
| Total Duration | estart(25). | estart(19). |
| MILP | ASP | |||||
|---|---|---|---|---|---|---|
| Time [s] | Step [#] | Succ. [#] | Time [s] | Step [#] | Succ. [#] | |
| (Min|Median|Max) | (Min|Median|Max) | (Min|Median|Max) | (Min|Median|Max) | |||
| 10 | 00.108|000.256|041.252 | 09|16.0|25 | 100 | 0.000|000.031|000.064 | 09|16.0|25 | 100 |
| 20 | 00.646|015.134|455.195 | 13|21.0|32 | 94 | 0.080|000.271|002.156 | 13|20.5|32 | 100 |
| 30 | 27.312|132.038|424.036 | 20|23.5|30 | 20 | 0.459|001.887|375.537 | 18|26.0|42 | 98 |
| 40 | — | — | 0 | 2.516|026.192|572.800 | 20|31.0|38 | 71 |
| 50 | — | — | 0 | 7.943|148.850|554.881 | 28|35.0|42 | 24 |
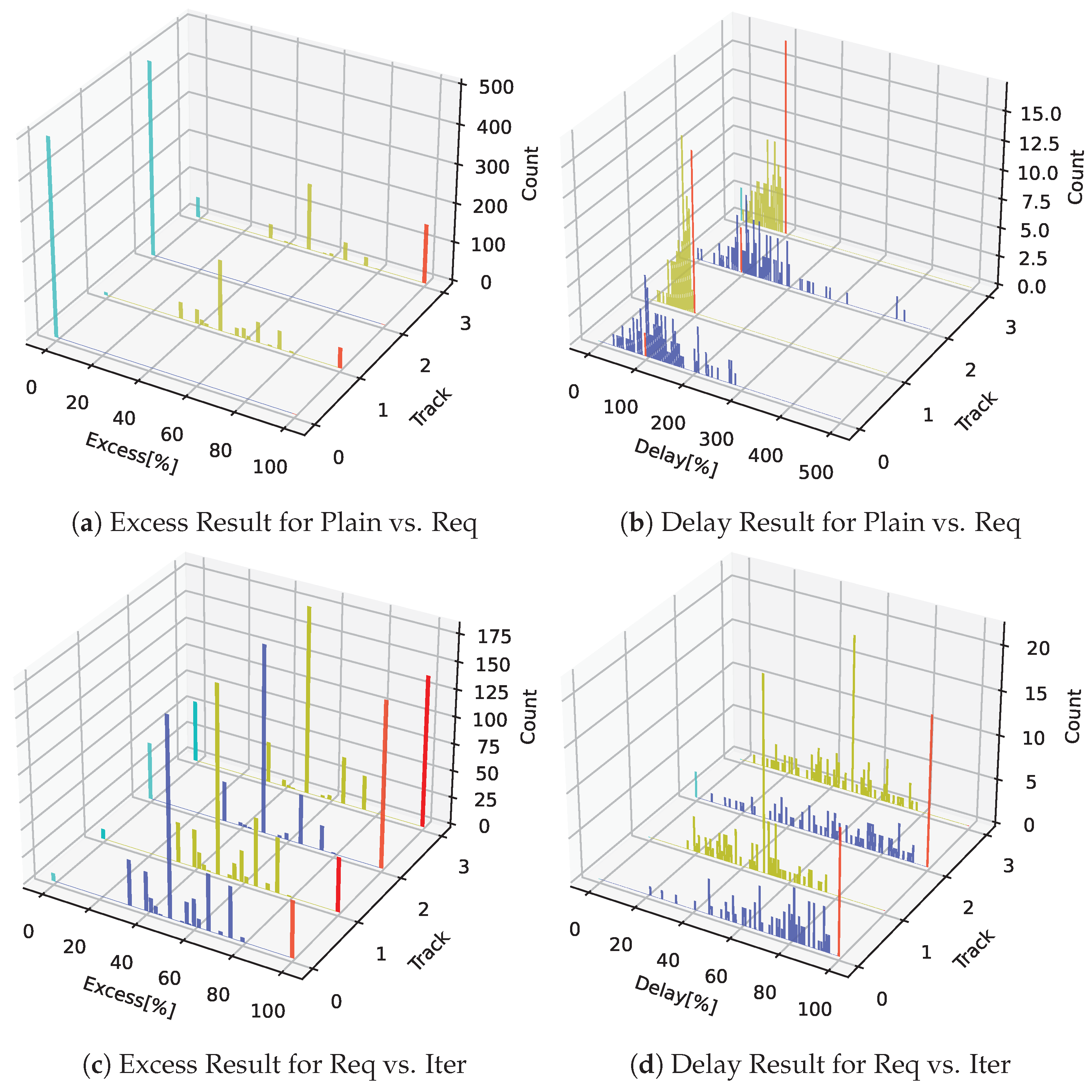
| Time [s] | Time [s] | Step [#] | Punctuality [#] | |
|---|---|---|---|---|
| (Min|Median|Max) | (Min|Median|Max) | (Min|Median|Max) | ||
| Plain | 0.095|0.446|30.191 | — | 13|21|40 | 35 |
| Req | 0.136|0.657|04.082 | 01.795|03.378|08.275 | 16|25|45 | 1000 |
| Iter | 0.121|0.648|04.285 | 06.669|13.864|35.994 | 16|25|45 | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Kim, K. Enhancing Urban Air Mobility Scheduling Through Declarative Reasoning and Stakeholder Modeling. Aerospace 2025, 12, 605. https://doi.org/10.3390/aerospace12070605
Kim J, Kim K. Enhancing Urban Air Mobility Scheduling Through Declarative Reasoning and Stakeholder Modeling. Aerospace. 2025; 12(7):605. https://doi.org/10.3390/aerospace12070605
Chicago/Turabian StyleKim, Jeongseok, and Kangjin Kim. 2025. "Enhancing Urban Air Mobility Scheduling Through Declarative Reasoning and Stakeholder Modeling" Aerospace 12, no. 7: 605. https://doi.org/10.3390/aerospace12070605
APA StyleKim, J., & Kim, K. (2025). Enhancing Urban Air Mobility Scheduling Through Declarative Reasoning and Stakeholder Modeling. Aerospace, 12(7), 605. https://doi.org/10.3390/aerospace12070605








