Flight Connection Planning for Low-Cost Carriers Under Passenger Demand Uncertainty
Abstract
1. Introduction
- 1.
- We develop an Uncertainty-Aware Integrated Connection Planning and Passenger Allocation Model (UICPPAM) for LCCs, which jointly optimizes the activation of connecting flights, transfer airports, and passenger allocation proportions guided by a discrete choice model. In this paper, the “activation of transfer airports” refers to the provision of transfer service functionality, such as through-checked baggage and seamless passenger transfer, at selected airports. Once activated, an airport is assumed to offer these services. Unlike existing studies that rely on deterministic or static demand assumptions, our model explicitly captures uncertainty across city-pair markets. It determines both the network configuration and passenger assignment within a unified framework that adapts to demand fluctuations.
- 2.
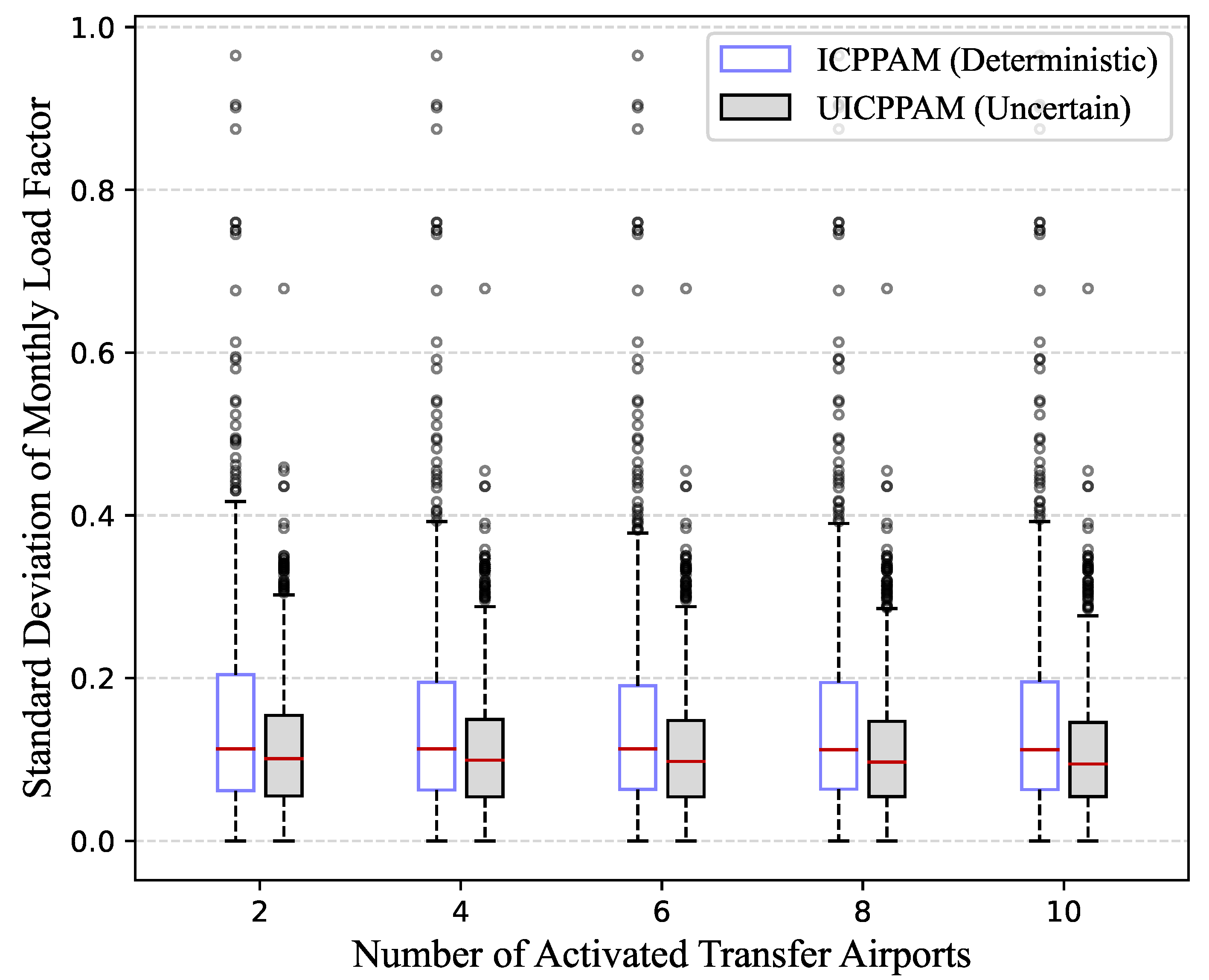
- We validate the practical applicability of UICPPAM using real-world data from Spring Airlines, the largest low-cost carrier in China. Numerical experiments show that UICPPAM outperforms the deterministic benchmark (ICPPAM) under demand uncertainty, providing more robust connection strategies. Specifically, under the same setting of activating ten transfer airports, our model generates 59.5% more feasible connecting itineraries compared to ICPPAM. Furthermore, when applying the connection strategies and passenger allocation solutions produced by both models to the ten representative demand scenarios we generated, UICPPAM reduces the average standard deviation of flight load factors by 26.1% compared to ICPPAM and increases the average success rate of implementing connection strategies from 77.1% under ICPPAM to 100%.
- 3.
- We highlight the importance of incorporating demand uncertainty into network planning and demonstrate the model’s potential to support resilient and data-driven decision making for LCCs.
2. Related Literature
2.1. Airline Network Planning
2.2. Development in LCC Networks
2.3. Demand Uncertainty in Airline Network Planning
3. Problem Statement and Model Formulation
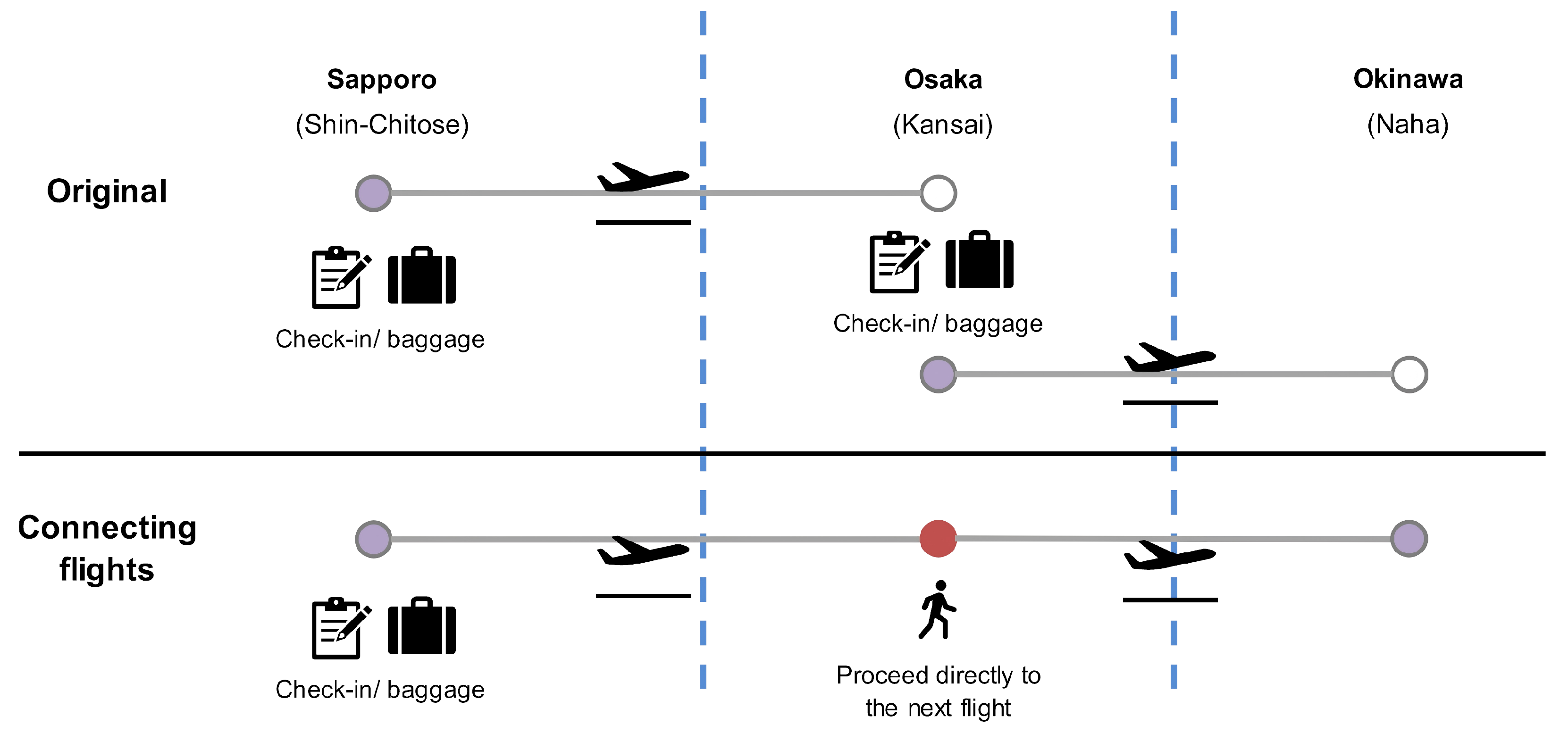
3.1. Problem Description
- Generation of feasible connections. First, we also construct potential connecting itineraries through a preprocessing procedure that ensures temporal and spatial feasibility, as well as other operational constraints (see Section 5.2 for details).
- Cost and modeling assumptions. Second, since the primary focus of this study is on generating robust connection and passenger allocation strategies under demand uncertainty, we adopt several similar cost-related assumptions and modeling rules, which are not the main subject of investigation in this work. Specifically, we assume that the existing flight schedule and capacity allocations remain unchanged and that the operational costs associated with current services are fixed and therefore excluded from the objective function. On the revenue side, the fare () is defined as the average ticket price associated with itinerary i. Regarding the costs associated with providing connecting services, we define two components: , representing the fixed cost of activating transfer airport h, and , representing the variable cost incurred per passenger for enabling seamless transfer services on the itinerary i.
- Endogenous demand modeling. Third, we model passenger demand as endogenous, allowing newly introduced connecting itineraries to compete with existing options by adopting a multinomial logit formulation (MNL) that captures how passengers choose among available itineraries [41]. This formulation estimates the probability of passengers selecting a specific itinerary based on the utility value (see Section 5.2 for details) they derive from it, thereby enabling the model to realistically account for demand redistribution within a given O&D market. Specifically, let be the set of city-pair markets and be the set of itineraries offered by the airline in market m. Each itinerary is associated with a utility value , and its attractiveness is defined as: . To capture the effect of external alternatives (e.g., itineraries offered by competitors), we define an aggregate attractiveness term: , where denotes the set of itineraries in the market m not offered by the target airline. Given this setup, the market share of itinerary i is computed as:where is a binary variable that indicates whether the airline chooses to offer itinerary i. Then, the number of passengers assigned to itinerary i is . This approach allows the model to account for both external and internal competition. External competition arises when other carriers serve the same market, while internal (or self) competition occurs when multiple feasible connecting itineraries from the same airline compete for the same O&D market.
3.2. Model Formulation
4. Solution Approach
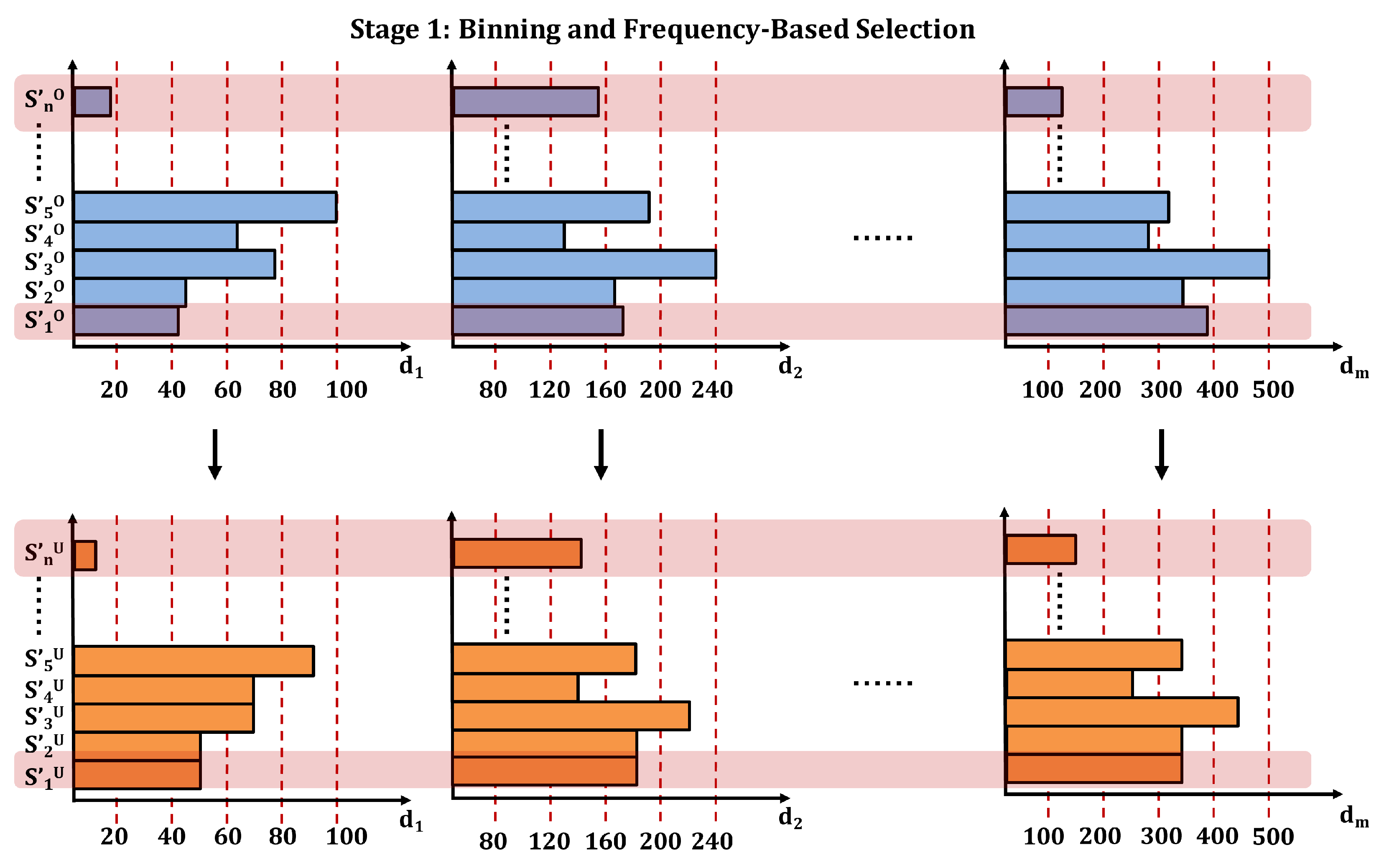
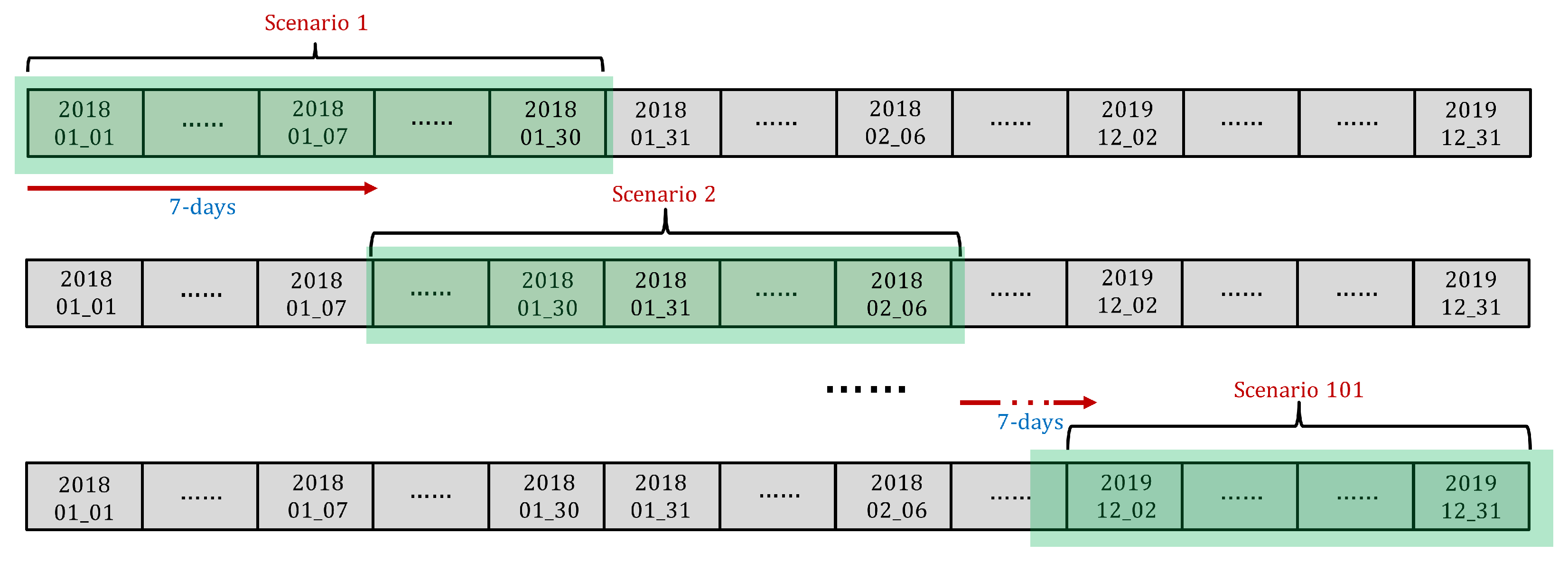
4.1. Scenario Generation
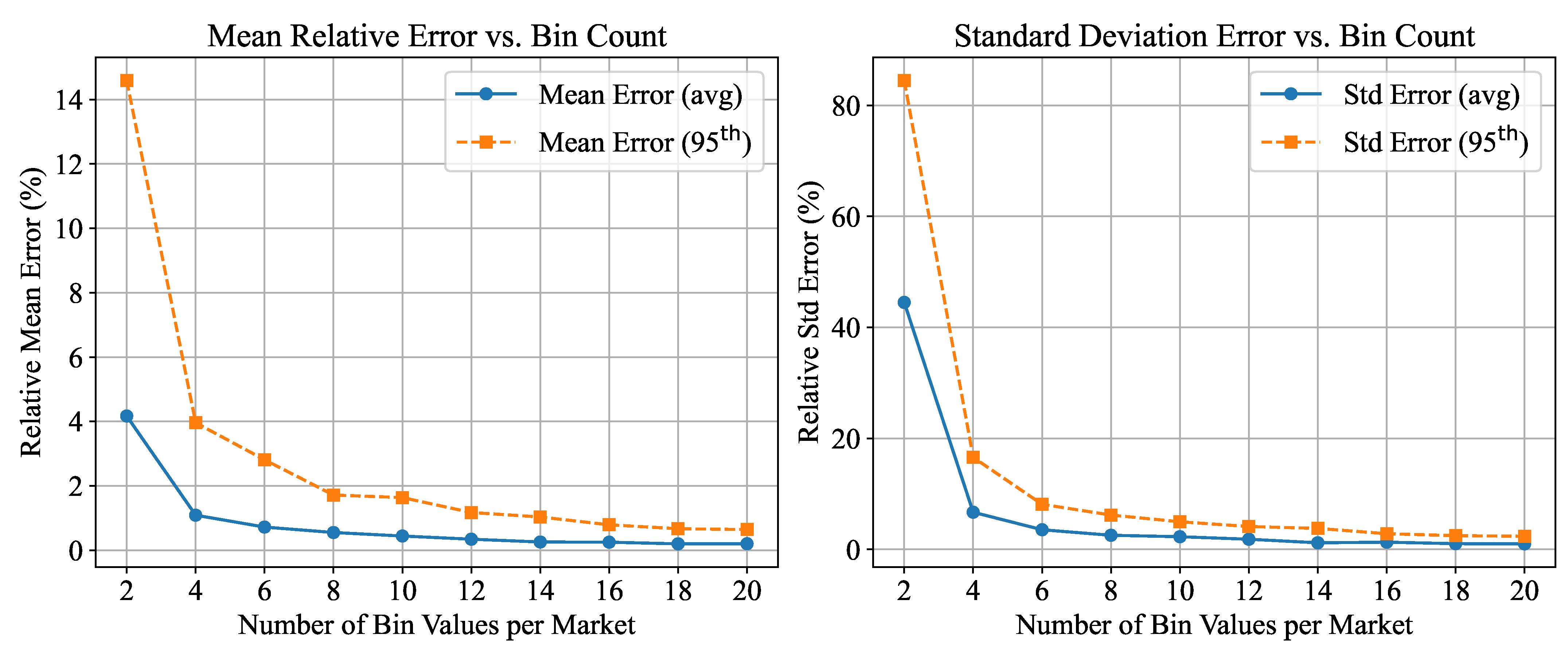
- Stage 1: Binning and Frequency-Based Selection
- Stage 2: Clustering of Remaining Sparse Combinations
4.2. Model Implementation and Setup
5. Case Study
5.1. Spring Airlines
5.2. Experimental Setup
5.3. Results
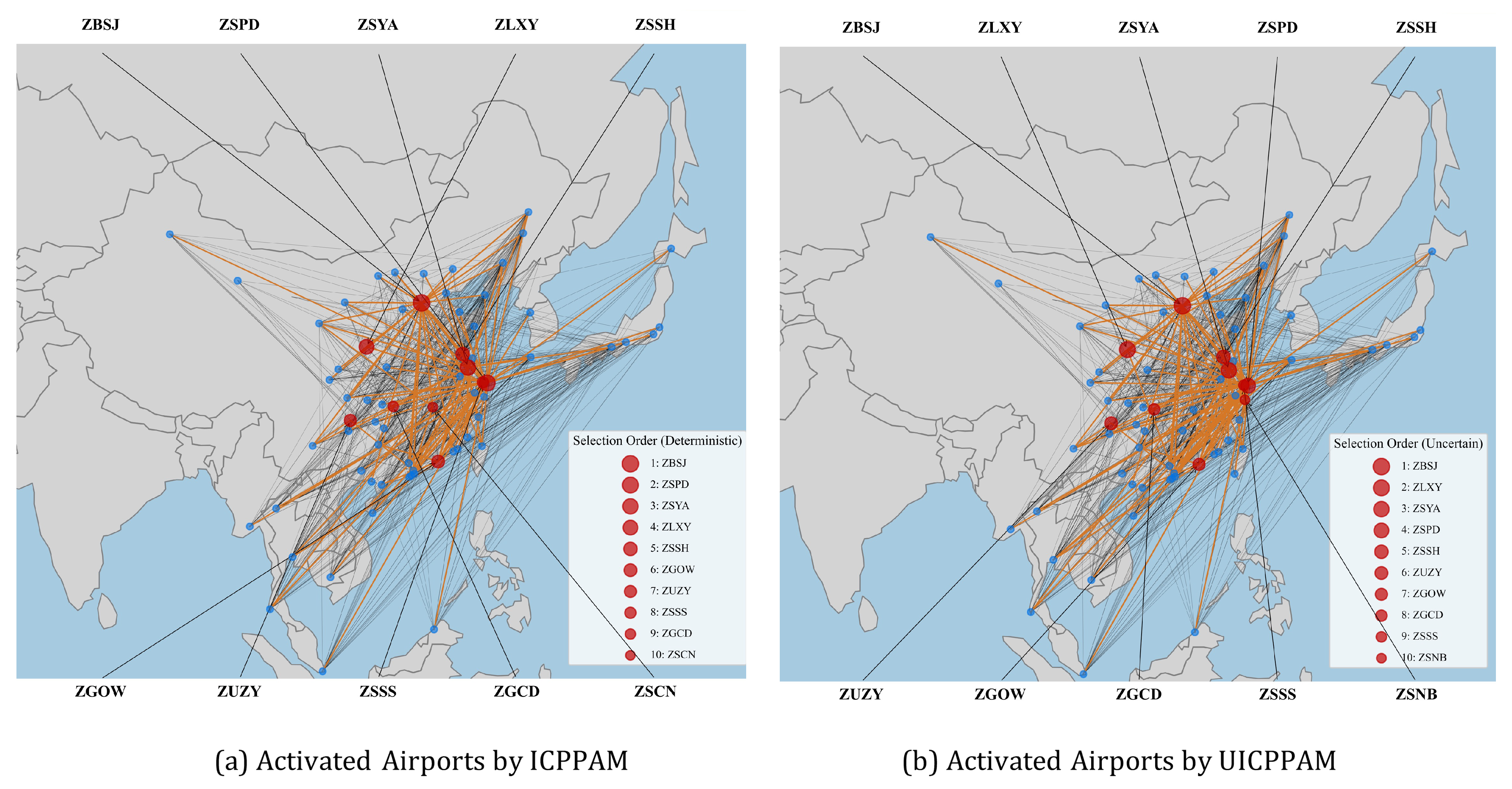
5.3.1. Selected Transfer Airports and Connecting Itineraries
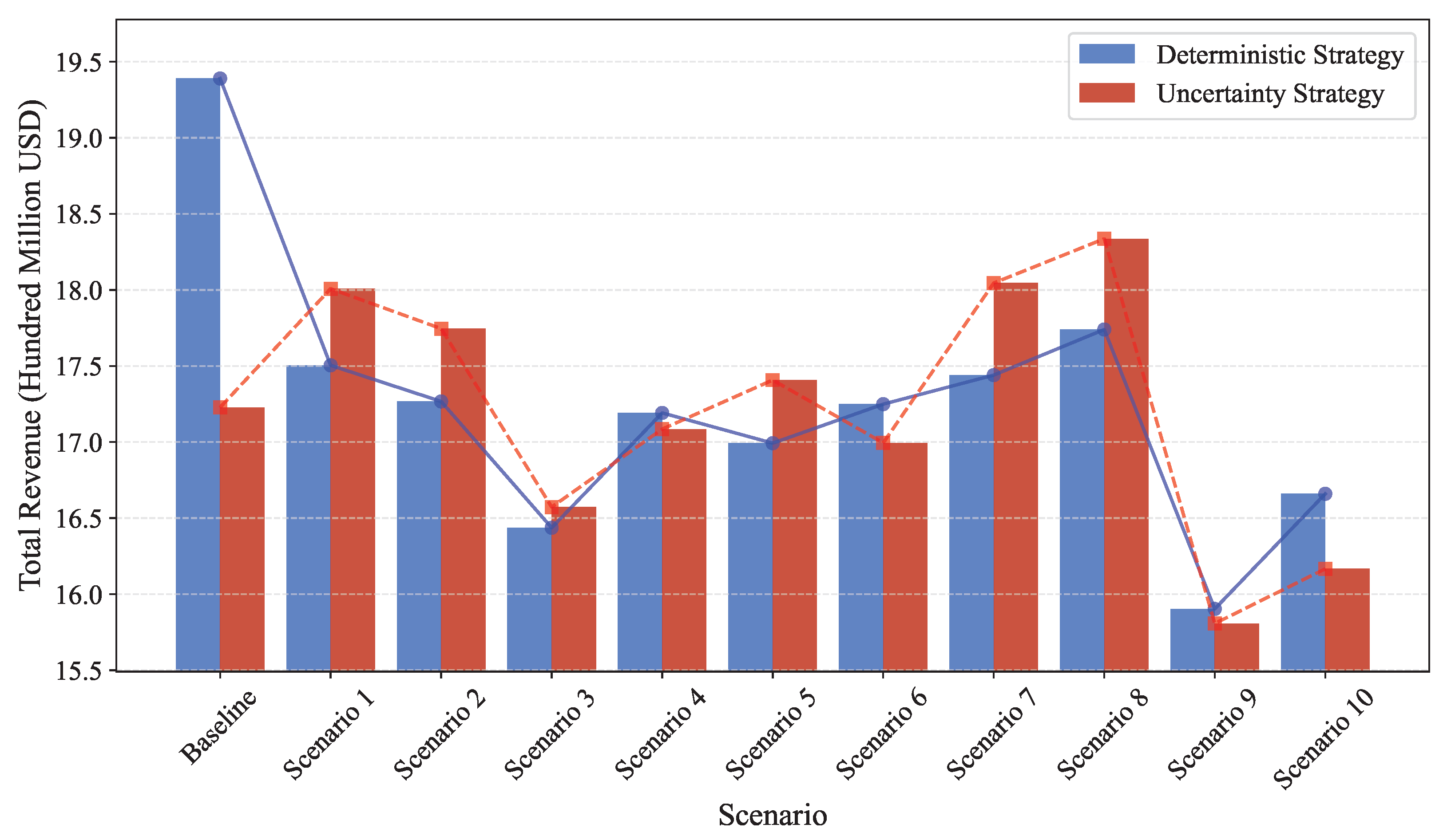
5.3.2. Robustness Analysis
- (i)
- In some one-stop itineraries, a local flight serves as the shared feeder for multiple connecting itineraries. When the total number of passengers allocated to this local flight exceeds its available seat capacity, the first leg of the connecting itineraries fails to operate, thereby preventing all subsequent connections from being activated. In Case 1, Flight CQH8592 (from ZYTL to ZSPD) reaches its seat capacity limit and thus cannot support any onward connections.
- (ii)
- As an extension of type (i), in some one-stop itineraries, a local flight serves as the shared feeder for multiple connecting itineraries. Although the total number of passengers allocated to this local flight does not exceed its seat capacity, the available seats are insufficient to accommodate all the connecting itineraries simultaneously. As a result, selective allocation must be performed, potentially leading to the failure of certain connections. In Case 2, if priority is given to passengers traveling from ZYTL to ZUCK, the connection to VYYY may fail. Alternatively, if priority is given to passengers traveling from ZYTL to VYYY, all connections can be preserved, but at the cost of losing more demand from ZYTL to ZUCK.
- (iii)
- In some one-stop itineraries, a local flight serves as the second leg for multiple connecting itineraries. When the direct demand allocated to this local flight exceeds its seat capacity, the flight cannot accommodate passengers from the preceding connections, leading to the failure of all upstream itineraries. In Case 3, Flight CQH8617 (from ZBSJ to ZBOW) reaches its seat capacity limit due to direct demand, leaving no capacity for any inbound connections.
- (iv)
- Similar to the second case, this failure type arises when a local flight serves as the downstream leg for multiple one-stop itineraries. Although the total number of allocated passengers does not exceed the seat capacity, the remaining seats are insufficient to accommodate all connections simultaneously. As a result, selective allocation becomes necessary, potentially leading to the failure of some connecting itineraries. Case 4 provides a concrete example of this situation.
| Algorithm 1: Priority-based dynamic allocation for passenger reallocation |
|
6. Discussion
7. Conclusions
7.1. Summary and Contributions
7.2. Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LCC | Low-Cost Carriers |
| P2P | Point-to-Point |
| H&S | Hub-and-Spoke |
| FSNCs | Full-Service Network Carriers |
| O&D | Origin-Destination |
| MNL | Multinomial Logit Formulation |
| MILP | Mixed-Integer Linear Programming |
| FSC | Full-Service Carriers |
Appendix A. List of Airports
| ICAO Code | Airport Name | Country | City |
|---|---|---|---|
| VYYY | Yangon International Airport | Myanmar | Yangon |
| ZBSJ | Shijiazhuang Zhengding International Airport | China | Shijiazhuang |
| ZBOW | Baotou Donghe International Airport | China | Baotou |
| ZLXY | Xi’an Xianyang International Airport | China | Xi’an |
| ZGCD | Changde Taohuayuan Airport | China | Changde |
| ZGOW | Jieyang Chaoshan International Airport | China | Jieyang |
| ZSAM | Xiamen Gaoqi International Airport | China | Xiamen |
| ZSCN | Nanchang Changbei International Airport | China | Nanchang |
| ZSNB | Ningbo Lishe International Airport | China | Ningbo |
| ZSPD | Shanghai Pudong International Airport | China | Shanghai |
| ZSSH | Huai’an Lianshui Airport | China | Huai’an |
| ZSSS | Shanghai Hongqiao International Airport | China | Shanghai |
| ZSYA | Yangzhou Taizhou International Airpor | China | Yangzhou |
| ZUCK | Chongqing Jiangbei International Airport | China | Chongqing |
| ZUZY | Zunyi Xinzhou Airport | China | Zunyi |
| ZYTL | Dalian Zhoushuizi International Airport | China | Dalian |
| ZYTX | Shenyang Taoxian International Airport | China | Shenyang |
References
- Oum, T.H.; Zhang, A.; Zhang, Y. Airline network rivalry. Can. J. Econ. 1995, 28, 836–857. [Google Scholar] [CrossRef]
- Klophaus, R.; Merkert, R.; Lordan, O. Mesh network as a competitive advantage for European LCCs: An alternative topology to hub-and-spoke for selling online connections. Transp. Policy 2021, 106, 196–204. [Google Scholar] [CrossRef]
- Zeigler, P.; Pagliari, R.; Suau-Sanchez, P.; Malighetti, P.; Redondi, R. Low-cost carrier entry at small European airports: Low-cost carrier effects on network connectivity and self-transfer potential. J. Transp. Geogr. 2017, 60, 68–79. [Google Scholar] [CrossRef]
- Klophaus, R.; Fichert, F. From low-cost carriers to network carriers without legacy? Evolving airline business models in Europe. In Airline Economics in Europe; Emerald Publishing Limited: Leeds, UK, 2019; Volume 8, pp. 57–75. [Google Scholar]
- Spring Airlines. Spring Airlines Annual Report 2023. 2025. Available online: https://ajax.springairlines.com/content/invester/%E6%98%A5%E7%A7%8B%E8%88%AA%E7%A9%BA%EF%BC%9A%E6%98%A5%E7%A7%8B%E8%88%AA%E7%A9%BA2023%E5%B9%B4%E5%B9%B4%E5%BA%A6%E6%8A%A5%E5%91%8A.pdf (accessed on 29 March 2025).
- Maertens, S.; Pabst, H.; Grimme, W. The scope for low-cost connecting services in Europe—Is self-hubbing only the beginning? Res. Transp. Bus. Manag. 2016, 21, 84–93. [Google Scholar] [CrossRef]
- Cattaneo, M.; Malighetti, P.; Paleari, S.; Redondi, R. Evolution of the European network and implications for self-connection. J. Air Transp. Manag. 2017, 65, 18–28. [Google Scholar] [CrossRef]
- Malighetti, P.; Paleari, S.; Redondi, R. Connectivity of the European airport network: “Self-help hubbing” and business implications. J. Air Transp. Manag. 2008, 14, 53–65. [Google Scholar] [CrossRef]
- Morlotti, C.; Birolini, S.; Cattaneo, M.; Redondi, R. Introducing connecting flights in LCCs’ business model: Ryanair’s network strategy. J. Air Transp. Manag. 2020, 87, 101849. [Google Scholar] [CrossRef]
- Birolini, S.; Besana, E.; Cattaneo, M.; Redondi, R.; Sallan, J.M. An integrated connection planning and passenger allocation model for low-cost carriers. J. Air Transp. Manag. 2022, 99, 102160. [Google Scholar] [CrossRef]
- Suh, D.Y.; Ryerson, M.S. Forecast to grow: Aviation demand forecasting in an era of demand uncertainty and optimism bias. Transp. Res. Part E Logist. Transp. Rev. 2019, 128, 400–416. [Google Scholar] [CrossRef]
- O’kelly, M.E. The location of interacting hub facilities. Transp. Sci. 1986, 20, 92–106. [Google Scholar] [CrossRef]
- O’Kelly, M.E.; Bryan, D.; Skorin-Kapov, D.; Skorin-Kapov, J. Hub network design with single and multiple allocation: A computational study. Locat. Sci. 1996, 4, 125–138. [Google Scholar] [CrossRef]
- Contreras, I.; Cordeau, J.F.; Laporte, G. Stochastic uncapacitated hub location. Eur. J. Oper. Res. 2011, 212, 518–528. [Google Scholar] [CrossRef]
- Tiwari, R.; Jayaswal, S.; Sinha, A. Competitive hub location problem: Model and solution approaches. Transp. Res. Part B Methodol. 2021, 146, 237–261. [Google Scholar] [CrossRef]
- O’Kelly, M.E.; Bryan, D. Interfacility interaction in models of hub and spoke networks. J. Reg. Sci. 2002, 42, 145–164. [Google Scholar] [CrossRef]
- Racunica, I.; Wynter, L. Optimal location of intermodal freight hubs. Transp. Res. Part B Methodol. 2005, 39, 453–477. [Google Scholar] [CrossRef]
- Barnhart, C.; Cohn, A. Airline schedule planning: Accomplishments and opportunities. Manuf. Serv. Oper. Manag. 2004, 6, 3–22. [Google Scholar] [CrossRef]
- Lohatepanont, M.; Barnhart, C. Airline schedule planning: Integrated models and algorithms for schedule design and fleet assignment. Transp. Sci. 2004, 38, 19–32. [Google Scholar] [CrossRef]
- Belobaba, P. Air Travel Demand and Airline Seat Inventory Management. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1987. [Google Scholar]
- Talluri, K.; Van Ryzin, G. An analysis of bid-price controls for network revenue management. Manag. Sci. 1998, 44, 1577–1593. [Google Scholar] [CrossRef]
- Hsiao, C.Y.; Hansen, M. A passenger demand model for air transportation in a hub-and-spoke network. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 1112–1125. [Google Scholar] [CrossRef]
- Wei, K.; Vaze, V.; Jacquillat, A. Airline timetable development and fleet assignment incorporating passenger choice. Transp. Sci. 2020, 54, 139–163. [Google Scholar] [CrossRef]
- Birolini, S.; Jacquillat, A.; Cattaneo, M.; Antunes, A.P. Airline Network Planning: Mixed-integer non-convex optimization with demand–supply interactions. Transp. Res. Part B Methodol. 2021, 154, 100–124. [Google Scholar] [CrossRef]
- Franke, M. Network design strategies. In Airline Operations; Routledge: London, UK, 2017; pp. 44–60. [Google Scholar]
- De Neufville, R. Low-cost airports for low-cost airlines: Flexible design to manage the risks. In Low Cost Carriers; Routledge: London, UK, 2017; pp. 163–196. [Google Scholar]
- Dobruszkes, F. An analysis of European low-cost airlines and their networks. J. Transp. Geogr. 2006, 14, 249–264. [Google Scholar] [CrossRef]
- De Wit, J.G.; Zuidberg, J. The growth limits of the low cost carrier model. In Low Cost Carriers; Routledge: London, UK, 2017; pp. 383–390. [Google Scholar]
- Fageda, X.; Suau-Sanchez, P.; Mason, K.J. The evolving low-cost business model: Network implications of fare bundling and connecting flights in Europe. J. Air Transp. Manag. 2015, 42, 289–296. [Google Scholar] [CrossRef]
- Wu, C.; Liao, M.; Zhang, Y.; Luo, M.; Zhang, G. Network development of low-cost carriers in China’s domestic market. J. Transp. Geogr. 2020, 84, 102670. [Google Scholar] [CrossRef]
- Franke, M. Competition between network carriers and low-cost carriers—retreat battle or breakthrough to a new level of efficiency? J. Air Transp. Manag. 2004, 10, 15–21. [Google Scholar] [CrossRef]
- Lordan, O. Study of the full-service and low-cost carriers network configuration. J. Ind. Eng. Manag. (JIEM) 2014, 7, 1112–1123. [Google Scholar] [CrossRef]
- Pearson, J.; O’Connell, J.F.; Pitfield, D.; Ryley, T. The strategic capability of Asian network airlines to compete with low-cost carriers. J. Air Transp. Manag. 2015, 47, 1–10. [Google Scholar] [CrossRef]
- Pels, E. Airline network competition: Full-service airlines, low-cost airlines and long-haul markets. Res. Transp. Econ. 2008, 24, 68–74. [Google Scholar] [CrossRef]
- Yang, T.H.; Huang, Y. Hub-and-spoke airline network design under competitive market. J. Ind. Prod. Eng. 2015, 32, 186–195. [Google Scholar] [CrossRef]
- Lee, J.; Marla, L.; Jacquillat, A. Dynamic disruption management in airline networks under airport operating uncertainty. Transp. Sci. 2020, 54, 973–997. [Google Scholar] [CrossRef]
- Yang, T.H. A two-stage stochastic model for airline network design with uncertain demand. Transportmetrica 2010, 6, 187–213. [Google Scholar] [CrossRef]
- Wang, Z.; Qi, M. Robust service network design under demand uncertainty. Transp. Sci. 2020, 54, 676–689. [Google Scholar] [CrossRef]
- Bauschert, T.; Büsing, C.; D’Andreagiovanni, F.; Koster, A.M.; Kutschka, M.; Steglich, U. Network planning under demand uncertainty with robust optimization. IEEE Commun. Mag. 2014, 52, 178–185. [Google Scholar] [CrossRef]
- De Koning, M.; Santos, B.F. Fleet Planning Under Demand Uncertainty: A Reinforcement Learning Approach; Technical report; Delft University of Technology: Delft, The Netherlands, 2020. [Google Scholar]
- Ben-Akiva, M.E.; Lerman, S.R. Discrete Choice Analysis: Theory and Application to Travel Demand; MIT Press: Cambridge, MA, USA, 1985; Volume 9. [Google Scholar]
- Kleywegt, A.J.; Shapiro, A.; Homem-de Mello, T. The sample average approximation method for stochastic discrete optimization. SIAM J. Optim. 2002, 12, 479–502. [Google Scholar] [CrossRef]
- King, A.J.; Wallace, S.W. Modeling with Stochastic Programming; Springer: New York, NY, USA, 2012; Volume 4. [Google Scholar]
- OAG. Official Airline Guide. 2025. Available online: https://www.oag.com/flight-data-sets (accessed on 10 June 2025).
- Birolini, S.; Cattaneo, M.; Malighetti, P.; Morlotti, C. Integrated origin-based demand modeling for air transportation. Transp. Res. Part E Logist. Transp. Rev. 2020, 142, 102050. [Google Scholar] [CrossRef]
- Serrano, F.; Kazda, A. The future of airports post COVID-19. J. Air Transp. Manag. 2020, 89, 101900. [Google Scholar] [CrossRef]
- Macilree, J.; Duval, D.T. Aeropolitics in a post-COVID-19 world. J. Air Transp. Manag. 2020, 88, 101864. [Google Scholar] [CrossRef]
- Bulchand-Gidumal, J.; Melián-González, S. Post-COVID-19 behavior change in purchase of air tickets. Ann. Tour. Res. 2021, 87, 103129. [Google Scholar] [CrossRef]

| Notation | Description |
|---|---|
| Sets | |
| Set of flights operated by the target airline, indexed by f | |
| Set of itineraries available to the target airline, indexed by i | |
| Set of markets, indexed by m | |
| Set of airports served by the target airline, indexed by a | |
| Set of candidate transfer airports, indexed by h | |
| Set of flight capacity, indexed by | |
| Subset of nonstop itineraries, indexed by i, | |
| Subset of connecting (one-stop) itineraries, indexed by i, | |
| Subset of itineraries containing flight f, | |
| Subset of itineraries in market m, indexed by i, | |
| Subset of connecting itineraries via transfer airport h, indexed by i, | |
| Subset of self-hubbing itineraries, indexed by i, | |
| Subset of handled itineraries, indexed by i, | |
| Subset of connecting itineraries with flight f as the first leg, indexed by i, | |
| Parameters | |
| Average price of itineraries i | |
| Capacity (number of seats) available on flight f, | |
| Total demand in market m, as a random parameter; equals in the deterministic case | |
| Attractiveness of itinerary i | |
| Aggregate attractiveness of the outside option in market m | |
| Activation costs defined for each transfer airport h | |
| Per passenger operating costs for one-stop handle itineraries, | |
| Decision variables | |
| Binary variables, where 1 indicates transfer airport is activated, and 0 otherwise. | |
| Binary variables, where 1 indicates itinerary is operated, and 0 otherwise. | |
| Market share captured by the outside option | |
| Market share on itinerary i | |
| Model | Apt () | Apt | Rev ($) | Rev (%) | AC (AC/PC) | Pax (%) | |
|---|---|---|---|---|---|---|---|
| Nonstop | One-Stop | ||||||
| ICPPAM | 1 | ZBSJ | 2.89 | 1.62% | 43 (8.0%) | −1.37% | – |
| 2 | ZSPD | 2.16 | 1.19% | 104 (19.3%) | −1.31% | +60.7% | |
| 3 | ZSYA | 2.12 | 1.15% | 127 (23.5%) | −1.05% | +41.2% | |
| 4 | ZLXY | 1.95 | 1.05% | 130 (24.1%) | −1.37% | +26.6% | |
| 5 | ZSSH | 1.46 | 0.78% | 141 (26.1%) | −0.28% | +11.8% | |
| 6 | ZGOW | 1.25 | 0.66% | 143 (26.5%) | −0.50% | +13.0% | |
| 7 | ZUZY | 1.21 | 0.64% | 143 (26.5%) | −0.43% | +9.3% | |
| 8 | ZSSS | 0.87 | 0.46% | 162 (30.0%) | −0.51% | +8.3% | |
| 9 | ZGCD | 0.78 | 0.40% | 167 (30.9%) | −0.35% | +6.3% | |
| 10 | ZSCN | 0.53 | 0.27% | 168 (31.1%) | −0.33% | +3.6% | |
| UICPPAM | 1 | ZBSJ | 2.57 | 1.62% | 50 (9.3%) | −2.65% | – |
| 2 | ZLXY | 1.91 | 1.20% | 54 (10.0%) | −1.53% | +45.8% | |
| 3 | ZSYA | 1.78 | 1.09% | 75 (13.9%) | −1.02% | +31.4% | |
| 4 | ZSPD | 1.73 | 1.05% | 193 (35.7%) | −4.73% | +51.8% | |
| 5 | ZSSH | 1.17 | 0.70% | 203 (37.6%) | −1.01% | +12.5% | |
| 6 | ZUZY | 1.08 | 0.64% | 205 (38.0%) | −0.58% | +9.1% | |
| 7 | ZGOW | 0.91 | 0.53% | 219 (40.6%) | −0.90% | +7.8% | |
| 8 | ZGCD | 0.74 | 0.43% | 224 (41.5%) | −0.37% | +5.2% | |
| 9 | ZSSS | 0.67 | 0.39% | 257 (47.6%) | −1.10% | +6.4% | |
| 10 | ZSNB | 0.54 | 0.31% | 268 (49.6%) | −0.65% | +4.2% | |
| Error Type | Mean (%) | Max (%) | 95th Percentile (%) |
|---|---|---|---|
| Mean Error | 1.37 | 59.91 | 3.98 |
| Std Error | 6.12 | 135.51 | 15.19 |
| 25th Quantile Error | 2.04 | 69.20 | 9.36 |
| 50th Quantile Error | 2.73 | 66.51 | 7.20 |
| 75th Quantile Error | 1.65 | 62.25 | 6.17 |
| Case | 1st Leg | Pax | 2nd Leg | Pax | AC Status | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ZYTL–ZSPD (CQH8592) | 95,197 | 5.4% | 5140 | 5022 | ZSPD–ZUCK (CQH6107) | 15,503 | 4.1% | 635 | - | failed |
| ZSPD–VYYY (CQH6243) | 252 | 20.4% | 51 | - | |||||||
| 2 | ZYTL–ZSPD (CQH8592) | 82,298 | 5.4% | 4444 | 5022 | ZSPD–ZUCK (CQH6107) | 15,742 | 4.1% | 645 | - | failed |
| ZSPD–VYYY (CQH6243) | 234 | 20.4% | 48 | - | |||||||
| 3 | ZYTX–ZBSJ (CQH8575) | 2366 | 77.1% | 1824 | – | ZBSJ–ZBOW (CQH8617) | 12,757 | 42.4% | 5408 | 5022 | failed |
| ZSAM–ZBSJ (CQH8976) | 1675 | 17.6% | 295 | – | |||||||
| 4 | ZYTX–ZBSJ (CQH8575) | 2234 | 77.1% | 1729 | – | ZBSJ–ZBOW (CQH8617) | 8018 | 42.4% | 3400 | 5022 | failed |
| ZSAM–ZBSJ (CQH8976) | 1546 | 17.6% | 272 | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, W.; Li, M.Z.; Itoh, E. Flight Connection Planning for Low-Cost Carriers Under Passenger Demand Uncertainty. Aerospace 2025, 12, 574. https://doi.org/10.3390/aerospace12070574
Ding W, Li MZ, Itoh E. Flight Connection Planning for Low-Cost Carriers Under Passenger Demand Uncertainty. Aerospace. 2025; 12(7):574. https://doi.org/10.3390/aerospace12070574
Chicago/Turabian StyleDing, Wenhao, Max Z. Li, and Eri Itoh. 2025. "Flight Connection Planning for Low-Cost Carriers Under Passenger Demand Uncertainty" Aerospace 12, no. 7: 574. https://doi.org/10.3390/aerospace12070574
APA StyleDing, W., Li, M. Z., & Itoh, E. (2025). Flight Connection Planning for Low-Cost Carriers Under Passenger Demand Uncertainty. Aerospace, 12(7), 574. https://doi.org/10.3390/aerospace12070574








