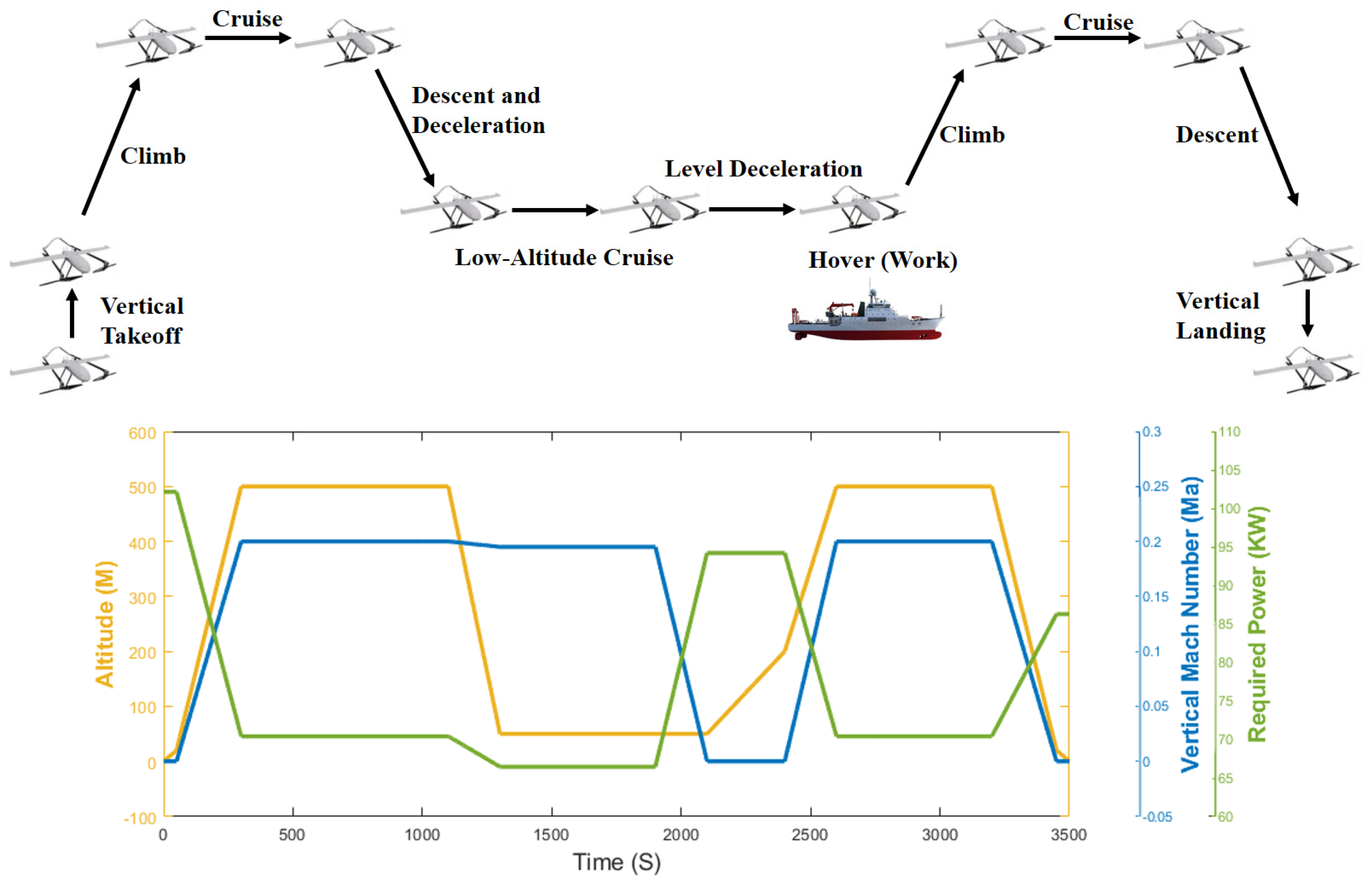
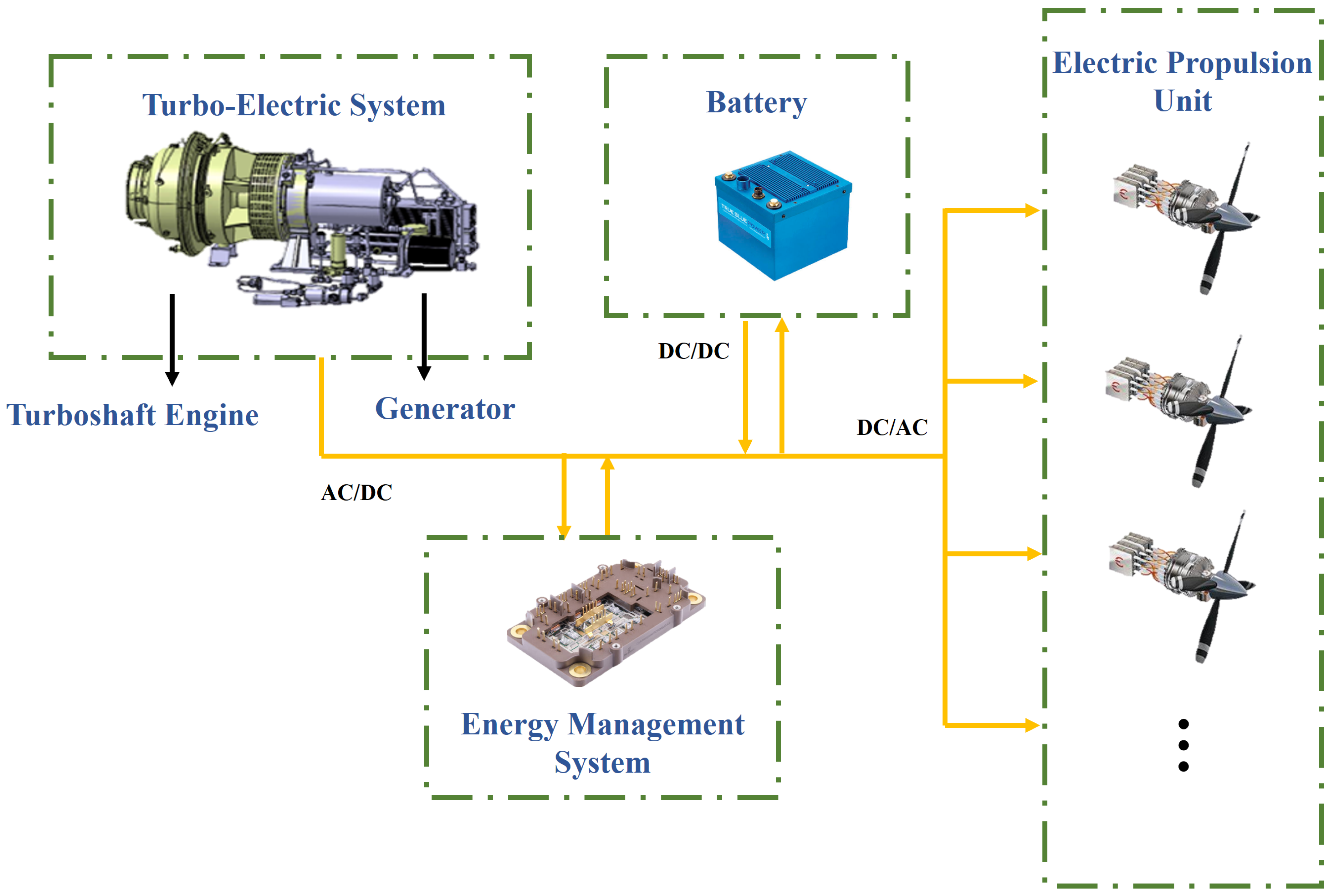
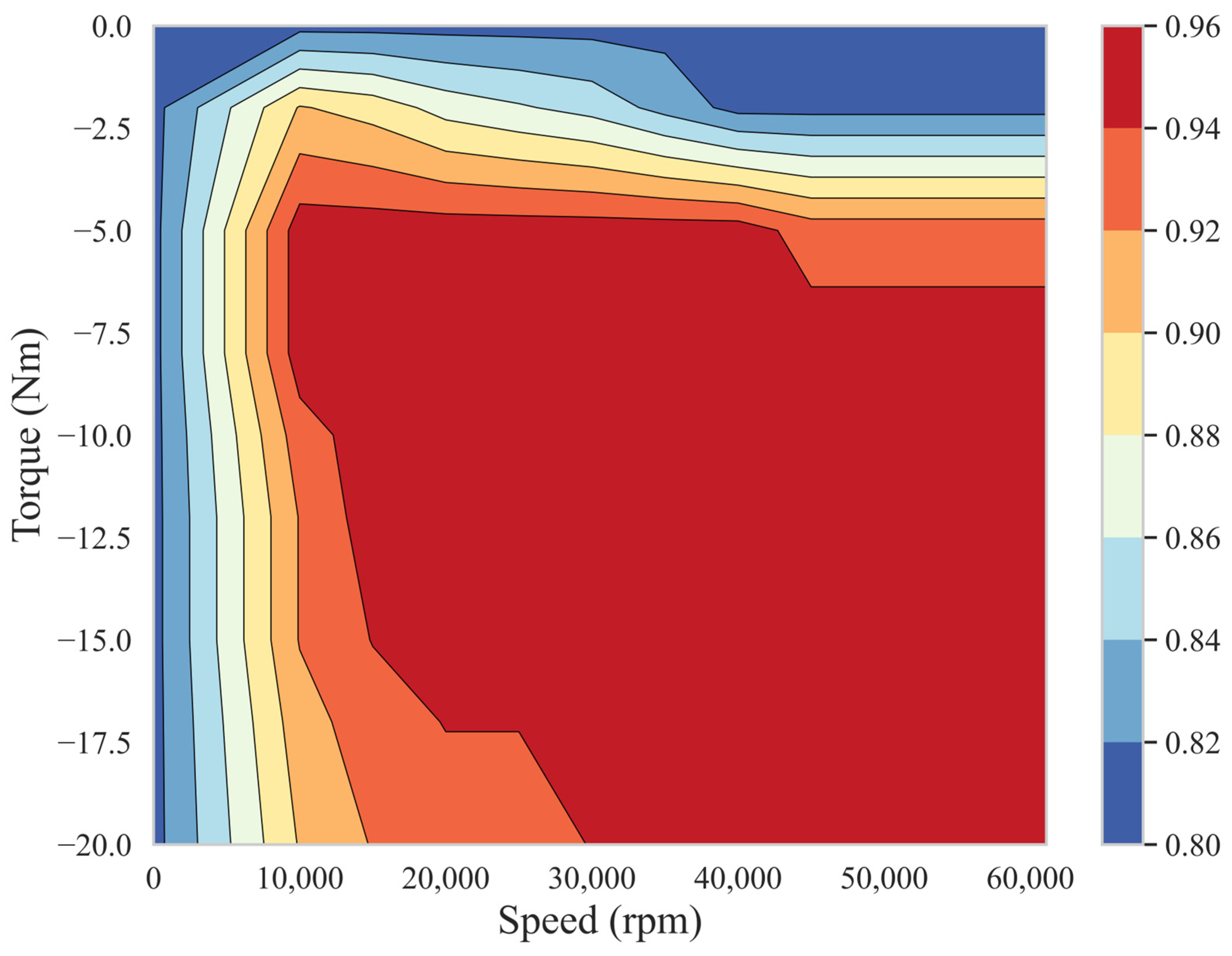
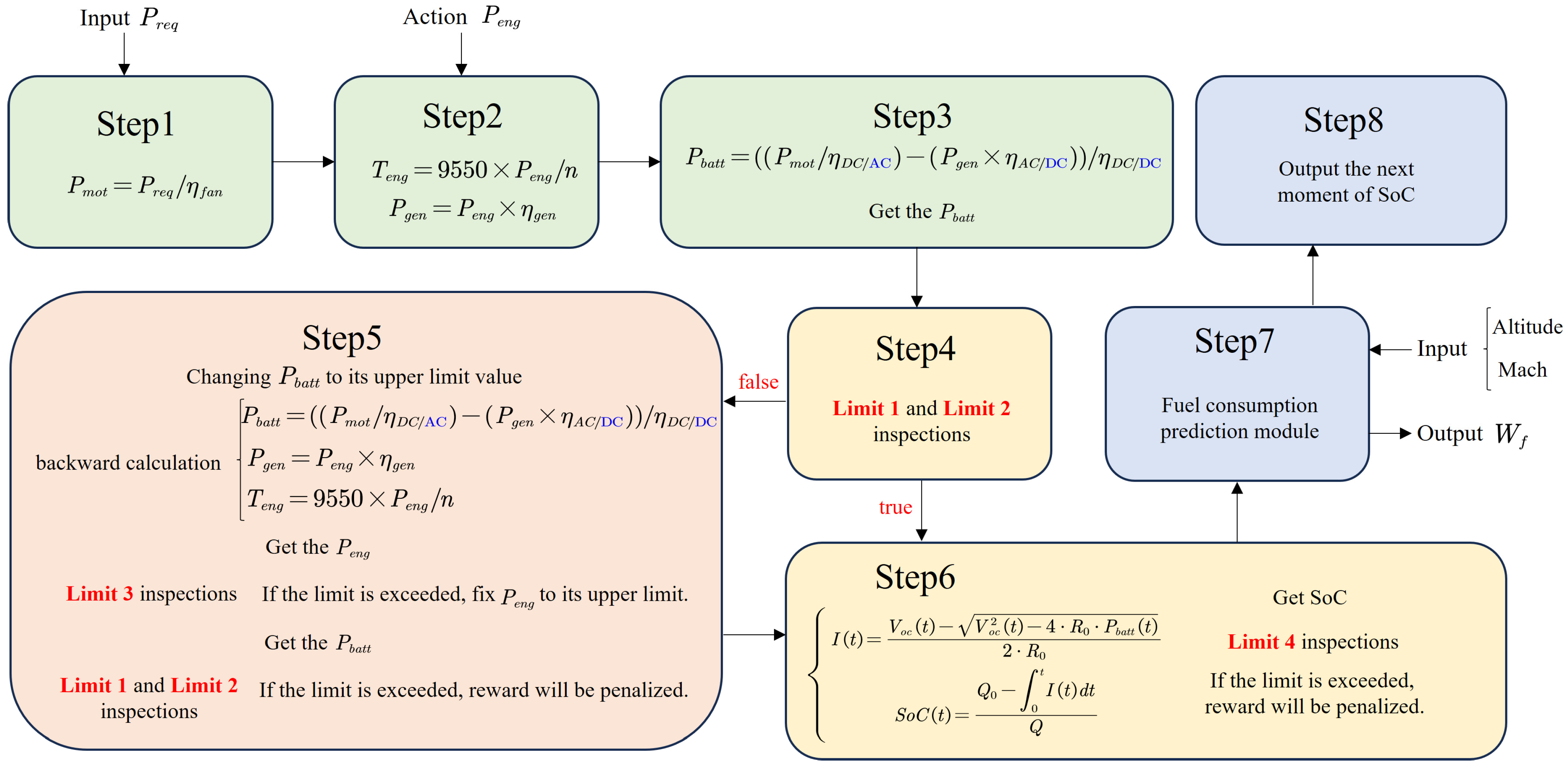
Compared to traditional multi-rotor unmanned aerial vehicles (UAVs) and fixedwing UAVs, electric vertical take-off and landing (eVTOL) [
1] aircraft exhibit flexible aerodynamic configurations and higher propulsion efficiency. These characteristics have showcased broad application prospects in fields such as low-altitude general aviation and logistics transportation, making eVTOL a key research focus in the global aerospace industry. However, due to the limitations of energy density in aviation batteries, eVTOL aircraft currently face challenges such as short flight duration and limited payload capacity, making it difficult to meet the requirements of high-load and long-duration missions. In contrast, hybrid power systems combine the advantages of electric propulsion with the maturity of traditional aeroengine. This not only enables distributed propulsion configurations but also effectively compensates for the endurance limitations of pure electric systems. As a result, turbo-electric hybrid propulsion system [
2] have emerged as an ideal propulsion solution for vertical take-off and landing aircraft in application scenarios such as regional logistics transportation and extended rescue missions in complex environments (e.g., mountainous or maritime areas). Internationally, NASA has developed a strategic roadmap to integrate hybrid power systems into the aviation sector by 2050 [
3]. General Electric [
4] has successfully tested megawatt-class hybrid propulsion systems, and other organizations such as Raytheon, Electra [
5], Safran, and VerdeGo have made significant progress in the development of hybrid propulsion systems. These technological advancements are laying the foundation for future air mobility solutions, with hybrid power systems expected to gradually achieve commercial application.
Energy management strategies (EMSs) are essential for optimizing the operation of turbo-electric hybrid propulsion systems. By employing advanced strategies to coordinate the use of aeroengine and battery power, an EMS ensures efficient energy use, minimizes fuel consumption, and reduces greenhouse gas emissions. Energy management strategies can generally be classified into three categories: (1) rule-based methods, which rely on predefined rules and heuristics; (2) optimization-based methods, which utilize mathematical models to find optimal solutions; (3) learning-based methods, which employ machine learning techniques to adaptively improve performance based on operational data. Rule-based energy management strategies are divided into deterministic and fuzzy rule approaches, which control the output power of hybrid power sources based on fixed, predefined rules without dynamically optimizing for specific objectives like efficiency or fuel economy. While simple and efficient, these strategies require human expertise and generally lack optimality [
6], especially in complex environments where they may exhibit poor stability, adaptability, and flexibility [
7,
8]. Consequently, they are often inadequate for real-time operations in such contexts. Optimization-based energy management strategies replace human intuition with computer algorithms, focusing on optimizing objectives like system efficiency and fuel economy. These strategies can be categorized into offline optimization (global optimization), which processes data and finds optimal solutions without time constraints, and online optimization, which adapts and responds in real-time to changing conditions. Dynamic programming (DP), a global optimization method, achieves optimal solutions under deterministic conditions but requires significant computational resources, making it an offline benchmark for energy management systems [
9]. In contrast, the Equivalent Consumption Minimization Strategy (ECMS) [
10] provides more practical, real-time optimization capabilities for control systems. ECMS has the advantage of obtaining an instantaneous optimal power allocation by equating the electric power consumption to the fuel consumption and has a low computational complexity. The disadvantages are that the global optimum cannot be achieved because only the current state is considered, the effect of the current control action on the future state of the system is neglected, and it can only be applied to a single optimization objective and cannot optimize multiple objectives at the same time. Traditional rule-based EMS systems suffer from poor optimality and adaptability to complex conditions, while optimization-based EMS systems face challenges due to high computational costs and limited real-time performance. Recently, learning-based EMS systems have emerged as viable solutions to these issues. Techniques such as convolutional neural networks (CNNs) [
11] and long short-term memory networks (LSTM) [
12] have shown promising results in EMS applications. In highly interactive real-time contexts, deep reinforcement learning (DRL) offers distinct advantages. Mnih et al. [
13] introduced the Deep Q Network (DQN), combining deep learning with Q learning to master Atari games directly from pixel inputs without manual feature engineering. Lillicrap et al. [
14] proposed the Deep Deterministic Policy Gradient (DDPG) algorithm, addressing continuous control problems using an actor–critic framework with deterministic policy gradients. Oh et al. [
15] developed a method integrating memory mechanisms and active perception in Minecraft to tackle complex tasks in partially observable environments. Schulman et al. [
16] introduced Trust Region Policy Optimization (TRPO), stabilizing policy updates via constrained optimization to improve training efficiency. Lastly, Kendall et al. [
17] demonstrated real-world end-to-end autonomous driving using deep reinforcement learning, achieving control with just 20 min of real-world training data. Zhang et al. [
18] looked at the development of energy management strategies in the field of hybrid vehicles, laying the foundation for the subsequent application of deep reinforcement learning on energy management strategies. Liu et al. [
19,
20] developed an EMS based on Q learning, which, compared to stochastic dynamic programming, showed notable improvements in computational efficiency, optimality, and adaptability. However, its reliance on discrete action and state spaces limits its applicability in more complex EMS scenarios that require continuous decision-making. Wu et al. [
21] extended this work by integrating Deep Q Learning (DQN) into EMSs, addressing the limitations of discrete actions and enhancing fuel economy and operational flexibility in real-world applications. Subsequently, Wu [
22] and Tan [
23] applied the Deep Deterministic Policy Gradient (DDPG) algorithm to EMS systems, using prioritized experience replay algorithms to approximate the effectiveness of dynamic programming, demonstrating superior performance in handling continuous actions and states.
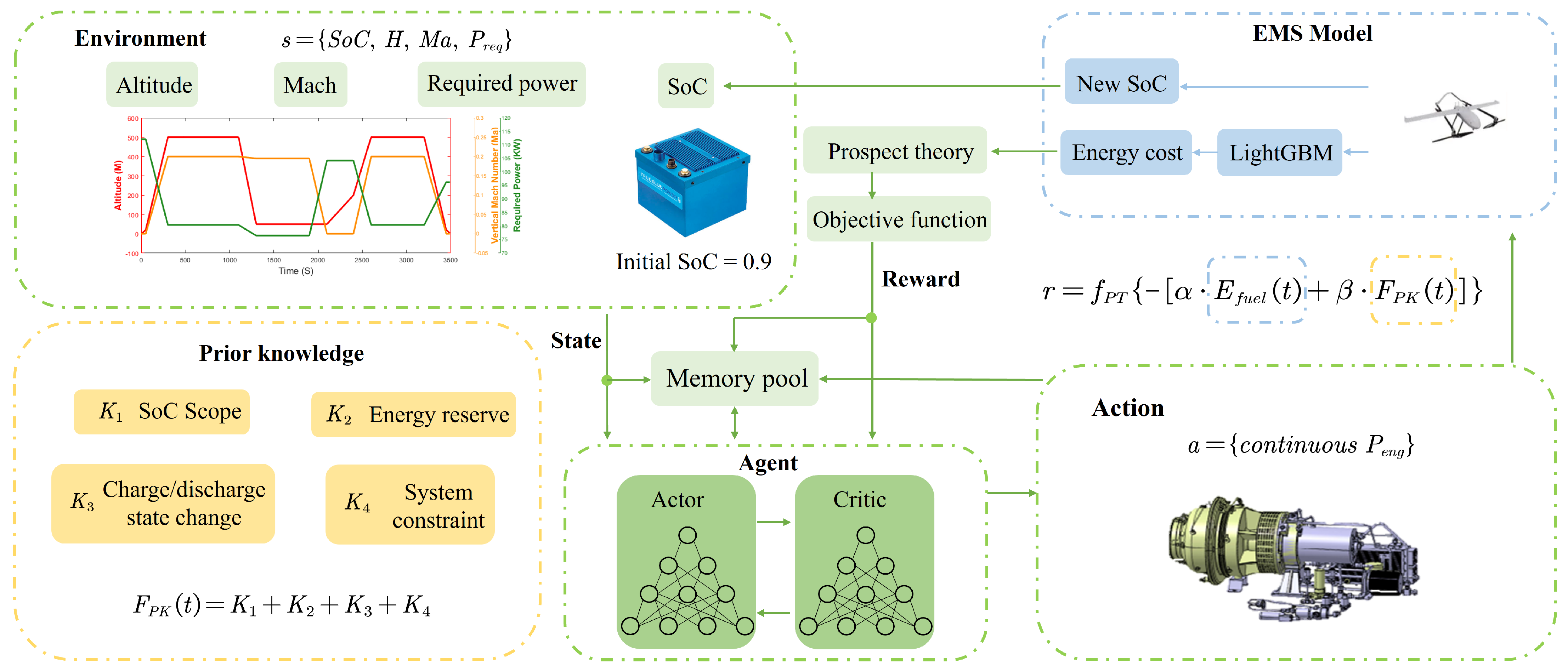
In the aviation field, including hybrid electric vertical take-off and landing (hVTOL), the intricate nature of aircraft power systems, with numerous operational constraints and safety requirements, has presented significant challenges for the widespread adoption of DRL in EMS systems. Conventional reinforcement learning methods often struggle to identify satisfactory or even reasonable strategies during the learning process due to the complexity of these environments. Reinforcement learning (RL) relies heavily on trial and error to maximize cumulative rewards through a policy [
24]. However, RL has limitations, particularly its dependence on large volumes of real samples during training, which can lead to inefficient sampling and local optima traps. Incorporating prior human knowledge into the RL training process can guide the exploration phase, imitating expert decision-making behaviors and effectively narrowing the search space for optimal solutions. In hVTOL EMS systems, prior knowledge, such as guidelines for battery charging and discharging power, recommendations for remaining battery energy, and advice on battery charge–discharge cycles, can significantly enhance sampling efficiency and reduce the risk of suboptimal solutions.
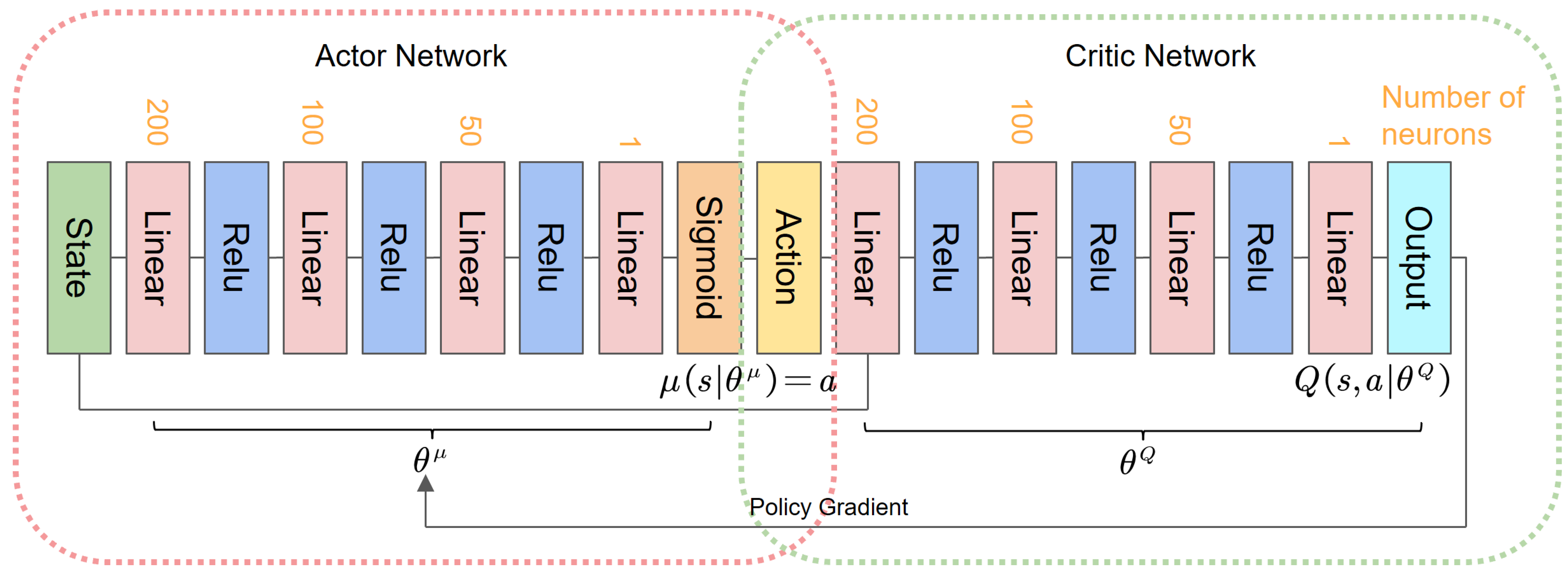
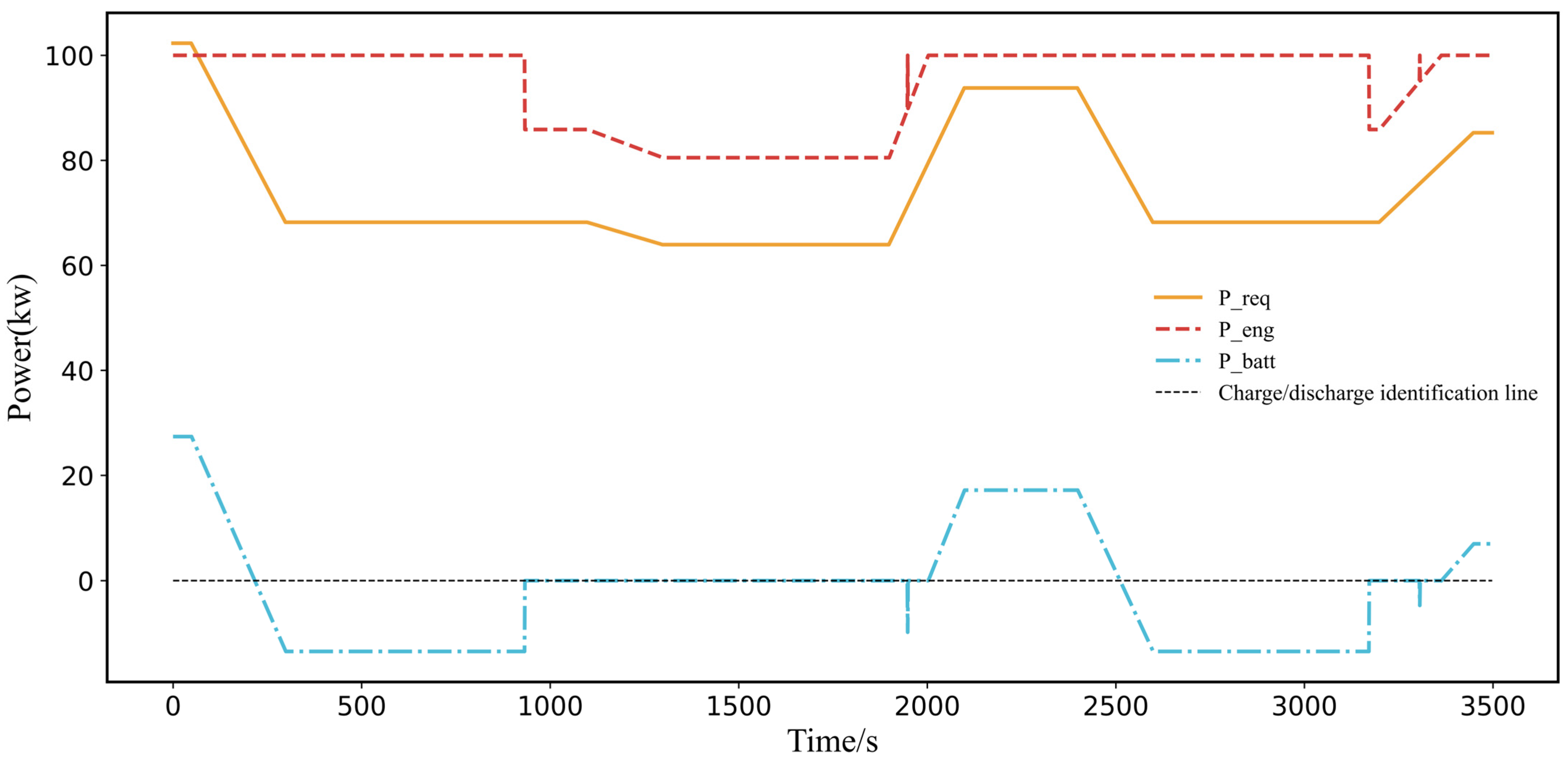
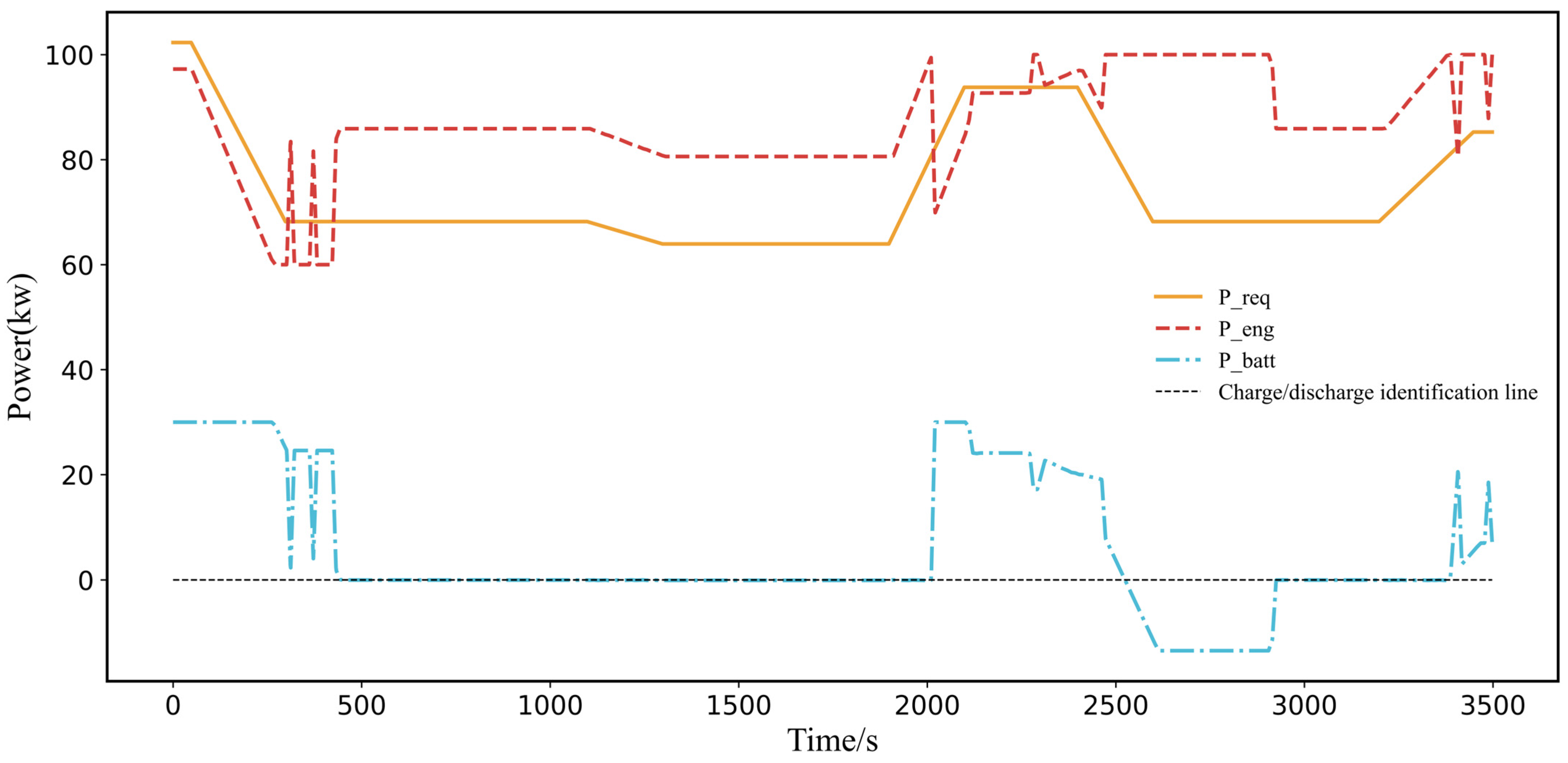
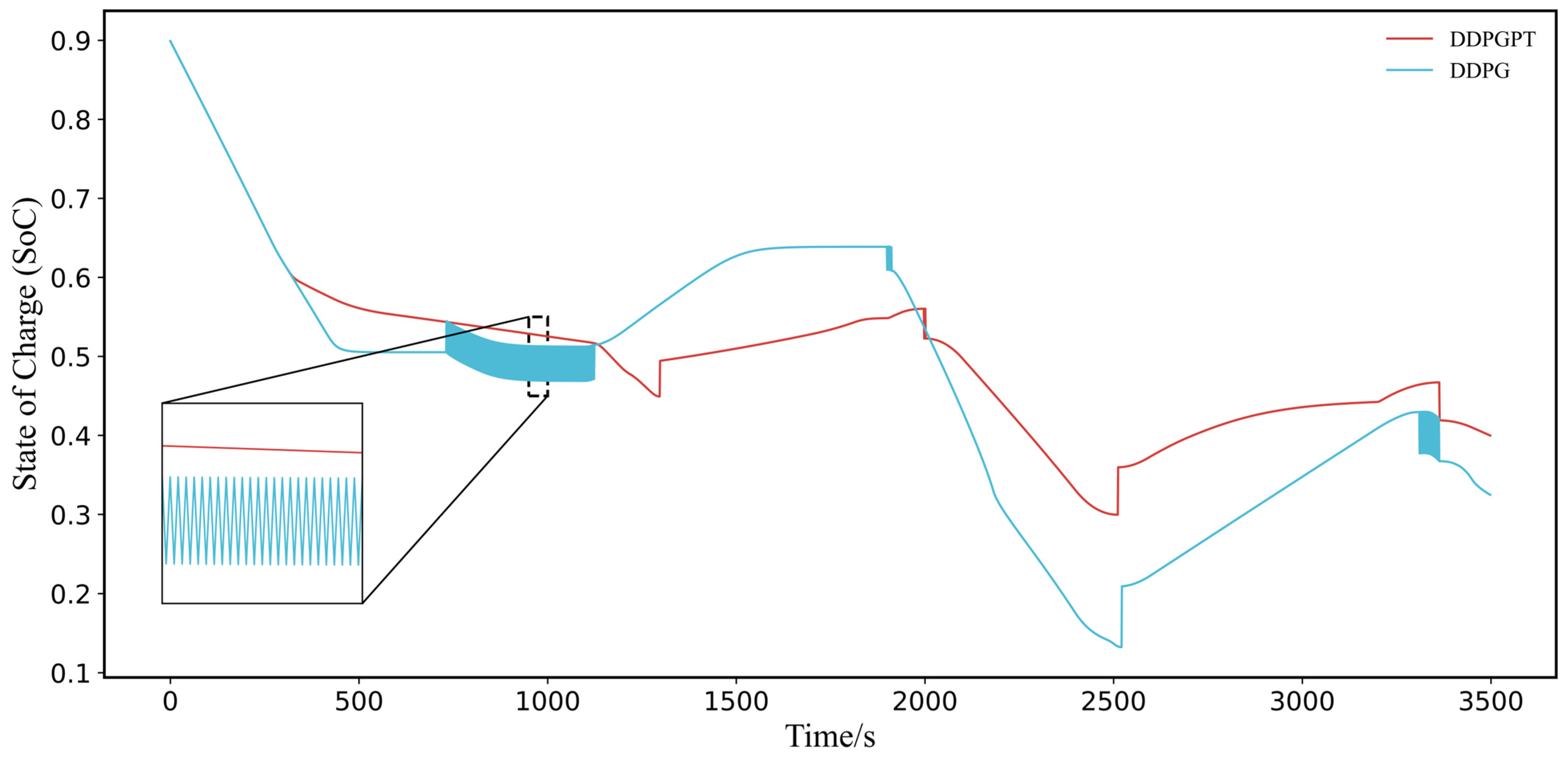
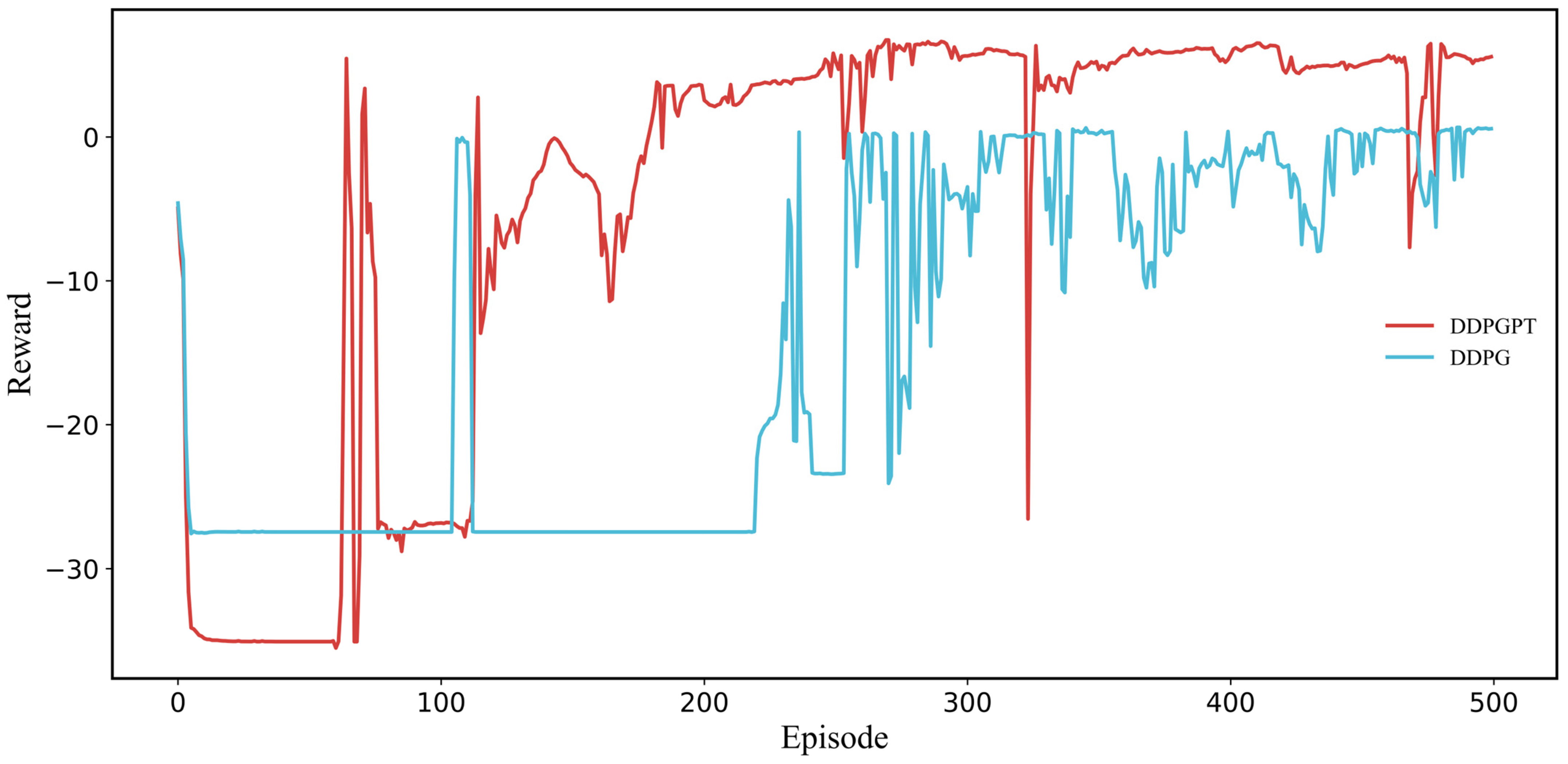
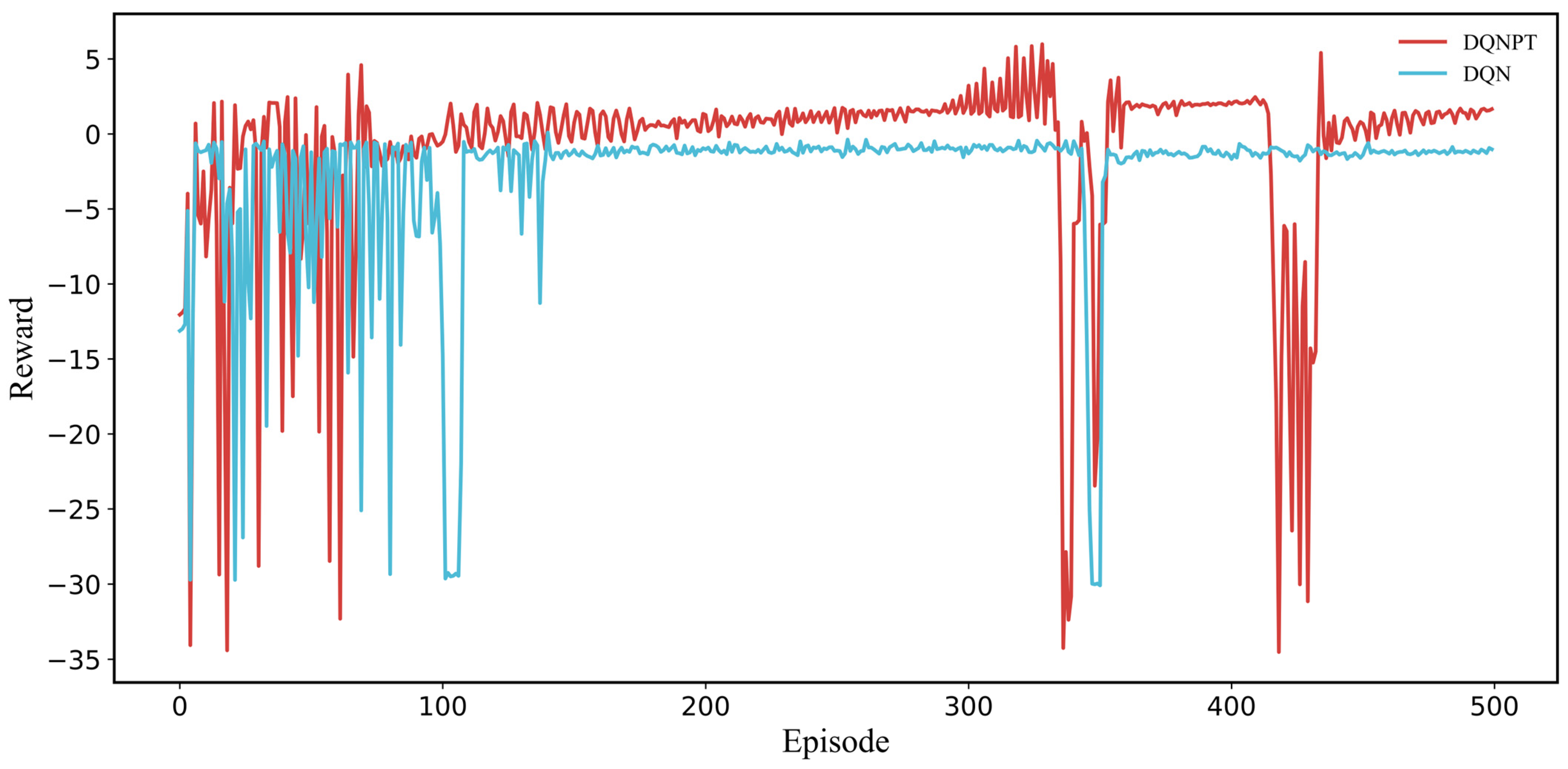
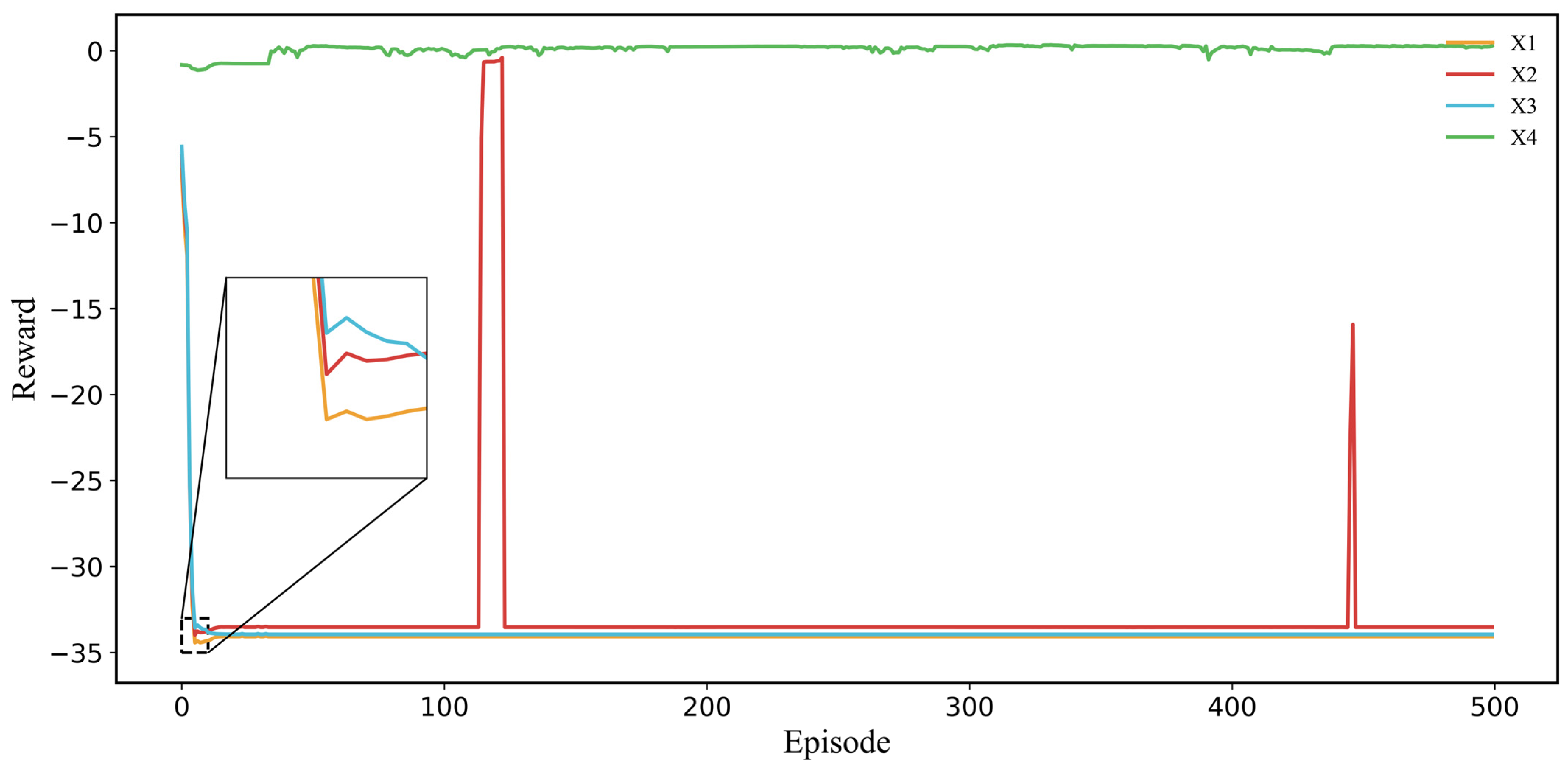
Building on these challenges and the potential of leveraging prior knowledge, this paper introduces a novel Prior Knowledge-Guided Deep Reinforcement Learning (PKGDRL) framework designed for energy management systems. The PKGDRL framework aims to enhance learning efficiency and fuel economy by integrating domain-specific insights with advanced DRL techniques.