Temperature Field and Thermal Stress Analysis of a Composite Wing Electric Heating System with Delamination Damage
Abstract
1. Introduction
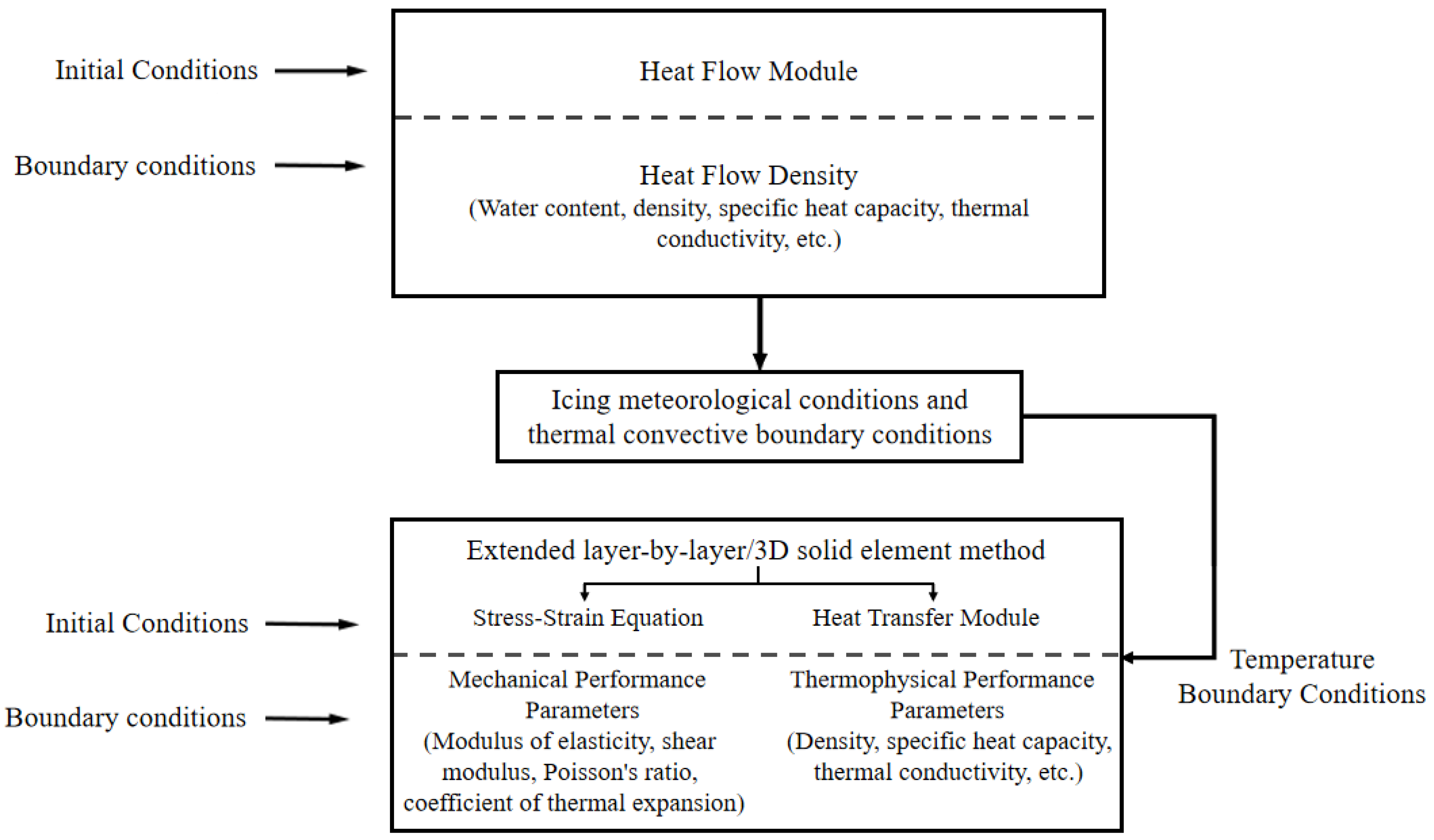
2. Composite Wing Leading Edge Modelling and Anti-Icing Environment Settings
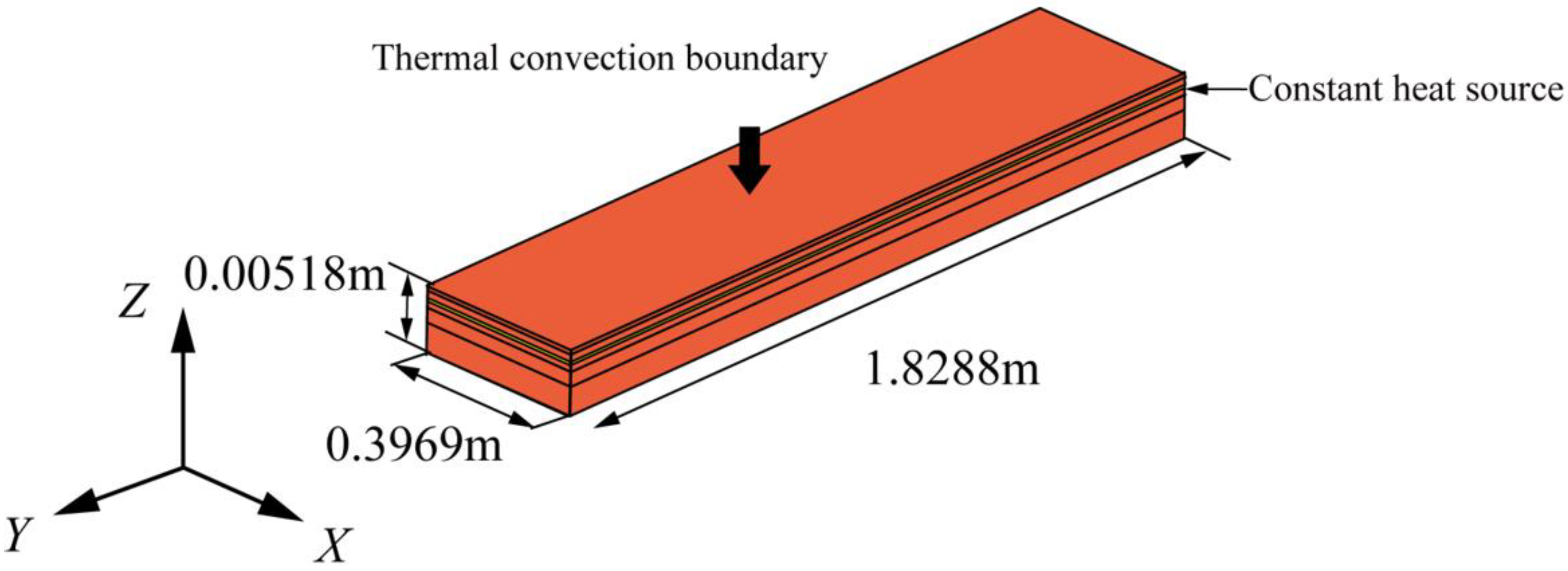
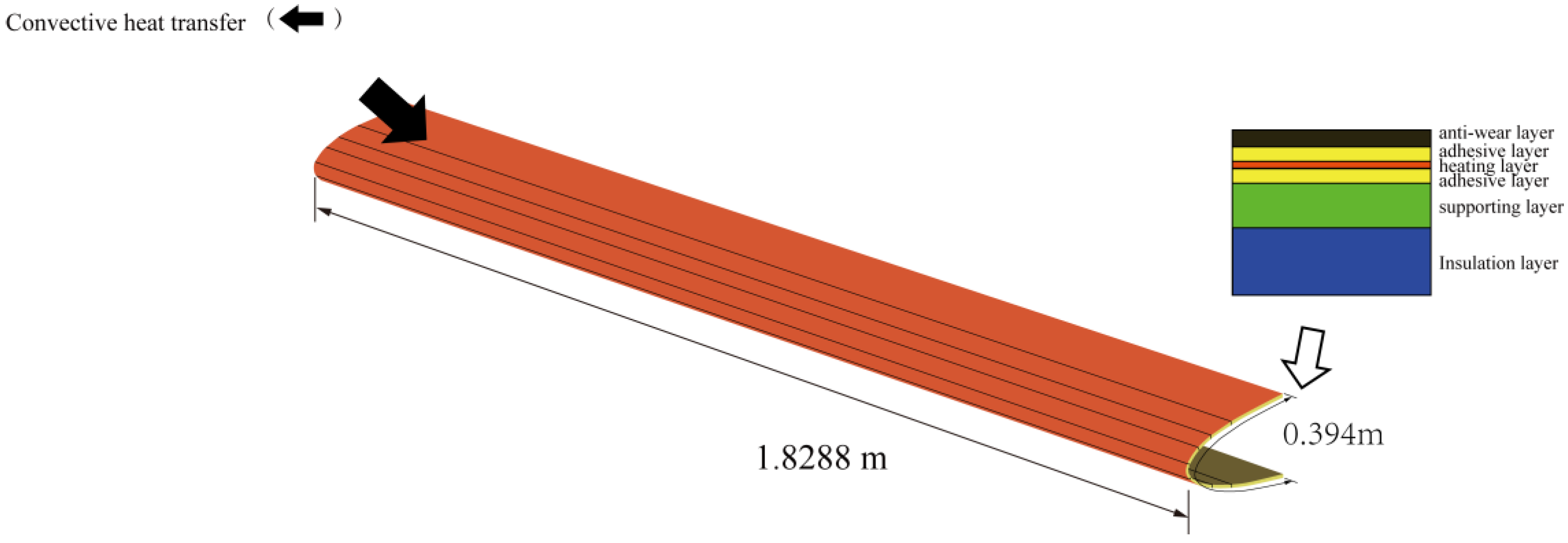
2.1. Composite Wing Leading Edge Modelling
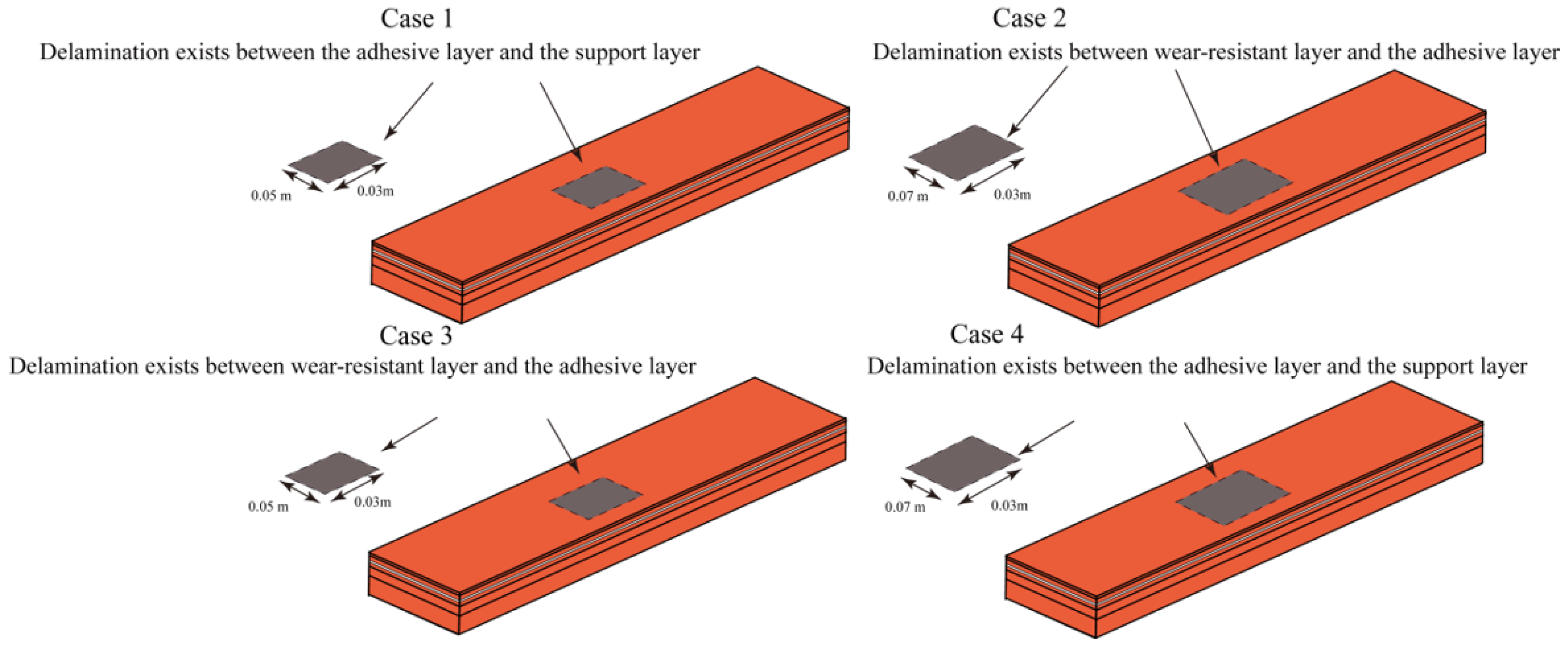
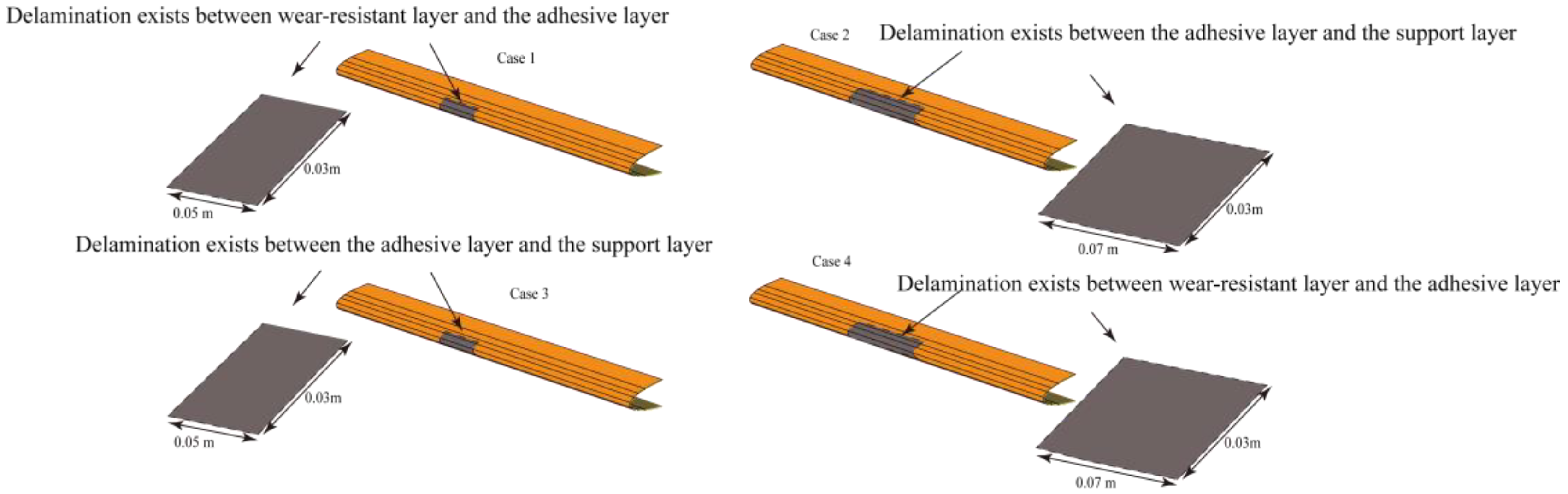
2.2. Composite Material Anti-Icing Environment and Delamination Damage Setting
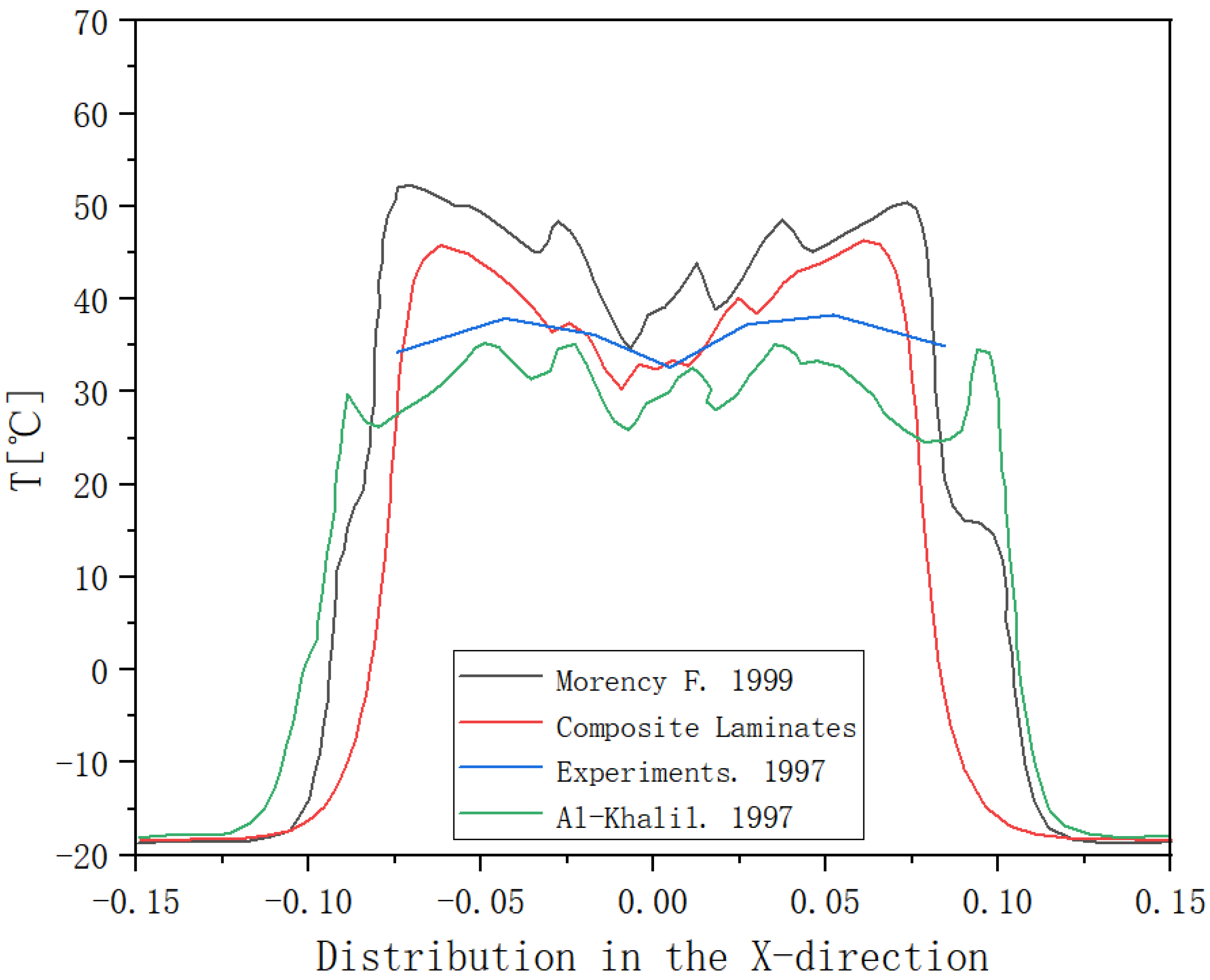
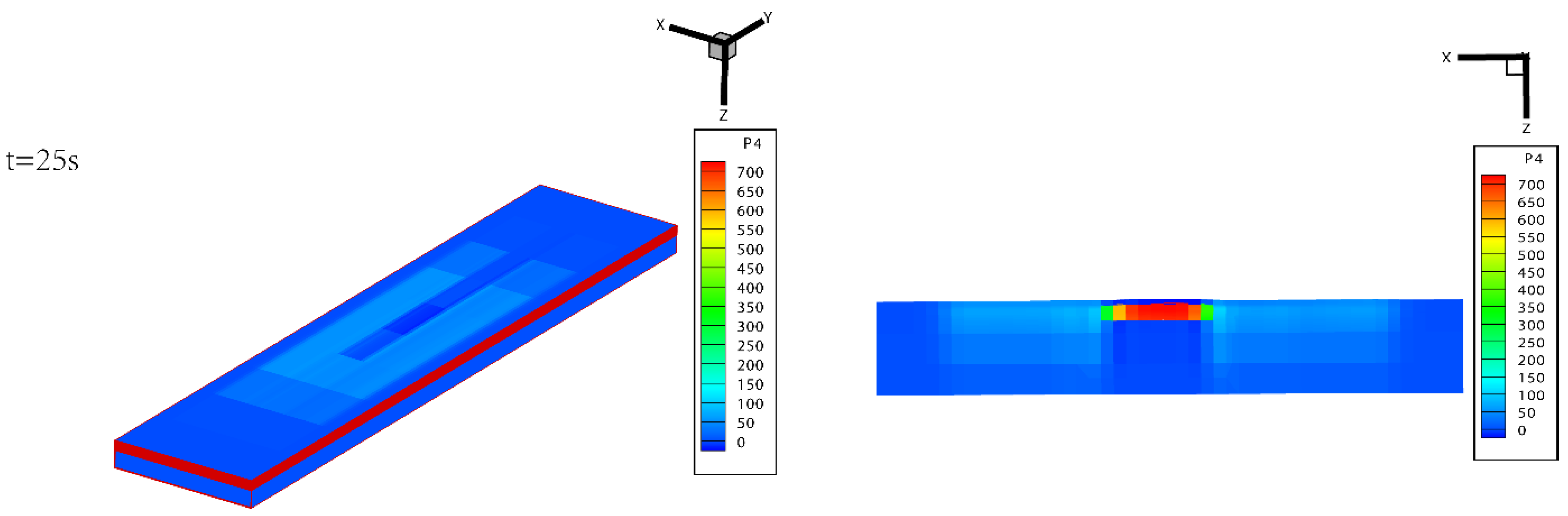
2.3. Validation of Calculation Methods
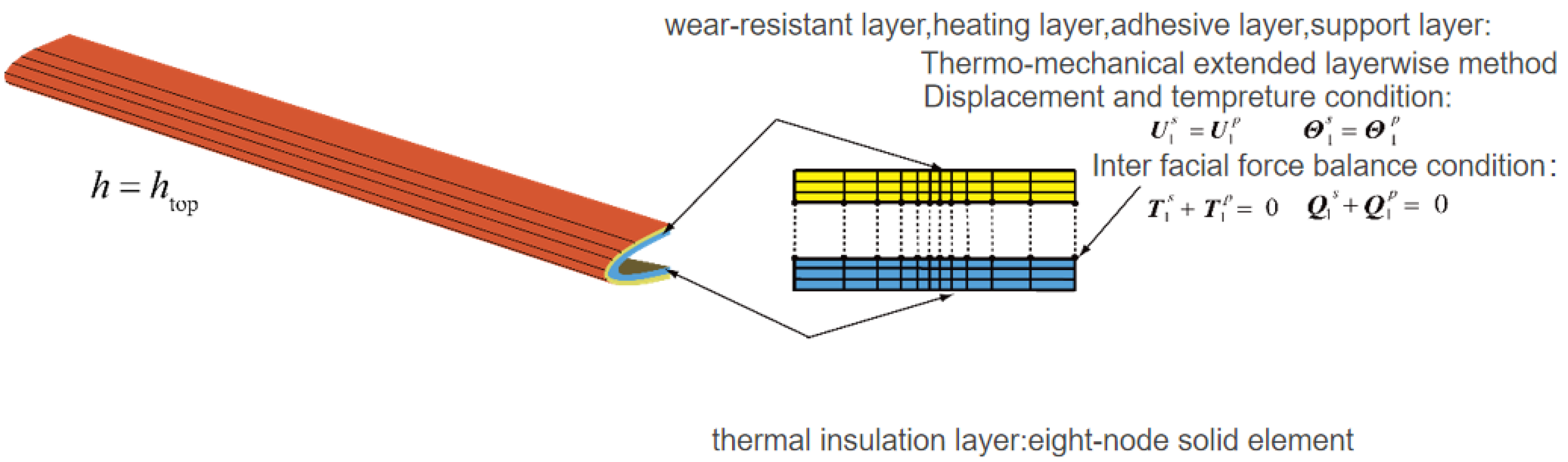
3. Finite Element Equations for Thermally Extended Layer-by-Layer/3D Solid Elements
3.1. Heat Mixed Variational Theorem
3.2. Finite Element Equation for Thermally Extended Layer-by-Layer/3D Solid Elements
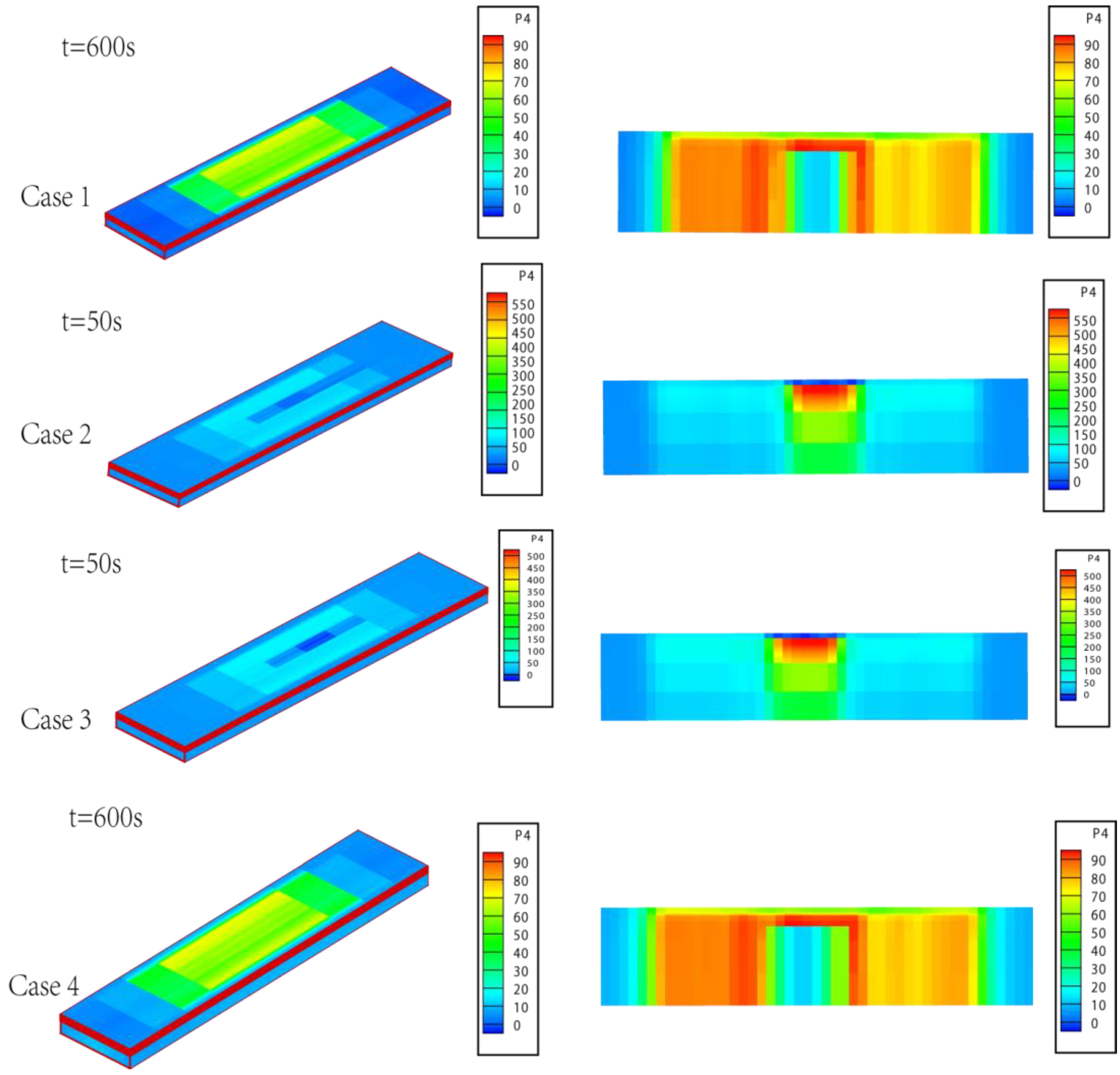
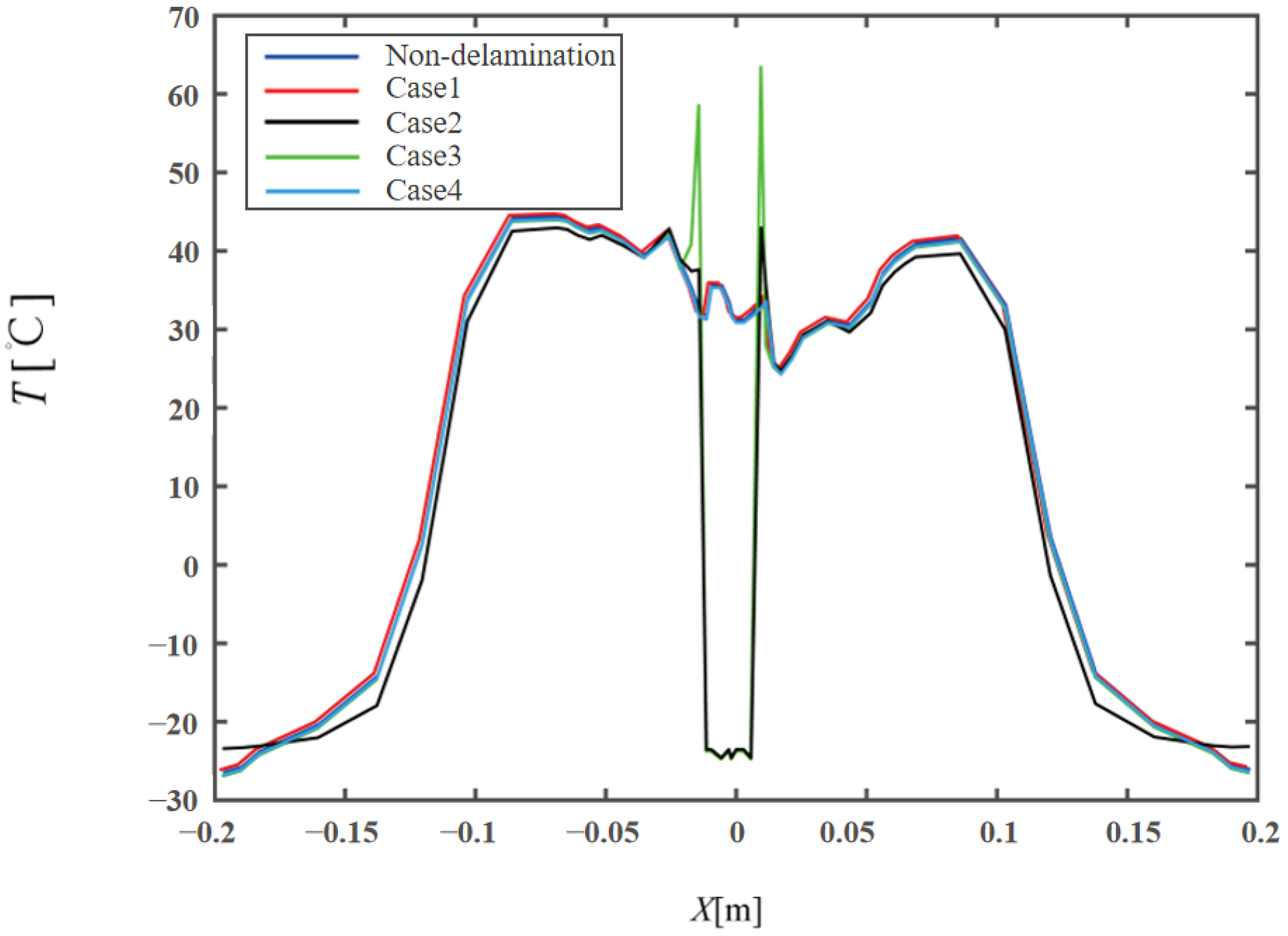
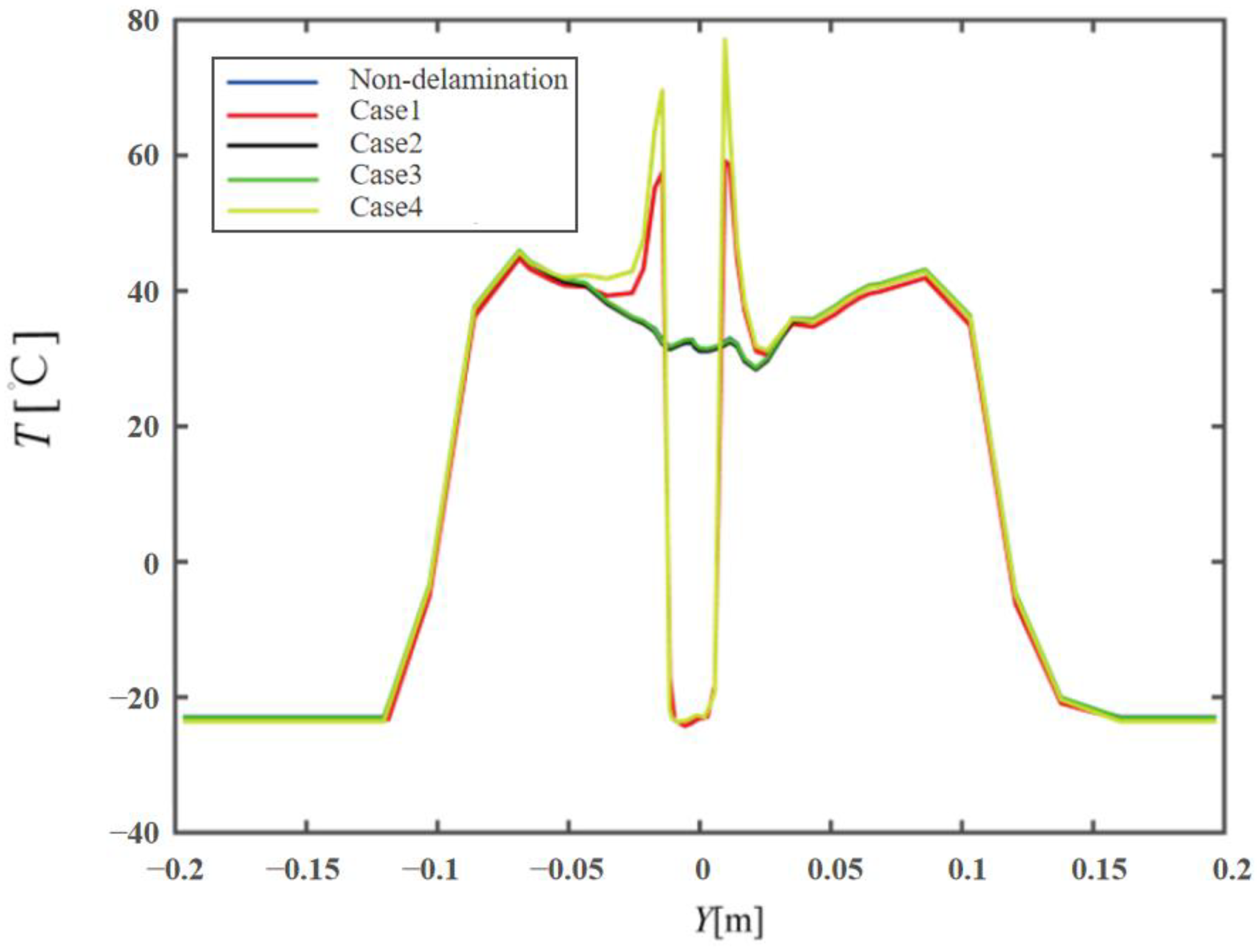
4. Temperature Distribution of Composites with Multiple Delamination Damage Events
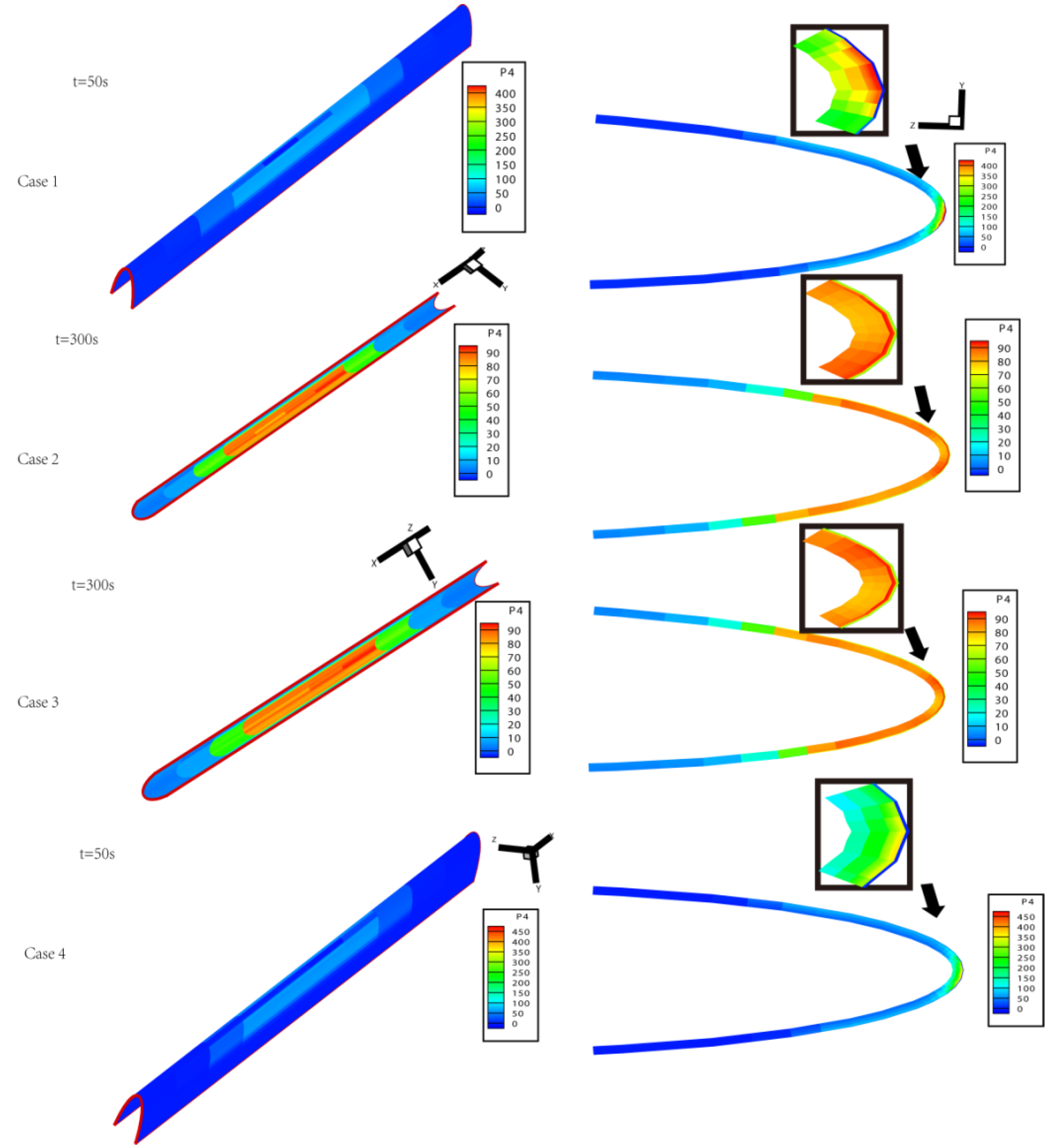
5. Surface Temperature and Thermal Stress Distribution of Aerofoils with Pre-Set Damage
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Lin, G.; Bu, X.; Shen, X. Aircraft Icing and Anti-Icing Techniques; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2016; pp. 1–46. [Google Scholar]
- Kong, F. Analysis of the impact of icing on aircraft flight safety and protection techniques. J. Artic. 2018, 69–70. [Google Scholar]
- Cao, S.; Wang, J. The development trend of low-speed Impact delamination damage of composite laminates. Metall. Mater. 2021, 41, 139–140. [Google Scholar]
- Cheng, X. Modelling and Detection of Delamination in Plate Structures. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2015. [Google Scholar]
- Johnson, A.; Holzapfel, M. Influence of delamination on impact damage in composite structures. Compos. Sci. Technol. 2004, 66, 807–815. [Google Scholar] [CrossRef]
- Li, S.; Reid, S.; Zou, Z. Modelling damage of multiple delaminations and transverse matrix cracking in laminated composites due to low velocity lateral impact. Compos. Sci. Technol. 2004, 66, 827–836. [Google Scholar] [CrossRef]
- Huo, L.; Kassapoglou, C.; Alderliesten, R.C. Influence of neighbouring damage on delamination growth in multiple indented composites. Mater. Des. 2023, 227, 111723. [Google Scholar] [CrossRef]
- Mao, Y. Analysis for Temperature Field and Thermal Stress of Composite Skin of Wings during Electrothermal Anti-Icing Process. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2018. [Google Scholar]
- Polla, A.; Frulla, G.; Cestino, E. Coupled Thermo-Mechanical Numerical Modeling of CFRP Panel under High-Velocity Impact. Aerospace 2023, 10, 367. [Google Scholar] [CrossRef]
- Tay, E.T. Analysis of Delamination Growth in Laminated Composites with Consideration for Residual Thermal Stress Effects. J. Compos. Mater. 2002, 36, 1299–1320. [Google Scholar] [CrossRef]
- Niu, Y.; Lu, C.; Yao, J. Effect of electro-thermal coupling on the residual strength of CFRP laminates containing prepositioning damage. Plast. Ind. 2023, 51, 108ߝ113+162. [Google Scholar]
- Reid, T.; Baruzzi, G.S.; Habashi, W.G. FENSAP-ICE: Unsteady conjugate heat transfer simulation of electrothermal de-icing. J. Aircr. 2012, 49, 1101–1109. [Google Scholar] [CrossRef]
- Zhengzhi, W.; Huanyu, Z.; Senyun, L. Numerical Simulation of Aircraft Icing under Local Thermal Protection State. Aerospace 2022, 9, 84. [Google Scholar] [CrossRef]
- Morita, K.; Kimura, S.; Sakaue, H. Hybrid System Combining Ice-Phobic Coating and Electrothermal Heating for Wing Ice Protection. Aerospace 2020, 7, 102. [Google Scholar] [CrossRef]
- Shen, X.; Liu, X.; Lin, G. Effects of anisotropic composite skin on electrothermal anti-icing system. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 5403–5413. [Google Scholar] [CrossRef]
- Lou, Y.; Bu, X.; Shen, X. Simulation of and experimental research on rivulet model onairfoil surface. Aerospace 2022, 9, 570. [Google Scholar] [CrossRef]
- Al-Khalil, K.; Horvath, C.; Miller, D.; Wright, W. Validation of NASA Thermal Ice Protection Computer Codes. III-The Validation of ANTICE; AIAA: Reno, NV, USA, 1997. [Google Scholar]
- Li, D.H.; Liu, Y.; Zhang, X. An extended layerwise method for composite laminated beams with multiple delaminations and matrix cracks. Int. J. Numer. Methods Eng. 2015, 101, 407–434. [Google Scholar] [CrossRef]
- Li, D.; Zhang, F.; Xu, J. Incompatible extended layerwise method for laminated composite shells. Int. J. Mech. Sci. 2016, 119, 243–252. [Google Scholar] [CrossRef]
- Li, D.; Zhang, X.; Sze, K.; Liu, Y. Extended layerwise method for laminated composite plates with multiple delaminations and transverse cracks. Comput. Mech. 2016, 58, 657–679. [Google Scholar] [CrossRef]
- Li, D.; Zhang, F. Full extended layerwise method for the simulation of laminated composite plates and shells. Comput. Struct. 2017, 187, 101–113. [Google Scholar] [CrossRef]
- Li, D. Delamination and transverse crack growth prediction for laminated composite platesand shells. Comput. Struct. 2016, 177, 39–55. [Google Scholar] [CrossRef]
- Li, D.; Fish, J. Thermomechanical extended layerwise method for laminated composite plates with multiple delaminations and transverse cracks. Compos. Struct. 2018, 185, 665–683. [Google Scholar] [CrossRef]
- Li, D.; Shan, W.; Zhang, F. Steady-state thermomechanical analysis of composite laminated plate with damage based on extended layerwise method. Arch. Appl. Mech. 2020, 90, 415–435. [Google Scholar] [CrossRef]
- Li, D.; Ma, S. Dynamic thermomechanical analysis on composite sandwich plates with damage. Contin. Mech. Thermodyn. 2021, 33, 2167–2201. [Google Scholar] [CrossRef]
- Morency, F.; Tezok, F.; Paraschivoiu, I. Anti-icing system simulation using CANICE. J. Aircr. 1999, 36, 999–1006. [Google Scholar] [CrossRef]
- Benjeddou, A.; Andrianarison, O. A heat mixed variational theorem for thermoelastic multilayered composites. Comput. Struct. 2006, 84, 1247–1255. [Google Scholar] [CrossRef]
- Li, D.; Ma, S. Study on Thermomechanical Extended-layewise/Solid-elements Method for Thermomechanical Problems of Thermal Barrier Coatings Structure with Damage. Aeronaut. Sci. Technol. 2021, 32, 12–24. [Google Scholar]
- Yang, Y. China’s aviation composites industry development outlook. Sci. Technol. Inf. 2022, 20, 161–163. [Google Scholar]
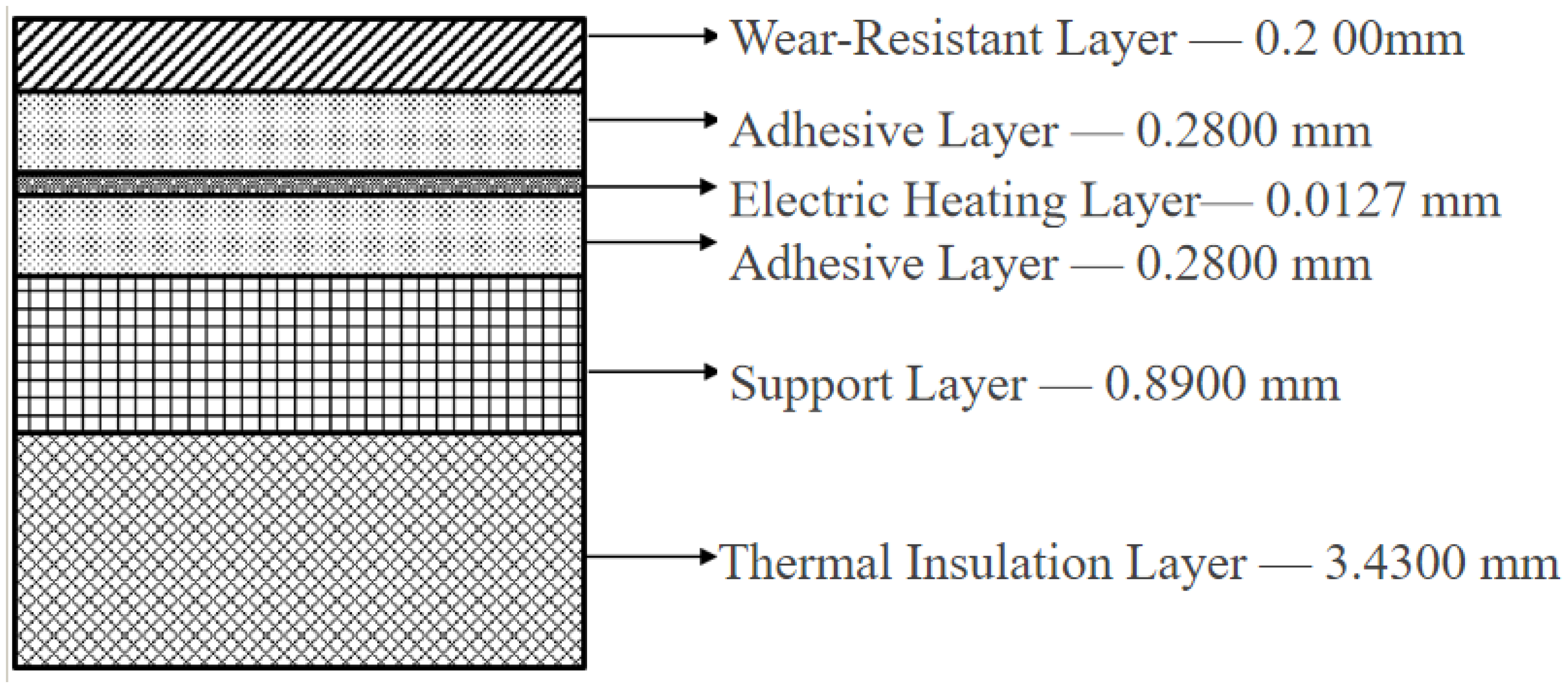




| λx W/(m·K) | λy W/(m·K) | λz W/(m·K) | ρ kg/m3 | Cp J/(kg·K) | |
|---|---|---|---|---|---|
| wear-resistant layer | 16.265 | 16.265 | 16.265 | 8026 | 502.4 |
| adhesive layer | 0.256 | 0.256 | 0.256 | 1384 | 1256 |
| electric heating layer | 41 | 41 | 41 | 8907 | 385.2 |
| support layer | 0.294 | 4.4 | 0.294 | 1796.5 | 1570 |
| thermal insulation layer | 0.121 | 0.121 | 0.121 | 648.8 | 1130.4 |
| Heating Unit | F | D | B | A | C | E | G |
|---|---|---|---|---|---|---|---|
| X-direction width (m) | 0.0381 | 0.0254 | 0.0254 | 0.01905 | 0.0254 | 0.0254 | 0.0381 |
| Electric heating power per unit volume (109 ) | 1.587 | 1.709 | 2.563 | 3.417 | 2.074 | 1.465 | 1.465 |
| Heating Unit | F | D | B | A | C | E | G |
| Elastic Modulus (GPa) | Liner Coefficient of Thermal Expansion (α × 10−6/°C) | Poisson’s Ratio | |
|---|---|---|---|
| wear-resistant layer | 193 | 16.5 | 0.29 |
| adhesive layer | 0.0078 | 200 | 0.49 |
| electric heating layer | 206 | 13.3 | 0.28 |
| thermal insulation layer | 3 | 40 | 0.35 |
| Elastic Modulus (GPa) | Liner Coefficient of Thermal Expansion (α × 10−6/°C) | Shear Modulus (GPa) | Poisson’s Ratio | ||
|---|---|---|---|---|---|
| X | 10 | 17.8 | XY | 5 | 0.3 |
| Y | 45 | 4.9 | YZ | 5 | 0.3 |
| Z | 10 | 17.8 | XZ | 3.8 | 0.4 |
| Case | 67A |
|---|---|
| V∞, m/s | 89.4 |
| T∞, ℃ | −21.6 |
| LWC, g/m3 | 0.55 |
| MVD, μm | 20 |
| Angle of attack, α | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Wang, Z.; Sun, X.; Chu, H.; Yao, J.; Niu, Y. Temperature Field and Thermal Stress Analysis of a Composite Wing Electric Heating System with Delamination Damage. Aerospace 2025, 12, 346. https://doi.org/10.3390/aerospace12040346
Hu X, Wang Z, Sun X, Chu H, Yao J, Niu Y. Temperature Field and Thermal Stress Analysis of a Composite Wing Electric Heating System with Delamination Damage. Aerospace. 2025; 12(4):346. https://doi.org/10.3390/aerospace12040346
Chicago/Turabian StyleHu, Xuelan, Ziyi Wang, Xiaoqing Sun, Hengyu Chu, Jiawei Yao, and Yifan Niu. 2025. "Temperature Field and Thermal Stress Analysis of a Composite Wing Electric Heating System with Delamination Damage" Aerospace 12, no. 4: 346. https://doi.org/10.3390/aerospace12040346
APA StyleHu, X., Wang, Z., Sun, X., Chu, H., Yao, J., & Niu, Y. (2025). Temperature Field and Thermal Stress Analysis of a Composite Wing Electric Heating System with Delamination Damage. Aerospace, 12(4), 346. https://doi.org/10.3390/aerospace12040346





