Abstract
An aeroengine faces multi-source uncertainty consisting of aeroengine epistemic uncertainty and the control system stochastic uncertainty during operation. This paper investigates actuator fault estimation under multi-source uncertainty to enhance the fault diagnosis capability of aero-engine control systems in complex environments. With the polynomial chaos expansion-based discrete stochastic model quantification, the optimal filter under multi-source uncertainty, the Hyperelliptic Kalman Filter, is proposed. Meanwhile, by treating actuator fault as unknown input, the Two-stage Hyperelliptic Kalman Filter (TSHeKF) is also proposed to achieve optimal fault estimation under multi-source uncertainty. However, considering that the biases of the model are often fixed for the individual, the TSHeKF-based fault estimation is robust and leads to inevitable conservativeness. By adding the additional estimation of the unknown deviation in state function caused by probabilistic system parameters, the hybrid fault observer (HFO) is proposed based on the TSHeKF and realizes conservativeness-reduced estimation for actuator fault under multi-source uncertainty. Numerical simulations show the effectiveness and optimality of the proposed HFO in state estimation, output prediction, and fault estimation for both single and multi-fault modes, when considering multi-source uncertainty. Furthermore, Monte Carlo experiments have demonstrated that the HFO-based optimal fault estimation is less conservative and more accurate than the Two-stage Kalman Filter and TSHeKF, providing better safety and more reliable aeroengine operation assurance.
1. Introduction
With the continuous development of aerospace technology, pursuing better performance also requires higher robustness and reliability of aeroengines [1]. In addition, the safety of aeroengine operation can be significantly assured by the contribution of fault diagnosis systems in detecting, isolating, and estimating faults [2,3]. Meanwhile, considering that uncertainty is an essential feature of complex systems [4], it can be classified as stochastic and epistemic uncertainty [5]. According to [6], the control system stochastic uncertainty and aeroengine epistemic uncertainty form the multi-source uncertainty affecting aeroengine operation. However, the traditional design process of the fault diagnosis system is based on a deterministic model and ignores the widespread uncertainty effects [2]. With the development of UQ, fault diagnosis of aeroengine control systems under multi-source uncertainty is gradually becoming a research hotspot, and fruitful results have been achieved in sensor fault diagnosis [6] and estimation [7]. But more research on actuator fault estimation is needed. Therefore, to improve the performance and effectiveness of the diagnostic system to ensure the safety of aeroengine operation, it is of great importance to consider multi-source uncertainty while designing the actuator fault estimation system.
Due to the higher interpretability and reliability of model-based methods, fruitful research results of actuator fault estimation are achieved by designing appropriate filters or observers [8,9]. The LKF is the most classical state-estimation method for linear dynamic systems, and Simon et al. designed a Kalman filter bank for the fault diagnosis of the aeroengine control system in 2003 [10,11]. It is widely known that the health management of aeroengines is mainly achieved by treating the unknown health parameters input as state and estimating them with the corresponding ASKF [12,13]. The actuator fault can also be treated as unknown input and is estimated in the same way as the health parameters. However, as the number of states increases, the computational effort of the ASKF increases geometrically [14]. To reduce computation ford while guaranteeing state estimation accuracy, TSKF, composed of two sub-filters, is proposed by introducing U-V transformations [14]. By extending the sub-filter of the TSKF from LKF to the extended Kalman filter [15] or unscented Kalman filter [16], the enhanced TSKF can realize more accurate fault estimation in a more extensive range. However, the above methods need to consider uncertainties sufficiently, and more advanced fault estimation methods are required for more complex environments [17,18]. Under non-Gaussian noise conditions, Lu et al. combined the particle swarm algorithm with LKF to propose the Kalman particle filter for state estimation and used it for aeroengine health management [19]. With the development of UQ, Combastel first proposed the ZKF and achieved optimal estimation of the state motion boundary [20]. And in 2021, Zhang et al. used ZKF for fault interval estimation [21]. However, the ZKF-based estimation is an interval estimation method and cannot characterize the distribution of states. PCE, the most popular way for UQ today, can adequately characterize the statistical properties of the state [22] and is increasingly used by scholars for state estimation [23,24], fault diagnosis [6] and performance monitoring [25].
In summary, research on fault estimation of aeroengine actuators under multi-source uncertainty needs to be revised, especially considering both stochastic processes and systems. On the foundation of PCE-based UQ of the discrete stochastic model, HeKF is proposed in this paper and realizes optimal filtering under multi-source uncertainty. Further, the TSHeKF is proposed and achieves optimal actuator fault estimation under multi-source uncertainty. Moreover, by adding estimation of the unknown state deviation, the HFO is established on the basis of the TSHeKF; it provides fault estimation with better stability and reliability and is less conservative.
This paper is organized as follows. The mathematical description of aeroengine under multi-source uncertainty is presented in Section 2. PCE-based discrete stochastic model quantification and the further optimal filtering under multi-source uncertainty are described in Section 3. The TSHeKF is proposed in Section 4, and the HFO is designed and realized conservativeness-reduced fault estimation. Numerical and MC simulations are presented in Section 5. Some brief conclusions are shown in Section 6.
Notation: In this article, represents the set of real numbers, and and denote real vectors and real matrices of appropriate dimensions shown in superscript, respectively. and represent the null matrix and identity square matrix, respectively; dimensions are also shown in the corresponding superscript. The bounded basic function set is represented by , and represents the space. For a given real vector , its square is written as and is defined as follows. Using to represent the sum of each element, for a given matrix , has the following expression.
2. Mathematical Description of the Problem
From [6], the multi-source uncertainty faced by aeroengines consists of the stochastic uncertainty of control system and the epistemic uncertainty of aeroengine. Based on uncertainty modeling of one type or a batch of aeroengines [26], the linear dynamical system considers the actuator fault with independent probabilistic parameters, as shown in Equation (2):
for with state functions ; similarly, input functions and output function . , and are continuous independent disturbance functions, which represent system noise, measurement noise and disturbance of actuator, respectively. is the expectation of and is the deterministic function which characterize the intensity of actuator stochastic uncertainty. , , , and denote the control matrices of appropriate dimensions with probabilistic system parameters which satisfy the controllability and the observability. is the additive actuator fault vector; and are fault-drive matrices with constant parameters. and are constant drive matrices; especially when the disturbance of each state or output is independent, and become diagonal matrices. Use to represent , , and , which is a continuous zero-mean random process with independent increments. According to [27], can only be expressed as , where is the Brownian motion. Using as the sampling time, the linear discrete stochastic dynamical system with actuator fault is shown in Equation (3):
where ; similarly, and obey the mutually independent multi-source Gaussian distribution. is used to substitute ; the superscript represents the discretization of the system matrix, which is obtained by Equation (4), where is the expansion order.
Temporarily ignoring the parameter uncertainty of the system matrix in Equation (3), the actuator failure can be optimally estimated based on either the ASKF [13] or TSKF [15] by treating as an augmented state. Moreover, the LKF, which is the basis for the ASKF and TSKF, needs to be replaced by optimal filtering considering multi-source uncertainty. However, since the above model is for a type or a batch of aeroengines rather than for a specific engine, the fault estimation based on Equation (3) is also optimal for a range of aeroengines, and robust for an individual one. In order to improve the accuracy of fault estimation for an individual aeroengine, the adaptiveness of the fault estimation needs to be enhanced. The linear discrete stochastic system for one specific aeroengine is shown in Equation (5):
where the overscore indicates the expectation of the stochastic matrix below, and represents the differences of the following control matrix between the aimed aeroengine and the expectation of the corresponding type or batch of aeroengines, which can also be seen as the uncertainty of the discrete model. It is obvious that both the state function and output function are affected. In order to improve the adaptiveness of the state estimation, the effect of model uncertainty on the state and output needs to be quantified. and are used to represent the bias of state and output caused by model uncertainty, respectively. By treating as unknown input, the effect of model uncertainty on the state can be estimated by the TSKF optimally. Moreover, since is additive to the output and does not affect the state, it is impossible to estimate by considering it as the augmented state. Considering that the optimal output estimation of an individual aeroengine is unachievable, the optimal output estimation for a range of aeroengines is the best available option. Therefore, the conservativeness-reduced actuator fault estimation system for individual aeroengine is designed optimally based on Equation (6).
To sum up, when considering multi-source uncertainty, TSKF, as the classical fault-estimation method when treating unknown inputs, is no longer feasible. TSKF, therefore, needs to be adapted from the optimal filtering under multi-source uncertainty to obtain optimal actuator fault estimation. However, directly using the optimal state estimation and output prediction for a batch of aeroengines would result in an unnecessary loss of accuracy by completely ignoring the differences between individuals. Because of the existence of and , the optimal output prediction for individual aeroengine does not exist. Therefore, by combining the adaptive state estimation for individual aeroengine with the optimal output estimation for the corresponding range of aeroengines, the accuracy of actuator fault estimation is maximized under multi-source uncertainty. With the optimal estimation of , the conservativeness-reduced estimation of is achieved based on the proposed HFO, which is the main contribution of this paper.
3. Optimal Filtering under Multi-Source Uncertainty
In this section, based on PCE, the statistical property of control matrices with independent probabilistic system parameters is quantified. Furthermore, the optimal state estimation of linear discrete stochastic dynamical system is provided. In addition, the actuator fault is temporarily not discussed.
3.1. PCE-Based UQ of Discrete Stochastic Model
3.1.1. Preliminaries of PCE
Considering a stochastic model , with the probabilistic input , which belongs to the probability space [27]. For stochastic analysis, the expansion of the model and the statistical property of are as follows:
where is the expansion order, is the expansion coefficient, which can be obtained by Galerkin projection [28,29], numerical integration [30], or collocation [31,32]. is the polynomial of orthogonal basis with the respect to the measure . and are the expectation and variance of , which can be directly estimated by .
Most realistic power systems combine multi random input and multi output, especially regarding the aeroengine. For with dimensional inputs and dimensional outputs, as an extension of one-dimensional PCE, the statistical property of can be quantized as follows:
where is the multi-variate polynomial orthonormal basis with as dimension. From [33], is determined by the dimension of the random inputs and the expansion order. In order to harmonize with one-dimensional PCE, is defined as multi-dimensional basis with zero-order expansion [33]. is the correlation between and output, and is the correlation matrix of the random vector.
To quantify the statistical property of the discrete model with probabilistic system parameters, the output of is further extended to . It is obvious that the expansion coefficients have the same size as the output. Moreover, considering the matrix computation demand in this paper, the correlation of the random matrix is indicated by the correlation matrix between row vectors or column vectors. The statistical property of is expressed by as follows:
where is the expectation, is the correlation matrix between and columns, and is based on row vectors. The subscript and represent the order of the column and row, respectively.
The statistical property of the product between the vector or matrix with probabilistic system parameters is discussed. With the assumption of mutual independence, the expectation of the product is simply equal to product of the individual expectation. Moreover, the correlation of the product is expressed in Equation (10) by extending the formula for variance of multiplied random variables [27]. Here, is Hadamard product, are random vectors with statistical property shown in Equation (8), and , are random matrixes with statistical property obey Equation (9).
3.1.2. Statistical Property of Discrete Stochastic Model
The statistical property of the stochastic model in Equation (3) is quantified based on multi-variate PCE. Considering the mutual independence between different outputs, the probabilistic parameters in and can be treated by row. Additionally, the multi-variate polynomial orthogonal basis of the dynamic model has the following form:
where represent the row of the matrix, and is the sort order with the max number of , , , and for each multi-variate polynomial orthonormal basis. Based on Equation (4), the discrete stochastic model is expressed by the random linear model and is determined by the relevant expansion coefficients. From [30], based on numerical integration, the expansion coefficient is calculated as follows:
where is the sort order and is support of the arbitrary measure [30,33]. Based on Equation (9), the statistical property of is quantified by . By respectively combining and , the expansion coefficient matrix and , which determines the statistical property of and , is shown in Equation (13).
From Equation (4), considering is a constant matrix, the randomness of is entirely caused by , and the expansion coefficient matrix , which expresses the statistical property of , has the following form:
Finally, since , the statistical property of can only be quantified based on Equation (10) with the statistical property of and , which can be obtained by and and has the following form.
3.2. Hyperelliptic Kalman Filter
For discrete stochastic system under multi-source uncertainty in Equation (3), the optimal state estimation is obtained by HeKF [6] and has the following form.
where are the one-step prediction and the optimal estimation of the state, which are both random processes due to the multi-source uncertainty. Based on Equation (8), the expectation and the correlation matrix together express the statistical property of the random vector, and and are assumed to be known. is the constant estimated gain matrix, which is optimized later. The statistical property of can be quantified by Equation (17).
where the , , and for both and are quantified in Section 3.1; the expectation and correlation matrix for is presented in Equation (18).
Next, the statistical property of is quantified as follows:
where , consistent with the case in Equation (17), the statistical properties of all the random parameters in Equation (19) can be quantified. is the optimal estimation of the state, and represent the disturbance intensity. Therefore, in order to obtain the optimal state estimation, the optimal gain matrix is required to minimize , since is a real symmetric positive definite matrix, and the diagonalization, , is introduced based on the transfer matrix which is determined by . Naturally, the trace of can be used as the evaluation of the disturbance intensity. Using as the optimization objective, it can be expressed as . For calculation convenience, can be simplified as follows based on Equation (10).
It is obvious that is the only unknown parameter in . Since is a real symmetric positive definite matrix, based on the calculation rules, is minimum only when , and the corresponding becomes the optimal gain matrix. Considering is not affect by , and thus, satisfying , also satisfies , and has the following form:
Moreover, combining Equations (19) and (21), can be simplified as follows:
Equations (17), (19), (21) and (22) together achieved the optimal state estimation considered multi-source uncertainty; using as the optimal prediction of output, the statistical property of can be expressed as Equation (23), where the statistical properties of all random variables have been quantified, and the calculation rules are presented in Equation (10).
4. Conservativeness-Reduced Fault Estimation under Multi-Source Uncertainty
In this section, the traditional TSKF-based fault estimation ideas are briefly described. Meanwhile, the TSKF is extended to the TSHeKF to provide optimal fault estimation of fault considered multi-source uncertainty. Moreover, by adding quantification of , the HFO is established on the basis of the TSHeKF, and the conservativeness-reduced fault estimation is achieved.
4.1. TSKF-Based Fault Estimation
By treating fault as unknown input, the TSKF is widely used in fault estimation [15,16], and the data flow of TSKF-based fault optimal estimation is shown in Figure 1. Where is the augmented state, which is composed of state and fault, is the ASKF-based optimal estimation. is the augmentation of and , which are estimated by TSKF, and is the estimation of fault. By introducing the potential U-V transformation, can reach the same estimation accuracy as with less computational cost. The design process of the TSKF can be divided into four parts, namely, ASKF, U-V transformation, decoupling, and TSKF, as shown in Figure 1, where ASKF presents the optimal estimation, which is also the aim of TSKF. U-V transformation is hypothetically present and is quantified, while the decoupling part establishes the conversion relationship between and . By repeating U-V transformation, is eliminated; moreover, the parts bounded by the dotted line in Figure 1 only contribute to the design process of the TSKF and are not involved its calculation. With the refresh of the U-V transformation matrix, the optimal state estimation can be formed by the linear combination of and , and becomes the optimal fault estimation. More detailed TSKF design processes can be found in [14,34]. However, due to the lack of consideration of multi-source uncertainty in the design process, the TSKF-based fault estimation needs to be improved. By combining with the optimal filtering in Section 3.2, the TSHeKF is proposed in the subsequent study and realizes optimal fault estimation considering multi-source uncertainty.
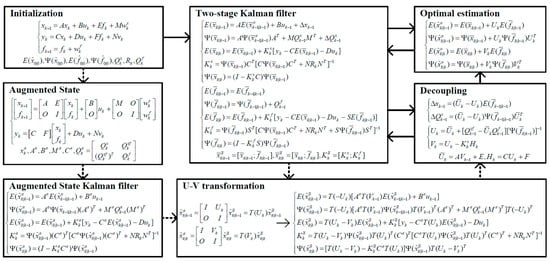
Figure 1.
TSKF-based optimal fault estimation.
4.2. TSHeKF-Based Optimal Estimation
Considering the multi-source uncertain environment, the basic filter of the TSKF needs to be replaced by HeKF proposed in Section 3.2. Meanwhile, in this section, the optimal fault estimation for one type or batch of aeroengines is proposed based on Equation (3). Same as the TSKF, the TSHeKF is designed in the same four-step process which shown in Figure 1.
- Augmented State estimator
Considering the dynamics of as , where and is independent from , , , . Treating as the augmented state, the optimal augmented state estimator under multi-source uncertainty is designed as follows:
where
Obviously, Equation (24) is a typical filter as in Equation (16), and presents the optimal state estimation , which is only used as the control group during the design process of the TSHeKF.
- U-V transformations
The filtering process of the sub-filter is indicated by an adding an upper underline in this paper, and the one-step prediction and the optimal state estimation have been augmented as and , the same as the optimal gain matrix . By introducing and as the gain of fault to state, meets the estimation accuracy as , and the U-V transformation for the TSHeKF is as follows:
where
Obviously, , and the inverse of is . By repeating the U-V transformation twice, the estimation of augmented state can be removed, and Equation (26) becomes:
Additionally, the statistical property of and is quantified below:
where represents the transpose of the corresponding part of partitioned matrix.
- Decoupling
By setting the correlation of state and fault in and to zero, the decoupling process is achieved and obtained:
where , . Moreover, the optimal sub-filter of fault has the following form:
Based on Equations (17), (19), (21), and (22), the statistical property of the optimal fault estimation is quantified as follows:
where . By adding the compensation of the unknown fault on the state , which is a random vector, the optimal sub-filter of state is expressed in Equation (34).
With and , the statistical property of the sub-filter-based state estimation is quantified as follows:
The sub-filters are all established, and based on Equations (29), (31), (33), and (35), the transformation matrices are quantified as:
Meanwhile, the statistical property of the random vector can be expressed based on Equations (31), (33), and (35) as follows:
- Optimal estimation under multi-source uncertainty
Finally, the design of the TSHeKF is completed based on the above steps and is optimal under multi-source uncertainty compared to standard TSKF. The optimal estimation of state and actuator fault is as follows:
where is the optimal estimation of state when considering multi-source uncertainty in Equation (3), and the statistical property of is quantified based on Equations (33), (35), (36), and (38) as follows. Meanwhile, the optimal output prediction can also be presented based on . Especially since the different sensors are mutually independent, is a diagonal matrix with variances of the outputs as the diagonal elements.
4.3. Conservativeness-Reduced Fault Estimation Based on HFO
The TSHeKF-based fault estimation in the previous section takes into account the multi-source uncertainty shown in Equation (3), which means it is optimal for the corresponding type or batch of aeroengines, but still retains conservativeness for the individual. Therefore, in order to improve the accuracy of estimation and reduce the conservativeness of the fault estimation system, multiple TSHeKFs are used for estimation of and , respectively, to achieve optimal fault estimation for individual aeroengines. The structure of the HFO is shown in Figure 2. The design process of the conservativeness-reduced fault estimation for individual aeroengines is based on Equation (6).
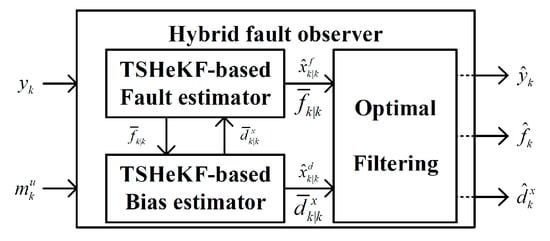
Figure 2.
Structure of HFO.
Where is the measurement of sensors, is the expectation of the control system output and can also be regarded as the expected input of the aeroengine. and are the TSHeKF-based unknown input estimations of fault and bias of state function, respectively. Moreover, and are both optimal state estimations of the corresponding TSHeKF, and together contribute to optimal state estimation of state under multi-source uncertainty. is the output prediction, is the estimation of actuator fault, and is the optimal quantification of the state function bias , which are all random vectors with the statistical property in Equation (8). Compared with the fault estimation in Section 4.2, the HFO-based fault estimation can accommodate the effect caused by model uncertainty in state function by adding the estimation of , which improves the adaptiveness and reduces the conservativeness. Since the output function bias cannot be quantified, the state optimal estimation process and output optimal prediction process are faced with multi-source uncertainty. Meanwhile, based on Equation (6), with the estimation of , there is no model uncertainty with the one-step prediction. Therefore, during the design process of the HFO, the one-step prediction of each filter follows the LKF, and the estimation of state and output should be handled by the proposed TSHeKF. The data flow of the HFO is shown in Figure 3, where the gain matrices and and the statistical properties of , , , are assumed to be known.
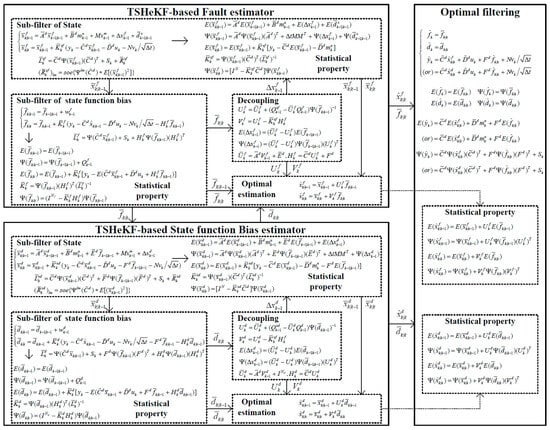
Figure 3.
Data flow of HFO.
5. Simulation
Performance of the proposed HFO is verified by numerical simulation under the MATLAB platform in this section. Meanwhile, the TSKF- and TSHeKF-based actuator fault estimation is used as a control group.
5.1. Linear Model under Multi-Source Uncertainty
The structure and the section definition of the biaxial separated exhaust turbofan engine, which is taken as an example, is shown in Figure 4. The nonlinear and uncertainty modeling processes are shown in [3,35], and the linearization processes are clearly described in [36]. The rotational speed of low-pressure rotor and high-pressure rotor together form the state of the linear system. Meanwhile, the control variables of the system are composed of fuel flow , variable stator vane (), and variable bleed valve (). In contrast, the actuator fault modes discussed in this paper correspond to the control variables. Concurrently, the output involves and , the total pressure on the outlet of the low-pressure compressor and high-pressure compressor , and the total temperature on the outlet of the high-pressure compressor , high-pressure turbine , and low-pressure turbine . Considering the ground state (H = 0 km, Ma = 0), with the working condition of (Percentage of ), the parameter of the above control and output variables are shown in Table 1 and Table 2. To facilitate the evaluation of the performance of actuator fault estimation, the fault drive matrices are normalized in this paper, as shown in Table 3. As for uncertainty modeling of state-space system, this paper follows [6], which assumes that the probabilistic system parameters obey Gaussian distribution, and the statistical property of control matrices of the state-space system for each element is shown in Table 4.

Figure 4.
Biaxial separated exhaust turbofan engine.

Table 1.
Turbofan engine control variables.

Table 2.
Turbofan engine output variables.

Table 3.
State-space model of turbofan engine normalized fault drive matrix.

Table 4.
State-space model of turbofan engine.
5.2. Optimal Filtering under Multi-Source Uncertainty
In this section, the performances of the TSKF, TSHeKF, and HFO are compared under fault-free conditions, and numerical simulation is carried out under multi-source uncertainty, as shown in Table 1, Table 2, Table 3 and Table 4. The simulation process is given as follows. The simulation duration is with a sampling time of , and a step of fuel flow is given from to . The comparative results of the TSKF, TSHeKF, and HFO-based state estimation, with and without accounting for probabilistic system parameters, are shown in Figure 5. The HFO-based optimal output prediction and estimation of state function bias are shown in Figure 6 and Figure 7, respectively.
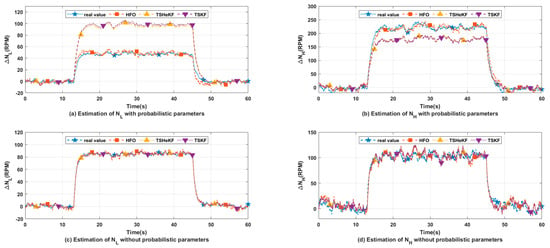
Figure 5.
State estimation with (without) probabilistic system parameters.
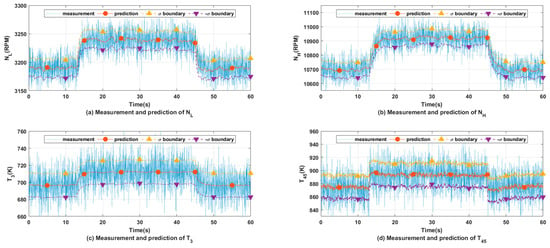
Figure 6.
Output prediction of HFO (partial).
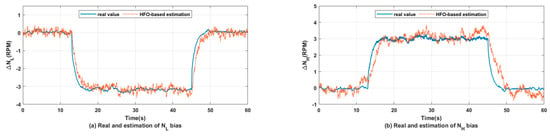
Figure 7.
HFO-based optimal estimation of .
As can be seen from Figure 5, when the model uncertainty is not considered, all of the three filters can realize precise state estimation. However, when considering systems with probabilistic parameters, neither the TSKF nor the TSHeKF can achieve accurate tracking of states. Due to the additional estimation of state function bias in Figure 7, only the HFO enables optimal state estimation under multi-source uncertainty. As it is well known that the probability of a Gaussian random variable takes value in the range of and is approximately equivalent to , it is referred to in this paper as σ-percentage for simplicity of description. Where both the states and outputs follow the Gaussian distribution, and also considering the mutually independence between different outputs, the for outputs at time are the corresponding diagonal elements of . For the output prediction in Figure 6, the σ-percentage for the shown outputs are , , , and . It is clear that the HFO-based predictions of σ-percentage of the outputs are basically equal to the theoretical value, which further illustrates that the HFO-based state estimation is optimal. As for Figure 7, since increment of state and input is around zero while the aeroengine is at the steady-state point, state function bias is only valued when system deviates from the steady-state. It is clear that after the step of fuel flow, gradually stabilizes to another steady-state, and the HFO realized accurate tracking of unknown input lays the foundation for optimal filtering under multi-source uncertainty.
To further validate the performance of different filters under multi-source uncertainty, the times MC simulation is designed, and the result is shown in Table 5. Firstly, from the aspect of mean relative error, the HFO-based output prediction is undoubtedly the best performer, due to the increased estimation of compared to the other two methods. Additionally, the TSHeKF slightly outperforms the standard TSKF, which is attributable to the proposed optimal filtering under multi-source uncertainty in Section 3.2. By adding the PCE-based UQ of the discrete stochastic model, compared with the TSKF, the TSHeKF achieves optimality under more uncertainties and proposes a more robust filter for the individual. Aiming at the minimum relative error, which means the best prediction of filtering, the prediction accuracies of the three methods are very close. This, again, demonstrates that in Figure 5c,d, all three methods achieve high confidence filtering when ignoring the model uncertainty. Finally, by comparing the maximum estimation error longitudinally, it is obvious that the standard TSKF is the least robust due to the fewest considerations of uncertainty in the design process. Meanwhile, compared to the TSHeKF, the proposed HFO greatly reduces the conservativeness by adding the estimation of state function bias which increases the adaptability to individuals. Therefore, the HFO-based state estimation balances both multi-source uncertainty for one type or batch of aeroengines and the model uncertainty of an individual aeroengine, and provides a theoretical basis for fault optimal estimation under multi-source uncertainty.

Table 5.
MC simulations for output prediction.
5.3. Actuator Optimal Fault Estimation
In this section, the accuracies of fault estimation based on the TSKF, TSHeKF, and HFO are evaluated firstly by keeping the control process of numerical simulation in Section 5.2 unchanged and adding fault inputs. Numerical simulations of step fault and ramp fault of fuel flow are used for verification, and the estimation results of different method are shown in Figure 8 and Figure 9, respectively. The step fault is of and remains between and ; meanwhile, the ramp fault starts from and maintains at , with a slope of .

Figure 8.
Estimation of fuel flow step fault.

Figure 9.
Estimation of fuel flow ramp fault.
As can be clearly seen from Figure 8 and Figure 9, the HFO provides optimal fault estimation when considering multi-source uncertainty. Meanwhile, errors in the TSKF or TSHeKF-based fault estimation are inevitably large due to the inability to achieve accurate tracking of states in the presence of probabilistic system parameters. To further illustrate the effectiveness of the proposed HFO under multi-source uncertainty and to verify its robustness to input noise, MC simulations are designed for each noise intensity of fuel flow, and the relative errors in the estimation of 10% step faults for are shown in Table 6.

Table 6.
MC simulations of fault estimation under different noise.
The following conclusions can be drawn from the data in Table 6. Firstly, as the noise intensity of the actuator output increases, the accuracy of fault estimation based on different methods decreases accordingly. Additionally, the three methods are ranked in the descending order of mean relative errors as the HFO, TSHeKF, and TSKF, which is also the order of the methods’ fault estimation performances under multi-source uncertainty. Same as the comparison of the output prediction accuracy, since the multi-source uncertainty is considered in the design process of the TSHeKF, the TSHeKF-based estimation outperformed that of the TSKF. Moreover, on the foundation of the TSHeKF, the HFO enhances the adaptiveness for individual aeroengines, thus enabling greater reduction in conservativeness of fault estimation and realizing adaptive optimal estimation under multi-source uncertainty. Secondly, by comparing the minimum mean estimation errors of the different methods, it can be seen that the precisions of the HFO and TSHeKF are comparable and slightly less than the precision of the TSKF. This is because the situation with minimal mean estimation error can be seen as a system without probabilistic parameters, and aiming at this situation, the TSKF is certainly optimal. Due to the adaptation of the HFO and TSHeKF to multi-source uncertainty, especially in the presence of model uncertainty, the estimation error increases in the above situation. Lastly, from the aspect of maximum estimation error and standard deviation, the TSHeKF provides more robust fault estimation than the TSKF. Moreover, compared to the TSHeKF, the HFO is able to adaptively follow the state function bias for each individual and can provide more accurate fault estimation. Therefore, the TSKF-based fault estimation is optimal for individual aeroengines when the model is completely known. Since uncertainty is widespread and unavoidable, the TSHeKF-based estimation is optimal for the corresponding type or batch but robust for the individual. Finally, the HFO further reduces the conservativeness by adding an estimation process of the state function bias. Considering the output function bias is not estimable, when considering multi-source uncertainty, the HFO-based fault estimation is optimal while satisfying achievability.
Next, the effectiveness of HFO-based multi-fault estimation is demonstrated in Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14. Each figure corresponds to a specific multi-actuator fault mode. The multi-fault modes are set by considering the components, type, sequence of occurrence, and duration of the fault, and following five fault mode were established for simulation verification.

Figure 10.
HFO-based actuator multi-fault estimation of .

Figure 11.
HFO-based actuator multi-fault estimation of .

Figure 12.
HFO-based actuator multi-fault estimation of .

Figure 13.
HFO-based actuator multi-fault estimation of .

Figure 14.
HFO-based actuator multi-fault estimation of .
- : step fault of start from , with step fault of start from ; both faults last for .
- : step fault of and step fault of ; both last from to .
- : a ramp fault of with slope of from to , and a step fault of start at and last for .
- : ramp faults of and , with slope of from to for and as slope starts from and stays at for .
- : ramp faults of and within to with slopes of and , respectively.
It is clear that the proposed HFO realizes optimal fault estimation with high accuracy whether the two faults occur simultaneously or are staggered, or whether they are step faults or ramp faults or both.
To sum up, compared with the commonly used fault estimation method, the HFO-based optimal fault estimation system has higher estimation accuracy, less conservativeness, and higher reliability under multi-source uncertainty.
6. Conclusions
This paper presents an innovative HFO for handling aeroengine actuator fault estimation under multi-source uncertainty consisting of system noise, measurement noise, input noise, and probabilistic system parameters. On the foundation of the PCE-based UQ of the discrete stochastic model, the optimal filtering under multi-source uncertainty is realized. Additionally, the TSHeKF-based fault estimation is also proposed by replacing the basic filter of the TSKF with HeKF, realizing optimal filtering for the linear stochastic system under multi-source uncertainty, and leading to the robust estimation for individuals. Since the bias in output function is relatively small and not estimable, by adding an estimate of state function bias, the HFO provides the best possible fault estimation for individuals and significantly reduces the conservativeness. Numerical simulations demonstrate the high accuracy of the HFO-based state estimation, output prediction, and unknown deviation estimation. Meanwhile, the effectiveness of the HFO in handling single and multiple faults has also been proven. Furthermore, MC simulations demonstrate that, compared with estimations based on the TSKF and TSHeKF, the proposed HFO has higher accuracy and better adaptiveness with guaranteed robustness when considering multi-source uncertainty. This enormously improves the fault diagnosis performance of the engine control system in complex environments and better ensures the safety and reliability of the aeroengine.
Author Contributions
Conceptualization, Y.W. and R.-Q.S.; methodology, R.-Q.S.; software, Y.W.; validation, Y.W., R.-Q.S. and L.-F.G.; formal analysis, Y.W.; investigation, R.-Q.S.; resources, L.-F.G.; data curation, Y.W.; writing—original draft preparation, Y.W.; writing—review and editing, R.-Q.S.; visualization, R.-Q.S.; supervision, R.-Q.S.; project administration, L.-F.G.; funding acquisition, L.-F.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by National Major Science and Technology Project (J2019-V-0010-0105); Science Center for Gas Turbine Project (P2022-A-V-001-001).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy and ethical concerns.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviation
| ASKF | Augmented State Kalman Filter |
| HFO | Hybrid Fault Observer |
| HeKF | Hyperelliptic Kalman Filter |
| LKF | Linear Kalman filter |
| MC | Monte Carlo |
| PCE | Polynomial Chaos Expansion |
| TSKF | Two-stage Kalman Filter |
| TSHeKF | Two-stage Hyperelliptic Kalman Filter |
| UQ | Uncertainty Quantification |
| ZKF | Zonotope Kalman Filter |
References
- Lv, C.; Chang, J.; Bao, W.; Yu, D. Recent research progress on airbreathing aero-engine control algorithm. Propuls. Power Res. 2022, 11, 1–57. [Google Scholar] [CrossRef]
- Rath, N.; Mishra, R.K.; Kushari, A. Aero engine health monitoring, diagnostics and prognostics for condition-based mainte-nance: An overview. Int. J. Turbo Jet Eng. 2024, 40, s279–s292. [Google Scholar] [CrossRef]
- Gou, L.; Sun, R.; Han, X. FDIA System for Sensors of the Aero-Engine Control System Based on the Immune Fusion Kalman Filter. Math. Probl. Eng. 2021, 2021, 6662425. [Google Scholar] [CrossRef]
- Roy, C.J.; Oberkampf, W.L. A comprehensive framework for verification, validation, and uncertainty quantification in sci-entific computing. Comput. Methods Appl. Mech. Eng. 2011, 200, 2131–2144. [Google Scholar] [CrossRef]
- Oberkampf, W.L.; Helton, J.C.; Joslyn, C.A.; Wojtkiewicz, S.F.; Ferson, S. Challenge problems: Uncertainty in system response given uncertain parameters. Reliab. Eng. Syst. Saf. 2004, 85, 11–19. [Google Scholar] [CrossRef]
- Sun, R.Q.; Han, X.B.; Chen, Y.X.; Gou, L.F. Hyperelliptic Kalman filter-based aeroengine sensor fault FDIA system under multi-source uncertainty. Aerosp. Sci. Technol. 2023, 132, 108058. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Z.; Wang, Y.; Ji, Z. Sensor fault estimation based on the constrained zonotopic Kalman filter. Int. J. Robust Nonlinear Control 2021, 31, 5984–6006. [Google Scholar] [CrossRef]
- Gou, L.; Shen, Y.; Zheng, H.; Zeng, X. Multi-Fault Diagnosis of an Aero-Engine Control System Using Joint Sliding Mode Observers. IEEE Access 2020, 8, 10186–10197. [Google Scholar] [CrossRef]
- Hamayun, M.T.; Edwards, C.; Alwi, H. Design and Analysis of an Integral Sliding Mode Fault-Tolerant Control Scheme. IEEE Trans. Autom. Control 2012, 57, 1783–1789. [Google Scholar] [CrossRef]
- Pourbabaee, B.; Meskin, N.; Khorasani, K. Sensor Fault Detection, Isolation, and Identification Using Multi-ple-Model-Based Hybrid Kalman Filter for Gas Turbine Engines. IEEE Trans. Control Syst. Technol. 2016, 24, 1184–1200. [Google Scholar] [CrossRef]
- Simon, D. A comparison of filtering approaches for aircraft engine health estimation. Aerosp. Sci. Technol. 2008, 12, 276–284. [Google Scholar] [CrossRef]
- Jin, P.; Lu, F.; Huang, J.; Kong, X.; Fan, M. Life cycle gas path performance monitoring with control loop parameters uncertainty for aeroengine. Aerosp. Sci. Technol. 2021, 115, 106775. [Google Scholar] [CrossRef]
- Lu, F.; Jiang, C.; Huang, J.; Qiu, X. A multi-rate sensor fusion approach using information filters for estimating aero-engine performance degradation. Chin. J. Aeronaut. 2019, 32, 1603–1617. [Google Scholar] [CrossRef]
- Hsieh, C.S.; Chen, F.C. Optimal solution of the two-stage Kalman estimator. IEEE Trans. Autom. Control 1999, 44, 194–199. [Google Scholar] [CrossRef]
- Hajiyev, C.; Cilden-Guler, D.; Hacizade, U. Two-Stage Kalman Filter for Fault Tolerant Estimation of Wind Speed and UAV Flight Parameters. Meas. Sci. Rev. 2020, 20, 35–42. [Google Scholar] [CrossRef]
- Chen, X.; Sun, R.; Wang, F.; Song, D.; Jiang, W. Two-stage unscented Kalman filter algorithm for fault estimation in space-craft attitude control system. IET Control Theory A 2018, 12, 1781–1791. [Google Scholar] [CrossRef]
- Patton, R.J.; Chen, J. On eigenstructure assignment for robust fault diagnosis. Int. J. Robust Nonlinear Control 2000, 10, 1193–1208. [Google Scholar] [CrossRef]
- Zhou, D.; Ma, S.; Chen, Y.; Wei, T.; Zhang, H.; Wei, F. A gas path fault diagnostic model for gas turbine based on deep belief network with prior information. In Proceedings of the 2018 IEEE International Conference on Prognostics and Health Management (ICPHM), Seattle, WA, USA, 11–13 June 2018; pp. 1–6. [Google Scholar]
- Lu, F.; Huang, J.; Lv, Y. Gas Path Health Monitoring for a Turbofan Engine Based on a Nonlinear Filtering Approach. Energies 2013, 6, 492–513. [Google Scholar] [CrossRef]
- Combastel, C. Zonotopes and Kalman observers: Gain optimality under distinct uncertainty paradigms and robust convergence. Automatica 2015, 55, 265–273. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Z.; Guo, S.; Shen, Y. Interval estimation of sensor fault based on zonotopic Kalman filter. Int. J. Control 2021, 94, 1641–1650. [Google Scholar] [CrossRef]
- Xiu, D. Numerical Methods for Stochastic Computations: A Spectral Method Approach; Princeton University Press: Princeton, NJ, USA, 2010; p. 125. [Google Scholar]
- Dutta, P.; Bhattacharya, R. Nonlinear estimation with polynomial chaos and higher order moment updates. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 3142–3147. [Google Scholar]
- Dutta, P.; Bhattacharya, R. Nonlinear Estimation of Hypersonic Flight Using Polynomial Chaos. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar]
- Sun, R.-Q.; Gou, L.-F.; Liu, Z.-Y.; Han, X.-B. Three-stage hyperelliptic Kalman filter for health and performance monitoring of aeroengine under multi-source uncertainty. Int. J. Engine Res. 2023, 25, 557–572. [Google Scholar]
- Ding, S.X. Model-Based Fault Diagnosis Techniques: Design Schemes, Algorithms and Tools; Springer: New York, NY, USA, 2013. [Google Scholar]
- Øksendal, B. Stochastic Differential Equations: An Introduction with Applications; Spring: New York, NY, USA, 2003. [Google Scholar]
- Xia, B.; Wu, H.; Qiu, Y.; Lou, B.; Song, Y. A Galerkin Method-Based Polynomial Approximation for Parametric Problems in Power System Transient Analysis. IEEE Trans. Power Syst. 2019, 34, 1620–1629. [Google Scholar] [CrossRef]
- Manfredi, P.; De Zutter, D.; Ginste, D.V. On the relationship between the stochastic Galerkin method and the pseudo-spectral collocation method for linear differential algebraic equations. J. Eng. Math. 2018, 108, 73–90. [Google Scholar] [CrossRef]
- Oladyshkin, S.; Nowak, W. Data-driven uncertainty quantification using the arbitrary polynomial chaos expansion. Reliab. Eng. Syst. Saf. 2012, 106, 179–190. [Google Scholar] [CrossRef]
- Shin, Y.; Xiu, D. Nonadaptive quasi-optimal points selection for least squares linear regression. SIAM. J. Sci. Comput. 2016, 38, A385–A411. [Google Scholar] [CrossRef]
- Constantine, P.G.; Gleich, D.F.; Iaccarino, G. Spectral methods for parameterized matrix equations. SIAM J. Matrix Anal. Appl. 2010, 31, 2681–2699. [Google Scholar] [CrossRef]
- Oladyshkin, S.; Nowak, W. Incomplete statistical information limits the utility of high-order polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2018, 169, 137–148. [Google Scholar] [CrossRef]
- Hsieh, C.S. Robust two-stage Kalman filters for systems with unknown inputs. IEEE Trans. Autom. Control 2000, 45, 2374–2378. [Google Scholar] [CrossRef]
- Montomoli, F.; Carnevale, M.; D’Ammaro, A.; Massini, M.; Salvadori, S. Uncertainty Quantification in Computational Fluid Dynamics and Aircraft Engines; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Gou, L.; Zeng, X.; Wang, Z.; Han, G.; Lin, C.; Cheng, X. A Linearization Model of Turbofan Engine for Intelligent Analysis Towards Industrial Internet of Things. IEEE Access 2019, 7, 145313–145323. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).