1. Introduction
The quest to improve wing efficiency has been an ongoing endeavor since Munk [
1] initially investigated and established the requirements to minimize vortex drag for planar unswept wings. For a constrained wingspan, aerodynamic efficiency may be improved through non-planarity, the most common embodiment of which is the winglet [
2]. Visually similar devices to the winglet include the tip sail [
3,
4] and the split tip [
5]. These devices serve to alter the spacial distribution of trailing vorticity. A winglet induces an upwash over the wing while itself experiencing no net normal wash if optimal [
2,
6]. In some instances, such as with swept wings, the winglet may also produce a forward thrust component, although this is not typically associated with optimal operation. Tip sails are visually consistent with the extended primary feathers of birds of prey (raptors) and function by thrust production on the forward-inclined elements of the sail [
3,
4]. Neither winglets nor tip sails scale particularly well to the dimensions consistent with small unmanned aerial vehicles. The resulting small chord of the tip sails or winglet yields very low Reynolds number flows, such that laminar separation without reattachment may occur, greatly reducing the efficiency of the device.
An alternative approach to improving efficiency is to camber the wing in the spanwise direction. Cone [
7] and Lowson [
8] showed that spanwise cambering is effective in reducing vortex drag. The non-planar wing captures a larger volume of air to generate the lift impulse; consequently, the downwash at a given point is lowered. As a result, the kinetic energy per unit length of the wake is reduced. Lowson [
8] showed that non-planarity is most effective near the wing tips, such that for a given non-planar height, an end plate may be most effective. Viscous effects must be considered when implementing non-planarity; a poorly designed end plate—wing junction may cause significant flow separation. When viewed in the context of small UAV-type vehicles, the benefits of spanwise camber must be weighed against penalties resulting from installation and poor performance at low Reynolds numbers. As shown by Jansen and Perez [
9], the optimal embodiment of non-planarity may depend on the function of the aircraft, i.e., long-range aircraft may benefit from a “C” wing [
5], whereas medium-range aircraft show greater benefit from wingtip modifications.
Lift augmentation using Gurney flaps (GFs) has received considerable attention [
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21] due to the ease of implementation and efficacy of these devices. The flap itself is little more than a thin strip of material that is commonly attached perpendicular to the airfoil’s lower surface at the trailing edge. The effect of the Gurney flap is outwardly similar to a conventional flap in that the zero-lift angle of attack becomes increasingly negative and the maximum lift coefficient increases [
11,
12,
13,
14,
15]. Unlike a conventional trailing edge flap, the stall angle is not always reduced [
12]. The minimum drag coefficient [
10,
11] may not increase if the flap does not project beyond the boundary layer. An increase in the lift curve slope caused by GFs has also been observed [
16]. The flap functions by essentially violating the Kutta condition at the trailing edge, creating a finite pressure differential. This has the effect of potentially lessening the adverse pressure gradient that the boundary layer must overcome, as well as increasing the upper surface dumping velocity. The lift curve slope increment is associated with thinning of the pressure side boundary layer with angle of attack, causing the effective flap height to increase. Additionally, the reduction in the upper surface displacement thickness (compared to a wing without the flap) reduces viscous decambering.
Given the current research focus on UAV technology, it is of interest to establish the behavior of Gurney flaps on spanwise-cambered wings. In this study, an experimental investigation is presented evaluating the impact of a Gurney flap on a wing with non-planarity in the form of a circular arc and a straight diagonal outboard section. This type of non-planarity would be easy to implement in the design of a small unmanned aerial vehicle. In addition, the non-planar extent of the wing would not have a reduced Reynolds number (due to a smaller chord), which can be problematic for winglets operating at low Re conditions. Force balance data are presented, and comparisons of the data with numerical estimates are also included.
2. Materials and Methods
Wind tunnel tests were conducted in Embry-Riddle’s 2 ft by 2 ft blower wind tunnel. This facility has a measured turbulence intensity of 0.25–0.5% and a jet uniformity better than 1% in the core (i.e., the local velocity does not deviate by more than 1% from the average velocity across the jet). Force balance measurements were undertaken using a 6-component NK biotechnical sting balance. Balance output voltages were digitized using a National Instruments 16-bit A/D board. Voltages were converted to loads using an internal calibration matrix in the data acquisition code. Each presented data point is the average of 5000 samples. The uncertainty for the lift, drag and pitching moment coefficient was estimated as 0.01, 0.005 and 0.01, respectively. The reference area used to obtain the aerodynamic coefficients corresponded to the wing’s projected area.
The model’s angle of attack was set and measured using a feedback loop in conjunction with a Midori angle sensor. Angle-of-attack repeatability was established as better than 0.1 degree. Wall corrections were not applied as the tests were comparative in nature. Wind tunnel testing was conducted at a free-stream velocity of 40 m/s, yielding a Reynolds number of 285,000 based on the reference chord length of 0.127 m. During testing, the model was pitched from −4 to 24 degrees in 2 degree increments. The model was then pitched down to ascertain whether hysteresis was present.
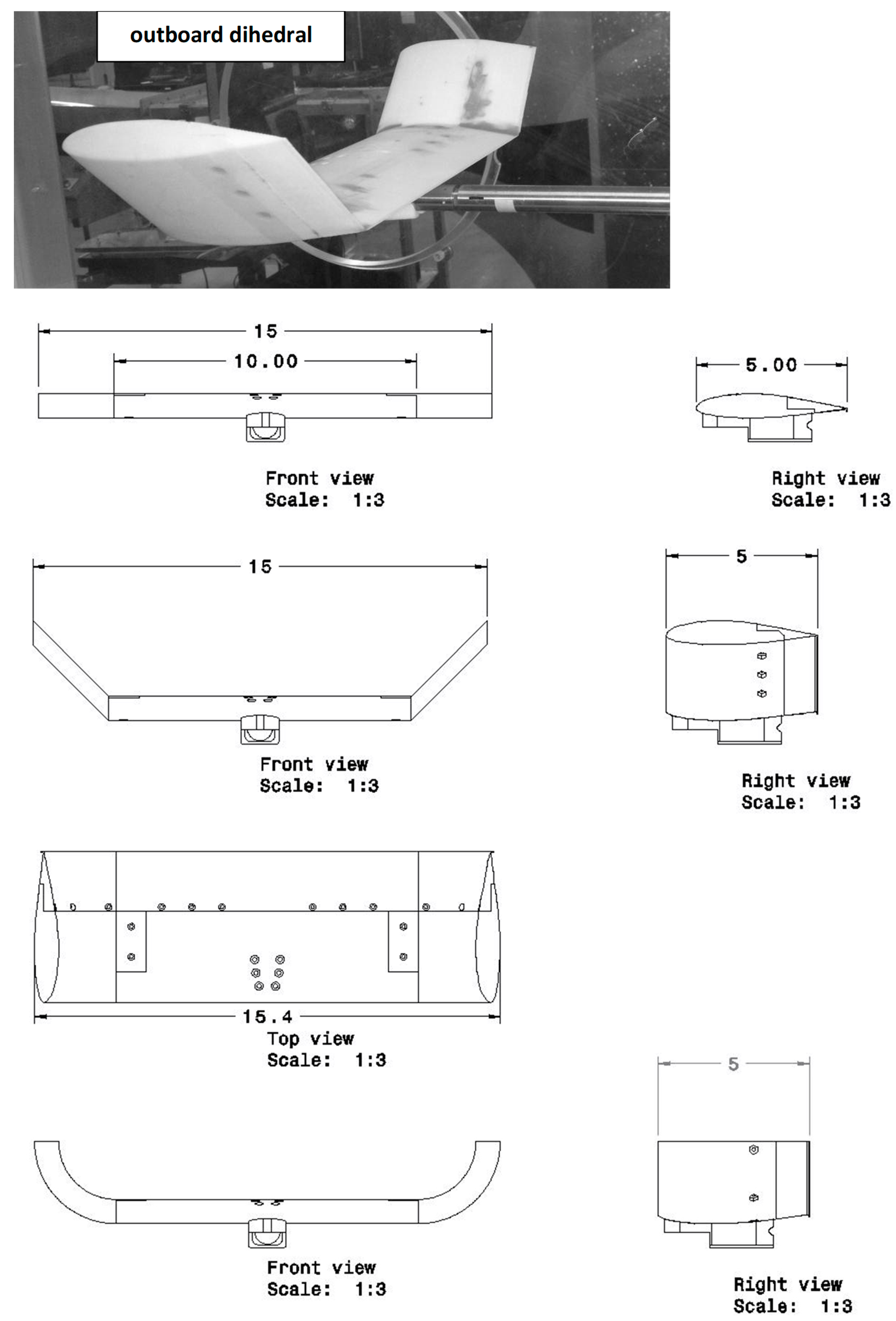
The wind tunnel model, see
Figure 1, was rapid-prototyped from acrylonitrile butadiene styrene (ABS) using Embry-Riddle’s rapid-prototyping facilities. All models had a projected AR of 3. The airfoil section was an S8036 with a thickness of 16%. The inner 2/3 of the projected span was common to all models. The outer 1/3 consisted of either a planar extension, a circular arc with a radius of 2.5 inches or a diagonal section with an angle of 45 degrees (
Figure 1). Dihedral was used for the outboard extents of the non-planar wings. A vortex lattice analysis would show no difference between outboard anhedral and dihedral. However, dihedral gives an additional lift increment due to a streamwise-induced velocity component along the planar wing panel, known as the induced lift effect.
The trailing edge section of the model could be removed and replaced with a section featuring a 2% Gurney flap molded into the trailing edge. A 2% flap was selected as prior studies have indicated marked lift modulation without a C
Dmin penalty [
11] for this profile. The pitching moment reference location was the quarter-chord.
Testing encompassed the effects of non-planarity on the measured coefficients with and without the Gurney flap. The spanwise distribution of the flap was also examined, with the flap extending over 2/3 of the projected wingspan (the inner 10-inch fixed section), as well as over the entire trailing edge spanwise extent.
3. Results
Table 1a presents a summary of the aerodynamic parameters extracted from the wind tunnel data, whereas
Table 1b shows the percentage change of these parameters from the flat wing without a flap case.
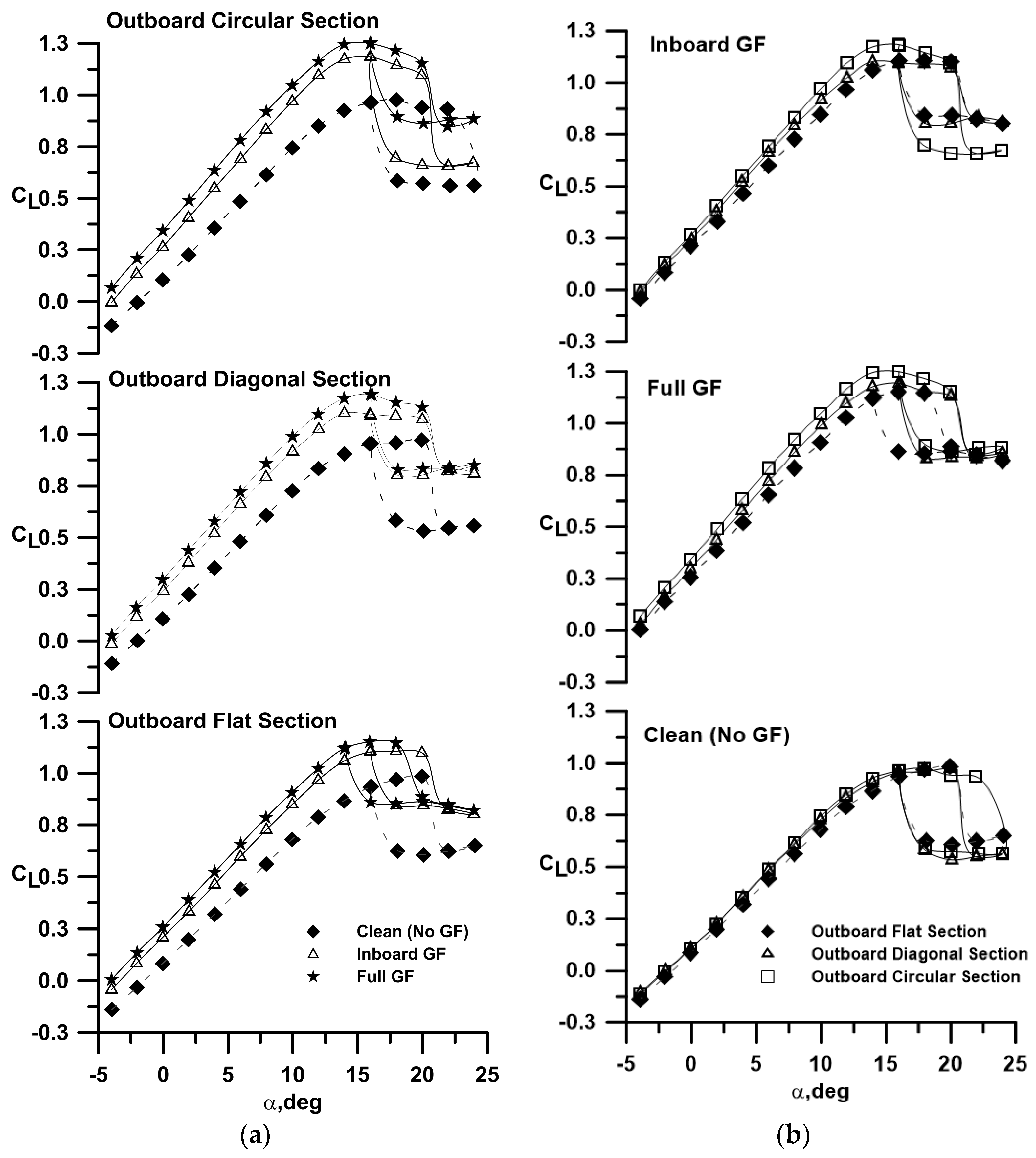
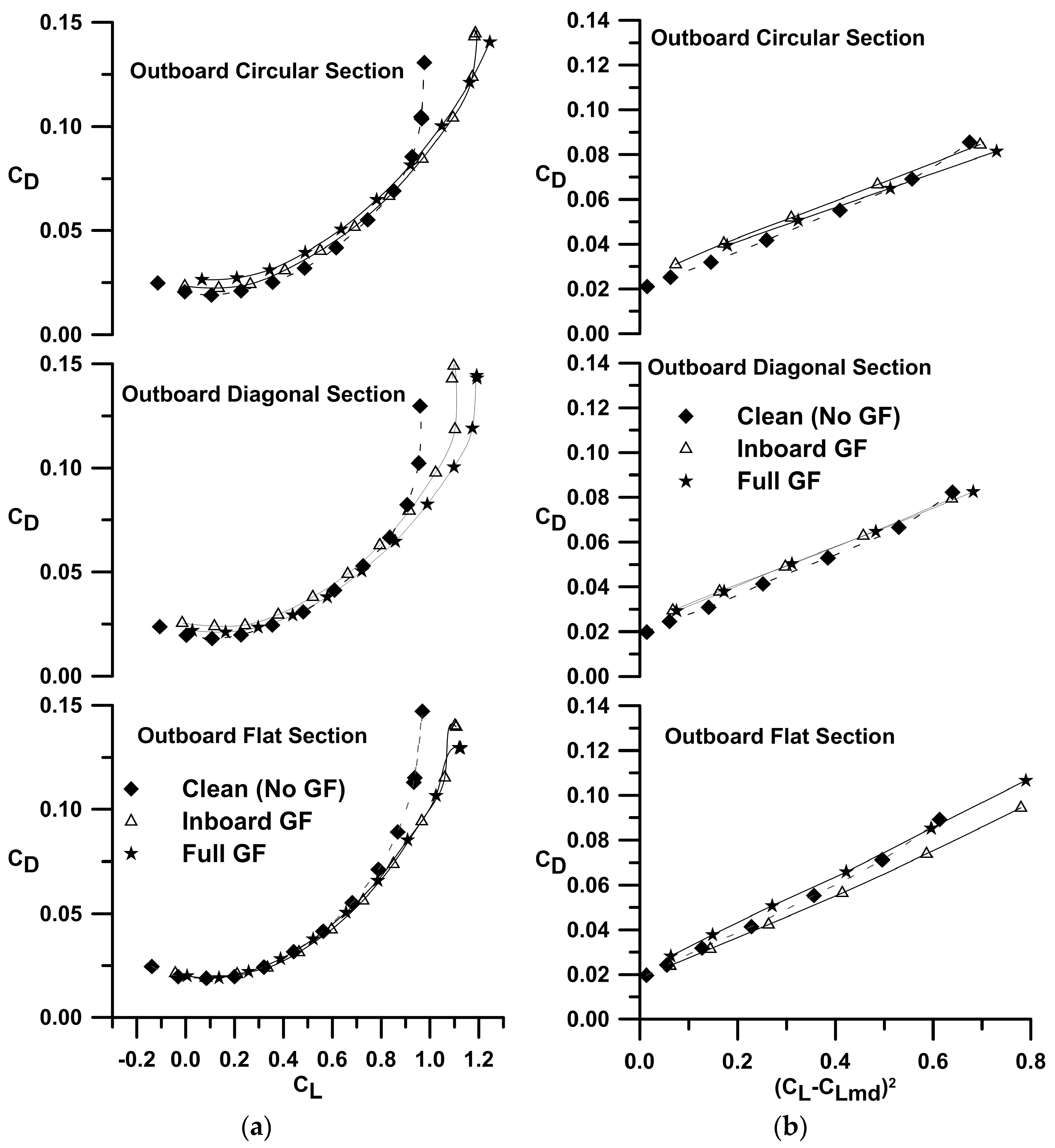
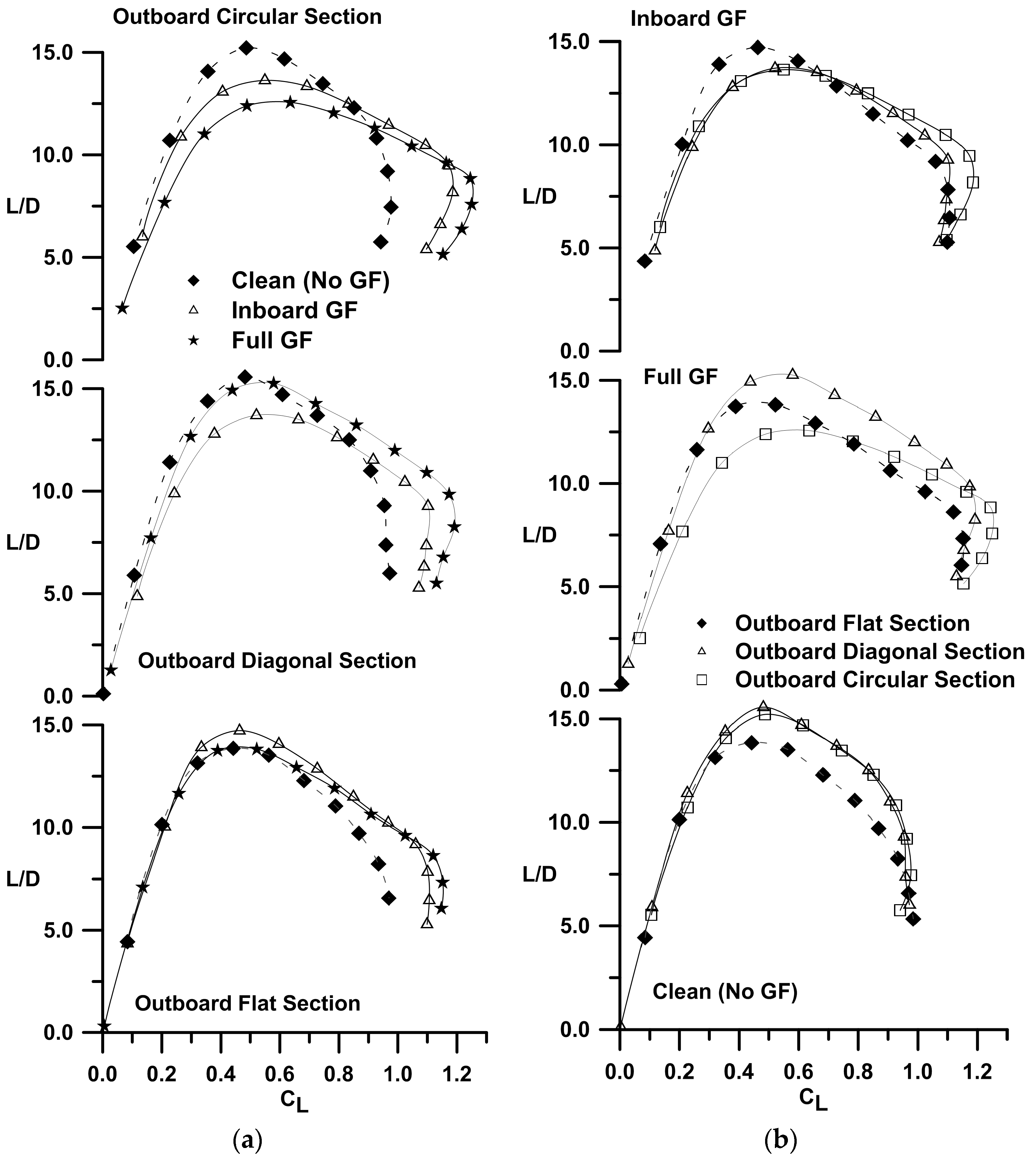
Figure 2a (grouped by extension type) and
Figure 2b (grouped by flap spanwise distribution) show the effect of the Gurney flap and its spanwise distribution on the three (planar, circular and diagonal) wing tip geometries. As shown in
Figure 2a, the flaps increased C
L for a given α through an α
ZL shift and an increase in C
Lα. The stall angle appears unaffected by the presence of the flap, as has been documented previously [
14]. In all cases, hysteresis was apparent, with its α angular extent unaffected by the flap. The presence of hysteresis indicates that the location of flow separation for a given angle of attack in the stall regime was different depending on whether the wing’s angle of attack was increasing or decreasing, i.e., there is a dependence on the history of the flow. As seen in
Figure 2a, the lift increment caused by the flaps (compared to the clean wing) was seen to increase with the non-planar outboard sections compared to the planar wing. Examining the maximum lift coefficient, the increase in C
Lmax with the full-span Gurney compared to the respective clean wing is 17%, 22% and 28% for the flat, diagonal and circular outboard sections, respectively.
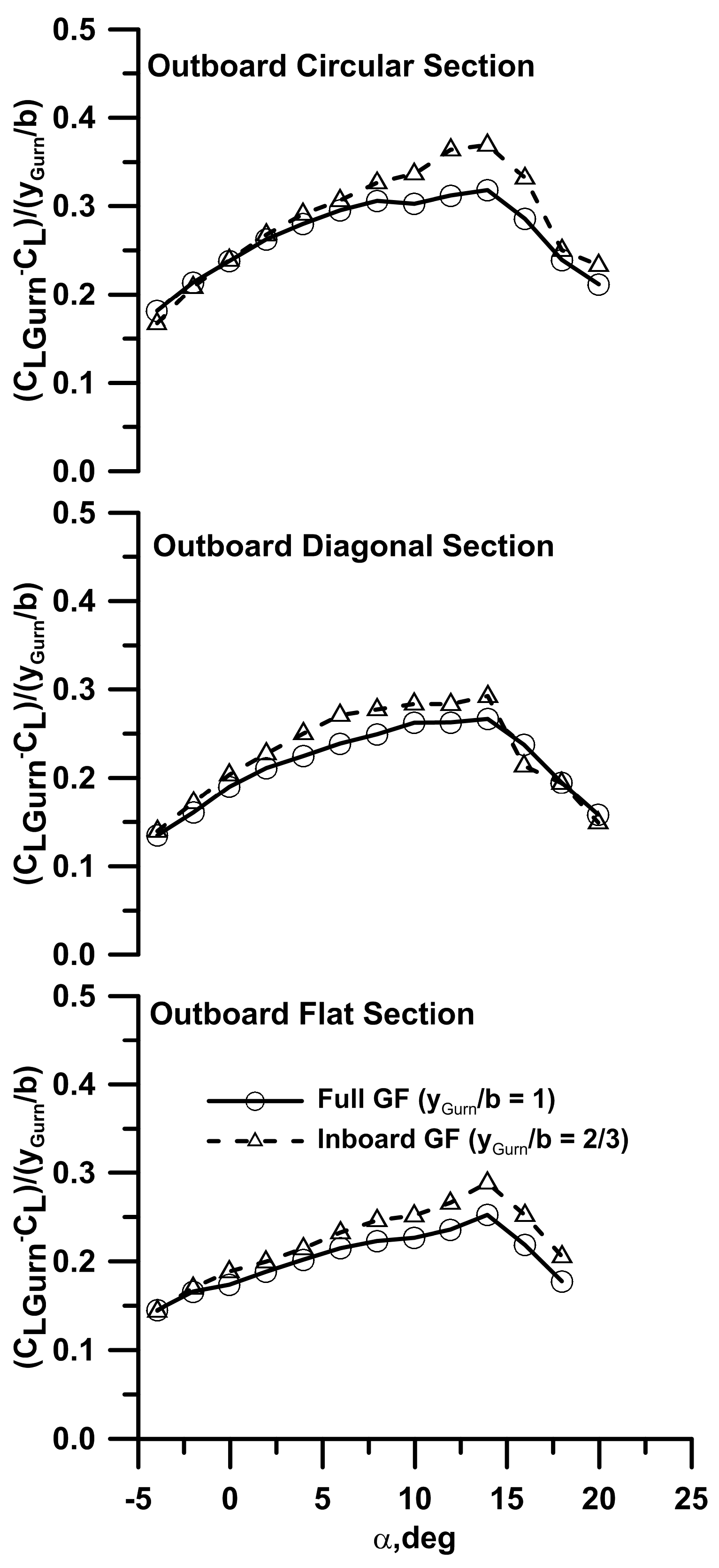
For h/c = 0 (no flap), non-planarity showed a small lift increment compared to the planar wing, caused by induced lift as well as a reduction in the downwash over the inner wing panel. The circular outboard section (h/c = 0) delayed stall moderately compared to the planar and diagonal extension. The effect of the spanwise distribution of the flap is explored in
Figure 3, where the lift increment of the flapped wing compared to the clean wing is shown reduced by the spanwise distribution of the flap. The inboard distribution of the flap is seen to yield the largest lift increment relative to its extent as lift augmentation extends beyond the width of the flap, especially for the circular arc section at higher angles of attack. The lift coefficient for the wing and Gurney flap combination may be expressed as follows:
That for the wing without a flap may be written as follows:
The incremental lift coefficient then follows:
Equation (3) shows explicitly that any variance in the lift curve slope compared to the clean wing (i.e., K > 1) will result in a lift increment that varies with α. As shown explicitly in
Table 1, non-planarity increases the lift curve slope by approximately 8% over the flat wing (no GF). This results from a net reduction in downwash due to the altered span load distribution. The addition of the Gurney flap also increased the wing lift curve slope, ranging from 10% to 11% for the tested geometries.
Table 1 also indicates that the α
ZL shift due to the Gurney flap was proportional to the spanwise distribution of the flap (i.e., the α
ZL shift for the inboard GFs was approximately two-thirds of that for the full-span GFs).
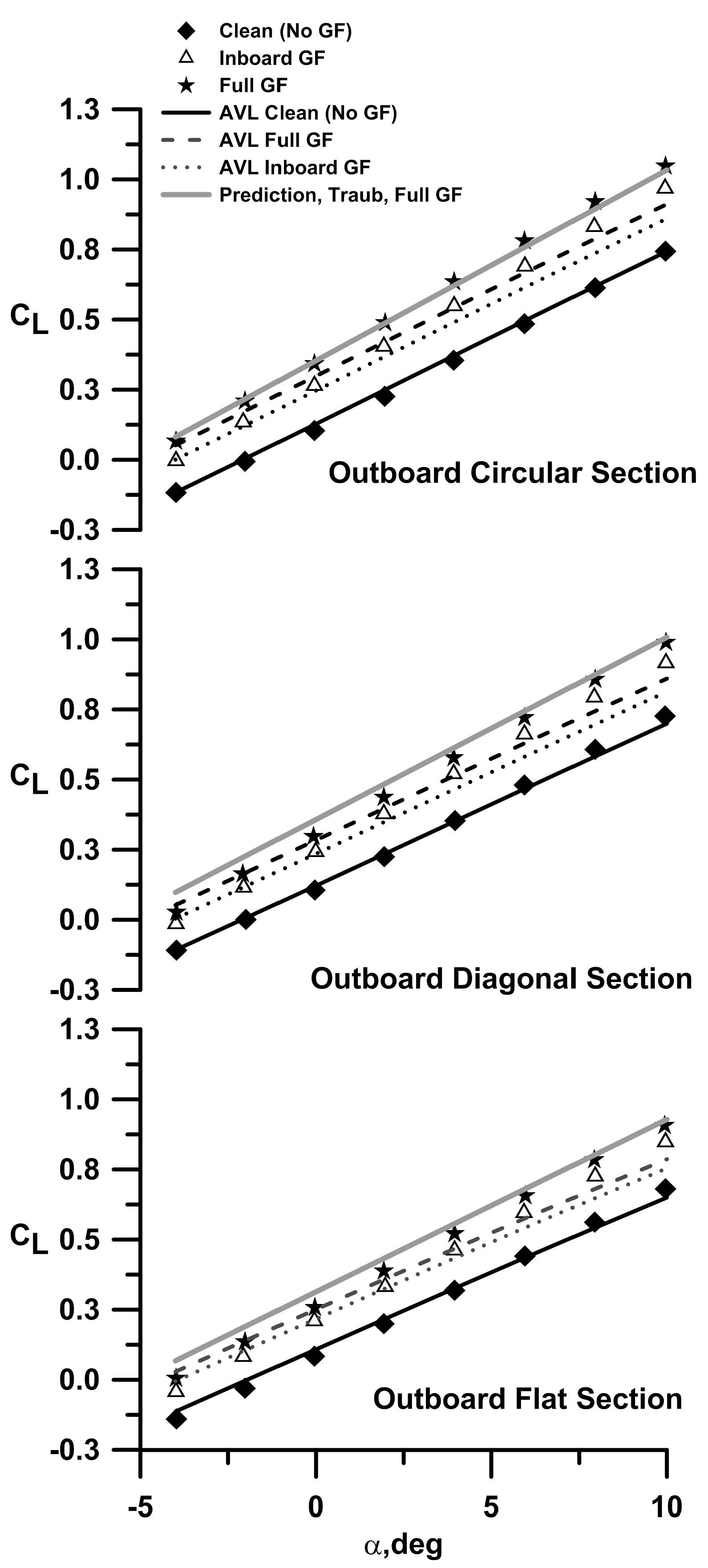
The effect of non-planarity was also investigated using a vortex lattice code, AVL (Athena Vortex Lattice:
https://web.mit.edu/drela/Public/web/avl/, accessed on 1 July 2024). AVL is a vortex lattice code that due to its method of input, can readily accommodate unconventional geometries. The impact of the Gurney flaps was simulated by accounting for their effect on α
ZL. A NACA 4420 profile simulated using Xfoil (Xfoil:
https://web.mit.edu/drela/Public/web/xfoil/, accessed on 3 July 2024) generated a similar zero lift angle of attack shift (≈−4 degrees) to that experimentally measured for the flaps. As the wing was not twisted and used a constant airfoil section throughout its span, α
ZL for the wing and its constituting airfoil profile would be similar. Xfoil is a panel method coupled with an accurate boundary layer routine that enables estimation of boundary layer transition, separation and reattachment. Consequently, this airfoil section was then used instead of the S8036 profile over the spanwise distribution of the flap in the simulations. Using this approach would not provide representative chordwise load distributions; however, net lift should be estimated effectively in the attached flow regime. AVL agreement with the clean (no GF) experimental data for all outboard geometries is good in terms of the lift curve slope and the zero lift angle of attack (
Figure 4). The vortex lattice estimate of the wing’s α
ZL with flaps was also well estimated. However, the lift curve slope was seen to be underestimated for all Gurney flap configurations, a consequence of the inviscid nature of AVL. The C
Lα increment associated with Gurney flaps is a viscous behavior and would not be modeled using an inviscid technique without explicit incorporation. In Ref. [
16], a semi-empirical equation is presented that accounts for the effect of Gurney flaps on both the zero lift angle of attack and the lift curve slope. This estimate is included in
Figure 4 (denoted as “Prediction, Traub”). As shown, the prediction is representative of the full span GFs in terms of C
Lα and α
ZL.
Figure 5a,b shows the drag polar and the linearized drag polar for the data grouped by outboard section. Gurney flap addition on the planar wing had little effect on C
Dmin (
Table 1). At higher lift coefficients, close to stall, the Gurney-flap-equipped models exhibited significantly lower drag than the non-GF models. This resulted from the flap augmenting lift in this regime, coupled with the GF attenuating pressure recovery demands on the boundary layer. For the non-planar geometries, flap addition caused an increase in C
Dmin due to greater arc length (i.e., increased wetted area). The addition of the Gurney flaps reduced drag due to lift, which is more clearly illustrated in
Figure 5b, which presents the linearized drag polar. The slope of the resulting curve relates directly to the drag due to lift and allows for easy comparison of aerodynamic efficiency. The reduced slope for all GF-equipped configurations compared to the corresponding clean wing implies greater aerodynamic efficiency. The AVL analysis suggests that the addition of the part-span and full-span flaps had little effect on the calculated e
i values (
Table 2). Thus, it can be inferred that the increase in aerodynamic efficiency was a consequence of a reduction in sectional pressure drag caused by attenuation of the adverse chordwise pressure gradient on the leeward surface for a given C
L. For the S8036 airfoil, an increase in the angle of attack caused a forward migration and contraction of the leeward laminar separation bubble [
22]. The addition of the flap caused a lift increment for a given angle of attack. However, this lift augmentation does not come at the expense of a stronger adverse pressure gradient [
14,
18] due to violation of the Kutta condition. Consequently, at a given α, the location of the laminar separation bubble was similar to the non-GF-equipped wing even though C
L was greater. Thus, the flap-equipped wing experienced a greater extent of laminar flow and a shorter extent of turbulent flow than a non-GF wing for the same C
L value.
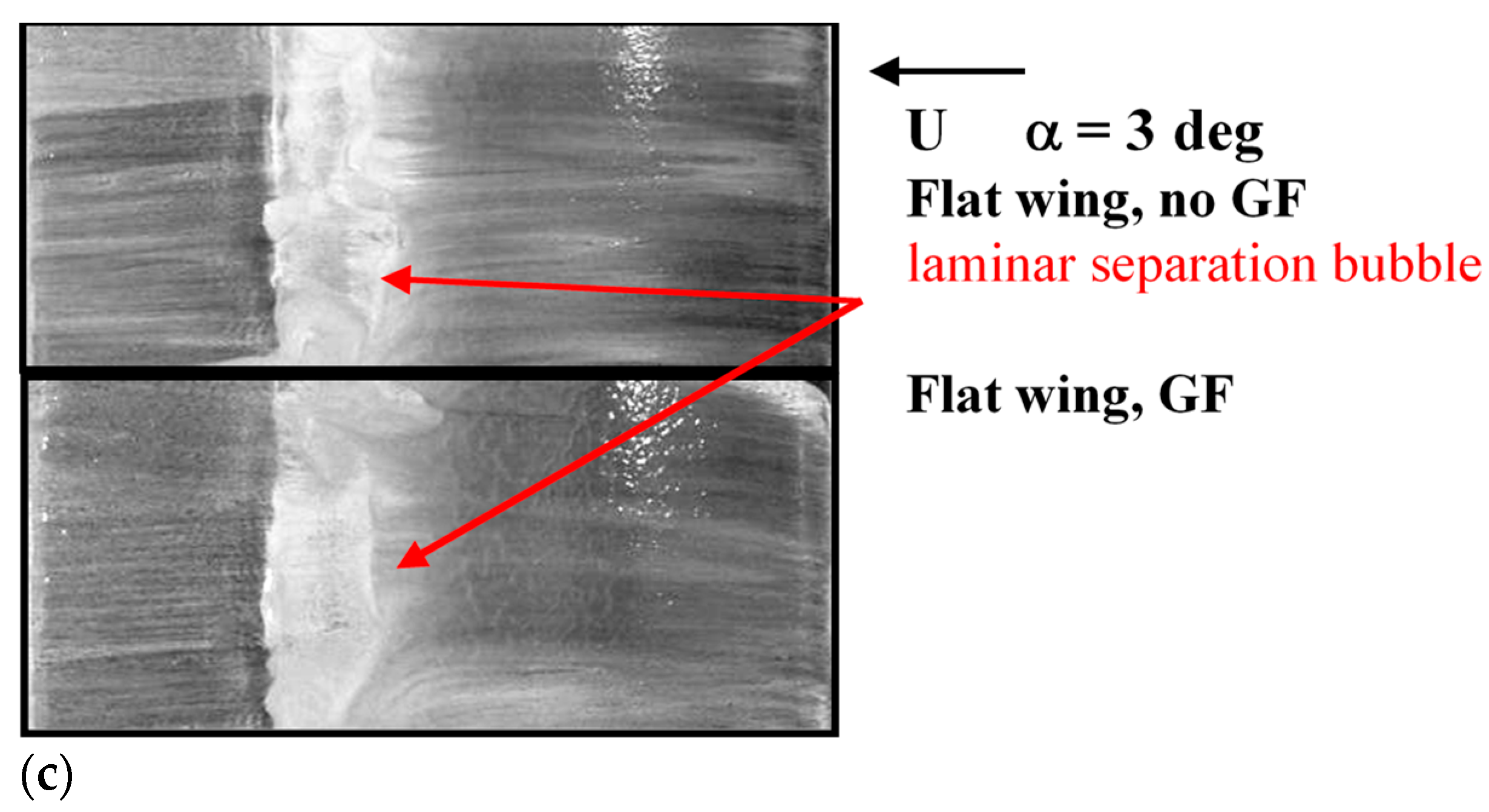
Figure 5c shows surface flow visualization (rendered using titanium dioxide suspended in paraffin and linseed oil) over a section of the wing, where the wing with and without a GF is presented at α = 3 degrees. Although the wing equipped with the GF produced more lift, the location and extent of its laminar separation bubble was very similar to that of the wing without the flap.
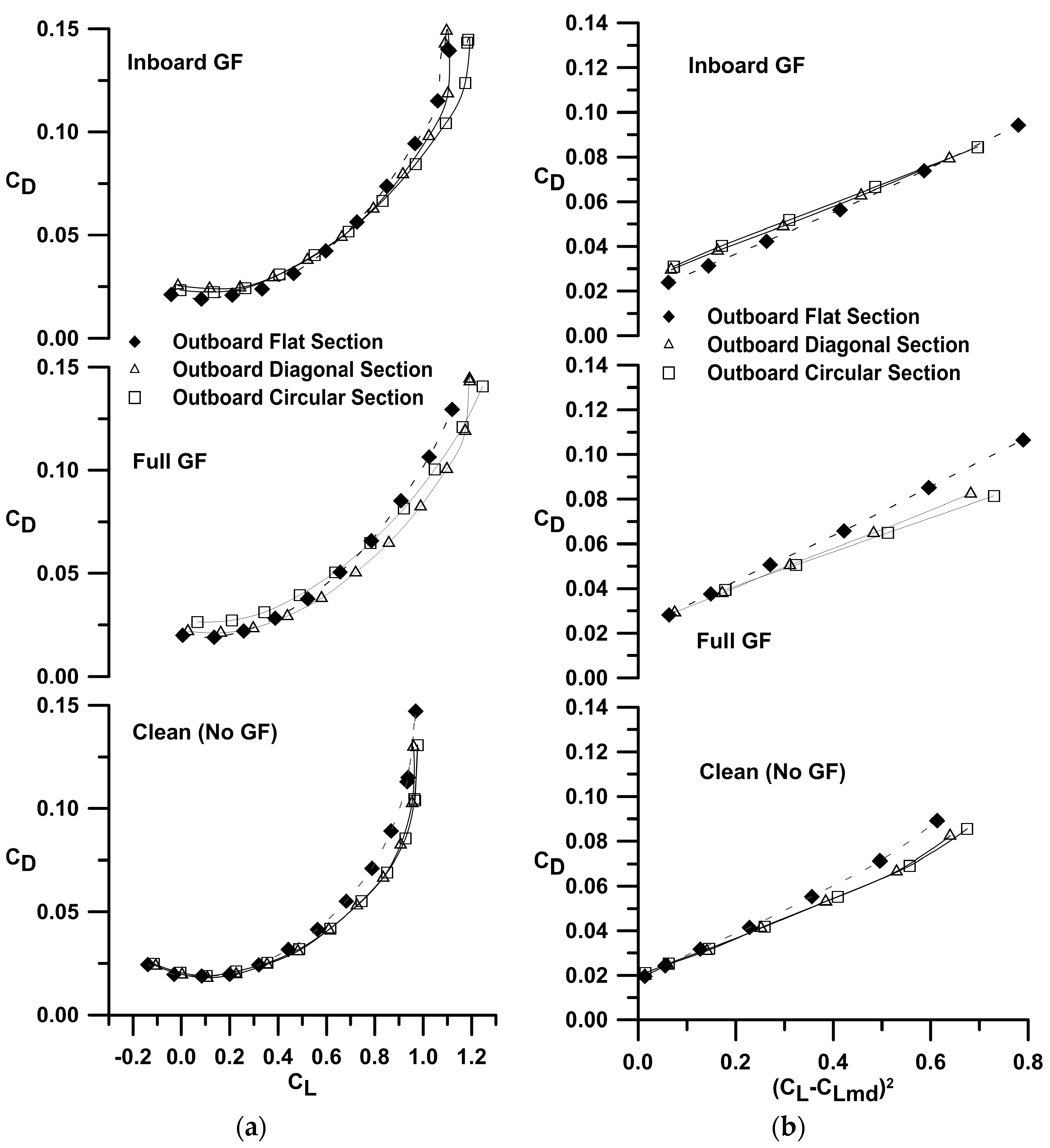
The effect of the outboard section (planar, dihedral or circular arc) for a given flap distribution is explored in
Figure 6a,b. For the clean wing (no GF) non-planarity had little effect on C
Dmin (
Table 1), while reducing the drag due to lift as shown explicitly in
Figure 6b, which is a direct benefit of non-planarity. With the full extent GF, a C
Dmin penalty was present, especially for the circular arc section. However, the induced efficiency was still greatly enhanced compared to the flat outboard section. A similar result was seen for the inboard GF distribution.
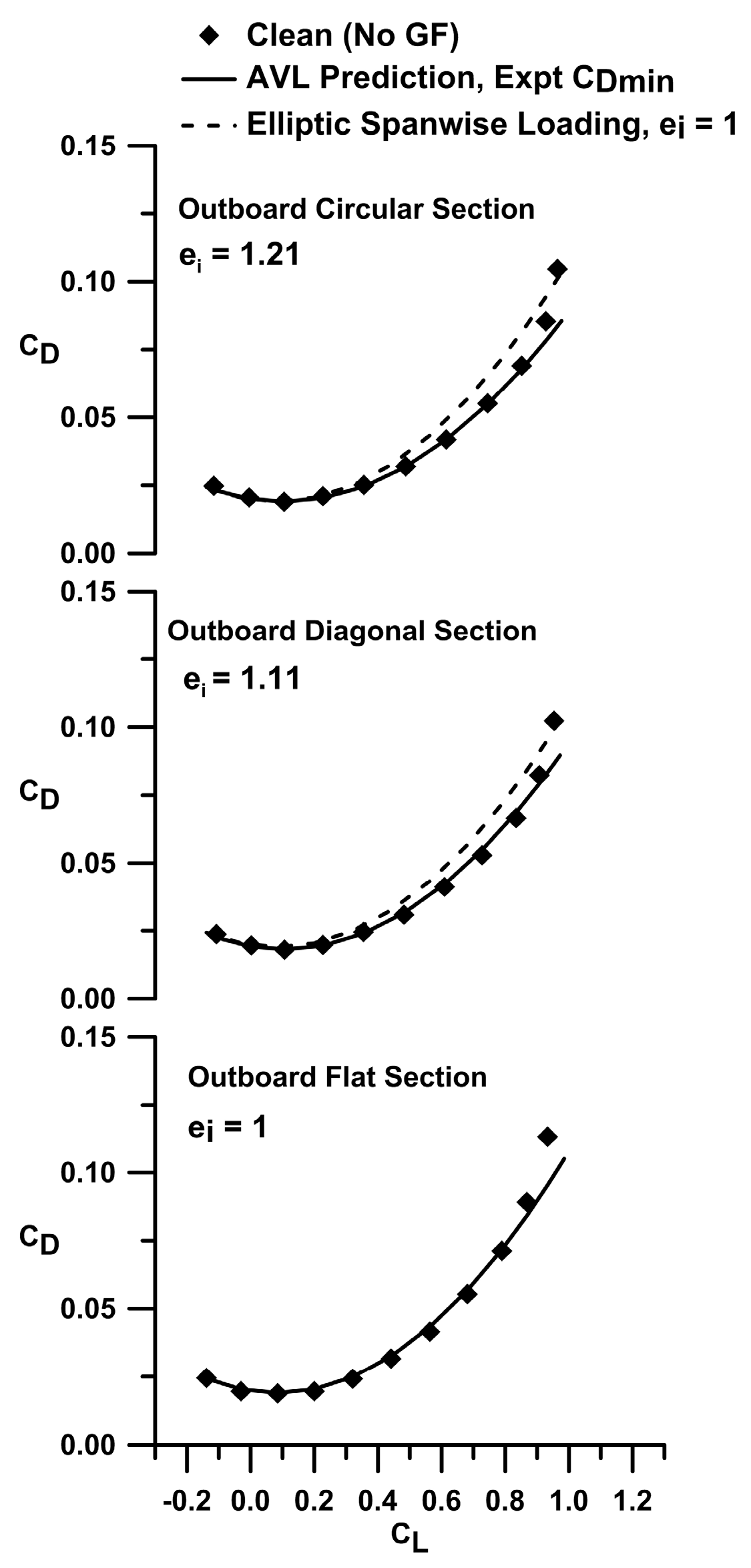
Estimates of the inviscid drag due to lift, using AVL-computed e
i, are shown for the clean (no GF) outboard circular, diagonal and flat sections in
Figure 7 (see
Table 2). The experimental C
Dmin was added to each estimate, such that the drag coefficient was calculated using
The numerical predictions show excellent agreement with the experimental data (i.e., clean). As Equation (4) does not account for sectional pressure drag it can be inferred that this quantity is small. Also included in
Figure 7 is the drag due to lift seen for elliptic spanwise loading (i.e., e
i = 1). The results clearly indicate that for a constrained span, efficiencies greater than those achievable using an optimal planar unswept wing may be achieved.
Aerodynamic benefits of non-planarity are often examined with reference to a simple planar extension of the non-planar element.
Figure 8 shows drag polars based on experimental data and assumes that the outboard diagonal and rectangular sections were flattened. Equation (4) was used in conjunction with the experimental value of e
i+p for the flat wing, replacing e
i. The aspect ratio values for the “flattened” wings were 3.42 and 3.57 for the outboard diagonal and circular arc sections, respectively. As shown, the (L/D)
max enhancement achieved through constrained span non-planarity exceeded that obtained by increasing the planar wing’s AR to match the arc length of the wing.
Figure 9 shows the experimental range parameter (lift-to-drag ratio) for the various configurations. For a given outboard geometry (
Figure 9a), addition of the GF reduced the peak C
L/C
D due to the increase in C
Dmin with flap addition. The reduction in the drag due to lift caused by the Gurney flap was negated by the increase in C
Dmin for the non-planar geometries, resulting in a decrease in (L/D)
max. The exception is the flat wing, where the negligible C
Dmin penalty with flap addition yielded a small improvement in the lift-to-drag ratio compared to the clean wing. Non-planarity resulted in significant increases in the maximum lift-to-drag ratio, with an increase of 12% over the planar wing (no GF) (
Figure 9b). As seen in
Figure 9a,b, the addition of GFs shifted the peak value of (C
L/C
D)
max to a higher C
L, whereas non-planarity without a GF had a similar effect. This shift resulted from the reduction in the slope (K
p) of the linearized polar for the non-planar wings, as well as with the addition of GFs. This can be expressed by showing the lift-to-drag ratio as follows:
Inverting for simplicity, differentiating and finding its minimum by equating the derivative to zero gives the following:
The lift coefficient for (C
L/C
D)
max follows as
(C
L/C
D)
max may be estimated by substituting Equation (6) into Equation (5).
Figure 5a and
Figure 6a indicate that all configurations have similar C
Lmd values. Equation (7) shows that a reduction in K
p, as associated with non-planarity or flap addition, can cause the maximum C
L/C
D to occur at a higher C
L.
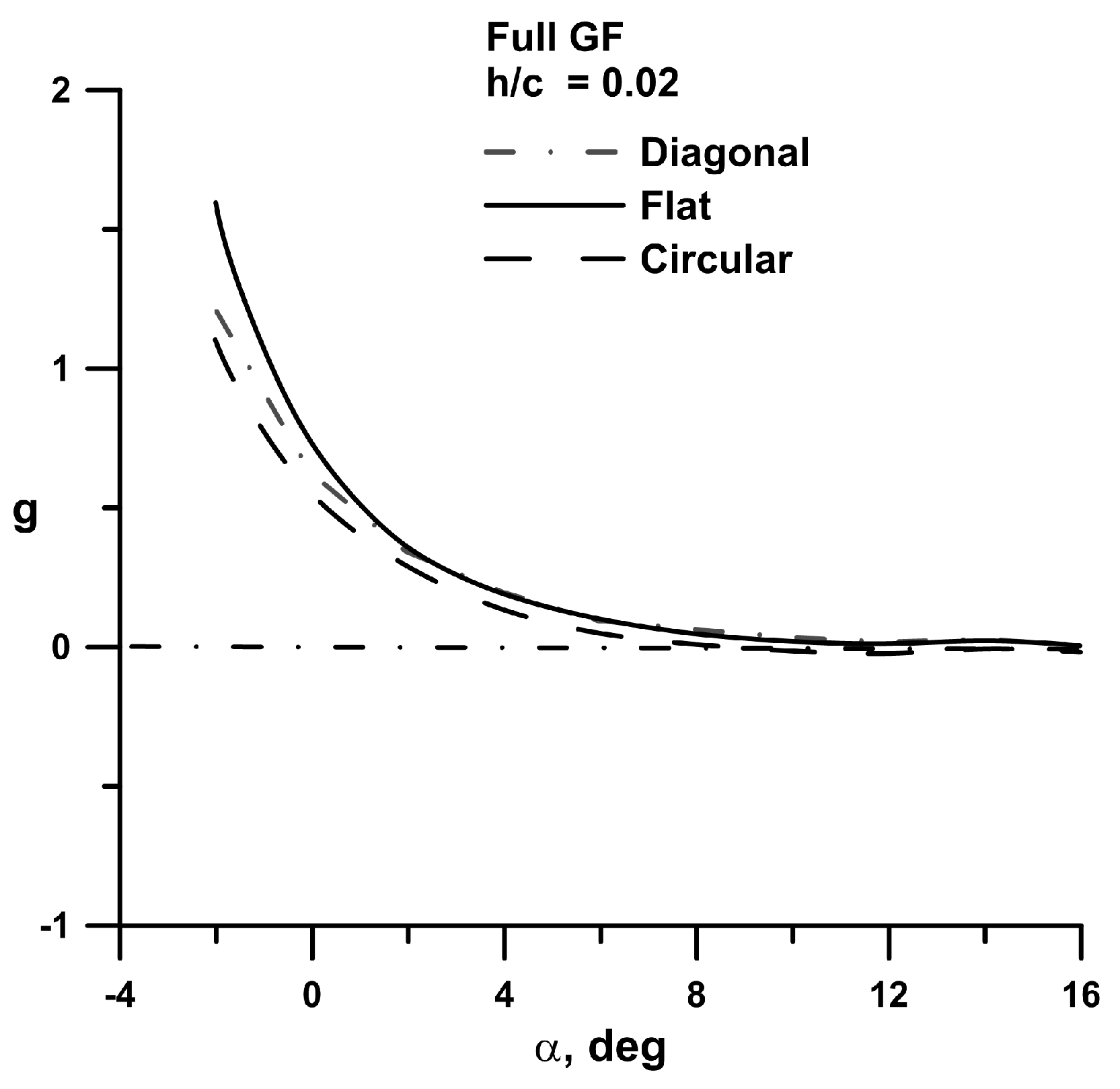
Liu [
19] suggests a “benefit” parameter, which evaluates the performance of an aerodynamic effect by accounting for its impact on both lift and drag. The relation is given by
where the differences are with respect to the clean wing without the flap. A g value greater than 0 indicates a net benefit. As seen in
Figure 10, the GF provided a benefit for all outboard geometries until α > 8 degrees. The planar wing exhibited the greatest advantage with flap addition, followed by the diagonal and circular arc tips.
The effect of non-planarity and GFs on the pitching moment coefficient is shown in
Figure 11a,b. Referring to
Figure 11a, the addition of the GF shifted the moment curve in the negative direction, which is common for a trailing edge flow effector (flap). The increase in aft loading associated with a GF is reflected in the rotation of the C
m curve, indicating a rearward shift of the wing’s aerodynamic center. This is quantified in
Table 1. The diagonal and circular tips caused a camber-like effect, shifting the moment curve negatively (
Figure 11b). This follows from the small C
L increase for a given α shown in
Figure 2b, which is consistent with flap addition.