Towards Autonomous Operation of UAVs Using Data-Driven Target Tracking and Dynamic, Distributed Path Planning Methods

Abstract

A hybrid real-time path planning method has been developed that employs data-driven target UAV trajectory tracking methods. It aims to autonomously manage the distributed operation of multiple UAVs in dynamically changing environments. The target tracking methods include a Gaussian mixture model, a long short-term memory network, and extended Kalman filters with pre-specified motion models. Real-time vehicle-to-vehicle communication is assumed through a cloud-based system, enabling virtual, dynamic local networks to facilitate the high demand of vehicles in airspace. The method generates optimal paths by adaptively employing the dynamic $A^{*}$ algorithm and the artificial potential field method, with minimum snap trajectory smoothing to enhance path trackability during real flights. For validation, software-in-the-loop testing is performed in a dynamic environment composed of multiple quadrotors. The results demonstrate the framework’s ability to generate real-time, collision-free flight paths at low computational costs.

1. Introduction

The increasing demand for Unmanned Air Systems (UASs) in low-altitude space requires the integration of UAS traffic management into the current airspace, which naturally leads to denser air traffic and increased complexity in traffic management [1]. Since 2012, the Federal Aviation Administration (FAA) has been developing the foundations of urban operations for UAVs in preparation for succeeding research works. NASA subsequently introduced the UAV Traffic Management (UTM) and urban air mobility (UAM) concepts, designed for safe and efficient future operations management [2], as well as the advent of urban air mobility (UAM) [3].

A robust, low-cost in computation, and scalable path planning framework becomes more important in managing the challenges of future urban air mobility. The purpose of the present study is to develop a computationally efficient and yet highly effective operation method to enable flight autonomy and safety. It should adapt to real-time conditions, generating collision-free paths without the need for offline training. This approach ensures scalability and reliability, making it suitable for dense UAV operations.

The major research components are as follows: (1) a ground cloud-based database system (CDS), (2) virtual and dynamic local networks, (3) data-driven target tracking models with consideration of uncertainty, and (4) an efficient hybrid path planning method without the need for offline training. These are integrated into a single operational framework and validated through software-in-the-loop simulations using a simple PID flight controller to demonstrate collision-handling capability, computational costs for path generation, and feasibility for a practical flight controller to track the planned route in real time.

The problem to solve is defined such that vehicles need to reach their pre-specified goal points in minimal traveling time without an intent of collaboration with other vehicles, while they should effectively avoid static obstacles and other moving vehicles. A key challenge is establishing a reliable communication system that allows each UAV to share its position information, enabling accurate recognition and coordination. Without a proper collision avoidance model, quadrotors are at risk of colliding, underscoring the necessity of robust target tracking methods. Additionally, guiding UAVs to their destinations requires a sophisticated path planning algorithm. To address these challenges, the proposed framework incorporates a communication module, a target tracking module for collision avoidance, and a path planning module. The validity and effectiveness of this framework are evaluated through software-in-the-loop testing, demonstrating its capability to solve the identified problem and meet the demands of dynamic UAV operation.

For communication, the ground-based cloud database system (CDS) is assumed, in line with recent practices by the FAA’s Remote ID for vehicle-to-vehicle (V2V) communication, to identify neighboring UAVs in close proximity. It receives and transmits a large number of various data, including trajectory history, in real time for UAVs sharing common airspace during operations. Along with the ground CDS, the virtual, dynamic, and local virtual network of an individual UAV becomes a fundamental unit to resolve any potential conflicts during the operation and can accommodate high-density operations, providing robust scalability almost independent of the number of UAVs in operation.

The framework utilizes data-driven target tracking methods, designed to accurately predict the near-future position of target vehicles based on their trajectory history. This approach addresses the limitations of traditional dynamic motion-based target tracking methods, particularly in predicting unknown controller types. A Gaussian mixture model (GMM) is employed to provide bounds for estimation uncertainty, which an AI-based prediction model alone cannot offer. This estimation uncertainty is utilized to enhance the calculation of safe distances from other UAVs. Along with the GMM, long short-term memory networks are employed, and the prediction results are directly compared with those of the traditional extended Kalman filter and Interacting Multiple Mode (IMM).

One of the key components of the proposed framework is hybridized dynamic path planning to leverage the complementary advantages of the A* search algorithm for robustness and the artificial potential field (APF) method for cost efficiency. A major difference compared with the existing methods to handle dynamic problems is that the utilization of the deterministic path planning module is superior in computation cost and does not require prior offline training, unlike with many machine learning or dynamic programming methods. As the UAV trajectory tracking is explicitly connected to the path planner, the uncertainty consideration becomes more flexible. The most significant mechanism lies in the adaptive switching of these two methods in response to dynamic environments in real time. It is straightforward to implement and ready for real-time simulation. The mechanism for collision avoidance varies according to the characteristics of the obstacles. Once the local virtual network forms due to neighboring UAVs in close proximity, a collision avoidance route is generated through A* search on a dynamic occupancy map that overlays three layers of position states at different physical times (past, present, and future). The collision avoidance behavior involves the simple adjustment of velocity to maintain the predefined right-of-way rules. Since the trackability of the planned route is critical but not considered during path planning, posteriori trajectory smoothing is employed by minimizing trajectory snap.

To demonstrate the validity of these operational methods, a software-in-the-loop simulation is conducted with four small-sized quadrotors flying with specified start and goal points, using trajectories for all UAVs informed by the past state from the CDS, predicted by the target tracking method, planned by the hybrid route generator, and tracked by the flight controller of the small-sized quadrotors.

One of the most significant contributions of this study is its scalability, which is nearly independent of the number of UAVs operating in shared airspace. All the methods operate within a local virtual network that dynamically changes over time. The computational cost of the route generator, the accuracy of the target tracking methods, and the trackability by the small-sized UVAs are presented in a statistical manner.

The ultimate goal of this study is to realize the distributed operation of a large number of UAVs of different types in a dynamically changing environment by enabling autonomy in situation awareness and decision making in route generation. The operational conditions assumed in this study are based on current practices in communication and onboard electronic systems.

The structure of this work is organized as follows. Section 3 introduces the concepts of data exchange and network formation for target tracking. Section 4 presents a data-driven target tracking approach, which leverages a statistical model based on a Gaussian mixture model (GMM) and a recurrent neural network (RNN) model using long short-term memory (LSTM). The mechanism underlying the hybrid path planning algorithm is detailed in Section 5. In Section 6, the performances of the data-driven methods are evaluated and compared with each other, as well as with the traditional target tracking method employing the extended Kalman filter. Finally, Section 7 simulates the proposed path planning algorithm in the context of multiple quadrotor operations.

2. Literature Review

2.1. Target Tracking Methods

Target tracking estimation, a pivotal sequential localization challenge, necessitates real-time position estimation algorithms [4]. Liu et al.’s groundbreaking work introduced a system for real-time target tracking and path planning for quadrotor UAVs in unmapped terrains [5]. They integrated tracking, learning detection with kernelized correction filters, enhancing tracking efficiency. Their elliptical tangential model bypasses traditional map-building.

Traditionally, the Kalman filter has been a foundational tool for estimating dynamic variables from noisy data [6]. Introduced in 1960 [7], the Kalman filter’s utility has expanded [8,9,10]. However, its single motion model struggles with intricate target behaviors [11]. Yaqi et al. [12] stressed the limitations of single-mode models in encapsulating dynamic target movements.

GPR is highly esteemed for delivering precise Bayesian analysis across a multitude of applications [13]. Recent studies emphasize its utility in motion state estimations for target tracking [14,15]. Notably, Aftab et al.’s work stands out, wherein GPR was employed for target shape estimations, further refining target motion using established models [16].

Building on these advances in target tracking, the field of machine learning has also seen significant developments. Deep neural networks (DNNs) have recently received renewed attention. Traditional feed-forward DNNs are composed of input and output layers linked through multiple hidden layers in between. These layers are fully connected and consist of artificial nodes that use weighted inputs and produce an output following a projection via activation functions [17]. Training a DNN typically involves the use of back-propagation and gradient descent to minimize the cost function or mean square error (MSE) of the estimated output with respect to the observed state variables [18]. Recent advances in graphics processing units (GPUs) have accelerated the evolution of neural networks, making them one of the most powerful methods in machine learning [19,20].

Further enhancing the capabilities of neural networks, recurrent neural networks (RNNs) were first introduced in the 1980s by Rumelhart, Hinton, and Williams [21], and have been an important focus of research and development since the 1990s. RNNs are designed to learn sequential or time-varying patterns [22], and are also trained using backpropagation. They contain a feedback loop, which utilizes the previous state of the nodes to determine the output at any given instant. This characteristic of temporal dependency is very effective for sequence-to-sequence problems. However, RNNs can encounter vanishing and exploding gradient problems for long-term sequences.

To resolve these issues, the long short-term memory (LSTM) was introduced by Hochreiter and Schmidhuber in 1997 [23]. LSTMs are a variant of RNNs and are designed to overcome the vanishing and exploding gradient problems associated with long-term sequences. LSTMs contain an additional common long short-term memory line, which is updated based on a nonlinear combination of its previous, current, and hidden states of the module. LSTMs have since become a very effective method and have been proven a significant advancement in a broad range of fields of study. Zhang et al. [24] and Liu et al. developed a DeepMTT network [25], with the recent inclusion of a specialized CNN-LSTM model for IoT by Hussain et al. [26]. Shu et al. [27] developed a deep neural network prediction model, utilizing a Stacked Bidirectional and Unidirectional LSTM (SBULSTM) network to predict future UAV positions.

*C14* Recently, transformer technology was introduced by [28]. It has revolutionized natural language processing through the use of a self-attention mechanism that effectively captures long-range dependencies in data, and this model architecture shows great potential for trajectory prediction as well, given its capability to manage long sequential data with intricate dependencies.

This research investigates data-driven target tracking models utilizing Gaussian Process Regression (GPR) and deep neural networks (DNNs) built on long short-term memory (LSTM). This paper presents a GPR-based target tracking method and an LSTM-based DNN model, comparing their ability to predict UAV positions and quantify collision probability in the estimated position. Details are in Section 6.

2.2. Path Planning Algorithms

Path planning algorithms have been widely used in various fields to address practical problems, such as mobile robots [29], planetary rovers [30], and autonomous sailboats [31]. The primary objective remains consistent: finding an optimal, conflict-free path in minimal time [32,33]. The artificial potential field (APF) method is favored for its computational efficiency [34], especially in UAV applications [35], but it struggles with local minima in complex terrains [36,37]. Heuristic search solvers, particularly the $A^{*}$ algorithm from the 50s to 70s, mitigate local minima issues and find optimal paths in intricate environments [38]. Their capabilities have been enhanced by Yao et al.’s weighted approach [39] and Tang et al.’s geometric innovation [40]. With the ascent of deep reinforcement learning, path planning has witnessed advancements, such as Xin et al.’s end-to-end mechanism [41] and Hu et al.’s proximal policy optimization for UAVs [42]. This study proposes a hybrid dynamic path planning algorithm, merging the APF and $A^{*}$ algorithm for effective UAV operations in both static and dynamic environments.

While graph search algorithms like $A^{*}$ and $D^{*}$ are effective, they can be time-consuming as they rely on cost maps that must be repeatedly generated and stored. In recent years, there has been increasing interest in artificial intelligence (AI)-based approaches to path planning problems, which use machine learning methods such as deep reinforcement learning, deep neural networks, or convolutional networks to minimize computation cost, while providing real-time conflict-free path planning to a target position. Many studies on AI-based path planning have been published since 2007, with examples including [43,44,45,46].

There has been increasing attention and extensive research on deep reinforcement learning. Xin et al. [41] proposed an end-to-end path planning method, named mobile robot path planning, using deep reinforcement learning, which aims to enable the robot to obtain the optimal action directly from the original visual perception without relying on handcrafted features and feature matching. Hu and colleagues [42] investigated the application of proximal policy optimization (PPO), a deep reinforcement learning algorithm, to provide secure and computationally efficient guidance for UAV operations while avoiding obstacles.

In this study, a hybrid dynamic path planning algorithm is proposed. It selectively uses a path planning algorithm between the $APF$ method and the $A^{*}$ algorithm based on the test domain size and state of environments for stability and efficient computation cost. Its performance is also compared with the results from the PPO-based path planning model.

3. Data Exchange and Network Formation for Target Tracking

The acquisition of data on the UAVs of interest is crucial for the target tracking method and is primarily accomplished through the central database system (CDS) on the ground. The establishment of the virtual formation of the local and dynamic network for the ego UAV is critical in defining the scope of the problem and contributes to the scalability of the operation. The data contents include trajectory history, UAV velocity, control station location, elevation, and more, depending on the communication module.

Variables to define mathematical formulations are defined as follows, if two-dimensional locations are considered,

$$\begin{array}{cccc}\hfill & {\mathit{T}}_k^{-,n_P}\hfill & \hfill =& \{{\mathit{X}}_k\left(t_{-i}\right)=(x_k\left(t_{-i}\right),y_k\left(t_{-i}\right),z_k\left(t_{-i}\right))|i=0,\cdots ,n_P\}\hfill \\ \hfill & {\mathit{T}}_k^{+,n_F}\hfill & \hfill =& \{{\mathit{X}}_k\left(t_{+i}\right)=(x_k\left(t_{-i}\right),y_k\left(t_{-i}\right),z_k\left(t_{-i}\right))|i=0,\cdots ,n_F\}\hfill \\ \hfill & {\widehat{\mathit{T}}}_{k^{*}}^{+,n_F}\hfill & \hfill =& \{{\widehat{\mathit{X}}}_{k^{*}}\left(t_{+i}\right)=({\widehat{x}}_{k^{*}}\left(t_{-i}\right),{\widehat{y}}_{k^{*}}\left(t_{-i}\right),{\widehat{z}}_{k^{*}}\left(t_{-i}\right))|i=0,\cdots ,n_F\}\hfill \end{array}$$

(1)

Symbol d is the dimension of input and is set to two in the present study, i.e., $(x_k,y_k)$ corresponds to the x and y coordinates of the kth UAV. The trajectory of the kth UAV is defined as ${\mathit{T}}_k={\mathit{T}}_k^{-,n_P}\cup {\mathit{T}}_k^{+,n_F}$, and the training sample dataset is $\mathit{D}=\left\{{\mathit{T}}_k\right|k=1,\cdots ,n_s\}$, where $n_s$ is the total number of sample points in the training set. Then, the trajectory of the target UAV is defined as ${\mathit{T}}_{k^{*}}={\mathit{T}}_{k^{*}}^{-,n_P}\cup {\mathit{T}}_{k^{*}}^{+,n_F}$ with the test set denoted as ${\mathit{D}}^{*}=\left\{{\mathit{T}}_{k^{*}}\right|k^{*}=1,\cdots ,n_{ts}\}$, where $n_{ts}$ is the number of sample points pre-selected for posterior validation. The network of the kth UAV at time t is defined as ${\mathcal{N}}_k\left(t\right)=\left\{{\mathit{T}}_i^{-,n_P}\right|i=1,\cdots ,n_{net}^k\left(t\right)\}$, where $n_{net}^k\left(t\right)$ represents the number of member UAVs within the local network at time t. In this study, $\widehat{(·)}$, ${(·)}^{-}$, ${(·)}^{+}$, and $\mathcal{E}$ represent estimated values, previous states, future states, and the sum of root mean square error (RMSE), respectively.

The target tracking methods utilized in this study are (1) an extended Kalman filter (EKF) method, (2) a Gaussian mixture model, and (3) a deep learning based long short-term memory network with encoder and decoder. A problem formulation for the method is as follows.

$$\begin{array}{cc}\hfill & \mathrm{Find}:\underset{{\widehat{x}}_i^{+},x_i}{\mathrm{minimize}}\mathcal{E}=\sum _{i=1}^{n_F}{\parallel {\widehat{\mathit{X}}}_{k^{*}}\left(t_{+i}\right)-{\mathit{X}}_{k^{*}}\left(t_{+i}\right)\parallel }_2\mathrm{given}{k}^{*}\hfill \\ \hfill & \mathrm{subject}\mathrm{to}:{\mathit{X}}_{k^{*}}\left(t_{+i}\right)\in {\mathit{D}}^{*}\hfill \end{array}$$

(2)

where $\mathcal{E}$ is a $l_{\infty }$ norm of the differences in the future state, positions only in the current study, between the true and the estimated values by a target tracking model.

3.1. Data Exchange and Communication via Central Database System (CDS)

A key operation concept of the study includes a ground central database system (CDS), real-time data exchange among multiple UAVs via the ground CDS, and a local and dynamic network of the UAVs that varies over time. A recent protocol of a remote ID [47] enables the broadcasting of the UAV information within about a 1 km range of the vehicle registration, GPS data, USS, FIMS, and sensor data, as well as take-off information. A ground CDS is set up in the present study as a cloud-based data storage and management system and constantly receives remote ID data from all UAVs during their entire mission. As the direct vehicle-to-vehicle communication is still limited in practice, an individual UAV receives data on a particular UAV of interest, sending a request to the ground CDS, and the data exchange is carried out in real time using Wi-Fi out of the other available communication modes of radio frequency, 5G, Long Range Wide Area Network (LoRAWAN) [48], or satellite transmission. The data collection rate is set to be 10 Hz to ensure compliance with the trajectory modeling time constraint.

While establishing the details of feasible communication protocols and time synchronization for vehicle-to-vehicle and vehicle-to-server interactions, such as ROS2 (Robot Operating System 2), is important, this paper primarily focuses on defining the essential structure and core concepts of our proposed framework. Key components of this framework include data exchange through a central database system (CDS) and the creation of a virtual, local dynamic network for UAV operations.

3.2. Virtual, Local Dynamic Network

Although a centralized operation system, where all information needs to be centralized in a single location [49], has the potential to achieve completeness and global optimization, it cannot effectively handle a large number of UAVs. When controlling a large number of UAVs, centralizing all information in a single location can lead to significant communication and computation overheads. The central system must process vast amounts of data in real-time, which can overwhelm the system, cause delays, and create bottlenecks, thereby reducing overall efficiency and responsiveness. Also, unexpected local events are best handled by local networks of the UAVs autonomously.

To manage heavy workloads, a network formation approach is proposed, where neighboring UAVs close to the ego UAVs are identified using a central cloud-based database system. The virtual and local dynamic network is a fundamental unit of the operation of an individual UAV for the target tracking of and collision avoidance with neighboring UAVs.

It is composed of an ego UAV and its neighboring UAVs within a pre-specified distance, and constantly changes, with its membership created and removed dynamically over time. It prohibits overload in communication and computation of an individual UAV, and enables the decentralized (i.e., distributed) operation based on autonomous decision making in optimal path planning and collision avoidance.

The coverage range of remote ID via LoRaWAN is extended up to 1 km through the utilization of an antenna with a transmission power of 14 dBm. The local dynamic network of the ego UAVs only allows membership to those UAVs that newly enter within the communication radius of 300 m.

Let ${\mathcal{N}}_k\left(t\right)$ represent the local dynamic network of the $k$-th UAV at time t, and it includes a set of trajectory histories of the neighboring UAVs within communication range.

$$\begin{array}{cc}\hfill & {\mathcal{N}}_k\left(t\right)=\left\{{\mathit{T}}_i^{-,n_P}\right|i=1,\dots ,n_{net}^k\left(t\right)\},\mathrm{given}k\hfill \end{array}$$

(3)

where $n_{net}^k\left(t\right)$ represents the total number of member UAVs at time t, and can vary over time. This allows greater autonomy and flexibility in decision making, without relying on a central system to coordinate their actions. This approach also enables UAVs to adapt to changes in the environment and handle complex scenarios more effectively.

4. Data-Driven Target Tracking Models

This section discusses target tracking models that utilize the trajectory histories of target UAVs within the proposed framework. Two types of models are examined: a statistical model and a neural network-based model.

4.1. Statistical Model: Gaussian Mixture Model

For diverse UAV trajectories, training the target tracking model requires extensive sample data, making a single GPR model insufficient. The Gaussian mixture model (GMM) [50] classifies trajectory types and predicts future paths. Rather than time-dependent GMM or GPR models, this study utilizes data classification by labels: past positions as labels and corresponding future positions as features.

The GMM is defined as a sum of M Gaussian distributions and can be defined as follows,

$$\begin{array}{cc}\hfill & p\left({\mathit{X}}_{k^{*}}\left(t_{+}\right)\right|{\mathit{X}}_{k^{*}}\left(t_{-}\right),{\mathit{T}}_{k=1:n_s}^{-,np},{\mathit{T}}_{k=1:n_s}^{+,nF})\hfill \\ \hfill & =\sum _{m=1}^M{\pi }_m\mathcal{N}({\mathit{X}}_{k^{*}}\left(t_{-}\right)\mid ,{\mathit{X}}_{k^{*}}\left(t_{+}\right),{\mu }_{\mathit{m}},{\pi }_{{\mathit{C}}_{\mathit{m}}})\hfill \end{array}$$

(4)

where Gaussian distribution is weighted by the parameter ${\pi }_m$, reflecting the proportion of data points in that Gaussian component. These mixing coefficients, ${\pi }_k$, satisfy $0\le {\pi }_k\le 1$ with their sum equaling 1 [51]. These coefficients are determined using the Expectation-Maximization (EM) algorithm, a method that iteratively refines latent variable distributions and model parameters to maximize the likelihood of the observed data.

All waypoints of any kth UAV, ${\mathit{X}}_k\left(t_{·}\right)$, along the trajectory of ${\mathit{T}}_k$ are assumed to follow the normal distribution of $\mathcal{N}({\mathit{X}}_k\left(t_{·}\right)\mid {\mu }_m,C_m)$, where ${\mu }_m$ and $C_m$ are the mean and covariance matrix, respectively, for the mth Gaussian component. Then, the estimation of the future state of the $k^{*th}$ target UAV follows the following probability distribution function based on the observation on the fixed duration of time in the past, $\{t_{-n_P},t_{-n_P+1},\cdots ,t_0\}$, where ${\mathit{X}}_{k^{*}}\left(t_{-}\right)$ and ${\mathit{X}}_{k^{*}}\left(t_{+}\right)$ are the approximated history and future trajectory in the current study of the target tracking. The parameters ${\pi }_{m}x$, ${\mu }_m$, and ${\pi }_{C_m}$ represent mixture weights, means, and covariance matrix, and can be found as,

$$\begin{array}{cc}\hfill {\pi }_m& ={\displaystyle \frac{{\pi }_{m}p(\mid {\mu }_{m,{\mathit{X}}_{k^{*}}\left(t_{-}\right)},C_{m,{\mathit{X}}_{k^{*}}\left(t_{-}\right),{\mathit{X}}_{k^{*}}\left(t_{-}\right)})}{{\sum }_{j=1}^M{\pi }_{j}p({\mathit{X}}_{k^{*}}\left(t_{-}\right)\mid {\mu }_{\mathit{j},{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{-}\right)},{\mathit{C}}_{\mathit{j},{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{-}\right),{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{-}\right)}}}\hfill \\ \hfill {\mu }_{\mathit{m}}& ={\mu }_{\mathit{m},{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{+}\right)}\hfill \\ \hfill & +{\mathit{C}}_{\mathit{m},{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{+}\right),{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{-}\right)}{\mathit{C}}_{\mathit{m},{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{+}\right),{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{-}\right)}^{-\mathbf{1}}({\mathit{X}}_{k^{*}}\left(t_{-}\right)\hfill \\ \hfill & -{\mu }_{m,{\mathit{X}}_{k^{*}}\left(t_{-}\right)})\hfill \\ \hfill {\pi }_{{\mathit{C}}_{\mathit{m}}}& ={\mathit{C}}_{\mathit{m},{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{+}\right),{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{+}\right)}-\hfill \\ \hfill & {\mathit{C}}_{\mathit{m},{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{+}\right),{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{-}\right)}{\mathit{C}}_{\mathit{m},{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{-}\right),{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{-}\right)}^{-\mathbf{1}}{\mathit{C}}_{\mathit{k},{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{-}\right),{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{+}\right)}\hfill \end{array}$$

(5)

where, $\mu$ and $\mathit{C}$ are composed of

$$\begin{array}{cc}\hfill {\mu }_{\mathit{m}}& =\left[\begin{array}{c}{\mu }_{\mathit{m},{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{-}\right)}\\ {\mu }_{\mathit{m},{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{+}\right)}\end{array}\right],\hfill \\ \hfill {\mathit{C}}_{\mathit{m}}& =\left[\begin{array}{cc}{\mathit{C}}_{\mathit{m},{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{-}\right),{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{-}\right)}& {\mathit{C}}_{\mathit{m},{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{-}\right),{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{+}\right)}\\ {\mathit{C}}_{\mathit{m},{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{+}\right),{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{-}\right)}& {\mathit{C}}_{\mathit{m},{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{+}\right),{\mathit{X}}_{{\mathit{k}}^{*}}\left({\mathit{t}}_{+}\right)}\end{array}\right]\hfill \end{array}$$

(6)

Finally, the mean and covariance matrices of the mixture model, $\mu$ and $\mathit{C}$, can be found,

$$\begin{array}{cc}\hfill \mu & =\sum _{m=1}^M{\pi }_m{\mu }_{\mathit{m}}\hfill \\ \hfill \mathit{C}& =\sum _{m=1}^M{\pi }_m\left({\mathit{C}}_{\mathit{m}}+({\mu }_{\mathit{m}}-\mu ){({\mu }_{\mathit{m}}-\mu )}^T\right)\hfill \end{array}$$

(7)

The state estimations, ${\widehat{\mathit{X}}}_{k^{*}}\left(t_{+}\right)$, are represented by $\mu$, and the covariance matrices, $\mathit{C}$, are used to calculate a $95\%$ confidence interval of estimation uncertainty for the data-driven target tracking method.

The pairwise collision probability at given time t between mth and nth UAVs is defined as $p_{collision}(m,n,t)$. For all member UAVs in the local network of the mth UAV, their corresponding sets of GMM models are built independently. The difference in the position state against the nth member UAV also follows the normal distribution, with mean ${\mu }_m\left(t\right)-{\mu }_n\left(t\right)$ and variance ${\sigma }_m^2\left(t\right)+{\sigma }_n^2\left(t\right)$

$$\begin{array}{cc}\hfill p_{collision}(m,n,t)& =p\left(\right|{\mathit{X}}_m\left(t_{+i}\right)-{\mathit{X}}_n\left(t_{+i}\right){|}_{\infty }\le d_{safe})\hfill \\ \hfill & =p(\underset{h=1,2}{max}\left(\right|x_{m,h}\left(t\right)-x_{n,h}\left(t\right)|\le d_{safe})\hfill \\ \hfill & =\prod _{h=1}^{d}p\left(\right|x_{m,h}\left(t\right)-x_{n,hf}\left(t\right)|\le r)\hfill \\ \hfill & =\prod _{h=1}^d\left[\Phi \left({\displaystyle \frac{d_{safe}-{\mu }_{m,h}\left(t\right)+{\mu }_{n,h}\left(t\right)}{\sqrt{{\sigma }_{m,h}^2+{\sigma }_{n,h}^2}}}\right)\right.\hfill \\ \hfill & \left.-\Phi \left({\displaystyle \frac{-d_{safe}-{\mu }_{m,h}\left(t\right)+{\mu }_{n,h}\left(t\right)}{\sqrt{{\sigma }_{m,h}^2+{\sigma }_{n,h}^2}}}\right)\right]\hfill \end{array}$$

(8)

4.2. Neural Network-Based Long Short-Term Memory

The LSTM encoder–decoder is a type of recurrent neural network designed specifically to solve sequence-to-sequence problems. Prediction is challenging as the input and output sequences can vary in length, while neural networks are designed to handle fixed-length inputs. To resolve this, multiple-length inputs are converted into fixed-length vectors through encoding, which are as fixed-length vectors. The LSTM architecture is suitable for predicting nonlinear motion trajectories in target tracking, where the size of input and output vectors differ. It takes in the trajectory history of neighboring UAVs as input and estimates the next predicted positions.

The LSTM cells in the architecture consist of four components: the input gate, forget gate, memory cell, and output gate. The input gate determines which parts of the current input should be stored in the memory cell, while the forget gate determines which parts of the previous state should be discarded. The memory cell is a type of memory that can selectively remember or forget information based on the input and previous state, and the output gate determines which parts of the memory cell should be used to generate the output.

$$\begin{array}{cc}\hfill {\mathit{i}}_t& =\sigma (W_i{\mathit{x}}_{k,t}^{-}+U_i{\widehat{\mathit{x}}}_{k,t-1}^{+}+b_i)\hfill \\ \hfill {\mathit{f}}_t& =\sigma (W_f{\mathit{x}}_{k,t}^{-}+U_f{\widehat{\mathit{x}}}_{k,t-1}^{+}+b_f)\hfill \\ \hfill {\mathit{C}}_t& ={\mathit{f}}_t{\mathit{C}}_{t-1}+{\mathit{i}}_{t}tanh(W_C{\mathit{x}}_{k,t}^{-}+U_C{\widehat{\mathit{x}}}_{k,t-1}^{+}+b_C)\hfill \\ \hfill {\mathit{o}}_t& =\sigma (W_o{\mathit{x}}_{k,t}^{-}+U_o{\widehat{\mathit{x}}}_{k,t-1}^{+}+b_o)\hfill \end{array}$$

(9)

where $i_t$, $f_t$, and $o_t$ are the input gate, forget gate, and output gate outputs at time t, respectively; $C_t$ is the memory cell state at time t; ${\mathit{x}}_k^{-}$ is the input vector at time t; ${\widehat{\mathit{x}}}_{t-1}^{+}$ is the previous LSTM output; $\sigma (·)$ is the sigmoid activation function; and $tanh(·)$ is the hyperbolic tangent activation function. $\mathit{W}$ and $\mathit{U}$ are weight matrices, and b is a bias vector. These components work together to resolve the problem of vanishing gradients in traditional RNNs and make LSTM networks more effective at handling sequential data. The ${\widehat{\mathit{x}}}_t^{+}$ is the LSTM output at time t and can be found as in Equation (10).

$$\begin{array}{c}\hfill {\widehat{\mathit{x}}}_t^{+}=tanh({\mathit{f}}_t\circ {\mathit{C}}_{t-1}+i_t\circ tanh(W_C{\mathit{x}}_{k,t}^{-}+{\mathit{U}}_C{\widehat{\mathit{x}}}_{k,t-1}^{+}+b_C))\end{array}$$

(10)

The LSTM network proposed for target tracking is designed to predict future positions based on sequences of past observations. The model processes input sequences of 10 time steps, each containing x, y, and z coordinates, through three LSTM layers. The first layer processes the sequence, the second reduces dimensionality, and the third generates predictions for the next three time steps. A RepeatVector layer ensures the correct output shape, and a TimeDistributed dense layer produces the final coordinates with a linear activation function. The model is trained using the Adam optimizer and MSE loss function over 2000 epochs and consists of 8543 trainable parameters.

In summary, these target trajectory tracking models are programmed into the real-time path planners that are explained in the following section to predict future collisions and generate optimal routes to the goal points.

5. Real-Time Hybrid and Dynamic Path Planning Algorithm

The problem formulation of optimal path planning is to find the shortest path from the start point to the goal point, and is given in Equation (11). The trajectory of the kth UAV was defined in Equation (1) as a time series in reference to the present time, $t_0$, but can also defined in terms of the order of the waypoints from the start point to the goal point, ${\mathit{T}}_k=\left\{{\mathit{X}}_k\left(p_j\right)\right|j=1,2,\cdots ,N_p\left(k\right)\}$, where $p_1$, $N_p\left(k\right)$, and $p_{N_p}\left(k\right)$ represent the total number of waypoints, a start point, and the goal point on the route of the kth UAV, respectively. The computation cost for path planning is constrained to less than one second, which is the time needed for the occupancy map update. The total distance traveled can be calculated by creating waypoints at each time step, as presented in Equation (11).

$$\begin{array}{cc}\hfill & \mathrm{Find}:\mathrm{minimize}\sum _{j=1}^{N_p\left(k\right)-1}\parallel {\mathit{X}}_k\left(p_{j+1}\right)-{\mathit{X}}_k\left(p_j\right)\parallel \mathrm{for}\mathrm{any}k\hfill \\ \hfill & \mathrm{subject}\mathrm{to}:t_{comp}<1\sec \hfill \\ \hfill & p_{collision}(k,l,t)\ge P_{ϵ},\mathrm{for}\mathrm{all}k\mathrm{and}l,k\ne l,\hfill \\ & \mathrm{and}k,l\in \{1,2,\cdots ,N_d\}\hfill \end{array}$$

(11)

where $p_{collision}(k,l,t)$ represents the collision probability at time t between the kth and the lth UAV, as defined in Equation (8), and $P_{ϵ}$ is a pre-specified threshold probability to enforce no-collision, e.g., 0.99.  $t_{comp}$ is the computation time for the path planning calculation at each time step. $N_d$ is the total number of neighboring UAVs in the host UAV’s local dynamic network.

5.1. Mechanism of a Hybrid Path Planner

An underlying mechanism of the hybrid path planner algorithm is dynamic switching between two different search methods. The algorithm selectively utilizes the APF method and the $A^{*}$ algorithm, as the switching is triggered when neighboring UAVs join the local virtual network of the host UAV, with the data communication rate at 10 Hz. Figure 1 highlights the drawback of the APF method in dealing with the local area of a complex environment, where the paths become trapped in local minima. The red triangles denote the starting points of each drone, while the inverted triangles mark their goal points. The solid blue lines represent the drones’ trajectories. To overcome the drawbacks, the hybrid planning method is developed.

At the beginning of the planning, the APF method is used to find a global conflict-free path to the pre-specified goal point, where the environment is fully known a priori and time-invariant with simple static obstacles of buildings, mountains, or geo-fences.

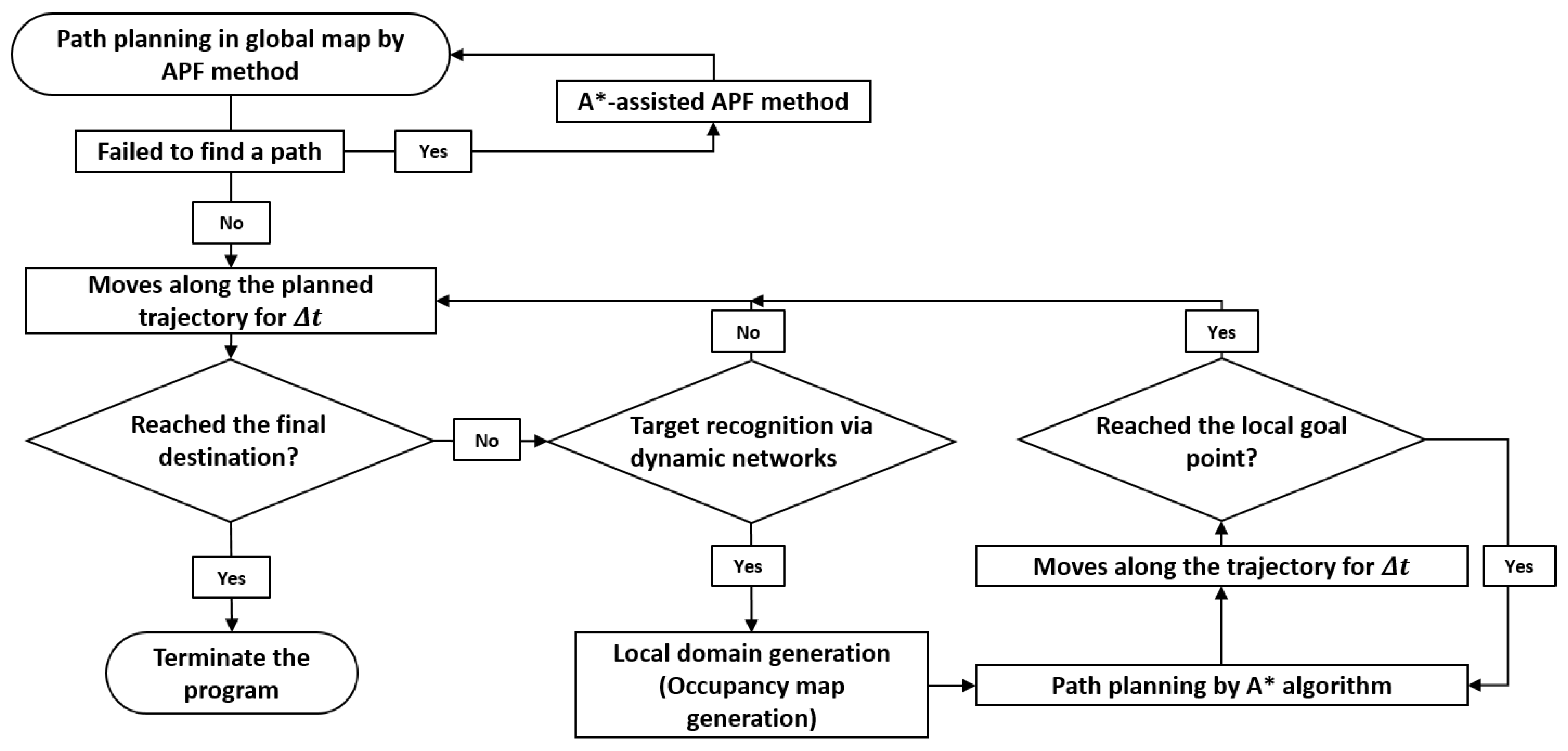
When neighboring UAVs enter the communication radius, $r_{comm}$, of the host UAS’s local dynamic network, the system switches from the APF method, used for global path planning, to the $A^{*}$ algorithm to address local path planning challenges. Figure 2 describes a flowchart of the hybrid dynamic path planning algorithm. Once the virtual local network has non-zero membership, the target tracking model is used to predict the behaviors of member UAVs during the instant future within the network, where the model is trained online with the dataset $D={({\mathit{X}}_i^{N_t},r_i^{N_H})}^N$. $N_t$ and $N_H$ indicate the length of the input and output vectors, respectively.

The path planning algorithm subsequently generates a local domain and defines a local goal point, which is at the intersection of the boundary of the local domain and the path planned initially by the APF method. The topological representation of the local virtual network is made by the occupancy map, which is explained in detail in Section 5.3, together with the local search algorithm. Based on the change in the dynamic environment, an instantaneous conflict-free path is repeatedly calculated until the neighboring UAVs are out of the bounds of the local domain or arrive at their own goal points. The local path planning process is terminated when the ego UAV reaches the local goal point, and the path planning algorithm turns the ego UAV back into the global conflict-free path, which has been calculated in the global path planning by the APF method. The hybrid dynamic path planning algorithm repeatedly executes transitions between the global and the local path planning until the UAV reaches the final destination. If a feasible path cannot be determined, the system initiates a fallback protocol, which may include returning to a safe location or awaiting further instructions, ensuring that the UAV operates safely. Algorithm 1 shows the pseudo algorithm for the hybrid dynamic path planning algorithm.

Algorithm 1 Pseudo Algorithm for Hybrid Dynamic Path Planning

1: while  ${\mathit{x}}_g\ne {\mathit{x}}_s$  do   2:    while $\mathrm{APF}\_\mathrm{reached}\ne 0$ do   3:      Run APF(${\mathit{x}}_s$)   4:      if $\mathrm{APF}\_\mathrm{reached}=0$ and $\mathrm{Goal}\ne \mathrm{Start}$ then   5:         Run $A^{*}$_assisted_APF(${\mathit{x}}_s$)   6:         $\mathrm{APF}\_\mathrm{reached}=0$   7:      end if   8:    end while   9:    $t=t+\Delta t$ 10:    Start = APF_method(t) 11:    if $d_k\leftarrow r_{comm}$ then 12:      Create Local_domain() 13:      while Goal_local $\ne {\mathit{x}}_g$ do 14:         Run occupancy_map(m,n) 15:         Run target_tracking(${\mathit{x}}^{-},{\mathit{x}}^{-}$) 16:         RUN $A^{*}$_algorithm($x_s,y_s$) 17:         $t_{total}=t_{total}+\Delta t_{total}$ 18:         ${\mathit{T}}_p=Astar\_path\left(t_{total}\right)$ 19:         $\{x_s,y_s\}={\mathit{T}}_p(t+\Delta t)$ 20:         ${\mathrm{start}}_{\mathrm{local}}$ = $\{x_s,y_s\}$ 21:      end while 22:      Terminate Local_domain() 23:    end if 24:    Start = ${\mathrm{Start}}_{\mathrm{local}}$ 25: end while

5.2. A*-Assisted Global Path Planning

The global path planning by the APF method can still fail to find a solution due to the presence of the local minima, even in a simple occupancy map with two or three obstacles. In such cases, the $A^{*}$ assisted APF method algorithm is performed to escape from the local minima by re-calculations of an optimal path from the waypoints. These waypoints are generated by the $A^{*}$ algorithm with a coarse grid once the APF method fails to find the path. The pseudo algorithm of the $A^{*}$ assisted APF method is provided in Algorithm 2.

Algorithm 2 $A^{*}$-Assisted APF Method

1: $m,n$← map matrix with a size of m by n   2: APF($x_s$, $y_s$)   3: if APF = 0 then   4:    Run occupancy_map(m, n)       // coarse grid generation   5:    ${\mathit{T}}_p=A^{*}algorithm(x_t,y_t)$               // uses the latest position of UAS($x_t$, $y_t$)   6:    ${\mathit{T}}_w=creat{e}_{w}a{y}_{p}oints\left(T_p\right)$             // based on solutions for $A^{*}$ algorithm   7:    n = 1   8:    while APF = 0 do   9:      { $x_n$, $y_n$ } = ${\mathit{T}}_w$ 10:      Run APF($x_n$, $y_n$)                       // Run at the n-th waypoint 11:      n = n + 1 12:    end while 13:    Run APF($x_{n-1}$, $y_{n-1}$) 14: end if

As the time complexity increases by $\mathcal{O}\left(n^2\right)$ in the 2D map, the size of grid is critical. The algorithm creates a coarse grid over the map, and the $A^{*}$ algorithm is then executed to calculate a conflict-free path to the desired goal point. Based on the solution, the algorithm generate a series of waypoints along the path, which are defined as the coordinates of new starting points of the APF method during re-planning. The algorithm picks the front point for the next run of the APF method and repeats the re-planning process until it finds an optimal path to the goal point.

5.3. Local Path Planning with Dynamic Occupancy Map

In local path planning, the environment is highly dynamic, with multiple UAVs operating nearby. To enable real-time decision making, a dynamic occupancy map is generated, consisting of multiple layers that reflect the continuously changing environment. The $A^{*}$ algorithm is utilized to navigate through these layers, identifying the optimal path while accounting for the presence of other UAVs. This section will explore the generation of the dynamic occupancy map and the collision avoidance methods used in the proposed framework.

Dynamic Occupancy Map

Topological representation of the dynamic environment is developed as an occupancy map to effectively handle both static objects and moving UAVs for local path planning within the virtual local network and effectively facilitate collision avoidance. The $A^{*}$ algorithm finds instantaneous conflict-free paths and is repeatedly executed with the updated state of other UAVs.

The occupancy map contains three layers of obstacle data, which are (1) an environment layer, (2) a position layer about all UAVs in the network, and (3) prediction layer state estimations of their future positions. Each layer is formulated as a matrix, and represents the location of the obstacles over the 2D coordinate system. The elements of a matrix are composed of integers of inf, 0, 1, where the value of each individual element is defined as follows,

$${\mathit{L}}_k(i,j)=\left\{\begin{array}{cc}\mathit{if}\mathrm{map}\mathrm{boundary},\hfill & {\mathit{L}}_k(i,j)=\inf \hfill \\ \mathit{else}\mathrm{if}\mathrm{occupied},\hfill & 1\le {\mathit{L}}_k(i,j,k)\le N_L\hfill \\ \mathit{else}\mathrm{empty},\hfill & {\mathit{L}}_k(i,j,k)=0\hfill \end{array}\right.$$

(12)

where $i\in \{1,2,3,\dots ,m\}$,$j\in \{1,2,3,\dots ,n\}$, and $k\in \{1,2,3,\dots ,N_L\}$. The occupancy map of ${\mathit{M}}_{\mathcal{O}}$ can be obtained by a sum of matrices of three layers, ${\mathit{M}}_{\mathcal{O}}={\mathit{L}}_1\cup {\mathit{L}}_2\cup {\mathit{L}}_3$, where $i\in \{1,2,3,\dots ,m\},\mathrm{and} j\in \{1,2,3,\dots ,n\}$. $N_L$ is the total number of layers (i.e., three in the present study), $\mathit{L}$ is the matrix of layers of the occupancy map, and m and n are the grid size of the local domain in the x and y directions, respectively. The environment layer represents the static state of the environment. The position layer shows the current coordinates of all UAVs, which are time-dependent and updated at each time step during local path planning. The prediction layer describes estimated positions of the moving UAVs in the near future by the target-tracking models, and the state predictions are projected onto the prediction layer as virtual obstacles. The three layers are combined to form an occupancy map that overlays the coordinates of all obstacles. The occupancy map evolves over time, with time step $\Delta t$, as illustrated in Figure 3. The dynamic obstacles are represented by small circles with a triangle at the center, while the static obstacles are depicted as a grey shaded area. Figure 3b,c show the changes in coordinates of dynamic obstacles evolving with time.

5.4. Collision Avoidance in Multiple Vehicle Operation

A multiple UAV operation with an individual UAV autonomously generating its own occupancy map is critical in collision-free path planning in a local region, where information on the coordinates of static obstacles, current and predicted positions of member UAVs received onto the UAV onboard system in real time from the ground CDS, and the pseudo code of the occupancy map in handling multiple UAVs are shown in Algorithm 3. At each iteration, the elements of the position and prediction layers are initialized to zero and then marked as one, corresponding to the coordinates of the estimated and current positions of each UAV, respectively. Meanwhile, the environment layer is initialized and updated once at the beginning of the local planning. By superimposing these layers, an occupancy map is updated with the current and estimated positions of the member UAVs in the local network.

Detection of the collision is set by the safety distance between any two UAVs, and a simple rule of right-of-way is applied in order to prevent the complexity of avoidance control. As an individual UAV can share this information by remote ID, the rule of right-of-way is a feasible choice at reduced cost. Similar to how autonomous vehicles on the road prioritize safety through predefined traffic protocols, utilizing right-of-way rules ensures streamlined and safer UAV operations. The closest point of approach (CPA) [52] was modified in the present study to take into account estimation uncertainty with 95% confidence in order to maintain a safe distance, $d_{safe}$, to the estimated position by Equation (13),

$$\begin{array}{cc}\hfill & d_{safe}=d_{cpa}+dea\hfill \\ \hfill & d_{cpa}=\sqrt{\parallel {\mathit{x}}_{\mathit{r}}{\parallel }^2+t_{cpa}{\mathit{x}}_{\mathit{r}}^T{\mathit{v}}_{\mathit{r}}}\hfill \\ \hfill & t_{cpa}=\left\{\begin{array}{cc}{\displaystyle \frac{-{\mathit{x}}_r^T{\mathit{v}}_r}{\parallel {\mathit{v}}_{\mathit{r}}{\parallel }^2}},\hfill & \mathrm{if}\parallel \mathit{v}\parallel \ne 0,\hfill \\ 0,\hfill & \mathrm{Otherwise}\hfill \end{array}\right.\hfill \end{array}$$

(13)

where ${\mathit{x}}_r$ and ${\mathit{v}}_r$ denote the vector of relative position and velocity between two UAVs, respectively. The distance and time remaining to the CPA are represented by $d_{cpa}$ and $t_{cpa}$, respectively.

In the current study, all UAVs are assigned a number, included in their PID, by their priority, and the lower numbers have the higher priority. All UAVs will stop and hover until a UAV with a higher hierarchy passes by and leaves their local virtual networks. A more elaborate way will be required for practical applications.

Algorithm 3 Pseudo Algorithm of Occupancy Maps in Dynamic State Environment with Multiple Neighboring UAVs

1: for $k=1$ to $N_L$ do   2:    $N_L$ is the number of layers of an occupancy map   3:    for $j=1$ to n do   4:      for $i=1$ to m do   5:         ${\mathit{L}}_{i,j,k}=0$ (Initializing layers)   6:      end for   7:    end for   8: end for   9: while Goal ≠ Start do 10:    for $k=2$ to $N_L$ do 11:      for $j=1$ to n do 12:         for $i=1$ to m do 13:           ${\mathit{L}}_{i,j,k}=0$ (Initializing layers) 14:           ${\mathit{M}}_O=0$ (Initializing occupancy map) 15:         end for 16:      end for 17:    end for 18:    ${\mathit{L}}_{i,j,1}({\mathit{x}}_{obs,s},{\mathit{y}}_{obs,s})=1$ (Coordinates of static obstacles) 19:    ${\mathit{L}}_{i,j,2}({\mathit{x}}_{obs,d},{\mathit{y}}_{obs,d})=1$ (Coordinates of UAS) 20:    ${\mathit{L}}_{i,j,3}({\mathit{x}}_{obs,p},{\mathit{y}}_{obs,p})=1$ (Coordinates of estimated position) 21:    for $k=1$ to $N_L$ do 22:      ${\mathit{M}}_O={\mathit{M}}_O+{\mathit{L}}_{i,j,k}$ 23:    end for 24: end while

6. Validation of Methods

The target tracking methods explained in Section 5 and path planners in Section 5 are integrated into a a software-in-the-loop (SITL) framework with virtual environment scenarios. The path planning algorithm dynamically switches between the APF method and the A* algorithm, adapting to changes in local network membership to ensure safe, collision-free trajectories. Additionally, minimum snap trajectory smoothing is applied for better trackability. By simulating dynamic scenarios, this framework demonstrates the robustness in managing multiple UAV operations.

6.1. Target Tracking Methods

For the validation of the various target tracking methods, the root mean squared error of the estimated positions of the target UAV in the near future against the true positions is calculated as follows, and compared with each other.

$$\begin{array}{c}\hfill RMSE({\widehat{\mathit{T}}}_{k^{*}}^{+,n_F},{\mathit{T}}_{k^{*}}^{+,n_F})=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^{n_F}{\parallel {\widehat{\mathit{X}}}_{k^{*}}\left(t_{+i}\right)-{\widehat{\mathit{X}}}_{k^{*}}\left(t_{+i}\right)\parallel }_2}{n_F}}}\end{array}$$

(14)

The extended Kalman filter (EKF) is employed with the three types of dynamic motion models of constant velocity (CV), constant acceleration (CA), and constant turn rate (CTR) models. They are denoted as ${\mathrm{EKF}}_{\mathrm{CV}}$, ${\mathrm{EKF}}_{\mathrm{CA}}$, and ${\mathrm{EKF}}_{\mathrm{CTR}}$, with the required inputs corresponding to the state at the current time, $t_0$, as $\left\{{\mathit{X}}_{k^{*}}\left(t_0\right)\right\},\{{\mathit{X}}_{k^{*}}\left(t_0\right),{\mathit{v}}_{k^{*}}\left(t_0\right)\},$ and $\{{\mathit{X}}_{k^{*}}\left(t_0\right),{\mathit{v}}_{k^{*}}\left(t_0\right),{\mathit{a}}_{k^{*}}\left(t_0\right)\}$, respectively.

On the other hand, the GMM and the LSTM encoder–decoder models require the history from the past to estimate unknown future states. The input vectors correspond to $\left\{{\mathit{X}}_{k^{*}}\left(t_{-i}\right)\right|i=0,1,2,\cdots ,n_P\}$. The prediction horizon is defined as $\left\{{\widehat{\mathit{X}}}_{k^{*}}\left(t_{+i}\right)\right|i=1,2,\cdots ,n_F\}$.

The GMM and the LSTM are trained offline using a total of 5000 sample points, each of which contains the position vectors from the eight previous time steps to estimate those of three time steps in the future. This corresponds to the training set $\mathit{D}=\{{\mathit{T}}_k={\mathit{T}}_k^{-,8}\cup {\mathit{T}}_k^{+,3}|k=1,\cdots ,5000\}$. The time step can vary depending on the required sampling frequency, but set to be one second in the validation study for simplicity.

A total of 10,000 sample training trajectories are generated, each within an environment with a random number of obstacles and unique starting and goal points. The APF method is employed for path generation, producing trajectories composed of coordinate pairs representing x and y positions. In addition, 5000 sample trajectories are employed for training purposes, while the subsequent 5000 are reserved for testing. The mean value of the RMSE over 5000 sample points is calculated to compare the estimation accuracy of each target tracking method.

Figure 4 shows the statistical analysis of the RMSE values by the EKF models and the GMM of the state estimates over 5000 test samples, with the average RMSE values summarized in

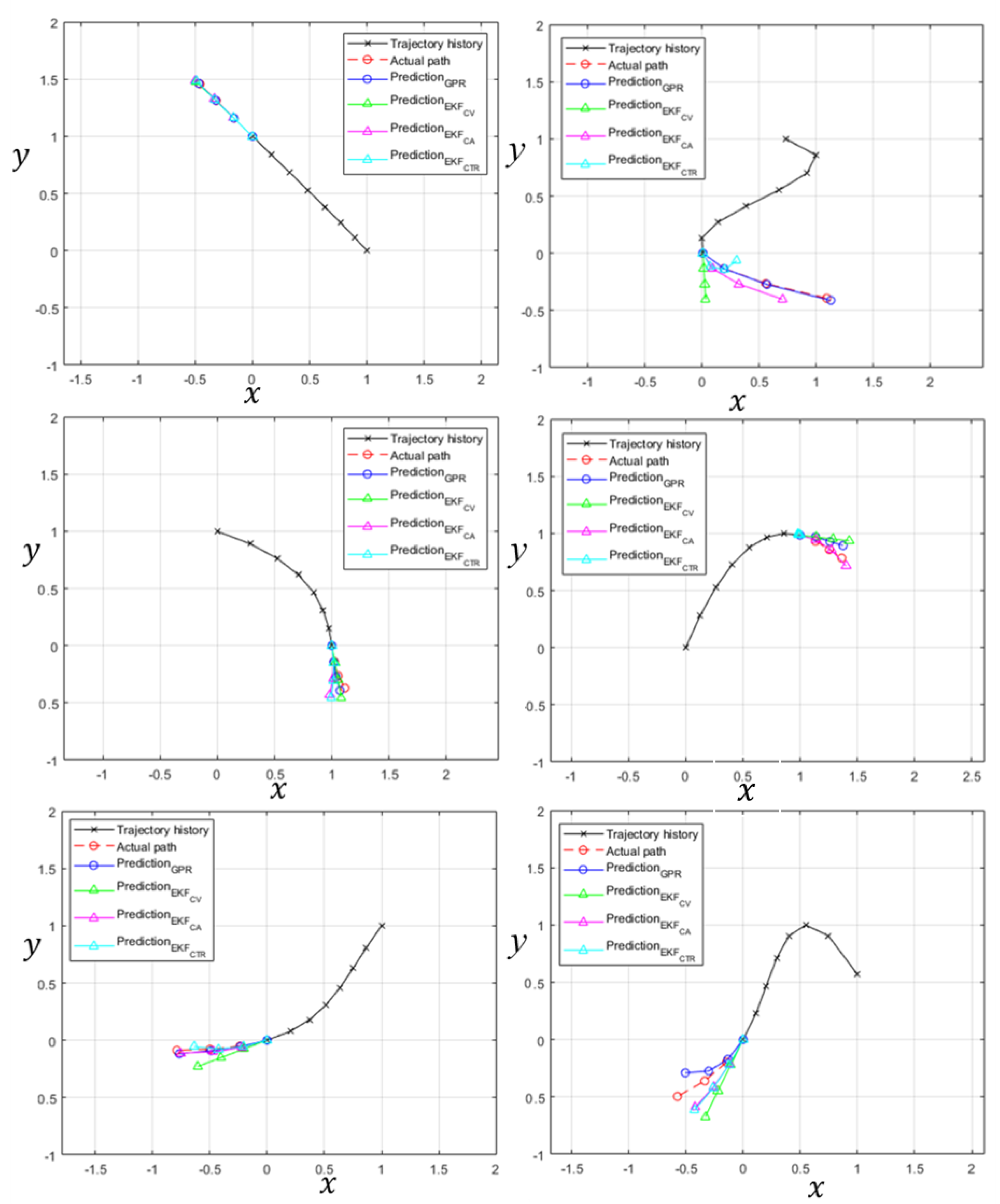
Table 1. The average RMSE values of the dynamic motion-based and statistical model-based target tracking methods: $EK{F}_{CV}$, $EK{F}_{CA}$, $EK{F}_{CTR}$, and GMM.

RMSE Values
Models	$EK{F}_{CV}$	$EK{F}_{CA}$	$EK{F}_{CTR}$	GMM
Average	0.0738	0.0527	0.1344	0.0121
Median	0.0706	0.0432	0.1336	0.0117
Variance	0.0684	0.0771	0.3035	0.0008

. The results show that the EKF with constant acceleration produces the most precise state estimates with the lowest median among all dynamic motion models. However, it should be noted that the GMM generally outperforms the dynamic model-based target tracking method. Six examples of test results out of 5000 test samples are shown in Figure 5 to demonstrate accuracy with respect to trajectories of varying curvature. The dynamic motion-based target tracking method with a single dynamic motion model hardly defines the behavior of an UAV with a single dynamic motion model as the degree of nonlinearity in UAV maneuvering increases.

The comparison between the statistical model of the GMM and the DNN model of the LSTM is carried out using the same two sets of 5000 sample points for training and test validation. Figure 6 shows the statistical analysis over 5000 test datasets, and the LSTM model slightly outperforms the GMM. This is partly because the LSTM is inherently developed for extrapolation, such as in sequence-to-sequence problems, whereas the GMM usually performs best in interpolation problems. The average RMSE values are summarized in

Table 2. The average RMSE values of the statistical model-based and DNN-based methods: GMM and LSTM.

RMSE Values
Models	GMM	LSTM
Average	0.0121	0.0115
Median	0.0117	0.0101
Variance	0.0008	0.0007

. Although the LSTM-based model can be more effective for state estimations in the present study, the GMM-based model is employed during path planning as it can provide estimation uncertainty bounds for collision avoidance.

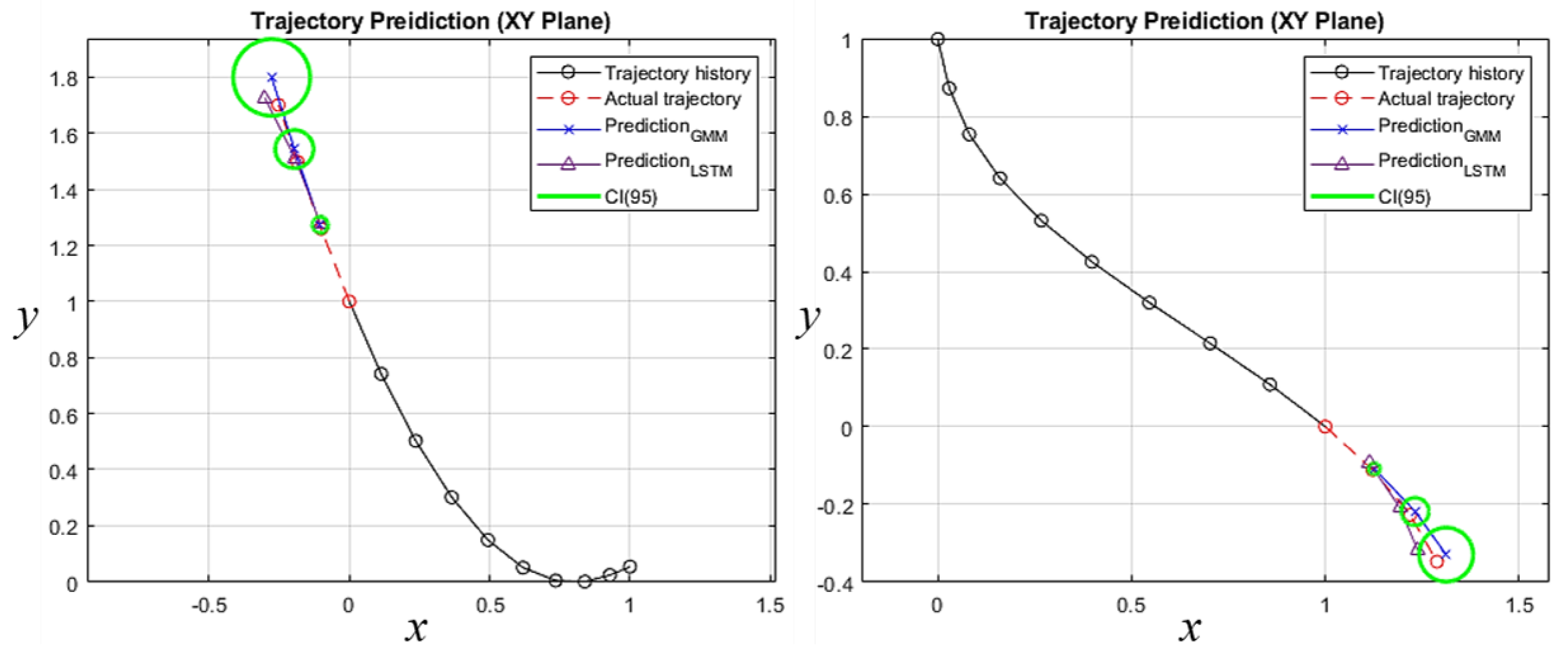
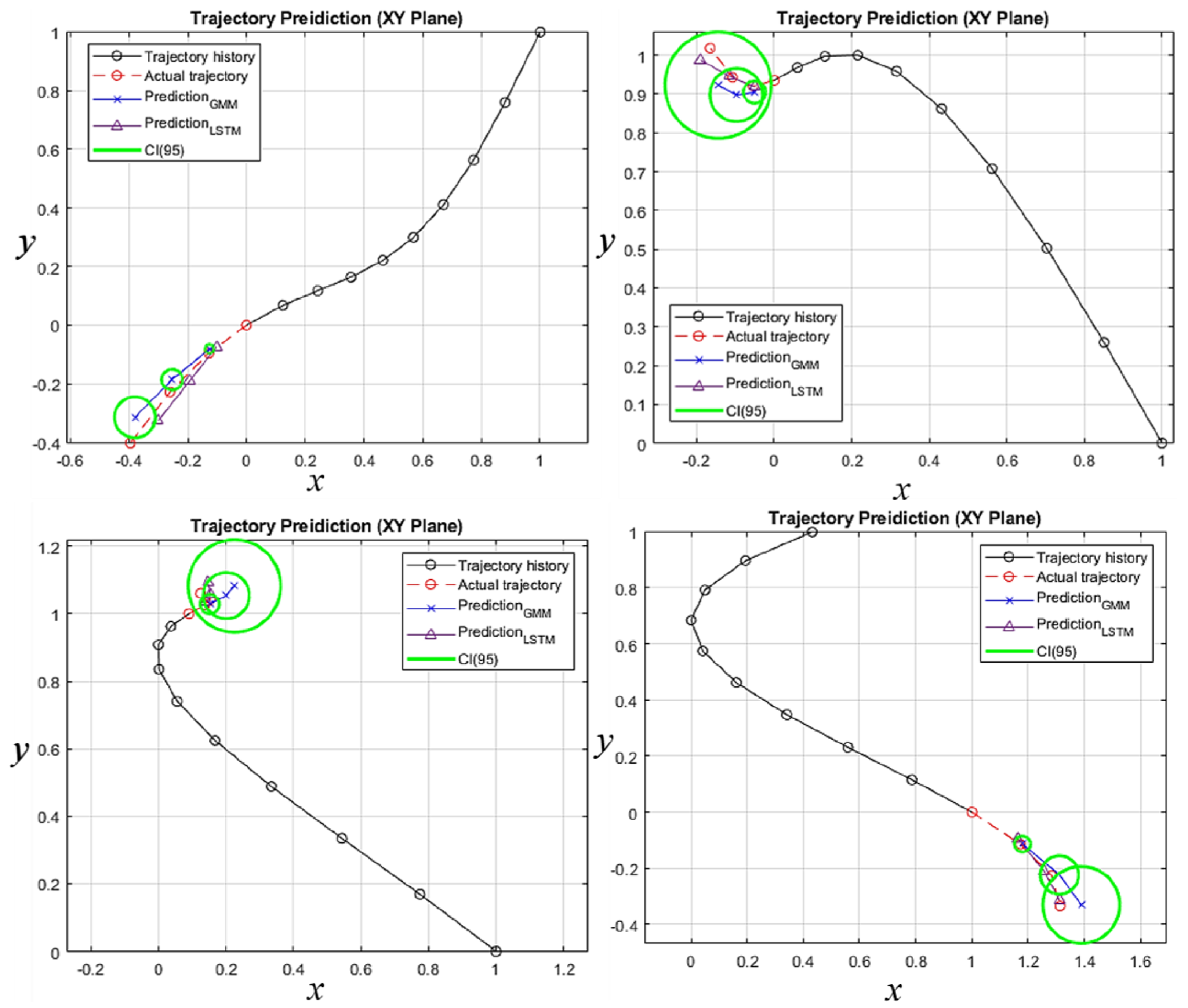
Figure 7 shows another six examples out of the 5000 test datasets. The state estimations by the GMM and the LSTM are shown by blue and purple solid lines, respectively. The green circles represent the safety buffer zone around the predicted mean value with the 95% confidence interval. The estimation uncertainties are effective in the path planning process to enhance deconfliction between UAVs with measurable safety provisions. The details are discussed in Section 6.2. Both data-driven methods yielded accurate state estimates with respect to the true state variables, which are shown by a red solid line with circles.

6.2. Distributed, Dynamic, Hybrid Path Planner

Validations of optimal path planning with target tracking in real time are performed in the operation of multiple UAVs within the virtual local network. The occupancy map is created to include a prediction layer to consider state estimations of UAVs over time.

In this simulation, the priority is given in the order UAV1-UAV2-UAV3. Figure 8 shows solutions from local path planning in a time series of snapshots of the virtual network of UAV1. The four UAVs are operating with the start and goal points, which are assigned on the local virtual network, in the environment with four static obstacles in circles in grey with different sizes. Trajectories of all member UAVs are predicted in the next two time steps and from the present state are predicted by the the GMM based on the state variables in the eight time steps in the past.

The black solid lines indicate the actual trajectory path traversed by an individual UAV, and the optimal paths are shown by blue solid lines. Trajectory predictions at two future time steps are in discrete blue circles. Although not shown explicitly in the plot, bounds of the estimation uncertainties are calculated from the target tracking model, and the areas within the bounds are set as obstacles in the occupancy map. The results show that solutions for the local path planning problems are successfully found and deliver optimal paths to the goal points.

To validate collision avoidance using the right-of-way rule, another scenario is tested where three UAVs are operating within the virtual local network in Figure 9. UAVs 1 and 2 are moving toward each other along their planned paths, which are predicted to intersect at a point, as shown in Figure 9b. When the distance between these UAVs becomes $d_{dist}\le d_{safe}$, UAV 2 stops or slows down to avoid a potential collision, as UAV 1 is assumed to have a higher priority in Figure 9c,d. After three seconds of yielding and when the distance between UAVs 1 and 2 reaches a pre-specified safe distance, UAV 2 resumes the path planning, as shown in Figure 9e,f, and advances to its goal point.

Comparison with a deep reinforcement learning method

Additionally, although different in searching strategies, popular deep reinforcement learning (DRL) methods are independently tested for a direct comparison. A major difference compared with the A*-assisted APF method is that the DRL is a model-free method, and an explicit target tracking method is not needed. Instead, time-consuming off-line training using the Markov decision process is required to avoid obstacles, either static or dynamic, with an objective of the shortest traveling time to the goal point. Detailed descriptions of the MDP definitions of state, action, and policy, as well as reward and penalty functions, are described in the co-author’s study [53]. Well-known DRL algorithms, i.e., the proximal policy optimization (PPO) and Twin Delayed Deep Deterministic policy gradient (TD3) algorithms, are employed. To improve the convergence rate, an artificial potential function is used to calculate attractive and repulsive forces, respectively, to numerically score penalty and rewards values.

Ten thousand flight scenarios with both static and dynamic obstacles are tested, and the statistical results of the success rates to reach pre-specified goal points are shown in Figure 10. Although not plotted in Figure 10, the A*-assisted APF method shows about a 90% success rate, similar to that of the APF-PPO.

Figure 11 presents one example of the path planning results, with snapshots at three different time steps obtained using the APF-PPO and APF-TD3 methods. Both of them successfully identified viable routes for the UAVs. Among these models, the APF-PPO approach generates a less optimal path, introducing unnecessary turns compared with the more efficient trajectory produced by the APF-TD3 model. The performance of the APF-PPO model could potentially be enhanced with further fine-tuning of the model, but that is not within the scope of the present study. Although the APF-DRL models achieved successful path planning, they require an offline training process, which the $A^{*}$ algorithm does not require.

7. Results: Software-in-the-Loop Demonstration

Although the best strategy to validate the operation method developed in the present study is a flight test in real time, the software-in-the-loop simulation is carried out prior to the field test with the PID controller implemented in the software.

7.1. Controller Tracking and Path Smoothing

The UAVs in the simulations are selected as quadrotors, and their state is represented by a six-dimensional vector of position and orientation, with the primary objective of tracking arbitrary trajectories through a four-dimensional vector that varies as a function of time. The quadrotor model includes nested feedback loops, comprising an inner loop for attitude control and an outer loop for position control, as illustrated in Figure 12.

A proportional–integral–derivative (PID) controller is used to design the inner feedback loop, which determines the orientation through feedback from the actual attitude, angular velocity, and roll, $\varphi$, pitch, $\theta$, and yaw angles, $\psi$, and rates, and computes $U_2$. The outer loop involves position feedback, requiring the specified position vector, specified yaw angle, actual position, and actual velocity to compute $U_1$, representing the sum of all thrust forces. The dynamics are linearized, assuming a hover position, and the linearized equations of motion are used to design the inner feedback loop and compute the error equation for position tracking. The aim is to minimize the error vector between the desired and actual positions and yaw angle, resulting in the determination of the commanded acceleration, the application of thrust, and the establishment of roll, pitch, and yaw angles using the linearized equations. The position control system leads to a fourth-order system, which requires at least four differentiable trajectories, motivating the use of minimum snap trajectories.

Minimum Snap Trajectory (MST) for Path Smoothing

The main problem of an $A^{*}$-generated optimal route is that it is non-smooth, which can be challenging for the UAV to track in real time. A method of the minimum snap trajectory is utilized to enhance the smoothness of the planned path, so that it is dynamically feasible for an UAV controller to track along. The order of the controller system of the quadrotor is up to the fourth derivative of the position, as shown in Figure 12. The minimum snap trajectory is used to minimize the fourth derivative of state variables integrated over time. The system of quadrotors is proven to be differentially flat, and all state as well as input variables can be determined in terms of four flat outputs of three outputs and the yaw angle, ${[x,y,z,\psi ]}^T$, and their derivatives [54]. The minimum snap trajectory passes through two consecutive points, $\mathit{r}\left(\mathbf{0}\right)$ and $\mathit{r}\left(\mathit{T}\right)$, in time T, and the minimum snap function can be expressed as below,

$$\begin{array}{c}\hfill \min {\int }_0^T{\left(x^{\left(4\right)\left(t\right)}\right)}^{2}dt=\min \sum _{i=1}^k{\int }_{t_{i-1}}^{t_i}{\left(x^4\left(t\right)\right)}^{2}dt\end{array}$$

(15)

Solving for the minimizing problem and integrating ${\mathit{r}}^{\left(8\right)}=0$ eight times, this yields the minimum snap trajectory as follows,

$$\begin{array}{cc}\hfill \mathit{x}\left(t\right)& =c_7{t}^7+c_6{t}^6+c_5{t}^5+c_4{t}^4+c_3{t}^3+c_2{t}^2+c_1{t}^1+c_0\hfill \end{array}$$

(16)

The trajectory is divided into n segments. The unknown eight coefficients can be found using constraints in boundary conditions at end points of each segments [55]. The MST is applied to the solutions of the real-time path planner from the $A^{*}$ algorithm. The minimum snap trajectory is then applied to resolve any abrupt changes in head angles and reshape, or smooth, the planned path. It returns a set of state profiles, which include desired position, velocity, and accelerations at a pre-specified rate, i.e., every 0.01 s. Figure 13(left) shows an example of a single UAV operation and the comparison between the original (blue dashed line) and the smoothed path (red solid line) produced by the minimum snap trajectory. The results show that the minimum snap trajectory replaces the sharp corners with continuous and smooth curvatures.

However, the update rate of the MST is much higher than that of the local path, 1 s vs. 0.1 s. It is applied to a few segments of the planned path for an efficient computation cost, while the length of the segment depends on the velocity of the agent UAV. Figure 13(right) shows that the planned path is partially refined in the vicinity of the UAV. It reduces the computation cost by five times compared with that for the entire path in this example.

7.2. Multi-Agent, Non-Collaborative UAV Operations

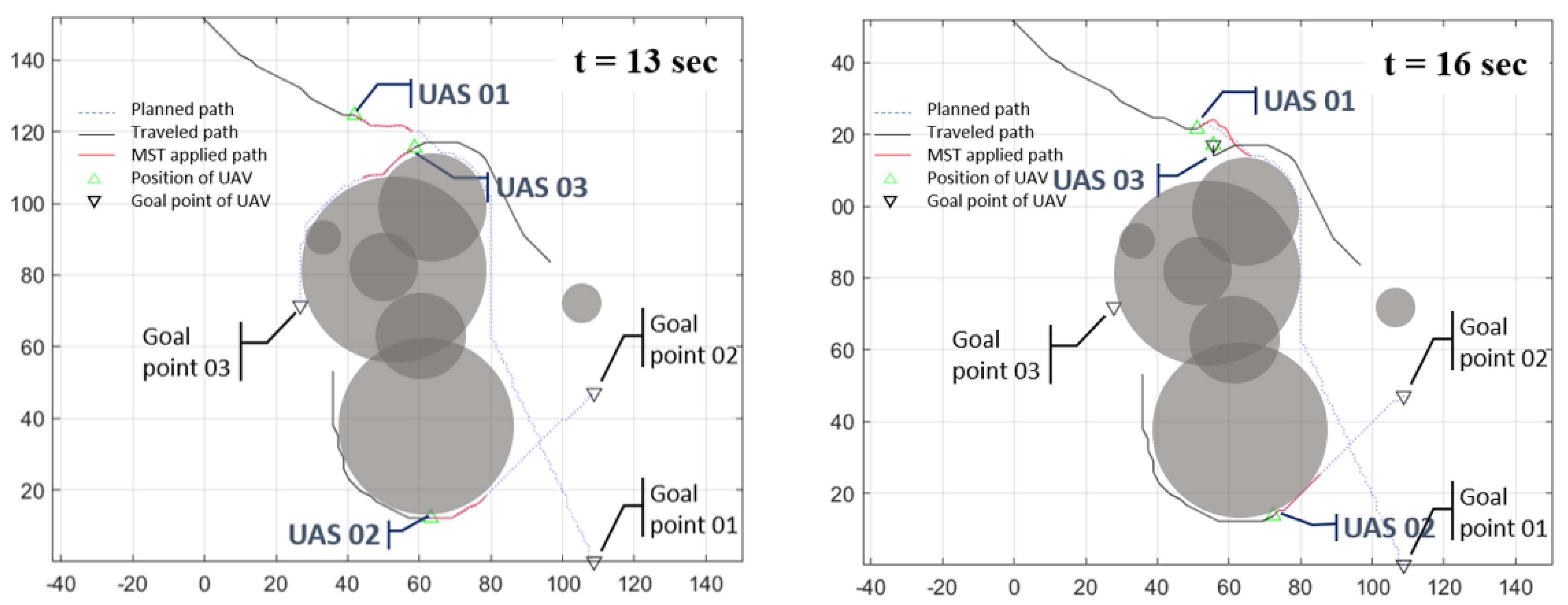
The real-time path smoothing by the minimum snap trajectory is also extended to multiple agent UAV operations. The hybrid dynamic path planning algorithm manages all four UAVs in both global and local domains to deliver conflict-free operations by calculating optimal paths for each individual UAV. The planned trajectories are reconstructed by the minimum snap trajectory. Figure 14 shows a snapshot of the path planning at four time instances of $t=$ 12, 13, 15, and 16 s out of 52 s, and reconstructed trajectories of four UAVs. Unlike path planning for a single target, changes in the states of multiple UAVs can affect the occupancy maps of the others, which may cause a complicate trajectory during the path planning more often. The planned trajectories for all three UAVs are smoothed by applications of the minimum snap trajectory.

7.3. Simulation Set Up

Although the UAV type is not limited to a specific model in the data-driven approach, three small quadrotors are selected for the SITL demonstration for simplicity. They are assumed to travel at a constant speed of 10 m/s. The total domain of operation spans 6750 m by 1890 m, within which the local domain has a size of 270 m by 270 m whenever $r_{comm}$ > $d_k$, where k∈$\{1,2,3,\cdots ,N_d\}$. The simulation is dynamic with all the key operation concepts of real-time data exchange via the ground CDS, GMM for the target tracking, hybrid path planning with the virtual and dynamic local networks, and the path smoothing by the MST. The data communication rate is at 10 Hz.

The main objective of the simulation is for an individual UAV to arrive at its goal point safely in an environment where two other UAVs share the airspace. The present study assumes a low-complexity environment, characterized by the absence of wind or gusts that may significantly impact the operations of UASs. The neighboring UAVs are programmed to hover for collision avoidance where the distance between any two UASs is less than the safety distance, $d_{safe}$. The GMM is trained using the dataset in Section 6.1 of $\mathit{D}=\{{\mathit{T}}_k={\mathit{T}}_k^{-,5}\cup {\mathit{T}}_k^{+,2}|k=1,\cdots ,5000\}$ to estimate ${\widehat{\mathit{X}}}_{k^{*}}^{+,2}$, given the input vector of ${\mathit{X}}_{k^{*}}^{-,5}$ using the GMM.

7.4. Results and Discussion

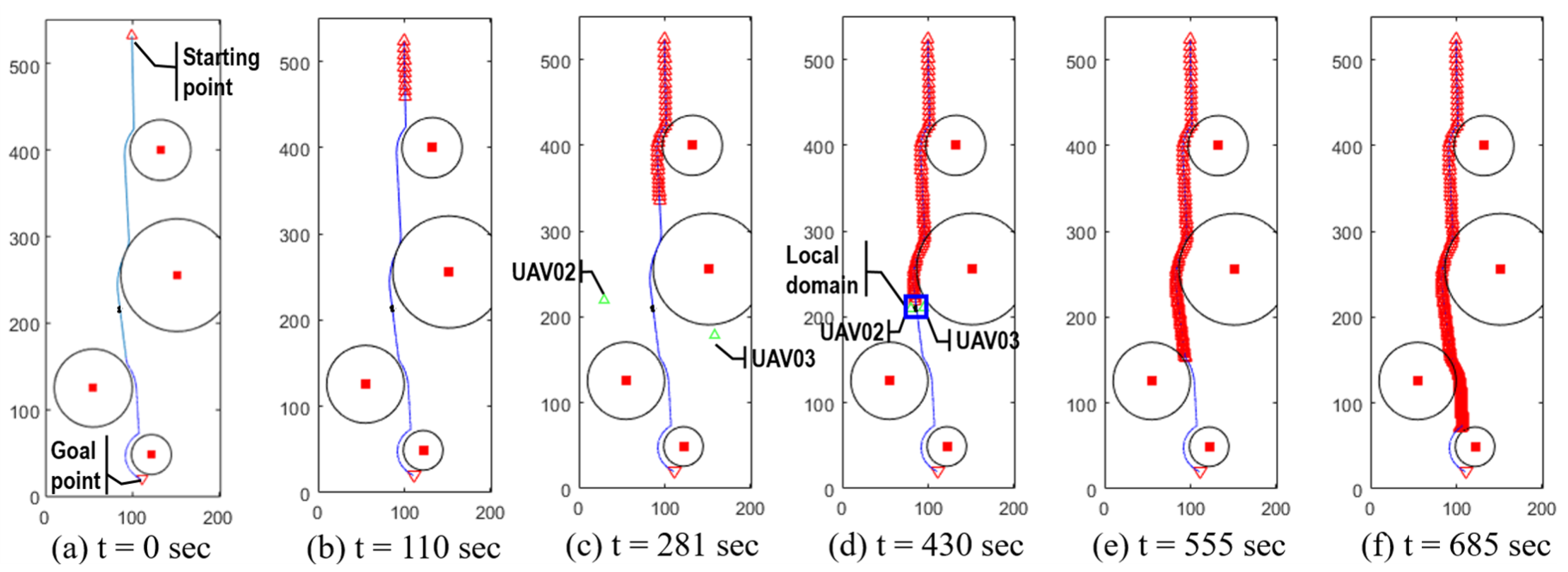
Figure 15 and Figure 16 illustrate the entire simulation from $t=0$ to $t=510$. The software-in-the-loop (SITL) demonstration was validated with the simple PID controller, and the simulation was represented by a series of snapshots at different time instances. Planned paths were locally smoothed at each update by the the minimum snap trajectory. In Figure 15a, the path planning by the APF method in the global domain is shown as a blue solid line, where four large obstacles are sparsely located. A series of red triangles indicate the trace of the ego UAV, with the the goal point at the bottom in the upside-down red triangle. Since the environment of the global domain is assumed to be static, only a single calculation of the global path planning was performed. With the event of the local minima, a series of new start points were generated offline by the $A^{*}$ algorithm in a much coarsened grid.

Using the ground CDS, the trajectory histories of the other UAVs were transferred every one second to the ego UAV (UAV01). The ego UAV had zero members in its local dynamic network, ${\mathcal{N}}_1\left(t\right)=\left\{\varphi \right\}$ until $t=429$ s. At $t=430$ s, the local dynamic network of the ego UAV included two member UAVs, ${\mathcal{N}}_1\left(429\right)=\{{\mathit{T}}_2^{-},{\mathit{T}}_3^{-}\}$, and the proposed algorithm subsequently created a local domain, as shown in Figure 15d. At $t=480$ s, the UAV02 arrived at its goal point and was removed from the local dynamic network, ${\mathcal{N}}_1\left(480\right)=\left\{{\mathit{T}}_3^{-}\right\}$. At $t=498$, the UAV3 was excluded from the local dynamic network of the ego UAV, and ${\mathcal{N}}_1(t=498)=\left\{\varphi \right\}$.

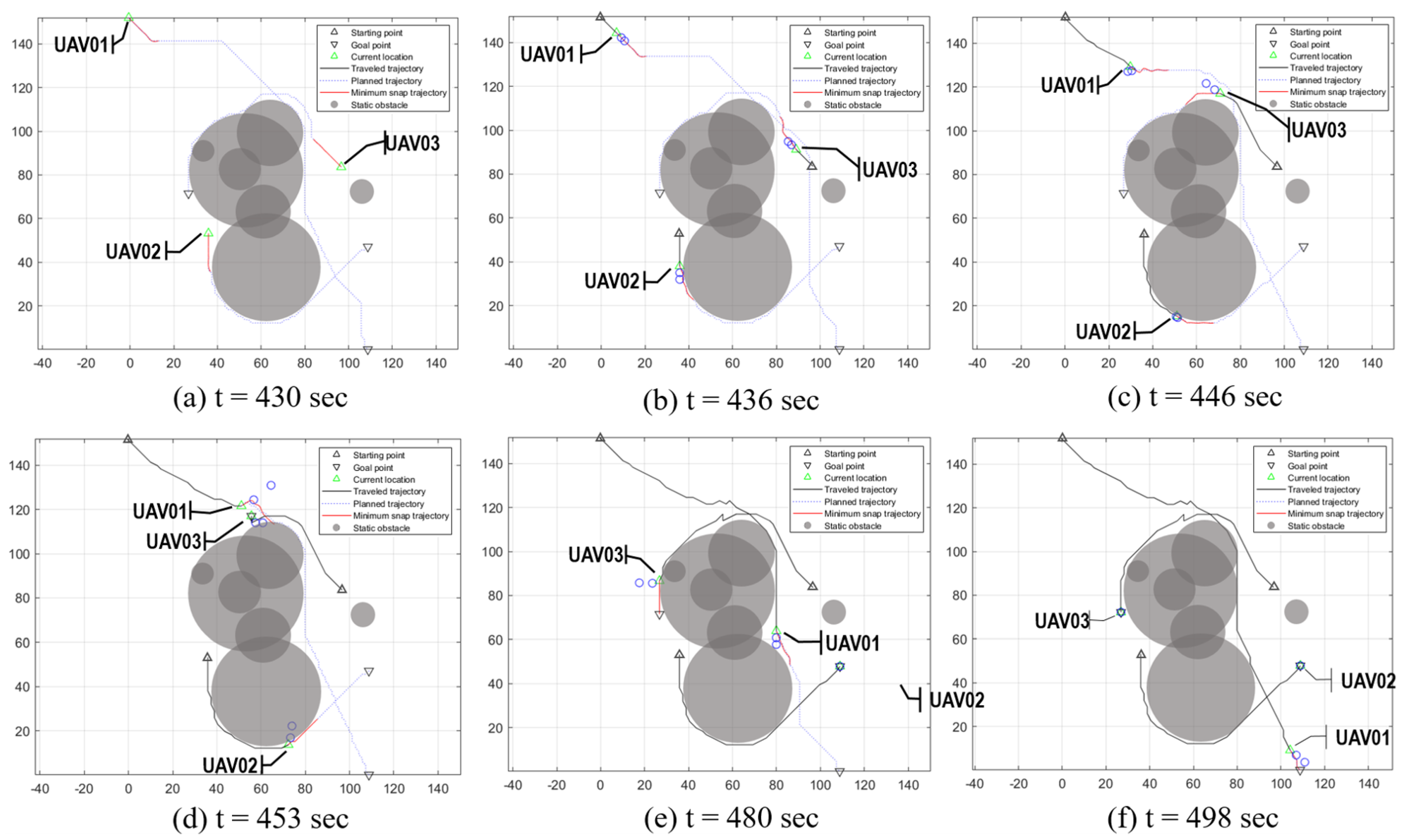
Within the local domain, the A* algorithm generated conflict-free locally optimal paths, as shown in Figure 16, where the perspective of the ego UAV (UAV01) is demonstrated. The green triangles represent the current locations of all UAVs, with their local goals in upside-down red triangles. The planned paths are shown as blue dotted lines, the paths smoothed by the MTS as red solid lines, and the routes successfully tracked by the PID controller as black solid lines.

The entire state information of UAVs is available every one second, and the path planning and update occur at each time step until the ego UAV (UAV01) reaches the goal point. UAV02 and UAV03 safely arrive at their goal points in Figure 16e,f, and these UAVs are excluded from the local dynamic network of the UAV01, ${\mathcal{N}}_0=\left\{\varphi \right\}$. Once the the ego UAV arrives at the local goal point, the virtual local network is removed instantly, and the ego UVA tracks along the globally optimal path generated at the beginning of the simulation, as shown in Figure 15e,f, until it reaches its own goal point.

To highlight the computational efficiency of the hybrid path planning method, Figure 17 shows a comparison of the computation time over the normalized traveled distance, ${\overline{d}}_{trav}$, between the proposed hybrid approach and the standalone $A^{*}$ algorithm. The SITL scenario with three UAVs with a fine grid size of 5025 by 1810 was used for the A* algorithm. The ${\overline{d}}_{trav}$ is non-dimensionalized by the total distance traveled, ${\overline{d}}_{trav}$$=d_{trav}/d_{total}$. The cumulative computation time is summed from the APF in blue and the $A^{*}$ algorithm in red from the global and the local path generation, respectively. Two different regions correspond to the APF method and the $A^{*}$ algorithm, represented by blue and red solid lines, respectively.

The computation time of the $A^{*}$ algorithm standalone application is depicted by the red dashed line. The linear increase of the blue solid line represents that the APF method can be effective in finding an optimal path independent of the size of the domain, while the local path planning exhibits a significant increase in computation cost with the $A^{*}$ algorithm. However, the total computation cost is significantly diminished compared with the scenario where the $A^{*}$ algorithm is exclusively applied to the whole domain with a fine grid to determine an optimal path, as shown in Figure 17. The significant reduction in computation time for the proposed hybrid approach shows its potential advantages.

8. Conclusions and Future Work

In this study, the hybrid dynamic path planning algorithm was developed to manage distributed dynamic path planning with multiple UAV operations. To estimate unknown state variables of UAVs, the data-driven target tracking method was developed based on the statistical model of the GMM and used with the proposed path planning algorithm. The state estimation results showed that the data-driven target tracking method outperformed the traditional target tracking methods, which used dynamic motion models, in terms of estimation accuracy. The GMM based data-driven target tracking method calculates bounds for estimation uncertainties, which can define constraints for the safety distance to the estimated state of UAVs in the path planning.

The proposed methods were validated in a software-in-the-loop (SITL) demonstration, with the simple PID controller of the UAVs implemented in the software program. The local dynamic of the network of the ego UAV was utilized with a centralized database system to ensure stable communication between UAVs for data exchange, such as trajectory history. The switching between different path planning methods in the hybrid dynamic path planning algorithm effectively addressed both global and local path planning problems with multiple UAV operations. A minimum snap trajectory was applied to the path planned by the $A^{*}$ algorithm, smoothing the conflict-free path to make it dynamically feasible for UAV tracking.

Future research may explore the application of deep learning models in real-time local path planning. The path-searching component of the current hybrid path planning algorithm could be enhanced by incorporating reinforcement learning, deep neural networks, or convolutional networks to identify optimal paths from a diverse range of perspectives. Additionally, transformer technology could be utilized and compared with LSTM models in trajectory prediction to assess their relative effectiveness. Furthermore, the implementation of communication protocols and time synchronization mechanisms, such as ROS2 (Robot Operating System 2), MQTT (Message Queuing Telemetry Transport), and DDS (Data Distribution Service), will be necessary for conducting actual field tests.