Global Attention-Based DEM: A Planet Surface Digital Elevation Model-Generation Method Combined with a Global Attention Mechanism
Abstract
1. Introduction
- A network combined with a global attention mechanism is proposed to generate high-precision DEMs from planetary images. Through the attention mechanism for the channel and spatial dimensions, the model can capture global height variance. Meanwhile, the ability to identify and reconstruct complex terrain features such as craters is significantly improved.
- A multi-order gradient fusion loss function that combines the first-order and second-order gradient is proposed. The organic fusion of the above loss functions through appropriate weights significantly improves the model’s ability to capture the rapid terrain changes and improve the precision of the generated DEM.
- Three datasets for the generation of DEMs of the Moon and Mars are created. These datasets not only rectify the mismatch between existing satellite imagery and digital elevation models (DEMs), but also concentrate on identifying typical terrains in planetary environments, thus providing invaluable data support for this work and future research.
2. Related Work
2.1. DEM Generation from Satellite Imagery
2.2. Attention Mechanism
3. Methods
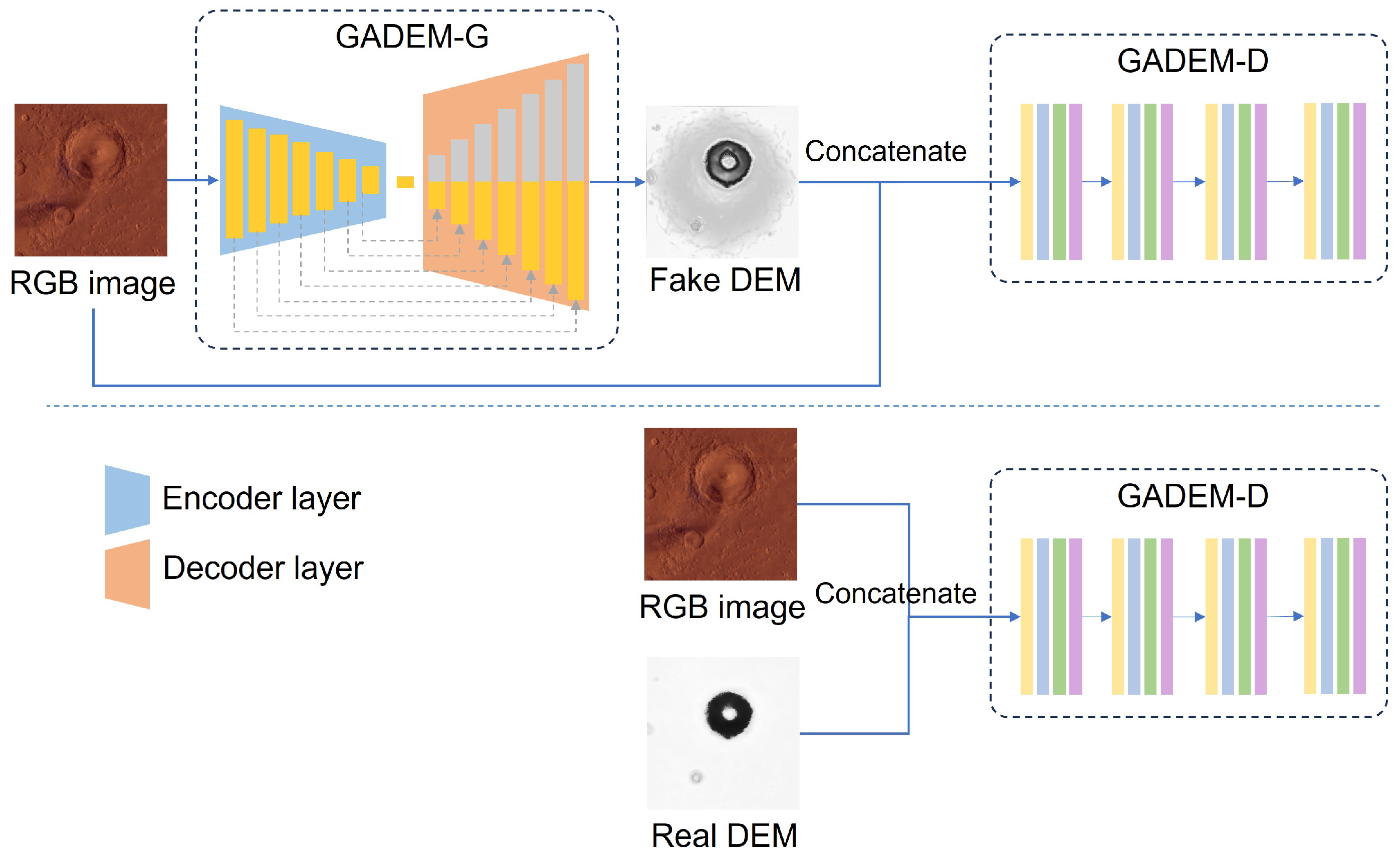
3.1. Entire Network Process
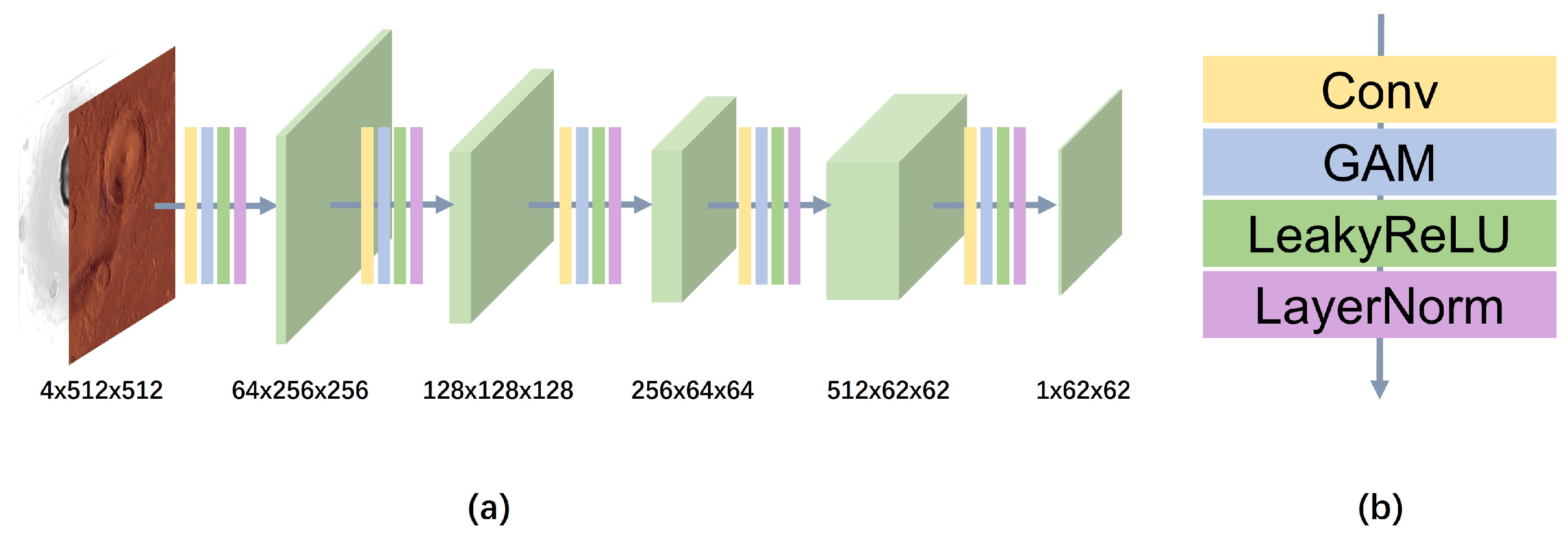
3.2. GADEM Network Structure
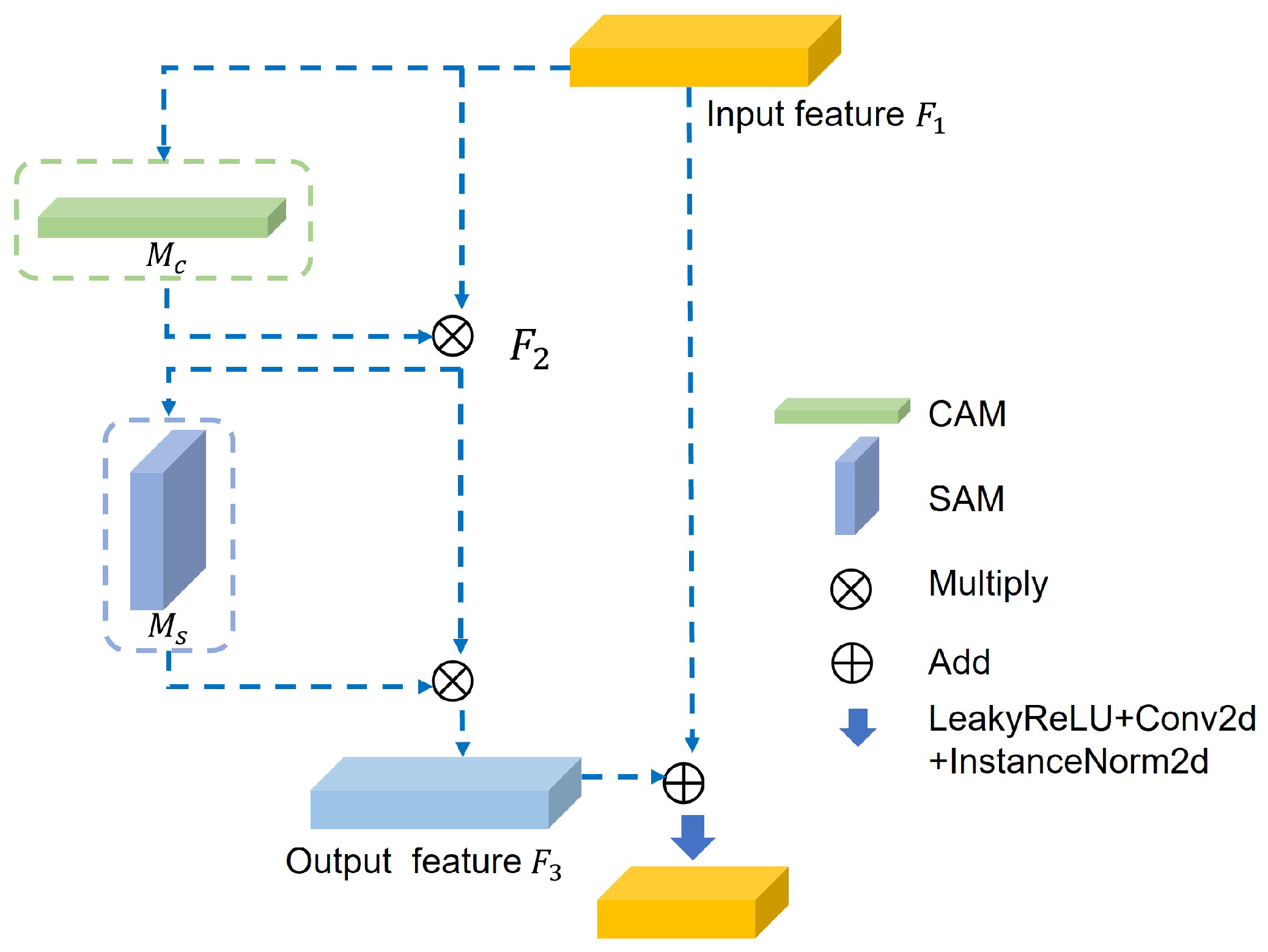
3.3. GAD
3.4. Multi-Order Gradient Fusion Loss Function
4. Experiments
4.1. Construction of Datasets
4.2. Evaluation Metrics
4.3. Experimental Plan
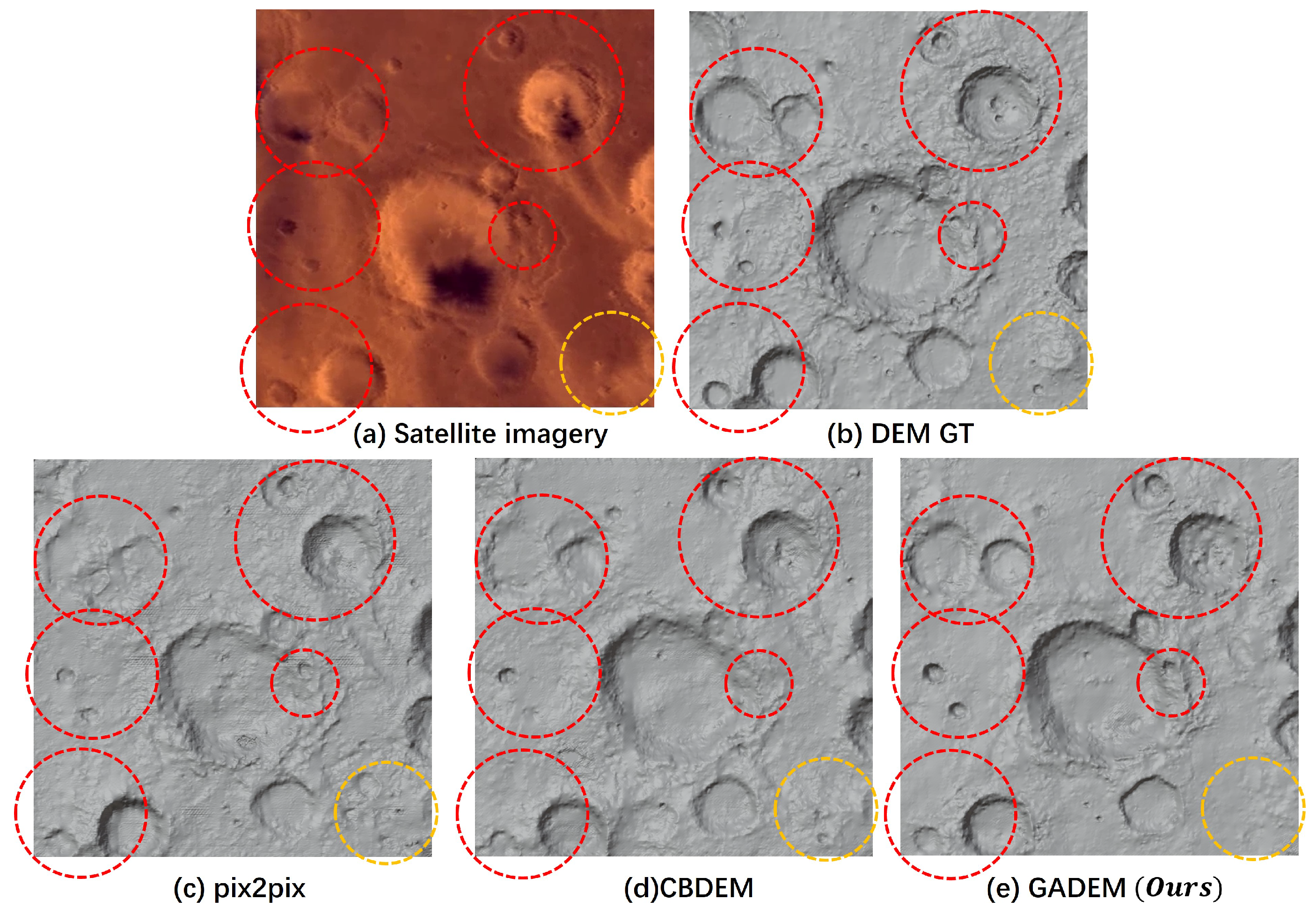
4.4. Experimental Results
4.5. Terrain Profile Analysis
4.6. Shadow Region Experiment
4.7. Ablation Experiment
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, R.; Zhang, Y. Fast path planning for long-range planetary roving based on a hierarchical framework and deep reinforcement learning. Aerospace 2022, 9, 101. [Google Scholar] [CrossRef]
- Hong, Z.; Sun, P.; Tong, X.; Pan, H.; Zhou, R.; Zhang, Y.; Han, Y.; Wang, J.; Yang, S.; Xu, L. Improved A-Star algorithm for long-distance off-road path planning using terrain data map. ISPRS Int. J. Geo-Inf. 2021, 10, 785. [Google Scholar] [CrossRef]
- Xu, X.; Fu, X.; Zhao, H.; Liu, M.; Xu, A.; Ma, Y. Three-Dimensional Reconstruction and Geometric Morphology Analysis of Lunar Small Craters within the Patrol Range of the Yutu-2 Rover. Remote Sens. 2023, 15, 4251. [Google Scholar] [CrossRef]
- Beckham, C.; Pal, C. A step towards procedural terrain generation with gans. arXiv 2017, arXiv:1707.03383. [Google Scholar]
- Panagiotou, E.; Chochlakis, G.; Grammatikopoulos, L.; Charou, E. Generating elevation surface from a single RGB remotely sensed image using deep learning. Remote Sens. 2020, 12, 2002. [Google Scholar] [CrossRef]
- Yao, S.; Cheng, Y.; Yang, F.; Mozerov, M.G. A continuous digital elevation representation model for DEM super-resolution. ISPRS J. Photogramm. Remote Sens. 2024, 208, 1–13. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, B.; Liu, W.C. Mars3DNet: CNN-based high-resolution 3D reconstruction of the Martian surface from single images. Remote Sens. 2021, 13, 839. [Google Scholar] [CrossRef]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar]
- Bhushan, S.; Shean, D.; Alexandrov, O.; Henderson, S. Automated digital elevation model (DEM) generation from very-high-resolution Planet SkySat triplet stereo and video imagery. ISPRS J. Photogramm. Remote Sens. 2021, 173, 151–165. [Google Scholar] [CrossRef]
- Ghuffar, S. DEM generation from multi satellite PlanetScope imagery. Remote Sens. 2018, 10, 1462. [Google Scholar] [CrossRef]
- Tao, Y.; Muller, J.P.; Conway, S.J.; Xiong, S. Large area high-resolution 3D mapping of Oxia Planum: The landing site for the ExoMars Rosalind Franklin rover. Remote Sens. 2021, 13, 3270. [Google Scholar] [CrossRef]
- Tao, Y.; Muller, J.P.; Xiong, S.; Conway, S.J. MADNet 2.0: Pixel-Scale Topography Retrieval from Single-View Orbital Imagery of Mars Using Deep Learning. Remote Sens. 2021, 13, 4220. [Google Scholar] [CrossRef]
- Mou, L.; Zhu, X.X. IM2HEIGHT: Height estimation from single monocular imagery via fully residual convolutional-deconvolutional network. arXiv 2018, arXiv:1802.10249. [Google Scholar]
- Gao, Q.; Shen, X. StyHighNet: Semi-supervised learning height estimation from a single aerial image via unified style transferring. Sensors 2021, 21, 2272. [Google Scholar] [CrossRef]
- Lu, J.; Hu, Q. Semantic Joint Monocular Remote Sensing Image Digital Surface Model Reconstruction Based on Feature Multiplexing and Inpainting. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4411015. [Google Scholar] [CrossRef]
- Alhashim, I.; Wonka, P. High quality monocular depth estimation via transfer learning. arXiv 2018, arXiv:1812.11941. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F.-F. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Tootell, R.B.; Hadjikhani, N.; Hall, E.K.; Marrett, S.; Vanduffel, W.; Vaughan, J.T.; Dale, A.M. The retinotopy of visual spatial attention. Neuron 1998, 21, 1409–1422. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7794–7803. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Park, J.; Woo, S.; Lee, J.Y.; Kweon, I.S. Bam: Bottleneck attention module. arXiv 2018, arXiv:1807.06514. [Google Scholar]
- Liu, Y.; Shao, Z.; Hoffmann, N. Global attention mechanism: Retain information to enhance channel-spatial interactions. arXiv 2021, arXiv:2112.05561. [Google Scholar]
- Zhang, J.; Zhou, Q.; Wu, J.; Wang, Y.; Wang, H.; Li, Y.; Chai, Y.; Liu, Y. A cloud detection method using convolutional neural network based on Gabor transform and attention mechanism with dark channel SubNet for remote sensing image. Remote Sens. 2020, 12, 3261. [Google Scholar] [CrossRef]
- Yu, Y.; Li, X.; Liu, F. Attention GANs: Unsupervised deep feature learning for aerial scene classification. IEEE Trans. Geosci. Remote Sens. 2019, 58, 519–531. [Google Scholar] [CrossRef]
- Gao, F.; He, Y.; Wang, J.; Hussain, A.; Zhou, H. Anchor-free convolutional network with dense attention feature aggregation for ship detection in SAR images. Remote Sens. 2020, 12, 2619. [Google Scholar] [CrossRef]
- Wang, L.; Yu, Q.; Li, X.; Zeng, H.; Zhang, H.; Gao, H. A CBAM-GAN-based method for super-resolution reconstruction of remote sensing image. IET Image Process. 2023, 18, 548–560. [Google Scholar] [CrossRef]
- Wang, W.; Tan, X.; Zhang, P.; Wang, X. A CBAM based multiscale transformer fusion approach for remote sensing image change detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6817–6825. [Google Scholar] [CrossRef]
- Ji, S.; Yu, D.; Shen, C.; Li, W.; Xu, Q. Landslide detection from an open satellite imagery and digital elevation model dataset using attention boosted convolutional neural networks. Landslides 2020, 17, 1337–1352. [Google Scholar] [CrossRef]
- Song, J.; Aouf, N.; Honvault, C. Attention-based DeepMoon for Crater Detection. In Proceedings of the CEAS EuroGNC 2022, Berlin, Germany, 3–5 May 2022. [Google Scholar]
- Li, W.; Wu, J.; Chen, H.; Wang, Y.; Jia, Y.; Gui, G. Unet combined with attention mechanism method for extracting flood submerged range. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6588–6597. [Google Scholar] [CrossRef]
- Li, Q.; Yan, D.; Wu, W. Remote sensing image scene classification based on global self-attention module. Remote Sens. 2021, 13, 4542. [Google Scholar] [CrossRef]
- Zhou, G.; Song, B.; Liang, P.; Xu, J.; Yue, T. Voids filling of DEM with multiattention generative adversarial network model. Remote Sens. 2022, 14, 1206. [Google Scholar] [CrossRef]
- Available online: https://svs.gsfc.nasa.gov/ (accessed on 1 September 2023).
- Available online: http://moon.bao.ac.cn (accessed on 1 September 2023).
- Rukundo, O.; Cao, H. Nearest neighbor value interpolation. arXiv 2012, arXiv:1211.1768. [Google Scholar]
- Polidori, L.; El Hage, M. Digital elevation model quality assessment methods: A critical review. Remote Sens. 2020, 12, 3522. [Google Scholar] [CrossRef]
- Flahaut, J.; Carpenter, J.; Williams, J.P.; Anand, M.; Crawford, I.; van Westrenen, W.; Füri, E.; Xiao, L.; Zhao, S. Regions of interest (ROI) for future exploration missions to the lunar South Pole. Planet. Space Sci. 2020, 180, 104750. [Google Scholar] [CrossRef]
- Hu, T.; Yang, Z.; Li, M.; van der Bogert, C.H.; Kang, Z.; Xu, X.; Hiesinger, H. Possible sites for a Chinese International Lunar Research Station in the Lunar South Polar Region. Planet. Space Sci. 2023, 227, 105623. [Google Scholar] [CrossRef]
- Barker, M.K.; Mazarico, E.; Neumann, G.A.; Smith, D.E.; Zuber, M.T.; Head, J.W. Improved LOLA elevation maps for south pole landing sites: Error estimates and their impact on illumination conditions. Planet. Space Sci. 2021, 203, 105119. [Google Scholar] [CrossRef]












| Datasets | Metrics | Pix2Pix | CBDEM | GADEM |
|---|---|---|---|---|
| Moon | MAE (m) ↓ | 2.978 | 2.571 | 2.465 |
| RMSE (m) ↓ | 3.165 | 2.623 | 2.498 | |
| R2 (m) ↑ | 0.351 | 0.554 | 0.616 | |
| SSIM (m) ↑ | 0.316 | 0.497 | 0.608 | |
| Mars | MAE (m) ↓ | 2.953 | 2.398 | 2.273 |
| RMSE (m) ↓ | 3.045 | 2.336 | 2.269 | |
| R2 (m) ↑ | 0.288 | 0.516 | 0.625 | |
| SSIM (m) ↑ | 0.321 | 0.522 | 0.614 |
| Datasets | Metrics | Pix2Pix | CBDEM | GADEM |
|---|---|---|---|---|
| Chang’e-2 | MAE (m) ↓ | 2.482 | 2.422 | 2.399 |
| RMSE (m) ↓ | 2.582 | 2.519 | 2.492 | |
| R2 (m) ↑ | 0.383 | 0.426 | 0.463 | |
| SSIM (m) ↑ | 0.285 | 0.360 | 0.386 |
| Datasets | Metrics | GAD | GradLoss | ||
|---|---|---|---|---|---|
| w/o | w | w | w | ||
| Moon | MAE (m) ↓ | 2.978 | 2.617 | 2.513 | 2.525 |
| RMSE (m) ↓ | 3.165 | 2.856 | 2.581 | 2.634 | |
| R2 (m) ↑ | 0.351 | 0.459 | 0.408 | 0.417 | |
| SSIM (m) ↑ | 0.316 | 0.439 | 0.418 | 0.432 | |
| Mars | MAE (m) ↓ | 2.953 | 2.557 | 2.434 | 2.447 |
| RMSE (m) ↓ | 3.045 | 2.680 | 2.551 | 2.574 | |
| R2 (m) ↑ | 0.288 | 0.466 | 0.424 | 0.451 | |
| SSIM (m) ↑ | 0.321 | 0.457 | 0.413 | 0.445 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Zhu, Z.; Sun, L.; Zhang, D. Global Attention-Based DEM: A Planet Surface Digital Elevation Model-Generation Method Combined with a Global Attention Mechanism. Aerospace 2024, 11, 529. https://doi.org/10.3390/aerospace11070529
Yang L, Zhu Z, Sun L, Zhang D. Global Attention-Based DEM: A Planet Surface Digital Elevation Model-Generation Method Combined with a Global Attention Mechanism. Aerospace. 2024; 11(7):529. https://doi.org/10.3390/aerospace11070529
Chicago/Turabian StyleYang, Li, Zhijie Zhu, Long Sun, and Dongping Zhang. 2024. "Global Attention-Based DEM: A Planet Surface Digital Elevation Model-Generation Method Combined with a Global Attention Mechanism" Aerospace 11, no. 7: 529. https://doi.org/10.3390/aerospace11070529
APA StyleYang, L., Zhu, Z., Sun, L., & Zhang, D. (2024). Global Attention-Based DEM: A Planet Surface Digital Elevation Model-Generation Method Combined with a Global Attention Mechanism. Aerospace, 11(7), 529. https://doi.org/10.3390/aerospace11070529







