Effect of Intake Acoustic Reflection on Blade Vibration Characteristics
Abstract
1. Introduction
2. Aerodynamic Model
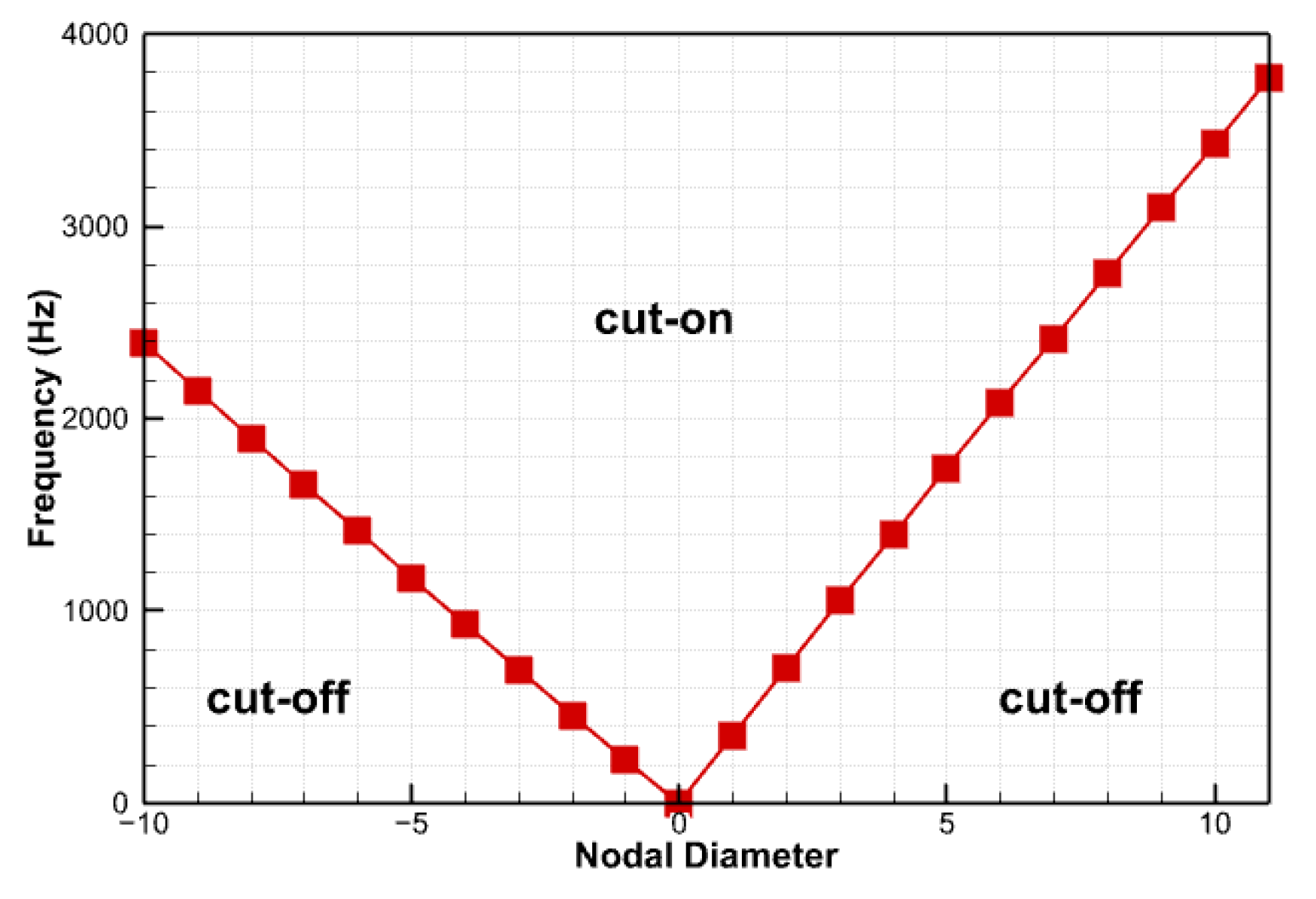
3. Acoustic Cut-On Frequency
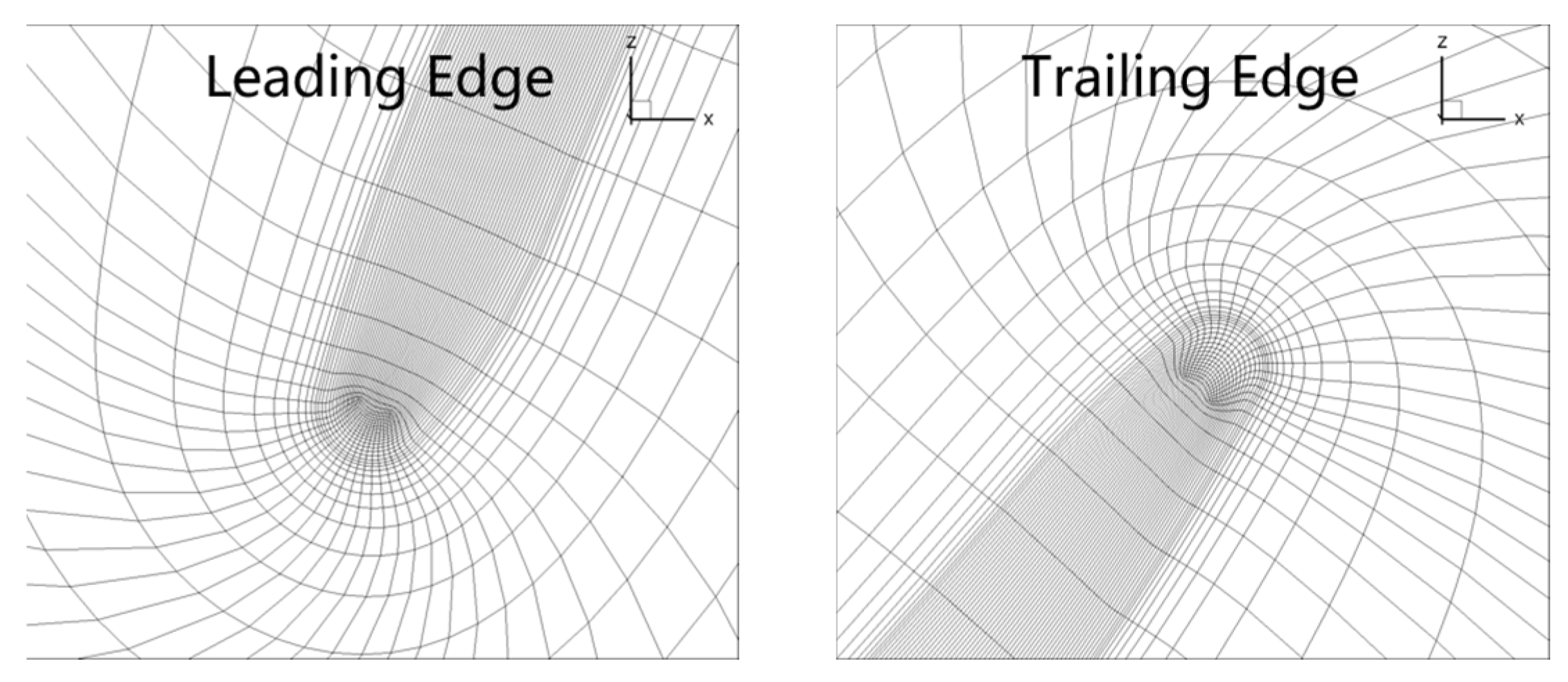
4. Numerical Setup
5. Flow Structures
6. Acoustic Flutter Analysis
6.1. Flow Field Acoustic Properties
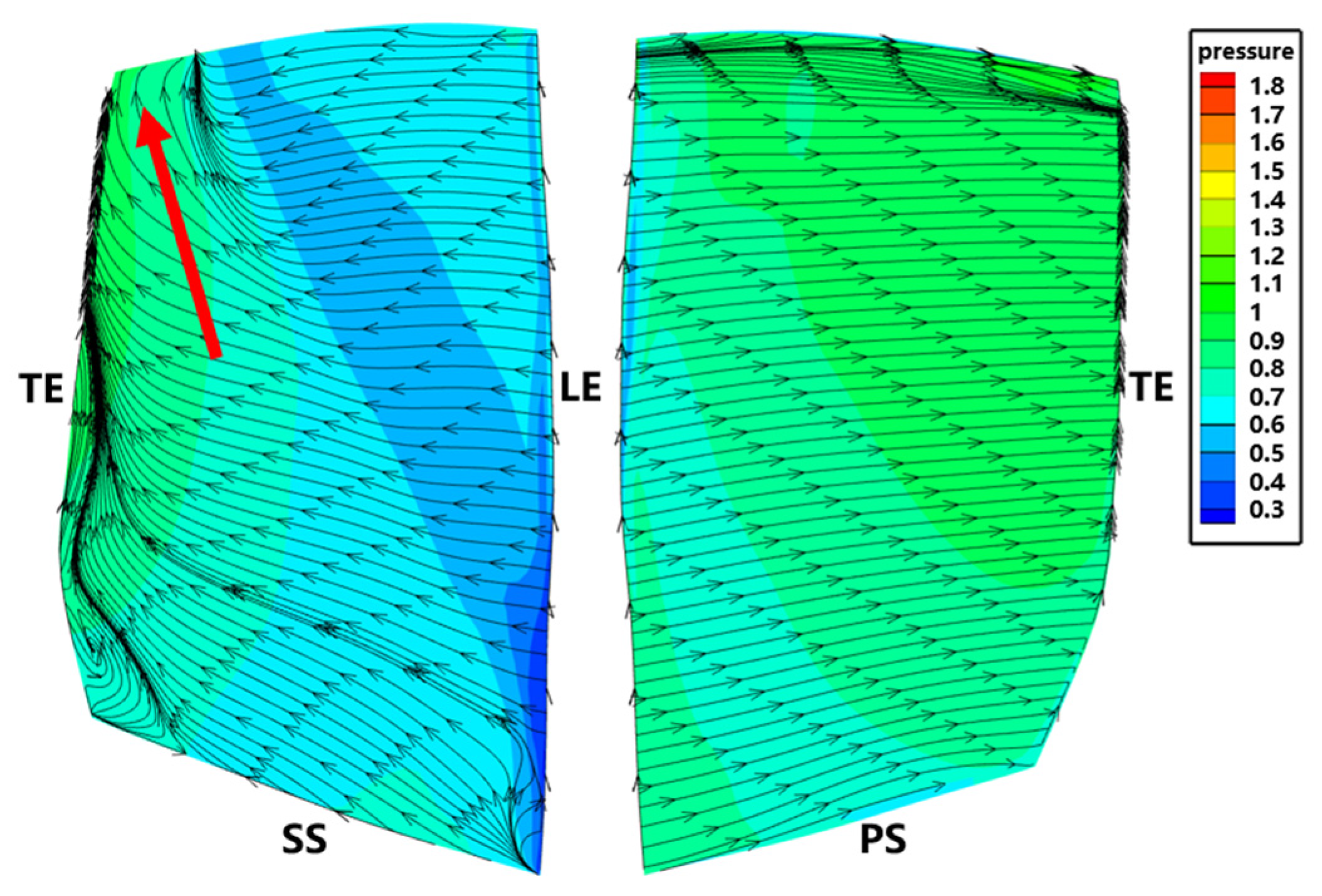
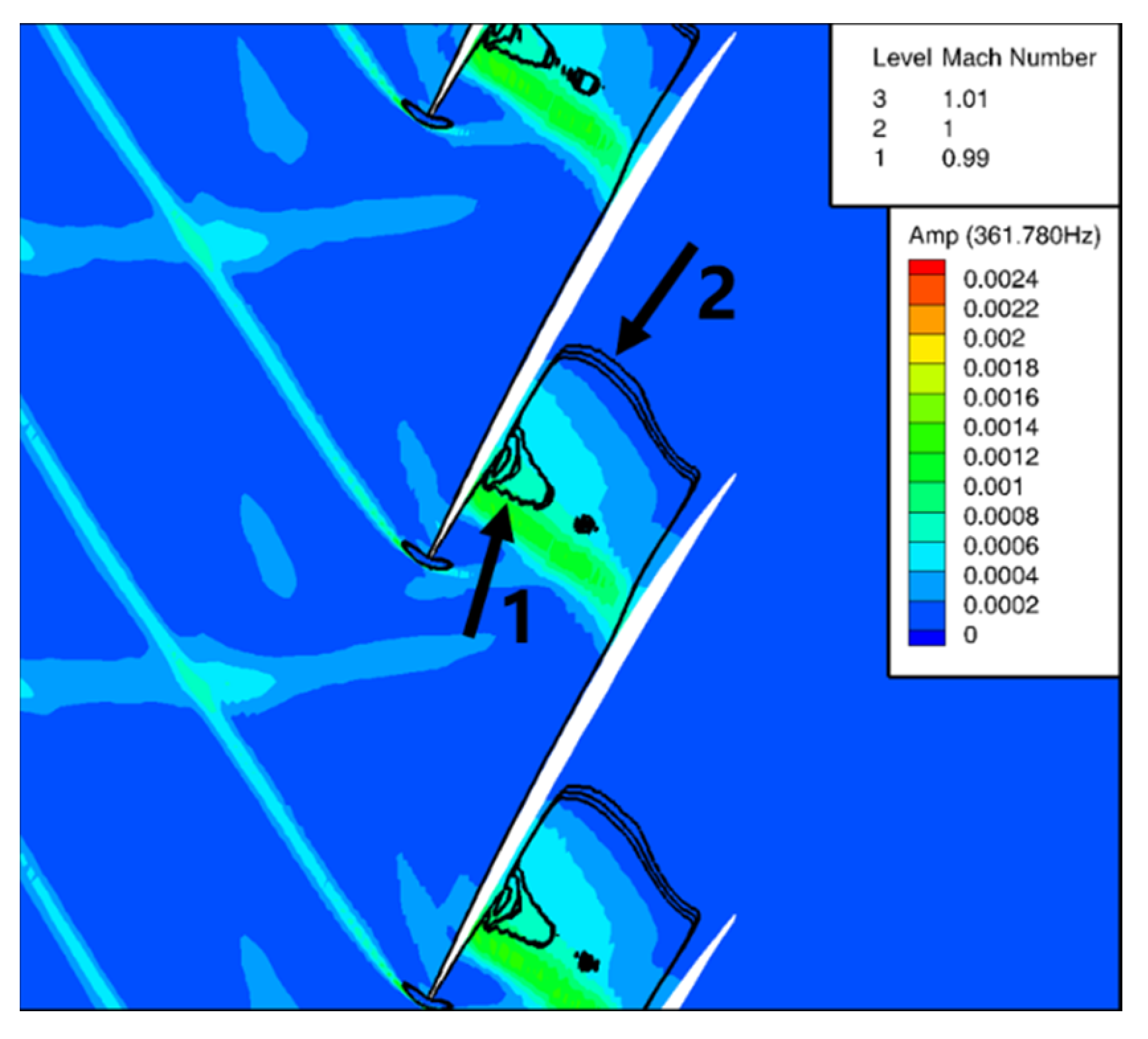
6.2. Relationship between the Pressure Waves and Flow Structure
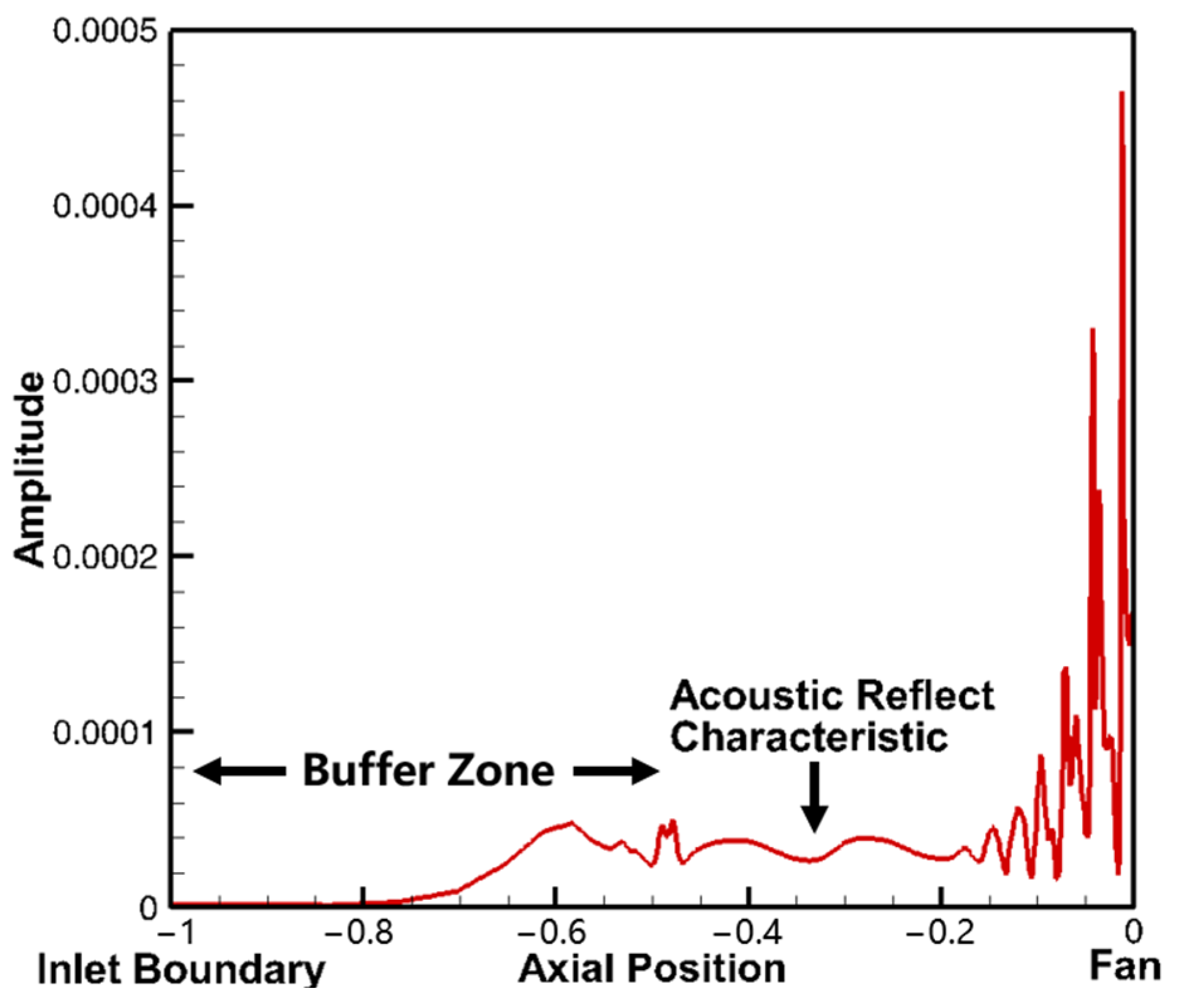
6.3. Acoustic Reflection Analyses
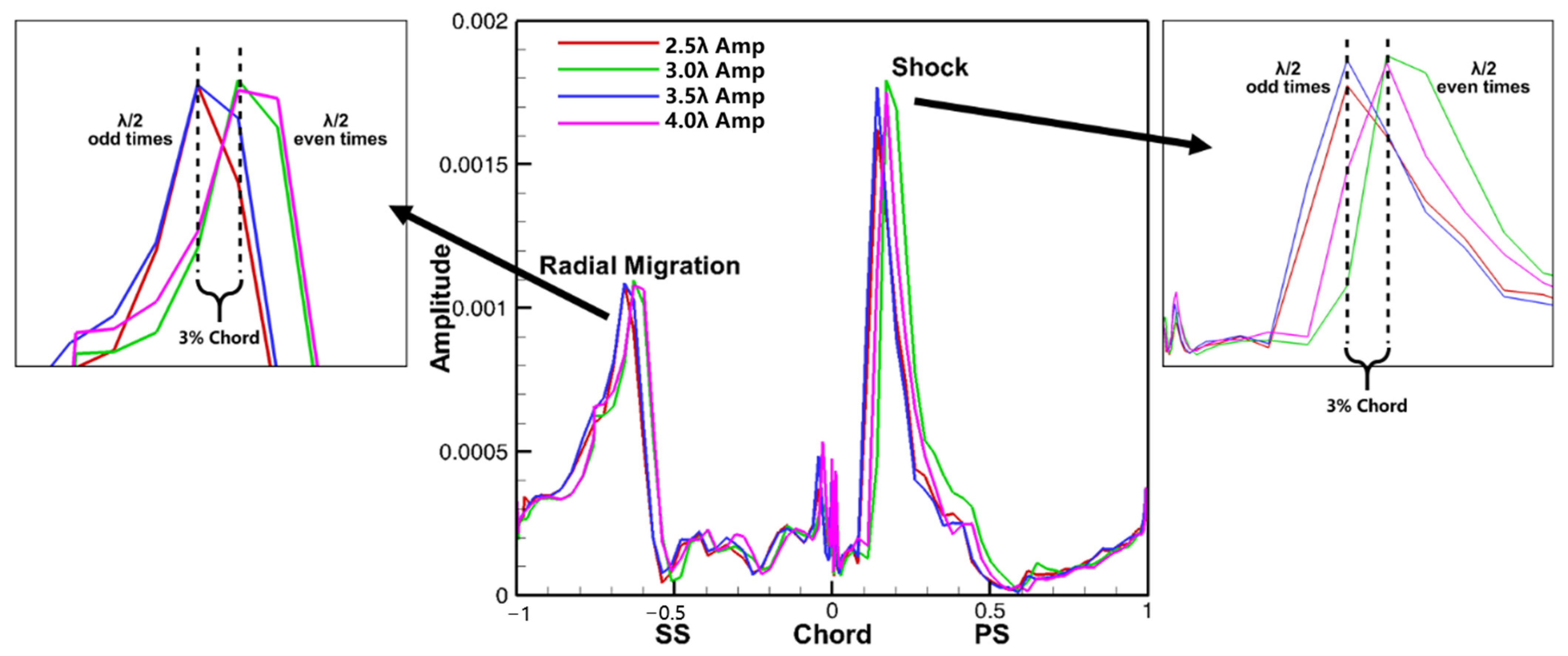
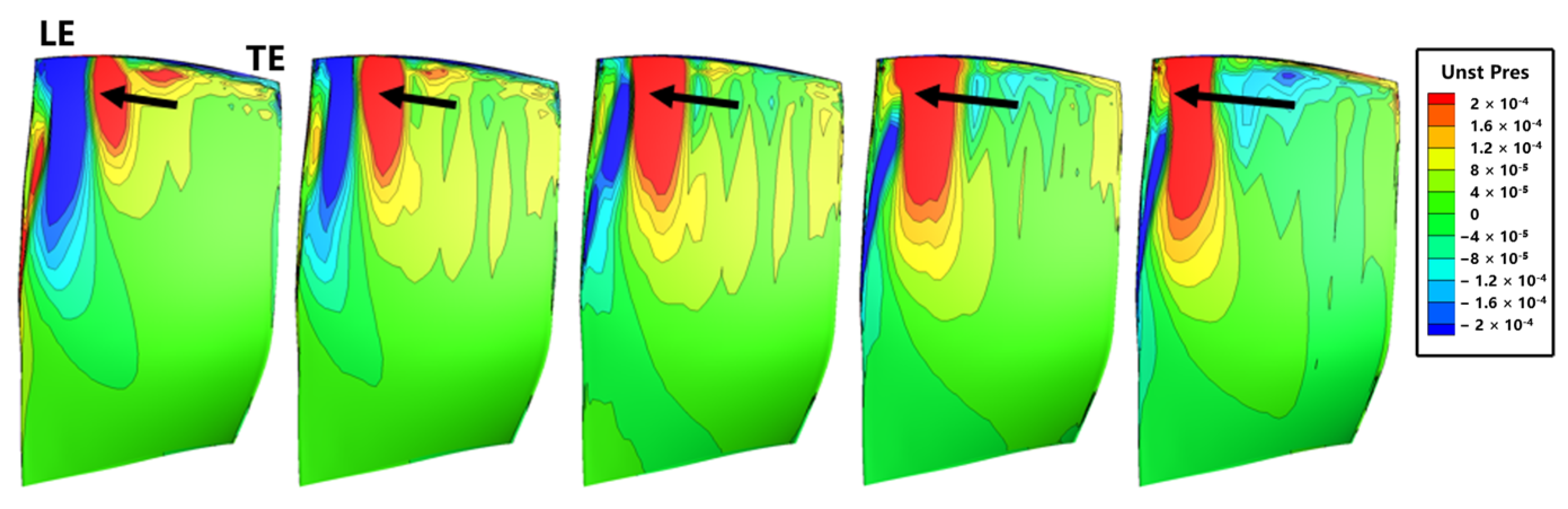
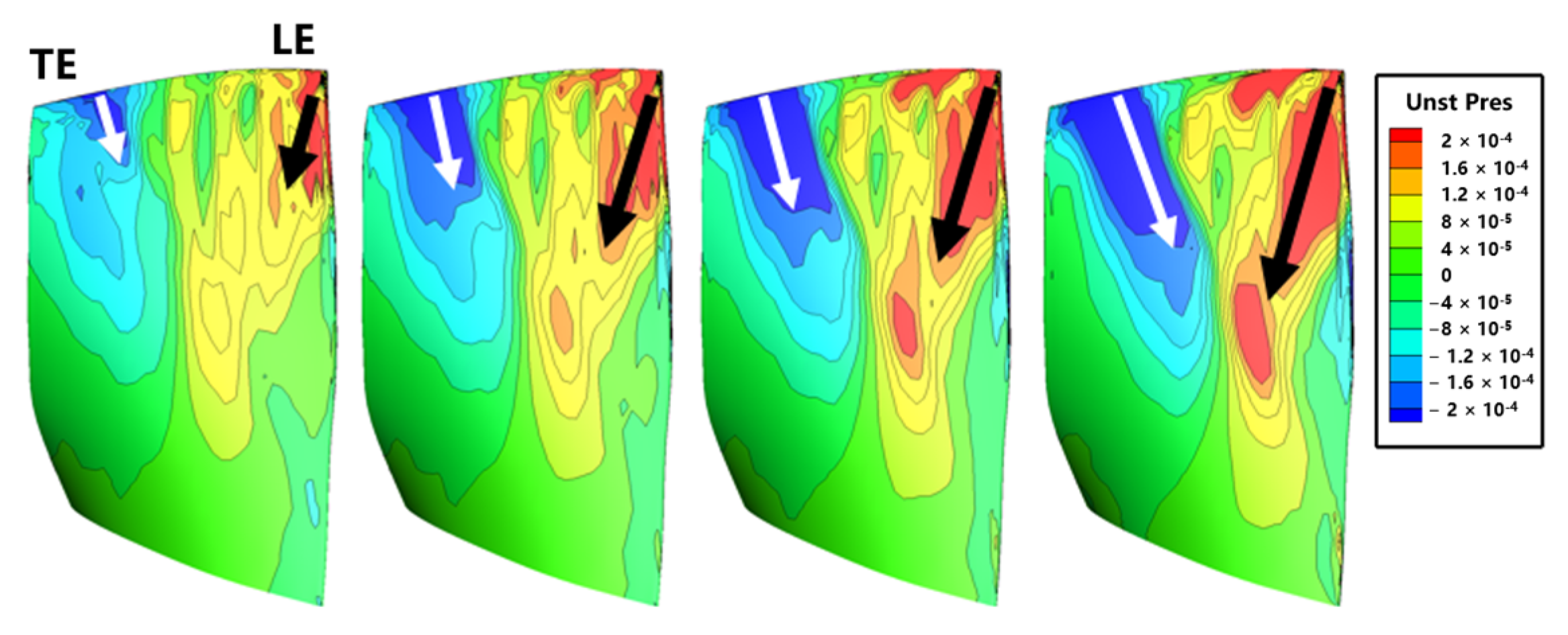
6.4. Unsteady Pressure Propagation Characteristics on Blade Surfaces
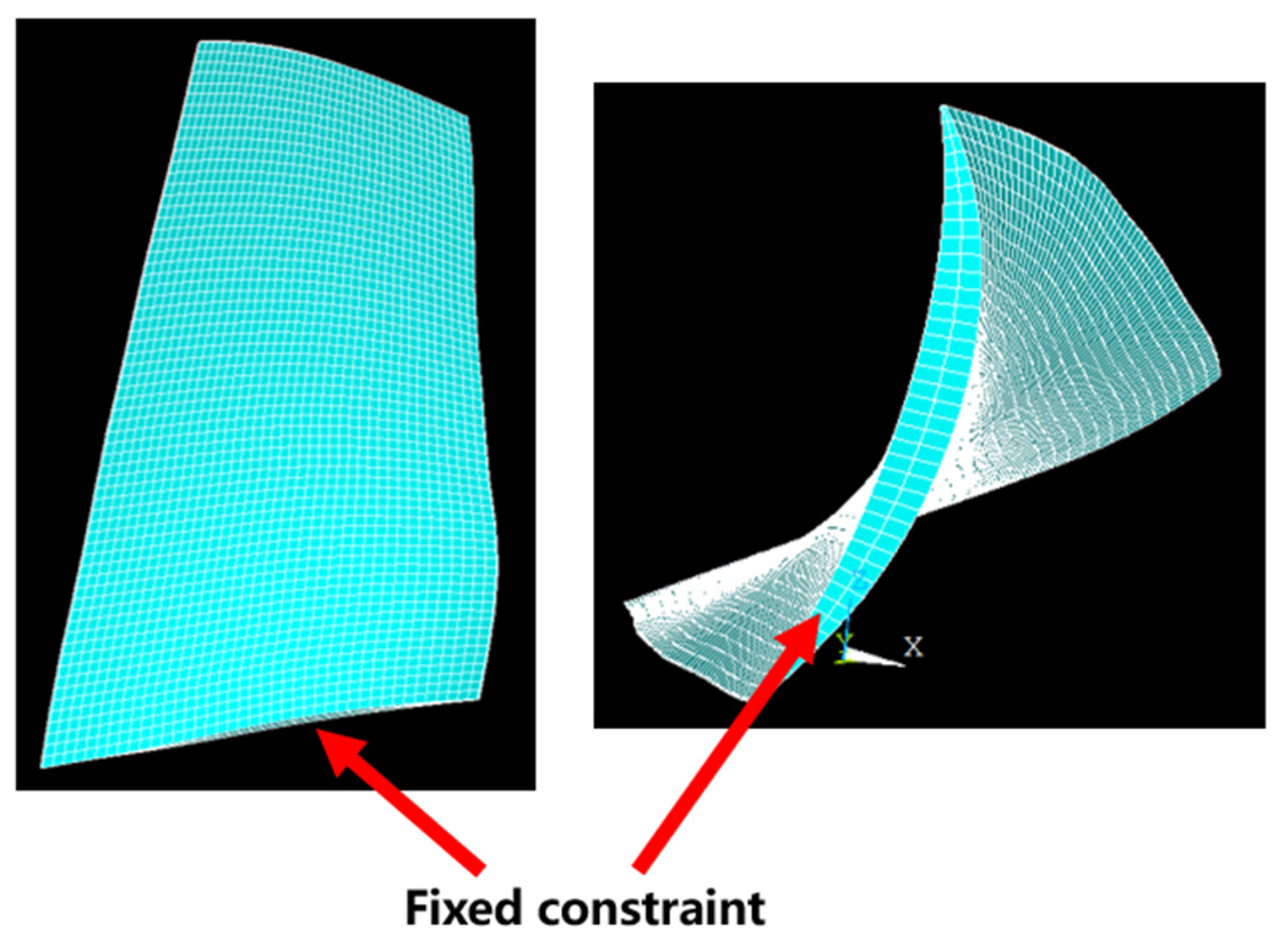
6.5. Blade Aeroelastic Stability
7. Conclusions
- The position of the shockwave is determined by the phase of the reflected acoustic waves, and the change in the shock wave position is the primary cause of the change in the blade aeroelastic stability under the influence of acoustic wave reflections. When wave reflection occurs upstream of the fan, the outgoing acoustic waves interfere with the reflected waves, resulting in a band-shaped axial distribution of the acoustic pressure. Different phases of the reflected waves represent varying magnitudes of the interfered acoustic pressure in front of the fan, consequently causing chordwise position variations in the shock wave and altering the blade aeroelastic stability.
- The effect of reflected waves on the local aeroelastic stability of blade surfaces varies in different zones dominated by different flow structures influencing the propagation of pressure waves. The amplitude variation of the pressure waves varies in the areas affected by the tip leakage flow and radial flow migration. This explains why the aerodynamic work on the suction surface always slightly deviates from the sinusoidal pattern.
- In prior studies, there has been a lack of attention directed toward investigating the influence of intake acoustic reflections on flow structures in the vicinity of blades. This study revealed that the influence of acoustic wave reflection on blade aeroelasticity cannot be dissociated from that of flow structures. Due to the interference of acoustic waves in the intake, the pressure in front of the fan changes, eventually leading to a shift in the position of the shock wave.
- The above findings imply that acoustic wave reflection plays an important role in the aeroelastic stability of the blade by affecting the flow structures. Thus, the intake geometry should be carefully selected. In our study, acoustic–vortex coupling is observed, but its effects on the blade aeroelastic stability are not discussed. Further study on this topic should help to clarify the physical mechanism of acoustic flutter.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Srinivasan, A.V. Flutter and Resonant Vibration Characteristics of Engine Blades. J. Eng. Gas Turbines Power 1997, 119, 742–775. [Google Scholar] [CrossRef]
- Isomura, K.; Giles, M.B. A Numerical Study of Flutter in a Transonic Fan. J. Turbomach. 1998, 120, 500–507. [Google Scholar] [CrossRef]
- Lane, F. System Mode Shapes in the Flutter of Compressor Blade Rows. J. Aeronaut. Sci. 1956, 23, 54–66. [Google Scholar] [CrossRef]
- Hansen, M.H. Aeroelastic instability problems for wind turbines. Wind Energy 2007, 10, 551–577. [Google Scholar] [CrossRef]
- Vogt, D.M.; Fransson, T.H. Experimental Investigation of Mode Shape Sensitivity of an Oscillating Low-Pressure Turbine Cascade at Design and Off-Design Conditions. J. Eng. Gas Turbines Power 2006, 129, 530–541. [Google Scholar] [CrossRef]
- Copeland, G.; Rey, G. Comparison of experiments and reduced-order models for turbomachinery high-incidence flutter. J. Fluids Struct. 2004, 19, 713–727. [Google Scholar] [CrossRef]
- Waite, J.J.; Kielb, R.E. Physical Understanding and Sensitivities of Low Pressure Turbine Flutter. J. Eng. Gas Turbines Power 2014, 137, 012502. [Google Scholar] [CrossRef]
- Srivastava, R.; Keith, T.G. Influence of Shock Wave on Turbomachinery Blade Row Flutter. J. Propuls. Power 2005, 21, 167–174. [Google Scholar] [CrossRef]
- Sanders, A.J.; Hassan, K.K.; Rabe, D.C. Experimental and Numerical Study of Stall Flutter in a Transonic Low-Aspect Ratio Fan Blisk. J. Turbomach. 2004, 126, 166–174. [Google Scholar] [CrossRef]
- Aotsuka, M.; Murooka, T. Numerical Analysis of Fan Transonic Stall Flutter. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition. Volume 7B: Structures and Dynamics, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar] [CrossRef]
- Vahdati, M.; Simpson, G.; Imregun, M. Mechanisms for Wide-Chord Fan Blade Flutter. J. Turbomach. 2011, 133, 041029. [Google Scholar] [CrossRef]
- Iseni, S.; Micallef, D.; di Mare, F. Sensitivity analysis of eigenmode variations on the flutter stability of a highly loaded transonic fan. In Proceedings of the GPPS Forum 18 Global Power and Propulsion Society, Montreal, QC, Canada, 7–9 May 2018. [Google Scholar]
- Purushothaman, K.; Naveen Kumar, N.R.; Jeyaraman, S.K.; Pratap, A. Aeroelastic instability evaluation of transonic compressor at design and off-design conditions. In Proceedings of the National Aerospace Propulsion Conference; Springer: Singapore, 2020; pp. 39–61. [Google Scholar]
- Dong, X.; Zhang, Y.; Zhang, Y.; Zhang, Z.; Lu, X. Numerical simulations of flutter mechanism for high-speed wide-chord transonic fan. Aerosp. Sci. Technol. 2020, 105, 106009. [Google Scholar] [CrossRef]
- Möller, D.; Jüngst, M.; Holzinger, F.; Brandstetter, C.; Schiffer, H.-P.; Leichtfuß, S. Mechanism of Nonsynchronous Blade Vibration in a Transonic Compressor Rig. J. Turbomach. 2016, 139, 011002. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, Y.; Zhang, Z.; Lu, X.; Zhang, Y. Effect of Tip Clearance on the Aeroelastic Stability of a Wide-Chord Fan Rotor. J. Eng. Gas Turbines Power 2020, 142, 091010. [Google Scholar] [CrossRef]
- Vahdati, M.; Sayma, A.I.; Breard, C.; Imregun, M. Computational Study of Intake Duct Effects on Fan Flutter Stability. AIAA J. 2002, 40, 408–418. [Google Scholar] [CrossRef]
- Lee, K.-B.; Wilson, M.; Vahdati, M. Numerical Study on Aeroelastic Instability for a Low-Speed Fan. J. Turbomach. 2017, 139, 071004. [Google Scholar] [CrossRef]
- Vahdati, M.; Smith, N.; Zhao, F. Influence of Intake on Fan Blade Flutter. J. Turbomach. 2015, 137, 081002. [Google Scholar] [CrossRef]
- Gallardo, J.M.; Sotillo, A.; Bermejo, Ó. Study of the Effect of the Scatter of Acoustic Modes on Turbine Flutter. J. Turbomach. 2019, 141, 101010. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, Y.; Lu, X.; Zhang, Y.; Gan, J. Numerical Investigation of the Fan Flutter Mechanism Related to Acoustic Propagation Characteristics. J. Turbomach. 2022, 144, 101009. [Google Scholar] [CrossRef]
- Oh, J.Y.; Ma, F.; Hsieh, S.-Y.; Yang, V. Interactions Between Shock and Acoustic Waves in a Supersonic Inlet Diffuser. J. Propuls. Power 2005, 21, 486–495. [Google Scholar] [CrossRef]
- Feldhusen, A.; Hartmann, A.; Klaas, M.; Schröeder, W. Impact of alternating trailing-edge noise on buffet flows. In Proceedings of the 31st AIAA Applied Aerodynamics Conference, San Diego, CA, USA, 24–27 June 2013. [Google Scholar] [CrossRef]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications; Elsevier BV: Amsterdam, The Netherlands, 2015; ISBN 9780080999951. [Google Scholar] [CrossRef]
- Zheng, Y.; Yang, H. Coupled Fluid-structure Flutter Analysis of a Transonic Fan. Chin. J. Aeronaut. 2011, 24, 258–264. [Google Scholar] [CrossRef]
- Roe, P. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- van Leer, B. Towards the Ultimate Conservative Difference Scheme. J. Comput. Phys. 1997, 135, 229–248. [Google Scholar] [CrossRef]
- Jameson, A. Time dependent calculations using multigrid, with applications to unsteady flows past airfoils and wings. In Proceedings of the 10th Computational Fluid Dynamics Conference, Honolulu, HI, USA, 24–26 June 1991. [Google Scholar] [CrossRef]
- Zheng, Y.; Jin, X.; Yang, H. Low-Engine-Order Forced Response Analysis of a Turbine Stage with Damaged Stator Vane. Entropy 2023, 26, 4. [Google Scholar] [CrossRef]
- Zheng, Y.; Gao, Q.; Yang, H. Forced Response Analysis of an Embedded Compressor Rotor Induced by Stator Disturbances and Rotor–Stator Interactions. Aerospace 2023, 10, 398. [Google Scholar] [CrossRef]
- Zheng, Y.; Jin, X.; Yang, H. Effects of Asymmetric Vane Pitch on Reducing Low-Engine-Order Forced Response of a Turbine Stage. Aerospace 2022, 9, 694. [Google Scholar] [CrossRef]
- Carta, F.O. Coupled Blade-Disk-Shroud Flutter Instabilities in Turbojet Engine Rotors. J. Eng. Power 1967, 89, 419–426. [Google Scholar] [CrossRef]
- Tyler, J.M.; Sofrin, T.G. Axial Flow Compressor Noise Studies. SAE Tech. Pap. 1962, 70, 309–332. [Google Scholar] [CrossRef]
- Hellmich, B.; Seume, J.R. Causes of Acoustic Resonance in a High-Speed Axial Compressor. J. Turbomach. 2008, 130, 031003. [Google Scholar] [CrossRef]
- Broatch, A.; García-Tíscar, J.; Roig, F.; Sharma, S. Dynamic mode decomposition of the acoustic field in radial compressors. Aerosp. Sci. Technol. 2019, 90, 388–400. [Google Scholar] [CrossRef]
- Buchwald, P.; Farahmand, A.; Vogt, D.M. On the Influence of Blade Aspect Ratio on Aerodynamic Damping. J. Turbomach. 2019, 141, 101007. [Google Scholar] [CrossRef]
- Spalart, P.R.; Allmaras, S.R. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar]
- Espinal, D.; Im, H.-S.; Zha, G.-C. Full-Annulus Simulation of Nonsynchronous Blade Vibration Excitation of an Axial Compressor. J. Turbomach. 2017, 140. [Google Scholar] [CrossRef]
- Stapelfeldt, S.; Brandstetter, C. Non-synchronous vibration in axial compressors: Lock-in mechanism and semi-analytical model. J. Sound Vib. 2020, 488, 115649. [Google Scholar] [CrossRef]
- Zhang, X.-Y.; Zhang, X.-Y.; Guo, S.-R. Efficient copper(I)-catalyzed C–S cross-coupling of thiols with aryl halides in an aqueous two-phase system. J. Sulfur Chem. 2011, 32, 23–35. [Google Scholar] [CrossRef]
- Kerrebrock, J.L. Small disturbances in turbomachine annuli with swirl. AIAA J. 1977, 15, 794–803. [Google Scholar] [CrossRef]











| Parameter | Unit | Value |
|---|---|---|
| Number of Blades | - | 22 |
| Tip Clearance | mm | 1.016 |
| Design Rotational Speed | rpm | 16,043 |
| Inlet Tip Diameter | cm | 51.4 |
| Outlet Tip Diameter | cm | 48.5 |
| Hub/Tip Radius Ratio at Leading Edge | - | 0.375 |
| Hub/Tip Radius Ratio at Trailing Edge | - | 0.478 |
| Mesh Level | Total Mesh Point | Mass Flow Rate | Pressure Ratio | Efficiency |
|---|---|---|---|---|
| Coarse | 752,763 | 34.1037 | 1.588 | 0.8976 |
| Medium | 1,207,325 | 34.0588 | 1.592 | 0.8996 |
| Fine | 1,565,434 | 34.0206 | 1.591 | 0.8991 |
| Elasticity Modulus (GPa) | Poisson Ratio | Density (kg/m3) |
|---|---|---|
| 110 | 0.33 | 4400 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Liang, H.; Zheng, Y. Effect of Intake Acoustic Reflection on Blade Vibration Characteristics. Aerospace 2024, 11, 358. https://doi.org/10.3390/aerospace11050358
Yang H, Liang H, Zheng Y. Effect of Intake Acoustic Reflection on Blade Vibration Characteristics. Aerospace. 2024; 11(5):358. https://doi.org/10.3390/aerospace11050358
Chicago/Turabian StyleYang, Hui, Hui Liang, and Yun Zheng. 2024. "Effect of Intake Acoustic Reflection on Blade Vibration Characteristics" Aerospace 11, no. 5: 358. https://doi.org/10.3390/aerospace11050358
APA StyleYang, H., Liang, H., & Zheng, Y. (2024). Effect of Intake Acoustic Reflection on Blade Vibration Characteristics. Aerospace, 11(5), 358. https://doi.org/10.3390/aerospace11050358







