Abstract
Satellites should be equipped with more and more deployable, large, flexible appendages to improve their service efficiency and reduce launch costs. The spring-driven deployment method of flexible appendages has been widely applied and generates great instantaneous shock loads on satellites, maybe affecting the safety of other flexible appendages, but the current related investigations for satellites with multiple large flexible appendages are insufficient. In this study, the deployment test of the antenna itself was conducted, and the attitude changes in a satellite during antenna deployment were telemetered. Then, a related dynamical model of the satellite was established and verified by the telemetry values of the satellite. Finally, the shock mechanism transmitted to solar arrays was analyzed, and the effect of solar array attitude was discussed. The results show that the simulated method of antenna deployment equivalent to the shock loads tested was thought to be efficient, though it could cause a small non-zero constant of the simulated angular velocities in the antenna deployment direction. The shock-induced moments, except the rotation direction of the solar array drive assembly (SADA), should be highlighted for the antenna deployment dynamic design of satellites, and the solar array attitude has few effects on the shock-induced loads at the SADA.
1. Introduction
In order to improve satellite service efficiency and reduce launch costs, satellites should be equipped with more and more deployable, large, flexible appendages, such as solar panels and mesh antennas [1,2]. Large flexible appendages are designed to be stowed within the fairing during launch, and then automatically deploy to the working state after entering orbit [3,4,5]. Large flexible appendages have a complex mechanical form, numerous constituent units and significant changes in mass properties during deployment, and whether they are successfully deployed in orbit generally affects the success or failure of satellite missions [6,7,8]. Therefore, deployment dynamical analysis and the design of large flexible appendages have become some of the key focuses in high-performance satellite design.
The dynamic design of large flexible appendages depends not only on their own deployment characteristics, but also on the dynamical behavior of the satellites. Many researchers have studied the dynamics behavior of the large flexible appendages themselves to ensure their reliable deployment in orbit. Wang et al. [9] designed a novel modular deployable structure for a rigid antenna driven by two brushless direct-current motors and proposed an equivalent dynamic analysis method for forecasting the motor driving force. Meng et al. [10], Bo et al. [11] and Siriguleng et al. [12] proposed structure design methods of basic units and their constructed regular polygonal prisms to describe the mechanism principles of motor-driven hoop truss antennas. Liu et al. [13], Wang et al. [14], Guo et al. [15,16], Takamatsu et al. [17] and Tian et al. [18,19] used experimental and numerical methods to design the truss structures, sliding hinges and driving springs of the truss antennas, aiming to ensure their reliable deployment driven by the elastic potential energy. Meanwhile, Li et al. [20] and Santoni et al. [21] studied the vibration characteristics of spring-deployed solar arrays on a satellite during deployment in orbit and found that the vibration of solar arrays has a larger amplitude and longer decay time under in-orbit vacuum conditions than on the ground. Thus, it can be summarized that there are mainly two ways to deploy flexible appendages, namely driven by a motor or by internal pre-compressed springs. The former contributes to the deployment controllability but requires a complex mechanism, usually for rigid and hoop truss antennas, while the latter has relatively simple mechanical structures but instantaneous shock load, often for solar arrays and truss antennas. In regard to these two deployment methods, Sureda et al. [22] compared them on the helix antenna of a 1U CubeSat and concluded that the spring-driven way is preferred due to the simpler mechanism, the higher reliability, the smaller volume and the lower cost.
Relatively few researchers have focused on the dynamical behavior of the satellites during the deployment of large flexible appendages. Liu et al. [23] performed dynamics modelling of a satellite with large motor-driven deployment of the hoop truss antenna. The results show that nonsynchronous deployment phenomena caused by the structural flexibility and the decay of the driving force should be considered in the design of the hoop truss antenna. Zheng et al. [24] built a dynamical model of a satellite during the spring-driven deployment of a truss antenna, but the simulation error of the peak shock force can reach 95%, and the error analysis of the shock force and the moment vs. time curves were not involved.
From the content mentioned above, it can be found that the deployment dynamics behavior of the large flexible appendages themselves has been thoroughly studied, in which the spring-driven deployment method has been widely applied due to the simple mechanism and the low cost. This deployment way inevitably generates great instantaneous shock loads on the satellite, and the larger size of the flexible appendage contributes to the greater shock loads, which may have negative effects on the satellite attitude and other flexible appendage safety, such as the root fracture of solar arrays. The current investigations about the dynamical behavior of satellites during spring-driven deployment of large flexible appendages are insufficient, especially regarding the effect of one flexible appendage deployment on the safety of another flexible appendage.
In this paper, the dynamic behavior of a satellite and its flexible solar arrays subjected to the spring-deployed shock of a large-scale flexible truss antenna was studied by tests and simulation. Firstly, the shock loads and the attitude changes in the satellite during antenna deployment were measured. Then, a corresponding dynamical model of the satellite was established and verified. Finally, the shock mechanism transmitted to solar arrays was analyzed and the effect of the solar array attitude is discussed based on the dynamical model. This paper can be used as a reference for the deployment dynamic design of satellites with multiple large flexible appendages.
2. Experimental Investigation
2.1. Deployment Test of Antenna Driven by Internal Spring Energy
A large-scale truss antenna like Figure 1a is studied in this paper. The design parameters of the antenna are consistent with Ref. [16]. A zero-gravity unloading device, composed of a support and ropes, was required during the deployment of the antenna. This support is a truss structure and its height is about twice that of the antenna aperture. The antenna hinges and the suspension point of the support were connected by the ropes to compensate the gravity effect of the truss antenna. Before deployment, the antenna was installed on the trolley through the riser with the same oblique angle as when deployed in orbit, and a six-direction load measurement sensor was installed between the riser and the trolley, as shown in Figure 1b. The shock data, obtained by the load measurement sensor, are shown in the local coordinate of Figure 1c. After the pyro devices on the clamp band initiated, the antenna began deploying. Then, the mass center of the antenna performed a circular motion centered on the suspension point of the unloading device. This made the measured shock loads not only include constant values for balancing gravity, but also include centrifugal forces caused by the circular motion, in which the latter led to some errors between the tested and in-orbit shock loads.
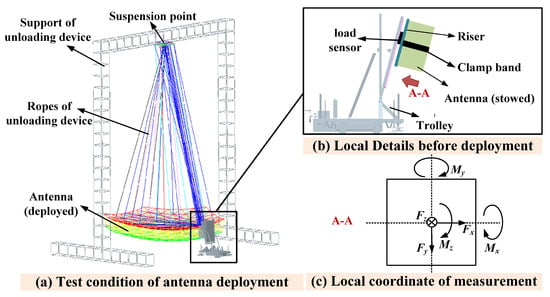
Figure 1.
The deployment test condition of the truss antenna.
The shock loads vs. time curves from the deployment test of the truss antenna were measured as shown in Figure 2a,b. It can be found that there is an obvious four-stage characteristic during the deployment process. The pyro device on the clamp band first initiated, causing huge pyro and mechanical shock loads from 0 to 0.8 s; the antenna then quickly extended, driven by the spring internal energy, from 0.8 s to 1.8 s, and next the antenna was locked after being deployed to the working position from 1.8 s to 2.8 s, generating great mechanical shock loads. Finally, the antenna vibrated and gradually attenuated to stability from 2.8 s to 5 s. In addition, the Z-direction shock force and Y-direction shock moment are obviously larger than the forces and moments in the other two directions, respectively. The former is because it is consistent with the antenna deployment direction where the mechanical shock loads from the spring release and the antenna lock is the greatest. The latter is due to the asynchronous phenomenon of the spring release and antenna lock of the antenna everywhere, causing the antenna in-plane moment, namely the Y-direction moment, to be the largest.
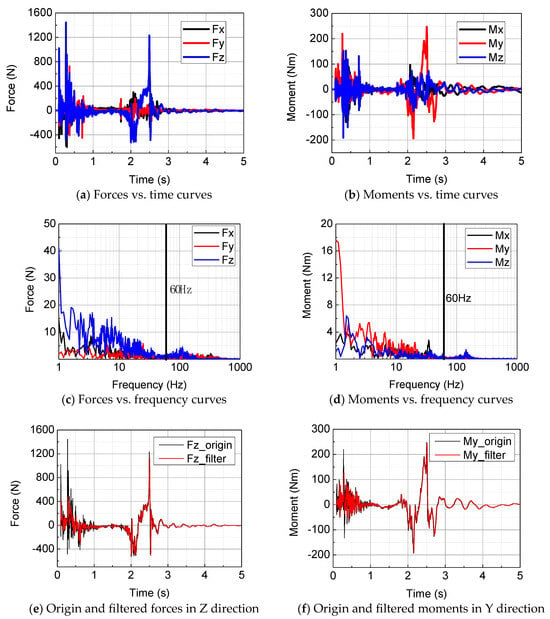
Figure 2.
Shock loads from the deployment test of the truss antenna in the local coordinate of Figure 1c.
In order to further investigate the shock loads of antenna deployment, fast Fourier transform was performed on the time-domain shock loads, as shown in Figure 2c,d. It can be found that the shock loads below 60 Hz are obviously larger than those over 60 Hz. Through the comparison of the shock loads without and with a low-pass filter of 60 Hz in Figure 2e,f, it can be seen that the filtered curves obviously reduce in the first stage but retain the mechanical shock loads in the third stage. Thus, it can be inferred that the mechanical and pyro shock loads are dominant in less and more than 60 Hz, respectively, and the front one is larger than the latter.
2.2. Attitude Test of Satellite during Antenna Shock Deployment
The deployment process of the truss antenna on a satellite with two flexible solar arrays was studied here, as shown in Figure 3. The two solar arrays were equipped on the ± Y sides of the satellite by solar array drive assemblies (SADAs), while the antenna was fixed on the riser of the stretch arm and the arm was fixed on the + X sides of the satellite. There are two solar panels in each solar array, and the detailed parameters of the solar panel are consistent with Ref. [25]. Before the deployment of the antenna began, the solar arrays and stretch arm were deployed to the specific position. After the initiation of pyro devices on the clamp band, the antenna was driven by spring internal energy from stowed to deployed statuses. The satellite angle and angular velocity were measured by the star sensor and gyroscope, respectively, and the data were downloaded to the ground by the telemetry, tracking and control (TT&C) subsystem of the satellite. There are designs of the global coordinate and local coordinate shown in Figure 3, in which the latter, consistent with that in Figure 1c, was only used to describe the shock loads and all other data in this paper were defined in the front one.
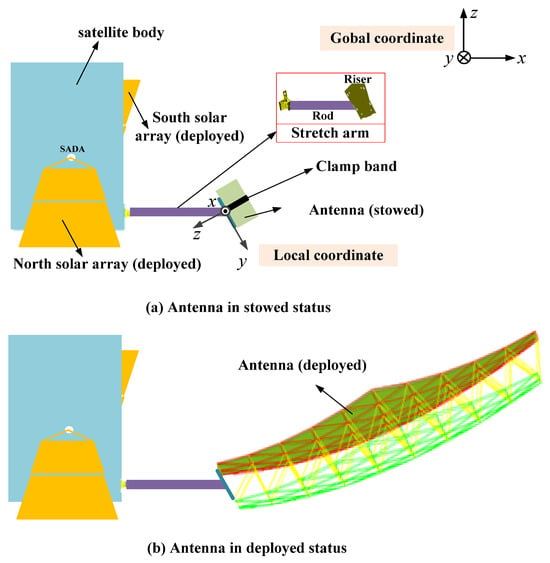
Figure 3.
The satellite configuration with the truss antenna from stowed to deployed statuses.
The angle and angular velocity vs. time curves of the satellite during the deployment of the antenna in the global coordinate of Figure 3 were obtained by the telemetry subsystem, as shown in Figure 4. Note that those curves are shown within 40 s from the antenna deployment, and the satellite has not started attitude intervention in this period. It can be found that both the angle and the angular velocity quickly increase within 5 s, which is consistent with the deployment time of the antenna itself. From 5 s to 40 s, the angular velocity gradually vibrantly decays to zero while the angle becomes a constant value due to conservation of the angular momentum. So, it is inferred that shock loads from the antenna deployment inevitably cause satellite attitude changes and solar array vibration, thereby extending the stability time. In addition, the maximum values of the angle and angular velocity are in the Y direction, middle values are in the Z direction, and the minimum values are in the X direction. This is because the maximum shock force is in the Z direction of the local coordinate, forming the maximum torque in the Y direction of the global coordinate. Similarly, the Y-direction angle and angular velocity are from the maximum shock moment in the Y direction of the local coordinate.
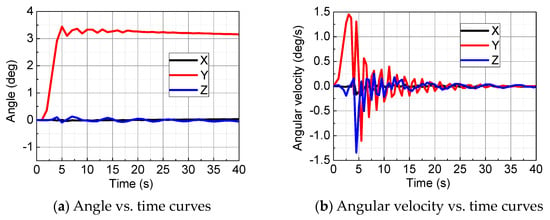
Figure 4.
The angle and angular velocity vs. time curves of the satellite during the deployment of the antenna in the global coordinate of Figure 3.
3. Dynamical Model
3.1. Modelling Details
The dynamical model of the satellite was established in ADAMS software [26] to simulate the deployment of the truss antenna, as shown in Figure 5. The antenna deployment was equivalent to the shock loads tested in Figure 2a,b, as shown in the red zones at A in Figure 5, due to the complexity of the accurate deployment model of the antenna with many constituent units. The two solar arrays, the stretch arm and the antenna were modelled as flexible bodies, while the satellite body involving all the remaining parts was simulated as a rigid body, as the natural frequency of the latter is two orders of magnitude larger than that of the front one. The stretch arm was fixed with the satellite body. The SADAs between the solar arrays and the satellite body were simulated by six-direction flexible joints like the red zones at C and D in Figure 5, with the equation as follows:
where Tx, Ty and Tz represent the translational motions in the X, Y and Z directions, respectively; Rx, Ry and Rz represent the rotational motions in the X, Y and Z directions, respectively; i denotes the direction of the SADA joint load; ki and ci represent the stiffness and damping coefficients in the i direction, respectively, and the values are from tests; and Fi and xi represent the joint load and displacement in the i direction, respectively. The SADA has a holding moment in the Y direction, that is, if the rotational moment in the Y direction is greater than 5 Nm, the blocking moment will always be 0.5 Nm.
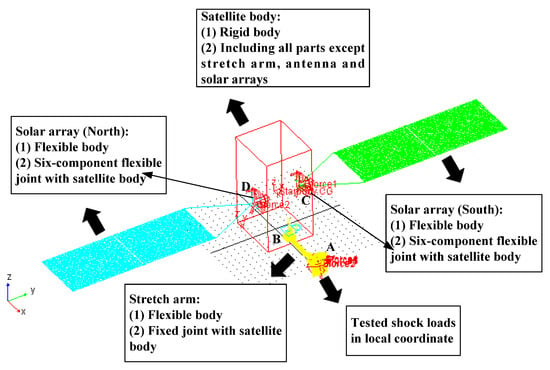
Figure 5.
The dynamical model of the satellite during the deployment of the truss antenna.
3.2. Prediction Verification
The load transmission induced by the truss antenna deployment is highlighted in the following discussion; thus, the accuracy of the dynamic model predicting the satellite’s angular acceleration should be verified. The angular accelerations cannot be obtained from the satellite’s telemetry subsystem, so the satellite’s angular velocities were applied to verify the efficiency of the model.
The telemetry and simulated angular velocity vs. time curves of the satellite during the deployment of the antenna in the global coordinates of Figure 3 are compared in Figure 6a–c. It can be found that the simulated angular velocities have more vibration and slightly larger peak values than telemetry values within 5 s, which may be because the telemetry acquisition interval of satellite angular velocities is only 0.5 s, and it is difficult to capture the rapid changes in satellite attitude during the antenna deployment phase. In addition, simulated Y-direction angular velocities attenuate to non-zero constants, as the shock loads used in the model include centrifugal forces caused by the unloading device, causing non-conservation of the angular momentum in this direction. The non-zero constant of about −0.1°/s is obviously smaller than the peak values of angular velocities induced by the antenna deployment, so the simulated method of antenna deployment equivalent to the shock loads tested was thought to be efficient. In addition, Figure 6d shows the simulated errors in terms of the peak values and attenuation frequency, in which an error is equal to 20 × lg(simulated value/telemetry value). It can be seen that all the errors are within 3 dB; thus, the model was thought to be efficient.
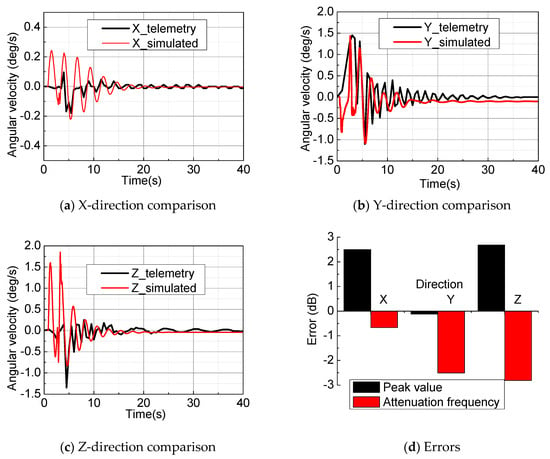
Figure 6.
Comparison of the telemetry and simulated angular velocity vs. the time curves of the satellite during the deployment of the antenna in the global coordinates of Figure 3.
4. Discussion
4.1. Shock Mechanism Transmitted to SADA
In order to study the propagation characteristics of shock loads from the antenna deployment on the satellite, four typical locations were selected, namely the point in the riser where was affected by shock loads (Point A in Figure 5), the joint between the stretch arm and the satellite body (Point B in Figure 5), and the SADAs on the ±Y sides (Point C and Point D in Figure 5).
The loads at four typical locations in the global coordinates of Figure 3 are compared in Figure 7. It can be found that the three direction forces and the X-direction moment from Point A to Point B are basically unchanged, while the moments in the Y and Z directions increase significantly. This is because the moments in the Y and Z directions at Point B include the bending moments formed by the forces at Point A, and the X-direction force at Point A cannot form the accumulated moment for the X-direction moment at Point B. The forces and moments at Point B drive the attitude rotation and position translation of the satellite body, forming the loads at Points C and D. It can be indicated that all the forces and Y-direction moments at the two points are quite small, while the X-direction and Z-direction moments are obviously greater. This is because the stiffness and damping coefficients of SADAs in the X and Z rotational directions are at least one order of magnitude larger than those in the Y rotational direction. Therefore, the shock-induced moments, except the SADA rotation direction, should be highlighted for the deployment dynamic design of satellites with multiple large flexible appendages.
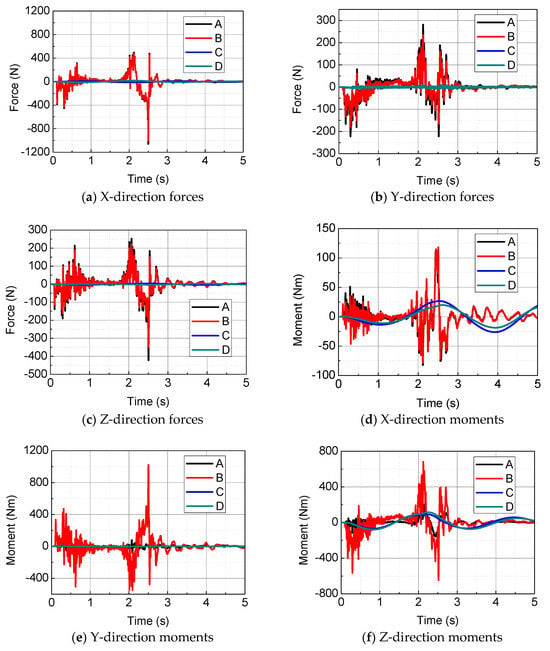
Figure 7.
Shock load transmission mechanism in the global coordinates of Figure 3.
4.2. Effect of Solar Array Attitude
In order to obtain the satellite strategy during the truss antenna deployment to protect the SADAs and solar arrays, the effect of the solar array attitude was discussed, including 0°, 45° and 90° attitudes, as shown in Figure 8. Note that the solar arrays do not rotate for their own service during antenna deployment.

Figure 8.
Three kinds of solar array attitudes.
Only the X-direction attitudes of the satellite as well as the X-direction and Z-direction loads at the SADAs with different solar array attitudes are shown in Figure 9, due to the similar rules in the other directions. It can be seen that the solar array attitude has few effects on the angular velocities of the satellite in the three directions and the Y-direction loads at the SADAs. Meanwhile, it affects the X-direction and Z-direction loads at the SADAs but did not composed loads of them. Therefore, it can be inferred that the solar array attitude has few effects on the shock-induced loads at the SADAs and there is no need to pay special attention to the design of the solar array attitude during antenna deployment.
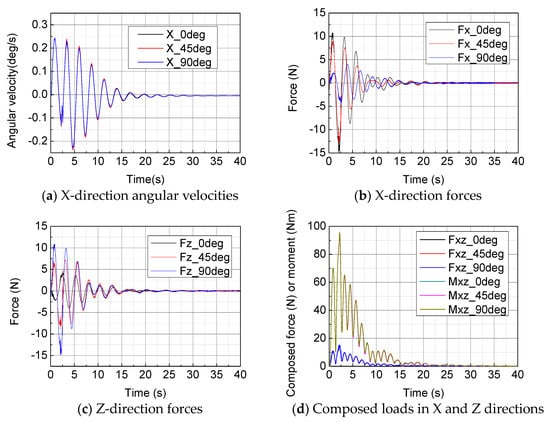
Figure 9.
The satellite attitudes and loads at SADAs with different solar array attitudes in the global coordinate of Figure 3.
5. Conclusions
In this paper, experimental and simulated methods are used to study the dynamic behavior of a satellite and its solar arrays subject to large-scale antenna deployment shock. The shock mechanism transmitted to solar arrays is analyzed and the effect of the solar array attitude is discussed. The following conclusions can be obtained:
- (1)
- The deployment of the truss antenna includes four stages, sequentially, the pyro unlocking of the antenna, the antenna extension driven by spring energy, the locking at a specified location and the antenna vibration attenuating to stability. Pyro shock and spring-induced mechanical shock are dominant at more and less than 60 Hz, respectively, and the former are smaller than the latter.
- (2)
- The stability time of the satellite subjected to the truss antenna deployment (40 s) is much larger than that of the truss antenna deployment by itself (5 s) due to the damped vibration of the solar arrays. In the dynamical model of the satellite, the simulated method of antenna deployment, equivalent to the shock loads tested, was thought to be efficient, though it could cause a small non-zero constant of the simulated Y-direction angular velocities.
- (3)
- The shock-induced moments, except the SADA rotation direction, should be highlighted for the antenna deployment dynamic design of satellites. The solar array attitude affects the X-direction and Z-direction loads at the SADAs but not their composed loads and Y-direction loads. Therefore, it can be inferred that there is no need to pay special attention to the design of the solar array attitude during antenna deployment.
Author Contributions
Conceptualization, J.Z., Q.H. and X.W.; methodology, J.Z. and Y.D.; software, J.Z.; validation, J.Z. and P.W.; formal analysis, J.Z.; investigation, J.Z. and P.W.; resources, J.Z., Q.H. and X.W.; data curation, J.Z.; writing—original draft preparation, J.Z., Q.H. and X.W.; writing—review and editing, J.Z., P.W. and Y.D.; supervision, J.Z. and Y.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Du, X.; Du, J.; Bao, H.; Sun, G. Deployment analysis of deployable antennas considering cable net and truss flexibility. Aerosp. Sci. Technol. 2018, 82, 557–565. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, J.; Xiao, Y.; Ma, X. Deployment Strategy and Dynamic Analysis of Large Ring Truss Antenna. Int. J. Aerosp. Eng. 2022, 2022, 4725423. [Google Scholar] [CrossRef]
- Dai, L.; Xiao, R. Optimal design and analysis of deployable antenna truss structure based on dynamic characteristics restraints. Aerosp. Sci. Technol. 2020, 106, 106086. [Google Scholar] [CrossRef]
- Sun, Z.; Yang, D.; Duan, B.; Kong, L.; Zhang, Y. Structural design, dynamic analysis, and verification test of a novel double-ring deployable truss for mesh antennas. Mech. Mach. Theory 2021, 165, 104416. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, R.Q.; Behdinan, K. Nonlinear dynamic analysis near resonance of a beam-ring structure for modeling circular truss antenna under time-dependent thermal excitation. Aerosp. Sci. Technol. 2019, 86, 296–311. [Google Scholar] [CrossRef]
- Freeman, M. On-orbit deployment anamolies, What can be done? In Proceedings of the the Seventeenth Space Simulation Conference. Terrestrial Test for Space Success, Baltimore, MD, USA, 9–12 November 1992; NASA Goddard Space Flight Center: Baltimore, MD, USA, 1992. [Google Scholar]
- Xu, Y.; Guan, F.L. Structure–electronic synthesis design of deployable truss antenna. Aerosp. Sci. Technol. 2013, 26, 259–267. [Google Scholar] [CrossRef]
- Takano, T.; Natori, M.; Miyoshi, K. A tension-truss deployable antenna for space-use and its obtainable characteristics. In Proceedings of the IEEE Antennas and Propagation Society International Symposium and URSI National Radio Science Meeting, Seattle, WA, USA, 20–24 June 1994; Volume 2, pp. 878–881. [Google Scholar]
- Wang, Y.; Liu, R.; Yang, H.; Cong, Q.; Guo, H. Design and deployment analysis of modular deployable structure for large antennas. J. Spacecr. Rocket. 2015, 52, 1101–1111. [Google Scholar] [CrossRef]
- Meng, Q.; Liu, X.J.; Xie, F. Structure design and kinematic analysis of a class of ring truss deployable mechanisms for satellite antennas based on novel basic units. Mech. Mach. Theory 2022, 174, 104881. [Google Scholar] [CrossRef]
- Han, B.; Xu, Y.; Yao, J.; Zheng, D.; Guo, L.; Zhao, Y. Type synthesis of deployable mechanisms for ring truss antenna based on constraint-synthesis method. Chin. J. Aeronaut. 2020, 33, 2445–2460. [Google Scholar] [CrossRef]
- Siriguleng, B.; Zhang, W.; Liu, T.; Liu, Y. Vibration modal experiments and modal interactions of a large space deployable antenna with carbon fiber material and ring-truss structure. Eng. Struct. 2020, 207, 109932. [Google Scholar] [CrossRef]
- Liu, R.Q.; Tian, D.K.; Deng, Z.Q.; Guo, H.W.; Liu, Z.J. Kinematics modeling and driving spring design of truss structure for deployable truss antenna. In Advanced Materials Research; Trans Tech Publications Ltd.: Wollerau, Switzerland, 2012; Volume 457, pp. 1337–1341. [Google Scholar]
- Wang, D.; Liu, R.; Wang, Y.; Guo, H.; Cong, Q.; Zhang, C. Deployment analysis of a planar deployable support truss structure. In Proceedings of the 2013 IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 4–7 August 2013; pp. 1287–1292. [Google Scholar]
- Guo, J.; Zhao, Y.; Zhang, G.; Liu, E.; Liu, B.; Xu, Y. Configuration synthesis and unfolding stiffness characteristics analysis of a truss antenna connecting mechanism based on URU-RR-URU hexagonal deployable unit. Mech. Mach. Theory 2022, 177, 105047. [Google Scholar] [CrossRef]
- Guo, J.; Zhao, Y.; Xu, Y.; Zhang, G. Mechanics analysis and structural design of a truss deployable antenna mechanism based on 3RR-3URU tetrahedral unit. Mech. Mach. Theory 2022, 171, 104749. [Google Scholar] [CrossRef]
- Takamatsu, K.A.; Onoda, J. New deployable truss concepts for large antenna structures or solar concentrators. J. Spacecr. Rocket. 1991, 28, 330–338. [Google Scholar] [CrossRef]
- Tian, D.; Liu, R.; Deng, Z. Spatial geometry modeling of truss structure and analysis of connection deviation for deployable truss antenna. In Proceedings of the 2010 International Conference on Measuring Technology and Mechatronics Automation, Changsha, China, 13–14 March 2010; Volume 3, pp. 427–432. [Google Scholar]
- Tian, D.; Deng, Z.; Liu, R.; Guo, H. Analysis on dynamic response of truss structure for deployable truss antenna. In Proceedings of the 2011 9th World Congress on Intelligent Control and Automation, Taipei, Taiwan, 21–25 June 2011; pp. 1185–1188. [Google Scholar]
- Li, D.X.; Liu, W.; Fan, C.Z. Dynamic characteristics of satellite solar arrays under the deployment shock in orbit. Shock. Vib. 2018, 2018, 6519748. [Google Scholar] [CrossRef]
- Santoni, F. Dynamics of spring-deployed solar panels for agile nanospacecraft. J. Aerosp. Eng. 2015, 28, 04014122. [Google Scholar] [CrossRef]
- Sureda, M.; Sobrino, M.; Millan, O.; Aguilella, A.; Solanellas, A.; Badia, M.; Munoz-Martin, J.F.; Fernandez, L.; Ruiz-De-Azua, J.A.; Camps, A. Design and testing of a helix antenna deployment system for a 1U CubeSat. IEEE Access 2021, 9, 66103–66114. [Google Scholar] [CrossRef]
- Liu, L.; Shan, J.; Zhang, Y. Dynamics modeling and analysis of spacecraft with large deployable hoop-truss antenna. J. Spacecr. Rocket. 2016, 53, 471–479. [Google Scholar] [CrossRef]
- Zheng, S.; Li, T.; Zhao, J.; Ma, X.; Zhu, J.; Huang, Z.; Lang, Y. Deployment Impact Experiment and Dynamic Analysis of Modular Truss Antenna. Int. J. Aerosp. Eng. 2022, 2022, 2038932. [Google Scholar] [CrossRef]
- Safak, O. Structural Design and Analysis of a Solar Array Substrate for a GEO Satellite. Master’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2013. [Google Scholar]
- Adams Dynamic Software; MSC Software Corporation: Santa Ana, CA, USA, 2016.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).