Dynamic Response of Phase Change Heat Exchange Unit with Layered Porous Media for Pulsed Electronic Equipment
Abstract
1. Introduction
2. Methodology
2.1. Physical Model
2.2. Governing Equations
2.2.1. Governing Equations for the Porous Medium Framework
- (1)
- The framework material is copper.
- (2)
- The porous medium exhibits isotropy in all directions.
- (3)
- Uniform pore density and constant porosity. The heat transfer within the copper framework is mathematically articulated through the energy control equation, as denoted by Equation (1).
2.2.2. Governing Equations for the PCM
- (1)
- The phase change material is pure paraffin.
- (2)
- The internal structure of the phase change material is isotropic.
- (3)
- The post-melting flow of the phase change material is laminar, incompressible, and includes a mushy zone during the phase transition.
- (4)
- The physical properties of paraffin remain constant in the solid and liquid phases, independent of temperature, while linearly varying in the mushy zone.
- (5)
- Post-melting paraffin adheres to the Boussinesq assumption, wherein density changes only affect the volume force term in the momentum equation.
- (6)
- The influence of surface tension is neglected.
2.3. Mesh Model
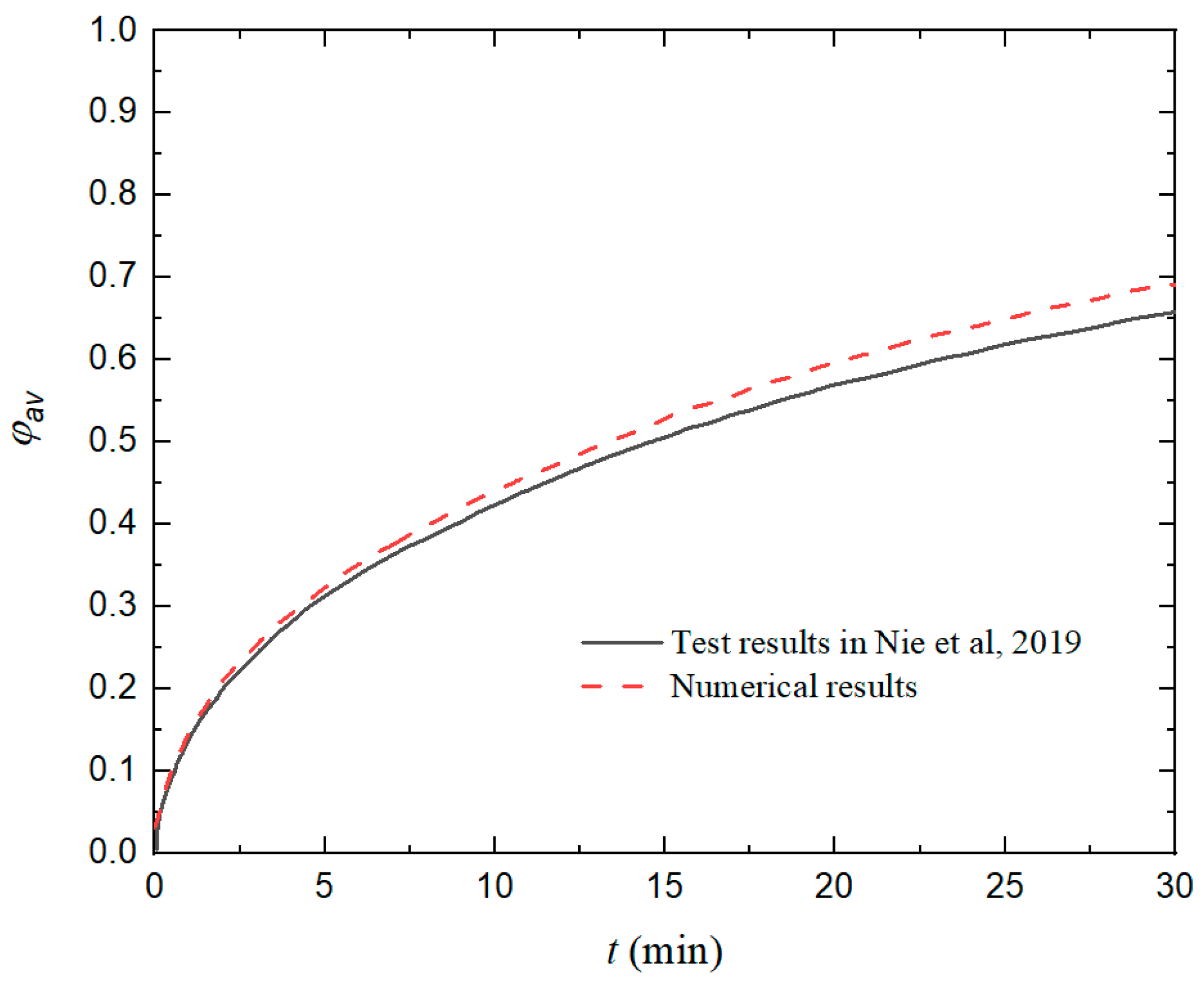
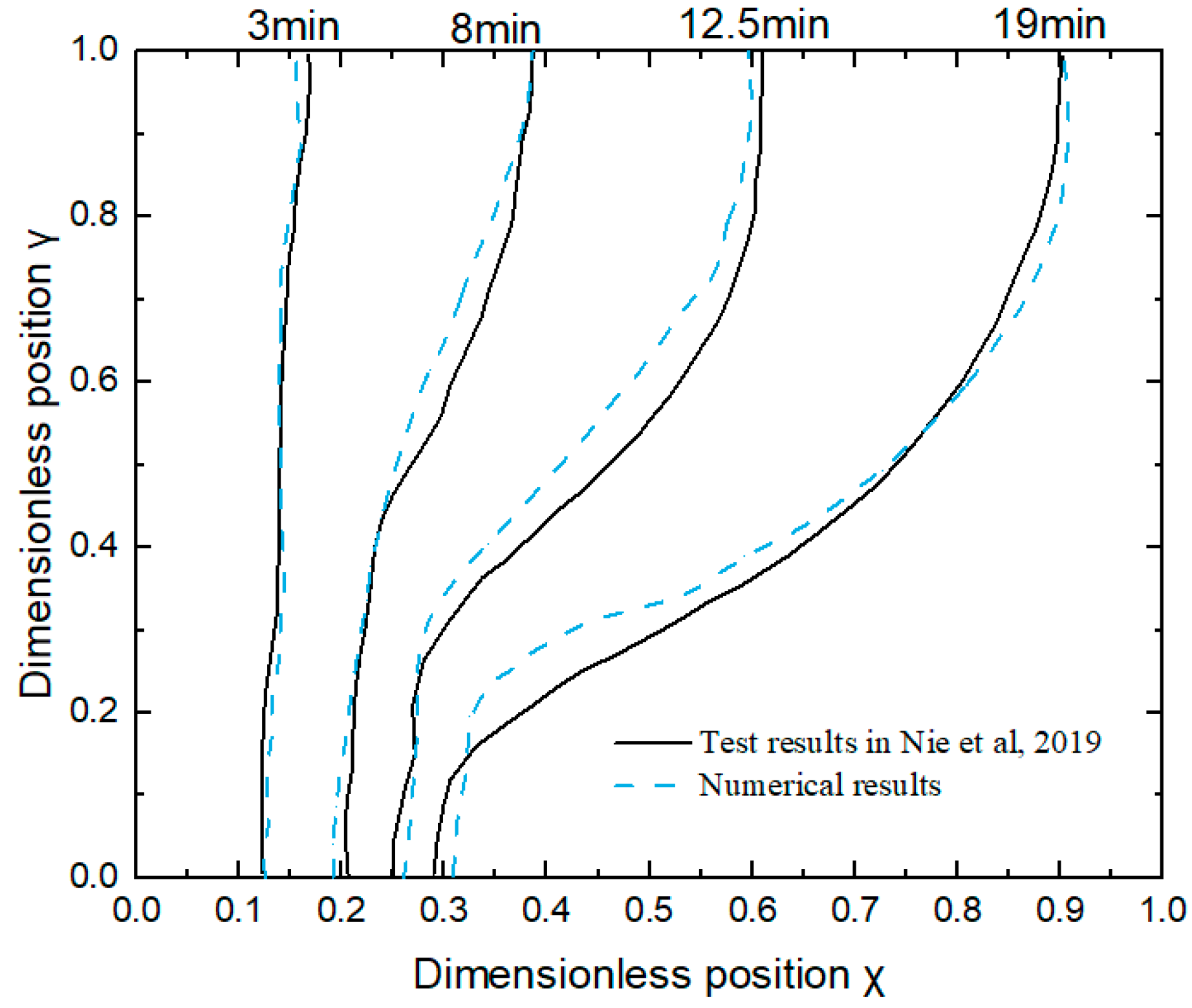
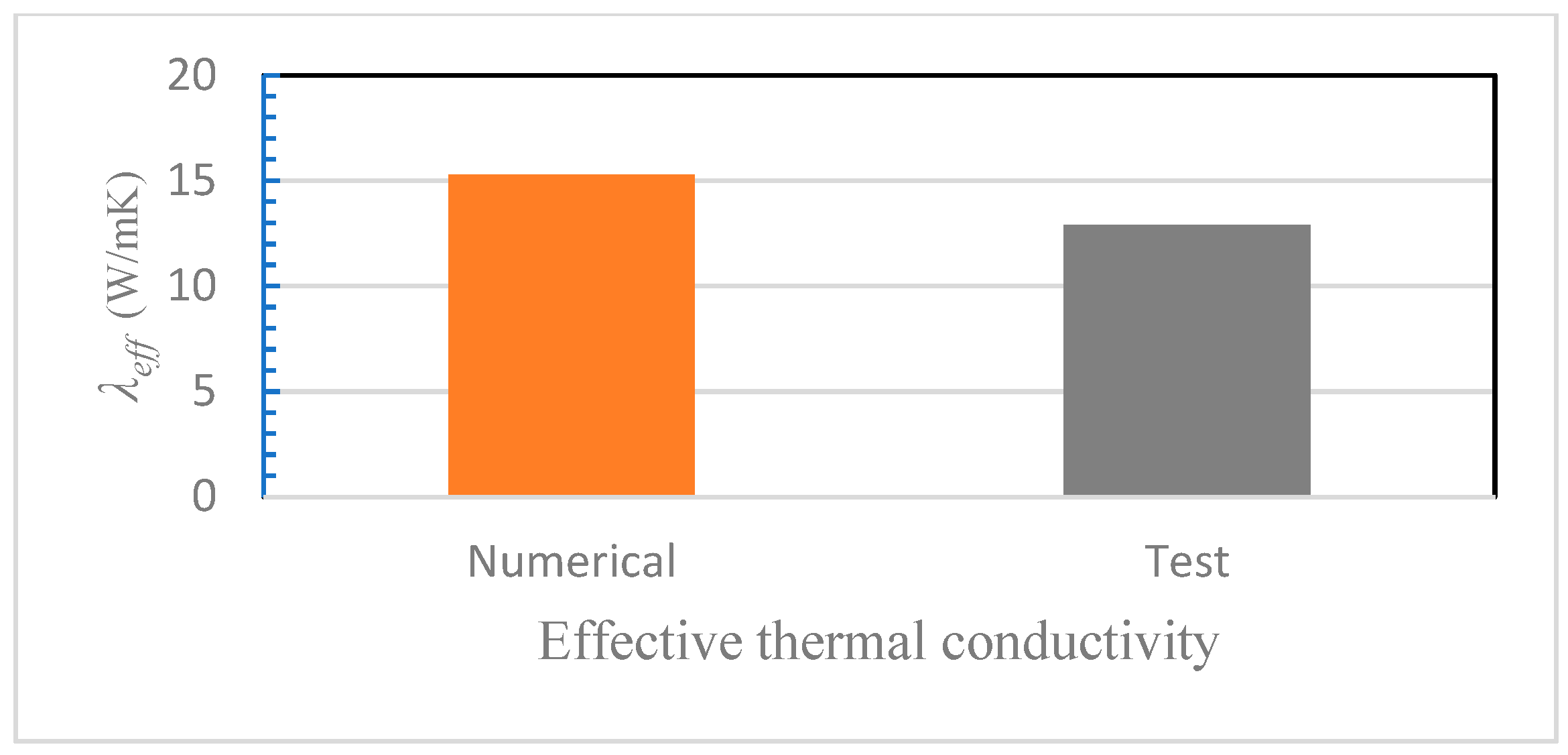
2.4. Model Validation
3. Simulation Results and Discussion
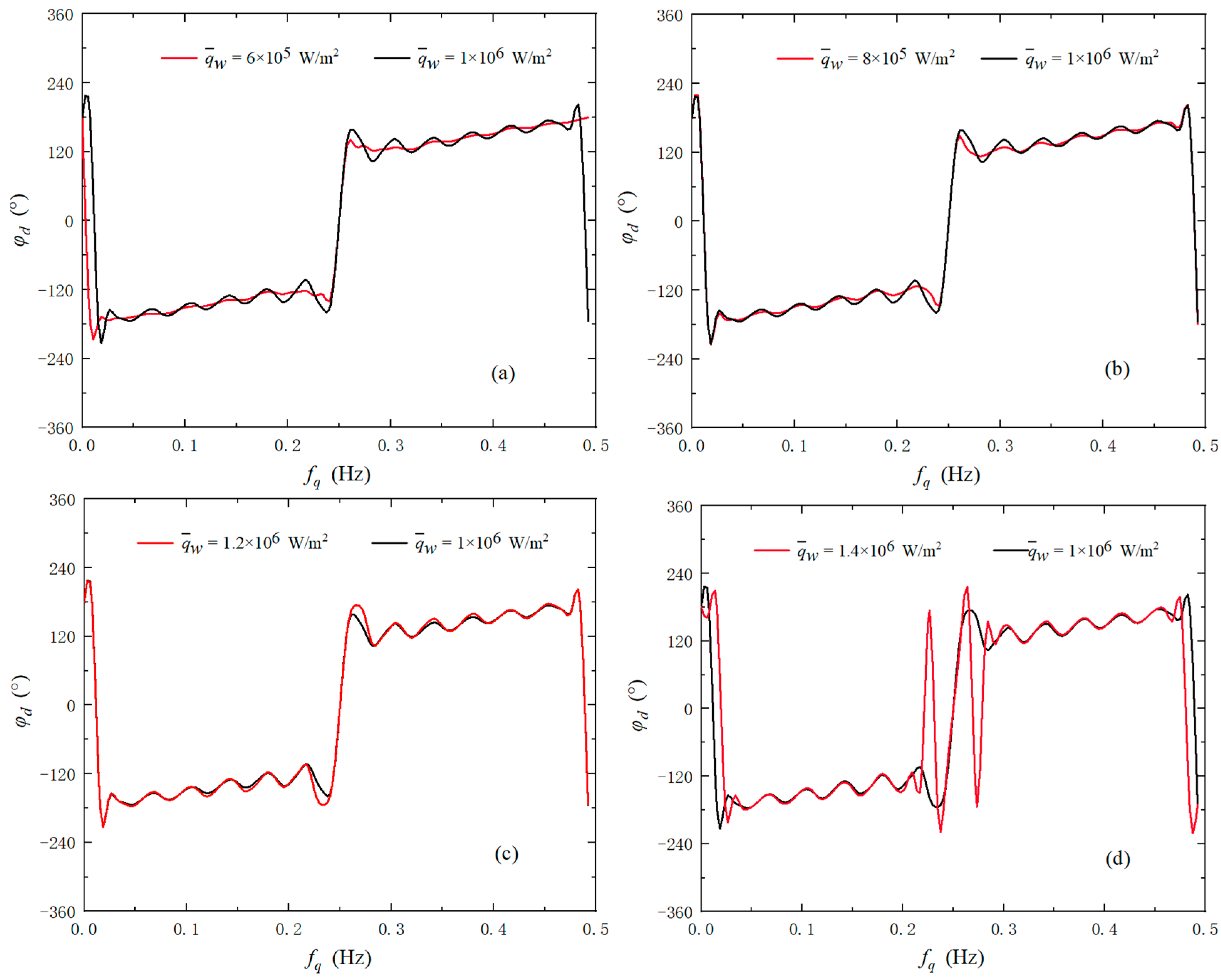
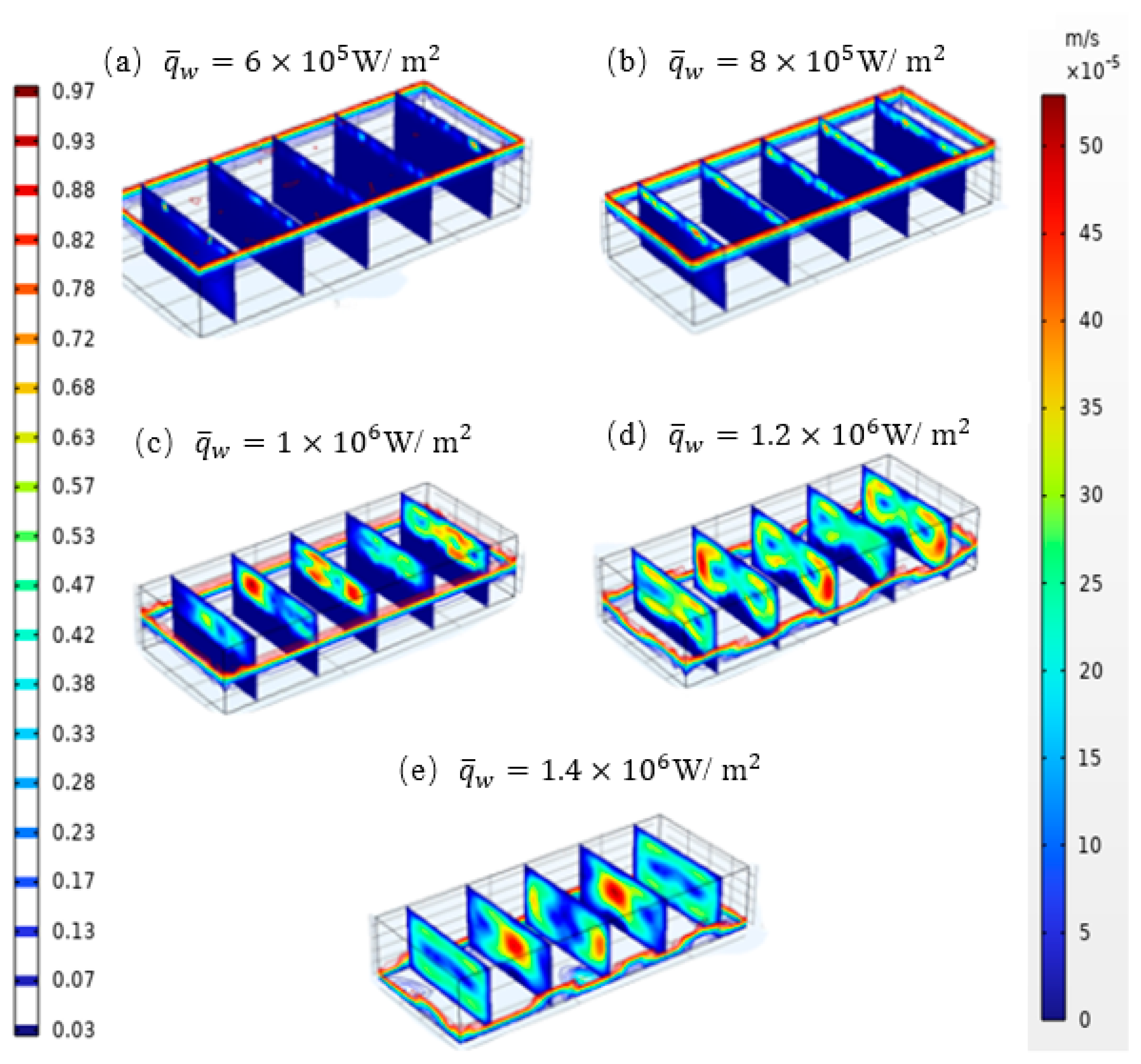
3.1. Variation in Heat Flow Amplitude
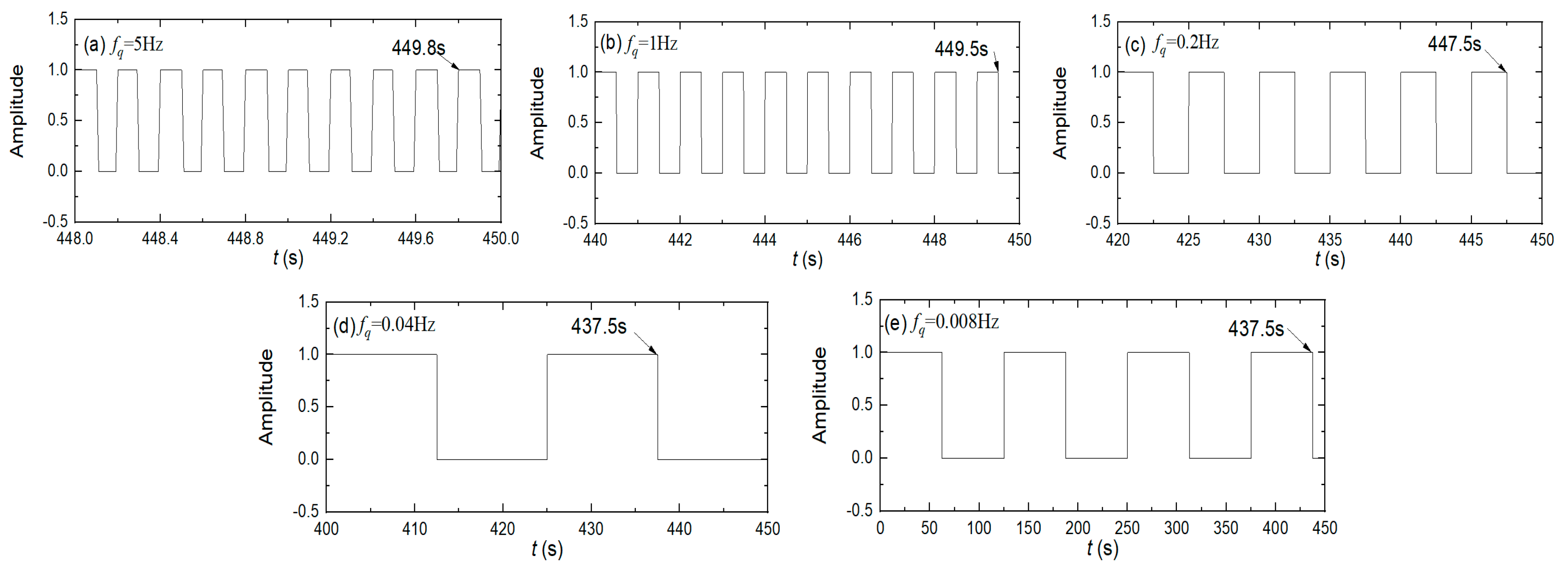
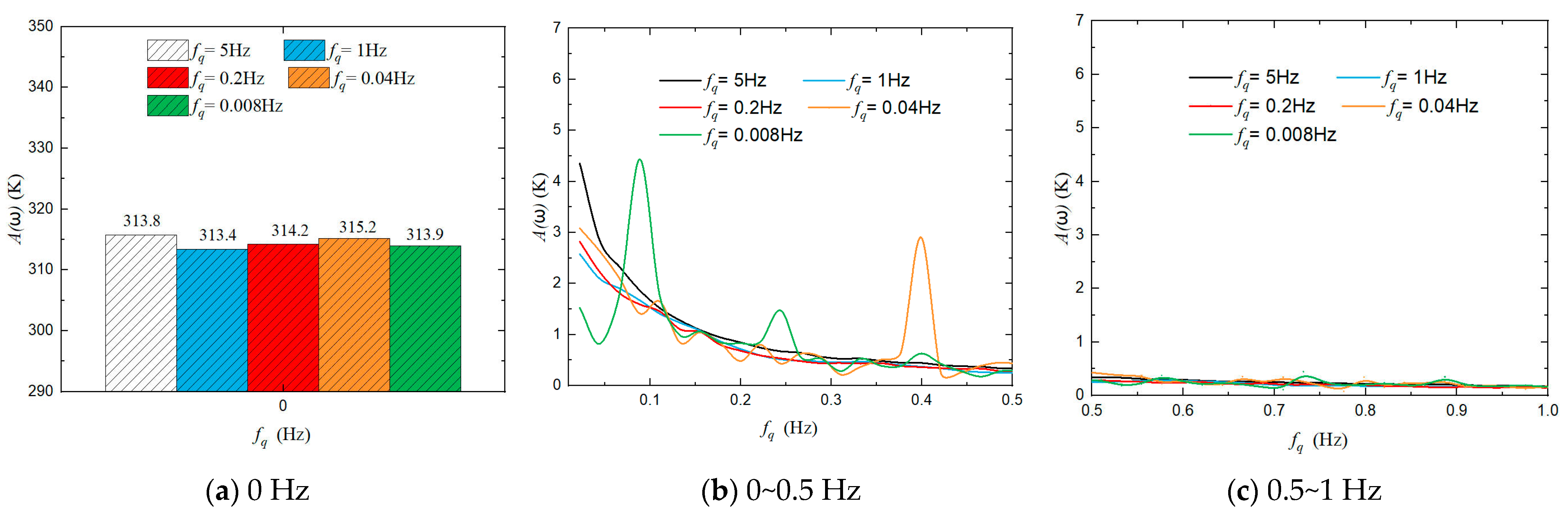
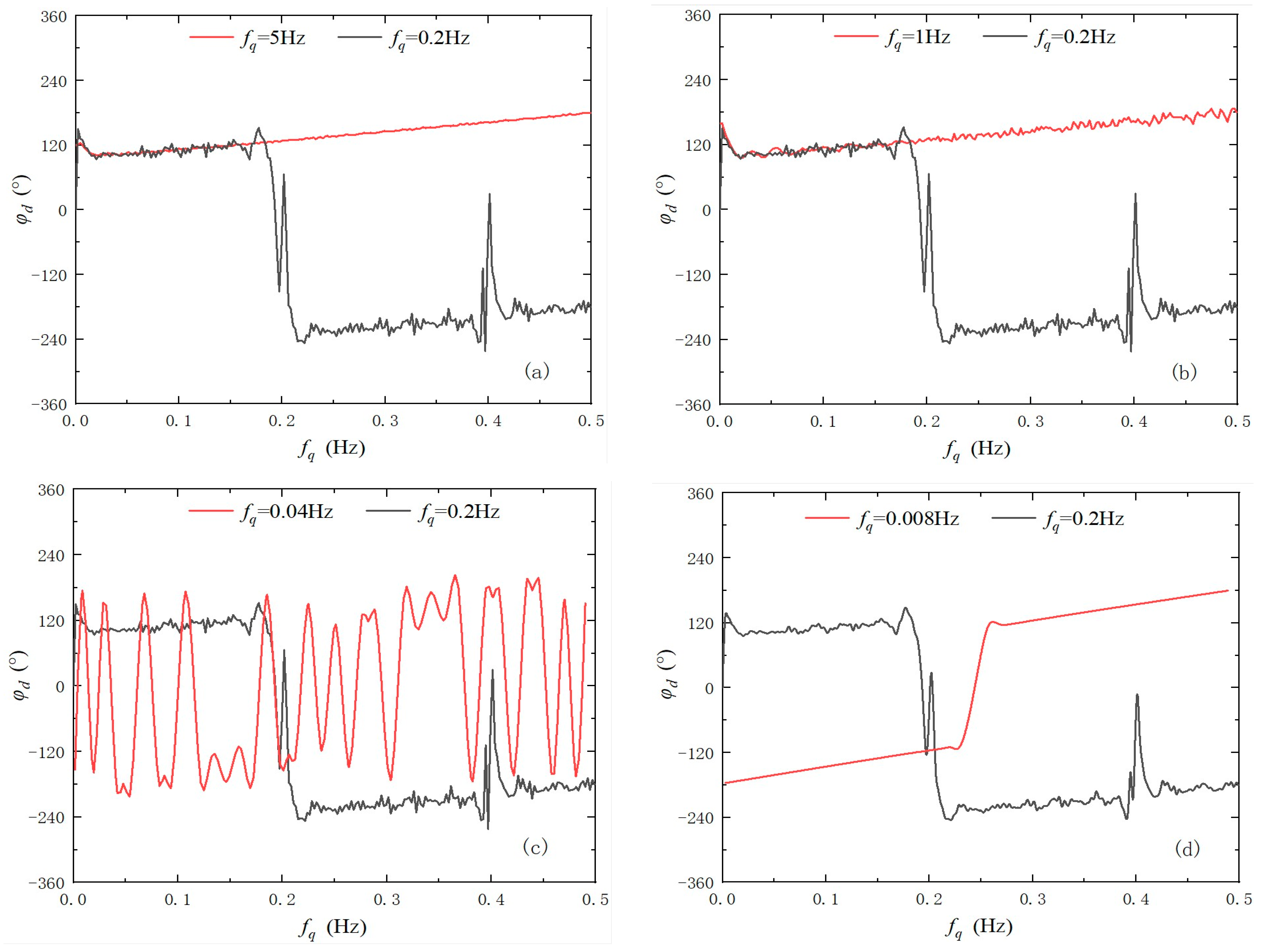
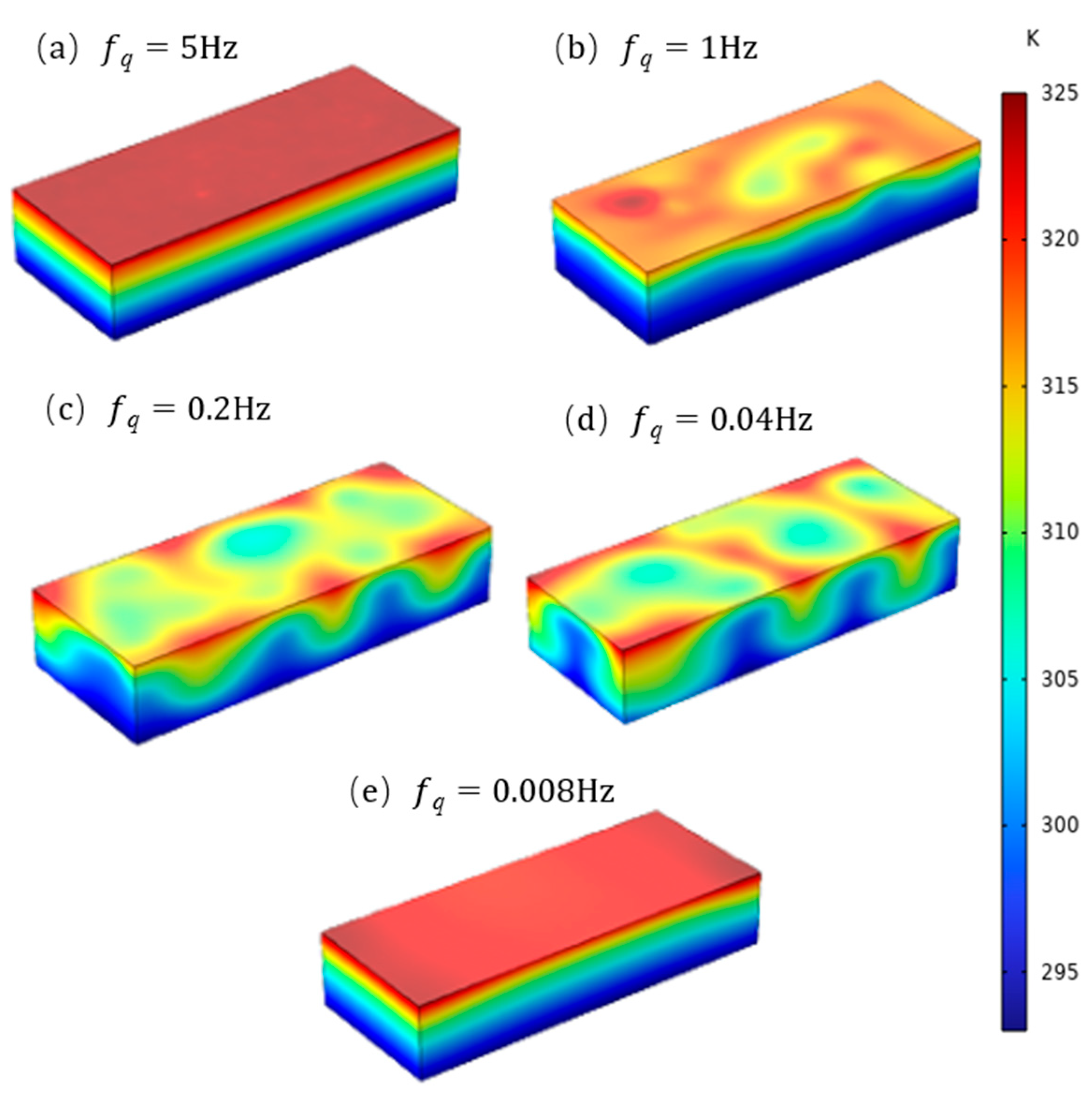
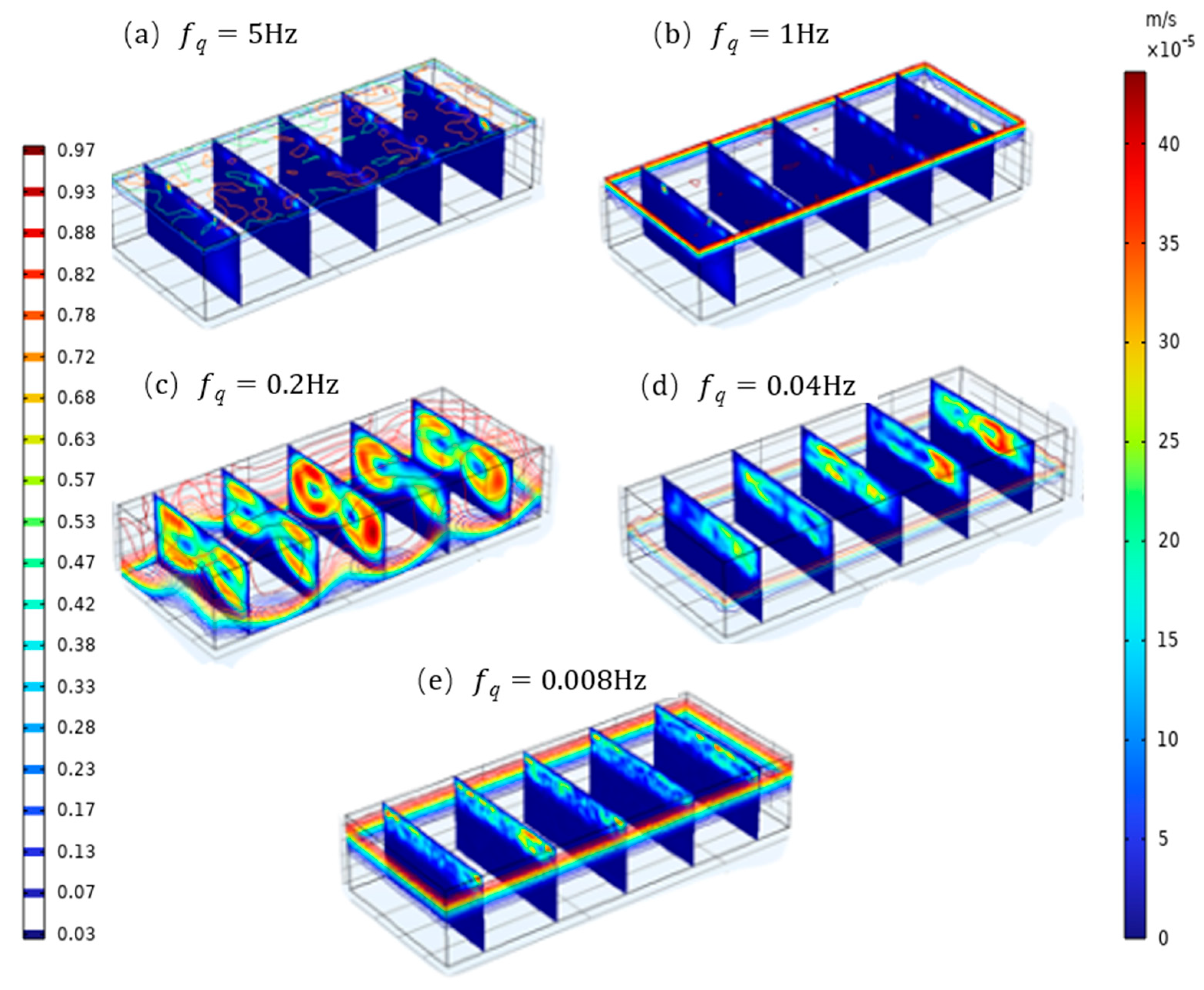
3.2. Variation in Heat Flow Frequency
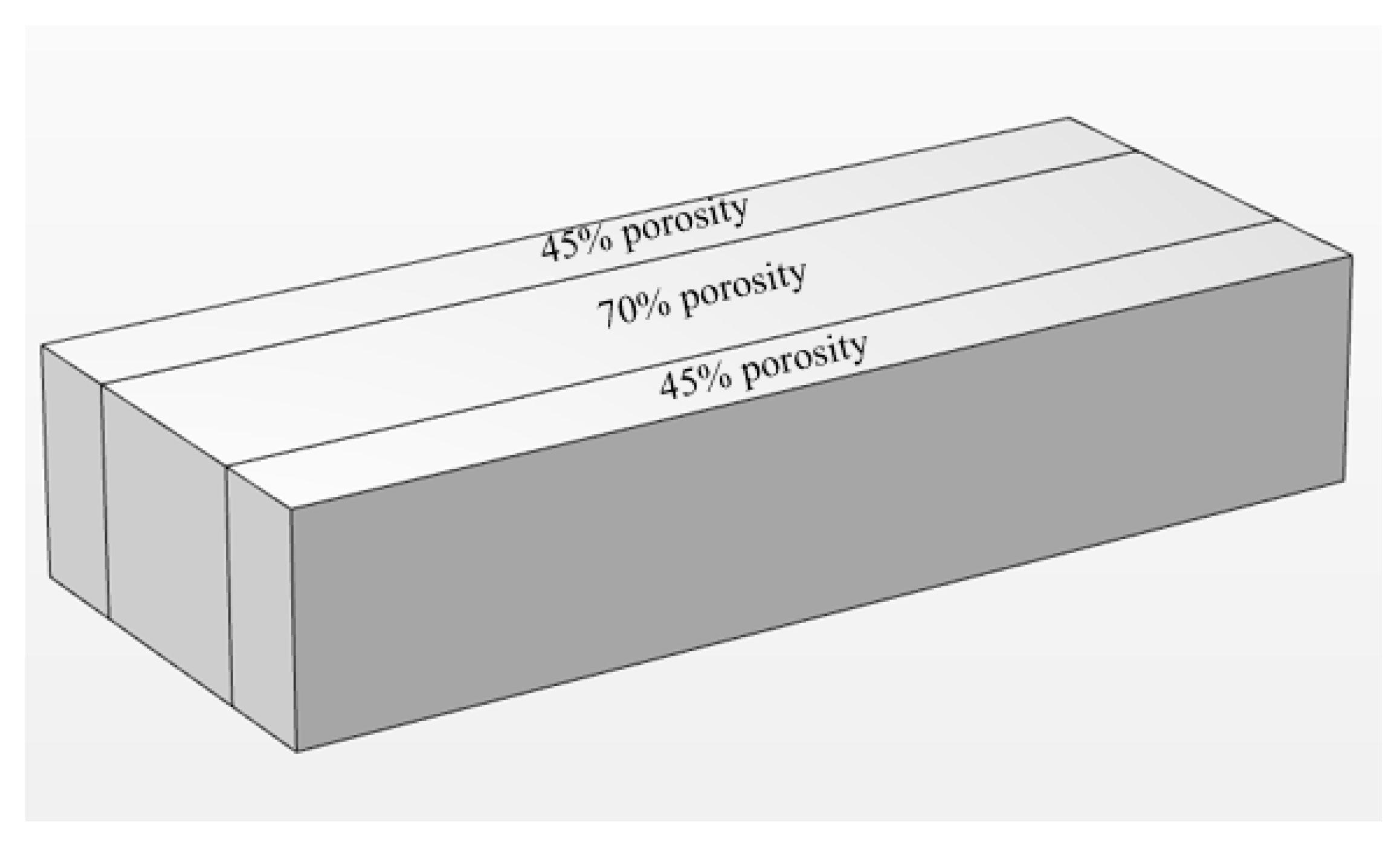
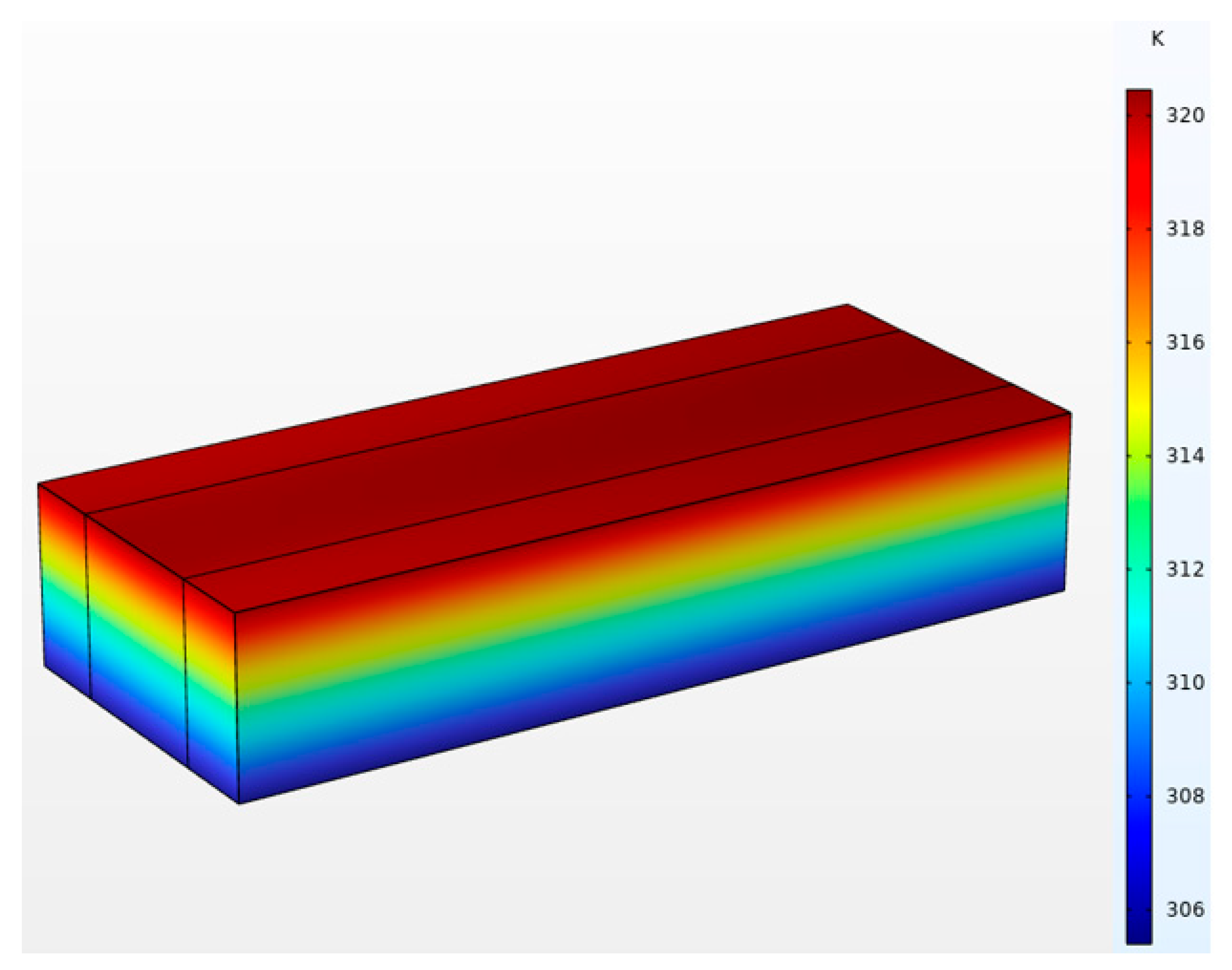
3.3. Variable Porosity Structure
4. Conclusions
- (1)
- It is crucial for the PCHEU–LPM to work within an appropriate amplitude of the pulse heat flow generated by the heat source. When the heat flow amplitude is excessively large, the heating surface and the surrounding PCM enter a superheated state. Conversely, when the amplitude is excessively small, they remain in a supercooled state. Neither extreme allows for the optimal utilization of latent heat during phase change, leading to the inadequate suppression of temperature fluctuations at the interface.
- (2)
- Natural convection in the liquid-phase region is attenuated when the PCHEU–LPM handles either high-frequency or low-frequency pulsed heat generation. As a result, the interface temperature exhibits a more uniform distribution. Specifically, when dealing with high-frequency heat flow (>1 Hz), the interface temperature fluctuation remains below 1 K. For medium-frequency heat flow (0.2 Hz to 0.04 Hz), the fluctuation ranges from approximately 4.5 K to 10 K, while low-frequency heat flow (<0.008 Hz) leads to fluctuations exceeding 14.5 K. Nevertheless, compared to heat sinks made of single-phase metal materials, the PCHEU–LPM still demonstrates superior suppression of temperature fluctuations when handling medium- and low-frequency heat flows.
- (3)
- If the thermal control of electronic devices inside cabins needs to further enhance the uniformity of spatial temperature distribution, one method is that a PCHEU–LPM with lower porosity can be used to suppress natural convection intensity. Another method is to make the pulse working mode of electronic devices ≥ 1 Hz or ≤0.008 Hz.
- (4)
- The design featuring high porosity in the central region and low porosity on the sides holds promise for enhancing the surface temperature uniformity of the PCHEU–LPM. Compared to the PCHEU–LPM with a porosity of 70%, which maintains a 70% porosity in the central region and reduces it to 45% on both sides to enhance thermal conductivity, this design improves surface temperature uniformity, reducing the maximum surface temperature difference from 11.3 K to 4.6 K. This configuration enables electronic devices within the payload bay of hypersonic aircraft to operate in pulsed mode at higher amplitude ranges and broader frequency spectrums.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclatures
| Parameter Name | ||
| L | Length | mm |
| Width | mm | |
| Height | mm | |
| Heat flow | W/m2 | |
| Temperature | K | |
| X-direction speed | m/s | |
| Y-direction speed | m/s | |
| Z-direction speed | m/s | |
| Body force | N/m3 | |
| s | Phase interface location | m |
| Convective heat transfer coefficient | W/m2-K | |
| Δh | Latent heat of phase change | KJ/kg |
| A | Area | m2 |
| Greek alphabet | ||
| Time | s | |
| Porosity or liquid phase ratio | ||
| Sport viscosity | Pa-s | |
| Density | kg/m3 | |
| Thermal conductivity | W/m-K | |
| Latent heat of phase change | KJ/kg | |
| Thermal diffusion coefficient | m2/s | |
| Permeability | m2 | |
| Subscript | ||
| l | Liquid phase | |
| Solid phase | ||
| Directional vector at the phase interface | ||
| w | External thermal excitation | |
| m | Phase change state | |
| c | Cold fluids | |
| 0 | Initial state | |
| ss | Steady-state, time-averaged value of transient temperature fluctuations | |
| h | Hot end | |
| c | Cold end |
References
- Sahoo, S.K.; Das, M.K.; Rath, P. Application of TCE-PCM Based Heat Sinks for Cooling of Electronic Components: A Review. Renew. Sustain. Energy Rev. 2016, 59, 550–582. [Google Scholar] [CrossRef]
- Gharbi, S.; Harmand, S.; Jabrallah, S.B. Experimental Study of the Cooling Performance of Phase Change Material with Discrete Heat Sources—Continuous and Intermittent Regimes. Appl. Therm. Eng. 2017, 111, 103–111. [Google Scholar] [CrossRef]
- Alshaer, W.G.; Nada, S.A.; Rady, M.A.; Del Barrio, E.P.; Sommier, A. Thermal Management of Electronic Devices Using Carbon Foam and PCM/Nano-Composite. Int. J. Therm. Sci. 2015, 89, 79–86. [Google Scholar] [CrossRef]
- Alimohammadi, M.; Aghli, Y.; Alavi, E.S.; Sardarabadi, M.; Passandideh-Fard, M. Experimental Investigation of the Effects of Using Nano/Phase Change Materials (NPCM) as Coolant of Electronic Chipsets, under Free and Forced Convection. Appl. Therm. Eng. 2017, 111, 271–279. [Google Scholar] [CrossRef]
- Chang, T.-C.; Lee, S.; Fuh, Y.-K.; Peng, Y.-C.; Lin, Z.-Y. PCM Based Heat Sinks of Paraffin/Nanoplatelet Graphite Composite for Thermal Management of IGBT. Appl. Therm. Eng. 2017, 112, 1129–1136. [Google Scholar] [CrossRef]
- Liu, L.; Su, D.; Tang, Y.; Fang, G. Thermal Conductivity Enhancement of Phase Change Materials for Thermal Energy Storage: A Review. Renew. Sustain. Energy Rev. 2016, 62, 305–317. [Google Scholar] [CrossRef]
- Rout, C.; Sharma, A. Recent Advancement in Phase Change Materials for Thermal Applications: A Review. In Proceedings of the AICTE Sponsored National Conference on RTEC, Bahal, India, 25–26 October 2013; p. 6. [Google Scholar]
- Asgharian, H.; Baniasadi, E. A Review on Modeling and Simulation of Solar Energy Storage Systems Based on Phase Change Materials. J. Energy Storage 2019, 21, 186–201. [Google Scholar] [CrossRef]
- Vargas-López, R.; Xamán, J.; Hernández-Pérez, I.; Arce, J.; Zavala-Guillén, I.; Jiménez, M.J.; Heras, M.R. Mathematical Models of Solar Chimneys with a Phase Change Material for Ventilation of Buildings: A Review Using Global Energy Balance. Energy 2019, 170, 683–708. [Google Scholar] [CrossRef]
- Cheng, W.-L.; Mei, B.-J.; Liu, Y.-N.; Huang, Y.-H.; Yuan, X.-D. A Novel Household Refrigerator with Shape-Stabilized PCM (Phase Change Material) Heat Storage Condensers: An Experimental Investigation. Energy 2011, 36, 5797–5804. [Google Scholar] [CrossRef]
- Abhilash, A.; Adarsh Murali Menon; Anirudh, K.; Aby Kurian, M. Nehru College of Engineering and Research Centre Comparison of a Conventional Domestic Refrigerator with a PCM Encapsulated Refrigerator. Int. J. Eng. Res. Technol. 2015, V4, IJERTV4IS100585. [Google Scholar] [CrossRef]
- Elarem, R.; Mellouli, S.; Abhilash, E.; Jemni, A. Performance Analysis of a Household Refrigerator Integrating a PCM Heat Exchanger. Appl. Therm. Eng. 2017, 125, 1320–1333. [Google Scholar] [CrossRef]
- Abdolmaleki, L.; Sadrameli, S.M.; Pirvaram, A. Application of Environmental Friendly and Eutectic Phase Change Materials for the Efficiency Enhancement of Household Freezers. Renew. Energy 2020, 145, 233–241. [Google Scholar] [CrossRef]
- Wang, J.-X.; Li, Y.-Z.; Zhang, H.-S.; Wang, S.-N.; Liang, Y.-H.; Guo, W.; Liu, Y.; Tian, S.-P. A Highly Self-Adaptive Cold Plate for the Single-Phase Mechanically Pumped Fluid Loop for Spacecraft Thermal Management. Energy Convers. Manag. 2016, 111, 57–66. [Google Scholar] [CrossRef]
- Zhong, M.-L.; Li, Y.-Z.; Guo, W.; Wang, S.-N.; Mao, Y.-F. Dynamic In-Loop Performance Investigation and Efficiency-Cost Analysis of Dual Heat Sink Thermal Control System (DHS-TCS) with a Sublimator for Aerospace Vehicles. Appl. Therm. Eng. 2017, 121, 562–575. [Google Scholar] [CrossRef]
- Lin, Y.; Jia, Y.; Alva, G.; Fang, G. Review on Thermal Conductivity Enhancement, Thermal Properties and Applications of Phase Change Materials in Thermal Energy Storage. Renew. Sustain. Energy Rev. 2018, 82, 2730–2742. [Google Scholar] [CrossRef]
- Zalba, B.; Marín, J.M.; Cabeza, L.F.; Mehling, H. Review on Thermal Energy Storage with Phase Change: Materials, Heat Transfer Analysis and Applications. Appl. Therm. Eng. 2003, 23, 251–283. [Google Scholar] [CrossRef]
- Casano, G.; Piva, S. Experimental and Numerical Investigation of the Steady Periodic Solid–Liquid Phase-Change Heat Transfer. Int. J. Heat Mass Transf. 2002, 45, 4181–4190. [Google Scholar] [CrossRef]
- Kalbasi, R.; Salimpour, M.R. Constructal Design of Phase Change Material Enclosures Used for Cooling Electronic Devices. Appl. Therm. Eng. 2015, 84, 339–349. [Google Scholar] [CrossRef]
- Ye, H.; Wang, Z.; Wang, L. Effects of PCM on Power Consumption and Temperature Control Performance of a Thermal Control System Subject to Periodic Ambient Conditions. Appl. Energy 2017, 190, 213–221. [Google Scholar] [CrossRef]
- Shao, G.; Hanaor, D.A.H.; Shen, X.; Gurlo, A. Freeze Casting: From Low-Dimensional Building Blocks to Aligned Porous Structures—A Review of Novel Materials, Methods, and Applications. Adv. Mater. 2020, 32, 1907176. [Google Scholar] [CrossRef]
- Nie, C.; Deng, S.; Guo, H.; Liu, J. Effects of Partially Thermally Active Walls on Simultaneous Charging and Discharging of Paraffin Wax in a Square Cavity. Energy Convers. Manag. 2019, 202, 112201. [Google Scholar] [CrossRef]








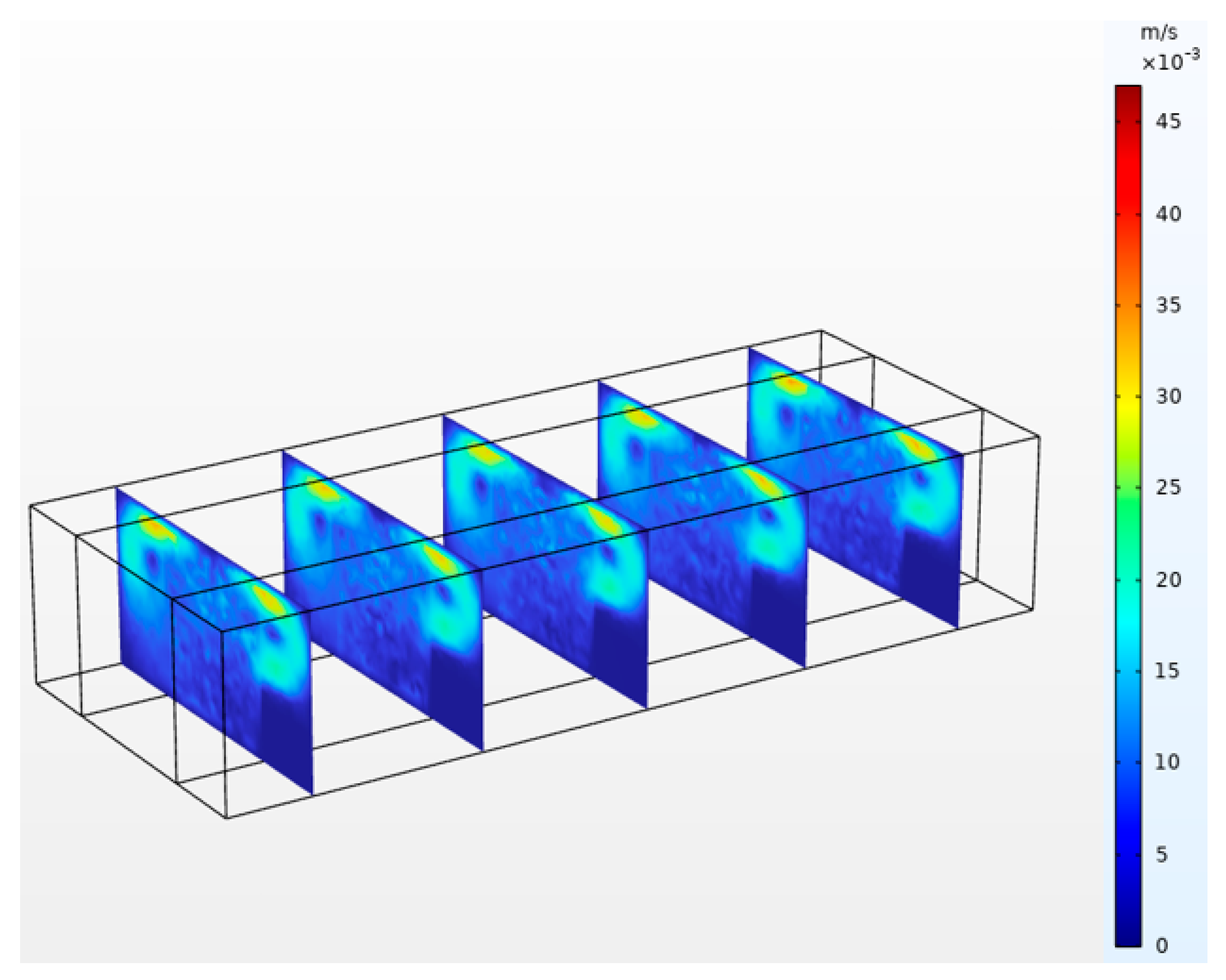
| Boundary Conditions | Location | Boundary Condition Parameters | ||
|---|---|---|---|---|
| Pulsed heat flux | Top | Heat flux 50,000 W/m2 | Pulse period 50 s | Pulse duty cycle 0.5 |
| Microchannel water cooling | Bottom | Mean flow rate 2 m/s | Refrigerant materials Water | Refrigerant incoming flow temperature 297 K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Zhang, J.; Zhang, J. Dynamic Response of Phase Change Heat Exchange Unit with Layered Porous Media for Pulsed Electronic Equipment. Aerospace 2024, 11, 331. https://doi.org/10.3390/aerospace11050331
Zhang R, Zhang J, Zhang J. Dynamic Response of Phase Change Heat Exchange Unit with Layered Porous Media for Pulsed Electronic Equipment. Aerospace. 2024; 11(5):331. https://doi.org/10.3390/aerospace11050331
Chicago/Turabian StyleZhang, Ruoji, Jingyang Zhang, and Jingzhou Zhang. 2024. "Dynamic Response of Phase Change Heat Exchange Unit with Layered Porous Media for Pulsed Electronic Equipment" Aerospace 11, no. 5: 331. https://doi.org/10.3390/aerospace11050331
APA StyleZhang, R., Zhang, J., & Zhang, J. (2024). Dynamic Response of Phase Change Heat Exchange Unit with Layered Porous Media for Pulsed Electronic Equipment. Aerospace, 11(5), 331. https://doi.org/10.3390/aerospace11050331






