Observer for Nonlinear Systems with Time-Varying Delays: Application to a Two-Degrees-of-Freedom Helicopter
Abstract
1. Introduction
2. Problem Statement
- (i)
- , such that sup.
- (ii)
- , such that .
3. Main Result
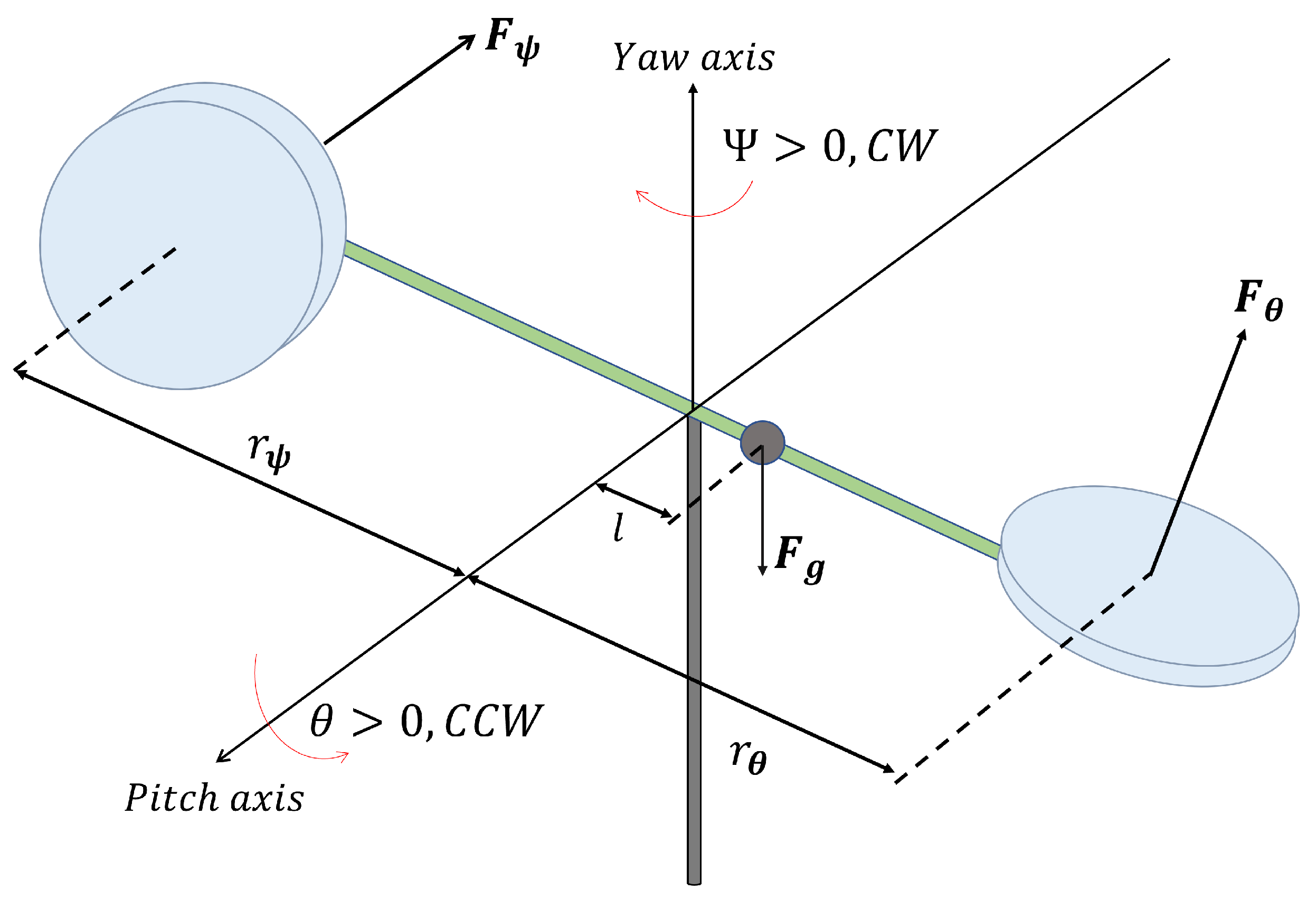
4. Application to Two-Degrees-of-Freedom Helicopter
4.1. Observer-Based Control
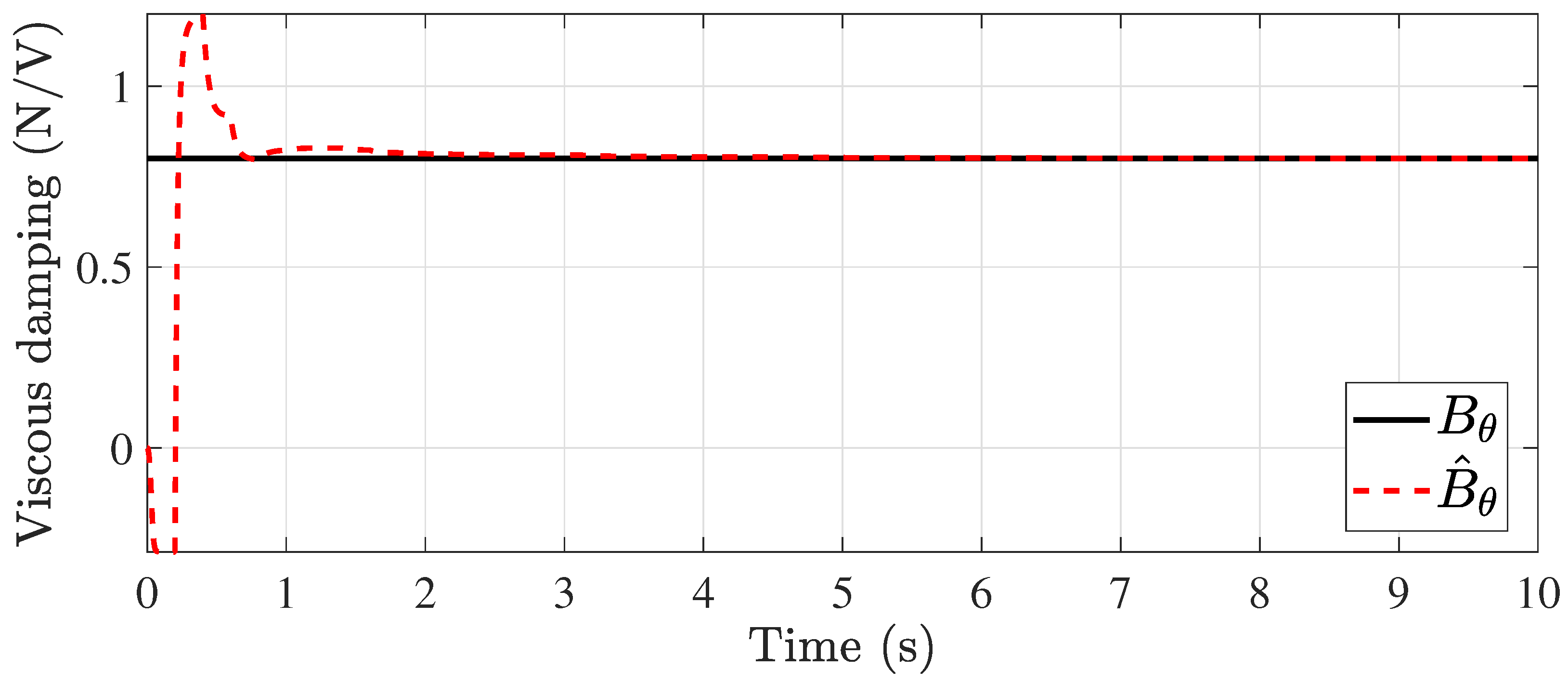
4.2. Estimation of Uncertainties
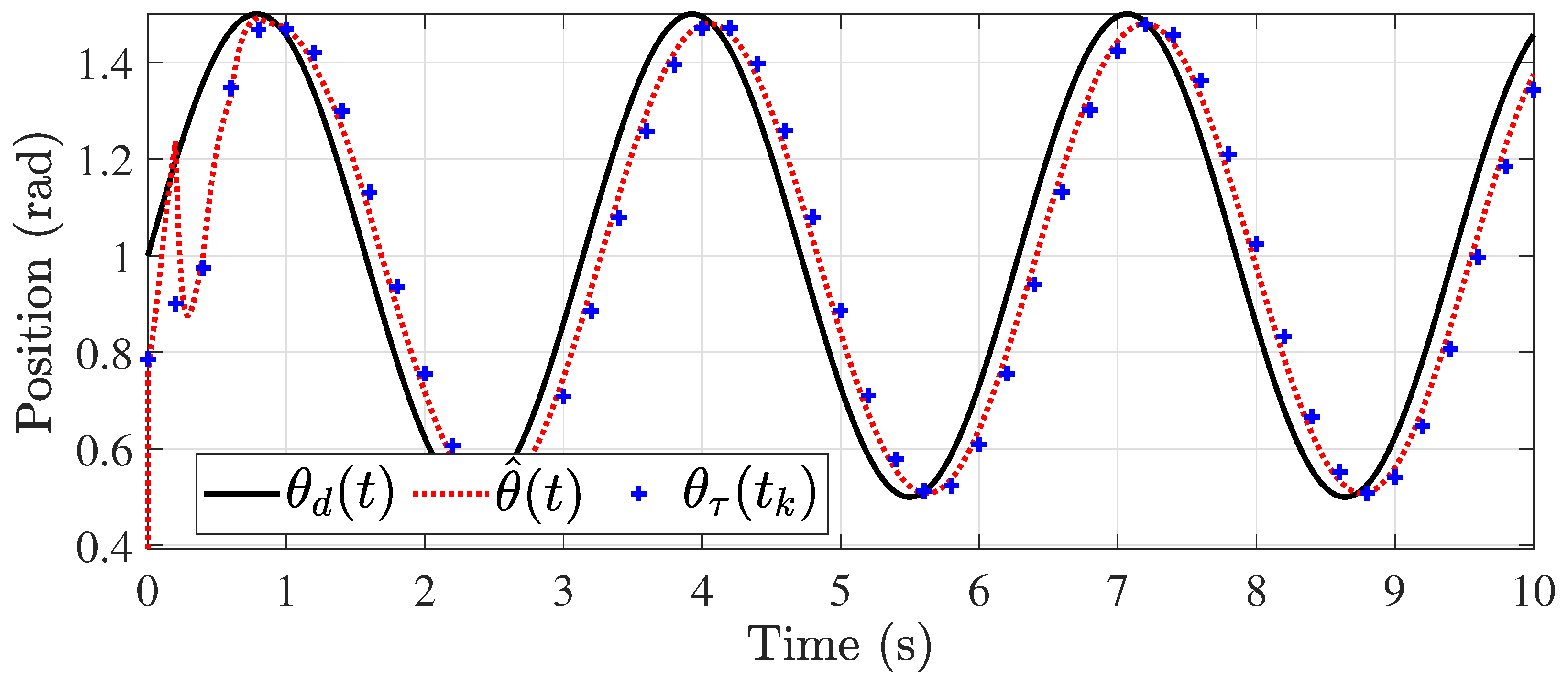
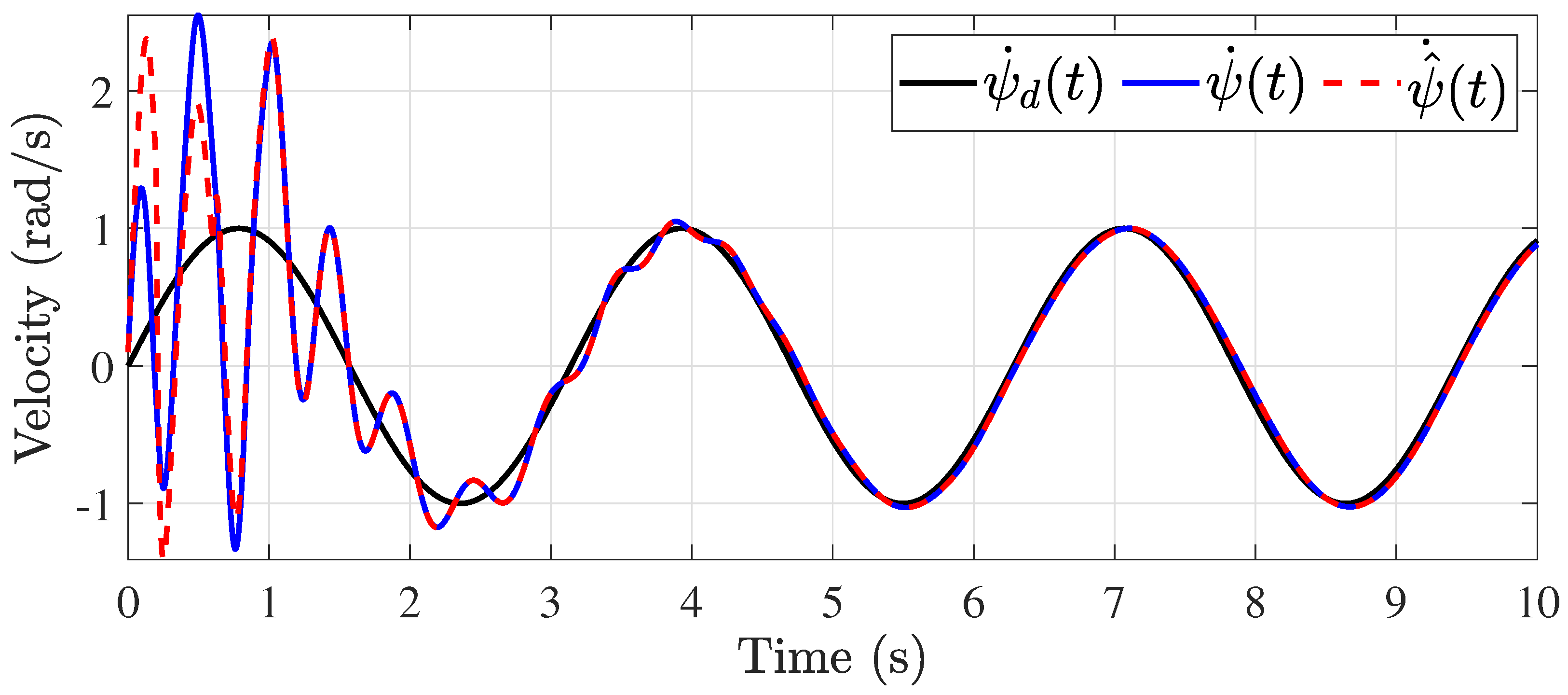
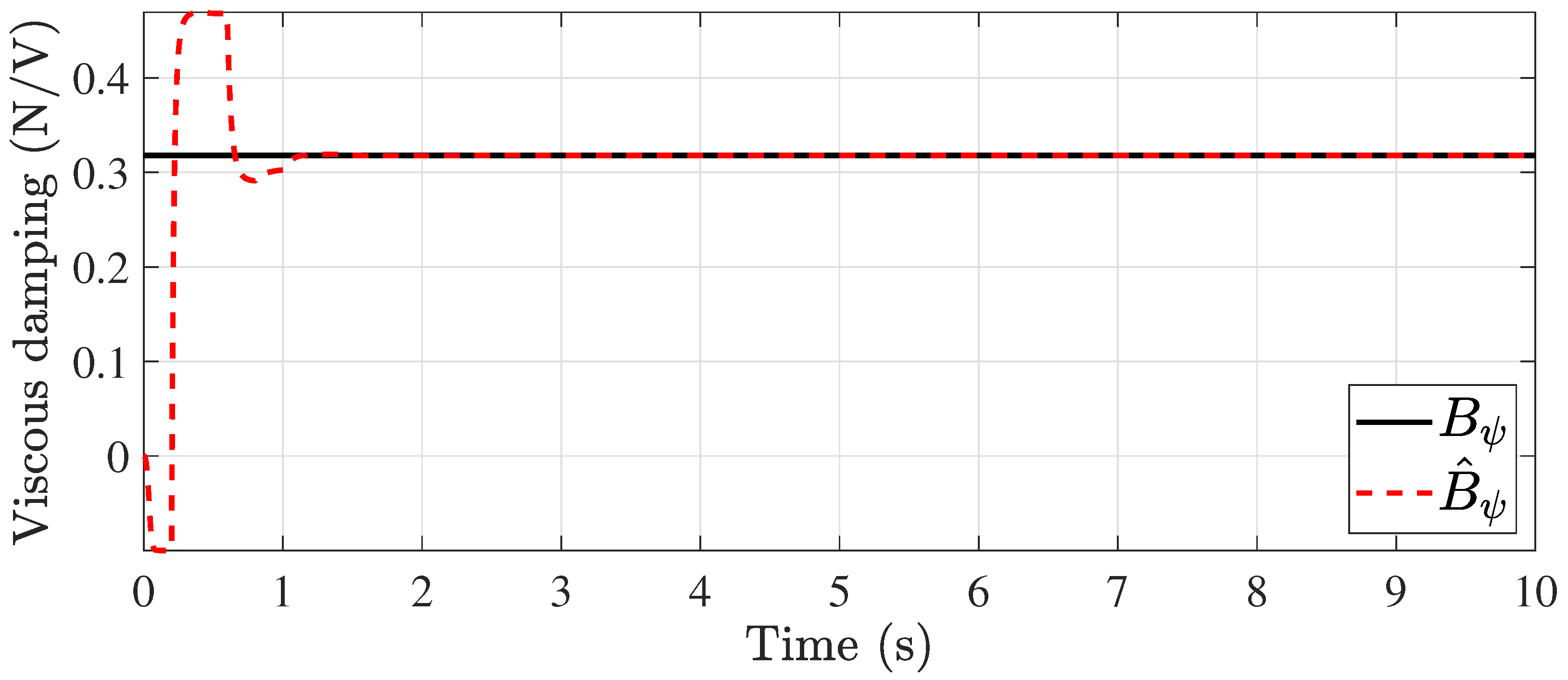
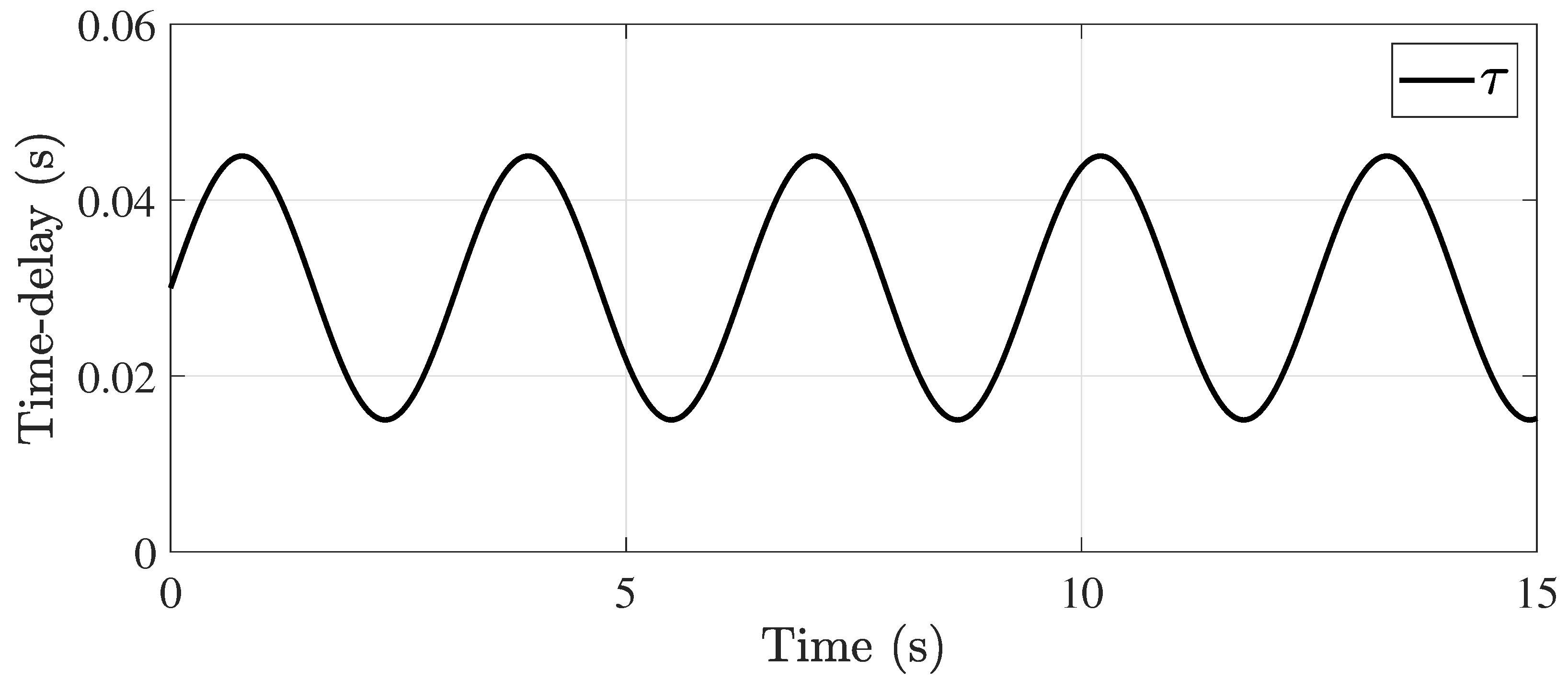
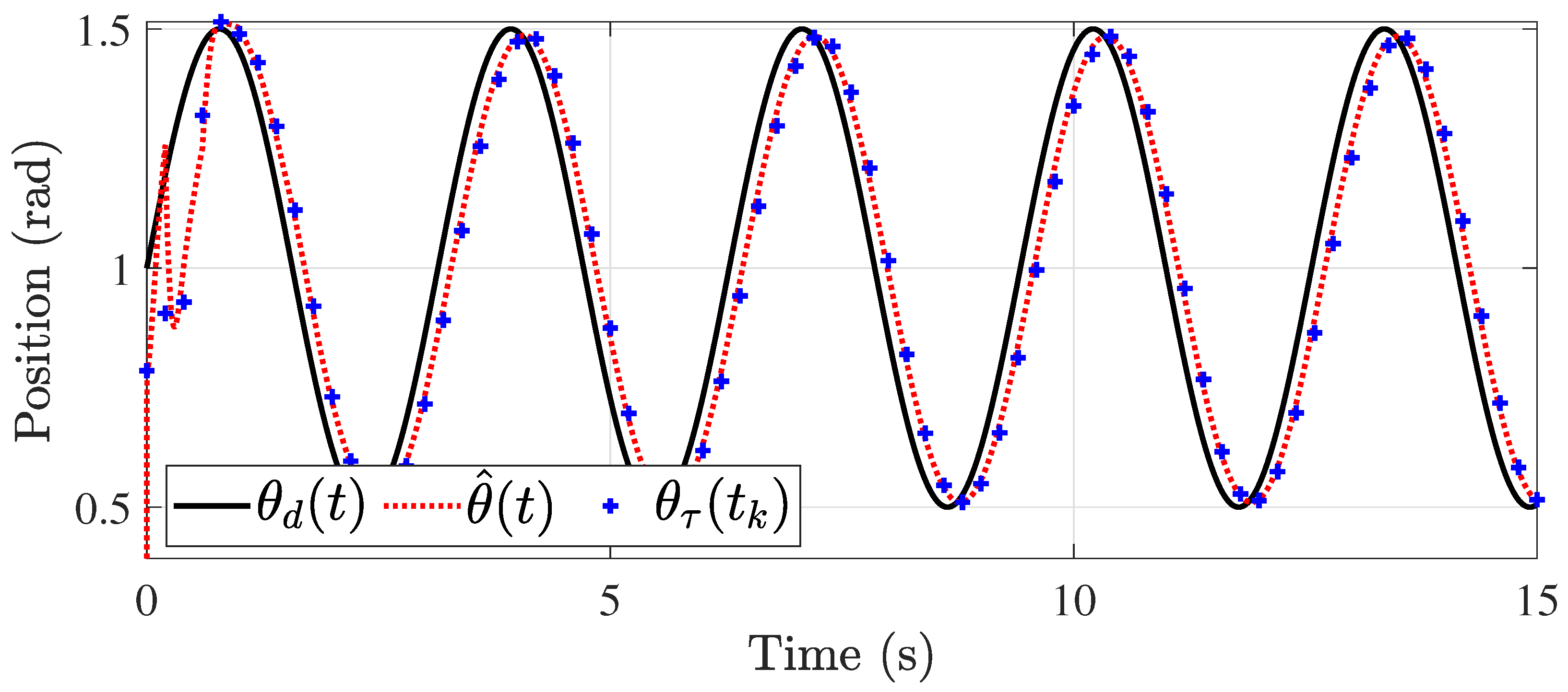
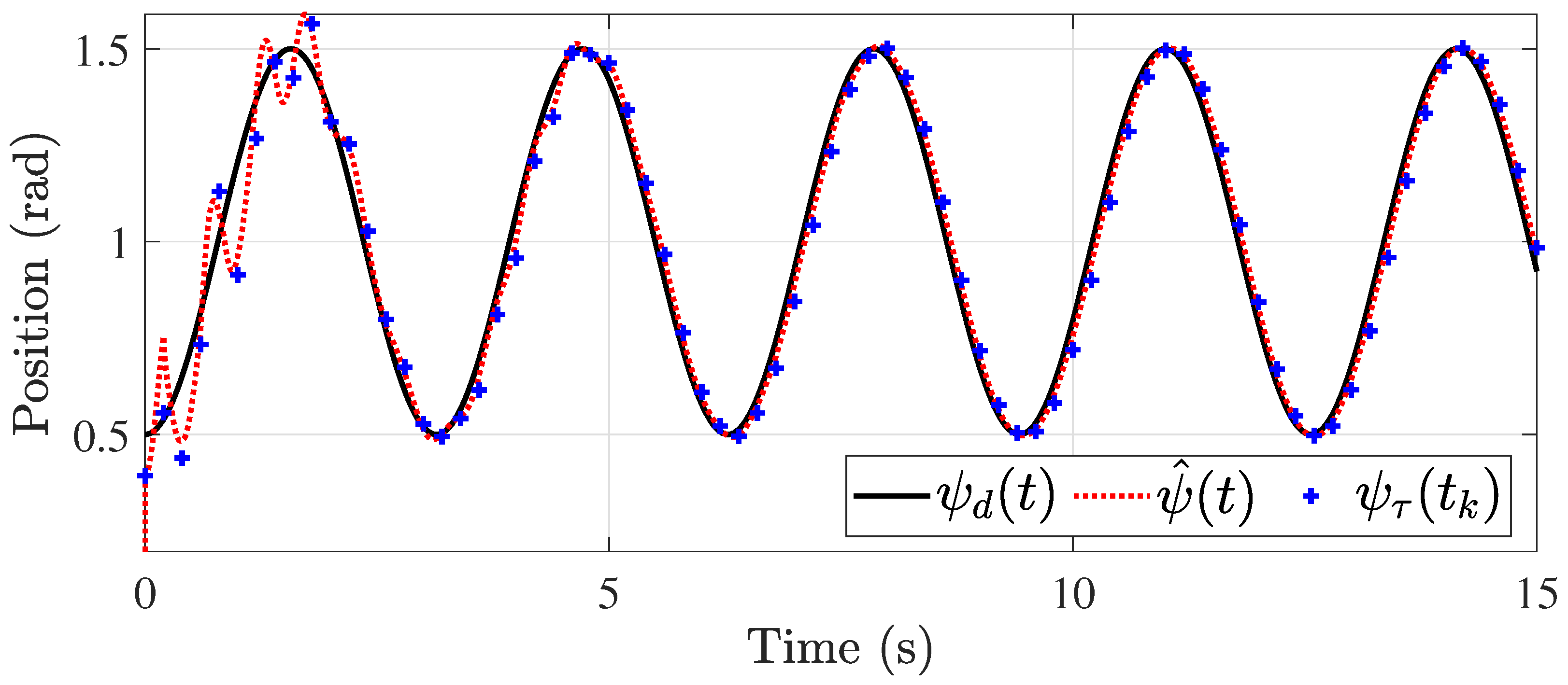
5. Numerical Results
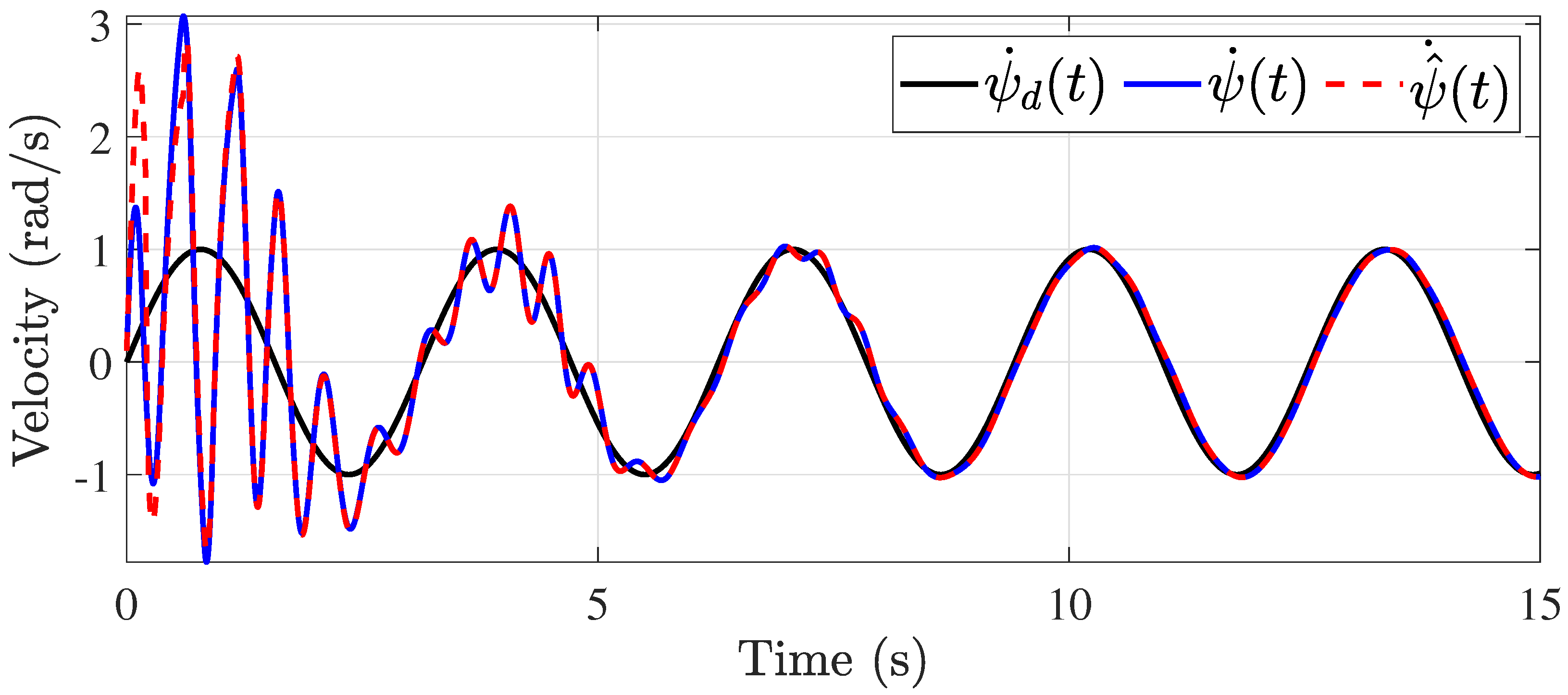
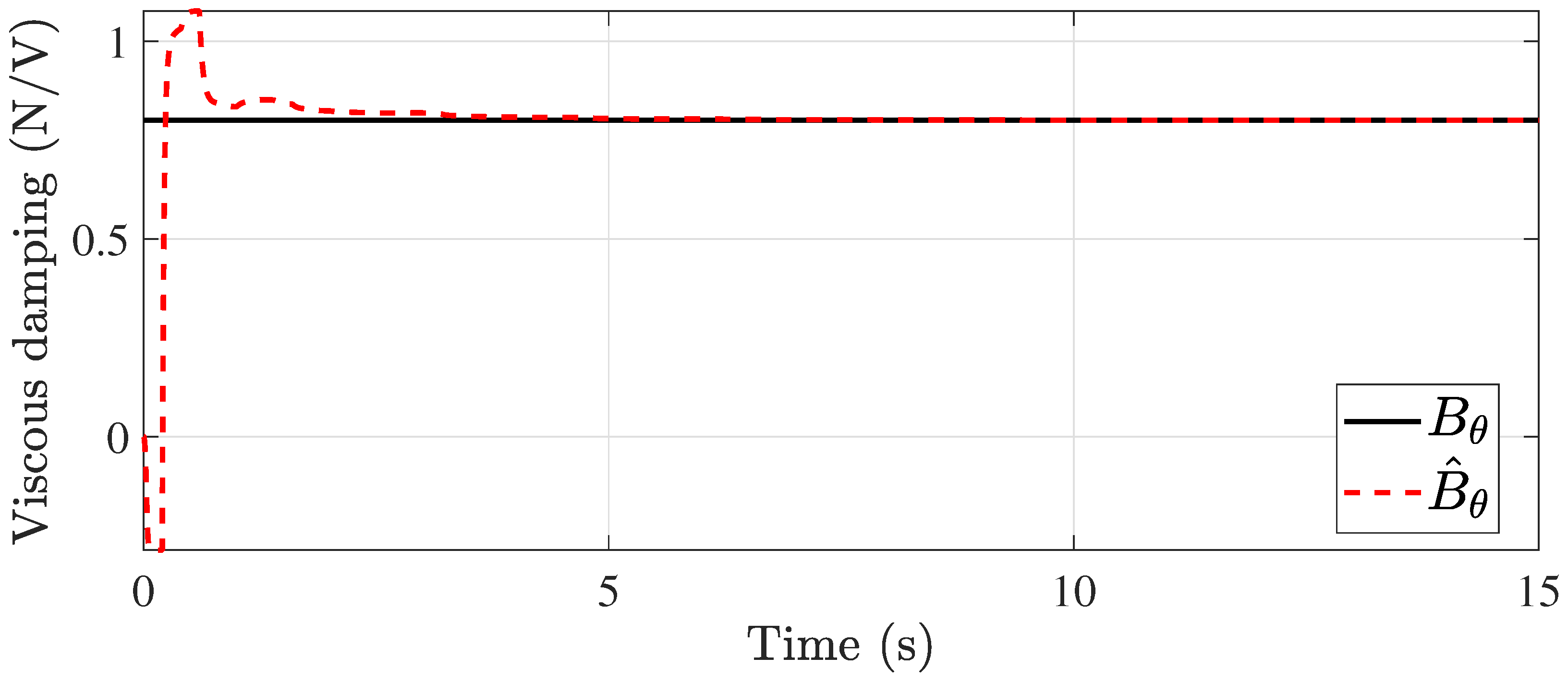
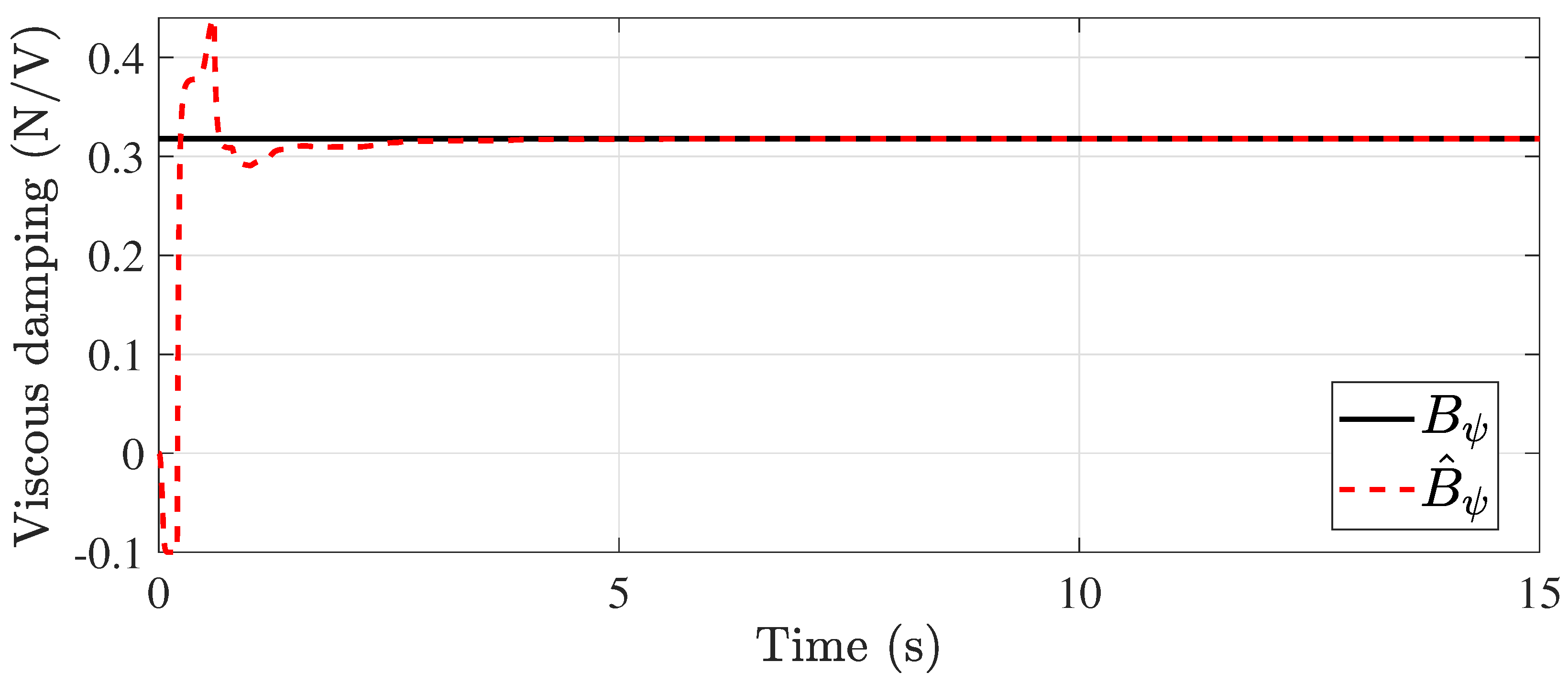
5.1. Constant Time-Delay Case
5.2. Time-Varying Delay Case
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abd, M.H.; Tahir, F.R.; Al-Suhail, G.A.; Pham, V.T. An adaptive observer synchronization using chaotic time-delay system for secure communication. Nonlinear Dyn. 2017, 90, 2583–2598. [Google Scholar] [CrossRef]
- Li, D.; Ma, W. Asymptotic properties of a HIV-1 infection model with time delay. J. Math. Anal. Appl. 2007, 335, 683–691. [Google Scholar] [CrossRef]
- Qi, W.; Kao, Y.; Gao, X.; Wei, Y. Controller design for time-delay system with stochastic disturbance and actuator saturation via a new criterion. Appl. Math. Comput. 2018, 320, 535–546. [Google Scholar] [CrossRef]
- Borri, A.; Cacace, F.; De Gaetano, A.; Germani, A.; Manes, C.; Palumbo, P.; Panunzi, S.; Pepe, P. Luenberger-like observers for nonlinear time-delay systems with application to the artificial pancreas: The attainment of good performance. IEEE Control. Syst. Mag. 2017, 37, 33–49. [Google Scholar] [CrossRef]
- Sanz, R.; García, P.; Fridman, E.; Albertos, P. Robust predictive extended state observer for a class of nonlinear systems with time-varying input delay. Int. J. Control. 2020, 93, 217–225. [Google Scholar] [CrossRef]
- Avilés, J.D.; Moreno, J.A.; Bejarano, F.J. Dissipative state observer design for nonlinear time-delay systems. J. Frankl. Inst. 2023, 360, 887–909. [Google Scholar] [CrossRef]
- Li, T.; Zheng, C.; Ma, Y.; Wang, Z. Interval estimation for discrete-time linear time-delay systems based on state augmentation. Eur. J. Control. 2023, 72, 100823. [Google Scholar] [CrossRef]
- Akbari, E.; Tabatabaei, S.M.; Yazdi, M.B.; Arefi, M.M.; Cao, J. Resilient backstepping control for a class of switched nonlinear time-delay systems under hybrid cyber-attacks. Eng. Appl. Artif. Intell. 2023, 122, 106128. [Google Scholar] [CrossRef]
- Di Ferdinando, M.; Di Gennaro, S.; Pepe, P. On Sontag’s formula for the sampled-data observer-based stabilization of nonlinear time-delay systems. Automatica 2023, 153, 111052. [Google Scholar] [CrossRef]
- Langueh, K.; Zheng, G.; Floquet, T. Impulsive fixed-time observer for linear time-delay systems. J. Frankl. Inst. 2018, 355, 3354–3366. [Google Scholar] [CrossRef]
- Islam, S.I.; Shi, P.; Lim, C.C. Robust functional observer for stabilising uncertain fuzzy systems with time-delay. Granul. Comput. 2020, 5, 55–69. [Google Scholar] [CrossRef]
- Ahmed-Ali, T.; Fridman, E.; Giri, F.; Kahelras, M.; Lamnabhi-Lagarrigue, F.; Burlion, L. Observer design for a class of parabolic systems with large delays and sampled measurements. IEEE Trans. Autom. Control. 2019, 65, 2200–2206. [Google Scholar] [CrossRef]
- Cacace, F.; Germani, A.; Manes, C. Predictor-based control of linear systems with large and variable measurement delays. Int. J. Control. 2014, 87, 704–714. [Google Scholar] [CrossRef]
- Du, S.L.; Wang, R.; Wang, S.; Yu, M. Observer-based H∞ stabilisation for linear systems with large delay periods. IET Control. Theory Appl. 2016, 10, 417–423. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, B. Extended observer based feedback control of linear systems with both state and input delays. J. Frankl. Inst. 2017, 354, 8232–8255. [Google Scholar] [CrossRef]
- Adil, A.; Hamaz, A.; N’doye, I.; Zemouche, A.; Laleg-Kirati, T.M.; Bedouhene, F. On high-gain observer design for nonlinear systems with delayed output measurements. Automatica 2022, 141, 110281. [Google Scholar] [CrossRef]
- Azmi, H.; Yazdizadeh, A. Robust adaptive fault detection and diagnosis observer design for a class of nonlinear systems with uncertainty and unknown time-varying internal delay. ISA Trans. 2022, 131, 31–42. [Google Scholar] [CrossRef] [PubMed]
- Ghanes, M.; De Leon, J.; Barbot, J.P. Simultaneous observation and identification for nonlinear systems under unknown time-varying delays. J. Frankl. Inst. 2016, 353, 2305–2318. [Google Scholar] [CrossRef]
- Gamiochipi, J.; Ghanes, M.; Aggoune, W.; De Leon, J.; Barbot, J.P. Observer design for a class of nonlinear systems under a persistent excitation. IFAC-PapersOnLine 2016, 49, 517–521. [Google Scholar] [CrossRef]
- Yang, Y.; Lin, C.; Chen, B. Nonlinear H∞ observer design for one-sided Lipschitz discrete-time singular systems with time-varying delay. Int. J. Robust Nonlinear Control. 2019, 29, 252–267. [Google Scholar] [CrossRef]
- Echi, N. Observer design and practical stability of nonlinear systems under unknown time-delay. Asian J. Control. 2021, 23, 685–696. [Google Scholar] [CrossRef]
- Shen, S.; Song, A.; Li, H.; Li, T. Cascade predictor for a class of mechanical systems under large uncertain measurement delays. Mech. Syst. Signal Process. 2022, 167, 108536. [Google Scholar] [CrossRef]
- Ramírez-Rasgado, F.; Astorga-Zaragoza, C.M.; Hernández-González, O.; Guerrero-Sánchez, M.E.; Osorio-Gordillo, G.L.; Reyes-Reyes, J. Observer Synthesis for Uncertain Nonlinear Systems with Nonuniformly Sampled and Delayed Output. IEEE Syst. J. 2022, 16, 4532–4540. [Google Scholar] [CrossRef]
- Nguyen, C.M.; Pathirana, P.N.; Trinh, H. Robust state estimation for non-linear systems with unknown delays. IET Control. Theory Appl. 2019, 13, 1147–1154. [Google Scholar] [CrossRef]
- Kalamian, N.; Khaloozadeh, H.; Ayati, M. Design of state-dependent impulsive observer for non-linear time-delay systems. IET Control. Theory Appl. 2019, 13, 3155–3163. [Google Scholar] [CrossRef]
- Peixoto, M.L.; Nguyen, A.T.; Guerra, T.M.; Palhares, R.M. Unknown input observers for time-varying delay Takagi-Sugeno fuzzy systems with unmeasured nonlinear consequents. Eur. J. Control. 2023, 72, 100830. [Google Scholar] [CrossRef]
- Dong, Y.; Hao, J.; Mei, S.; Deng, M. Observer design for one-sided Lipschitz uncertain descriptor systems with time-varying delay and nonlinear uncertainties. Circuits Syst. Signal Process. 2021, 40, 4779–4798. [Google Scholar] [CrossRef]
- Taghieh, A.; Shafiei, M.H. Observer-based robust model predictive control of switched nonlinear systems with time delay and parametric uncertainties. J. Vib. Control. 2021, 27, 1939–1955. [Google Scholar] [CrossRef]
- Yang, Y.; Lin, C.; Chen, B.; Wang, Q.G. Reduced-order observer design for a class of generalized Lipschitz nonlinear systems with time-varying delay. Appl. Math. Comput. 2018, 337, 267–280. [Google Scholar] [CrossRef]
- Léchappé, V.; De Leon, J.; Moulay, E.; Plestan, F.; Glumineau, A. Delay and state observation for SISO nonlinear systems with input delay. Int. J. Robust Nonlinear Control. 2018, 28, 2356–2368. [Google Scholar] [CrossRef]
- Farza, M.; Sboui, A.; Cherrier, E.; M’Saad, M. High-gain observer for a class of time-delay nonlinear systems. Int. J. Control. 2010, 83, 273–280. [Google Scholar] [CrossRef]
- Hernández-González, O.; Ramírez-Rasgado, F.; Astorga-Zaragoza, C.M.; Guerrero-Sánchez, M.E.; Valencia-Palomo, G.; Rodriguez-Mata, A.E. Observer for non-linear systems with sampled measurements: Application to the friction factor estimation of a pipeline. IET Control. Theory Appl. 2021, 15, 432–445. [Google Scholar] [CrossRef]
- Cacace, F.; Conte, F.; Germani, A.; Palombo, G. Delay identification for a class of nonlinear systems. Int. J. Control. 2016, 89, 2350–2359. [Google Scholar] [CrossRef]
- Ramírez-Rasgado, F.; Hernández-González, O.; Farza, M.; M’Saad, M.; Astorga-Zaragoza, C.; Dahhou, B. On high-gain observer redesign with respect to the nature of the available outputs. In Proceedings of the 2022 10th International Conference on Systems and Control (ICSC), Marseille, France, 23–25 November 2022; pp. 190–195. [Google Scholar] [CrossRef]
- Boukadida, W.; Benamor, A.; Messaoud, H.; Siarry, P. Multi-objective design of optimal higher order sliding mode control for robust tracking of 2-DoF helicopter system based on metaheuristics. Aerosp. Sci. Technol. 2019, 91, 442–455. [Google Scholar] [CrossRef]
- Castañeda, H.; Salas-Peña, O.S.; de León-Morales, J. Extended observer based on adaptive second order sliding mode control for a fixed wing UAV. ISA Trans. 2017, 66, 226–232. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, S.; Wang, S.; Wang, X.; Duan, H. Distributed bearing-based formation maneuver control of fixed-wing UAVs by finite-time orientation estimation. Aerosp. Sci. Technol. 2023, 136, 108241. [Google Scholar] [CrossRef]
- Guerrero-Sánchez, M.E.; Hernández-González, O.; Valencia-Palomo, G.; López-Estrada, F.R.; Rodríguez-Mata, A.E.; Garrido, J. Filtered observer-based ida-pbc control for trajectory tracking of a quadrotor. IEEE Access 2021, 9, 114821–114835. [Google Scholar] [CrossRef]
- Hernández-González, O.; Guerrero-Sánchez, M.E.; Farza, M.; Ménard, T.; M’Saad, M.; Lozano, R. High gain observer for a class of nonlinear systems with coupled structure and sampled output measurements: Application to a quadrotor. Int. J. Syst. Sci. 2019, 50, 1089–1105. [Google Scholar] [CrossRef]
- Hashim, H.A. Exponentially stable observer-based controller for VTOL-UAVs without velocity measurements. Int. J. Control. 2023, 96, 1946–1960. [Google Scholar] [CrossRef]
- Aligia, D.A.; Roccia, B.A.; De Angelo, C.H.; Magallan, G.A.; Gonzalez, G.N. An orientation estimation strategy for low cost IMU using a nonlinear Luenberger observer. Measurement 2021, 173, 108664. [Google Scholar] [CrossRef]
- Berkane, S.; Tayebi, A.; De Marco, S. A nonlinear navigation observer using IMU and generic position information. Automatica 2021, 127, 109513. [Google Scholar] [CrossRef]



| Constant | Description | Value | Unit |
|---|---|---|---|
| Total moment of inertia about pitch axis | 0.0384 | kg·m2 | |
| Total moment of inertia about yaw axis | 0.0432 | kg·m2 | |
| Viscous damping about pitch axis | 0.8000 | N/V | |
| Viscous damping about yaw axis | 0.3180 | N/V | |
| Thrust torque of pitch motor | 0.2040 | N·m/V | |
| Thrust torque of yaw motor | 0.0720 | N·m/V | |
| Thrust torque of pitch axis from yaw motor | 0.0068 | N·m/V | |
| Thrust torque of yaw axis from pitch motor | 0.0219 | N·m/V | |
| m | Mass of the helicopter | 1.3872 | kg |
| l | Center of mass length along helicopter body from a pitch axis | 0.1860 | m |
| g | Gravitational acceleration | 9.81 | m/s2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-González, O.; Ramírez-Rasgado, F.; Farza, M.; Guerrero-Sánchez, M.-E.; Astorga-Zaragoza, C.-M.; M’Saad, M.; Valencia-Palomo, G. Observer for Nonlinear Systems with Time-Varying Delays: Application to a Two-Degrees-of-Freedom Helicopter. Aerospace 2024, 11, 206. https://doi.org/10.3390/aerospace11030206
Hernández-González O, Ramírez-Rasgado F, Farza M, Guerrero-Sánchez M-E, Astorga-Zaragoza C-M, M’Saad M, Valencia-Palomo G. Observer for Nonlinear Systems with Time-Varying Delays: Application to a Two-Degrees-of-Freedom Helicopter. Aerospace. 2024; 11(3):206. https://doi.org/10.3390/aerospace11030206
Chicago/Turabian StyleHernández-González, Omar, Felipe Ramírez-Rasgado, Mondher Farza, María-Eusebia Guerrero-Sánchez, Carlos-Manuel Astorga-Zaragoza, Mohammed M’Saad, and Guillermo Valencia-Palomo. 2024. "Observer for Nonlinear Systems with Time-Varying Delays: Application to a Two-Degrees-of-Freedom Helicopter" Aerospace 11, no. 3: 206. https://doi.org/10.3390/aerospace11030206
APA StyleHernández-González, O., Ramírez-Rasgado, F., Farza, M., Guerrero-Sánchez, M.-E., Astorga-Zaragoza, C.-M., M’Saad, M., & Valencia-Palomo, G. (2024). Observer for Nonlinear Systems with Time-Varying Delays: Application to a Two-Degrees-of-Freedom Helicopter. Aerospace, 11(3), 206. https://doi.org/10.3390/aerospace11030206












