Multi-Objective Optimization Design of an Origami-Inspired Combined Cushion Airbag
Abstract
1. Introduction
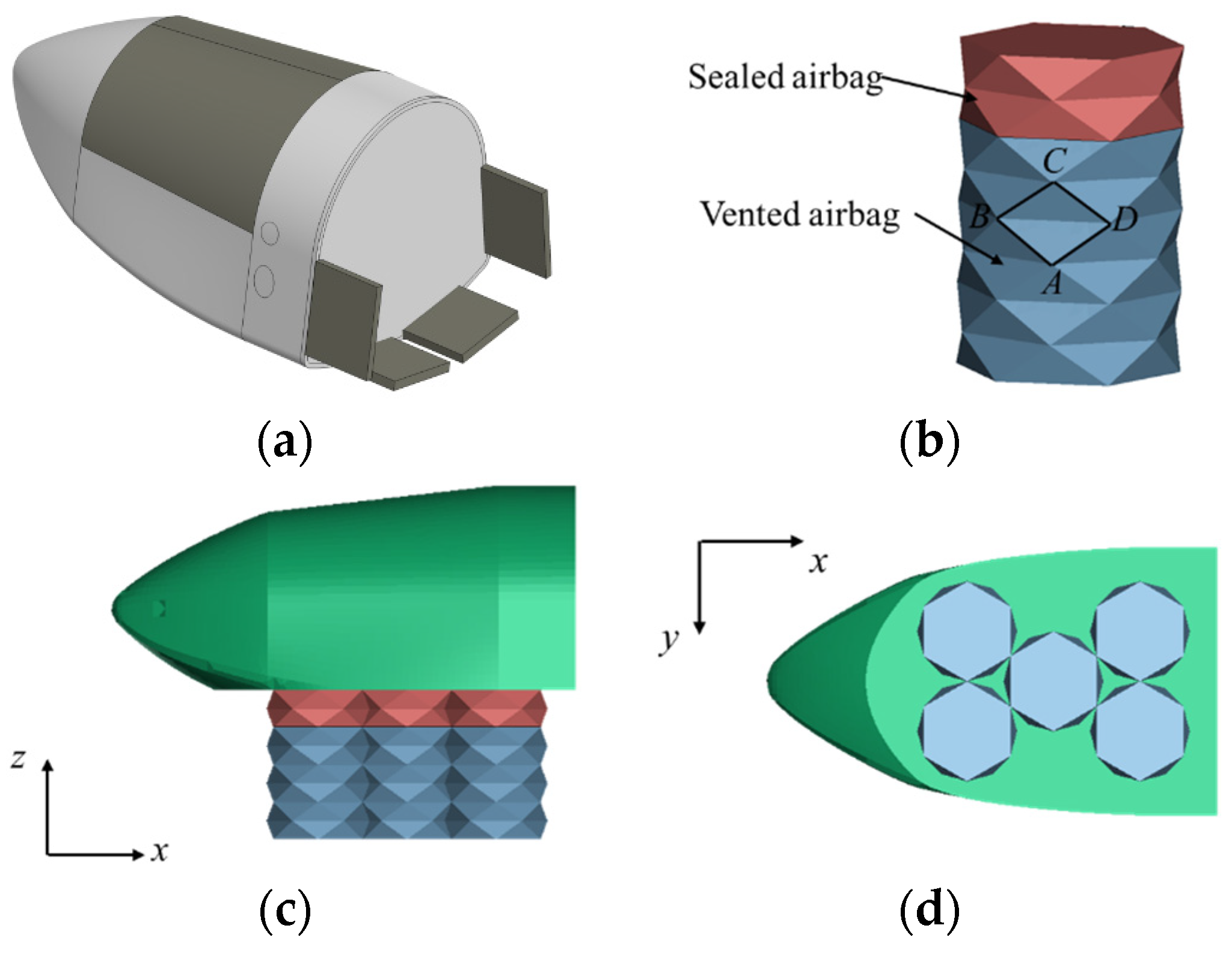
2. Design of Combined Cushion Airbag
2.1. Design of Airbag Height
2.2. Design of the Exhaust Vent
2.3. Origami Pattern Design
3. Finite Element Modeling and Analysis
3.1. Material Design and Test
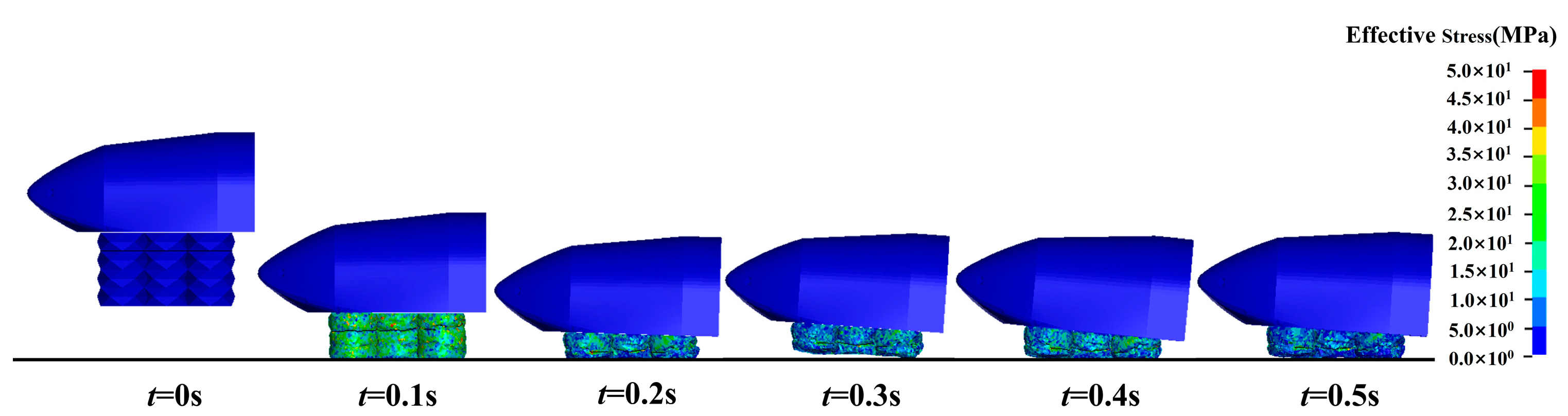
3.2. Analysis Model
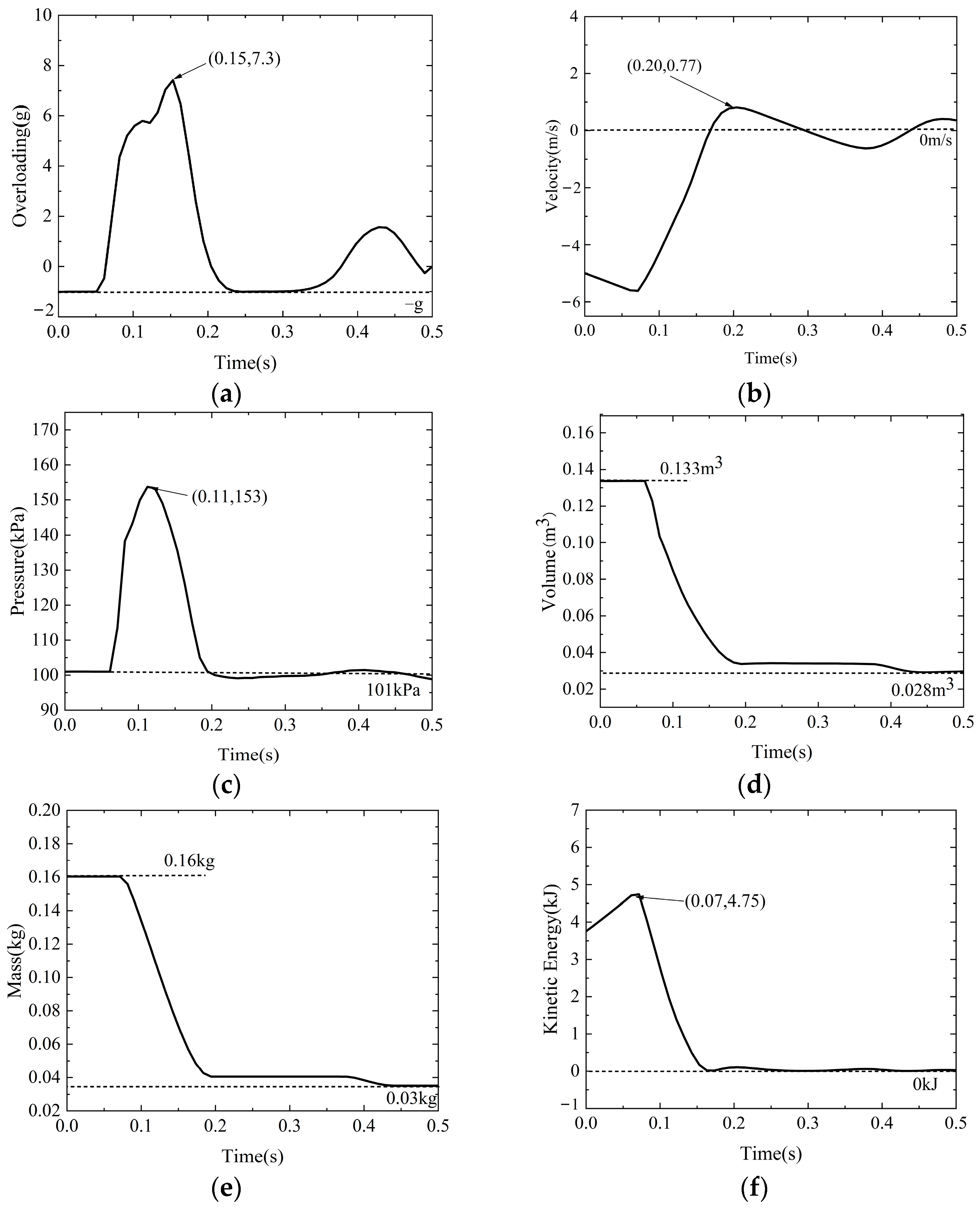
3.3. Analysis Results
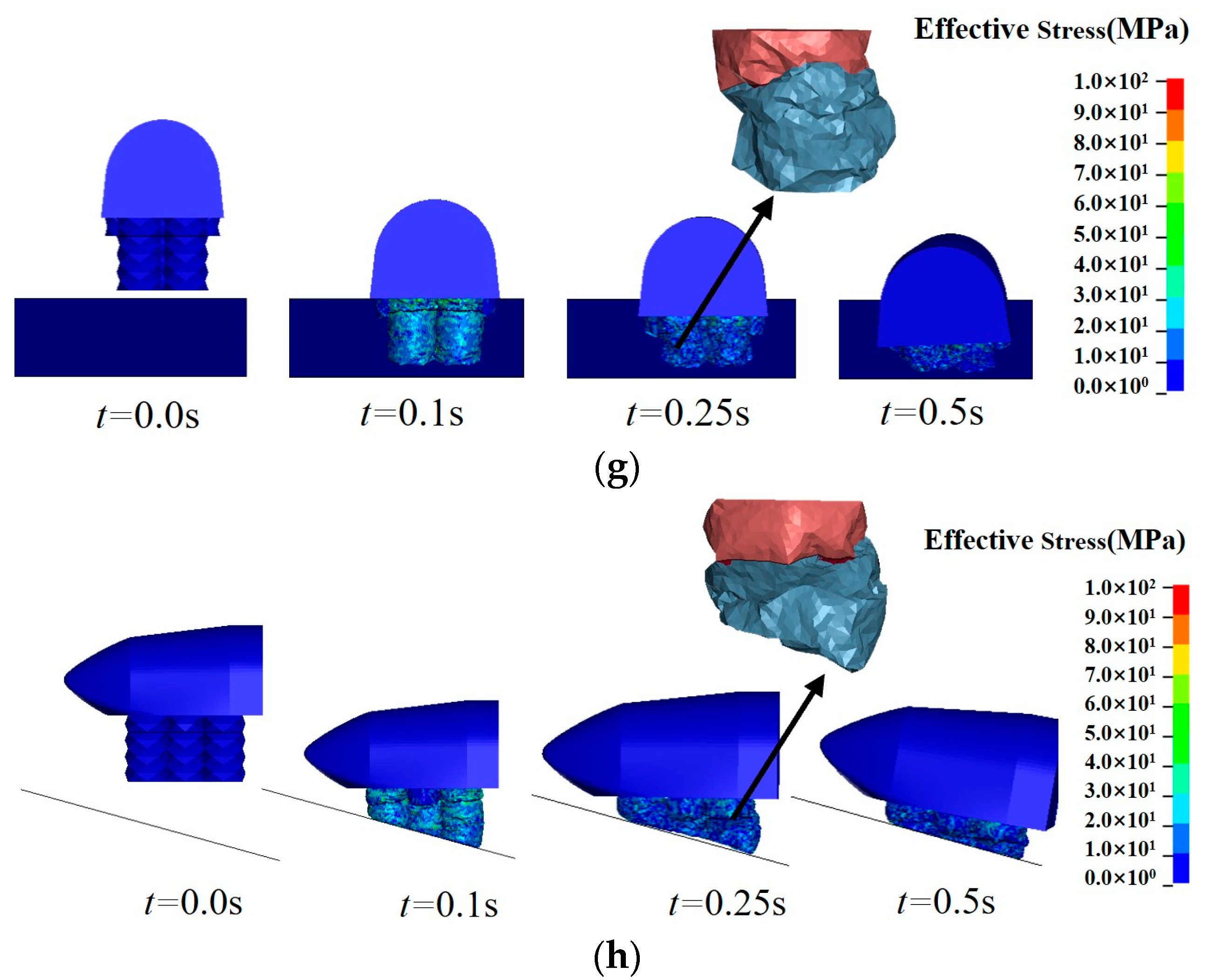
4. Analyses for Complex Landing Environments
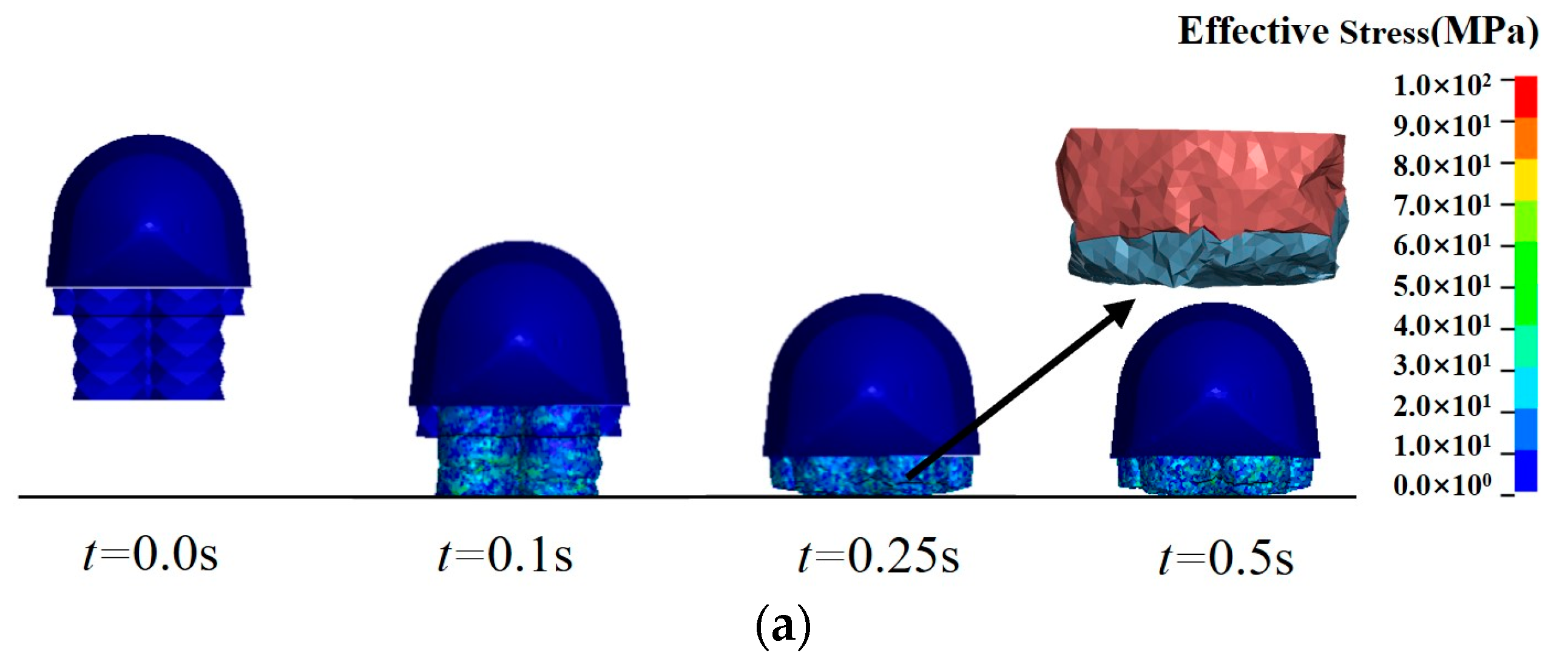
4.1. Anti-Rollover Design
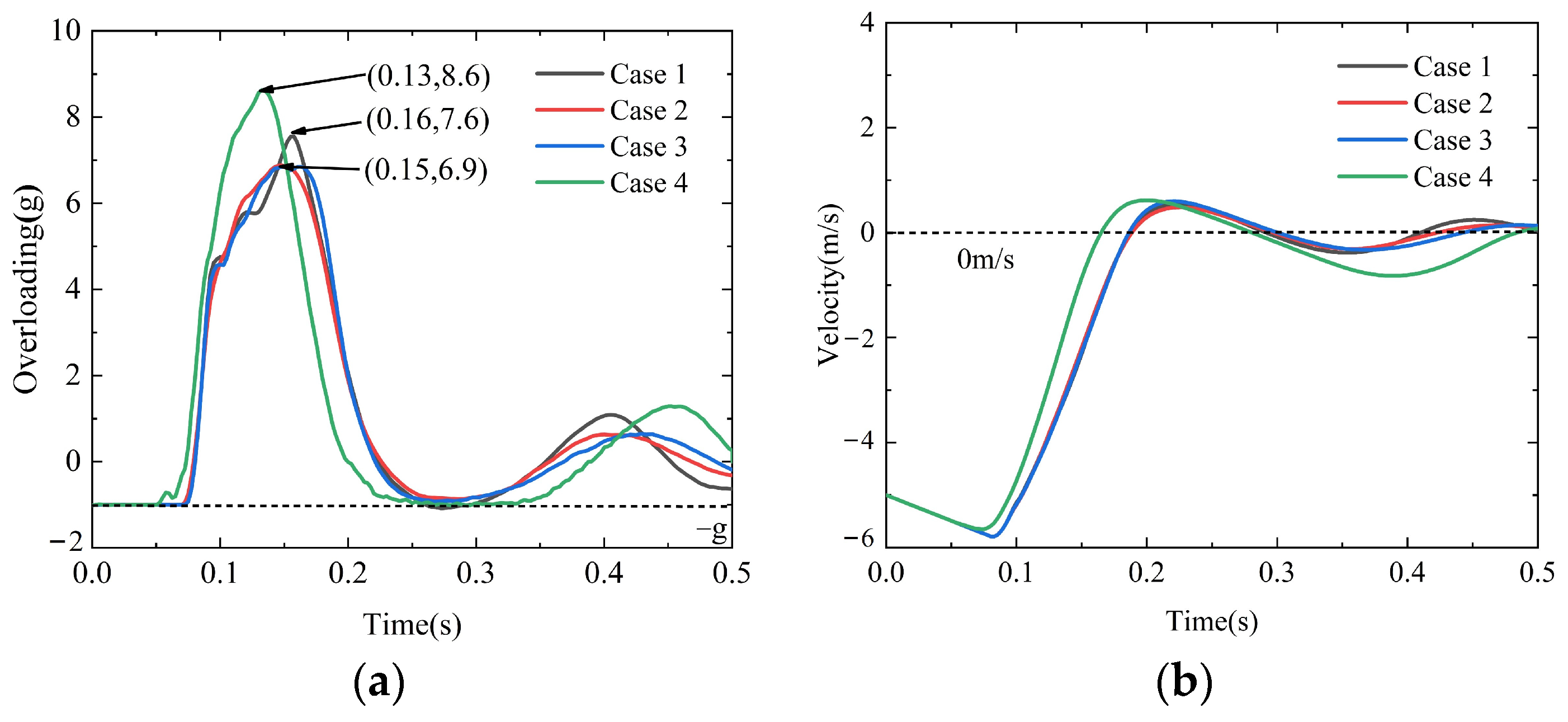
4.2. Analysis Cases for Complex Environments
5. Multi-Objective Optimization
5.1. Selection of Optimization Variables
5.2. Multi-Objective Optimization Model
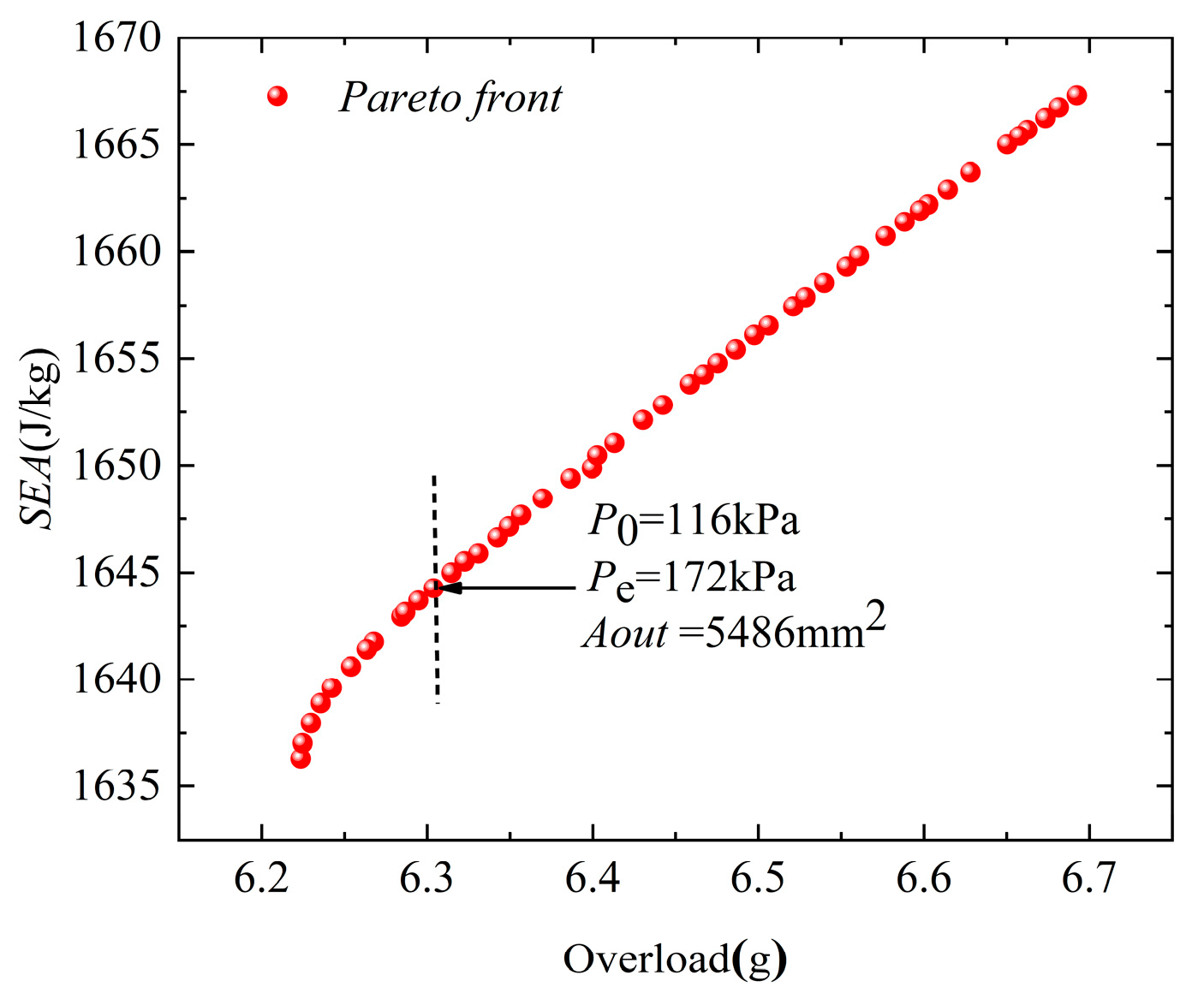
5.3. Optimization Design Method
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, X.; Zhou, S.; Li, D.; Cui, D.; Dong, C. Research on design and cushioning performance of combined lunar landing airbag. Acta Astronaut. 2022, 191, 55–78. [Google Scholar] [CrossRef]
- Wang, H.Y.; Hong, H.J.; Hao, G.X.; Deng, H.; Rui, Q.; Li, J. Characteristic verification and parameter optimization of airbag cushion system for airborne vehicle. Chin. J. Mech. Eng. 2015, 27, 50–57. [Google Scholar] [CrossRef]
- Tutt, B.; Sandy, C.; Corliss, J. Status of the development of an airbag landing system for the Orion Crew Module. In Proceedings of the 20th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Seattle, WA, USA, 4–7 May 2009; pp. 1–13. [Google Scholar]
- Timmers, R.; Hardy, R.; Welch, J. Modeling and simulation of the second-generation Orion Crew Module airbag landing system. In Proceedings of the AIAA SPACE 2009 Conference & Exposition, Pasadena, CA, USA, 14–17 September 2009; pp. 1–14. [Google Scholar]
- Slade, R.; Sharp, P.; Jones, R.; Toropov, V. Analysis, optimization and probabilistic assessment of an airbag landing system for the ExoMars space mission. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA, USA, 6–8 September 2006; pp. 1–9. [Google Scholar]
- Wang, J.T.; Nefske, D.J. A New CAL3D Airbag Inflation Model; SAE Transactions; SAE: Warrendale, PA, USA, 1988; pp. 697–706. [Google Scholar]
- He, H.; Chen, Z.; He, C.; Ni, L.; Chen, G. A hierarchical updating method for finite element model of airbag buffer system under landing impact. Chin. J. Aeronaut. 2015, 28, 1629–1639. [Google Scholar] [CrossRef]
- Wang, H.Y.; Hong, H.J.; Li, J.Y.; Rui, Q. Study on multi-objective optimization of airbag landing attenuation system for heavy airdrop. Def. Technol. 2013, 9, 237–241. [Google Scholar] [CrossRef]
- Zhou, X.; Zhou, S.; Li, D.; Zhou, A. Direct folding method of cylindrical airbag and its application in landing buffer. J. Aerosp. Eng. 2022, 35, 04022083. [Google Scholar] [CrossRef]
- Dmitri, F.; Nitin, L.; Lars, F. On airbag simulation in LS-DYNA with the use of the arbitrary Lagrangian-Eulerian method. In Proceedings of the 4th European LS-DYNA Users Conference, Ulm, Germany, 22–23 May 2003. [Google Scholar]
- Ma, J.; Chai, S.; Chen, Y. Geometric design, deformation mode, and energy absorption of patterned thin-walled structures. Mech. Mater. 2022, 168, 104269. [Google Scholar] [CrossRef]
- Gattas, J.M.; Lv, W.; Chen, Y. Rigid-foldable tubular arches. Eng. Struct. 2017, 145, 246–253. [Google Scholar] [CrossRef]
- Garrett, D.; You, Z.; Gattas, J.M. Curved crease tube structures as an energy absorbing crash box. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016; p. 50169. [Google Scholar]
- Xiang, X.M.; Lu, G.; You, Z. Energy absorption of origami inspired structures and materials. Thin-Walled Struct. 2020, 157, 107130. [Google Scholar] [CrossRef]
- Liu, X.; Li, D.H. Analysis of diamond-patterned origami tubes under axial crushing forces. Appl. Math. Mech. 2017, 38, 163–169. [Google Scholar]
- Yuan, L.; Shi, H.; Ma, J.; You, Z. Quasi-static impact of origami crash boxes with various profiles. Thin-Walled Struct. 2019, 141, 435–446. [Google Scholar] [CrossRef]
- Yang, K.; Xu, S.; Zhou, S.; Xie, Y.M. Multi-objective optimization of multi-cell tubes with origami patterns for energy absorption. Thin-Walled Struct. 2018, 123, 100–113. [Google Scholar] [CrossRef]
- Faraj, R.; Popławski, B.; Gabryel, D.; Kowalski, T.; Hinc, K. Adaptive airbag system for increased evacuation safety. Eng. Struct. 2022, 270, 114853. [Google Scholar] [CrossRef]
- Wu, Q.; Yu, L.; Yao, X.R. Study on the cushioning properties of airbag and the effect of vent size. Comput. Simul. 2016, 33, 85–89. [Google Scholar]
- Zhang, X.; Chen, Y. The diamond thick-panel origami and the corresponding mobile assemblies of plane-symmetric bricard linkages. Mech. Mach. Theory 2018, 130, 585–604. [Google Scholar] [CrossRef]
- Willey, C.; Sandy, C.; Welch, J.; Timmers, R. Impact attenuating airbags for earth and planetary landing systems. In Proceedings of the AIAA SPACE 2007 Conference & Exposition, Long Beach, CA, USA, 18–20 September 2007; p. 6172. [Google Scholar]
- Gao, H.H.; Wang, H.H.; Zhang, H.Y.; Tong, M.B. Experimental Research on Buffer Performance of Recycling Airbag for a Drone. Spacecr. Recovery Remote Sens. 2021, 42, 30–38. (In Chinese) [Google Scholar]
- Zhang, P.F.; Wei, J.Z.; Chen, X.Y.; Tan, H.F.; Zhu, M.F. Analysis and multi-objective optimization for buffer performance of heavy landing airbags. J. Vib. Shock 2020, 39, 91–98,142. (In Chinese) [Google Scholar]
- Sadollaha, A.; Eskandarb, H.; Kim, J.H. Water cycle algorithm for solving constrained multi-objective optimization problems. Appl. Soft Comput. 2015, 27, 279–298. [Google Scholar] [CrossRef]






| Elastic Modulus (MPa) | Poisson Ratio | Density (kg/m3) | |
|---|---|---|---|
| Cushion airbag | 9.3 × 102 | 0.35 | 1.60 × 103 |
| Returnable spacecraft | 3.0 × 105 | 0.30 | 1.25 × 104 |
| Ground | 3.0 × 105 | 0.30 | 7.80 × 103 |
| Number of FEA Elements | 27,960 | 60,986 | 101,680 |
|---|---|---|---|
| Peak overload (g) | 7.25 | 7.05 | 7.08 |
| Pressure peak (KPa) | 153 | 161 | 157 |
| Calculation cost (minute) | 32 | 68 | 115 |
| Descending Velocity (m/s) | Horizontal Velocity (m/s) | Lateral Velocity (m/s) | Landing Pitch Angle (°) | |
|---|---|---|---|---|
| Case 1 | −5 | 2 | 0 | 0 |
| Case 2 | −5 | 0 | 2 | 0 |
| Case 3 | −5 | 2 | 2 | 0 |
| Case 4 | −5 | 0 | 0 | 15 |
| Case | (mm2) | Initial Pressure P0 (kPa) | Venting Threshold Pressure Pe (kPa) | Polygon Edge Number L | Maximum Overload Value amax (g) | Maximum Rebound Velocity v2 (m/s) | Specific Energy Absorption SEA (J/kg) |
|---|---|---|---|---|---|---|---|
| 5 | 3000 | 101 | 130 | 6 | 7.5 | 0.96 | 1637 |
| 6 | 4000 | 101 | 130 | 6 | 7.3 | 0.77 | 1655 |
| 7 | 5000 | 101 | 130 | 6 | 6.5 | 0.69 | 1661 |
| 8 | 6000 | 101 | 130 | 6 | 8.7 | 1.29 | 1598 |
| 9 | 7000 | 101 | 130 | 6 | 11.9 | 1.77 | 1521 |
| 10 | 4000 | 101 | 101 | 6 | 8.2 | 0.81 | 1651 |
| 11 | 4000 | 101 | 160 | 6 | 7.3 | 0.44 | 1676 |
| 12 | 4000 | 101 | 190 | 6 | 9.2 | 0.67 | 1663 |
| 13 | 4000 | 130 | 190 | 6 | 7.4 | 0.22 | 1683 |
| 14 | 4000 | 160 | 190 | 6 | 6.2 | 0.51 | 1672 |
| 15 | 4000 | 190 | 190 | 6 | 6.1 | 0.61 | 1666 |
| 16 | 4000 | 101 | 160 | 8 | 8.4 | 0.45 | 1675 |
| 17 | 4000 | 101 | 160 | 10 | 8.4 | 0.52 | 1672 |
| 18 | 4000 | 101 | 160 | ∞ | 8.6 | 0.46 | 1675 |
| Exhaust Vent Area (mm2) | Initial Pressure (kPa) | Venting Threshold Pressure (kPa) | Maximum Overload (g) | SEA (J/kg) | |
|---|---|---|---|---|---|
| Before optimization | 4000 | 101 | 130 | 7.3 | 1648 |
| After optimization | 5486 | 116 | 172 | 6.1 | 1667 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Yang, Y.; Huang, H.; Chen, G.; Li, G.; Chen, H. Multi-Objective Optimization Design of an Origami-Inspired Combined Cushion Airbag. Aerospace 2024, 11, 169. https://doi.org/10.3390/aerospace11030169
Xu Y, Yang Y, Huang H, Chen G, Li G, Chen H. Multi-Objective Optimization Design of an Origami-Inspired Combined Cushion Airbag. Aerospace. 2024; 11(3):169. https://doi.org/10.3390/aerospace11030169
Chicago/Turabian StyleXu, Yan, Yilong Yang, He Huang, Gang Chen, Guangxing Li, and Huajian Chen. 2024. "Multi-Objective Optimization Design of an Origami-Inspired Combined Cushion Airbag" Aerospace 11, no. 3: 169. https://doi.org/10.3390/aerospace11030169
APA StyleXu, Y., Yang, Y., Huang, H., Chen, G., Li, G., & Chen, H. (2024). Multi-Objective Optimization Design of an Origami-Inspired Combined Cushion Airbag. Aerospace, 11(3), 169. https://doi.org/10.3390/aerospace11030169






