Bayesian Identification of High-Performance Aircraft Aerodynamic Behaviour
Abstract
1. Introduction
1.1. Related Works
1.2. Research Motivation
1.3. Research Contribution
2. Aircraft Modelling
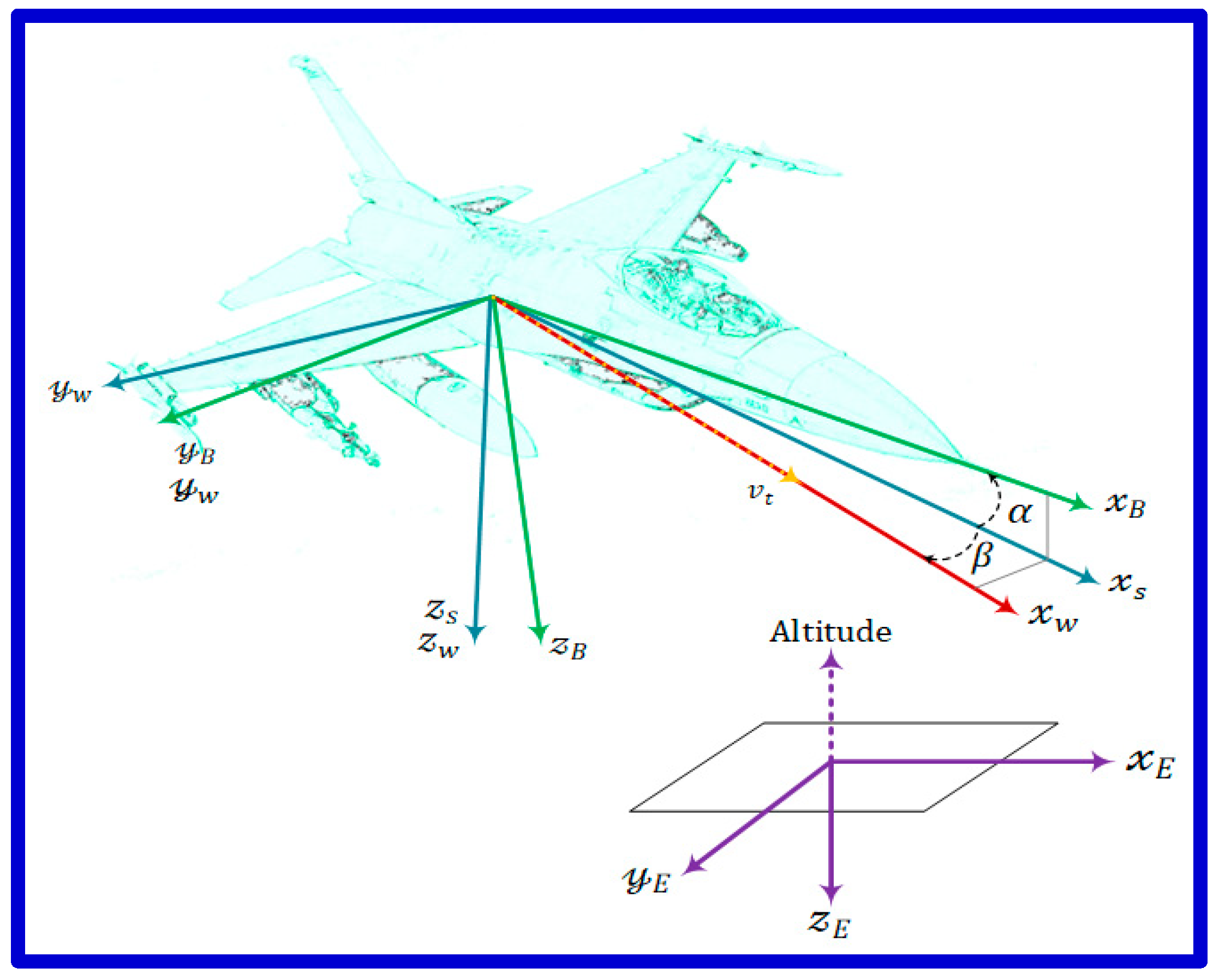
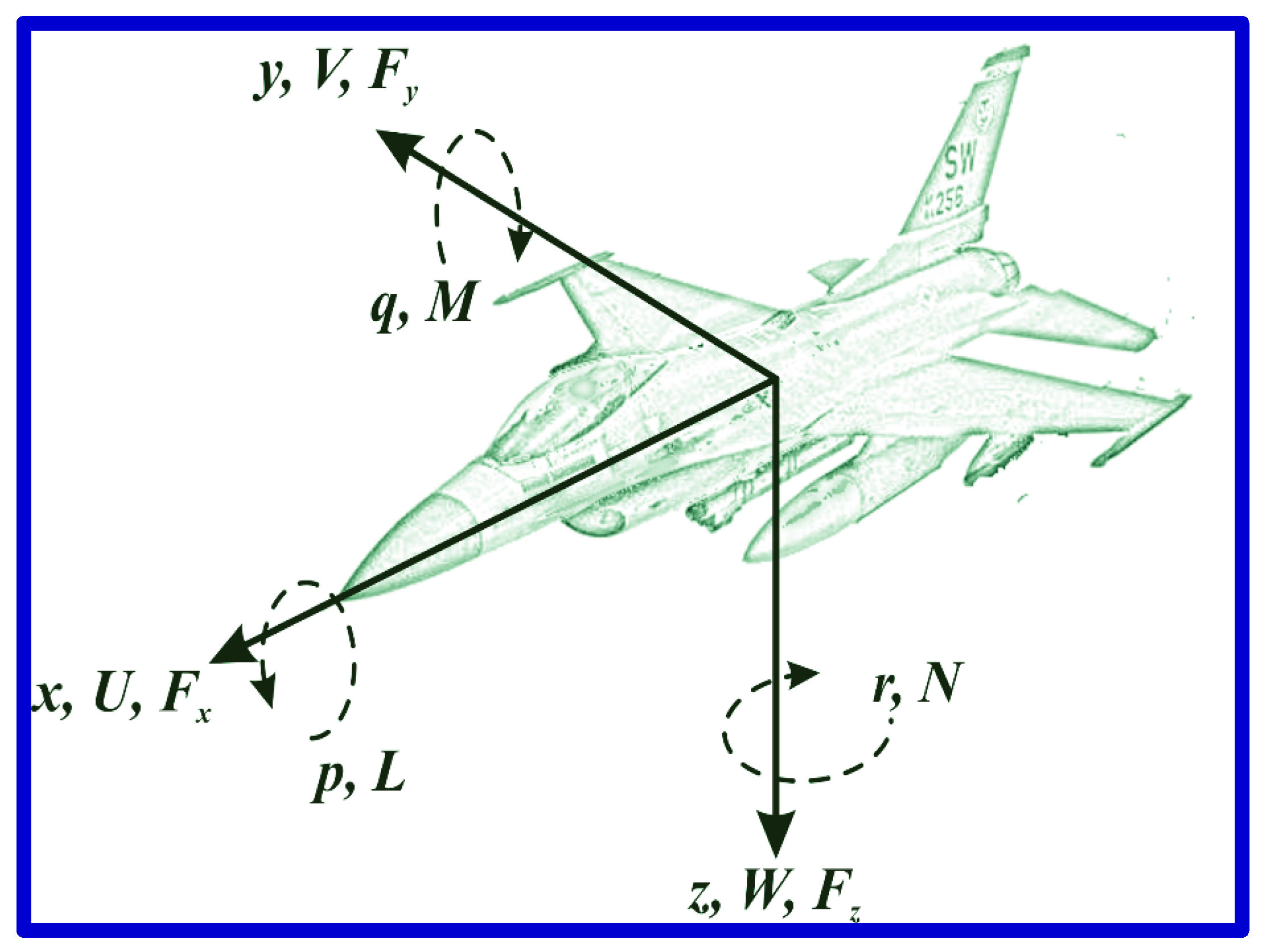
2.1. Mathematical Formulations
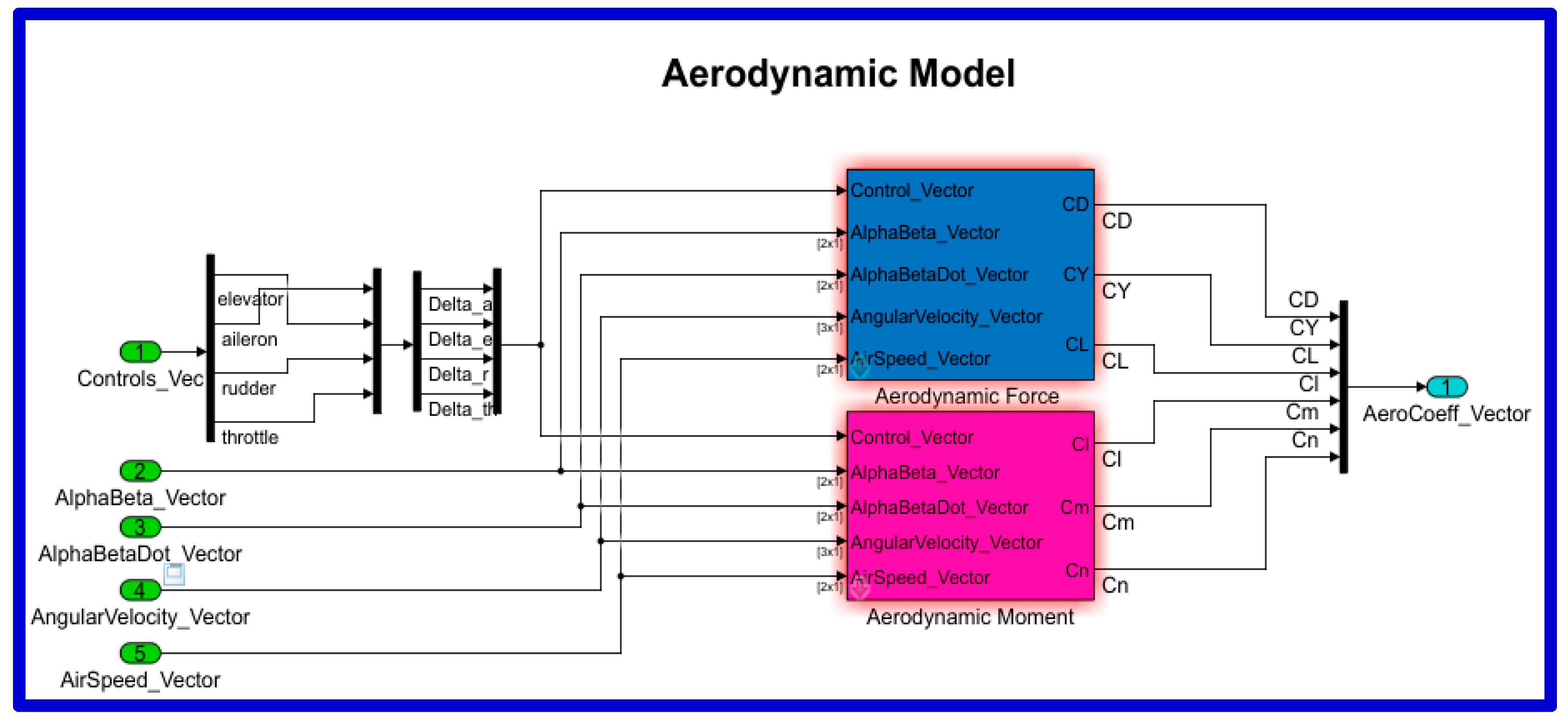
2.2. Development of FDM
2.3. Analysis of Aircraft Lateral-Directional Model
2.3.1. Step 1: Numerical Linearization to Obtain Trim Points
| Algorithm 1: Aircraft Steady State Points |
| Input: 1. Specify inputs and states (); inputs States Iterations: 2. Set tolerance value = 1 × 10−8 2.1. Compute (state derivatives) from inputs and states . 2.2. Compute cost function: J = a1∗, a2∗… an∗. 2.3. Apply minimization algorithm (Nelder Mead Algorithm) on cost function. 2.4. Stopping criteria: Tolerance value achieved—terminate the iterations. Output: 3. Display Trim data: Vt, . |
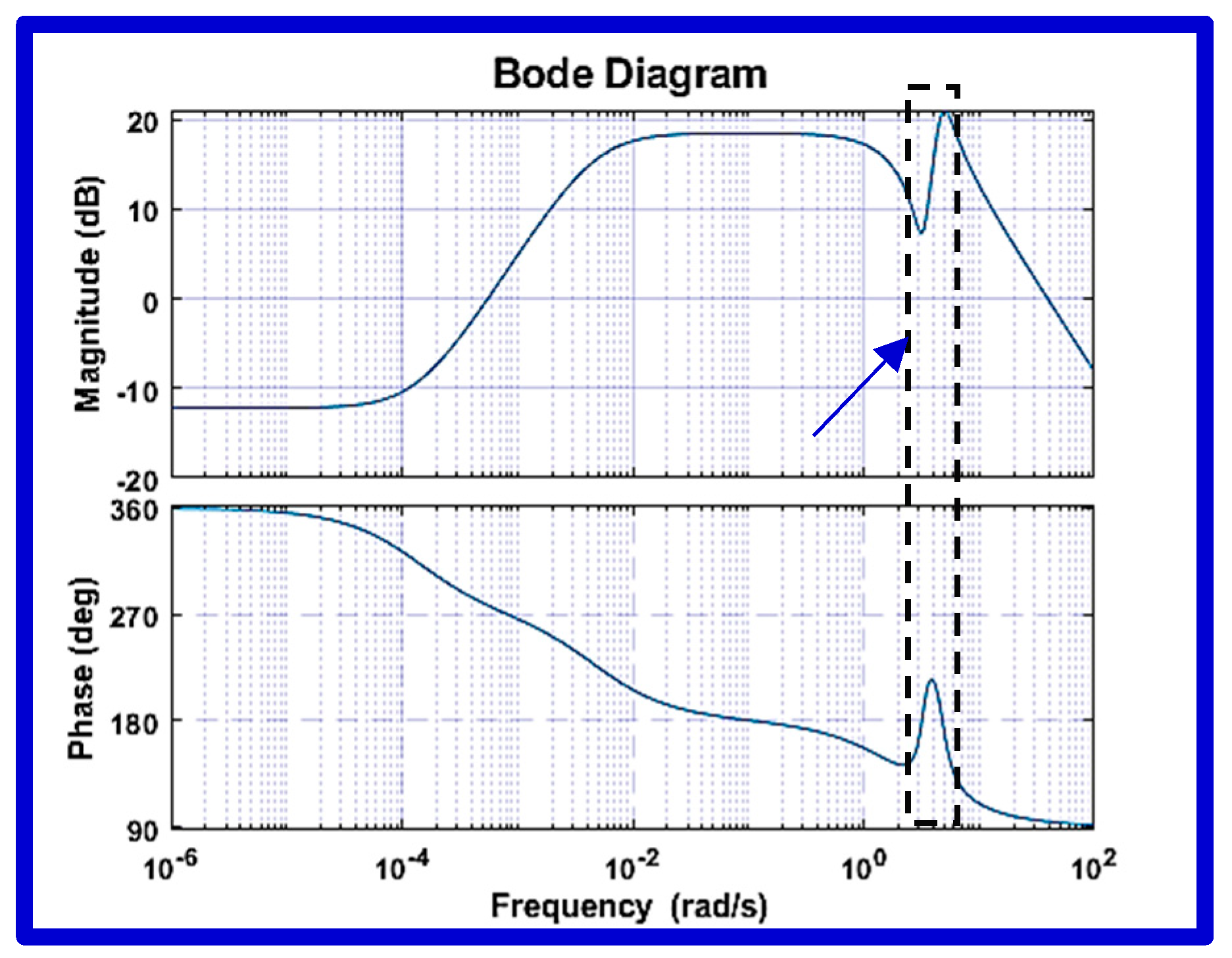
2.3.2. Step 2: Non-Parametric (FIR) Modelling
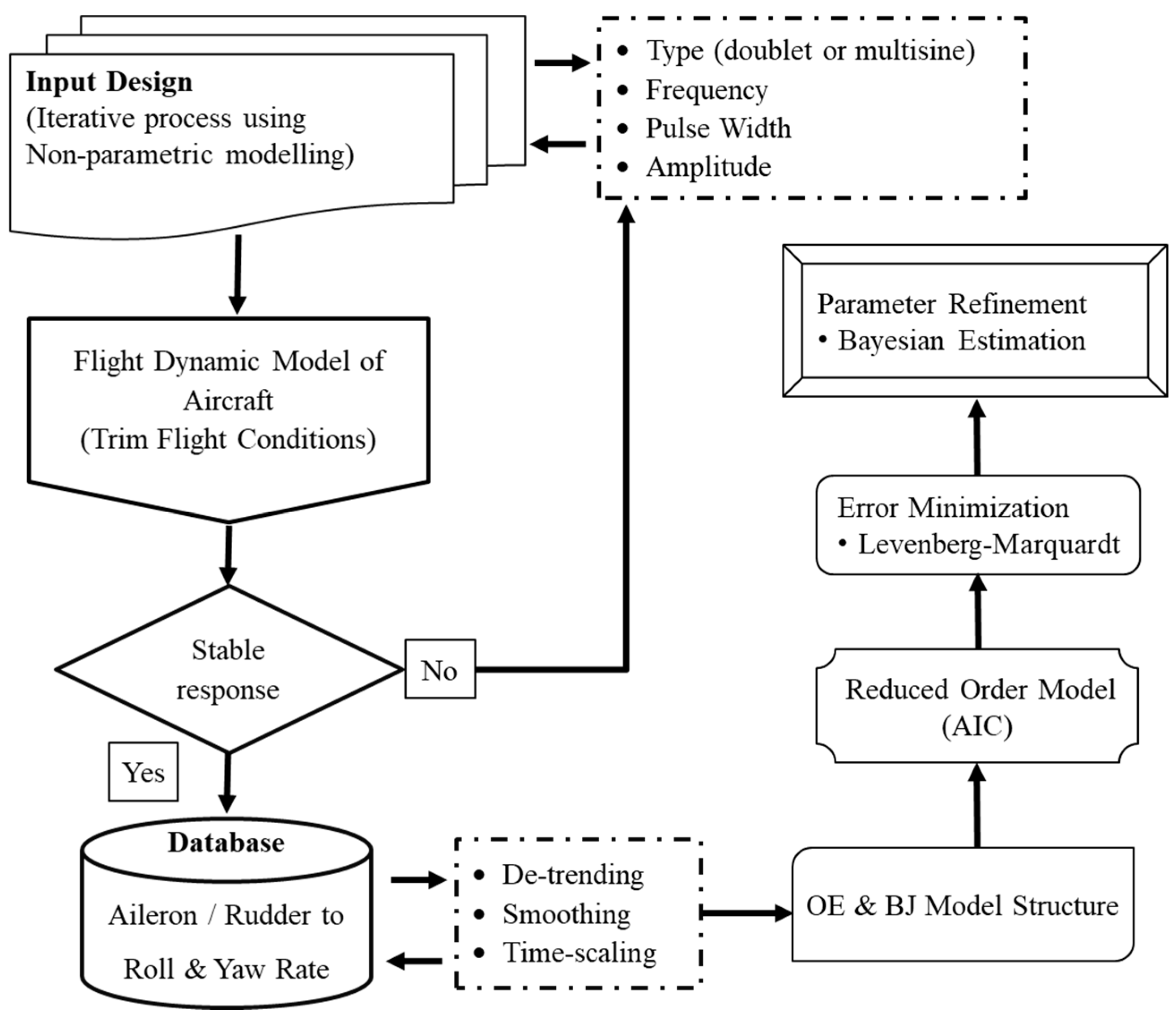
3. Methodology
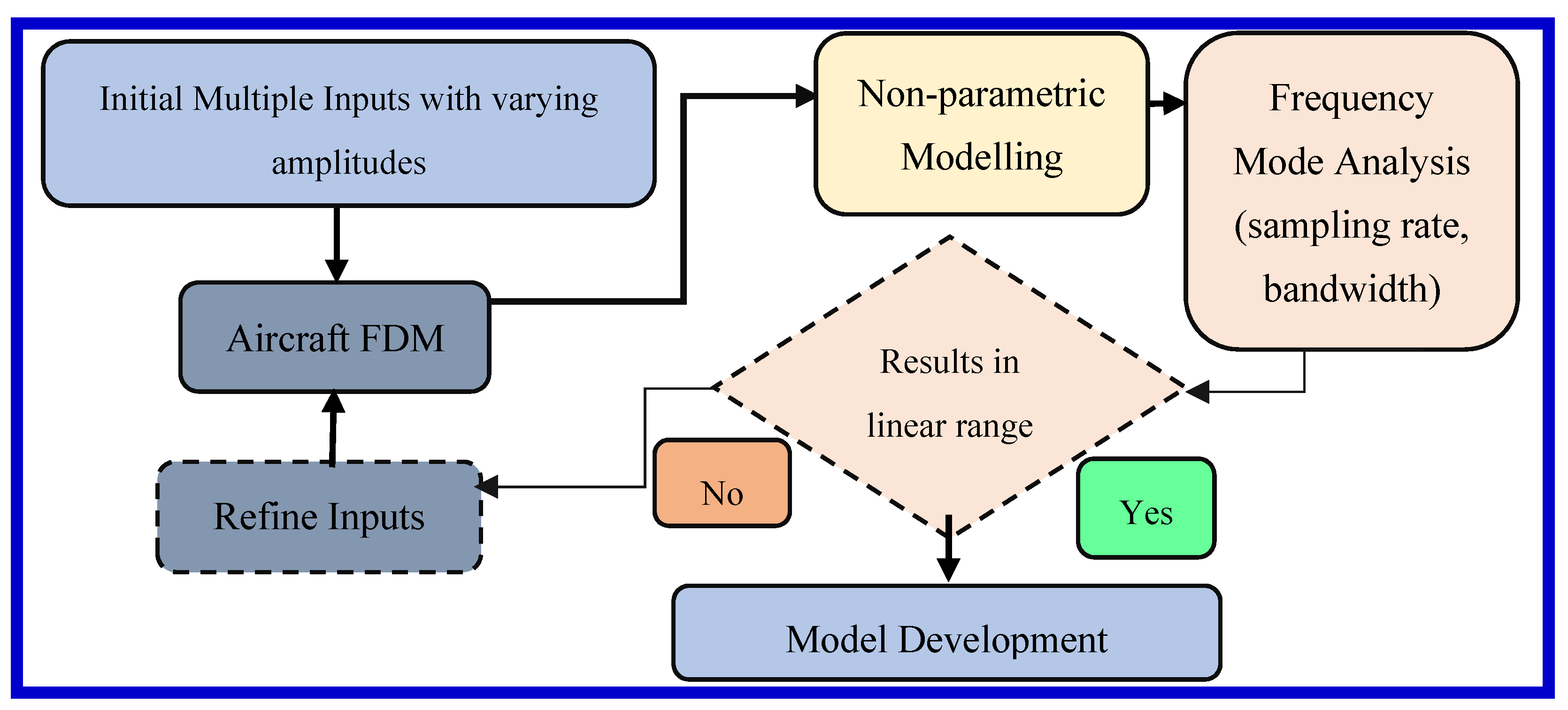
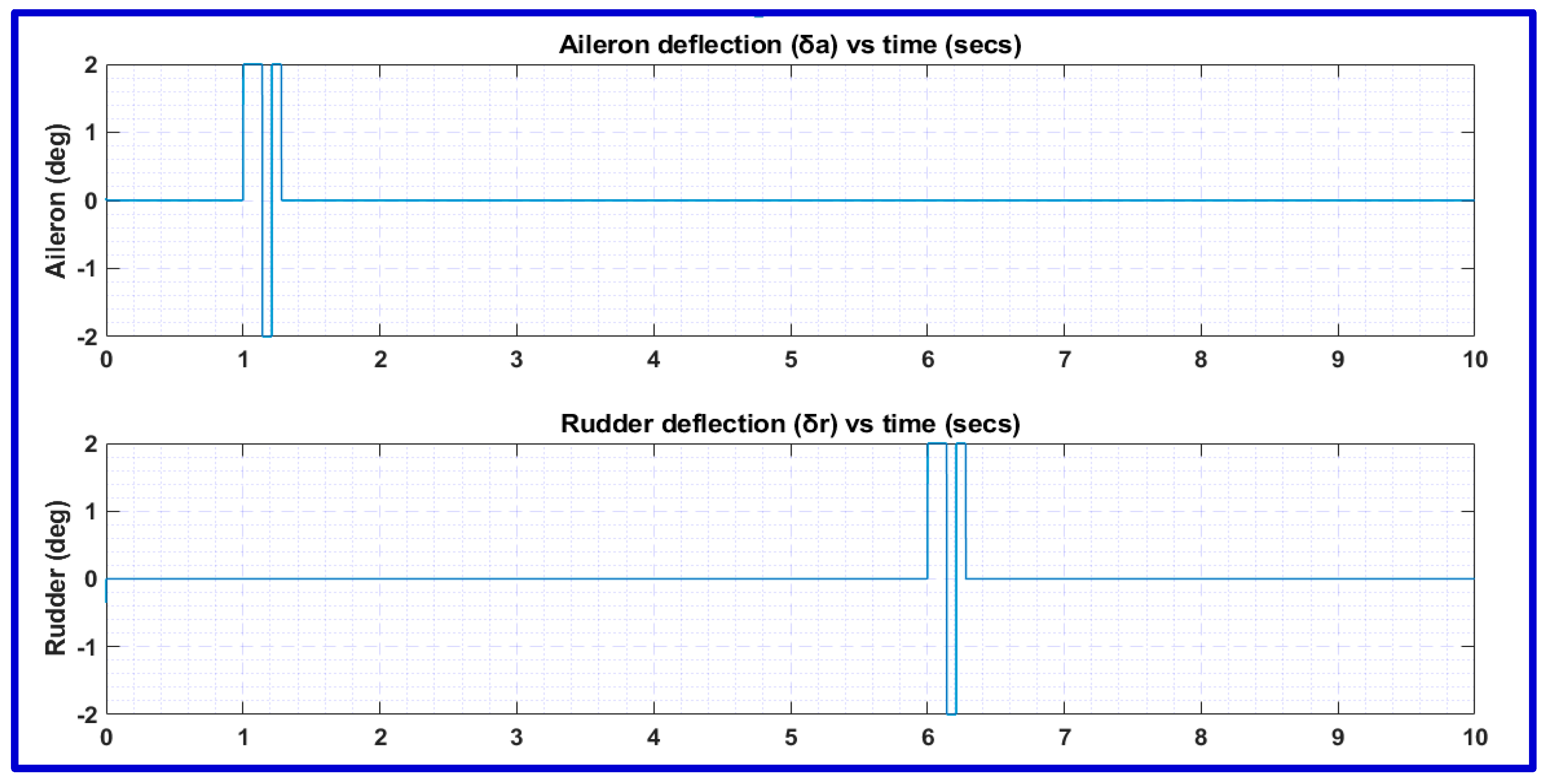
3.1. Input Design
| Algorithm 2: Determine BJ Structure |
Input:
Iterations:
Output:
|
3.2. Model Postulation—OE and BJ Structures
3.3. Reduced Order Model—(AIC)
3.4. Error Minimization—L-M Algorithm
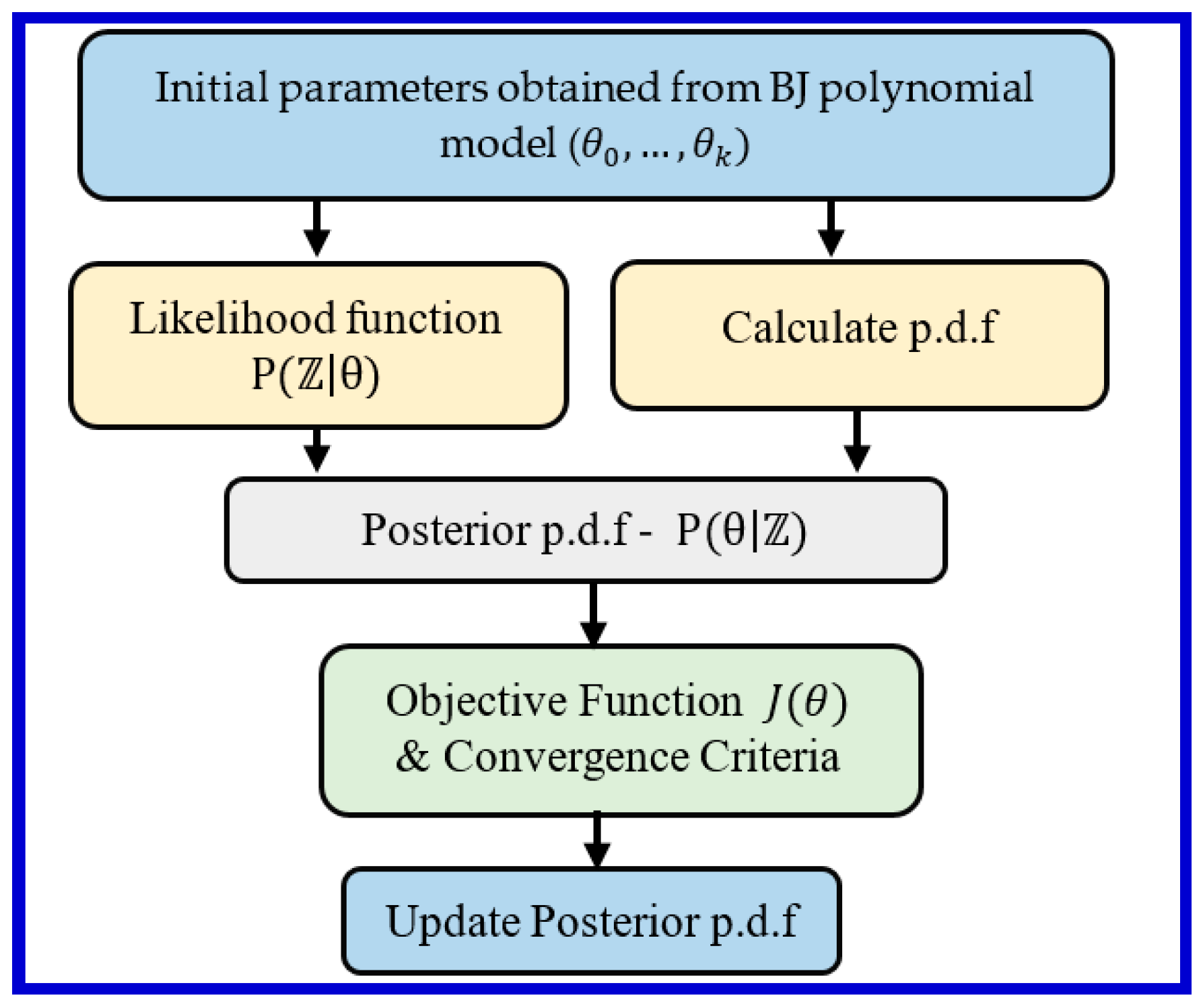
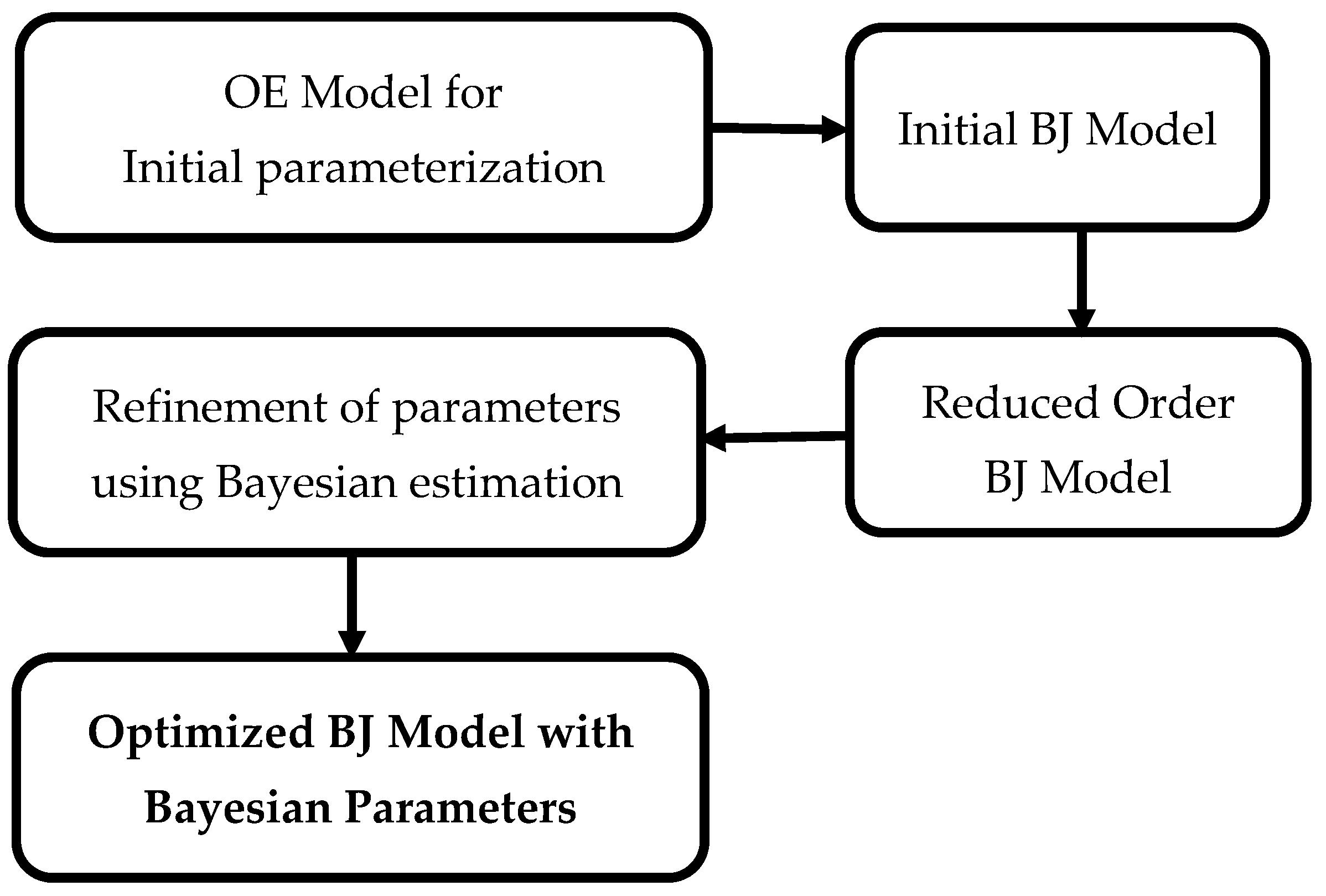
3.5. Model Optimization—Bayesian Approach
| Algorithm 3: L-M Algorithm |
| Input: 1. Initial parameters obtained from Nonlinear Least square estimation of BJ structure. 2. Set regularization value to 0.001. Iterations: 3. Set tolerance value. 4. Initial hessian matrix (∇2) using Newton-Raphson Technique: xn + 1 = xn − (xn)/f’(xn) 5. Compute Jacobean matrix 6. Compute Modified Hessian Matrix 7. Compute cost function: < 0.001 8. Update vector. 9. Stopping criteria: Tolerance value achieved Output: 10. Optimized parameters |
| Algorithm 4: Bayesian Estimation |
| Input: 1. Initial guess of parameters obtained from BJ model Iterations: 2. Set Convergence criteria: ϵ = 1 × 10−5 3. Iterate for 4. Compute and 5. Compute 6. Compute as the solution of 7. Stopping criteria: until or Output: 8. Estimated parameters |
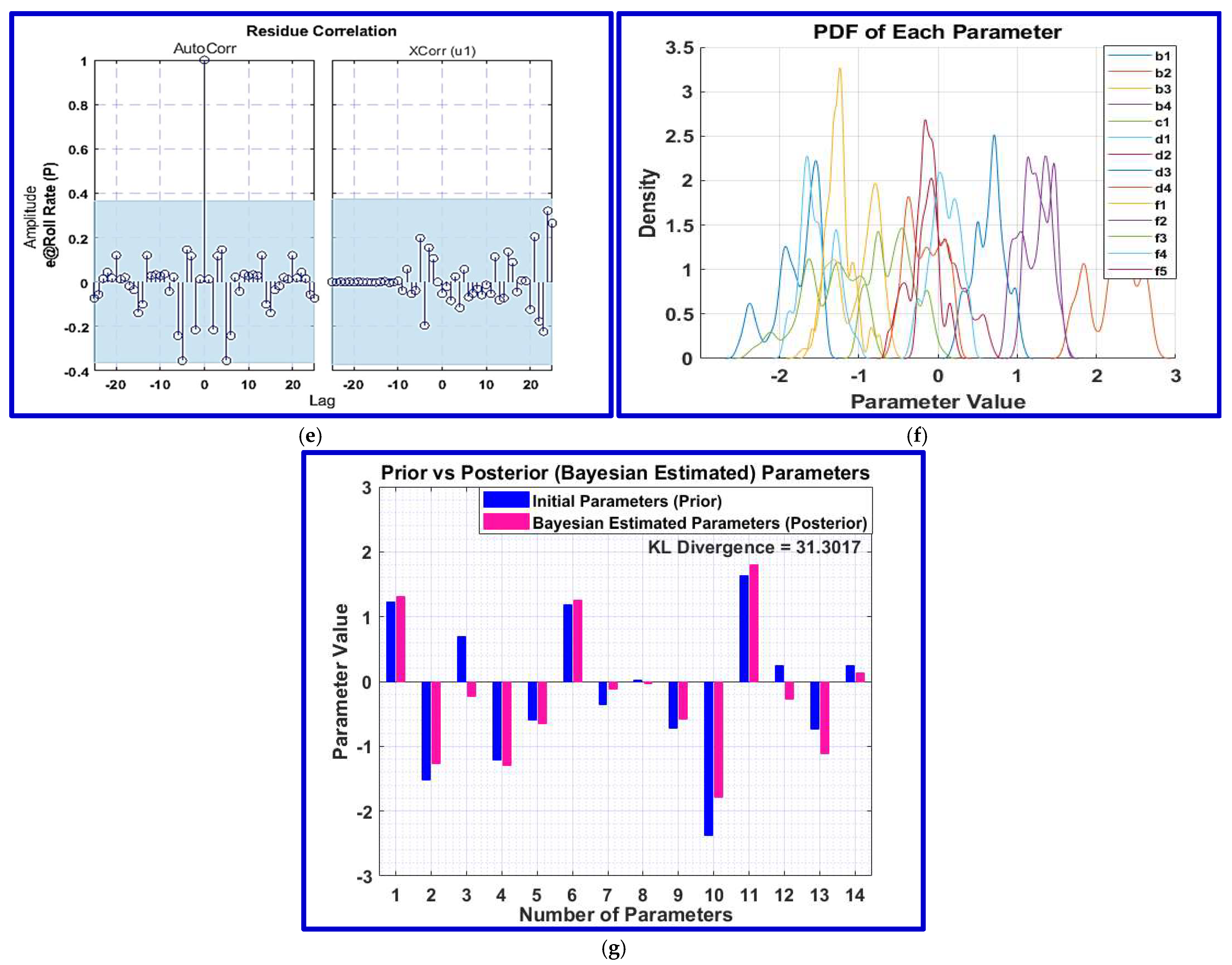
Bayesian Sensitivity Analysis
4. Results and Discussion
4.1. Aircraft FDM
4.2. Aircraft Trim Conditions
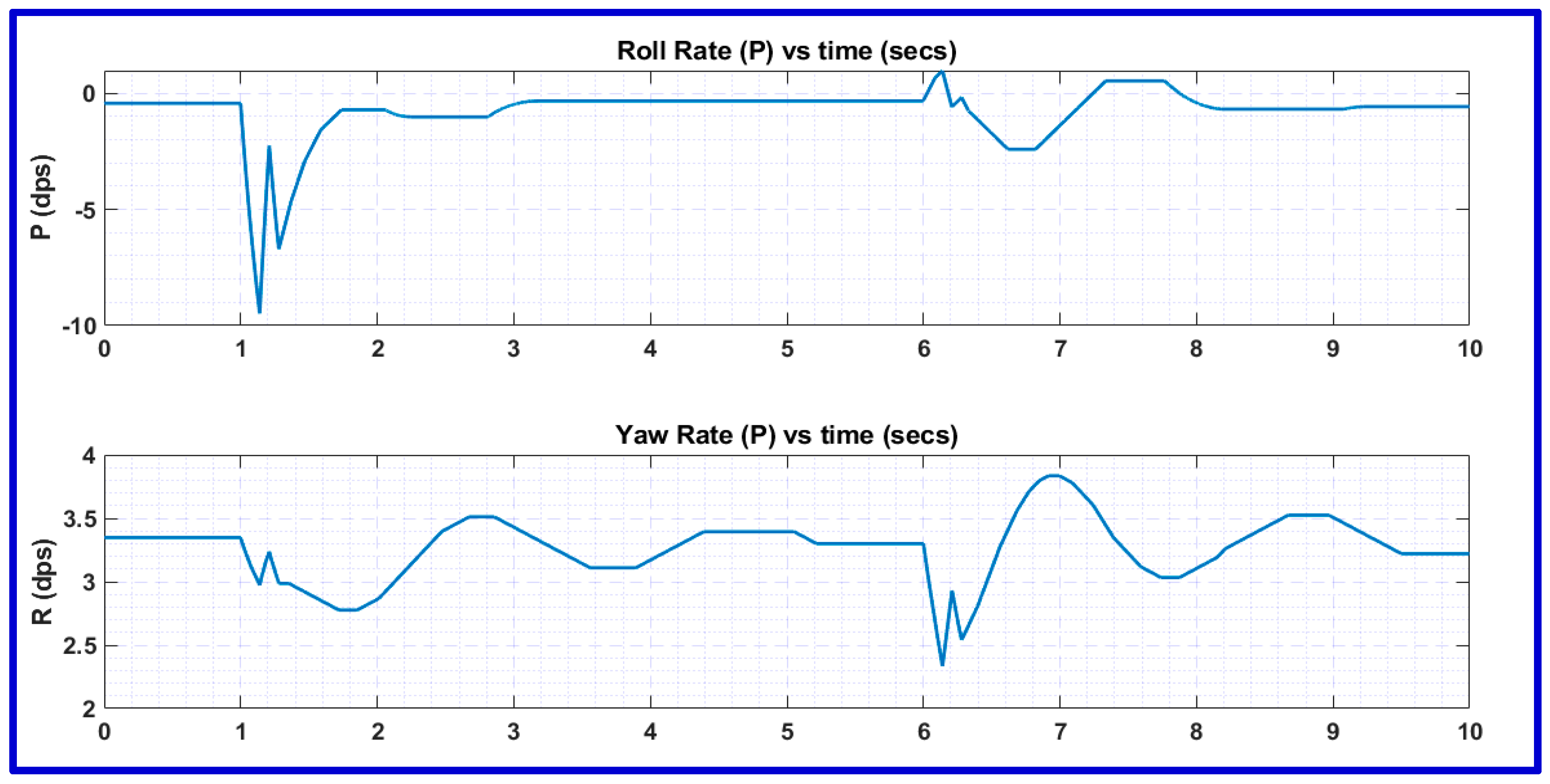
4.3. Optimum Input Design
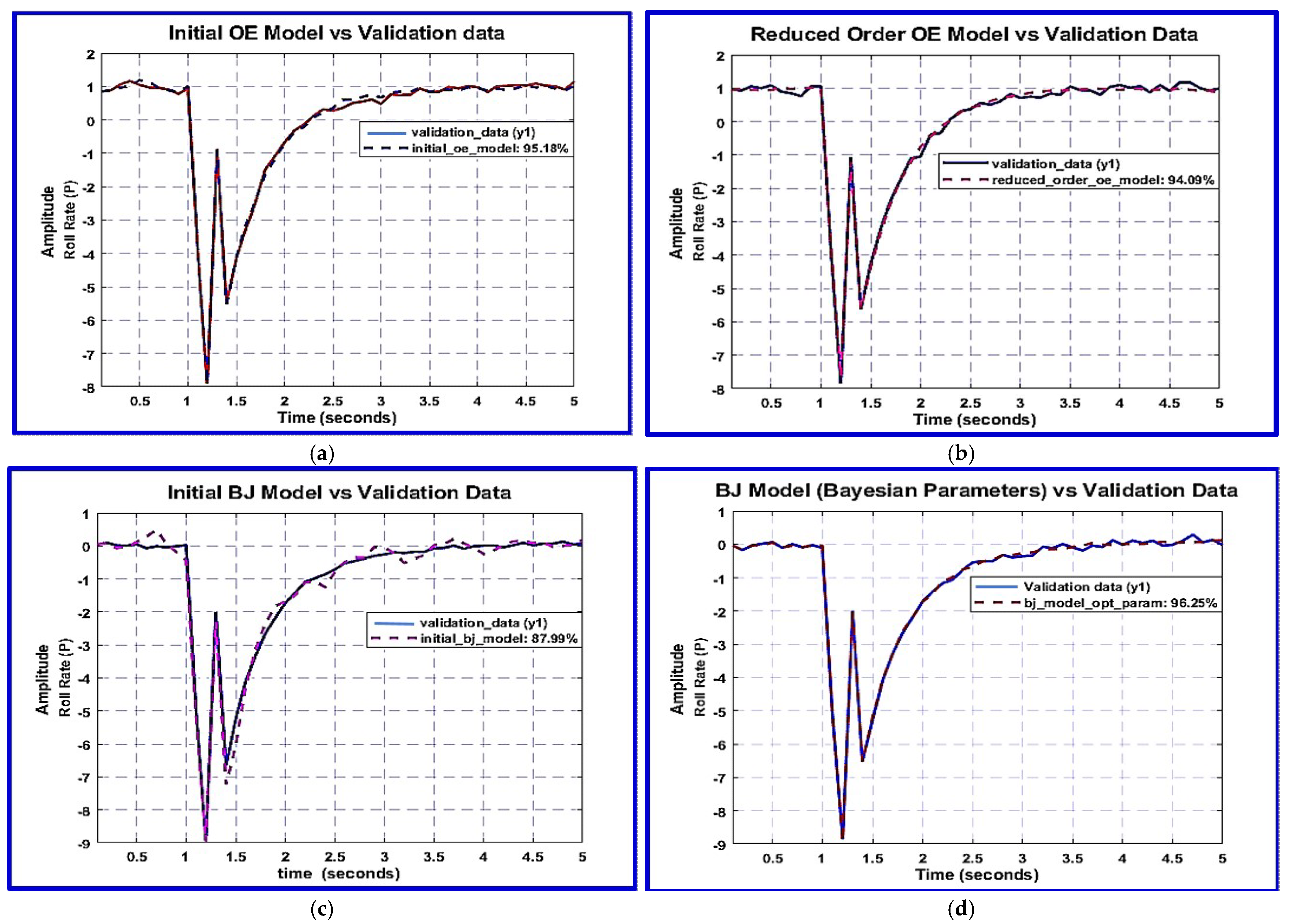
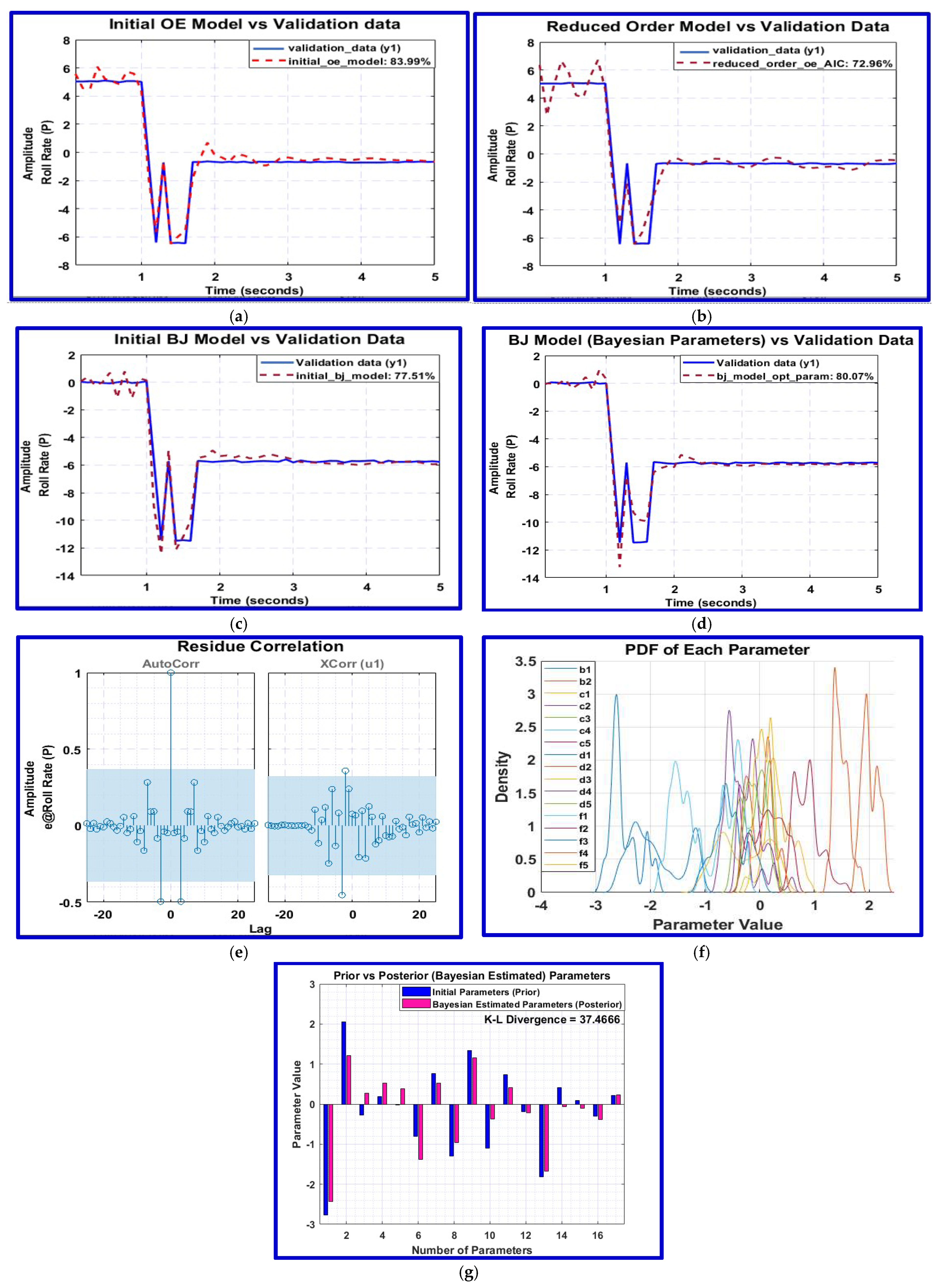
4.4. Model Identification and Parameter Refinement
C(z) = 1 − 0.9291 z−1
D(z) = 1 − 1.138 z−1 + 0.2772 z−2 + 0.2227 z−3 − 0.4422 z−4
F(z) = 1 + 0.4055 z−1 − 1.211 z−2 − 0.3027 z−3 + 0.3932 z−4 − 0.009715 z−5
C(z) = 1 − 0.9973 z−1 + 0.134 z−2 + 0.1181 z−3 − 1.096 z−4 + 0.8415 z−5
D(z) = 1 − 1.626 z−1 + 0.6488 z−2 + 0.1839 z−3 − 0.3126 z−4 + 0.1056 z−5
F(z) = 1 − 0.6974 z−1 + 0.1451 z−2 + 0.07067 z−3 − 0.2726 z−4 + 0.2265 z−5
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
Roman
Greek
|
Superscripts
|
References
- Tangirala, A.K. Principles of System Identification Theory and Practice; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Klein, V.; Morelli, E. Aircraft System Identification Theory and Practice; American Institute of Aeronautics & Astronautics: Reston, VA, USA, 2006. [Google Scholar]
- Stevens, B.L.; Lewis, F.L. Aircraft Control and Simulation, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Tulleken, H.J.A.F. Grey-box Modelling and Identification Using Physical Knowledge and Bayesian Techniques. Automatica 1993, 29, 285–308. [Google Scholar] [CrossRef]
- Morelli, E.A.; Grauer, J.A. Advances in Aircraft System Identification at NASA Langley Research Center. J. Aircr. 2023, 60, 1354–1370. [Google Scholar] [CrossRef]
- Morelli, E.A.; Grauer, J.A. Practical Aspects of Frequency-Domain Approaches for Aircraft System Identification. J. Aircr. 2020, 57, 268–291. [Google Scholar] [CrossRef]
- Oznurlu, C. Data-Driven Model Discovery and Control of Lateral-Directional Fighter Aircraft Dynamics. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2022. [Google Scholar]
- Belge, E.; Kaba, H.K.; Parlak, A.; Altan, A.; Hacioğlu, R. Estimation of small unmanned aerial vehicle lateral dynamic model with system identification approaches. Balk. J. Electr. Comput. Eng. 2020, 8, 121–126. [Google Scholar] [CrossRef]
- Bnhamdoon, O.A.A.; Hanif, N.H.H.M.; Akmeliawati, R. Identification of a quadcopter autopilot system via Box–Jenkins structure. Int. J. Dyn. Control 2020, 8, 835–850. [Google Scholar] [CrossRef]
- Pillonetto, G.; Dinuzzo, B.F.; Chenc, T.; Nicolao, G.D.; Ljung, L. Kernel methods in system identification, machine learning and function estimation: A survey. Automatica 2014, 50, 657–682. [Google Scholar] [CrossRef]
- Kwad, A.M.; Hanafi, D.; Omar, R.; Rahman, H.A. Development of system identification from traditional concepts to real-time soft computing based. IOP Conf. Ser. Mater. Sci. Eng. 2020, 767, 012050. [Google Scholar] [CrossRef]
- Ji, Y.; Jiang, X.K.; Wan, L.J. Hierarchical least squares parameter estimation algorithm for two-input Hammerstein finite impulse response systems. J. Frankl. Inst. 2020, 357, 5019–5032. [Google Scholar] [CrossRef]
- Millidere, M. Optimal Input Design and System Identification for an Agile Aircraft. Ph.D. Thesis, Middle East Technical University, Ankara, Turkey, 2021. [Google Scholar]
- Morelli, E.A. Practical Aspects of the Equation-Error Method for Aircraft Parameter Estimation. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Keystone, CO, USA, 21–24 August 2006. [Google Scholar]
- Roeser, M.S.; Fezans, N. Method for designing multi-input system identification signals using a compact time-frequency representation. CEAS Aeronaut. J. 2021, 12, 291–306. [Google Scholar] [CrossRef]
- Lopez, M.J.S.; Ruckel, P.; Berrigan, C.S. Bell V-280 System Identification and Model Validation with Flight Test Data Using the Joint Input-Output Method. In Proceedings of the Vertical Flight Society’s 76th Annual Forum & Technology Display, Virginia Beach, VA, USA, 5–8 October 2020. [Google Scholar]
- Simmons, B.M.; McClelland, H.G.; Woolsey, C.A. Nonlinear Model Identification Methodology for Small, Fixed-Wing, Unmanned Aircraft. J. Aircr. 2019, 56, 1056–1067. [Google Scholar] [CrossRef]
- Dutra, D.A.A. Collocation-Based Output-Error Method for Aircraft System Identification. In Proceedings of the AIAA Aviation Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar]
- Mukhopadhaya, J.; Whitehead, B.T.; Quindlen, J.F.; Alonso, J.J. Multi-fidelity modeling of probabilistic aerodynamic databases for use in aerospace engineering. Int. J. Uncertain. Quantif. 2020, 10, 425–447. [Google Scholar] [CrossRef]
- Wang, Q.; Zheng, F.; Qian, W.; Ding, D. A practical filter error method for aerodynamic parameter estimation of aircraft in turbulence. Chin. J. Aeronaut. 2022, 36, 17–28. [Google Scholar] [CrossRef]
- Srivastava, A.; Kumar, A.; Ghosh, A.K. Determination of Parameters during Quasi-Steady Stall Maneuver Using Genetic Algorithm. Int. J. Aviat. Aeronaut. Space 2019, 6, 4. [Google Scholar]
- Zainuddin, F.A.; Samad, M.F.A. Crossover of genetic algorithm for linear and nonlinear system identification. In Proceedings of the Innovative Research and Industrial Dialogue, Melaka, Malaysia, 17 December 2020. [Google Scholar]
- Ordóñez, C.; Lasheras, F.S.; Roca-Pardiñas, J.; Juez, F.J.d.C. A hybrid ARIMA–SVM model for the study of the remaining useful life of aircraft engines. J. Comput. Appl. Math. 2019, 346, 184–191. [Google Scholar] [CrossRef]
- Gen, M.; Cheng, R. Genetic Algorithm and Engineering Optimization; Institute of Technology: Ashikaga, Japan, 2000. [Google Scholar]
- Fatima, S.K.; Abbas, S.M.; Mir, I.; Gul, F.; Forestiero, A. Flight Dynamics Modeling with Multi-Model Estimation Techniques: A Consolidated Framework. J. Electr. Eng. Technol. 2023, 18, 2371–2381. [Google Scholar] [CrossRef]
- Bagherzadeh, S.A. Flight dynamics modeling of elastic aircraft using signal decomposition methods. J. Aerosp. Eng. 2019, 233, 4380–4395. [Google Scholar] [CrossRef]
- Alessandrini, M.; Falaschetti, L.; Biagetti, G.; Crippa, P.; Turchetti, C. Nonlinear Dynamic System Identification in the Spectral Domain Using Particle-Bernstein Polynomials. Electronics 2022, 11, 3100. [Google Scholar] [CrossRef]
- Ram, P.R.M.; Römer, U.; Semaan, R. Bayesian Dynamical System Identification with Unified Sparsity Priors And Model Uncertainty. arXiv 2021, arXiv:2103.05090. [Google Scholar]
- Piga, D.; Breschi, V.; Bemporad, A. Estimation of Jump Box–Junction Models. Automatica 2020, 120, 109126. [Google Scholar] [CrossRef]
- Carr, J. 2014. An Introduction to Genetic Algorithms [Online]. Available online: https://www.whitman.edu.USA (accessed on 25 May 2024).
- Hamilton, J.; Wall, D.G.; Saddington, A.J.; Economou, J.T. Hypersurface normalised gain-scheduled controller for a non-linear 6-DOF fast jet. Aerosp. Sci. Technol. 2020, 106, 106155. [Google Scholar] [CrossRef]
- Rémy, P.; Hugo, G.; Ian, C.; Stephane, D.; Youssef, D.; Nathalie, B. An efficient application of Bayesian optimization to an industrial MDO framework for aircraft design. In Proceedings of the AIAA Aviation Forum, Virtual, 15–19 June 2020. [Google Scholar]
- Botero, E.M. Generative Bayesian Networks for Conceptual Aircraft Design. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2019. [Google Scholar]
- Kim, D.; Oh, H.S.; Moon, I.C. Black-box Modeling for Aircraft Maneuver Control with Bayesian Optimization. Int. J. Control Autom. Syst. 2019, 17, 1558–1568. [Google Scholar] [CrossRef]
- Saves, P.; Bartoli, N.; Diouane, Y.; Lefebvre, T.; Morlier, J. Constrained Bayesian Optimization over Mixed Categorical Variables, with Application to Aircraft Design. In Proceedings of the AeroBest, Lisbonne, Portugal, 21–23 July 2021. [Google Scholar]
- Scoggins, J.B.; Wignall, T.J.; Nakamura-Zimmerer, T.; Bibb, K. Multihierarchy Gaussian Process Models for Probabilistic Aerodynamic Databases using Uncertain Nominal and Off-Nominal Configuration Data. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023; NASA Langley Research Centre: Hampton, VA, USA, 2023. [Google Scholar]
- Napolitano, M.R. Aircraft Dynamics: From Modelling to Simulation; Scitus Academics LLC: Wilmington, DE, USA, 2012. [Google Scholar]
- Nguyen, L.T.E.A. Simulator Study of Stall/Post-Stall Characteristics of a Fighter Airplane with Relaxed Longitudinal Static Stability [F16]; NASA: Washington, DC, USA, 1979.
- F 16 Jet Design, Collimator. 2024. Designing an F 16 Fighter Jet [Online]. Available online: https://www.collimator.ai/tutorials/simulating-a-nonlinear-f16-model (accessed on 25 May 2024).
- Mohajerani, M.H. Frequency-Domain System Identification for Unmanned Helicopters from Flight Data. Master’s Thesis, Concordia University, Montreal, QC, Canada, 2014. [Google Scholar]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Muhammad, W.; Ahsan, A. Airship aerodynamic model estimation using unscented Kalman filter. J. Syst. Eng. Electron. 2020, 31, 1318–1329. [Google Scholar] [CrossRef]
- Rundel, M.C.M.Ç.-R.C.; Banks, D.; Chai, C.; Huang, L. An Introduction to Bayesian Thinking. A Companion to the Statistics with R Course; Taylor and Francis: Abingdon, UK, 2020. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Grauer, J.; Morelli, E. Method for real-time frequency response and uncertainty estimation. J. Guid. Control Dyn. 2014, 37, 336–344. [Google Scholar] [CrossRef]


| Ref. | Bayesian Methodology | Application |
|---|---|---|
| Herbert et al. [4] | Bayesian framework to estimate aerodynamic model parameters | Aircraft parameter estimation |
| Mukhopadhaya et al. [19] | Gaussian Process Regression, close to Bayesian estimation, for improvement of uncertainty of aerodynamic database | Aerodynamic Modelling using database |
| Rémy Priem et al. [32] | Using Bayesian approach for optimization in Aircraft design configurations | Aircraft Design Configurations |
| Emilio M. Botero [33] | Using Generative Bayesian Network for conceptual design of aircraft | Aircraft Design |
| Kim et al. [34] | Bayesian network optimization for data-driven controller of the aircraft using black box modelling | Data-driven controller design for aircraft maneuver |
| Paul Saves et al. [35] | Aircraft design optimization using Bayesian approach and Gaussian Process. | Aircraft Design |
| James et al. [36] | Mathematical framework for modelling probabilistic aerodynamic datasets using conditional coupled with Gaussian Processes | Aerodynamic Modelling |
| ] | |
|---|---|
| 1 to 3 | Not worth a bare mention |
| 3 to 20 | Positive |
| 20 to 150 | Strong |
| >150 | Very strong |
| Symbol | Value | Unit |
|---|---|---|
| b | 30 | ft |
| 11.32 | ft | |
| S | 300 | |
| W | 20,500 | Lbs |
| gd | 32.17 | |
| Vt | 502 | ft/s |
| h | 30 | ft |
| 300 | psf | |
| Xcg | ft | |
| Ixx | 9496 | |
| Iyy | 55,814 | |
| Izz | 63,100 | |
| Ixz | 982 |
| Symbol | Steady Straight and Level Flight | Coordinated Turn Flight | Unit |
|---|---|---|---|
| Vt | 502 | 502 | ft/s |
| h | 30 | 30 | ft |
| 300 | 300 | psf | |
| Xcg | ft | ||
| 0.03 | 0.24 | rad | |
| 0 | 0 | rad | |
| φ | 0 | 1.3 | rad |
| 0.15 | 0.05 | rad | |
| P | 0 | −0.01 | rad/s |
| Q | 0 | 0.29 | rad/s |
| R | 0 | 0.06 | rad/s |
| 0 | 0.15 | rad/s |
| Poles | Damping | Frequency (rad/s) | Time Constant (s) |
|---|---|---|---|
| −4.78 × 10−3 | 1.00 | 4.78 × 10−3 | 2.09 × 102 |
| −2.22 | 1.00 | 2.22 | 4.50 × 10−1 |
| −9.24 × 10−1 + 4.67i | 1.94 × 10−1 | 4.76 | 1.08 |
| −9.24 × 10−1 − 4.67i | 1.94 × 10−1 | 4.76 | 1.08 |
| Parameter Estimates and Errors | |||
|---|---|---|---|
| Parameters | NLS MSE: 9.3 × 10−2 % fit—87.99% | MLE MSE: 5.2 × 10−3 % fit—95.75% | Bayesian MSE: 3.9 × 10−3 % fit—96.25% |
| b1 | 1.2319 ± 0.5224 | 1.1129 ± 0.0113 | 1.1036 ± 0.0690 |
| b2 | −1.5237 ± 1.4569 | −0.6976 ± 0.2309 | −0.9870 ± 0.6327 |
| b3 | 0.6885 ± 0.2685 | 0.5832 ± 0.4312 | 0.6799 ± 0.5177 |
| b4 | −1.2097 ± 0.2557 | −1.1414 ± 0.6314 | −1.1567 ± 0.4477 |
| c1 | −0.5983 ± 0.3882 | −0.2188 ± 0.2424 | −0.3291 ± 0.3066 |
| d1 | 1.1822 ± 0.2840 | 0.5998 ± 0.32984 | 0.7939 ± 0.2365 |
| d2 | −0.3579 ± 0.2333 | −0.4501 ± 0.2069 | −0.3026 ± 0.1699 |
| d3 | 0.0206 ± 0.0841 | 0.0566 ± 0.0988 | 0.0716 ± 0.1455 |
| d4 | −0.7206 ± 0.1603 | −0.0619 ± 0.1422 | −0.0752 ± 0.1399 |
| f1 | −2.3801 ± 0.2184 | −1.444 ± 0.1977 | −1.3332 ± 0.2503 |
| f2 | 1.6348 ± 0.1954 | 1.5924 ± 0.3166 | 1.7412 ± 0.3417 |
| f3 | 0.2456 ± 0.1134 | 1.1868 ± 0.2959 | 1.1912 ± 0.2789 |
| f4 | −0.7353 ± 0.1399 | −0.8423 ± 0.0978 | −0.7926 ± 0.1255 |
| f5 | 0.2426 ± 0.2953 | −0.3576 ± 0.0463 | −0.3525 ± 0.0132 |
| Parameter Estimates and Errors | |||
|---|---|---|---|
| Parameters | NLS MSE: 0.2838 % fit—77.51% | MLE MSE: 0.1549 % fit—72.27% | Bayesian MSE: 0.1076 % fit—80.07% |
| b1 | −2.7703 ± 0.5224 | −2.6948 ± 0.6282 | −2.8416 ± 0.3352 |
| b2 | 2.0599 ± 1.4569 | 1.8639 ± 1.0505 | 1.2786 ± 0.8046 |
| c1 | −0.2802 ± 0.2685 | 0.0832 ± 0.4141 | 0.0058 ± 0.9224 |
| c2 | 0.1900 ± 0.2557 | 0.6910 ± 0.2599 | 0.7222 ± 0.2309 |
| c3 | −0.0267 ± 0.3882 | 0.7470 ± 0.3367 | 0.8252 ± 0.2990 |
| c4 | −0.8072 ± 0.2840 | −0.6734 ± 0.3529 | −0.6921 ± 0.2244 |
| c5 | 0.7626 ± 0.2333 | 0.7639 ± 0.1813 | 0.4692 ± 0.9028 |
| d1 | −1.3011 ± 0.0841 | −0.5260 ± 0.1892 | −0.7591 ± 0.8219 |
| d2 | 1.3436 ± 0.1603 | 1.3588 ± 0.2941 | 1.0851 ± 0.9780 |
| d3 | −1.0987 ± 0.2184 | −1.0939 ± 0.2717 | −0.9738 ± 0.4596 |
| d4 | 0.7316 ± 0.1954 | 0.8825 ± 0.2487 | 0.6657 ± 0.4727 |
| d5 | −0.1844 ± 0.1134 | −0.4063 ± 0.1648 | −0.0999 ± 0.2929 |
| f1 | 0.4115 ± 0.1399 | −1.1599 ± 0.3476 | −1.5465 ± 0.2038 |
| f2 | −1.8137 ± 0.2953 | 0.5206 ± 0.1862 | 0.4772 ± 0.1453 |
| f3 | 0.0845 ± 0.1730 | 0.0990 ± 0.0824 | 0.6454 ± 0.0428 |
| f4 | −0.2993 ± 0.0574 | −0.3032 ± 0.0737 | −0.2414 ± 0.0276 |
| f5 | 0.2120 ± 0.0577 | 0.2268 ± 0.0962 | 0.4398 ± 0.0652 |
| Parameter Estimates and Errors | |||
|---|---|---|---|
| Parameters | NLS MSE: 6.8 × 10−1 % fit—78.66% | MLE MSE: 1.3 × 10−1 % fit—80.75% | Bayesian MSE: 1.4 × 10−2 % fit—95.49% |
| b1 | −0.0399 ± 0.2376 | −0.2424 ± 0.2980 | −0.3906 ± 0.0531 |
| b2 | 0.3101 ± 0.1375 | 0.3612 ± 0.1519 | 0.1206 ± 0.2529 |
| c1 | −1.9760 ± 1.0797 | −1.9883 ± 0.7384 | −0.6182 ± 0.854 |
| c2 | 0.9760 ± 0.9234 | 0.9895 ± 1.2943 | 0.8582 ± 0.7253 |
| d1 | −0.8397 ± 0.2274 | −0.9174 ± 0.2912 | −2.5870 ± 1.212 |
| d2 | −0.4616 ± 0.5261 | −0.6852 ± 0.4727 | 2.3138 ± 2.3003 |
| d3 | 0.5737 ± 0.5613 | 0.8832 ± 0.3967 | −0.6969 ± 1.215 |
| f1 | −0.6638 ± 0.5958 | −1.5629 ± 0.3434 | −1.4591 ± 0.728 |
| f2 | −0.7063 ± 0.6085 | 0.3123 ± 0.9005 | 0.4699 ± 0.7319 |
| f3 | 0.4186 ± 0.4558 | 1.2015 ± 0.9578 | 1.1084 ± 0.1574 |
| f4 | 0.0585 ± 0.3124 | 0.1958 ± 0.8334 | 0.0446 ± 0.1438 |
| f5 | 0.2305 ± 0.3142 | 0.4038 ± 0.3982 | 0.0814 ± 0.1458 |
| Parameter Estimates and Errors | |||
|---|---|---|---|
| Parameters | NLS MSE: 4.4 × 10−2 % fit—82.93% | MLE MSE: 4.3 × 10−2 % fit—83.75% | Bayesian MSE: 3.9 × 10−2 % fit—85.49% |
| b1 | 0.6851 ± 0.0904 | −0.3410 ± 0.0980 | −0.3465 ± 0.0987 |
| b2 | −2.6887 ± 0.4530 | 0.3602 ± 0.1286 | 0.3642 ± 0.1184 |
| c1 | 2.4674 ± 0.6864 | −0.4502 ± 0.7700 | −0.6261 ± 0.863 |
| c2 | −0.7786 ± 0.2789 | 0.2385 ± 0.7396 | 0.3914 ± 0.8208 |
| d1 | −2.2853 ± 0.1387 | −1.6688 ± 0.6378 | −1.6878 ± 0.614 |
| d2 | 2.3718 ± 0.2871 | 1.4156 ± 1.0789 | 1.4251 ± 1.0266 |
| d3 | −1.3191 ± 0.2246 | −0.7082 ± 0.6029 | −0.7017 ± 0.5427 |
| f1 | 0.3695 ± 0.0686 | −1.9609 ± 0.3877 | −1.9085 ± 0.360 |
| f2 | −2.1439 ± 0.1189 | 1.2114 ± 0.5484 | 1.1118 ± 0.5213 |
| f3 | 2.1391 ± 0.2527 | −0.1710 ± 0.4755 | −0.1088 ± 0.484 |
| f4 | −1.0981 ± 0.2341 | 0.0248 ± 0.4961 | 0.0107 ± 0.502 |
| f5 | 0.1920 ± 0.1106 | −0.0220 ± 0.3423 | −0.0126 ± 0.344 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazhar, M.F.; Abbas, S.M.; Wasim, M.; Khan, Z.H. Bayesian Identification of High-Performance Aircraft Aerodynamic Behaviour. Aerospace 2024, 11, 960. https://doi.org/10.3390/aerospace11120960
Mazhar MF, Abbas SM, Wasim M, Khan ZH. Bayesian Identification of High-Performance Aircraft Aerodynamic Behaviour. Aerospace. 2024; 11(12):960. https://doi.org/10.3390/aerospace11120960
Chicago/Turabian StyleMazhar, Muhammad Fawad, Syed Manzar Abbas, Muhammad Wasim, and Zeashan Hameed Khan. 2024. "Bayesian Identification of High-Performance Aircraft Aerodynamic Behaviour" Aerospace 11, no. 12: 960. https://doi.org/10.3390/aerospace11120960
APA StyleMazhar, M. F., Abbas, S. M., Wasim, M., & Khan, Z. H. (2024). Bayesian Identification of High-Performance Aircraft Aerodynamic Behaviour. Aerospace, 11(12), 960. https://doi.org/10.3390/aerospace11120960








