Abstract
As the complexity of air gaming scenarios continues to escalate, the demands for heightened decision-making efficiency and precision are becoming increasingly stringent. To further improve decision-making efficiency, a particle swarm optimization algorithm based on positional weights (PW-PSO) is proposed. First, important parameters, such as the aircraft in the scenario, are modeled and abstracted into a multi-objective optimization problem. Next, the problem is adapted into a single-objective optimization problem using hierarchical analysis and linear weighting. Finally, considering a problem where the convergence of the particle swarm optimization (PSO) is not enough to meet the demands of a particular scenario, the PW-PSO algorithm is proposed, introducing position weight information and optimizing the speed update strategy. To verify the effectiveness of the optimization, a 6v6 aircraft gaming simulation example is provided for comparison, and the experimental results show that the convergence speed of the optimized PW-PSO algorithm is 56.34% higher than that of the traditional PSO; therefore, the algorithm can improve the speed of decision-making while meeting the performance requirements.
1. Introduction
With the increasing complexity of modern air gaming scenarios, air gaming has gradually become a diversified challenge covering multi-domain applications [1,2]. The collaborative gaming strategy, due to its significant cost-effectiveness, high flexibility and adaptability, and powerful information fusion capability, has firmly occupied the forefront of international research and strategic deployment [3,4,5]. In this context, cluster countermeasures, as an emerging and highly promising research trend [6,7,8,9], are gradually transitioning from being the subject of theoretical explorations to real-world applications. In a coordinated multi-target decision-making environment, air gaming decision-making is not only directly related to victory or defeat on the battlefield but also involves complex problems such as massive data processing, real-time situational assessment, and dynamic target allocation [10,11,12,13]. This means that traditional algorithms face great challenges in dealing with such problems and need to rely on more advanced artificial intelligence, machine learning, big data analysis, and other modern technological means to realize deep mining, intelligent analysis, and rapid decision-making using information.
By reviewing the related literature, it can be observed that when solving air gaming decision-making problems, numerous studies tend to use a single algorithm or fuse multiple algorithms. However, air gaming problems are highly specific, requiring a precise grasp of our needs and complex judgments regarding the position of the aircrafts, which increases the complexity of the problem. In view of this, this paper carries out an in-depth analysis of specific scenarios in the process of air gaming and unifies the criteria regarding the parameters of the decision-making method and the evaluation system. Through simulating an air gaming problem, a way to improve the algorithm is obtained. A set of reasonable air gaming simulation experiments is designed, and an accurate evaluation of the decision-making method can be realized.
Achieving more efficient real-time decision-making in the highly dynamic and changing air gaming environment remains a challenge. Considering the complexity of air gaming systems and the extremely high demands regarding reaction speed, this paper proposes an innovative position weight-based particle swarm optimization algorithm (PW-PSO), which retains the high decision-making accuracy of the traditional PSO algorithm. Through the introduction of position weight information, the velocity update strategy can be optimized. This optimization strategy can intelligently and dynamically adjust the search speed of particles according to the distance between the current decision and the global optimal solution, thus accelerating the convergence of the algorithm while ensuring the accuracy of the decision-making results, which provides a more efficient and reliable solution for decision-making during air gaming.
The following sections are structured as follows: Section 2 describes the related works. Section 3 describes the specific air gaming problem and applies the AHP method to assign weights to the indicators at each level. Section 4 provides an in-depth introduction to the principles and implementations of the PW-PSO algorithm. Section 5 comprehensively verifies the effectiveness and operational efficiency of the proposed PW-PSO algorithm through simulation experiments. Section 6 summarizes the research.
2. Related Works
In the complex battlefield environment of large-scale air gaming, the efficient assignment of tasks among aircrafts is particularly important. This is not only related to whether each aircraft can fully utilize its performance advantages but also directly affects the overall effectiveness during gaming [14,15,16,17]. Nantogma, S, constructed a strategy-generating agent based on learning classifier-inspired coordination mechanism, which was inspired by an artificial immune system, skillfully fusing the strengths of a learning classifier system and an artificial immune algorithm to achieve intelligent learning for combat threat assessment and weapon allocation [18]. Liu, S, on the other hand, applied the partial triangular fuzzy number method to accurately define the relative distance and angle of the missile ships as key parameters of their formation, and then proposed an adaptive algorithm that integrates simulated annealing and particle swarm optimization (SA-PSO), which effectively solves the optimization problem of missile formation [19]. In addition, Liang, Z. et al. innovatively proposed a distributed self-organizing CISCS strategy for the challenges in multi-unmanned-aerial-vehicle (UAV) cooperative operations, which integrates finite-time formation control, the distributed ant colony optimization task assignment based on improved Q-Learning, and real-time obstacle avoidance path planning, significantly improving the efficiency of cooperative reconnaissance and operations [20]. Li et al. proposed a constrained strategy game approach to generate intelligent decisions for multiple UCAVs in a complex air combat environment by utilizing situational air combat information and time-sensitive information, and proposed a constrained strategy game-solving algorithm based on linear programming and linear inequalities (CSG-LL) [21].
In the process of multi-aircraft collaborative decision-making, the establishment of an appropriate air gaming performance indicator model will directly affect the effectiveness, accuracy, and real-time abilities of the decision-making system [22,23]. FANG et al., in response to the insufficient objectivity in air warfare threat assessment indicators, proposed an empowerment method combining the Analytical Hierarchy Process (AHP) method and the CRITIC method, realizing the combined empowerment of threat assessment indicators by using the AHP method to synthesize the expert’s judgment of the indicator’s weights and then determining the linkage between the objective data according to the CRITIC method [24]. Zhang et al. proposed an air attack target threat metrics ranking method based on the fusion of entropy and the AHP method to solve the problem of strong subjectivity and stereotyped logic of ranking in the evaluation of the target threat during traditional air defense operations [25].
PSO algorithm [26], as a stochastic optimization method based on group intelligence, is known for its rapid computation and excellent optimization ability, and is widely used in various scenarios of air combat decision-making [27]. Ding, Y. et al. constructed an effectiveness evaluation model based on the PSO-BP neural network by combining the fuzzy analysis method and BP neural network in the field of unmanned-surface-vehicle cooperative combat effectiveness evaluation [28]. Cheng, Z. et al. used agent-based modeling technology to deeply analyze the structure and function of the ballistic missile defense system and successfully applied the PSO algorithm to construct a multi-agent decision support system containing missile agents [29]. Wu et al. proposed an improved PSO algorithm based on the Zaslavskii chaos. The Zaslavskii chaotic mapping formulation is used to generate chaotic sequences, which improves the inertia weights and random variables of the particle swarm algorithm for solving the path planning problem of unmanned combat aerial vehicles (UCAVs) in threatened battlefields [30]. Zhao et al. proposed the SHOPSO algorithm, which combines a selfish population optimizer (SHO) and a PSO to maximize and minimize the cost of UAVs to avoid enemy radar reconnaissance and artillery attacks [31].
3. A Model of the Air Gaming Decision Problem
3.1. Description of the Problem
In the decision-making process of the air game, the platforms of the two sides of the aircraft and the decision-making results are not a simple one-to-one correspondence; locking accuracy, both sides of the position, attitude, distance and other factors will affect the final gaming results. However, as simulations involve more factors, their implementation becomes more challenging, so this paper simplifies the decision-making problem by reducing the gaming scenario from three dimensions to two. Next, the factors affecting the results are identified through AHP, which can be used to calculate the probability of the opposing equipment locking on to our platform and the probability of our equipment successfully locking on to the opposing aircraft.
Assuming both the other side and we have N aircrafts, in a period, an aircraft can only launch one. is the success rate of the i-th aircraft lock on to the j-th opposing aircraft; the mission of the i-th aircraft is assigned to the j-th opposing aircraft, the probability of the j-th opposing aircraft surviving is . Correspondingly, the opposing aircraft can also use lock on us on our N aircrafts. is the success rate of the opposant’s i-th aircraft destroying our j-th target. represents the result of the decision of aircraft i against opposing aircraft j, where 0 means no action is taken and 1 means action is taken. Meanwhile, denotes the decision result of opposing aircraft locking on our aircraft under our judgment.
The success probability of all N aircrafts’ actions in concert for the opposant:
Correspondingly, in the case of an opposant’s action, the success probability of escape for our aircraft j is
Set the number of our aircrafts at 6 and the number of opposing aircrafts at 6. In this paper, we randomly generated the position and attitude of 12 air aircrafts within a 1000 × 1000 grid.
3.2. AHP-Based Constraint Establishment
Multi-aircraft air gaming has various attributes, a complex structure, and difficulties in quantitatively assessing the evaluation of the object. The aircraft launching an action must consider multiple factors, requiring a more comprehensive and specific approach to account for various elements. This ensures the authenticity of the experiment during the simulation process. Therefore, this paper chooses the AHP method to evaluate the factors that need to be considered for launching an action, determining the multi-level and multi-element constraints on the aircraft’s action evaluation.
The basic idea of the AHP method is to decompose the complex problem into various constituent factors, and then group the factors according to their dominant relationship to form a hierarchical structure. The relative importance of each factor in the hierarchy is determined by pairwise comparison, combining quantitative and qualitative analysis, using the experience of the decision-maker to judge the relative importance of each criterion for measuring whether the goal can be achieved, and reasonably giving the weight of each criterion for each decision-making scheme, and using the weights to find out the order of the scheme’s advantages and disadvantages.
3.2.1. Hierarchical Modeling
The multi-level structural model is constructed as shown in Figure 1. Among them, the target layer is the air gaming capability index, the criterion layer includes four items of the environment, aircraft flight performance, weapon system, and aircraft hardware performance, and the indicator layer covers three items of aircraft attack range D, aircraft detection range R and aircraft attack angle A. The action capability of the aircraft is also reflected through the above three indicators.
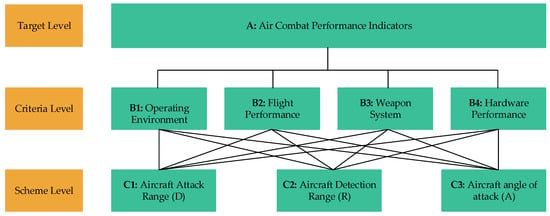
Figure 1.
Structural model for air gaming performance evaluation.
3.2.2. Judgment Matrix Construction
Two-by-two comparisons were made for each factor at the same level to assess their importance relative to specific criteria at the previous level. This process uses a 1–9 scale to quantitatively express the relative importance between factors, and a judgment matrix is constructed accordingly. The generation of the judgment matrix is based on expert evaluation, and sub-indicators are obtained for each assessment indicator, resulting in a matrix of assessment indicator values A. It is worth noting that the matrix A exhibits positive reciprocity, i.e., the elements in the matrix satisfy the following:
This characteristic ensures the consistency and rationality of the judgment matrix. The judgment matrices obtained in this paper are shown in Table A2 in Appendix A.
3.2.3. Calculation of Relative Weights of Elements
The square root method is a technical tool to compute the normalized relative importance vector of each element associated with a particular element in its upper layer. Specifically, the calculations are based on the following formula:
By applying this formula to the five judgment matrices constructed in Section 3.2.2, we can calculate the relative importance vectors corresponding to each judgment matrix. The results of the calculations are exhaustively organized and presented in Table A2 in Appendix A.
3.2.4. Consistency Test
In hierarchical analysis, consistency tests must be performed to verify the reasonableness and feasibility of the judgment matrix obtained. Two key indicators commonly used in this process are the consistency indicator (C.I.) and the consistency ratio (C.R.). The specific formulas for calculating these two indicators are as follows:
where denotes the i-th component of the vector AW.
In the hierarchical analysis method, the Random Index (R.I.) is used as the average random consistency indicator, and its value is given through Table A1 in Appendix A, which shows the average random consistency indicator from 1000 calculations based on the positive inverse matrices of order 1 to 14. Since R.I. represents the average level of the consistency indicator of the same-order stochastic judgment matrices, its introduction effectively mitigates the problem that the consistency judgment indicator may significantly increase as the matrix order n increases.
Eventually, the calculated C.R. values, are shown in Table A2 in Appendix A, all the listed C.R. values satisfy the criterion of less than 0.1. This result shows that the degree of inconsistency of the above judgment matrix is controlled within acceptable limits, thus validating the reasonableness and effectiveness of the judgment matrix.
Table 1 summarizes the results of the stratified analysis of the overall importance of the indicators:

Table 1.
Table of indicator weights.
Based on the table above, the importance weights for each of the three indicators in the indicator layer can be determined. Subsequently, when constructing the objective function, the weights assigned to these indicators will directly refer to the corresponding data in Table 1.
By using the AHP method, the factors influencing the success or failure of an aircraft action and the corresponding weights are determined, in which the relationship between the parameters of the aircraft attack range D, the angle of the opposing aircraft relative to us A, and the detection range R of the aircraft is shown in Figure 2.
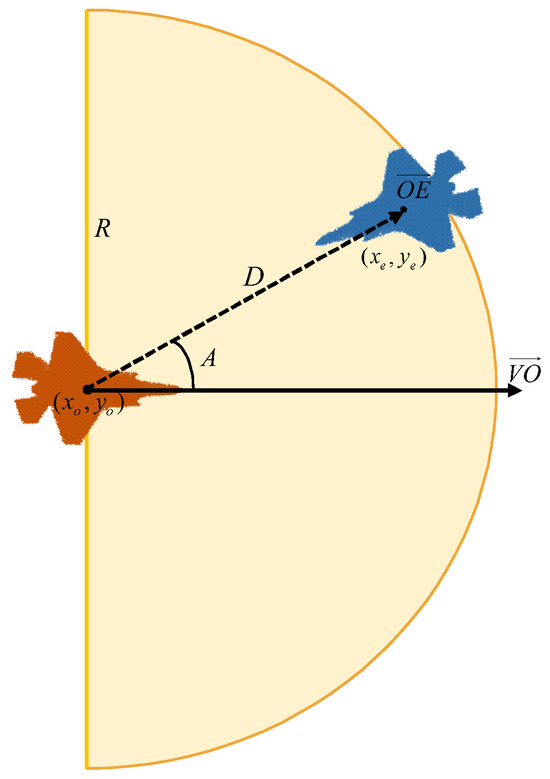
Figure 2.
Schematic diagram of indicator parameters.
In the above figure, orange aircraft indicates our aircraft, blue indicates opposing aircraft, and yellow areas indicate the attackable range of our aircraft. is the direction vector of our aircraft, is the vector of the opposing aircraft relative to our aircraft, D is the distance of the opposing aircraft relative to our aircraft, and R is the detection range of our aircraft. The angle at which our aircraft can action includes only 180° in front of the aircraft. Only when the distance of the enemy aircraft relative to our aircraft is less than the detection range R of our aircraft and the angle of the opposing aircraft relative to our aircraft is within the detection range of our aircraft:
In addition, since an aircraft can select only one opposing aircraft in an operation, no more than N actions are made by all the aircraft of our team in an operation and no more than 1 action is made by one aircraft:
The constraints generated are based on a combination of the aircraft’s current relevant information and the action constraints set by the weapon system, as described in the previous section.
3.3. Objective Function
In the air gaming problem, the main task is to eliminate the maximum loss to us from the target, i.e., to ensure the maximum damage to the opposant while minimizing the loss to ourselves. Firstly, in terms of ensuring the maximum loss to the opposant from our side, the assignment is expressed by the formula:
And in terms of ensuring that we minimize the loss incurred to our side, the assignment is expressed as follows:
The main point of importance is to decide which opposing aircraft to attack by judging their loss value to us. If the opposant’s aircraft is not within our action range, then takes the maximum value of the opposant’s threat to our aircraft.
The air gaming decision-making problem is a multi-objective function problem, which is simplified and solved using a particle swarm algorithm. In this paper, we use the linear weighted sum method to simplify the two objective functions, set the weight coefficients according to the importance of the two objective functions, and set the weight coefficient of the objective function (11) to be , and the weight coefficient of the objective function (12) to be . Then, the objective function can be simplified into
The primary purpose of the air gaming decision is to inflict damage on the enemy; therefore, the initialization sets the weight coefficients and .
4. Particle Swarm Algorithm Based on Position Weight Velocity Update Strategy
4.1. Particle Swarm Algorithm (PSO)
The PSO algorithm is an intelligent optimization algorithm inspired by the foraging behavior of bird flocks. In this algorithm, a population of randomly distributed particles is first initialized, with each particle representing a potential solution to the problem. Subsequently, each particle dynamically adjusts its flight speed and position based on its own historical best position (the individual optimal solution) as well as the global best position (the global optimal solution) discovered by the entire flock so far. This adjustment mechanism enables the particles to efficiently search for and approximate the optimal solution in the solution space.
The updating of position and velocity in particle swarm algorithms usually follows the following formula:
where is the velocity of particle i at the t-th iteration on dimension d; is the inertia weight, which is used to control the degree of inheritance of the particle’s velocity; and are the learning factors, that regulate the step size of the particle’s leaning towards the individual optimum and global optimum; is the individual optimal position; is the value of the global optimal position on dimension d; is the position of particle i at the t-th iteration on dimension d.
By iteratively performing the above velocity and position updating process, the particle swarm algorithm can induce the entire population of particles to gradually converge to or approach the optimal solution region of the problem.
When dealing with large-scale complex problems, PSO often experiences high consumption of computational resources and takes a long time to explore and converge to the optimal solution. However, a common challenge in the process of approximating the optimal solution is the rapid slowdown of the particles or the limitation of the updating mechanism, which may weaken the fineness of the search and make it difficult for the algorithm to pinpoint the globally optimal solution accurately. To overcome this challenge, this paper innovatively proposes a velocity updating strategy based on position weights, aiming to improve the search precision and efficiency of the algorithm.
4.2. Speed Update Strategy Based on Positional Weights (PW-PSO)
To achieve a more rapid and accurate judgment of strategies in an intense air gaming environment, we have targeted and optimized the velocity update mechanism in the particle swarm algorithm. By incorporating a position weight parameter into the velocity update formula, we provide the algorithm with a kind of intelligent adjustment capability: when the decision judged by a particle (potential strategy) is at a large distance from the optimal decision, the parameter will automatically increase, prompting the particle to accelerate in the optimal direction to quickly narrow the gap; when the decision is close to the optimal solution, the weight will be reduced accordingly, slowing down the speed of the particle, making the search process more detailed and avoiding missing potential better solutions near the optimal solution.
According to the idea of the dynamic adjustment of the speed of the decision and the distance from the optimal solution, this design, in which the position weight parameter is introduced, adds the parameter r and weight, and updates the speed formula, which will be adjusted as follows:
The main steps of the proposed PW-PSO method are as Algorithm 1, where eval is the number of times the function is evaluated and MaxEval is the maximum number of times the function is evaluated.
| Algorithm 1: PW-PSO-based air gaming decision-making |
| Begin |
| for each particle i do: |
| Randomly initialize the position ; |
| Randomly initialize the velocity ; |
| Calculate fitness value EFFECT(); |
| Set individual optimal position ; |
| Set the global optimal position as the position of the particle with the best fitness value among all ; |
| while eval ≤ MaxEval do |
| if r < 0.6 then |
| for each particle i do |
| Update the velocity according Equation (16); |
| Update position according to Equation (15); |
| Calculate the fitness value; |
| eval++; |
| end for |
| else |
| for each particle i do |
| Update the velocity according Equation (14); |
| Update position according to Equation (15); |
| Calculate the fitness value; |
| eval++; |
| end for |
| end if |
| Update the and in the population; |
| end while |
| End |
5. Simulation Analysis
This paper takes the two-dimensional static multi-objective air gaming decision-making problem as the research object, establishes a mathematical model, and formulates an objective function according to the two directions of maximizing the action effect of our side and minimizing the loss level of the opposant; and applies the linear weight method to simplify the multi-objective function into a single objective function. According to the constraints, the objective function is corrected in the process of randomly generating the initial solution to make it conform to the constraints, and the PW-PSO is utilized for the solution calculation. Moreover, under the same conditions, the problem is solved using the original PSO algorithm, and the two are compared and analyzed to observe the capability enhancement effect of the PW-PSO algorithm. The computer configuration chosen for the experiment was equipped with an Intel(R) Core(TM) i5-10400F CPU running Windows 10 operating system, and MATLAB 2022a was used as the experimental software.
5.1. Randomized Parameter Setting
Within the framework of the simulation experiments in this paper, the pre-positional attitude information is obtained by random generation. For the position information part, the x and y coordinates are randomly selected within a wide range of [0, 1000] to simulate different spatial positions. The angle A, as the angle between the direction towards which the aircraft is facing and the x-axis, has a value randomly determined within a complete circle of [0, 360] degrees, as shown in the representation below. In the experiment, we recorded the specific data generated randomly once, as shown in Table 2.

Table 2.
Aircraft position attitude numeric.
Converting the data in Table 2 into a graphical representation, we can visualize the 2D planar position map of the aircraft, as shown in Figure 3. In this figure, the orange markers represent the position and attitude of our aircraft, while the blue markers indicate position and orientation of the opposing aircraft.
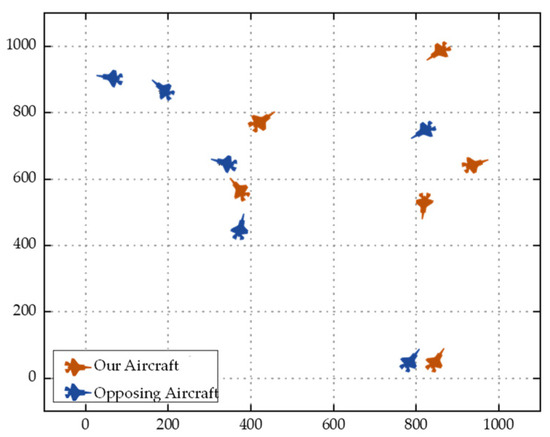
Figure 3.
Aircraft 2D positional attitude map.
5.2. Results and Analysis
Based on the position and attitude information obtained in the previous section, combined with the constraints defined in Section 3 and the designed fitness function, four optimization algorithms, namely genetic algorithm (GA) [32], PSO algorithm, adaptive particle swarm algorithm (Adaptive-PSO) [33], and PW-PSO, were selected for the experiments in this study. All the algorithms reached the same maximum value of 1.10301 in the experiments. To further evaluate the accuracy and stability of these algorithms, each algorithm independently conducted 100 repetitions of the experiments for the purpose of counting the number of times that each of them reached the known maximum value. Based on the results of these experiments, the accuracy assessment of each algorithm is shown in Figure 4.
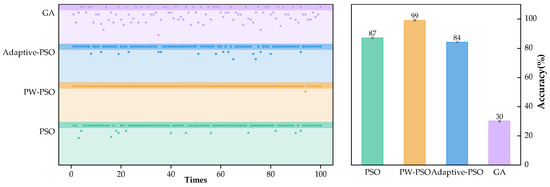
Figure 4.
Algorithm accuracy comparison.
As can be obtained from Figure 4, the accuracy of experiments using PSO and its two improved versions (Adaptive-PSO and PW-PSO) both exceeded 80%, demonstrating the superior performance of the PSO and its variants in dealing with the specific problem. In contrast, the GA exhibited a lower accuracy of 30%, indicating that the GA may not be the best choice in this application scenario. In light of these results, the following section focuses on more in-depth experiments with these three high-performing PSO to explore and compare their convergence rates.
Comparative experiments of the three PSO algorithms were conducted to obtain Figure 5 and Figure 6. Figure 5 shows the fitness function curves of the three algorithms during one of the experiments. Figure 6 shows a box plot of the number of generations of convergence of the three algorithms after 100 experiments on the three algorithms.
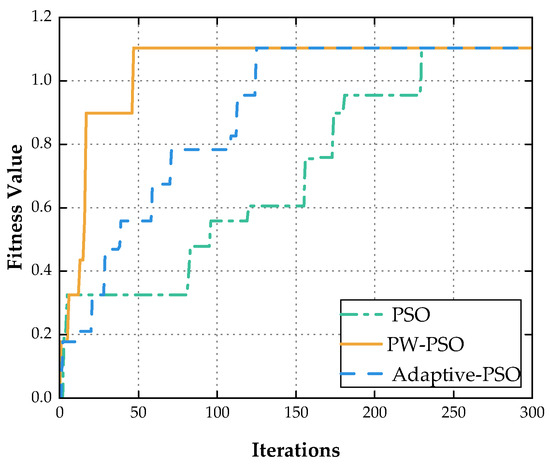
Figure 5.
Comparison plot of fitness function curves.
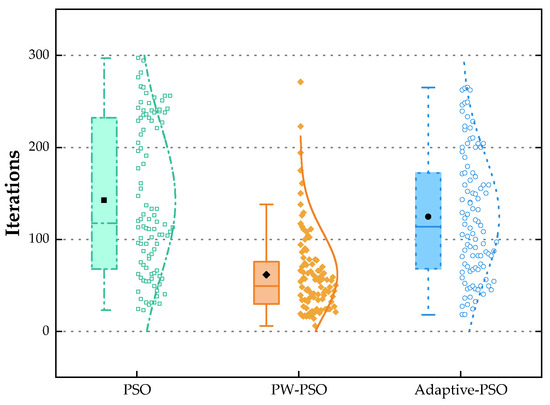
Figure 6.
Convergence algebra comparison.
From Figure 5 and Figure 6, it is obvious that the distribution of convergence generations of the PSO algorithm is broader, mainly focusing on the range of 0 to 300 iterations, showing greater volatility, and the average number of convergent generations of the algorithm is about 142 times. In contrast, the Adaptive-PSO algorithm shows improvement in convergence speed, and its average number of convergent generations is reduced to about 124, indicating that the adaptive mechanism helps to accelerate the convergence process of the algorithm.
The PW-PSO algorithm shows a significant improvement in convergence speed, and most of its convergent generations are concentrated in the smaller range of 0 to 100 iterations, with an average number of convergent generations of 62 approximately. This result indicates that the convergence speed of the PSO algorithm is improved by introducing the position weighting mechanism to optimize the PSO algorithm, which can significantly improve the convergence performance and stability.
In addition, to comprehensively evaluate the performance of the three algorithms, the key indexes of the algorithms, such as the success rate, the average convergence value, and the average number of convergence generations, are counted and summarized in Table 3.

Table 3.
Summary of experimental results data.
The PW-PSO algorithm performs well in 100 independent experiments, with 80 experiments converging significantly faster than the PSO algorithm, which proves the significant improvement of PW-PSO in convergence efficiency. In addition, the experimental success rate of PW-PSO is as high as 98%, which is not only much higher than the 87% of PSO but also higher than the 84% of Adaptive-PSO, which demonstrates its high stability and reliability.
Further analysis of the average convergence value and the variance of the convergence value reveals that PW-PSO also shows advantages in precision and accuracy, outperforming both PSO and Adaptive-PSO. This indicates that PW-PSO can not only converge quickly in the process of searching for the optimal solution, but also approach the true optimal value with higher precision, reducing the volatility and error of the results.
In particular, the average number of convergence generations of PW-PSO is only 62, which is a significant reduction compared to 142 generations of PSO and 124 generations of Adaptive-PSO. The 56.34% improvement in the number of convergence generations for PW-PSO compared to PSO is a figure that intuitively reflects the dramatic improvement in the convergence speed of the algorithm.
In summary, the PW-PSO algorithm outperforms the traditional PSO and Adaptive-PSO algorithms in several aspects such as convergence speed, success rate, precision, and accuracy.
6. Conclusions
With the increasing complexity of air gaming scenarios, more stringent requirements are imposed on the efficiency and accuracy of the decision-making process. To effectively deal with this challenge, this paper innovatively proposes PW-PSO. The algorithm first extracts and models the key parameters of the aircraft and environment in air gaming, and transforms them into a complex multi-objective optimization problem. Subsequently, the multi-objective problem is successfully transformed into a more manageable single-objective optimization problem by skillfully applying hierarchical analysis and linear weighting techniques. To address the shortcoming of the traditional PSO algorithm’s insufficient convergence speed in air gaming scenarios, the PW-PSO algorithm achieves a significant improvement in the performance through the introduction of the concept of positional weights and the optimization speed update mechanism. To verify this optimization result, we designed a 6v6 air gaming simulation scenario for comparison experiments. The experimental data clearly show that, compared to the traditional PSO algorithm, the convergence speed of the PW-PSO algorithm is improved by 56.34%, and at the same time, the decision-making process is significantly accelerated under the premise of satisfying the performance constraints, which lays a solid foundation for the efficient execution of air gaming decisions.
Although the PW-PSO algorithm shows significant advantages in convergence speed and stability, it may still fall into a local optimal solution under specific situations. Furthermore, when applying the PW-PSO algorithm to actual air gaming decision-making scenarios, it is necessary to consider numerous practical variables, including the dynamic changes in the environment and the differences in the performance of equipment, etc., which may limit the application of the algorithm to a certain extent. The limitations in the above two areas are also directions for further improvement of the algorithm.
For the limitations of the PW-PSO algorithm, the algorithm can be further optimized in the future to improve its efficiency and accuracy in dealing with complex problems. For the problem of falling into local optimal solutions, more advanced parameter tuning methods can be explored to reduce the dependence on parameter settings and improve the global search capability of the algorithm. To overcome the challenge of limited complex scenarios, more complex simulation scenarios can be designed to consider more practical factors in order to evaluate the performance of the algorithm more comprehensively.
Author Contributions
Conceptualization, all authors; methodology, A.X. and Y.H.; software, A.X.; investigation, Y.H. and G.L.; resources, H.L.; writing—original draft preparation, A.X.; writing—review and editing, G.L.; project administration, H.L.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (52102453), the Natural Science Foundation of Sichuan Province (2022NSFSC0037, 2024NSFSC0021), the Sichuan Science and Technology Programs (MZGC20230069), the Fundamental Research Funds for the Central Universities (ZYGX2023K025, ZYGX2024K028).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data in our paper are included within the article.
Conflicts of Interest
All the authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendix A
This appendix exhaustively describes the steps of air gaming effectiveness indicator assessment using the hierarchical analysis method and is accompanied by empirical data from practical applications. Among them, Table A1 specifically lists the average stochastic consistency index values of the positive reciprocal inverse matrices of order 1 to 14; while Table A2 demonstrates the construction of the A-B and B-C judgment matrices at two levels and their subsequent processing.

Table A1.
Average random consistency indicator.
Table A1.
Average random consistency indicator.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R.I. | 0 | 0 | 0.52 | 0.89 | 1.12 | 1.26 | 1.36 | 1.41 | 1.46 | 1.49 | 1.52 | 1.54 | 1.56 | 1.58 |

Table A2.
A-B and B-C two-level judgment matrices and processing.
Table A2.
A-B and B-C two-level judgment matrices and processing.
| A | B1 | B2 | B3 | B4 | |||||
| B1 | 1 | 1/2 | 1/3 | 1/4 | 0.452 | 0.097 | 4.104 | ||
| B2 | 2 | 1 | 1/2 | 1/3 | 0.759 | 0.164 | 4.078 | ||
| B3 | 3 | 2 | 1 | 2 | 1.861 | 0.401 | 4.226 | ||
| B4 | 4 | 3 | 1/2 | 1 | 1.565 | 0.338 | 4.205 | ||
| B1 | C1 | C2 | C3 | ||||||
| C1 | 1 | 1/3 | 2 | 0.874 | 0.230 | 3.002 | |||
| C2 | 3 | 1 | 5 | 2.466 | 0.648 | 3.004 | |||
| C3 | 1/2 | 1/5 | 1 | 0.464 | 0.122 | 3.005 | |||
| B2 | C1 | C2 | C3 | ||||||
| C1 | 1 | 1/3 | 1/5 | 0.406 | 0.105 | 3.036 | |||
| C2 | 3 | 1 | 1/3 | 1.000 | 0.258 | 3.040 | |||
| C3 | 5 | 3 | 1 | 2.466 | 0.637 | 3.040 | |||
| B3 | C1 | C2 | C3 | ||||||
| C1 | 1 | 7 | 3 | 2.759 | 0.682 | 3.003 | |||
| C2 | 1/7 | 1 | 1/2 | 0.415 | 0.103 | 3.003 | |||
| C3 | 1/3 | 2 | 1 | 0.874 | 0.215 | 3.002 | |||
| B4 | C1 | C2 | C3 | ||||||
| C1 | 1 | 3 | 2 | 1.817 | 0.540 | 3.009 | |||
| C2 | 1/3 | 1 | 1/2 | 0.550 | 0.163 | 3.010 | |||
| C3 | 1/2 | 2 | 1 | 1.000 | 0.297 | 3.008 | |||
References
- Xue, S.; Wang, Z.; Bai, H.; Yu, C.; Deng, T.; Sun, R. An Intelligent Bait Delivery Control Method for Flight Vehicle Evasion Based on Reinforcement Learning. Aerospace 2024, 11, 653. [Google Scholar] [CrossRef]
- Karali, H.; Inalhan, G.; Tsourdos, A. Advanced UAV Design Optimization Through Deep Learning-Based Surrogate Models. Aerospace 2024, 11, 669. [Google Scholar] [CrossRef]
- Li, S.; Wang, Y.; Zhou, Y.; Jia, Y.; Shi, H.; Yang, F.; Zhang, C. Multi-UAV Cooperative Air Combat Decision-Making Based on Multi-Agent Double-Soft Actor-Critic. Aerospace 2023, 10, 574. [Google Scholar] [CrossRef]
- Tian, C.; Song, M.; Tian, J.; Xue, R. Evaluation of Air Combat Control Ability Based on Eye Movement Indicators and Combination Weighting GRA-TOPSIS. Aerospace 2023, 10, 437. [Google Scholar] [CrossRef]
- Wang, L.; Wang, J.; Liu, H.; Yue, T. Decision-Making Strategies for Close-Range Air Combat Based on Reinforcement Learning with Variable-Scale Actions. Aerospace 2023, 10, 401. [Google Scholar] [CrossRef]
- Dong, P.; Chen, W.; Wang, K.; Zhou, K.; Wang, W. Research on Combat Mission Configuration of Unmanned Aerial Vehicle Maritime Reconnaissance Based on Particle Swarm Optimization Algorithm. Complexity 2024, 2024, 1–12. [Google Scholar] [CrossRef]
- Khelifi, M.; Butun, I. Swarm Unmanned Aerial Vehicles (SUAVs): A Comprehensive Analysis of Localization, Recent Aspects, and Future Trends. J. Sens. 2022, 2022, 8600674. [Google Scholar] [CrossRef]
- Mcgrew, J.S.; How, J.P.; Williams, B.; Roy, N. Air-Combat Strategy Using Approximate Dynamic Programming. J. Guid. Control Dyn. 2010, 33, 1641–1654. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Y.; Sun, M.; Chen, Z. Air Combat Maneuver Decision Based on Deep Reinforcement Learning with Auxiliary Reward. Neural Comput. Appl. 2024, 36, 13341–13356. [Google Scholar] [CrossRef]
- Xing, D.; Zhen, Z.; Gong, H. Offense-Defense Confrontation Decision Making for Dynamic UAV Swarm versus UAV Swarm. Proc. Inst. Mech. Eng. 2019, 233, 5689–5702. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, Q.; Shi, G.; Yi, L.; Yong, W. UAV Cooperative Air Combat Maneuver Decision Based on Multi-Agent Reinforcement Learning. J. Syst. Eng. Electron. 2021, 32, 18. [Google Scholar]
- You, H. Mission-Driven Autonomous Perception and Fusion Based on UAV Swarm. Chin. J. Aeronaut. 2020, 33, 2831–2834. [Google Scholar]
- Guo, J.; Hu, G.; Guo, Z.; Zhou, M. Evaluation Model, Intelligent Assignment, and Cooperative Interception in Multimissile and Multitarget Engagement. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3104–3115. [Google Scholar] [CrossRef]
- Li, W. Autonomous Maneuver Decision of Air Combat Based on Simulated Operation Command and FRV-DDPG Algorithm. Aerospace 2022, 9, 658. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Sun, C.; Ru, C. Intelligent Maneuver Decision Method of UAV Based on Reinforcement Learning and Neural Network. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 8544–8549. [Google Scholar]
- Jia, L.; Cai, C.; Wang, X.; Ding, Z.; Xu, J.; Wu, K.; Liu, J. Multi-Intent Autonomous Decision-Making for Air Combat with Deep Reinforcement Learning. Appl. Intell. 2023, 53, 29076–29093. [Google Scholar] [CrossRef]
- Dou, X.; Tang, G.; Zheng, A.; Wang, H.; Liang, X. Research on Autonomous Decision-Making in Manned/Unmanned Coordinated Air Combat. In Proceedings of the 2023 9th International Conference on Control, Automation and Robotics (ICCAR), Beijing, China, 21 April 2023; pp. 170–178. [Google Scholar]
- Nantogma, S.; Xu, Y.; Ran, W.Z. A Coordinated Air Defense Learning System Based on Immunized Classifier Systems. Symmetry 2021, 13, 271. [Google Scholar] [CrossRef]
- Liu, S.; Huang, F.; Yan, B.; Zhang, T.; Liu, R.; Liu, W. Optimal Design of Multimissile Formation Based on an Adaptive SA-PSO Algorithm. Aerospace 2022, 9, 21. [Google Scholar] [CrossRef]
- Liang, Z.; Li, Q.; Fu, G. Multi-UAV Collaborative Search and Attack Mission Decision-Making in Unknown Environments. Sensors 2023, 23, 7398. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Chen, M.; Wang, Y.; Wu, Q. Air Combat Decision-Making of Multiple UCAVs Based on Constraint Strategy Games—ScienceDirect. Def. Technol. 2022, 18, 16. [Google Scholar]
- Yin, H.; Li, D.; Li, Y.W. Adaptive Dynamic Occupancy Guidance for Air Combat of UAV. Unmanned Syst. 2024, 12, 29–46. [Google Scholar] [CrossRef]
- Ren, Z.; Zhang, D.; Tang, S.; Xiong, W.; Yang, S.H. Cooperative Maneuver Decision Making for Multi-UAV Air Combat Based on Incomplete Information Dynamic Game. Def. Technol. 2023, 27, 308–317. [Google Scholar] [CrossRef]
- Fang, C.; Kou, Y.; Xu, A.; Deng, S.; Peng, M. A VIKOR Method for Threat Assessment in Air Combat Based on AHP-CRITIC Combination Weighting. Electron. Opt. Control 2021, 28, 24–28. [Google Scholar]
- Zhang, Y.; Yang, G.; Meng, H.; Wang, R.; Qi, B. Threat measurement and sequencing of air raid targets based on entropy method fused with AHP. J. Telem. Track. Command. 2020, 41, 57–64. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the Icnn95-international Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Sun, B.; Zeng, Y.; Zhu, D. Dynamic Task Allocation in Multi Autonomous Underwater Vehicle Confrontational Games with Multi-Objective Evaluation Model and Particle Swarm Optimization Algorithm. Appl. Soft Comput. 2024, 153, 111295. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, C.; Lu, Q.; Zhu, M. Effectiveness Evaluation of UUV Cooperative Combat Based on GAPSO-BP Neural Network. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 4620–4625. [Google Scholar]
- Cheng, Z.; Fan, L.; Zhang, Y. Multi-agent decision support system for missile defense based on improved PSO algorithm. J. Syst. Eng. Electron. 2017, 28, 514–525. [Google Scholar]
- Wu, P.; Li, T.; Song, G. UCAV Path Planning Based on Improved Chaotic Particle Swarm Optimization. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 1069–1073. [Google Scholar]
- Zhao, R.; Wang, Y.; Xiao, G.; Liu, C.; Hu, P.; Li, H. A Method of Path Planning for Unmanned Aerial Vehicle Based on the Hybrid of Selfish Herd Optimizer and Particle Swarm Optimizer. Appl. Intell. Int. J. Artif. Intell. Neural Netw. Complex. Probl.-Solving Technol. 2022, 52, 16775–16798. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Zhan, Z.H.; Zhang, J.; Li, Y.; Chung, H.S.-H. Adaptive Particle Swarm Optimization. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2009, 39, 1362–1381. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).