Adaptive Robust Time-Varying Formation Control of Quadrotors under Switching Topologies: Theory and Experiment
Abstract
:1. Introduction
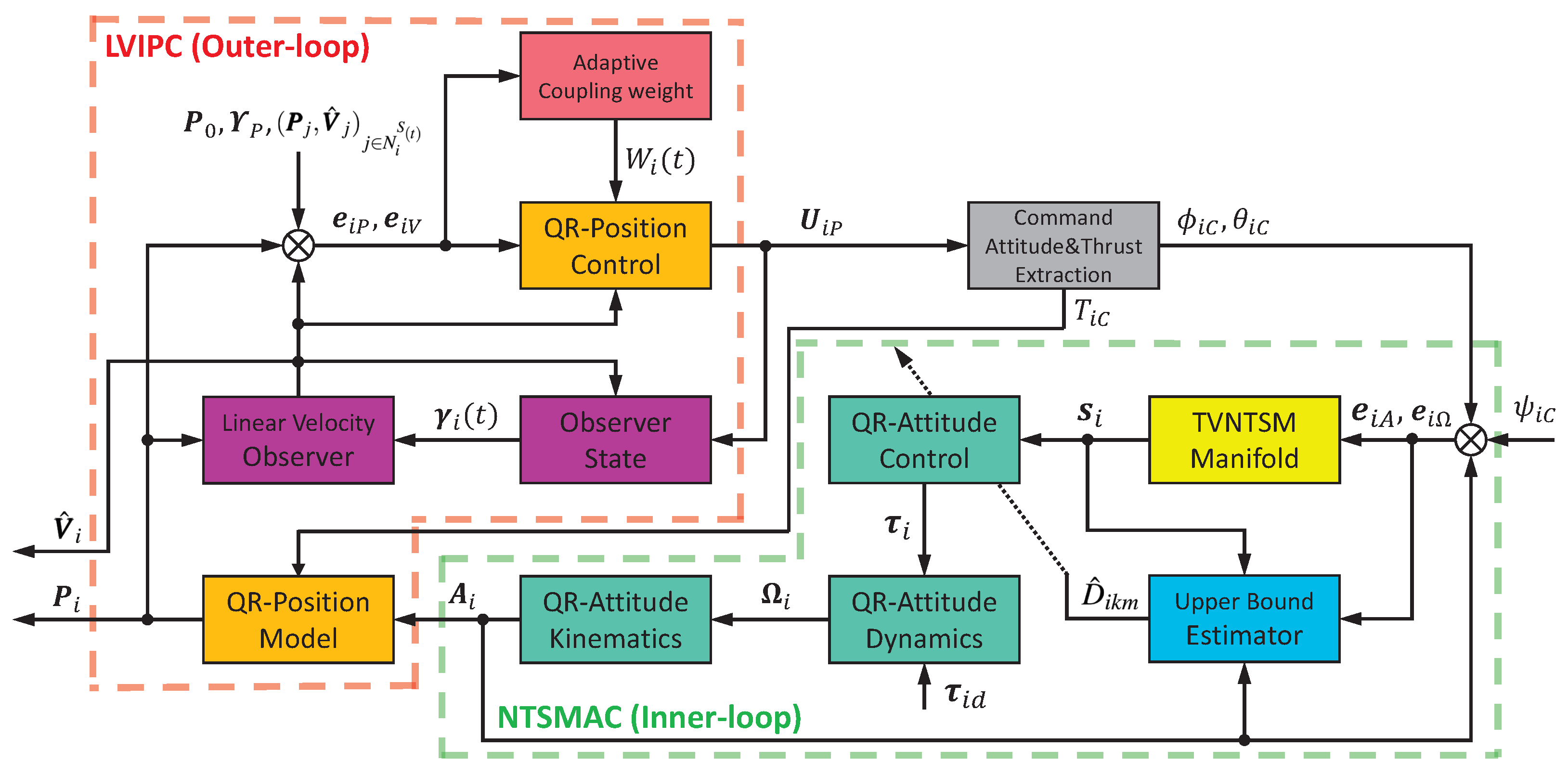
- In terms of theory, firstly, for easy application, adaptive laws were adopted to remove the reliance on the prior knowledge of the unknown upper bound of lumped uncertainties. Secondly, the TVNTSM manifold was designed to suppress the impact of the reaching phase on system robustness and guarantee the convergence of the system state in adjustable finite time, thereby improving practicality. Thirdly, distributed observers were employed to eliminate the measurement of linear velocity, with the possibility of realizing formation control without any global topology information, thereby making it fully distributed. Fourthly, both formation pattern and directed topology could be dynamically adjusted, making it suitable for scenarios such as target enclosing, area coverage, and target tracking.
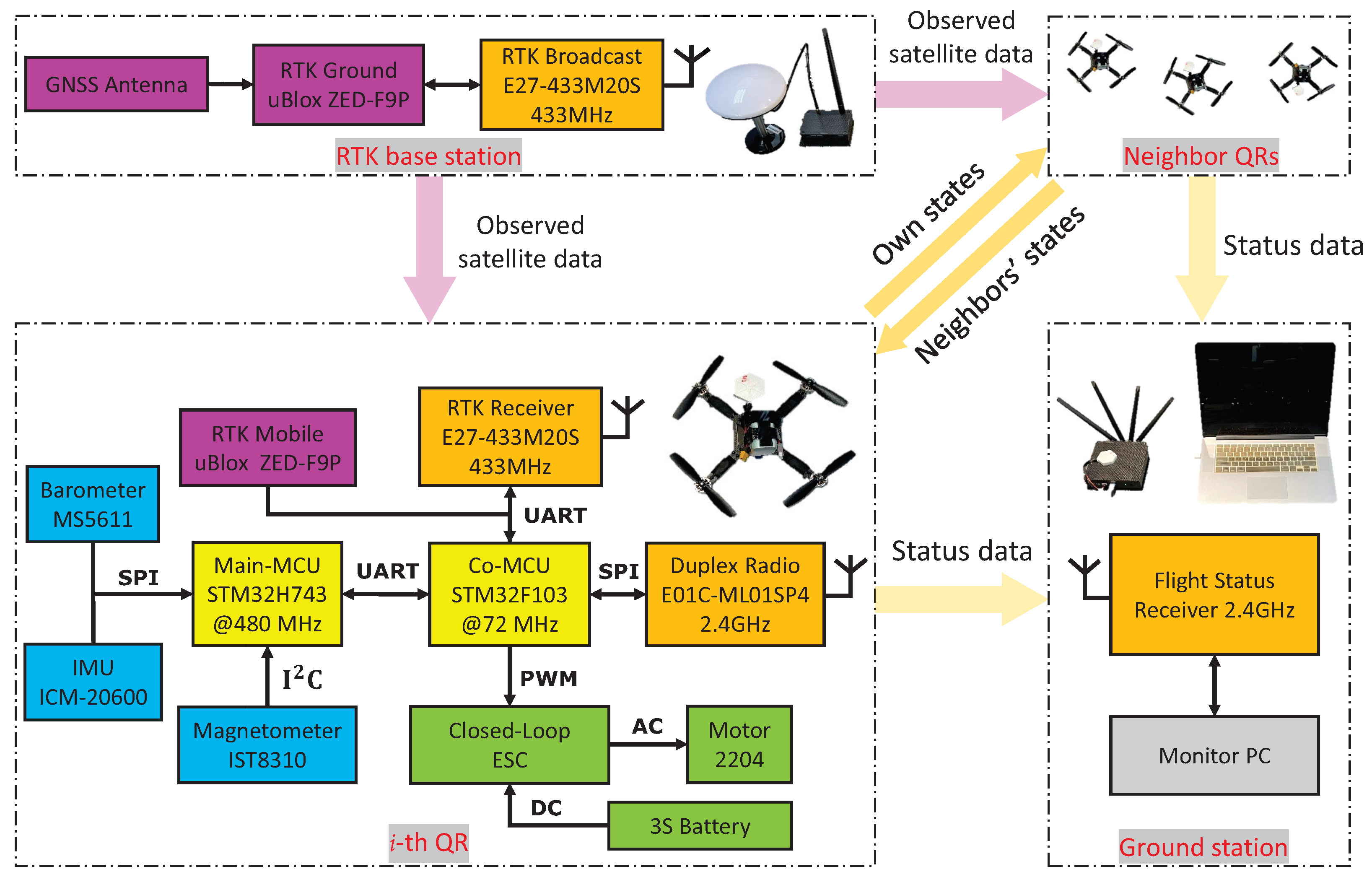
- In terms of application, this study differs from most previous research that only conducted experimental verification in ideal indoor environments based on motion capture or UWB positioning. Instead, an outdoor scheme was designed for this study, with all QRs flying in natural disturbed environments. Their positions were provided by the RTK system in accordance with actual working conditions. In addition, unlike most previous research that relied on a robot operating system (ROS) with high hardware requirements or Wi-Fi with a limited range to establish the interconnection of UAVs, this paper utilized bi-directional wireless modules to build the QR network, such that total control could be achieved through micro control unit (MCU)-based hardware solutions, which is currently the mainstream solution used in the drone industry.
2. Preliminaries and Problem Formulation
2.1. Notations
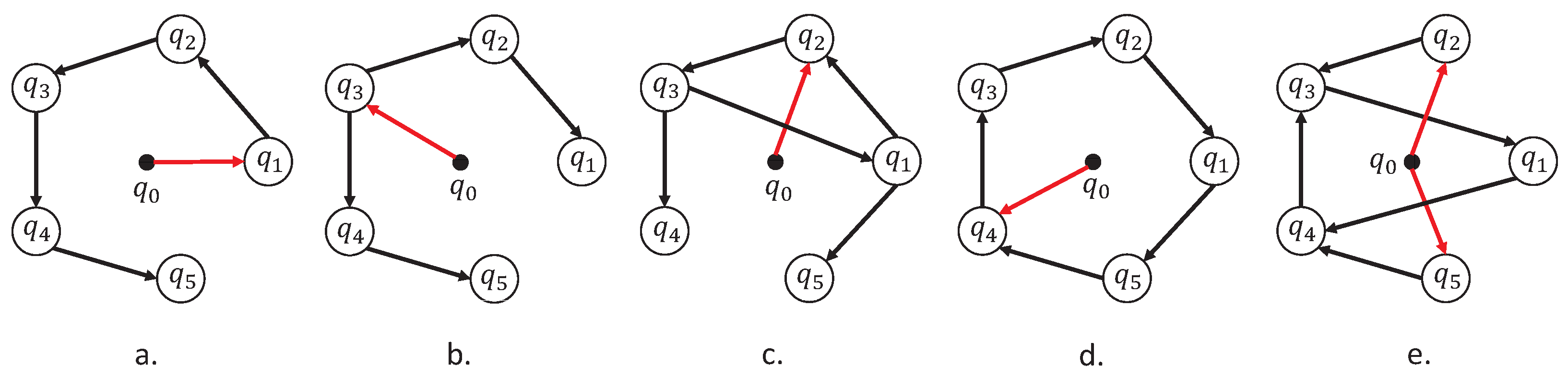
2.2. Graph Theory
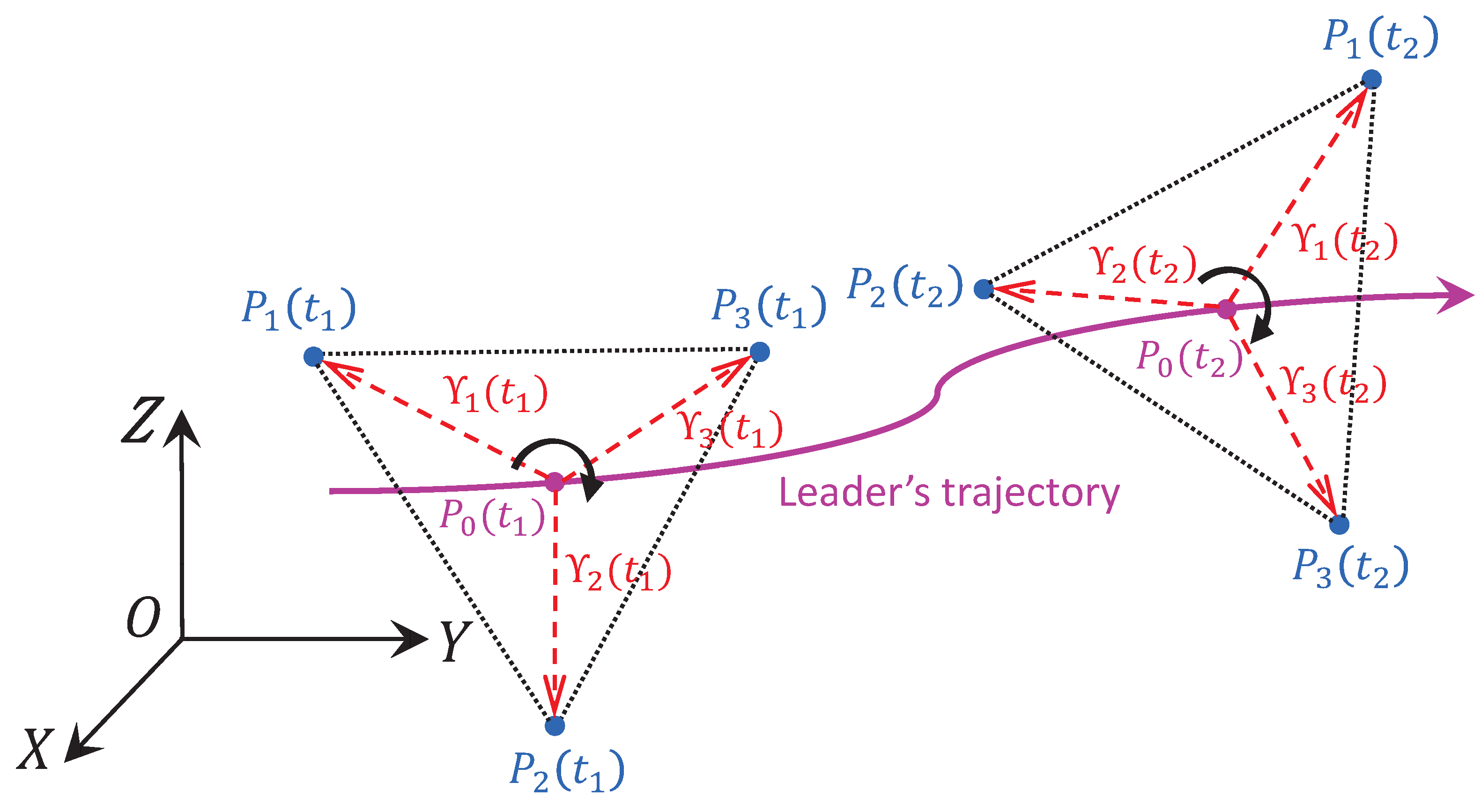
2.3. Problem Formulation
2.4. Control Objective
- The QR’s formation pattern and directed topology can be dynamically adjusted under the fully distributed TVFC protocol;
- The measurement and transmission of the QR’s linear-velocity can be eliminated by distributed observers;
- The influence of the reaching phase can be suppressed by adopting TVNTSM, and the finite convergence time of the attitude tracking error can be adjusted;
- The reliance on the prior knowledge of the unknown upper bound of lumped uncertainty can be removed by adaptive laws.
3. Main Results
3.1. Design of LVIPC
3.2. Design of NTSMAC
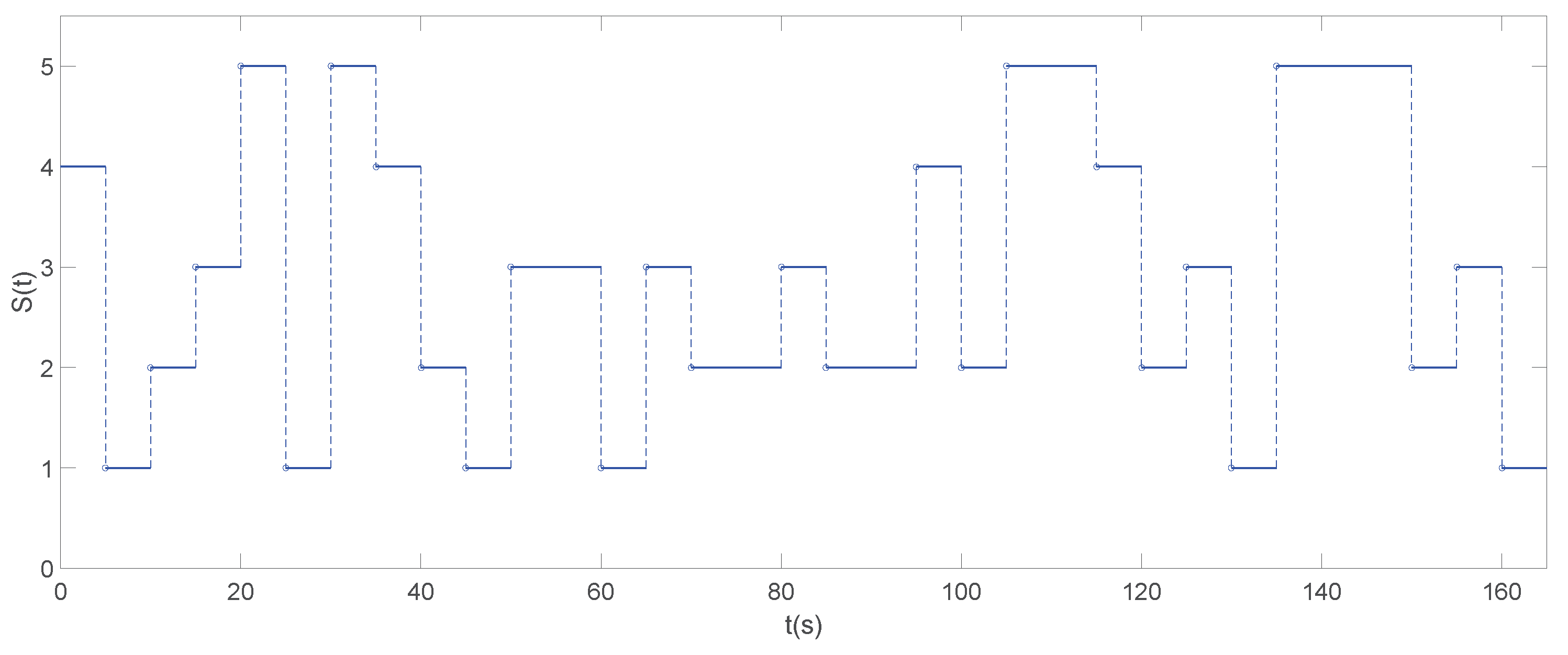
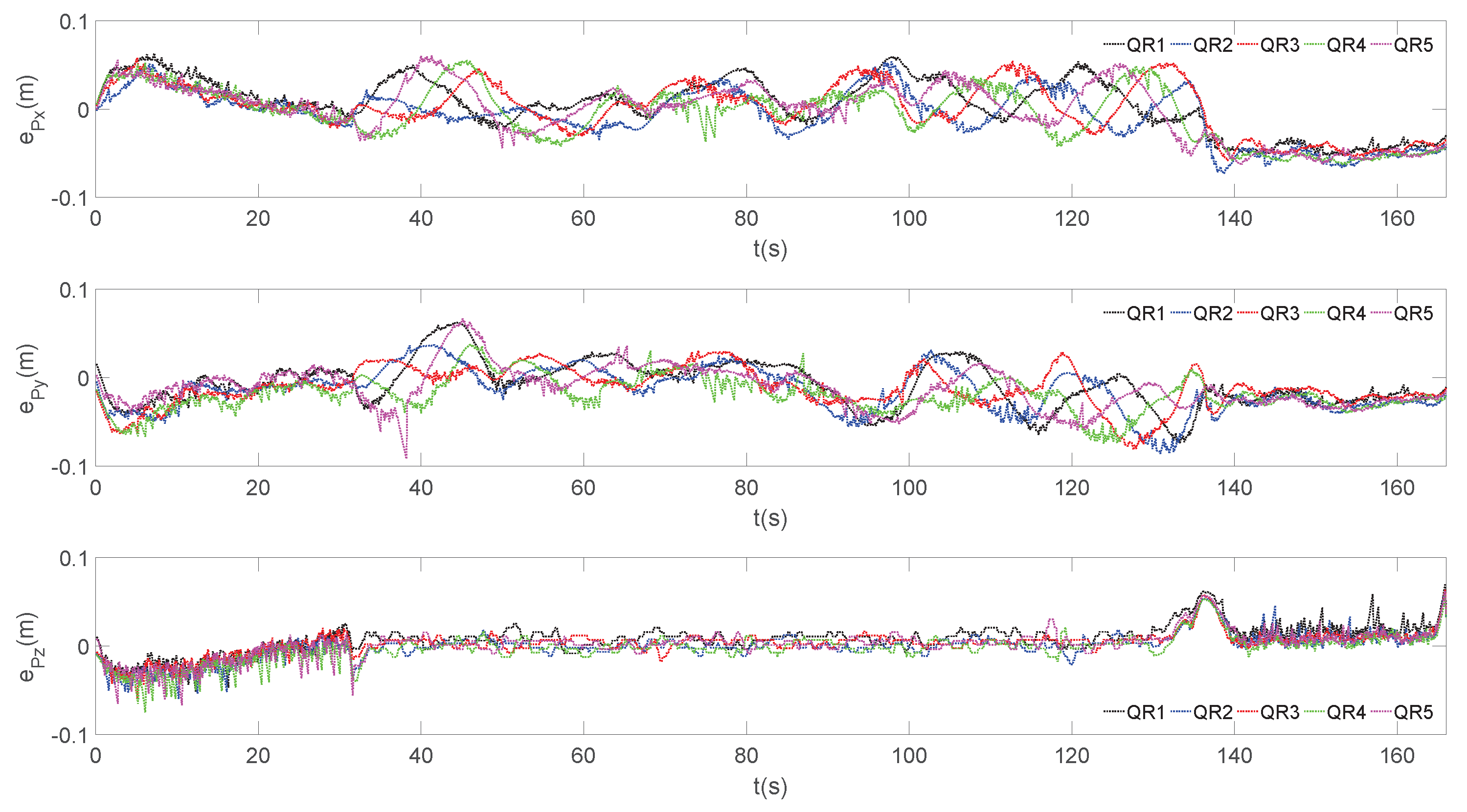
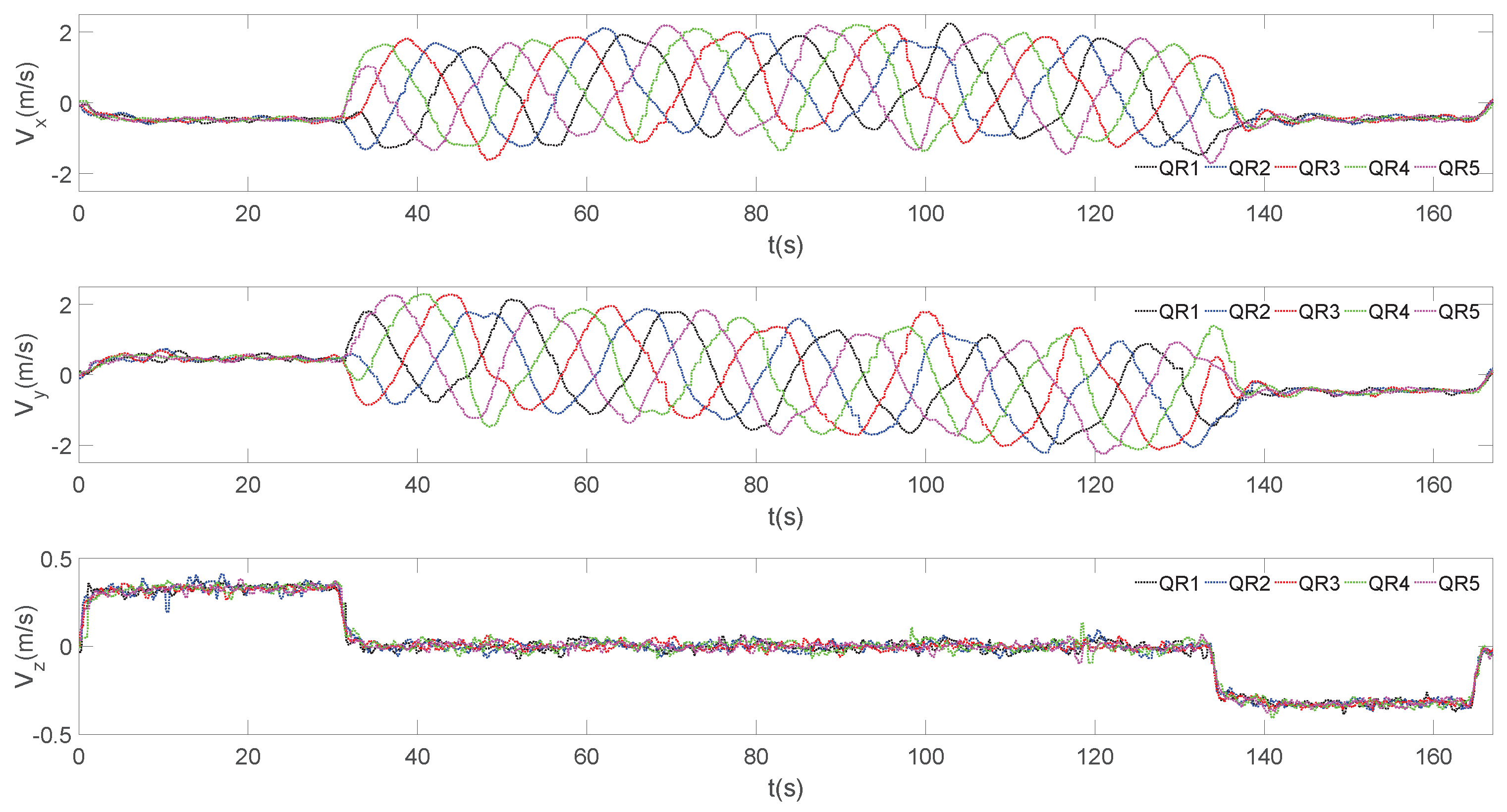
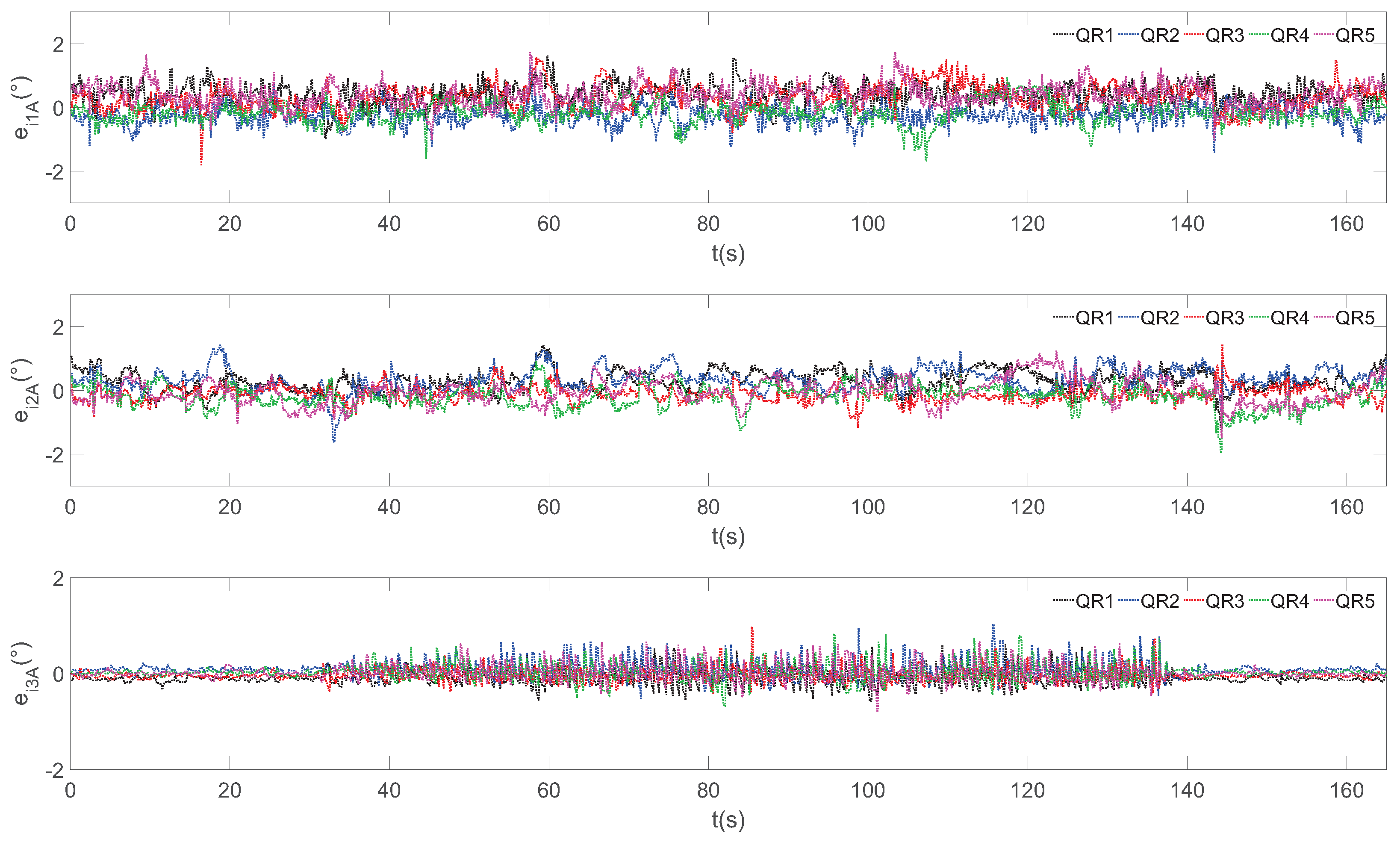
4. Experiment Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raja, G.; Baskar, Y.; Dhanasekaran, P.; Nawaz, R.; Yu, K. An Efficient Formation Control mechanism for Multi-UAV Navigation in Remote Surveillance. In Proceedings of the 2021 IEEE Globecom Workshops (GC Wkshps), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Pan, Z.; Zhang, C.; Xia, Y.; Xiong, H.; Shao, X. An Improved Artificial Potential Field Method for Path Planning and Formation Control of the Multi-UAV Systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1129–1133. [Google Scholar] [CrossRef]
- Xie, Y.; Han, L.; Dong, L.; Li, Q.; Ren, Z. Bio-inspired adaptive formation tracking control for swarm systems with application to UAV swarm systems. Neurocomputing 2021, 453, 272–285. [Google Scholar] [CrossRef]
- Idrissi, M.; Salami, M.; Annaz, F. A Review of Quadrotor Unmanned Aerial Vehicles: Applications, Architectural Design and Control Algorithms. J. Intell. Robot. Syst. 2022, 104, 22. [Google Scholar] [CrossRef]
- Zhao, Z.; Zheng, Z.; Zhu, M.; Wu, Z. Adaptive fault tolerant attitude tracking control for a quadrotor with input saturation and full-state constraints. In Proceedings of the 2017 13th IEEE International Conference on Control & Automation (ICCA), Ohrid, Macedonia, 3–6 July 2017; pp. 46–51. [Google Scholar]
- Pounds, P.; Mahony, R.; Corke, P. Modelling and control of a large quadrotor robot. Eng. Pract. 2010, 18, 691–699. [Google Scholar] [CrossRef]
- Guo, J.; Qi, J.; Wang, M.; Wu, C.; Ping, Y.; Li, S.; Jin, J. Collision-free formation tracking control for multiple quadrotors under switching directed topologies: Theory and experiment. Aerosp. Sci. Technol. 2022, 131, 108007. [Google Scholar] [CrossRef]
- Mechali, O.; Xu, L. Distributed fixed-time sliding mode control of time-delayed quadrotors aircraft for cooperative aerial payload transportation: Theory and practice. Adv. Space Res. 2023, 71, 3897–3916. [Google Scholar] [CrossRef]
- Wang, J.; Bi, C.; Wang, D.; Kuang, Q.; Wang, C. Finite-time distributed event-triggered formation control for quadrotor UAVs with experimentation. ISA Trans. 2022, 126, 585–596. [Google Scholar] [CrossRef]
- Mechali, O.; Xu, L.; Xie, X.; Iqbal, J. Theory and practice for autonomous formation flight of quadrotors via distributed robust sliding mode control protocol with fixed-time stability guarantee. Control Eng. Pract. 2022, 123, 105150. [Google Scholar] [CrossRef]
- Yang, K.; Dong, W.; Tong, Y.; He, L. Leader-follower Formation Consensus of Quadrotor UAVs Based on Prescribed Performance Adaptive Constrained Backstepping Control. Int. J. Control Autom. Syst. 2022, 20, 3138–3154. [Google Scholar] [CrossRef]
- Koksal, N.; An, H.; Fidan, B. Backstepping-based adaptive control of a quadrotor UAV with guaranteed tracking performance. ISA Trans. 2020, 105, 98–110. [Google Scholar] [CrossRef]
- Baek, J.; Kang, M. A Synthesized Sliding-Mode Control for Attitude Trajectory Tracking of Quadrotor UAV Systems. IEEE/ASME Trans. Mechatron. 2023, 28, 2189–2199. [Google Scholar] [CrossRef]
- Hegde, N.T.; George, V.I.; Nayak, C.G.; Vaz, A.C. Application of robust H-infinity controller in transition flight modeling of autonomous VTOL convertible Quad Tiltrotor UAV. Int. J. Intell. Unmanned Syst. 2021, 9, 204–235. [Google Scholar] [CrossRef]
- Azar, A.T.; Serrano, F.E.; Koubaa, A.; Kamal, N.A. Backstepping H-Infinity Control of Unmanned Aerial Vehicles with Time Varying Disturbances. In Proceedings of the 2020 First International Conference of Smart Systems and Emerging Technologies (SMARTTECH), Riyadh, Saudi Arabia, 3–5 November 2020; pp. 243–248. [Google Scholar]
- Chen, F.; Jiang, R.; Zhang, K.; Jiang, B.; Tao, G. Robust Backstepping Sliding-Mode Control and Observer-Based Fault Estimation for a Quadrotor UAV. IEEE Trans. Ind. Electron. 2016, 63, 5044–5056. [Google Scholar] [CrossRef]
- Razmi, H.; Afshinfar, S. Neural network-based adaptive sliding mode control design for position and attitude control of a quadrotor UAV. Aerosp. Sci. Technol. 2019, 91, 12–27. [Google Scholar] [CrossRef]
- Hamadi, H.; Lussier, B.; Fantoni, I.; Francis, C.; Shraim, H. Observer-based Super Twisting Controller Robust to Wind Perturbation for Multirotor UAV. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; pp. 397–405. [Google Scholar]
- Tian, B.; Cui, J.; Lu, H.; Liu, L.; Zong, Q. Attitude control of UAVs based on event-triggered supertwisting algorithm. IEEE Trans. Ind. Inform. 2020, 17, 1029–1038. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, J.; She, H.; Jin, H. Quadrotor UAV flight control via a novel saturation integral backstepping controller. Automatika 2019, 60, 193–206. [Google Scholar] [CrossRef]
- Liu, W.; Cheng, X.; Zhang, J. Command filter-based adaptive fuzzy integral backstepping control for quadrotor UAV with input saturation. J. Frankl. Inst. 2023, 360, 484–507. [Google Scholar] [CrossRef]
- John, M.; David, W.L. Output feedback sliding mode control in the presence of unknown disturbances. Syst. Control Lett. 2009, 58, 188–193. [Google Scholar]
- Fei, J.; Ding, H. Adaptive sliding mode control of dynamic system using RBF neural network. Nonlinear Dyn. 2012, 70, 1563–1573. [Google Scholar] [CrossRef]
- Mofid, O.; Mobayen, S.; Zhang, C.; Esakki, B. Desired tracking of delayed quadrotor UAV under model uncertainty and wind disturbance using adaptive super-twisting terminal sliding mode control. ISA Trans. 2022, 123, 455–471. [Google Scholar] [CrossRef]
- Ghadiri, H.; Emami, M.; Khodadadi, H. Adaptive super-twisting non-singular terminal sliding mode control for tracking of quadrotor with bounded disturbances. Aerosp. Sci. Technol. 2021, 112, 106616. [Google Scholar] [CrossRef]
- Lian, S.; Meng, W.; Lin, Z.; Shao, K.; Zheng, J.; Li, H.; Lu, R. Adaptive Attitude Control of a Quadrotor Using Fast Nonsingular Terminal Sliding Mode. IEEE Trans. Ind. Electron. 2022, 69, 1597–1607. [Google Scholar] [CrossRef]
- Hassani, H.; Mansouri, A.; Ahaitouf, A. Robust autonomous flight for quadrotor UAV based on adaptive nonsingular fast terminal sliding mode control. Int. J. Dyn. Control 2021, 9, 619–635. [Google Scholar] [CrossRef]
- Bartoszewicz, A.; Nowacka-Leverton, A. SMC without the reaching phase–the switching plane design for the third-order system. IET Control Theory Appl. 2007, 1, 1461–1470. [Google Scholar] [CrossRef]
- Al-khazraji, A.; Essounbouli, N.; Hamzaoui, A.; Nollet, F.; Zaytoon, J. Type-2 fuzzy sliding mode control without reaching phase for nonlinear system. Eng. Appl. Artif. Intell. 2011, 24, 23–38. [Google Scholar] [CrossRef]
- Nechadi, E.; Harmas, M.N.; Hamzaoui, A.; Essounbouli, N. A new robust adaptive fuzzy sliding mode power system stabilizer. Int. J. Electr. Power Energy Syst. 2012, 42, 1–7. [Google Scholar] [CrossRef]
- González-Sierra, J.; Ríos, H.; Dzul, A. Quad-rotor robust time-varying formation control: A continuous sliding-mode control approach. Int. J. Control 2020, 93, 1659–1676. [Google Scholar] [CrossRef]
- Dey, S.; Giri, D.K.; Gaurav, K.; Laxmi, V. Robust nonsingular terminal sliding mode attitude control of satellites. J. Aerosp. Eng. 2021, 34, 06020003. [Google Scholar] [CrossRef]
- Wang, J.; Du, J.; Li, J. Distributed finite-time velocity-free robust formation control of multiple underactuated AUVs under switching directed topologies. Ocean Eng. 2022, 266, 112967. [Google Scholar] [CrossRef]
- Wang, W.; Huang, J.; Wen, C.; Fan, H. Distributed adaptive control for consensus tracking with application to formation control of nonholonomic mobile robots. Automatica 2014, 50, 1254–1263. [Google Scholar] [CrossRef]
- Wu, Z.; Guan, Z.; Wu, X.; Li, T. Consensus Based Formation Control and Trajectory Tracing of Multi-Agent Robot Systems. J. Intell. Robot. Syst. 2007, 48, 397–410. [Google Scholar] [CrossRef]
- Garcia-Aunon, P.; Roldán, J.J.; Barrientos, A. Monitoring traffic in future cities with aerial swarms: Developing and optimizing a behavior-based surveillance algorithm. Cogn. Syst. Res. 2019, 54, 273–286. [Google Scholar] [CrossRef]
- Hacene, N.; Mendil, B. Behavior-based Autonomous Navigation and Formation Control of Mobile Robots in Unknown Cluttered Dynamic Environments with Dynamic Target Tracking. Int. J. Autom. Comput. 2021, 18, 766–786. [Google Scholar] [CrossRef]
- Low, C.B. A dynamic virtual structure formation control for fixed-wing UAVs. In Proceedings of the 2011 9th IEEE International Conference on Control and Automation (ICCA), Santiago, Chile, 19–21 December 2011; pp. 627–632. [Google Scholar]
- Askari, A.; Mortazavi, M.; Talebi, H.A. UAV formation control via the virtual structure approach. Int. J. Autom. Comput. 2015, 28, 04014047. [Google Scholar] [CrossRef]
- Chen, F.; Dimarogonas, D.V. Leader–follower formation control with prescribed performance guarantees. IEEE Trans. Control Netw. Syst. 2020, 8, 450–461. [Google Scholar] [CrossRef]
- Liu, W.; Wang, X.; Li, S. Formation Control for Leader–Follower Wheeled Mobile Robots Based on Embedded Control Technique. IEEE Trans. Control Syst. Technol. 2022, 31, 265–280. [Google Scholar] [CrossRef]
- Jin, X.; Che, W.; Wu, Z.; Deng, C. Robust adaptive general formation control of a class of networked quadrotor aircraft. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 7714–7726. [Google Scholar] [CrossRef]
- Yan, D.; Zhang, W.; Chen, H. Design of a Multi-Constraint Formation Controller Based on Improved MPC and Consensus for Quadrotors. Aerospace 2022, 9, 94. [Google Scholar] [CrossRef]
- Li, Q.; Chen, Y.; Liang, K. Predefined-time formation control of the quadrotor-UAV cluster’position system. Appl. Math. Model. 2023, 116, 45–64. [Google Scholar] [CrossRef]
- Yue, X.; Shao, X.; Zhang, W. Elliptical encircling of quadrotors for a dynamic target subject to aperiodic signals updating. IEEE Trans. Intell. Transp. Syst. 2021, 23, 14375–14388. [Google Scholar] [CrossRef]
- Elmokadem, T. Distributed coverage control of quadrotor multi-UAV systems for precision agriculture. IEEE Trans. Intell. Transp. Syst. 2019, 52, 251–256. [Google Scholar] [CrossRef]
- Kang, Y.; Luo, D.; Xin, B.; Cheng, J.; Yang, T.; Zhou, S. Robust Leaderless Time-Varying Formation Control for Nonlinear Unmanned Aerial Vehicle Swarm System with Communication Delays. IEEE Trans. Cybern. 2022, 53, 5692–5705. [Google Scholar] [CrossRef] [PubMed]
- Ajwad, S.A.; Moulay, E.; Defoort, M.; Menard, T.; Coirault, P. Distributed time-varying formation tracking of multi-quadrotor systems with partial aperiodic sampled data. Nonlinear Dyn. 2022, 108, 2263–2278. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhu, M.; Zhang, X. Target Enclosing and Coverage Control for Quadrotors with Constraints and Time-Varying Delays: A Neural Adaptive Fault-Tolerant Formation Control Approach. Sensors 2022, 22, 7497. [Google Scholar] [CrossRef] [PubMed]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Ullah, N.; Mehmood, Y.; Aslam, J.; Wang, S.; Phoungthong, K. Fractional order adaptive robust formation control of multiple quad-rotor UAVs with parametric uncertainties and wind disturbances. Chin. J. Aeronaut. 2022, 35, 204–220. [Google Scholar] [CrossRef]
- Steinleitner, A.; Ballam, R.; McFadyen, A. Practical consensus-based formation control for quadrotor systems. In Proceedings of the 2022 International Conference on Unmanned Aircraft Systems (ICUAS), Dubrovnik, Croatia, 21–24 June 2022; pp. 1510–1519. [Google Scholar]
- Mechali, O.; Xu, L.; Xie, X. Nonlinear homogeneous sliding mode approach for fixed-time robust formation tracking control of networked quadrotors. Aerosp. Sci. Technol. 2022, 126, 107639. [Google Scholar] [CrossRef]
- Xu, W.; He, W.; Ho, D.W.; Kurths, J. Fully distributed observer-based consensus protocol: Adaptive dynamic event-triggered schemes. Automatica 2022, 139, 110188. [Google Scholar] [CrossRef]
- Wang, H.; Shan, J. Fully Distributed Event-Triggered Formation Control for Multiple Quadrotors. IEEE Trans. Ind. Electron. 2023, 70, 12566–12575. [Google Scholar] [CrossRef]
- Cheng, M.; Tian, Y.; Liu, H.; Li, J. Fully Distributed Time-Varying Formation Control of Quadrotors. In Proceedings of the 2022 International Conference on Guidance, Navigation and Control, Harbin, China, 5–7 August 2022; pp. 1–6. [Google Scholar]
- Huang, Y.; Meng, Z. Bearing-based distributed formation control of multiple vertical take-off and landing UAVs. IEEE Trans. Control Netw. Syst. 2021, 8, 1281–1292. [Google Scholar] [CrossRef]
- Matouk, D.; Gherouat, O.; Abdessemed, F.; Hassam, A. Quadrotor position and attitude control via backstepping approach. In Proceedings of the International Conference on Modelling, Identification and Control (ICMIC), Algiers, Algeria, 15–17 November 2016; pp. 73–79. [Google Scholar]
- Bhatia, A. Matrix Analysis, 3rd ed.; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2001; pp. 168–174. [Google Scholar]
- Ma, Z.; Sun, G. Dual terminal sliding mode control design for rigid robotic manipulator. J. Frankl. Inst. 2018, 355, 9127–9149. [Google Scholar] [CrossRef]
- Zhao, D.; Li, S.; Gao, F. A new terminal sliding mode control for robotic manipulators. Int. J. Control 2009, 82, 1804–1813. [Google Scholar] [CrossRef]
- Yao, Q. Adaptive finite-time sliding mode control design for finite-time fault-tolerant trajectory tracking of marine vehicles with input saturation. J. Frankl. Inst. 2020, 357, 13593–13619. [Google Scholar] [CrossRef]
- Bo, G.; Xin, L.; Hui, Z.; Ling, W. Quadrotor helicopter Attitude Control using cascade PID. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 5158–5163. [Google Scholar]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]




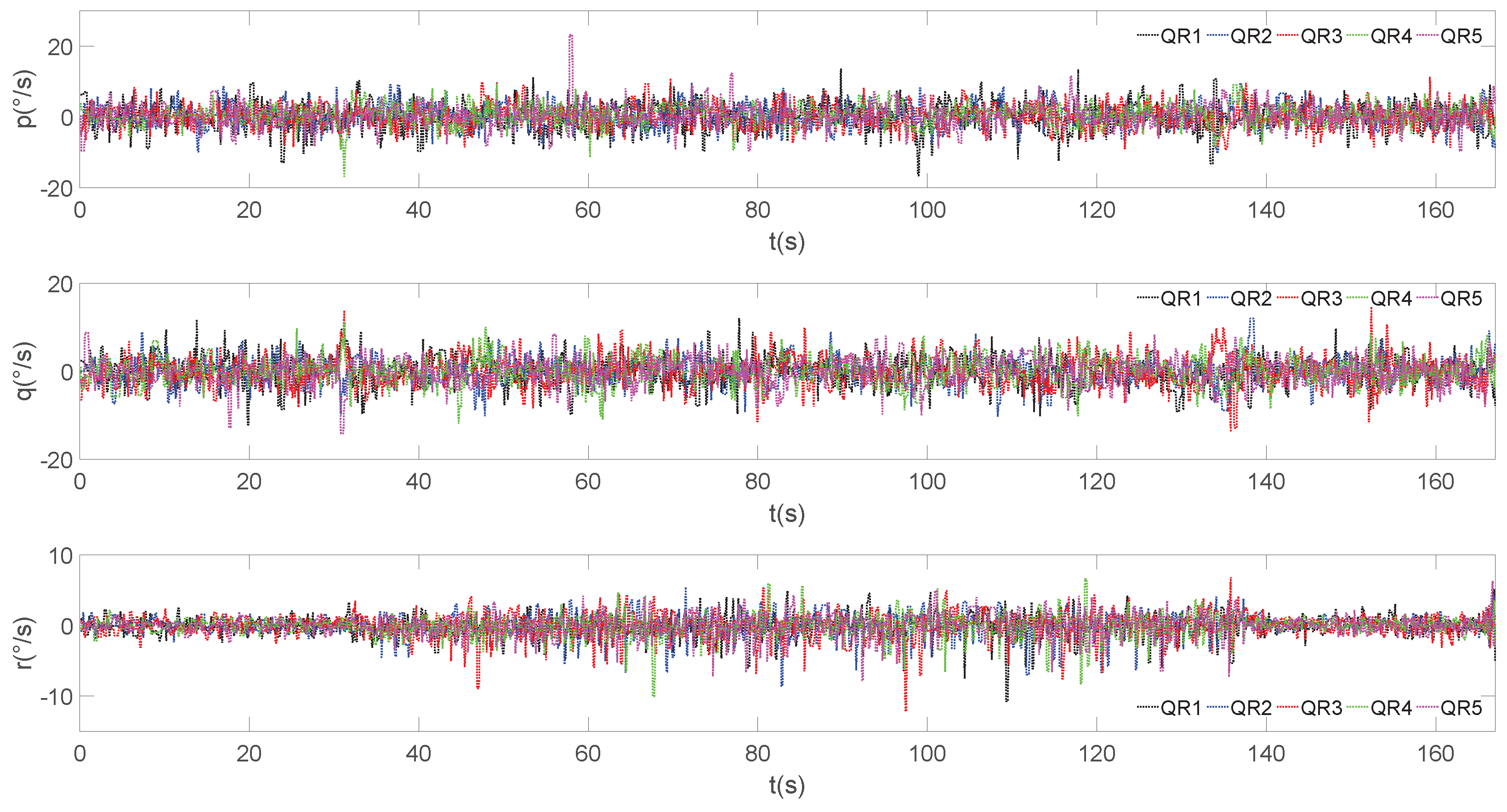
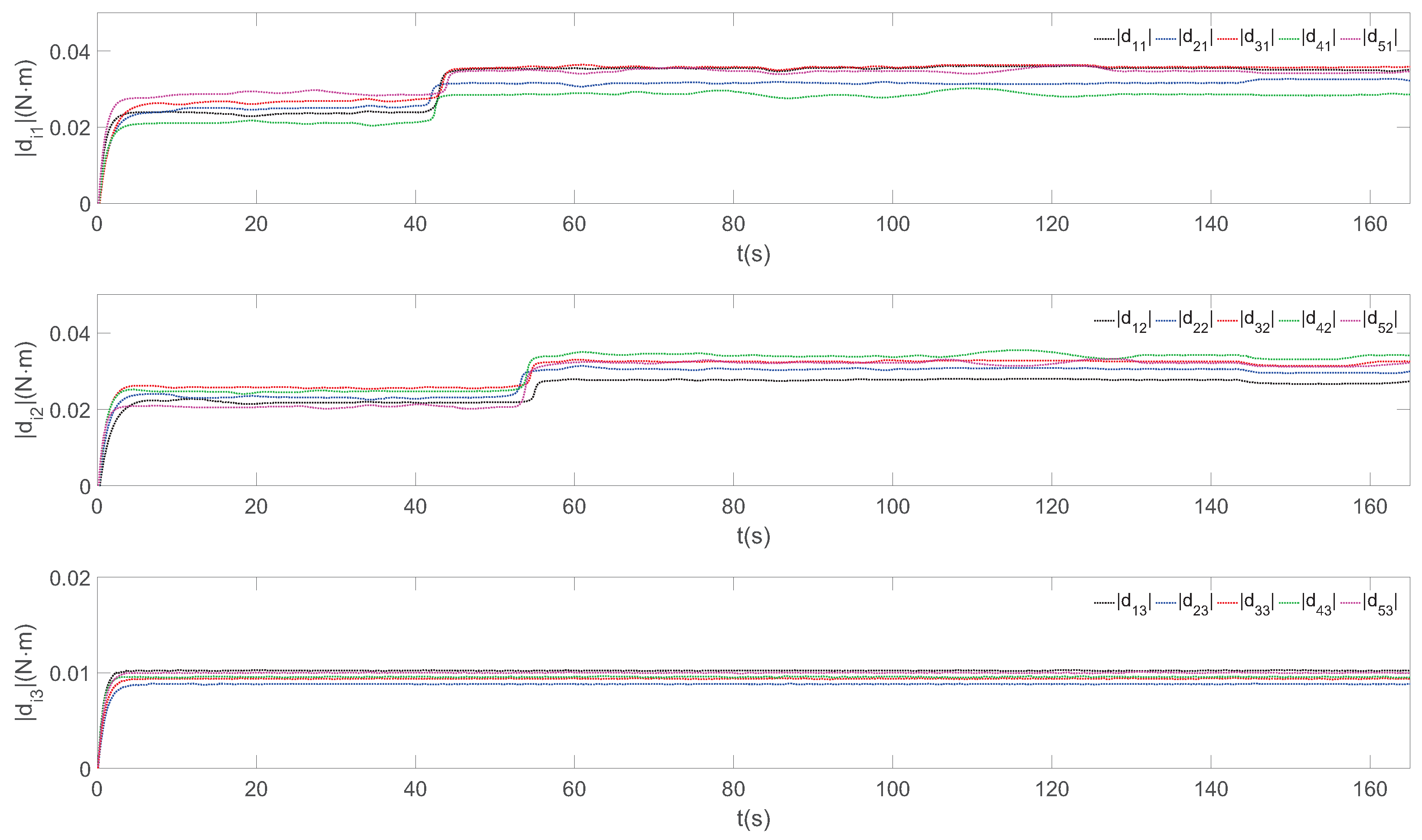
| Channel | ||||
|---|---|---|---|---|
| Roll | 5.2 | 0.31 | 0.03 | 0.0012 |
| Pitch | 4.85 | 0.28 | 0.025 | 0.0011 |
| Yaw | 2.5 | 0.62 | 0.015 | 0 |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| 19.5 | 4 | 243 | |||
| 235 | 42.6 | 2150 | |||
| 0.006 | 42.6 | 2920 | |||
| 36 | 22.2 |
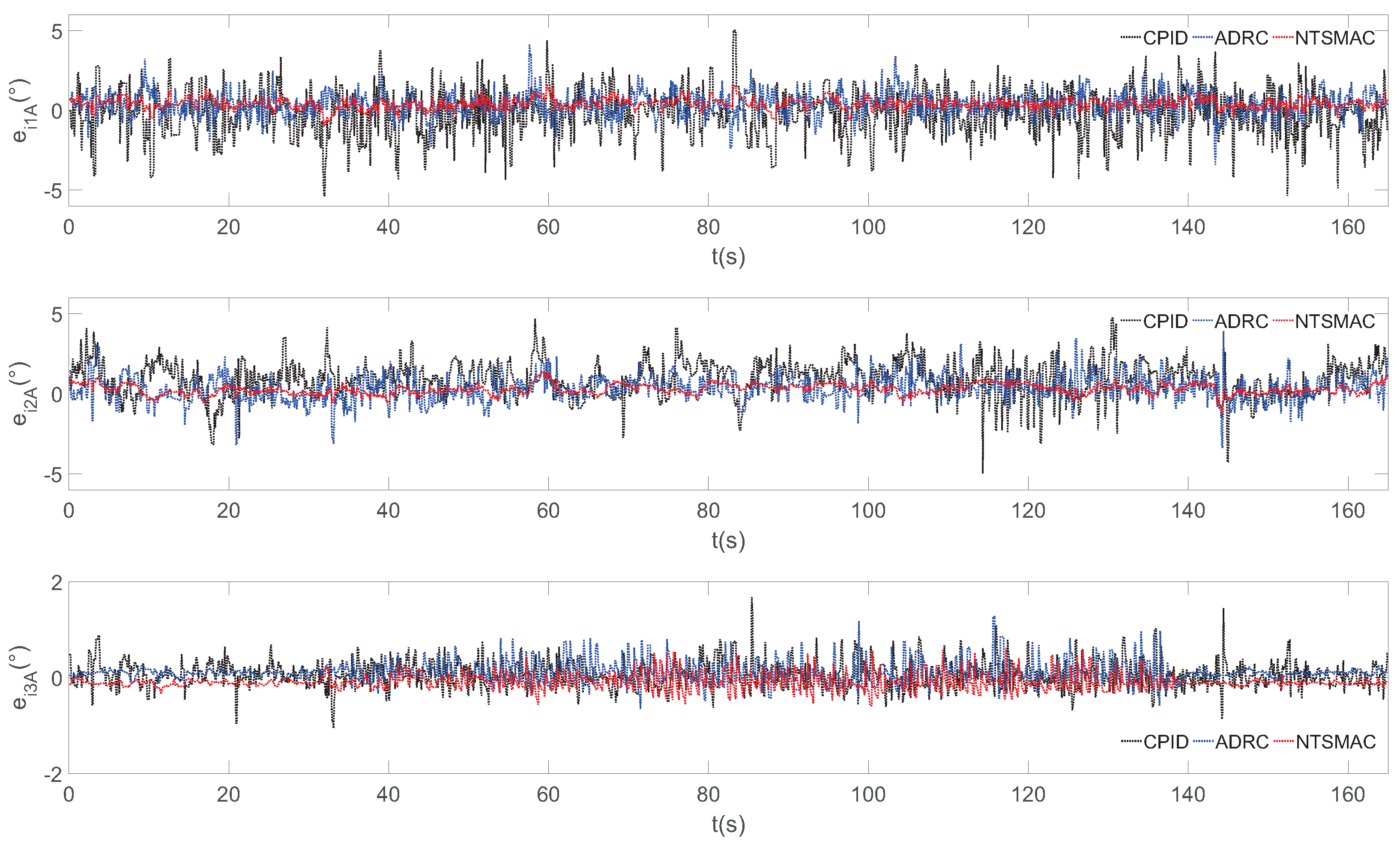
| Channel | |||||||
|---|---|---|---|---|---|---|---|
| QR’s ID | Controller | Roll | Pitch | Yaw | |||
| RMSE | MAXE | RMSE | MAXE | RMSE | MAXE | ||
| CPID | 2.944 | 5.347 | 2.807 | 4.936 | 0.989 | 1.691 | |
| 1 | ADRC | 1.847 | 3.855 | 2.286 | 4.104 | 0.627 | 1.299 |
| NTSMC | 0.776 | 1.653 | 0.850 | 1.499 | 0.362 | 0.714 | |
| CPID | 2.874 | 4.985 | 3.340 | 5.732 | 1.022 | 1.547 | |
| 2 | ADRC | 1.758 | 3.673 | 2.194 | 3.890 | 0.754 | 1.107 |
| NTSMC | 0.825 | 1.420 | 0.784 | 1.427 | 0.323 | 1.020 | |
| CPID | 2.901 | 5.104 | 2.905 | 5.300 | 0.856 | 1.603 | |
| 3 | ADRC | 2.641 | 4.012 | 2.008 | 3.922 | 0.878 | 1.318 |
| NTSMC | 0.951 | 1.834 | 0.863 | 1.422 | 0.434 | 0.966 | |
| CPID | 3.113 | 5.073 | 3.502 | 5.112 | 1.104 | 1.707 | |
| 4 | ADRC | 2.372 | 3.976 | 2.223 | 4.207 | 0.823 | 1.243 |
| NTSMC | 0.998 | 1.678 | 0.790 | 1.972 | 0.412 | 0.820 | |
| CPID | 2.975 | 5.217 | 3.476 | 4.876 | 1.020 | 1.824 | |
| 5 | ADRC | 2.406 | 3.874 | 1.983 | 4.046 | 0.796 | 1.192 |
| NTSMC | 0.932 | 1.738 | 0.905 | 1.384 | 0.433 | 0.649 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Zhu, M.; Qin, J. Adaptive Robust Time-Varying Formation Control of Quadrotors under Switching Topologies: Theory and Experiment. Aerospace 2023, 10, 735. https://doi.org/10.3390/aerospace10080735
Zhao Z, Zhu M, Qin J. Adaptive Robust Time-Varying Formation Control of Quadrotors under Switching Topologies: Theory and Experiment. Aerospace. 2023; 10(8):735. https://doi.org/10.3390/aerospace10080735
Chicago/Turabian StyleZhao, Ziqian, Ming Zhu, and Jiazheng Qin. 2023. "Adaptive Robust Time-Varying Formation Control of Quadrotors under Switching Topologies: Theory and Experiment" Aerospace 10, no. 8: 735. https://doi.org/10.3390/aerospace10080735
APA StyleZhao, Z., Zhu, M., & Qin, J. (2023). Adaptive Robust Time-Varying Formation Control of Quadrotors under Switching Topologies: Theory and Experiment. Aerospace, 10(8), 735. https://doi.org/10.3390/aerospace10080735





