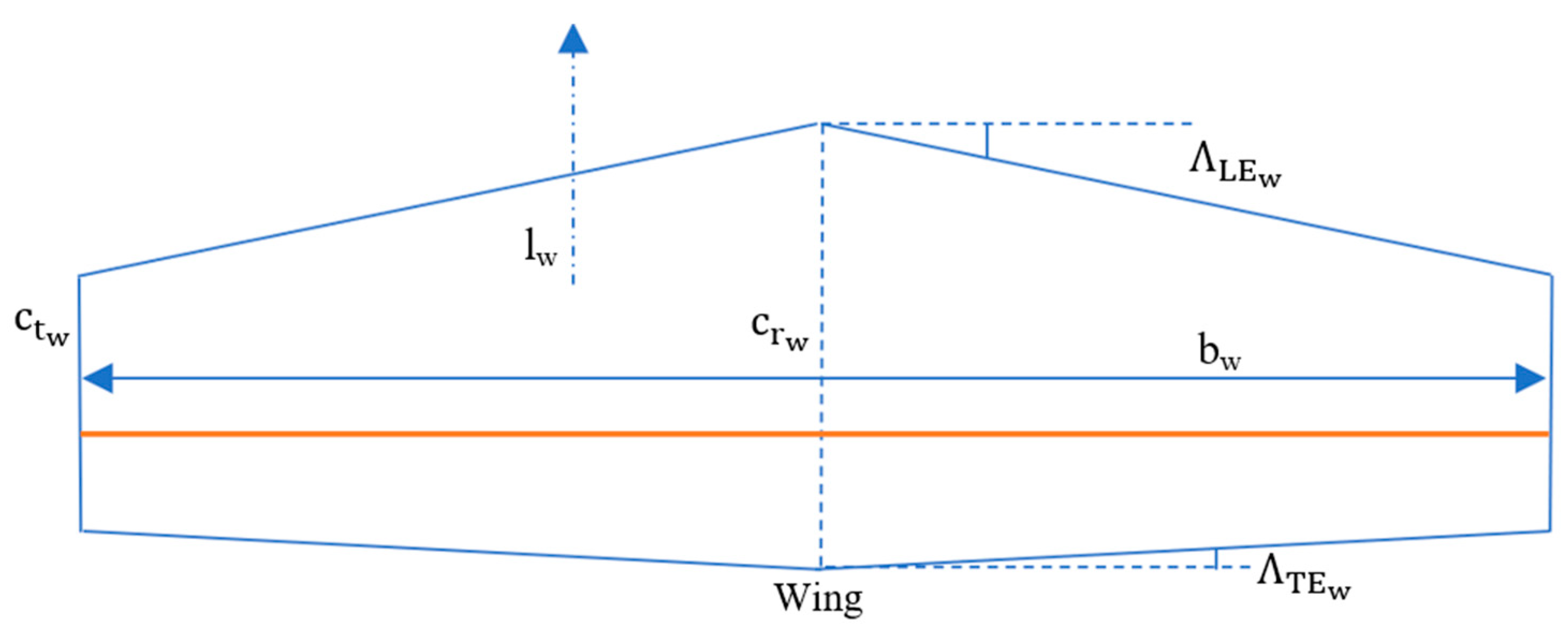
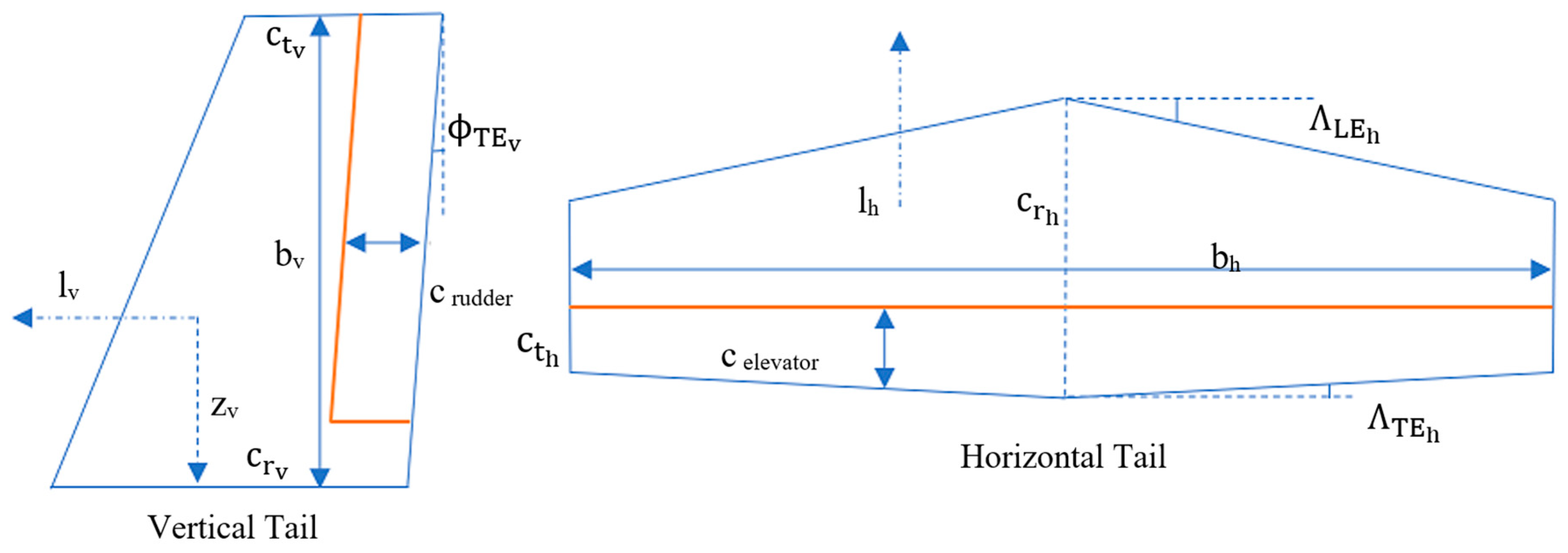
In this case, the main concern was sizing the empennage and wing, where the optimization was completed by altering the defining geometry whilst satisfying the requirements of the design given by the aircraft geometry, electrical propulsion characteristics, and different flight circumstances. The involved disciplines were aerodynamics, weight and balance, propulsion, as well as stability and control. An initial sizing of the electric propulsion system was accomplished to estimate the required number of engines along with the number, mass, and volume of batteries.
2.1. MAPLA
The semi-empirical analysis program MAPLA, devised for the optimization of light, general aviation aircraft, was enhanced for use with electric vertical take-off and landing (eVTOL) vehicles. The original implementation includes five disciplines: aerodynamics, propulsion, performance, weight and balance as well as stability and control, all built with state-of-the-art analytical procedures and design data collections combined into a fully automated method. For this investigation, the electric propulsion submodule was developed including the following considerations: engine/propeller positioning and sizing, off-design analysis of blades, noise analysis, mass calculation, volume determination, and battery specifications.
In a series of previous investigations, this tool was demonstrated to be capable of modelling the characteristics of small aircraft with acceptable precision [
39,
40,
41,
42,
43]. In these cases, the modelled aircraft were all using conventional configurations, a requirement imposed by the semi-empirical methods which underpin many of MAPLA’s analyses. These limitations are still present in the current version of the tool, and as such only eVTOL aircraft which resemble a conventional aircraft while in cruise can be successfully modelled; atypical or hybrid configurations cannot be analyzed with MAPLA.
For the purpose of this study, initially, a small propeller-driven aircraft was chosen and first analyzed by MAPLA. In the next step, the corresponding aerodynamic characteristics predicted by MAPLA were compared with those of the wind tunnel test results for the small aircraft [
44,
45] to validate the calculated results.
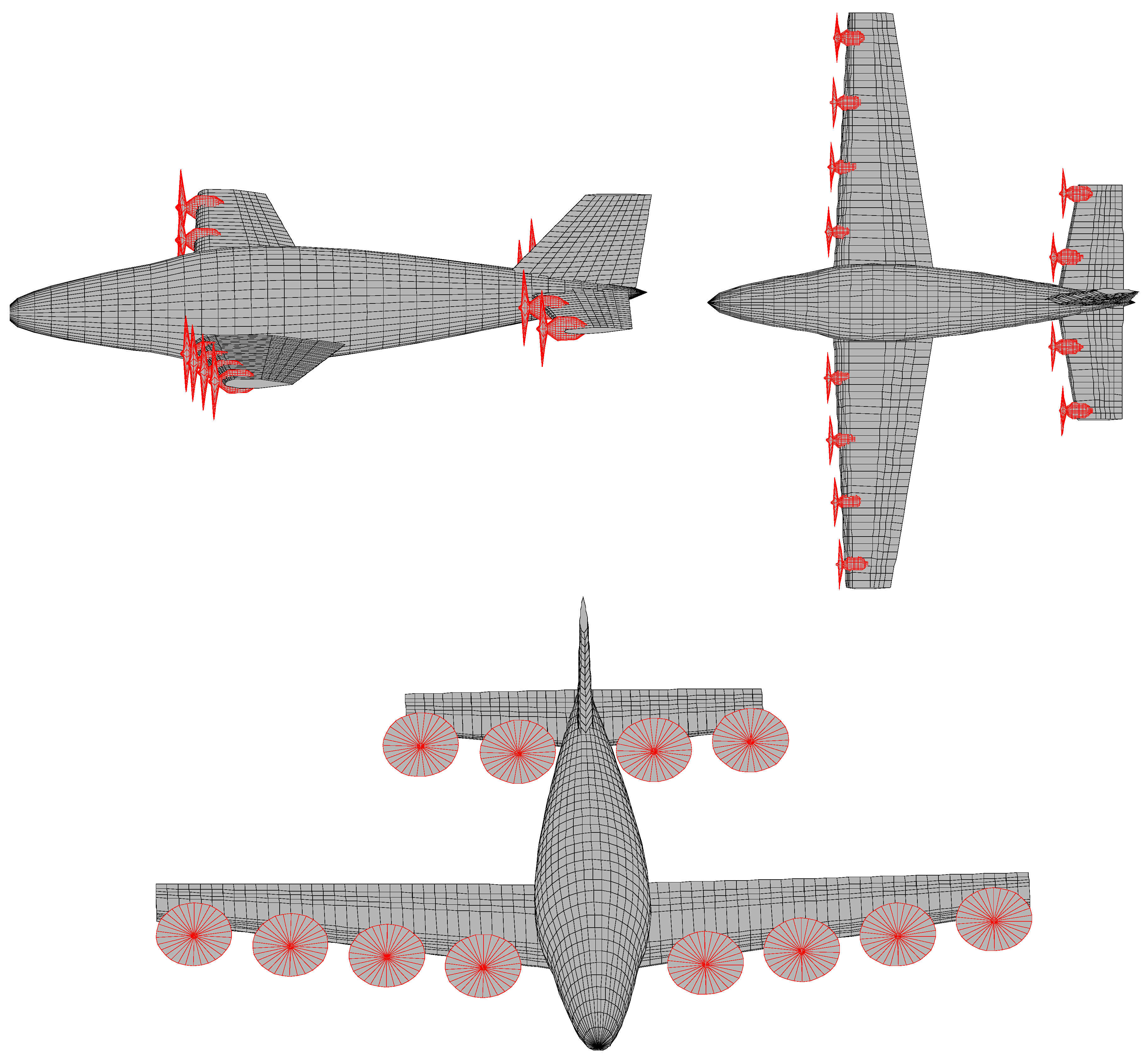
Figure 3a,b shows the geometry of the original aircraft model and the modelled aircraft using MAPLA, respectively. The general characteristics of the airplane and properties of the investigated flight condition are presented in
Table 1.
In the following, in
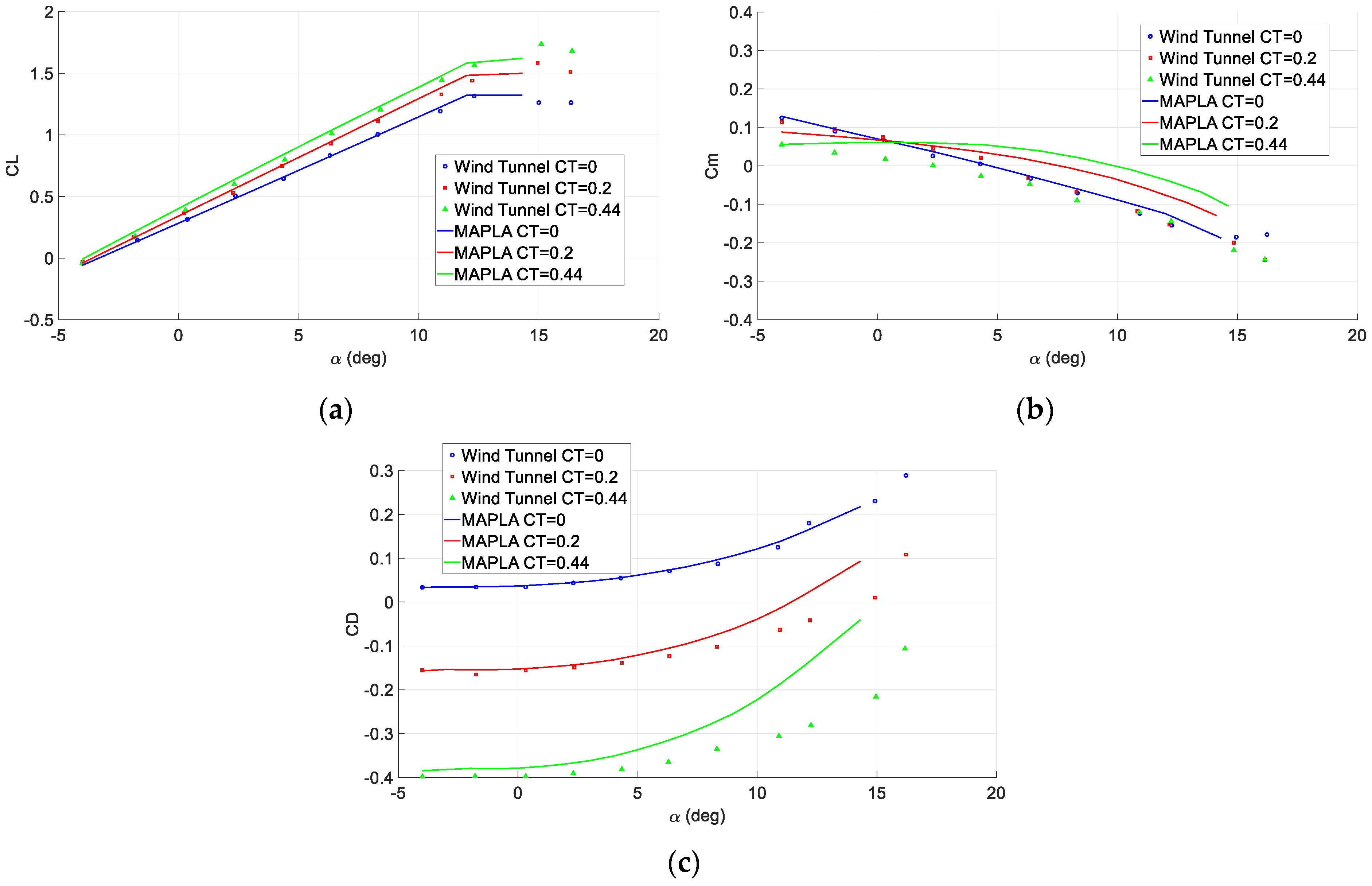
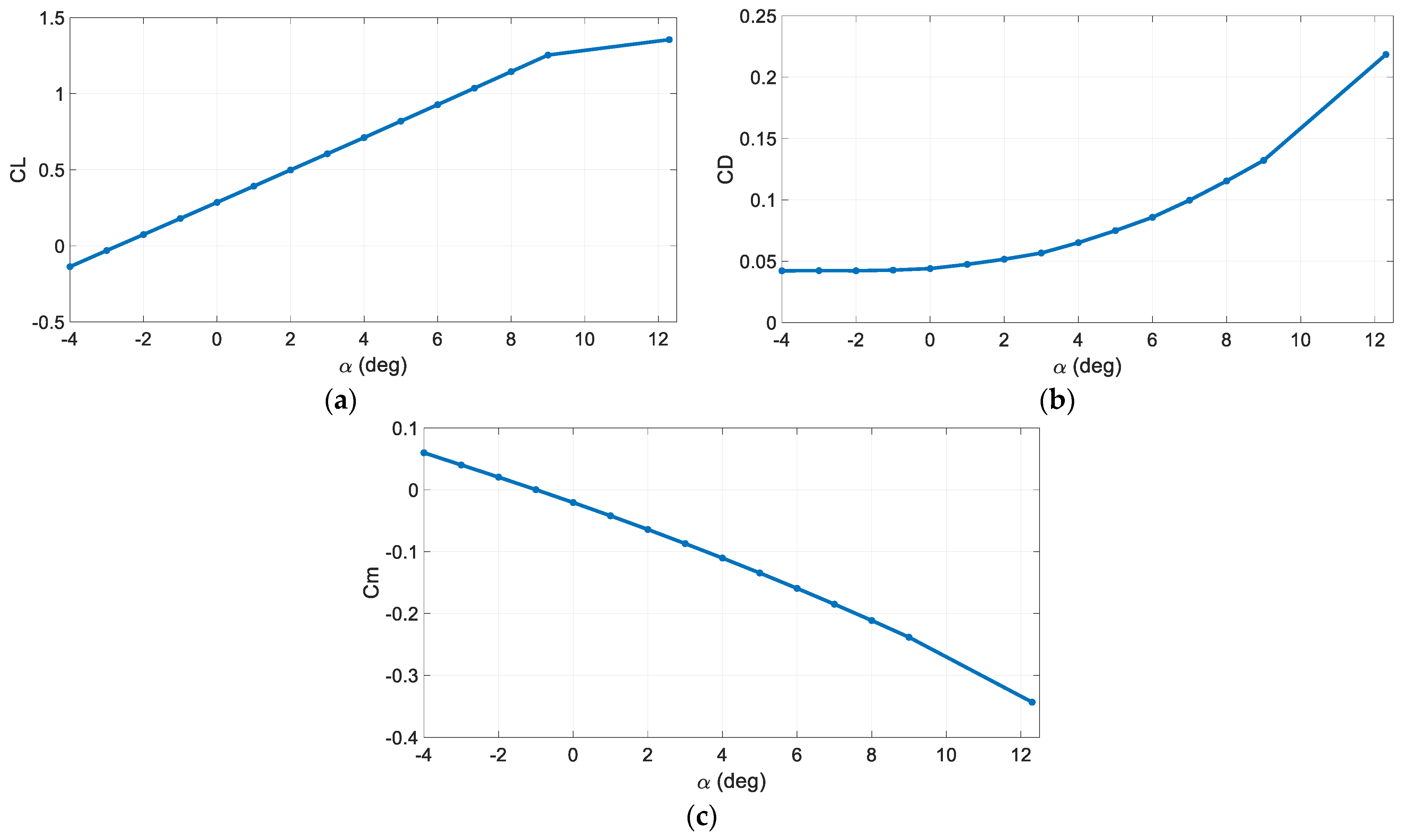
Figure 4a–c, the longitudinal aerodynamic characteristics of the investigated airplane are presented for the corresponding flight condition.
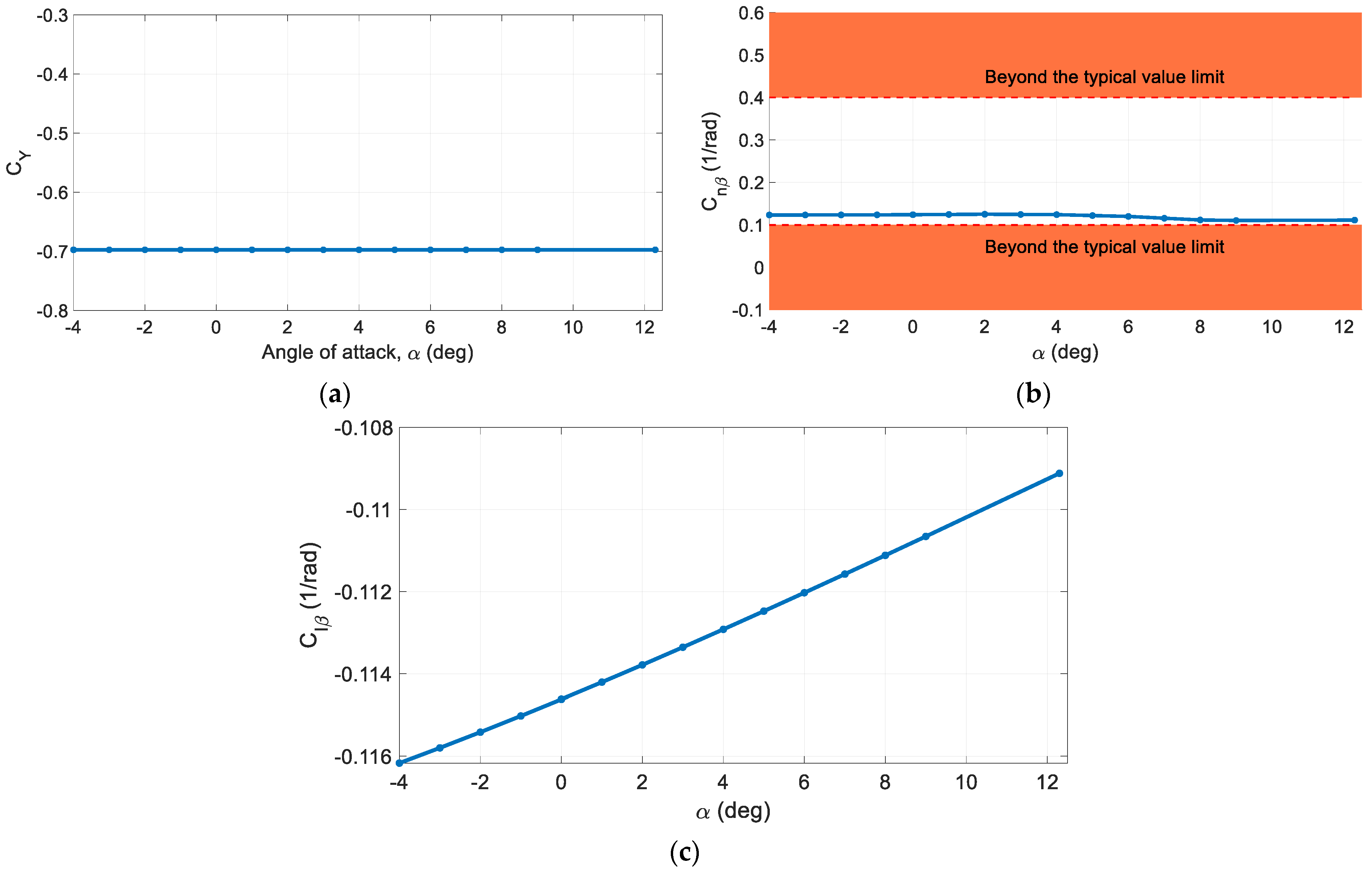
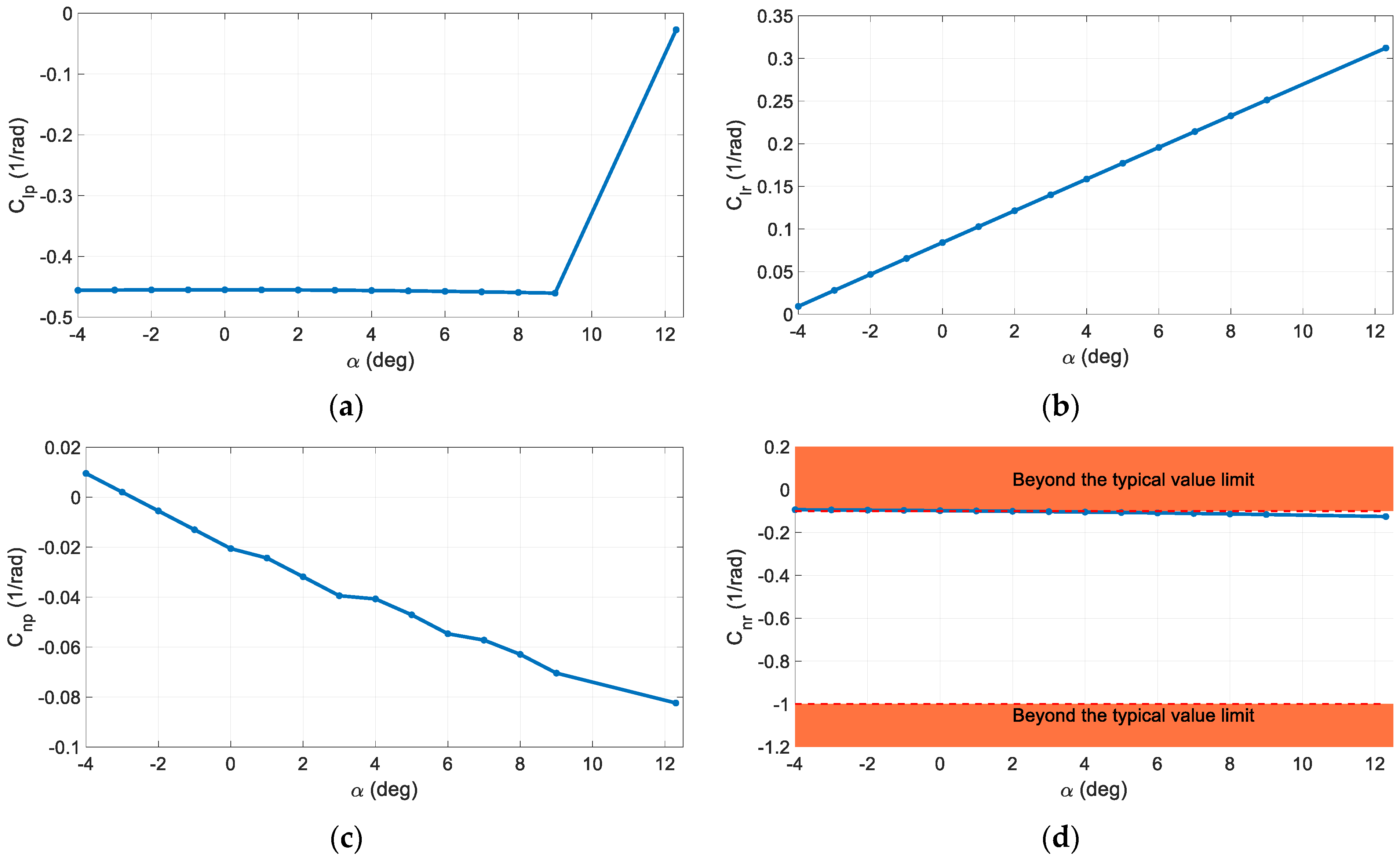
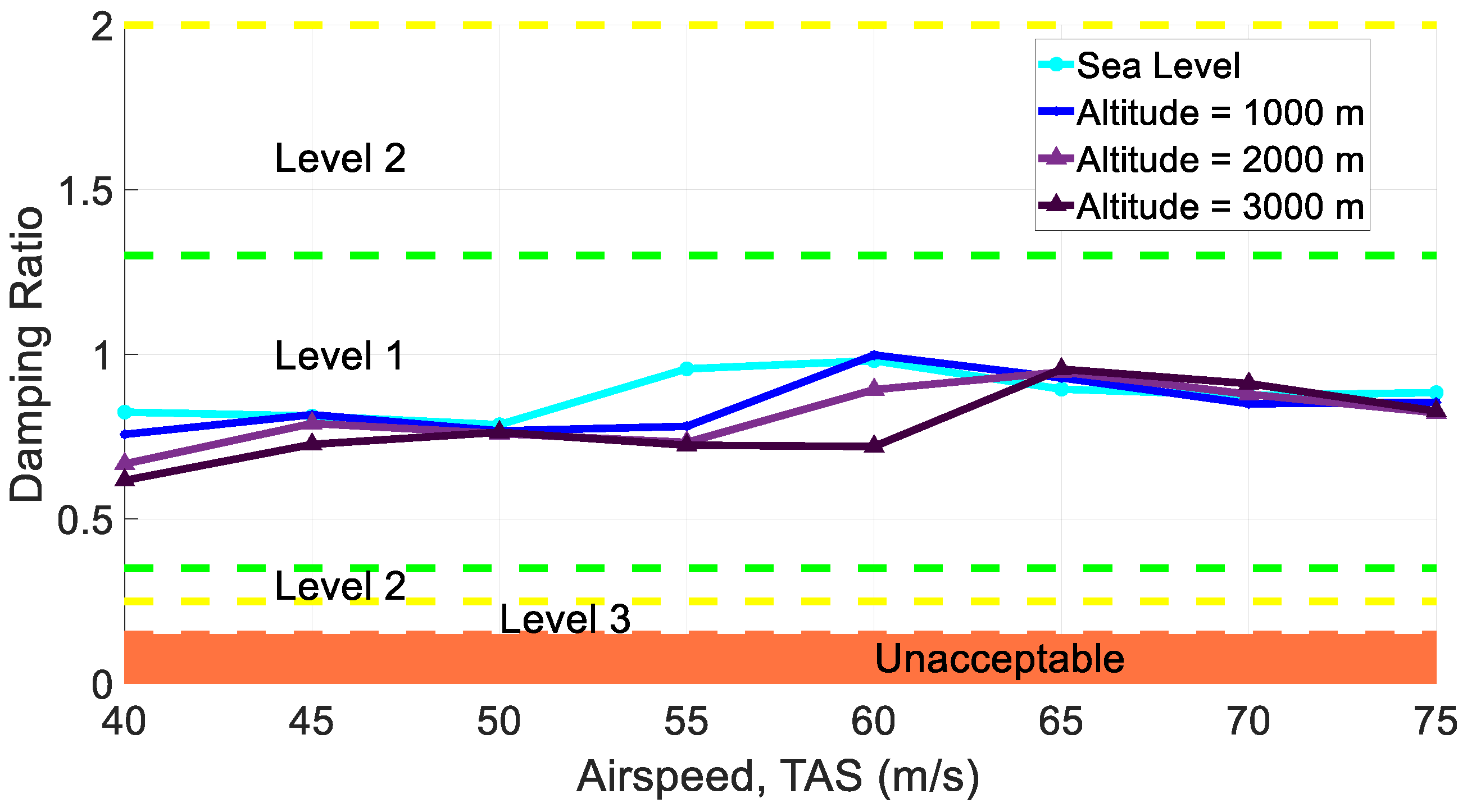
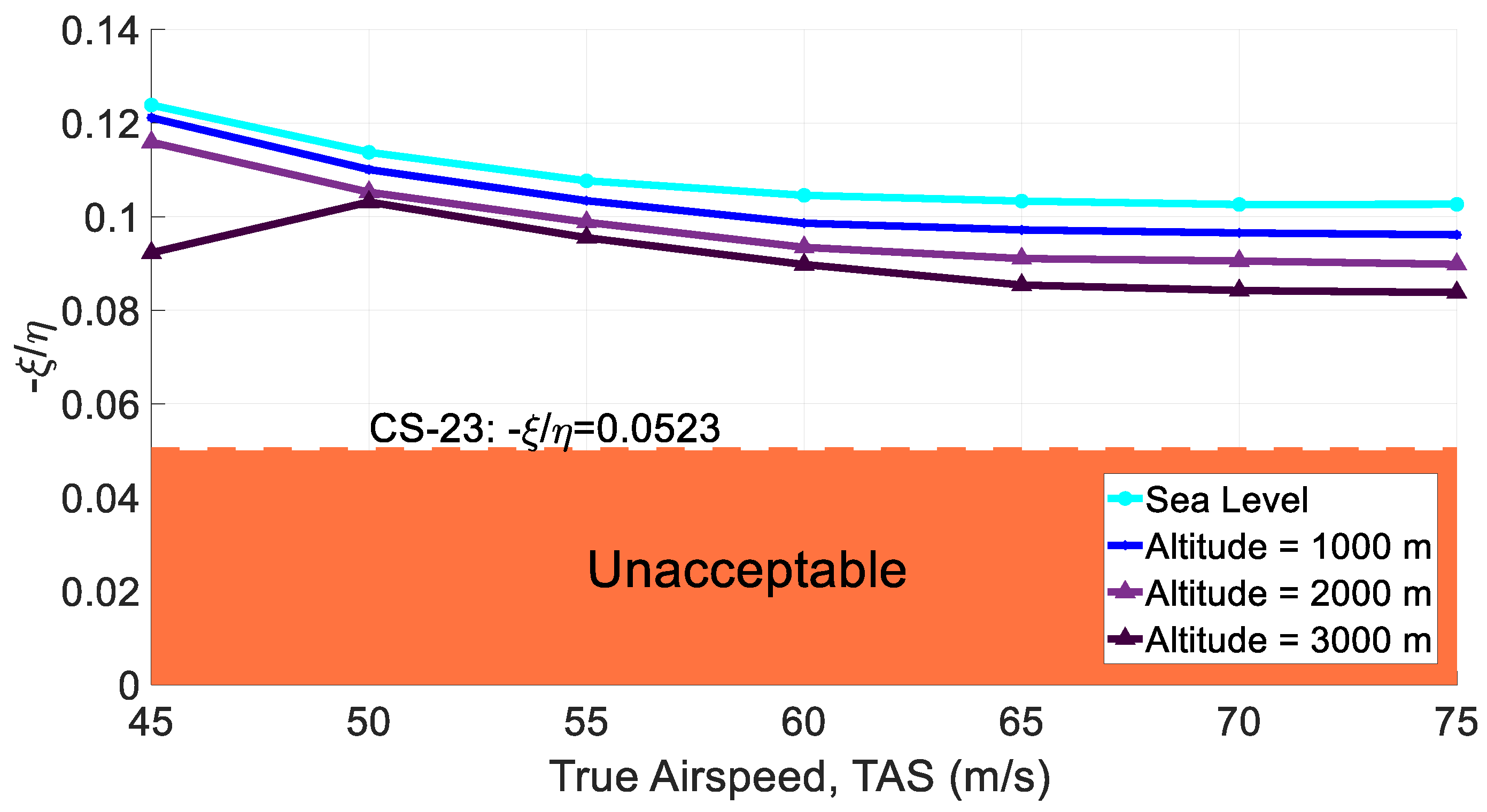
Figure 5a,b presents the lateral-directional aerodynamic characteristics of the twin-engine propeller-driven small aircraft using MAPLA and the available wind tunnel test results [
44,
45]. Compared to the longitudinal characteristics, the lateral-directional results show higher deviation from the wind tunnel test results. A probable reason for this deviation could be the propeller effects and power contributions. Particularly, these effects change the flow characteristics over the empennage and change its contribution to aerodynamics.
2.2. Initial Design and Sizing of the Propulsion System
To size the electric propulsion system, the number of engines needs to be selected first. Deciding between having fewer larger engines or several smaller engines requires consideration of the following factors [
46]:
Disk loading: bigger propeller disk is better in hover due to lower disk loading.
Ground clearances: smaller propellers would result in more ground clearance when the horizontal tail and the wing are in a horizontal position.
Propeller-wing interaction: larger propellers would have a higher slipstream height, which results in more lift because of the propeller slipstream in the same slipstream speed.
Propeller-propeller interaction: smaller propellers with lower slipstream heights allow easier placement of the engines such that the horizontal tail propellers do not lose their slipstream. This slipstream loss can lead to a reduction in thrust from the horizontal tail propellers and an increase in noise emissions.
Blade rotation mechanism: using very small propellers makes it more difficult to alter the pitch of the blades.
Safety in OEI conditions: using more and smaller engines, a failure of one would result in less effect on controllability in hover and on a loss of thrust.
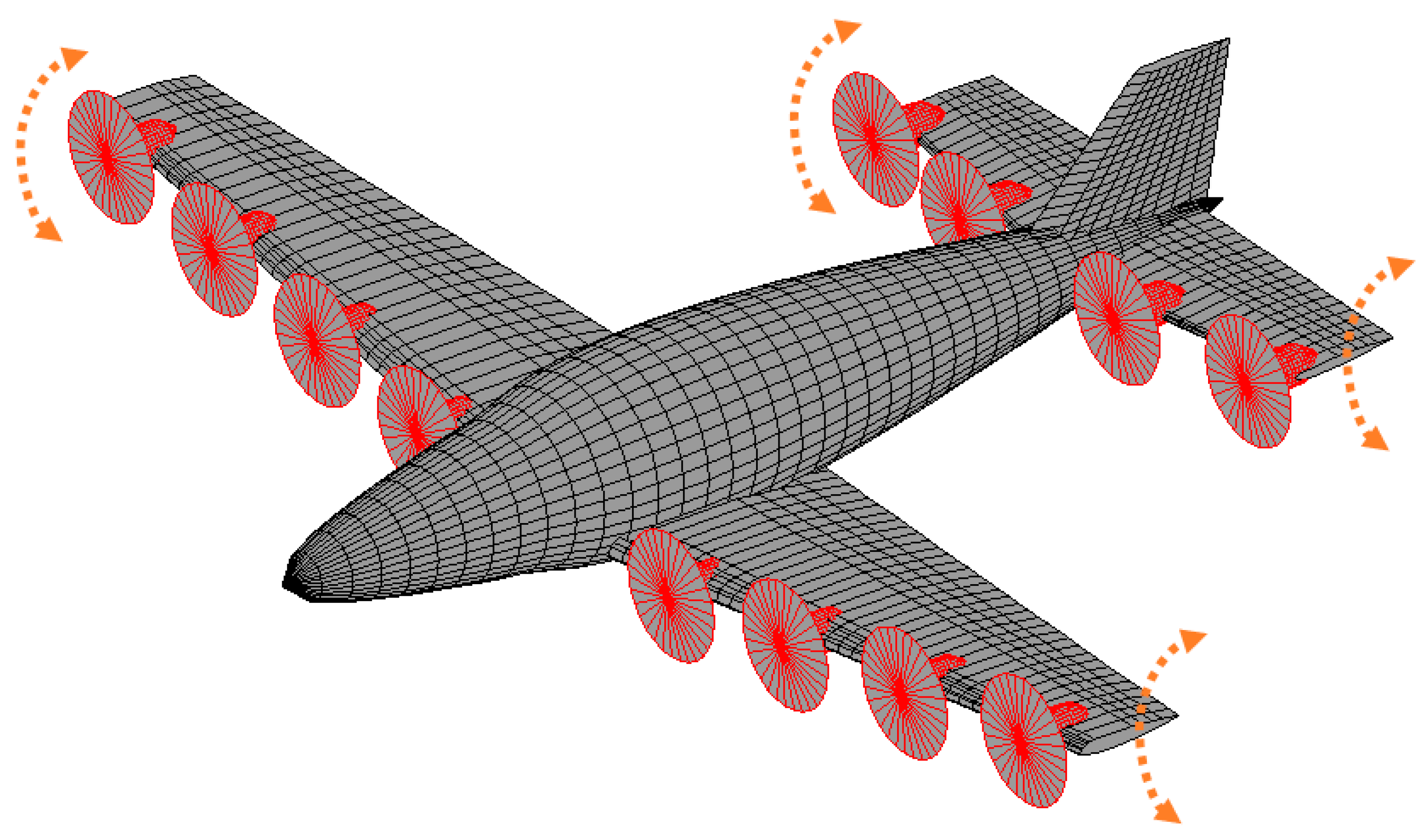
The aircraft features two sets of electric engines with variable-pitch and variable-speed open rotors with six blades, and it was decided to use the same size to minimize differences in propeller loading and provide cheaper manufacturing. A great proportion of the engines are placed on the wing as it is closer to the CG location and requires higher thrust during hover. After considering the criteria for the number of engines and using MAPLA’s electric propulsion module, the desired number of engines was found to be 12 (8 for the wing and 4 for the horizontal tail) with a radius of 0.5 m and a maximum allowable rpm level of ~4800. For controllability purposes, the maximum thrust-to-weight ratio was found to be approximately 1.5. For an MTOW of 2500 kg and 12 propellers, this results in a required maximum thrust of about 3100 N per propeller with a pitch down of 45 deg. The design point for the flight condition was set to the cruise speed of 70 m/s at a 1 km altitude.
The solid-state lithium battery with a specific energy of 500 Wh/kg, a volumetric energy density of 1000 Wh/L, and a power density of 6500 W/kg was chosen. Each battery cell has an internal capacitance of 5 Ah and a nominal voltage of 3.7 V. Future-oriented battery specifications were chosen for the eVTOL tilt-wing aircraft [
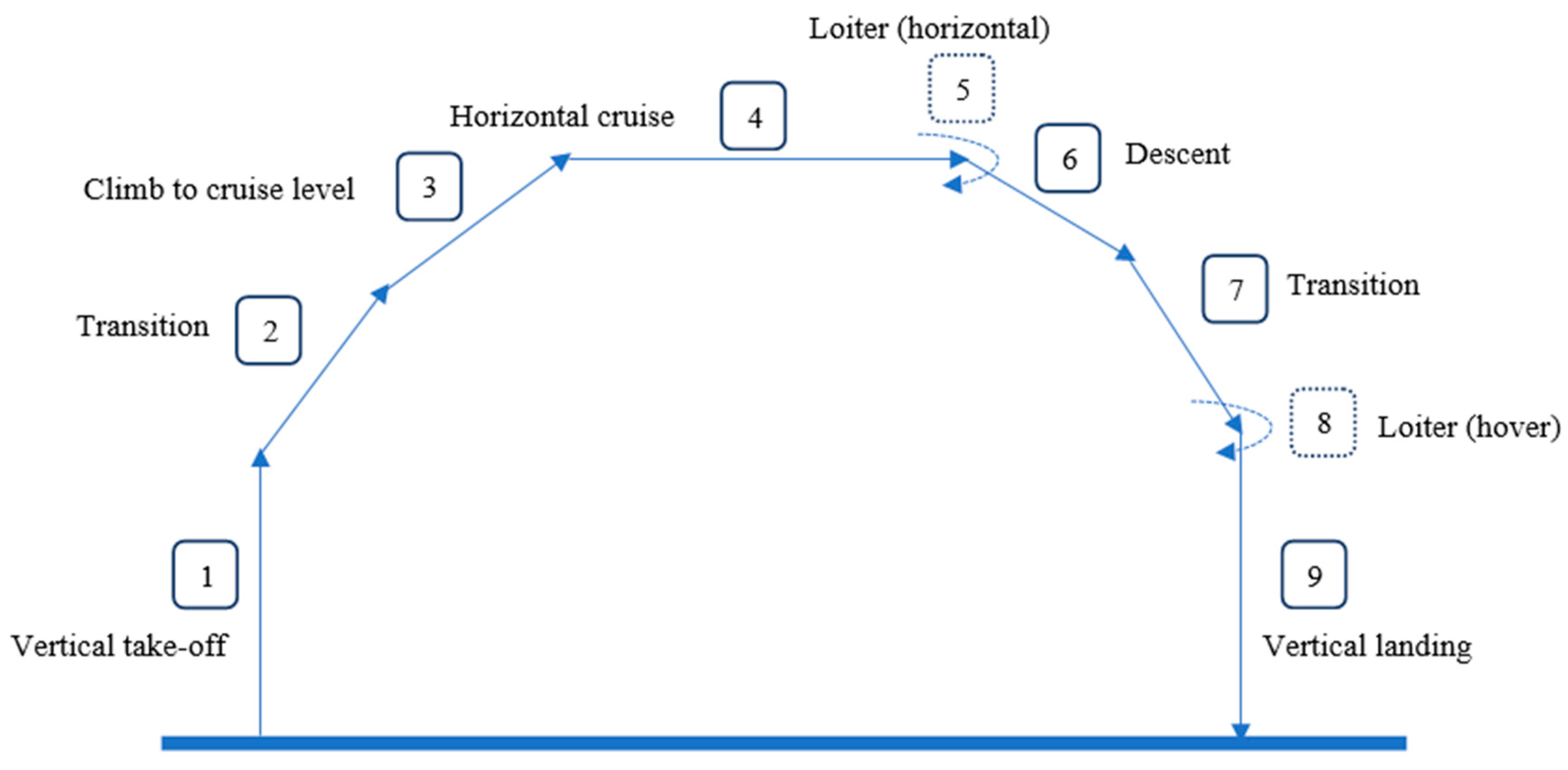
46]. The regular mission profile as shown in
Figure 6 was defined according to the VTOL aircraft flight requirements including 1. Vertical take-off; 2. The transition from hover to climb; 3. Climb to cruising altitude; 4. Cruise; 5. Loiter in horizontal flight; 6. Descent; 7. Transition to hover; 8. Loiter in hover; and 9. Landing [
46].
To calculate the energy used during flight using the method presented in [
46], thrust at different flight regimes was calculated and converted to power. Accordingly, for take-off and landing, the following relation was used:
where T accounts for the thrust, V
∞ is the speed perpendicular to the propeller disk, factor k corrects for the power losses, equal to 1.2 in this case, and A is the disc area.
To calculate the required thrust during take-off and landing the following equations of motion were used [
46].
where
represents the rotated wing incidence with respect to the horizontal axis, x-axis, and
and
are the corresponding accelerations in the x-axis and y-axis, respectively. To find the fuselage drag contribution, it was assumed that the fuselage is at 90 degrees when flying vertically.
For cruise flight conditions, the suggested relation from [
46] for power estimation was used
where η is the propulsive efficiency at the given speed for cruise flight conditions. Finally, the required energy to be stored by batteries for the entire mission profile can be calculated by [
46,
47]
Consequently, the energy required for a 300 km range flight with 15 min loiter (~86 min) using equations 1 through 5 was estimated to be ~1400 MJ with a maximum power requirement during take-off of ~2.1 MW.
To calculate the battery weight, the following equations according to the energy demands and maximum power were used [
46]
where DoD is the depth of discharge and EOLC is the end-of-life capacity, and they are both varying between 0 and 1. And the volume of the battery was estimated using [
46]:
where
is the specific energy in Wh/kg and
stands for the volumetric energy density in Wh/m
3 [
46]. Consequently, using MAPLA’s electric propulsion module with the total energy and maximum power requirements, the total battery mass for energy storage was estimated to be 776 kg with a required volume of 0.4 m
3.
In the following, the total voltage of batteries and the total current, assuming they are connected in series are presented [
46].
where
is the capacity and
stands for nominal cell voltage. Also, the required number of battery cells for the electric engines obtained from [
46]
where
describes the number of battery cells,
stands for the energy percentage that goes into the motors and
is the energy stored in each individual cell. However, the relation requires additional corrections as a battery package not only needs to provide energy but also requires the correct voltage. Accordingly, the number of batteries required could be calculated using the following relations considering parallel and series connections [
46].
The total number of battery cells for the electric propulsion system and other electronic devices was estimated to be 20,763. Based on the required voltage of 500 V for motors taken from Calnetix [
46], using MAPLA’s propulsion module, the number of cells in series is 135 and the required number of battery cells in parallel arrangement is 154 which would result in 20,790 cells due to rounding. As for the proposed eVTOL aircraft, 12 propellers were selected and 2 batteries were required for each engine, giving a total of 24 batteries. Hence, the total number of battery cells in parallel should increase to 164 to allow the modular set of 7 cells in parallel for 24 batteries. Consequently, the total number of cells will be 22,140 with a total mass of 827 kg and a volume of about 0.43 m
3.
2.3. PBDO Method Outline
A deterministic gradient optimizer was coupled to a possibility-evaluation algorithm to carry out the design optimization under uncertainty. This gives a comparable framework to the Sequential Optimization and Reliability Assessment (SORA) method developed for use with PBDO [
48,
49]. Here, the Performance Measure Approach (PMA) was used to implement the possibility evaluation on each constraint. This algorithm employs a separate optimization loop to find the worst-case scenario for each individual constraint. Using this, the value of each uncertain variable is determined within its possibilistic interval and adjusted to ensure that even in extreme cases the constraints will not be violated by an implementation of the output design [
37,
50]. After this step, for each iteration, a deterministic optimization followed to progress the design. This method of interwoven optimization and possibility evaluation, here achieved by applying Sequential Quadratic Programming (SQP) for each, allows the design to be iteratively altered until a final configuration is selected which is guaranteed to adhere to the constraints [
37].
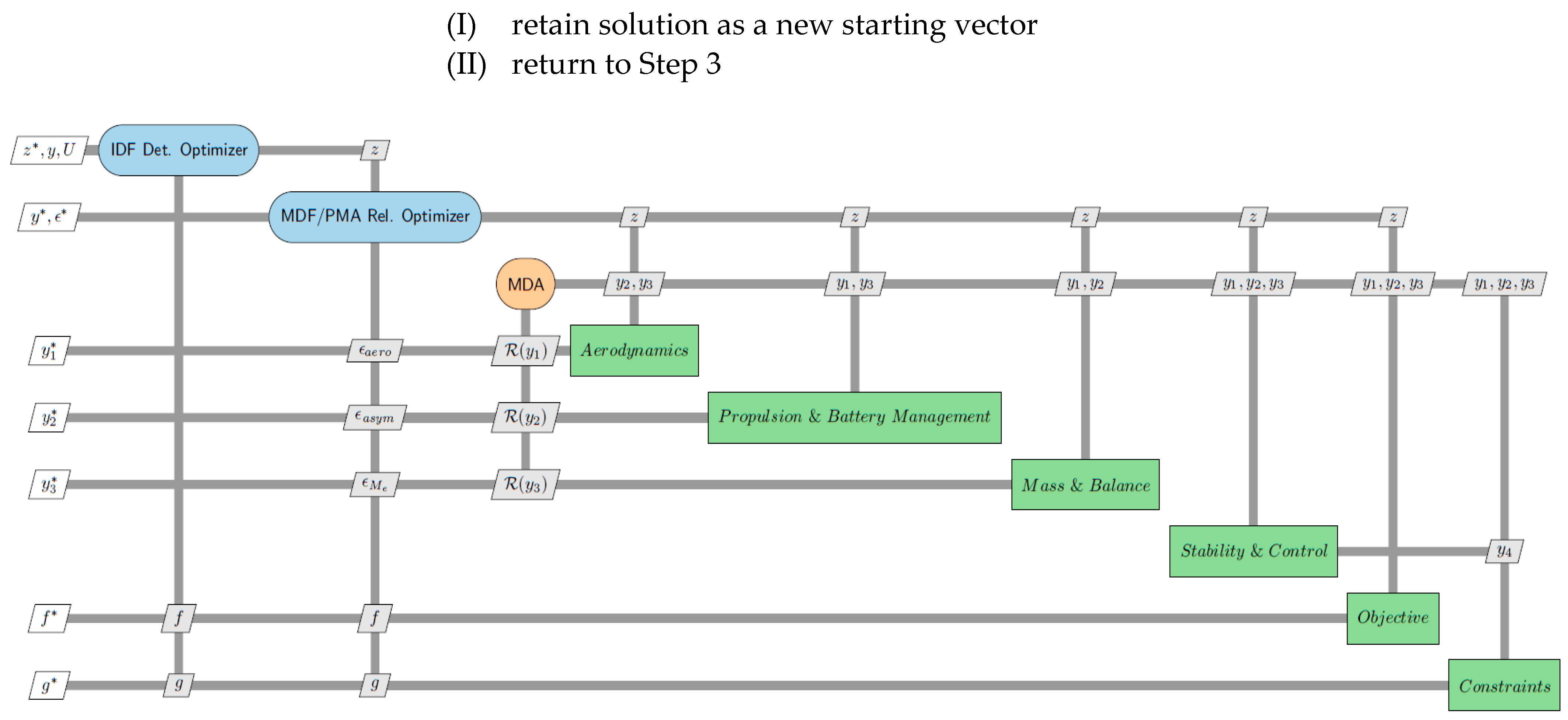
The MDF approach is a single-level MDO procedure where the shared design and coupling variables are consistent across all disciplines, achieved by using an MDA loop. The MDA loop starts with the given design variable states, x and z, introduced by the optimizer using an initial estimation of the coupling variable vector, y. Each discipline is then computed sequentially to update its coupling variable using values from the output of the previous discipline. The loop continues until the coupling variable vector converges. The mathematical representation of a deterministic MDF approach for an optimization problem is presented as follows:
where the shared design variables are defined by z and the local design variables are defined by x. The coupling variables, y, are found using an MDA loop each time the system and the local variables are updated.
The mathematical representation of a reliability-based MDF approach that was used in this study is shown as follows:
where P is the probability of feasibility for each constraint and p is the uncertain parameters. The optimizer alters z and x. The coupling variables, y, are estimated internally by the MDA loop and are not in the system optimizer.
The IDF method was used to reduce the iterations of the computationally costly MDA loop by eliminating the feasibility for every design assessed by the optimizer. Design feasibility, or rather the consistency of the coupling and shared variables, is only assured at the end. New auxiliary constraints are defined to reduce the discrepancy between the discipline responses and the estimated quantities at the optimum point. The mathematical representation of a deterministic IDF approach for an optimization case is presented as follows:
where the coupling variables,
, are determined by calculating each discipline’s result using the coupling variable states,
, defined by the system optimizer. The coupling variables,
, are defined for the system optimization variables in the IDF-based PBDO method considering the auxiliary constraints. With respect to the PMA-based reliability analysis,
IDF approaches are also achievable using a revised reliability analysis loop with a double loop or sequential PBDO methods.
Validation of the implemented framework was completed previously [
43]. Accordingly, the following nonlinear single-discipline PBDO test example was solved with various methods [
51,
52]:
Table 2 shows the results of the comparison between various methods including the double-loop PMA approach, the double-loop Reliability Index Approach (RIA), and the sequential PMA method.
Of the tested configurations, the single-loop approach diverged from PMA and RIA methods for large values of and as such, was not selected. Overall, the PMA method was found to require fewer iterations when compared to its RIA counterparts; with the sequential PMA approach requiring fewer iterations than its double-loop implementation. For this reason, it was the approach that was ultimately selected, with the hope that fewer iterations for this problem would translate to a more rapid aircraft optimization process.
The speed and stability of this method were also assessed by running the optimization procedure through 100 starting values. It was found to, on average, have an error below
%, and require less time than the double loop methods [
43].
For further validation of the MDO methodology, the following multi-discipline problem was solved and compared with different methods [
43,
53].
where the uncertain variables of
and
were considered to have a variation coefficient of 0.04 defined as the standard deviation,
, to the random variable mean value,
. After solving the problem using different methods at a reliability level of
and finding the optimum points, the results are presented along with the number of function evaluations,
in
Table 3.
The results indicated that the IDF method with a sequential PMA strategy for the PBDO method achieved the most efficient results. Although MDF-based methods were also accurate, the effort needed to solve the problem and find the most optimized case with regard to the was considered to be excessive.