A Reinforcement Learning Method Based on an Improved Sampling Mechanism for Unmanned Aerial Vehicle Penetration
Abstract
1. Introduction
2. Related Works
3. Problem Description
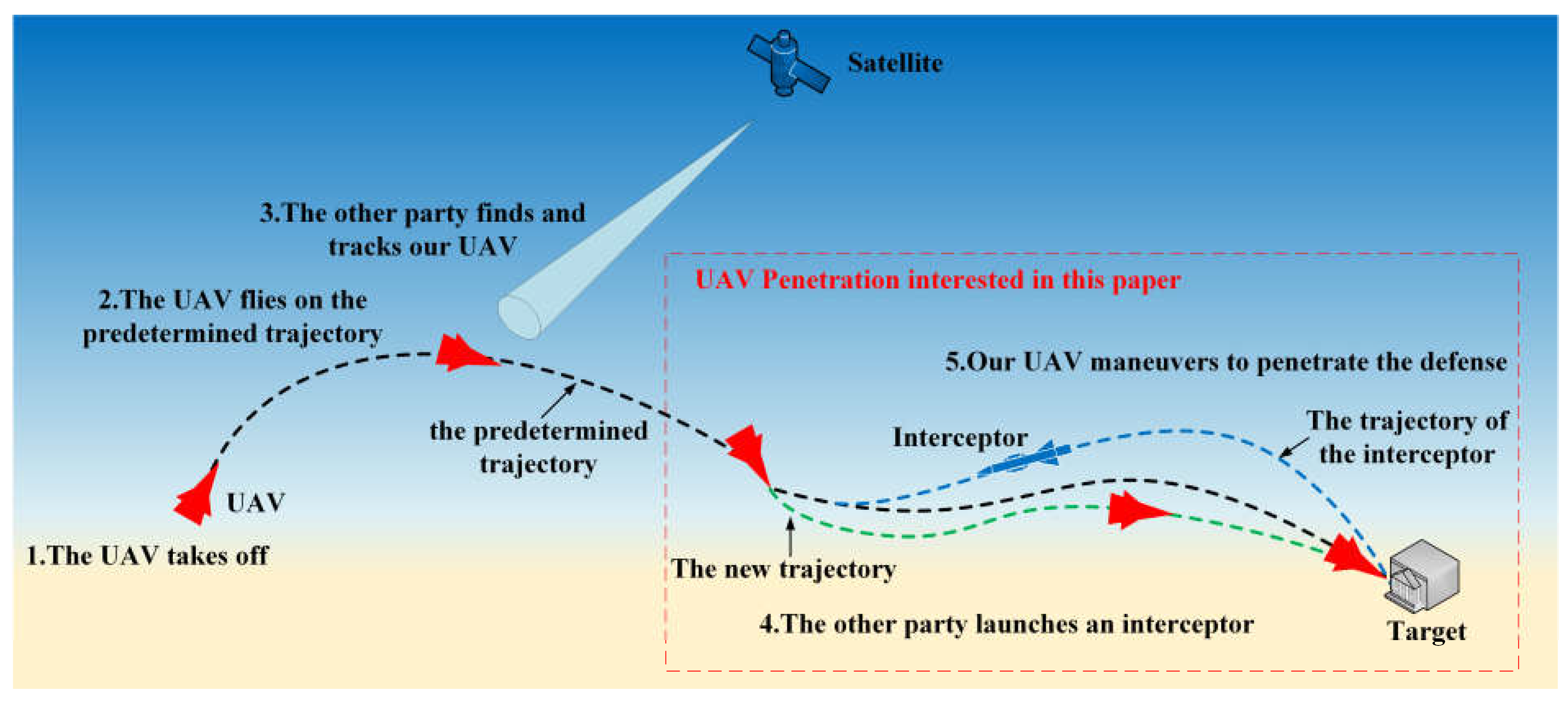
3.1. UAV Penetration
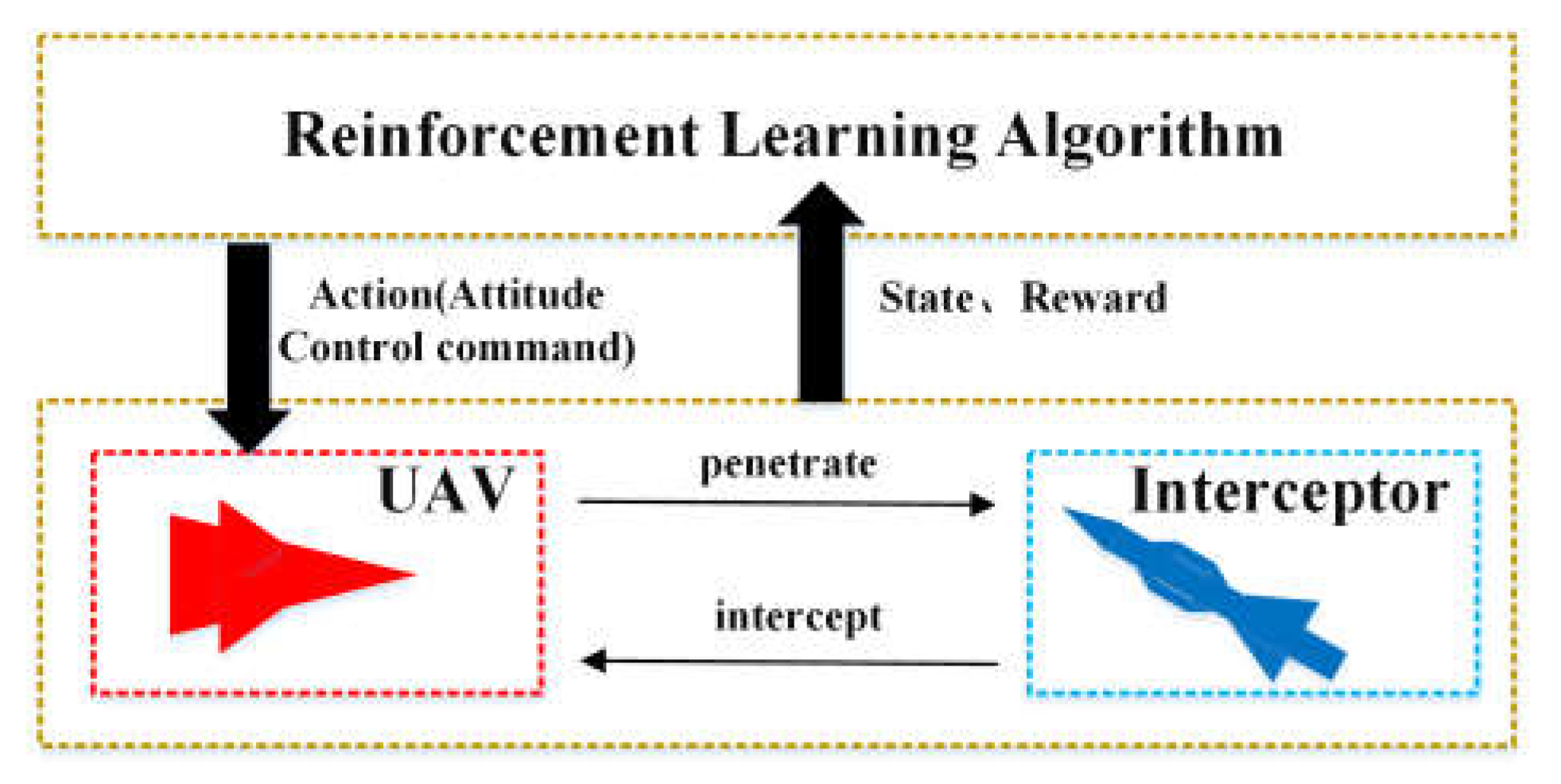
3.2. Reinforcement Learning Description of UAV Penetration
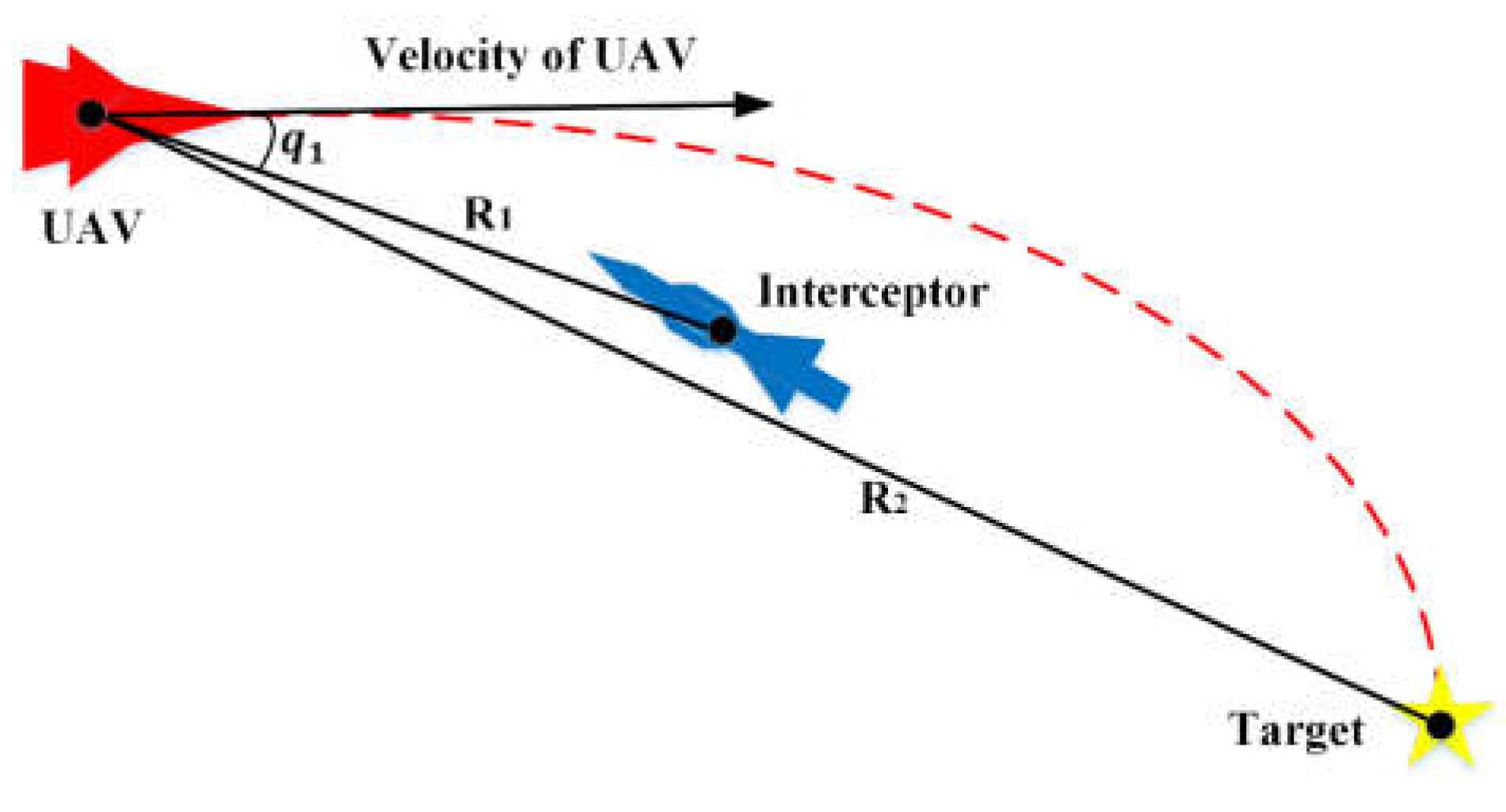
3.2.1. State and Action Specification
3.2.2. Reward Shaping
- (a).
- Guiding the UAV through interception defenses
- (b).
- Guiding the UAV to hit the target after penetration
| Function 1: Reward Function of UAV Penetration. |
If the UAV is intercepted: , where , is the increasing function of , where , , is the increasing function of If the UAV penetrates successfully: , where , is the instant reward for successful penetration If the UAV fails to penetrate: , where , is the immediate penalty for failed penetration If the UAV successfully penetrates and before landing: , where , , is the decreasing function of If the UAV lands and hits the target: , where , is the instant reward for hitting the targetIf the UAV lands and misses the target: , where , is the immediate penalty for missing the target |
4. TCD-SAC Algorithm
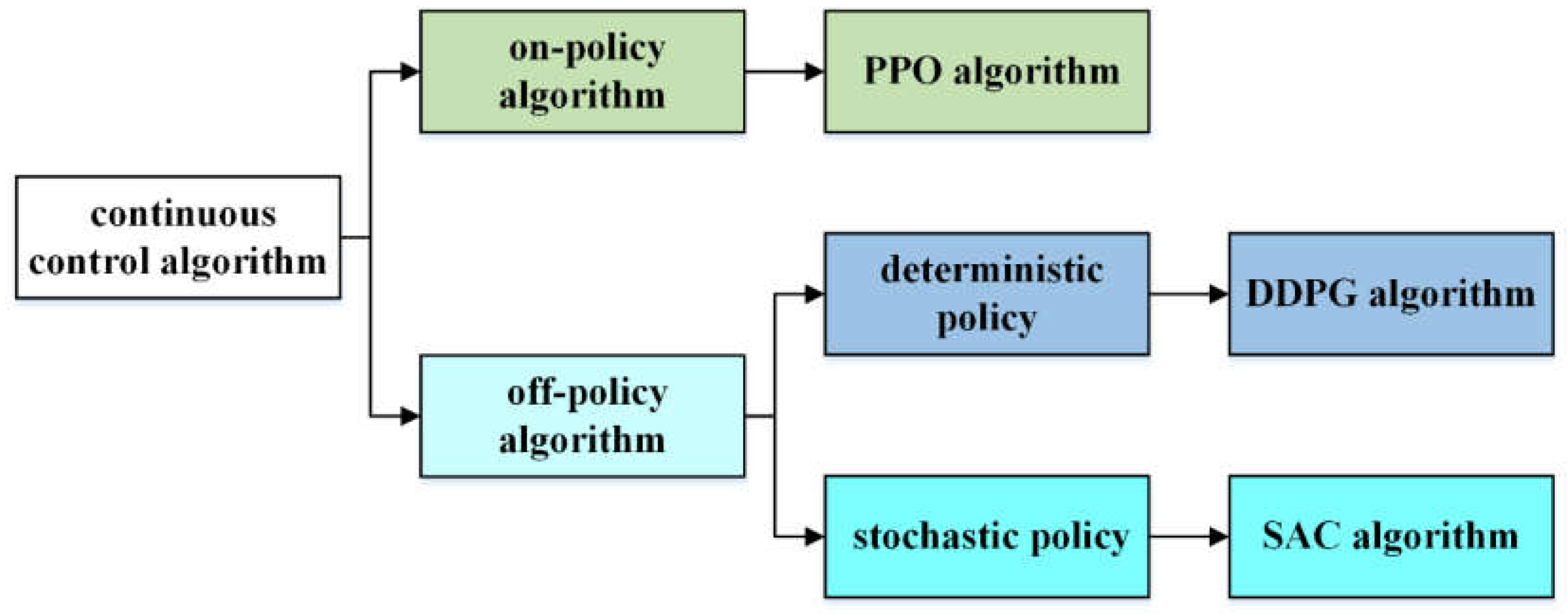
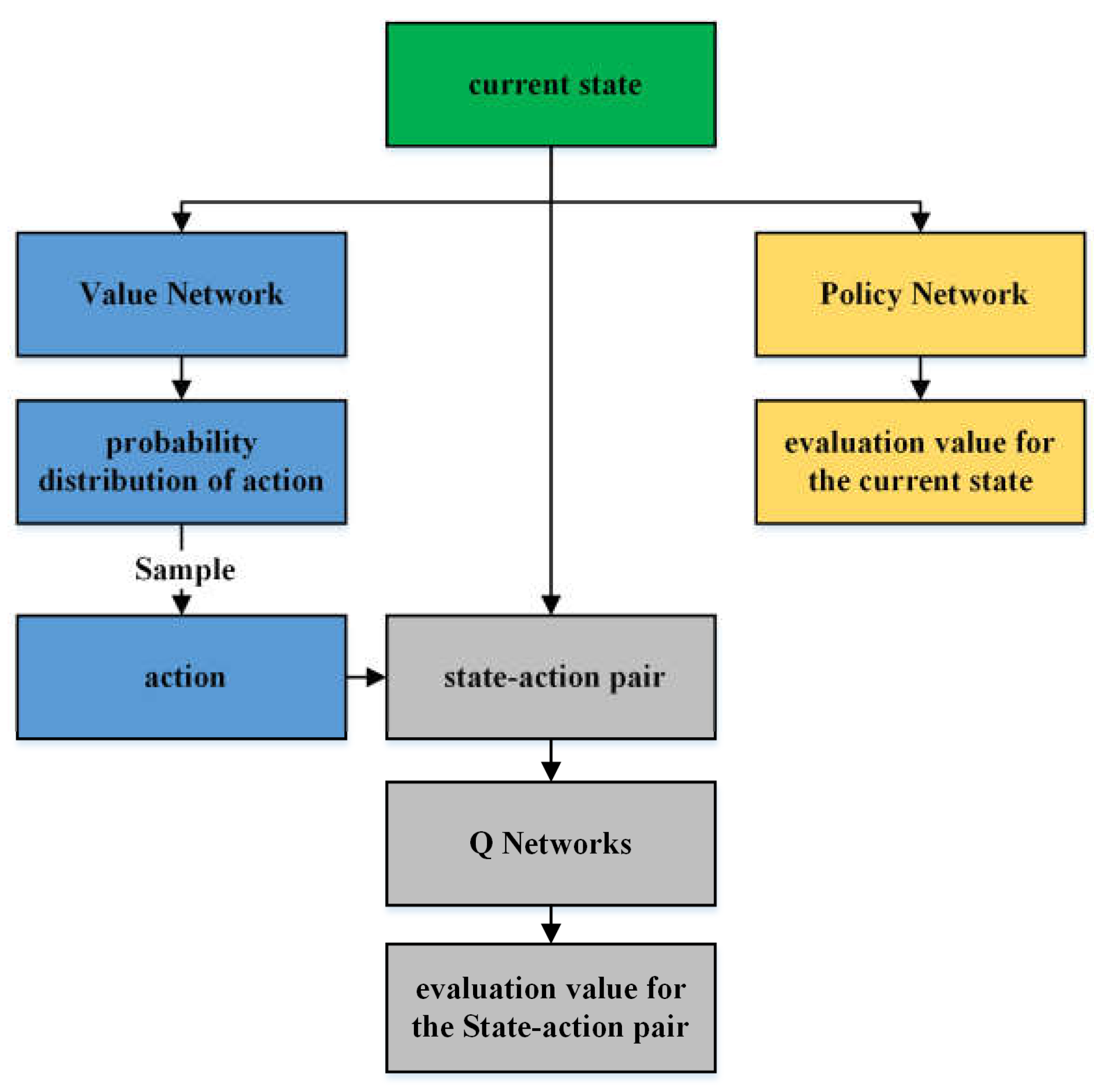
4.1. SAC Algorithm
4.2. Task Completion Division
| Algorithm 1: Task completion division (TCD) algorithm |
| Given: a reinforcement learning algorithm a reward function : . Initialize Initialize replay buffer for episode = 1, do Set a task and sample an initial state . For do Sample an action using the behavioral policy from : Execute the action and observe the next state end for for do Store the transition in for do Store the transition in end for end for for do Sample a minibatch from the replay buffer Perform one step of optimization using and minibatch end for end for |
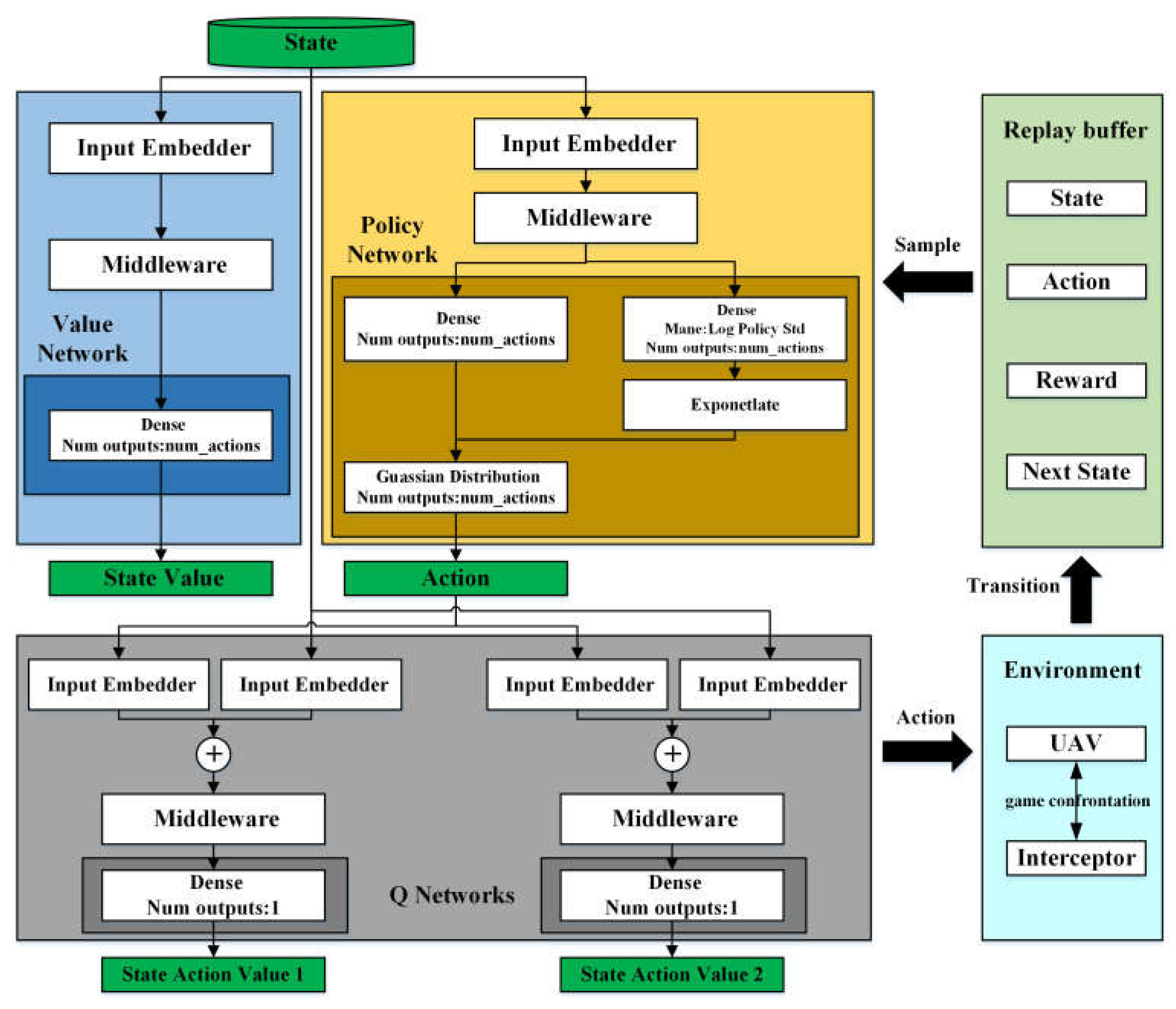
4.3. TCD-SAC Algorithm
| Algorithm 2: Task completion division–soft actor critic (TCD-SAC) algorithm |
| Input:, , , for each iteration do for each environment step do for do end for end for for each gradient step do end for end for Output:, , |
5. Environmental Results and Discussion
5.1. Training and Testing Environment
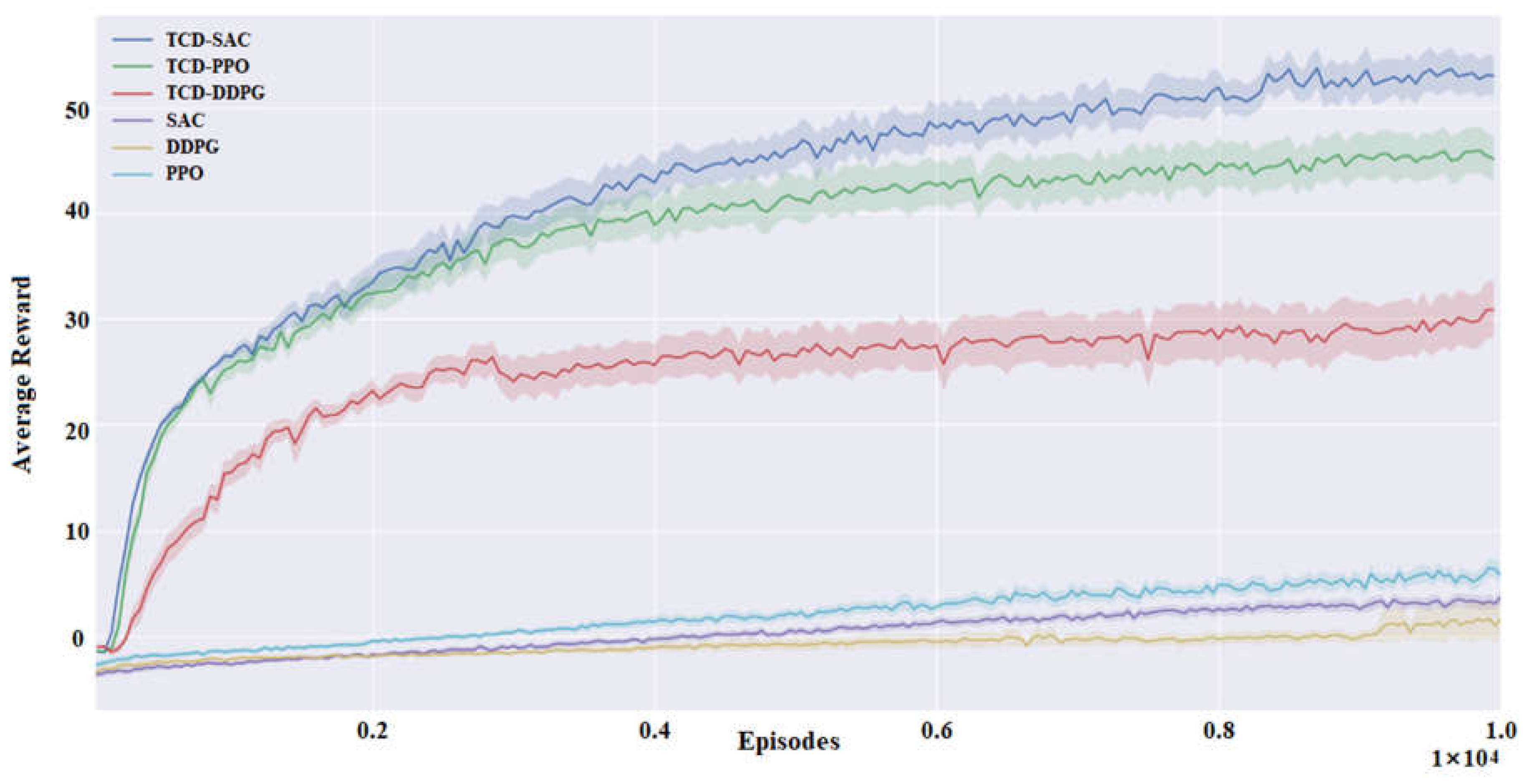
5.2. Performance in Training Experiment
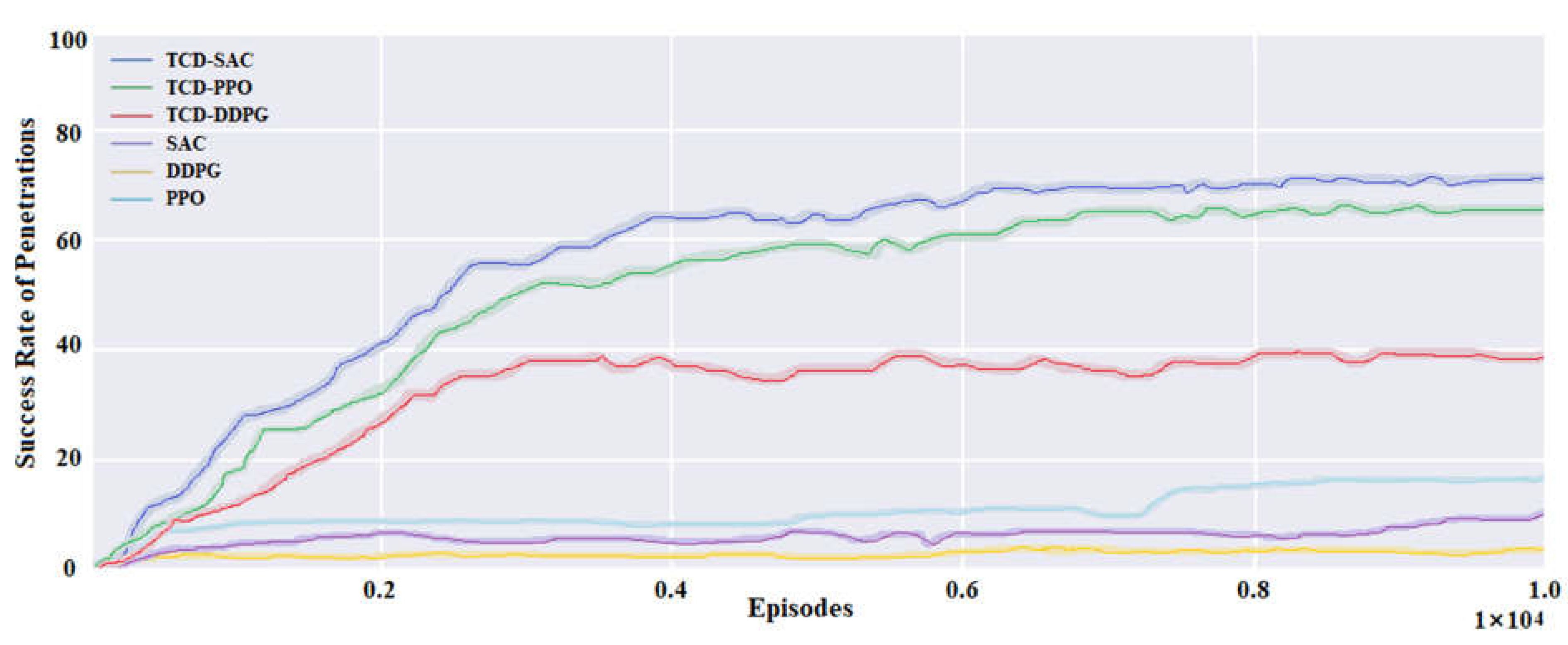
5.3. Performance in Test Experiment
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Kumar, G.N.; Sarkar, A.; Mangrulkar, K.; Talole, S. Atmospheric vehicle trajectory optimization with minimum dynamic pressure constraint. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 837–846. [Google Scholar] [CrossRef]
- Chai, R.; Savvaris, A.; Tsourdos, A.; Chai, S.; Xia, Y.; Wang, S. Solving trajectory optimization problems in the presence of probabilistic constraints. IEEE Trans. Cybern. 2019, 50, 4332–4345. [Google Scholar] [CrossRef]
- Xu, J.; Dong, C.; Cheng, L. Deep neural network-based footprint prediction and attack intention inference of hypersonic glide vehicles. Mathematics 2022, 11, 185. [Google Scholar] [CrossRef]
- Gao, Y.; Cai, G.; Yang, X.; Hou, M. Improved tentacle-based guidance for reentry gliding hypersonic vehicle with no-fly zone constraint. IEEE Access 2019, 7, 119246-58. [Google Scholar] [CrossRef]
- Liao, Y.; Li, H. Trajectory optimization for terminal phase flight of hypersonic reentry vehicles with multi-constraints. In Proceedings of the 2013 25th Chinese Control and Decision Conference (CCDC), Guiyang, China, 25–27 May 2013; pp. 571–576. [Google Scholar]
- Sana, K.S.; Weiduo, H. Hypersonic reentry trajectory planning by using hybrid fractional-order particle swarm optimization and gravitational search algorithm. Chin. J. Aeronaut. 2021, 34, 50–67. [Google Scholar] [CrossRef]
- Chai, R.; Savvaris, A.; Tsourdos, A.; Chai, S.; Xia, Y. Improved gradient-based algorithm for solving aeroassisted vehicle trajectory optimization problems. J. Guid. Control Dyn. 2017, 40, 2093–2101. [Google Scholar] [CrossRef]
- Wan, K.; Gao, X.; Hu, Z.; Wu, G. Robust motion control for uav in dynamic uncertain environments using deep reinforcement learning. Remote Sens. 2020, 12, 640. [Google Scholar] [CrossRef]
- Luo, J.; Liang, Q.; Li, H. Uav penetration mission path planning based on improved holonic particle swarm optimization. J. Syst. Eng. Electron. 2023, 34, 197–213. [Google Scholar] [CrossRef]
- Fu, J.; Sun, G.; Yao, W.; Wu, L. On trajectory homotopy to explore and penetrate dynamically of multi-uav. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24008–24019. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, J.; Dai, J.; He, C. A novel real-time penetration path planning algorithm for stealth uav in 3d complex dynamic environment. IEEE Access 2020, 8, 122757–122771. [Google Scholar] [CrossRef]
- Luo, Y.; Song, J.; Zhao, K.; Liu, Y. Uav-cooperative penetration dynamic-tracking interceptor method based on ddpg. Appl. Sci. 2022, 12, 1618. [Google Scholar] [CrossRef]
- Li, Y.; Han, W.; Wang, Y. Deep reinforcement learning with application to air confrontation intelligent decision-making of manned/unmanned aerial vehicle cooperative system. IEEE Access 2020, 8, 67887–67898. [Google Scholar] [CrossRef]
- Kaifang, W.; Bo, L.; Xiaoguang, G.; Zijian, H.; Zhipeng, Y. A learning-based flexible autonomous motion control method for uav in dynamic unknown environments. J. Syst. Eng. Electron. 2021, 32, 1490–1508. [Google Scholar] [CrossRef]
- Liang, L.; Deng, F.; Wang, J.; Lu, M.; Chen, J. A reconnaissance penetration game with territorial-constrained defender. IEEE Trans. Autom. Control 2022, 67, 6295–6302. [Google Scholar] [CrossRef]
- Bellman, R. A markovian decision process. J. Math. Mech. 1957, 6, 679–684. [Google Scholar] [CrossRef]
- Li, S.; Lei, H.; Shao, L.; Xiao, C. Multiple model tracking for hypersonic gliding vehicles with aerodynamic modeling and analysis. IEEE Access 2019, 7, 28011–28018. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y.; Wang, S.; Huang, W. Backstepping attitude control for hypersonic gliding vehicle based on a robust dynamic inversion approach. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2014, 228, 543–552. [Google Scholar] [CrossRef]
- Li, G.; Zhang, H.; Tang, G. Maneuver characteristics analysis for hypersonic glide vehicles. Aerosp. Sci. Technol. 2015, 43, 321–328. [Google Scholar] [CrossRef]
- Shen, Z.; Yu, J.; Dong, X.; Hua, Y.; Ren, Z. Penetration trajectory optimization for the hypersonic gliding vehicle encountering two interceptors. Aerosp. Sci. Technol. 2022, 121, 107363. [Google Scholar] [CrossRef]
- Yan, B.; Liu, R.; Dai, P.; Xing, M.; Liu, S. A rapid penetration trajectory optimization method for hypersonic vehicles. International J. Aerosp. Eng. 2019, 2019, 11. [Google Scholar] [CrossRef]
- Chai, R.; Tsourdos, A.; Savvaris, A.; Chai, S.; Xia, Y.; Chen, C.P. Six-dof spacecraft optimal trajectory planning and real-time attitude control: A deep neural network-based approach. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 5005–5013. [Google Scholar] [CrossRef] [PubMed]
- Xiang, J.; Li, Q.; Dong, X.; Ren, Z. Continuous control with deep reinforcement learning for mobile robot navigation. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 1501–1506. [Google Scholar]
- Wenjun, N.; Ying, B.; Di, W.; Xiaoping, M. Energy-optimal trajectory planning for solar-powered aircraft using soft actor-critic. Chin. J. Aeronaut. 2022, 35, 337–353. [Google Scholar]
- Eteke, C.; Kebüde, D.; Akgün, B. Reward learning from very few demonstrations. IEEE Trans. Robot. 2020, 37, 893–904. [Google Scholar] [CrossRef]
- Han, S.-C.; Bang, H.; Yoo, C.-S. Proportional navigation-based collision avoidance for uavs. Int. J. Control Autom. Syst. 2009, 7, 553. [Google Scholar] [CrossRef]
- Wang, Z.; Cheng, X.X.; Li, H. Hypersonic skipping trajectory planning for high l/d gliding vehicles. In Proceedings of the 21st AIAA International Space Planes and Hypersonics Technologies Conference, Xiamen, China, 6–9 March 2017; p. 2135. [Google Scholar]
- Tripathi, A.K.; Patel, V.V.; Padhi, R. Autonomous landing of fixed wing unmanned aerial vehicle with reactive collision avoidance. IFAC-PapersOnLine 2018, 51, 474–479. [Google Scholar] [CrossRef]
- Maeda, R.; Mimura, M. Automating post-exploitation with deep reinforcement learning. Comput. Secur. 2021, 100, 102108. [Google Scholar] [CrossRef]
- Sackmann, M.; Bey, H.; Hofmann, U.; Thielecke, J. Modeling driver behavior using adversarial inverse reinforcement learning. In Proceedings of the 2022 IEEE Intelligent Vehicles Symposium (IV), Aachen, Germany, 5–9 June 2022; pp. 1683–1690. [Google Scholar]
- Hu, Y.; Gao, C.; Li, J.; Jing, W.; Li, Z. Novel trajectory prediction algorithms for hypersonic gliding vehicles based on maneuver mode on-line identification and intent inference. Meas. Sci. Technol. 2021, 32, 115012. [Google Scholar] [CrossRef]
- Alzahrani, B.; Oubbati, O.S.; Barnawi, A.; Atiquzzaman, M.; Alghazzawi, D. Uav assistance paradigm: State-of-the-art in applications and challenges. J. Netw. Comput. Appl. 2020, 166, 102706. [Google Scholar] [CrossRef]
- Kontogiannis, S.G.; Ekaterinaris, J.A. Design, performance evaluation and optimization of a uav. Aerosp. Sci. Technol. 2013, 29, 339–350. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.; Di, B.; Song, L. Cellular uav-to-x communications: Design and optimization for multi-uav networks. IEEE Trans. Wirel. Commun. 2019, 18, 1346–1359. [Google Scholar] [CrossRef]
- Oubbati, O.S.; Atiquzzaman, M.; Ahanger, T.A.; Ibrahim, A. Softwarization of uav networks: A survey of applications and future trends. IEEE Access 2020, 8, 98073–98125. [Google Scholar] [CrossRef]
- Koch, W.; Mancuso, R.; West, R.; Bestavros, A. Reinforcement learning for uav attitude control. ACM Trans. Cyber-Phys. Syst. 2019, 3, 1–21. [Google Scholar] [CrossRef]

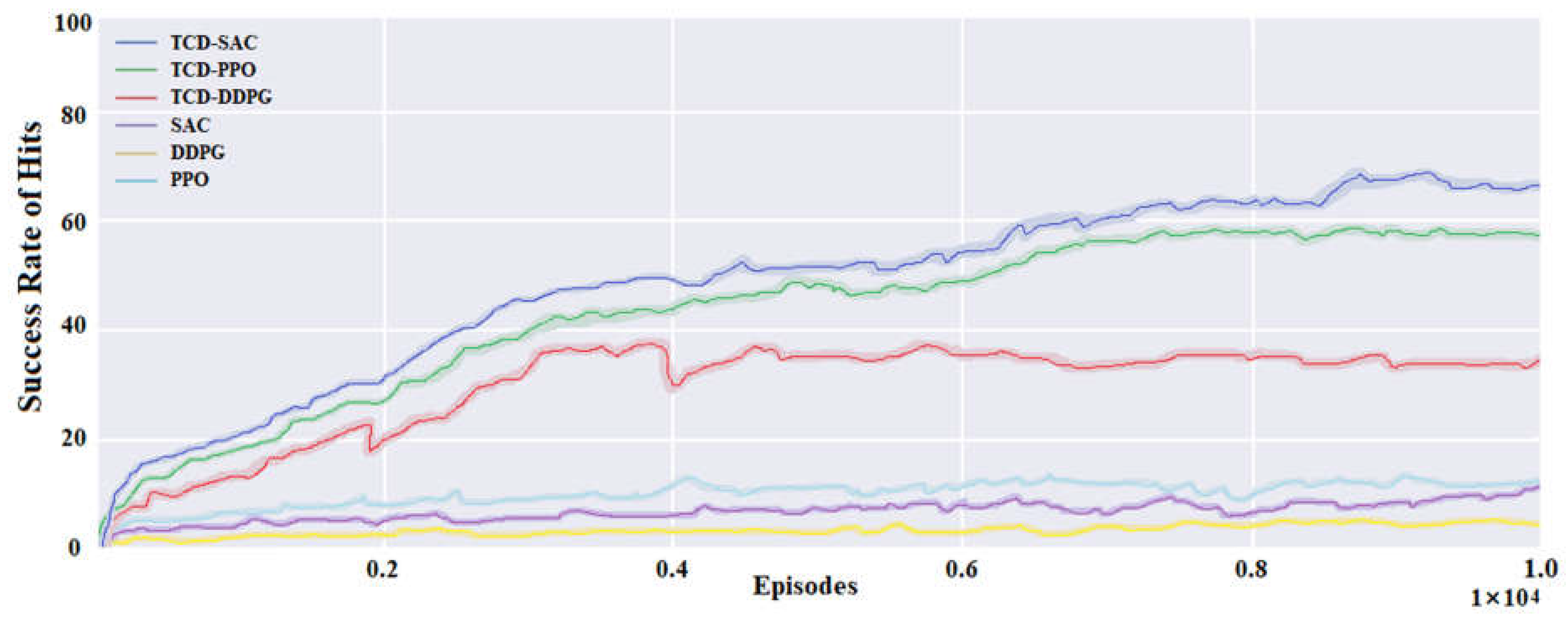
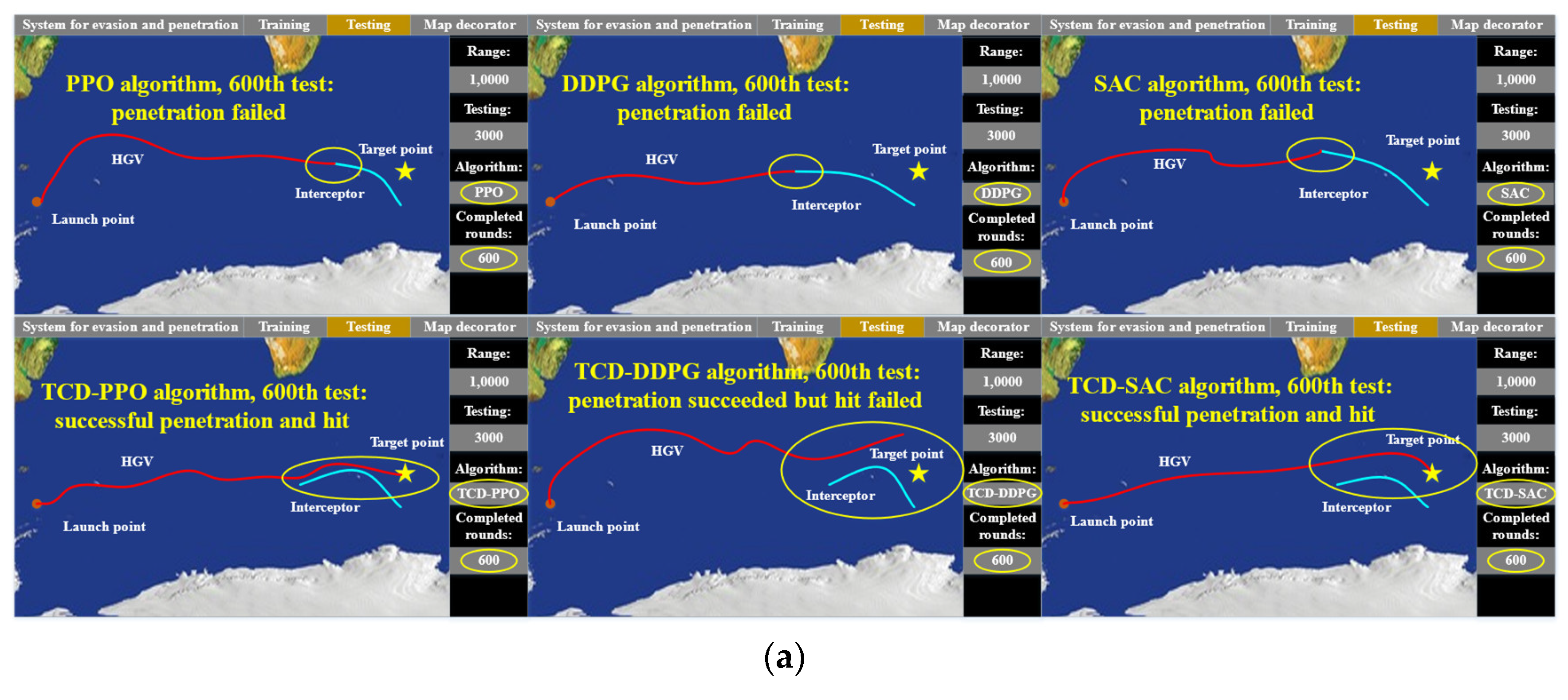


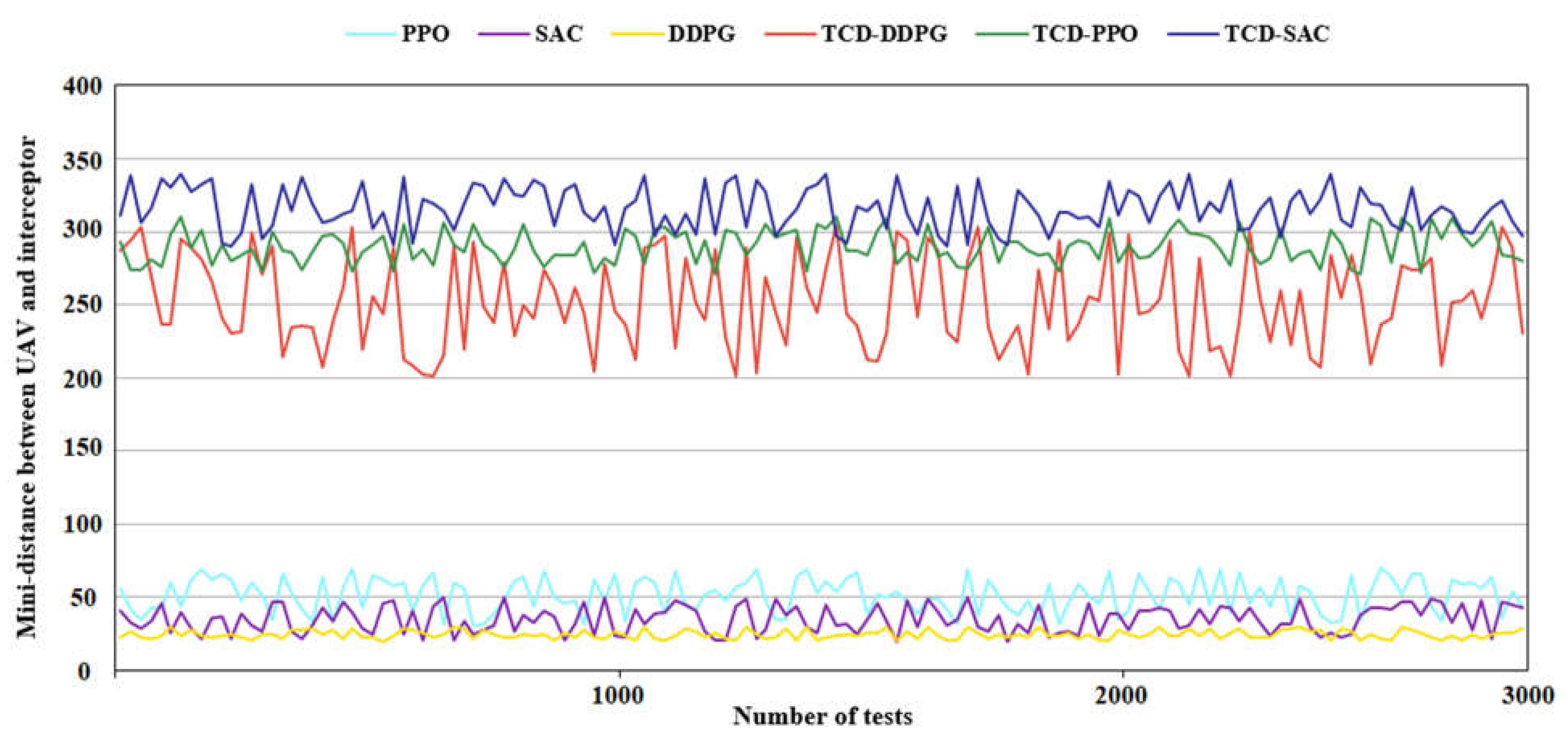

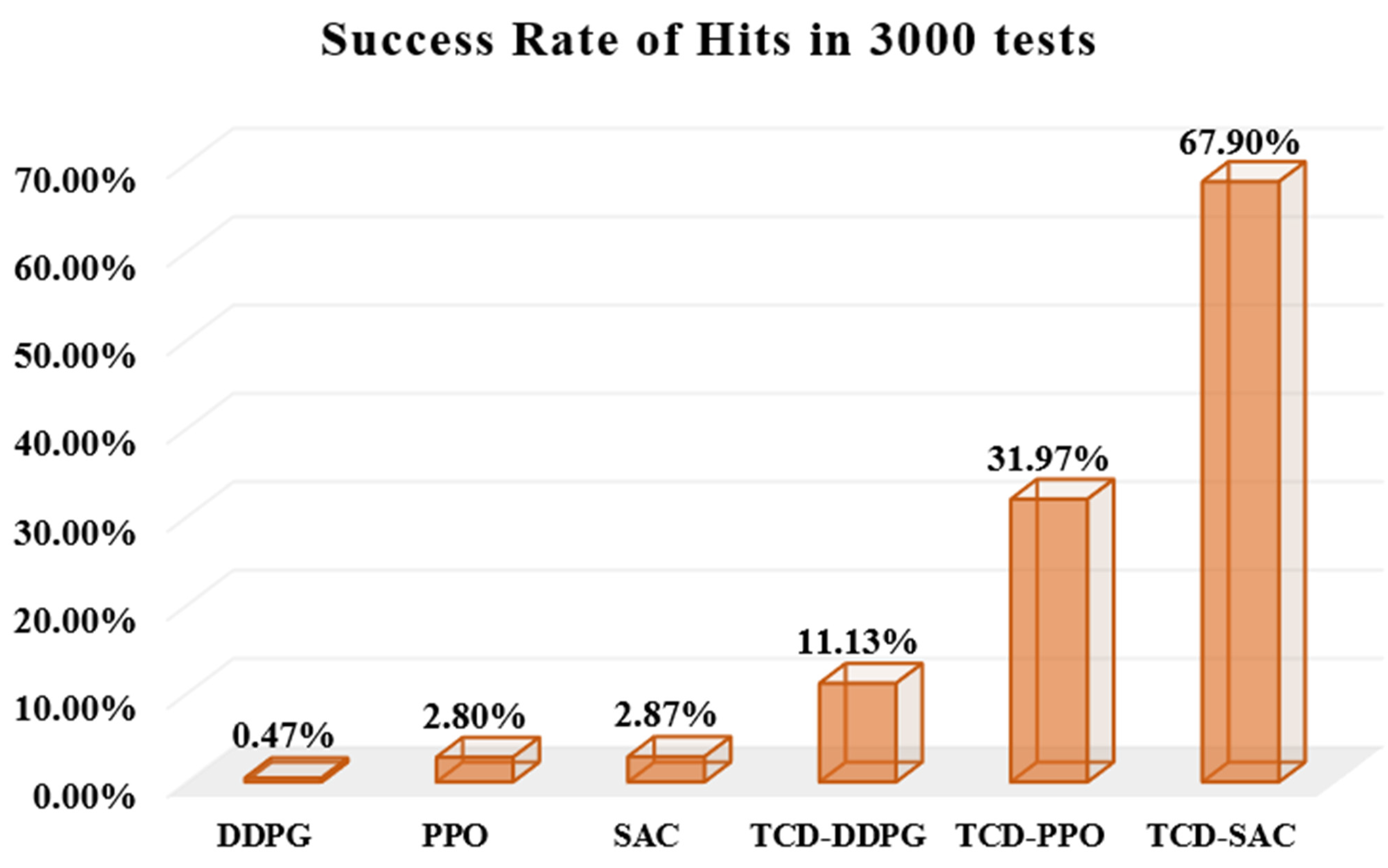
| Performance | Value |
|---|---|
| range | 4000~6000 km |
| maximum boost height | 120~180 km |
| glide height | 30~40 km |
| gliding speed | 4~6 Ma |
| Algorithm | Network Dimension Number | Network Layer Number | Replay Buffer | Batch Size | Update Times | Discount Factor |
|---|---|---|---|---|---|---|
| SAC | 128 | 4 | 217 | 128 | 1024 | 0.998 |
| DDPG | 256 | 4 | 217 | 256 | 512 | 0.997 |
| PPO | 128 | 8 | 217 | 128 | 1024 | 0.994 |
| TCD-SAC | 128 | 4 | 217 | 128 | 1024 | 0.995 |
| TCD-DDPG | 256 | 4 | 217 | 256 | 512 | 0.991 |
| TCD-PPO | 128 | 8 | 217 | 128 | 1024 | 0.997 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, K.; Zhuang, X.; Liu, X.; Li, H. A Reinforcement Learning Method Based on an Improved Sampling Mechanism for Unmanned Aerial Vehicle Penetration. Aerospace 2023, 10, 642. https://doi.org/10.3390/aerospace10070642
Wang Y, Li K, Zhuang X, Liu X, Li H. A Reinforcement Learning Method Based on an Improved Sampling Mechanism for Unmanned Aerial Vehicle Penetration. Aerospace. 2023; 10(7):642. https://doi.org/10.3390/aerospace10070642
Chicago/Turabian StyleWang, Yue, Kexv Li, Xing Zhuang, Xinyu Liu, and Hanyu Li. 2023. "A Reinforcement Learning Method Based on an Improved Sampling Mechanism for Unmanned Aerial Vehicle Penetration" Aerospace 10, no. 7: 642. https://doi.org/10.3390/aerospace10070642
APA StyleWang, Y., Li, K., Zhuang, X., Liu, X., & Li, H. (2023). A Reinforcement Learning Method Based on an Improved Sampling Mechanism for Unmanned Aerial Vehicle Penetration. Aerospace, 10(7), 642. https://doi.org/10.3390/aerospace10070642






