Abstract
Integration of Uncrewed Aircraft into unsegregated airspace requires robust and objective risk assessment in order to prevent exposure of existing airspace users to additional risk. A probabilistic Mid-Air Collision risk model is developed based on surveillance traffic data for the intended operational area. Simulated probable traffic scenarios are superimposed on a desired Uncrewed Aircraft operation and then sampled using Monte Carlo methods. The results are used to estimate the operation-specific collision probability with known uncertainty in the output. The methodology is demonstrated for an example medical logistics operation in the United Kingdom, and a Target Level of Safety is used as a benchmark to decide whether the operation should be permitted.
1. Introduction
The integration of Uncrewed Aircraft Systems (UAS), colloquially referred to as “drones”, into airspace poses a number of challenges. In most jurisdictions, the operation of UAS is still restricted to segregated airspace, where the UAS should be the only aircraft operating within the defined volume of airspace. This approach, whilst almost eliminating the Mid-Air Collision (MAC) risk, is a very inefficient use of airspace and is neither scalable nor sustainable for multiple UAS operations. The deployment of segregated airspace in the United Kingdom (UK), taking the form of a Temporary Danger Area (TDA), has drawn complaints from the General Aviation (GA) community, who are usually the airspace users most affected as the segregated airspace is usually set up within uncontrolled airspace [1]. This is where the majority of GA operations take place, and the introduction of segregated airspace reduces the airspace available to GA and could contribute to higher MAC risk between GA aircraft as a result. In part due to these circumstances, the integration of UAS into non-segregated airspace is a desirable future outcome that has received considerable research interest.
In order to facilitate the integration of UAS, the risks posed to other airspace users must be considered. This includes the risk of a MAC between a UAS and another crewed aircraft. As GA aircraft operating within uncontrolled airspace are by definition not under the control of Air Traffic Control (ATC), they often use the concept of See and Avoid to tactically deconflict from other aircraft. This poses a problem when it comes to UAS, as they can be considerably smaller than other crewed aircraft. This means that it is very difficult and, at times, impossible to visually identify them with sufficient time to avoid them. This work, therefore, addresses this case.
The goal of this methodology was to find the unmitigated Mid-Air Collision (uMAC) probability. Concretely, this means that the methodology disregarded the contributions of any tactical deconfliction means ranging from pilot intervention to technologies such as TCAS to the reduction in MAC risk. This was done intentionally to provide a worst-case but still realistic estimate of the uMAC upper bound value. The rationalisation was then that any additional mitigation measures could only improve (reduce) this uMAC risk value. Additionally, this removed a large amount of complexity from the modelling and simulation, allowing very fast run times for the simulations and the achievement of the required large number of samples for the Monte Carlo methodology used.
The novel contribution of this work is the introduction of spatiotemporal, localised altitude distributions allowing more realistically distributed background traffic. This allows the application of the presented methodology both in the vicinity of aerodromes and en route at specific times of the day. This forms part of an unmitigated mid-air collision (uMAC) risk quantification methodology that is operation-centric and extensible, employing Monte Carlo methods. Additionally, a provision is made to include non-transponder-equipped traffic in the analysis. Whilst simulation approaches are commonly discounted as requiring an infeasible number of simulations, we successfully demonstrate the use of the approach in a reasonable computational time.
In Section 2, we present the methodology and demonstrate an application to a case study in Southern England; in Section 3.5 the results of the case study are presented; in Section 5, we discuss the results, their wider applicability and the strengths and weakness of the methodology; finally, we draw conclusions in Section 5.
2. Related Works
Endoh [2] presented comprehensive analytical models for MAC rate from first principles based up on traffic density, aircraft speed, and dimensions. The model was stochastic in nature and applicable to airspace with known individual (or averaged) parameters for the input variables. Holt et al. [3] also related surveillance accuracy and separation standards to MAC rate to allow for real-time collision hazard prediction. Knecht [4] examined the mathematical assumptions behind the “Big Sky Theory”; a concept that states that a pair of stochastically flying aircraft are unlikely to collide due to the relative size of three-dimensional free space compared to the size of the aircraft in question. The work employed a Gas Law-based approach to initially model the theory that was then validated by Monte Carlo simulations. The input parameters were the same as that for Endoh, namely traffic density, speed, and size. The results suggested that physical collisions were relatively rare; however, the infringement of formal separation standards was common. Patlovany [5] used a Monte Carlo model to compare several different systems of rules for aircraft to reduce the MAC rate themselves and, in addition, model the effects of compliance to the given rules. The results suggested that the MAC risk is directly proportional to compliance to the given rules. Additionally, the model was focused on an en route environment where there were usually far fewer climbing or descending aircraft that could affect the MAC risk. A similar analysis was performed by Sunil et al. [6] who examined the MAC rate of several different airspace constructs in order to determine the optimal airspace design for reduced MAC risk. They validated their model using fast-time simulations.
The preceding literature examined the MAC in idealised environments. Jardin [7] developed a binomial random variable model to predict conflict counts as a function of traffic density. Real-world surveillance data was combined with simulation data to fit the model, which was then tested in both a free route uncontrolled environment and a strategically deconflicted Air Traffic Management environment. In the free route environment, it was found that the binomial random variable model was well suited to the modelling of conflict counts. La Cour-Harbo and Schiøler [8] used real world data to estimate the probability of several classes of GA aircraft being below a set altitude threshold and, therefore, at risk of MAC with UAS in Denmark. They applied these fitted probability distributions of altitude to a derived analytical model of MAC probability that was specific to GA aircraft and low altitude environments, but was uniformly applied to a large area rather than specific to a given location. McFadyen and Martin [9] also used a data-driven approach to find high MAC risk areas from which UAS should be excluded, based upon a risk-opportunity metric from their analysis. They used real traffic data for a low altitude area of Brisbane, Australia, to demonstrate the methodology and its real-world application. The approach was specific to a given location and, similarly to la Cour-Harbo and Schiøler, was a probabilistic risk assessment methodology. In a further work, McFadyen [10] determined maximum altitudes for UAS in the vicinity of a major aerodrome based upon a Target Level of Safety. This work was most similar to Lee et al. [11], who analysed the MAC risk for a region of interest located around Grand Forks, USA, by collating one year of traffic data and replacing historic traffic positions with probability distributions to generate a “continuous traffic model”. This enabled the integration of an intended path and associated conflict volume across the continuous traffic model in order to determine the probability of encountering traffic.
3. Methodology
A Monte Carlo method (MC) was used to sample positions of traffic within a specific operational scenario. The process could be split into a number of steps that provide insightful information in their own right, particularly as a result of the traffic data analysis.
The methodology aimed to characterise the position of traffic in the desired area of operation probabilistically, then reconstruct a probable traffic scenario with the addition of the UAS that we wished to introduce into the real environment, referred to as the ownship. For each sample, the distance between each of the traffic entities and the ownship was calculated along the ownship path and any conflicts were returned.
The method allows for the flexible inclusion or exclusion of any number of additional factors that may affect the uMAC of the operation, therefore is extensible and accommodating of constraints or conditions that are specific to a given operation. The only theoretical limitation is the ability to model this within the traffic scenario samples, although practical consideration should also be made for the computational cost this could incur. This differs from the “airspace-centric” approach by McFadyen and Martin [9]. The method presented here can be considered an “operation-centric” approach to risk assessment.
The method consists of a number of steps: Operational Area definition, Traffic Surveillance data collection/ingestion, traffic data analysis, MC sampling of traffic scenarios, and, finally, analysis of MC outputs.
3.1. Surveillance Data Analysis
As the simulations are stochastic, there is little to be gained from modelling traffic operating under the control of Air Traffic Control (ATC) within controlled airspace, that is airspace where all traffic motion is dictated by ATC. The group that UAS pose the highest MAC risk to is General Aviation (GA), who routinely operate in uncontrolled airspace and are under no obligation to be in receipt of ATC services. We, therefore, emphasised the inclusion of GA in the data.
3.1.1. Data Ingestion
Once the analysis area had been established, the ingestion of the traffic data could begin. This was obtained from the OpenSky network [12], a research data repository that collates (primarily) ADS-B returns that are collected by a global network of ADS-B receivers that are run usually by volunteers or institutions. In this sense, it is very similar to commercial products such as FlightRadar24, which also rely on individual receivers donating their data to the network.
A year was chosen as the time horizon for the data as it was judged to be suitably long to encompass trends and a full cycle of the seasons, and, therefore, the weather. This is particularly important as the range of weather conditions that General Aviation can and do fly in is much narrower than commercial aviation. Additionally, General Aviation is not scheduled and has much lower commercial pressures, if any; therefore, if the weather is unfavourable, any flying will usually be deferred or cancelled. There is also a time and server loading cost to downloading large amounts of data, therefore only downloading as much as is required makes the analysis process faster and the data provider hosting more sustainable. As an example, for the year of 2019, the traffic data for the south of England, widely considered very busy airspace, consisted of 110GiB uncompressed.
The data are provided in the form of state vectors, . These are single geographic positions specified by their latitude, , longitude, , and altitude above mean sea level h and associated with a time, t. The state vectors can trivially be reassembled into a trajectory of I points, . There are a considerable number of other variables that are associated with each state vector, such as the ICAO transponder address, the callsign, and the “squawk” code. These additional data were not useful for the analysis, however; therefore, they were discarded in order to reduce the size and therefore reduce the amount of data needing processing.
It must be recognised that there is a significant self-selection bias in the data. This is inherent to the method used to collect the data as they depend on the carriage of a ADS-B transponder onboard the aircraft. Transponders are a form of Electronic Conspicuity (EC) that send additional information about the aircraft. This additional information includes identification, speed, and altitude and can be received by other suitable receivers, which is how the majority of ADS-B data are collected. This additional information can be crucial in areas of complex airspace. Primary radar, whilst requiring no additional equipment onboard the aircraft, can only calculate the slant range of the aircraft; this means that the altitude of the aircraft is either impossible to determine or must rely upon multi-lateration, where the time taken to receive a reflection from an irradiated target is accurately calculated from multiple receivers with known locations to find the distance to each receiver.
Transponders can be expensive equipment and are, at time of writing, not mandatory in the UK. It is estimated by the UK General Aviation Alliance (GAA) that approximately 5000 out of 23,000 Sport and Recreation General Aviation aircraft are equipped with transponders, which is equivalent to 21.7% equipage. These data that we have obtained could therefore only capture approximately that percentage of the actual traffic in the skies. With a lack of any additional spatial information, it was impossible to determine how this equipage is distributed. It was conjectured that a higher proportion of aircraft operating in the South of England and around more complex airspace would be equipped with transponders, as there is greater incentive in terms of safety and airspace access compared to rural areas with little to no controlled airspace and much lower traffic densities. Additionally, we conjectured that fewer aircraft would be equipped with transponders at lower heights, owing to the greater diversity of different aircraft types such as paragliders and sailplanes. A discussion of how this was handled is included in the following section.
3.1.2. Data Aggregation
The flight trajectories, , were then filtered and cleaned of spurious data points. This was done using a median filter across the positional variables, , within the state vector. This implicitly assumed that aircraft would follow a broadly “smooth” trajectory, which is reasonable for the vast majority of aircraft. Every trajectory was uniformly resampled to a frequency of 10 s, such that
where obtains the time of the state vector S. After filtering, the number of unique trajectories considered in the dataset, J, was 44,222.
A traffic count map was generated with lateral cell resolutions of m, such that each cell had the number of unique intersecting trajectories. The map, , was obtained directly through aggregation of the data, which include only EC-equipped flights. The estimation of non-EC-equipped (NEC) aircraft consisted of scaling to obtain the total traffic count map, :
This was a reasonable assumption that generally constitutes the worst case for the traffic density because, as previously discussed, most high traffic density regions are likely to have a higher EC equipage. This resulted in a traffic count map such as that in Figure 1.

Figure 1.
Scaled annual traffic density in uncontrolled airspace in Southern England for the year 2019.
A standard geographic projection, , was used to map geographic coordinates to a local Cartesian coordinate system.
As the distributions were unknown and upon inspection did not conform to a standard parameterised distribution, a non parametric characterisation had to be found. For this same reason, it was not valid to approximate the characteristic traffic variables as a standard distribution and proceed analytically. The lateral positional variables were modelled for the entire operational area as Kernel Density Estimates:
The kernel function, K, used was the Epanechnikov kernel [13]:
for the support . The bandwidth parameter w was found by minimising the Mean Integrated Square Error (MISE) between the KDE and unknown density function. The bandwidth is a smoothing parameter and its selection is of critical importance when using a KDE.
The altitude distributions were specific to each cell midpoint location and were similarly fitted KDEs with Epanechnikov kernels.
For locations with an insufficient number of samples, the immediate neighbour cells were used instead to fit a KDE for that cell.
The temporal aspects of the problem are addressed next. The traffic density map, , was found by normalising to the volume of the cell and by 365 (days) as the surveillance data used encompassed a year. The daily temporal distribution of the traffic (such as that in Figure 2) was used to scale the mean daily traffic distribution, to a given hour of the day, .
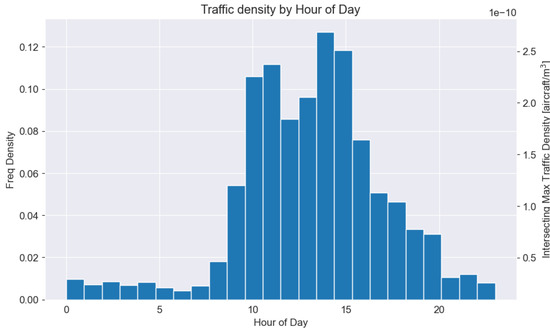
Figure 2.
Frequency density and corresponding traffic densities by hour of day for operational area.
3.2. Simulation
Samples were generated for the bounds of the desired operational area. Each sample could be considered a semi-static Agent Based Simulation (ABS). Within the ABS, there exist two types of agent: background traffic agents (referred to as traffic or traffic agents) and the ownship agent. These are representative of aircraft in the analysed traffic environment, and the ownship, whose introduction into the environment we wished to analyse for uMAC risk, respectively. Therefore, the ownship(s) were representative of the UAS(s) that we wished to introduce to the traffic environment. Within each individual simulation environment, the traffic agents did not move and only the ownship(s) were stepped forward through the simulation time.
The ownship followed a similarly defined trajectory . Whilst each cell could be responsible for the probabilistic determination of containing traffic agent(s), such as in [14], in the simulation approach taken here it may result in a large range of total numbers of traffic agents, therefore this was determined centrally prior to simulation sampling. The traffic density was found from the maximum intersecting traffic density, .
Each sample had an associated random seed that initialised a dedicated pseudo-random number generator (RNG) that was used for the generation of all random numbers for that sample. For each sample , a set of random numbers was generated to sample each positional variable KDE, , and . The lateral position was sampled first, then the corresponding altitude distribution was used to determine the vertical position. This created the static traffic set for that sample, , which was probabilistically representative of the real world traffic environment. Within the simulation world space, each background traffic aircraft was represented by the delta function. The delta function represented the position of a single aircraft. Cumulatively, they represented all traffic within the simulation run. , therefore, provided a continuous representation of the probability of traffic being located at the position .
In order to check for MACs in the environment, conflict distances were defined laterally and vertically from the ownship, as seen in Figure 3. Within these distances in their respective dimensions, a conflict was counted. This aimed to capture the physical collision probability rather than an infringement of defined separation minima. The number of MACs within each sample, , was then found by the piecewise linear integration of the simulation world space along the ownship trajectory. The piecewise linear integration scheme was similar to that in [11], therefore details are omitted for brevity.
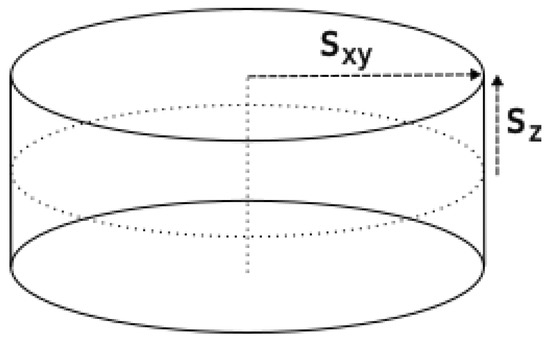
Figure 3.
Conflict Volume Definition.
3.3. Monte Carlo Analysis
As a single sample is equivalent to a single execution of the operation in the real world, it was not able to generate any useful statistical data about the uMAC probability. In order to estimate the uMAC probability, we turned to Monte Carlo (MC) methods. The core issue with the application of MC to the rare event simulation problem is the requirement for a significant number of samples in order to draw useful statistical inferences. This means the variance of the resulting output could feasibly be an order of magnitude or more than the actual result if insufficient samples are made.
The variance in the estimate reduces with in the current configuration, commonly referred to as crude Monte Carlo (CMC). The actual relative error value can be found from Equation (15). There is substantial literature on variance reduction for MC methods that can be applied in order to reduce the number of samples required to achieve the same variance value. This will be considered in future work.
The results of all the ABS runs were collected into a database that associated the run ID, random seed used and the number of conflicts for each ABS. These data also allowed for the replication and reproduction of the results, primarily for validation and traceability. An unbiased estimator, , for the true uMAC probability, p, was found by Equation (14), where N is the number of MC samples (ABS runs) and is the number of unmitigated conflicts in the n-th sample. As the effects of tactical deconfliction systems was not simulated, this is the unmitigated mid-air collision probability.
Of critical importance is the estimation of error in the result. Two measures of error could be utilised: the relative bias (RB) and relative error (RE). As the estimator in the CMC method is unbiased, the RB is negligible for large N [15] and was not considered here. The relative error is a measure of the dispersion of the estimator. This is given by Equation (15) [15] and can also be used for estimation of the required MC samples for a given estimated probability. Additionally, the convergence of the uMAC rate could be plotted against the number of samples, such as in Figure 4. This provided a more empirical validation of the convergence of the solution to cross check.
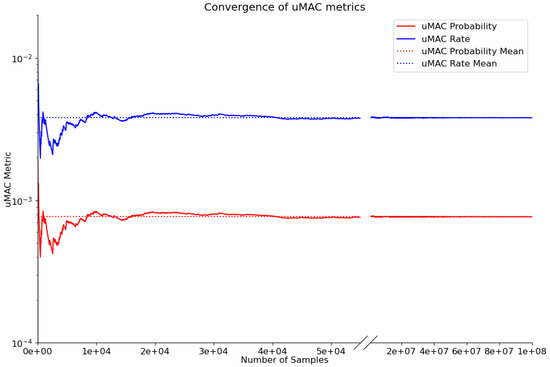
Figure 4.
Convergence of uMAC metrics across MC samples.
The confidence interval in the result could be found using the Central Limit Theorem using a common method:
where is the confidence level and is the Standard Normal inverse CDF. As the confidence interval is symmetric around the estimator value, the uMAC probability is not sensitive to the confidence level in this case.
The output could be expressed either as a uMAC probability per operation (as in Equation (14)) or uMAC rate per flight hour, given in Equation (18), where is the total number of timesteps simulated for the n-th ABS run.
By tracking the ownship position when a conflict occurs, the probability of uMAC could be determined spatially along the ownship trajectory, .
3.4. Implementation
The implementation is divided into data analysis and simulation orchestration. The former was performed in Python using the Traffic library [16], the ADS-B surveillance data were obtained from OpenSky [12], and additional sailplane data were obtained and integrated to partially account for Non-EC-equipped traffic. The latter was a custom implementation written in GoLang. The integration in Equation (13), was performed numerically by stepping along the ownship trajectory O, such that no “stepping over” of potential conflicts occurs. The step distance was empirically set to . This made the implementation function as a semi-static Agent Based Simulation (ABS), where only the ownship agent(s) were moved with every timestep.
From a computational perspective, the problem of running many samples was trivially parallel, and, therefore, easily accommodated on modern computers and easily scaled to “cloud” remote computing services. There was no requirement to synchronise or transfer any information between samples during their execution. The fast execution was, of course, predicated on the complexity of the operation being simulated and was particularly sensitive to the number of traffic agents (therefore the traffic density and size of the analysis volume) and the length of the ownship path.
3.5. Simulation Validation
The traffic simulation environment was validated by correlation of the outputs with the original input distributions for each cell. The positions of all generated traffic agents from samples was used to fit a KDE for the altitude of each cell of an arbitrary operational area. The lateral position KDEs were similarly fitted from the same data. A two-sample Kolmogorov–Smirnov test [17] was performed on all corresponding distributions between the surveillance data derived reference distribution and simulation environment collected distributions. The test statistic was calculated between the empirical distribution functions and for the reference and simulation distributions of sizes , respectively.
They were tested to be identical distributions to 95% confidence ()
All corresponding distributions were tested to this level, thus validating the simulation implementation.
4. Results
The methodology was applied to the air risk assessment of a case study operation between Portsmouth, UK to Newport, UK. This case study was based upon a potential future medical logistics operation that has only been operated in segregated airspace at time of writing. The analysed trajectory was fixed in altitude at 1000 ft above ground level (AGL), although the flexibility of the method allows these to be varied. This altitude was selected for demonstration, as previously conjectured lower altitudes were likely to have greater proportion of aircraft that are not featured in the data. The lateral trajectory can be seen overlaid on the local daily traffic density in Figure 5. In the vicinity of the operational area there are three busy GA airfields. Additionally, there is good ADS-B receiver coverage reported by the surveillance data provider used. A lateral and vertical conflict distance of m and m, respectively, were selected. The analytical derivation of the separation distances was considered out of scope for this work, as the model allows this to be set parametrically; we refer the reader to past works that have considered this further [18,19].
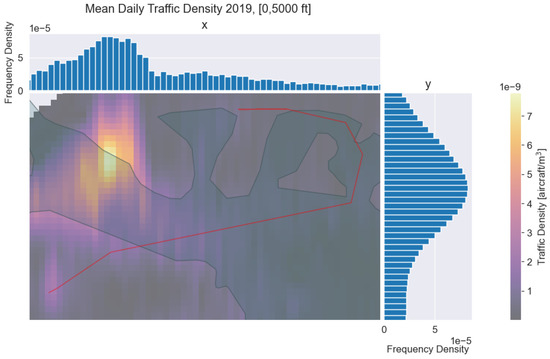
Figure 5.
Analysed flight trajectory with local traffic density overlaid. The trajectory is fixed at 1000 ft AGL.
The UK Civil Aviation Authority (CAA) defines Flight Restriction Zones (FRZs) around airfields and critical infrastructure. There are FRZs around two of the three aforementioned airfields, as shown in Figure 6.
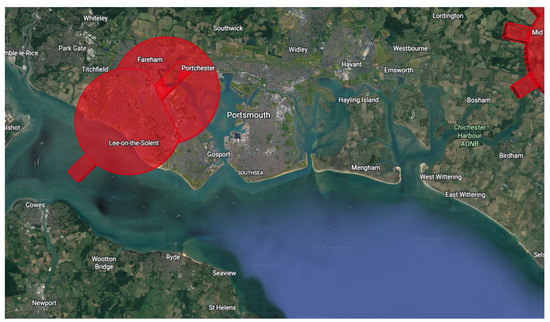
Figure 6.
Locations of FRZs in the operational area.
Surveillance traffic data were obtained for the entirety of 2019 for a region up to 5000 ft. The year of 2019 was chosen as to exclude any effects on the data due to COVID-19. It was important that sufficient data samples were captured to draw representative and valid distributions from. The data were processed as detailed in Section 2 to yield probability distributions in the traffic characteristic variables, shown in Figure 2 and Figure 5. It is important to reiterate that the traffic density values were multiplied by in order to estimate non-ADS-B-equipped traffic.
The operation was selected to take place at 1400 h. This is the busiest time of day in the operational area, shown by Figure 2, accounting for a relative frequency of 0.1218. The traffic density for the operational area is shown in Table 1. The values represent the traffic densities for a mean day across the time horizon of the data, in this case one year, within the entire operational area and for only the cells that the trajectory intersects. Figure 2 also shows the maximum traffic density of all intersecting cells by hour of day on the right vertical axis. This results in a max traffic density of aircraft/m corresponding to the operation time of 1400. The minimum and mean values for the intersecting traffic densities are aircraft/m and aircraft/m, respectively. However, the realistic worst case was desired; therefore, the maximum intersecting traffic density was used.

Table 1.
Traffic Density statistics for an averaged day in the case study operational areas.
We made an a priori estimate of the uMAC probability at with a desired maximum relative error of 10%. These values were used to estimate the number of MC samples required, as per Equation (15). The estimated MC samples required was found to be a minimum of . The simulations were set up and queued for batch execution on a machine with a 12-core Intel 12700K processor and 16GiB RAM. The total execution time took approximately 3 h. The uMAC probability converged to () and the convergence to this value could be verified by plotting the uMAC probability against the number of samples, shown in Figure 4. Likewise the uMAC rate converged to (). More samples than initially required were made in order to verify the convergence of the value.
The localised conflict probability is shown in Figure 7. As expected, this is seen to correlate with the traffic density map in Figure 5. This allows for further refinement of the path to avoid identified high uMAC risk regions of the originally intended flightpath.
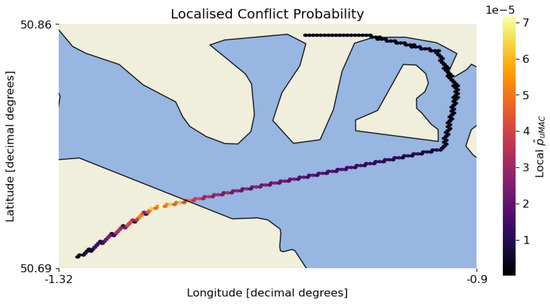
Figure 7.
values along the ownship trajectory.
5. Discussion
The results presented demonstrate the combination of a CMC method with ABS to estimate the uMAC probability of a specific operation. The ABS traffic environment is set up to probabilistically replicate the real world operational environment, both spatially and temporally. Additional UAS(s) can then be introduced to assess the probability of them colliding with the existing traffic agents in this environment.
The methodology presented is designed to assess the unmitigated MAC probability. As such, it is assumed that any further mitigations improve this base uMAC probability value and make it less likely that a MAC will occur. These mitigations can take the form of Detect and Avoid (DAA) technologies, such as EC measures, or on-board realtime sensors, such as radars or electro-optical (EO) systems. This approach is in line with the SORA [20]
In a safety assessment and operation approval context, this allows objective quantification of the air risk posed by the UAS and the monitoring of compliance to a target level of safety (TLoS). The value of the TLoS is of debate, with previous work using the TLoS of fatalities per flight hour [21]. Previous data from the FAA suggest fatalities per flight hour for all aircraft movements for the period 2007–2011. Ultimately, the responsibility falls to the regulator to set the TLoS. For a proposed operation, an agreed TLoS can be specified in the Operational Safety Case (OSC) and the proposed flightpath(s) can be verified using the presented methodology.
This approach is complementary to the quantification of ground risk posed by UAS [22] and the use of both methods enables a holistic, objective, and quantified assessment of the risks posed by UAS operations. It is suggested that both the air and ground risk components be normalised to estimate the number of fatalities per single sortie of an operation and combined to a single value representing the probability of a fatality occurring. This should then be the figure of merit compared to the TLoS to establish whether an operation is permitted.
The CMC approach is not particularly computationally efficient; however, it is relatively straightforward to validate and is tenable for the speed of the current implementation. This could form the basis for validation of more advanced methods.
It is assumed a MAC would result in at least a single fatality; therefore, we used the uMAC rate as the fatality rate. In the presented case, the operation should not be allowed to operate at the given time of day on the basis of a TLoS of fatalities per flight hour. The air risk could be mitigated by selecting a different time of day or routing.
To demonstrate this, the method was repeated for a different time of day. A time of 0700 was selected for the same operation, corresponding to a traffic density of aircraft/m. After samples, the uMAC rate converged to () per operation flight hour. This is still above the prescribed TLoS; therefore, a change in routing is required.
6. Conclusions
In this work, we have demonstrated the use of a crude Monte Carlo method sampling Agent-Based Simulations of a realistic traffic environment to determine an estimate of unmitigated mid-air collision probability. The environment traffic motion is based upon the analysis of surveillance traffic for the intended operational area. The operation-centric methodology presented here forms an alternative to airspace-centric approaches with the former allowing for higher flexibility and consideration of special conditions and constraints that may be imposed on a specific operation.
A case study of a specific operation in the South of the UK has been presented and the air risk determined based upon an assumed time of day for the operation. The results suggest that the case study operation does not reach an assumed Target Level of Safety desired and therefore should not be allowed to proceed for the given time of day.
Future Work
There are numerous avenues for future work that could stem from this study. A key path is that of variance reduction of the MC method. This could result in a much faster analysis time due to the requirement for fewer samples. This would allow for feasible analysis of more complex operations, particularly those including multiple UAS (ownship agents) and the introduction of specific scenarios that are not necessarily characterised in the surveillance traffic data but are of particular importance, such as the transit of emergency medical helicopter flights in the vicinity of the operation. Techniques from the field of Rare Event Simulation are highly applicable in this case and methods such as importance sampling and simulation splitting show great promise for the improvement of this methodology. This would allow a sensitivity analysis of the presented methodology, as this is currently computationally intractable.
The spatial partitioning of the methodology may also be desirable, especially for particularly long range operations, this would allow the method to be more scalable and the modelling of different variations of sections of the UAS trajectory.
The inclusion of other UAS, either as part of the traffic or as an ownship, is also technically feasible and can cover the case of multiple UAS operating in the same environment.
Author Contributions
Conceptualization, A.P., J.S. and M.F.; methodology, A.P.; software, A.P.; validation, A.P., J.S. and M.F.; formal analysis, A.P.; investigation, A.P.; resources, A.P.; data curation, A.P.; writing—original draft preparation, A.P.; writing—review and editing, A.P., J.S. and M.F.; visualization, A.P.; supervision, J.S. and M.F.; project administration, J.S.; funding acquisition, J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Engineering and Physical Sciences Research Council grant numbers EP/V002619/1 and EP/R009953/1.
Data Availability Statement
Not applicable.
Acknowledgments
The authors wish to thank Chris Fox for his assistance in obtaining glider flight data.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Grote, M.; Pilko, A.; Scanlan, J.; Cherrett, T.; Dickinson, J.; Smith, A.; Oakey, A.; Marsden, G. Sharing Airspace with Uncrewed Aerial Vehicles (UAVs): Views of the General Aviation (GA) Community. J. Air Transp. Manag. 2022, 102, 102218. [Google Scholar] [CrossRef]
- Endoh, S. Aircraft Collision Models. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1982. [Google Scholar]
- Holt, J.; Marner, G. Separation Theory in Air Traffic Control System Design. Proc. IEEE 1970, 58, 369–376. [Google Scholar] [CrossRef]
- Knecht, W.R. Modeling the Big Sky Theory. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2001, 45, 87–91. [Google Scholar] [CrossRef]
- Patlovany, R.W. U.S. Aviation Regulations Increase Probability of Midair Collisions. Risk Anal. 1997, 17, 237–248. [Google Scholar] [CrossRef]
- Sunil, E.; Hoekstra, J.; Ellerbroek, J.; Bussink, F.; Nieuwenhuisen, D.; Vidosavljevic, A.; Kern, S. Metropolis: Relating Airspace Structure and Capacity for Extreme Traffic Densities. In Proceedings of the 11th USA/Europe Air Traffic Management Research and Development Seminar, ATM 2015, Lisbon, Portugal, 23–26 June 2015; p. 11. [Google Scholar]
- Jardin, M.R. Analytical Relationships Between Conflict Counts and Air-Traffic Density. J. Guid. Control. Dyn. 2005, 28, 1150–1156. [Google Scholar] [CrossRef]
- La Cour-Harbo, A.; Schiøler, H. Probability of Low-Altitude Midair Collision Between General Aviation and Unmanned Aircraft. Risk Anal. 2019, 39, 2499–2513. [Google Scholar] [CrossRef] [PubMed]
- Mcfadyen, A.; Martin, T. Terminal Airspace Modelling for Unmanned Aircraft Systems Integration. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016. [Google Scholar] [CrossRef]
- McFadyen, A. Probabilistic Determination of Maximum Safe Altitudes for Unmanned Traffic Management. In Proceedings of the 2019 IEEE/AIAA 38th Digital Avionics Systems Conference (DASC), San Diego, CA, USA, 8–12 September 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Lee, H.T.; Meyn, L.; Kim, S. Probabilistic Safety Assessment of Unmanned Aerial System Operations. J. Guid. Control. Dyn. 2013, 36, 610–617. [Google Scholar] [CrossRef]
- Schäfer, M.; Strohmeier, M.; Lenders, V.; Martinovic, I.; Wilhelm, M. Bringing Up OpenSky: A Large-scale ADS-B Sensor Network for Research. In Proceedings of the IPSN-14—13th International Symposium on Information Processing in Sensor Networks, Berlin, Germany, 15–17 April 2014; pp. 83–94. [Google Scholar]
- Epanechnikov, V.A. Non-Parametric Estimation of a Multivariate Probability Density. Theory Probab. Appl. 1969, 14, 153–158. [Google Scholar] [CrossRef]
- Kochenderfer, M.J.; Edwards, M.W.M.; Espindle, L.P.; Kuchar, J.K.; Griffith, J.D. Airspace Encounter Models for Estimating Collision Risk. J. Guid. Control. Dyn. 2010, 33, 487–499. [Google Scholar] [CrossRef]
- Kroese, D.P.; Rubinstein, R.Y. Monte Carlo Methods. Wiley Interdiscip. Rev. Comput. Stat. 2012, 4, 48–58. [Google Scholar] [CrossRef]
- Olive, X. Traffic, a Toolbox for Processing and Analysing Air Traffic Data. J. Open Source Softw. 2019, 4, 1518. [Google Scholar] [CrossRef]
- Smirnov, N. Table for Estimating the Goodness of Fit of Empirical Distributions. Ann. Math. Stat. 1948, 19, 279–281. [Google Scholar] [CrossRef]
- Zhu, G.; Wei, P. Low-Altitude UAS Traffic Coordination with Dynamic Geofencing. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016; AIAA AVIATION Forum. American Institute of Aeronautics and Astronautics: Reston, DC, USA, 2016. [Google Scholar] [CrossRef]
- Hu, J.; Erzberger, H.; Goebel, K.; Liu, Y. Probabilistic Risk-Based Operational Safety Bound for Rotary-Wing Unmanned Aircraft Systems Traffic Management. J. Aerosp. Inf. Syst. 2020, 17, 171–181. [Google Scholar] [CrossRef]
- JARUS. JARUS Guidelines on Specific Operations Risk Assessment (SORA) v2.5. p. 30. Available online: https://www.easa.europa.eu/en/domains/civil-drones-rpas/specific-category-civil-drones/specific-operations-risk-assessment-sora (accessed on 15 May 2023).
- Dalamagkidis, K.; Valavanis, K.; Piegl, L. On Unmanned Aircraft Systems Issues, Challenges and Operational Restrictions Preventing Integration into the National Airspace System. Prog. Aerosp. Sci. 2008, 44, 503–519. [Google Scholar] [CrossRef]
- Pilko, A.; Sóbester, A.; Scanlan, J.P.; Ferraro, M. Spatiotemporal Ground Risk Mapping for Uncrewed Aircraft Systems Operations. J. Aerosp. Inf. Syst. 2023, 20, 126–139. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).