Numerical Investigation of Gas Dynamic Foil Bearings Conjugated with Contact Friction by Elastic Multi-Leaf Foils
Abstract
1. Introduction
2. Computational Method
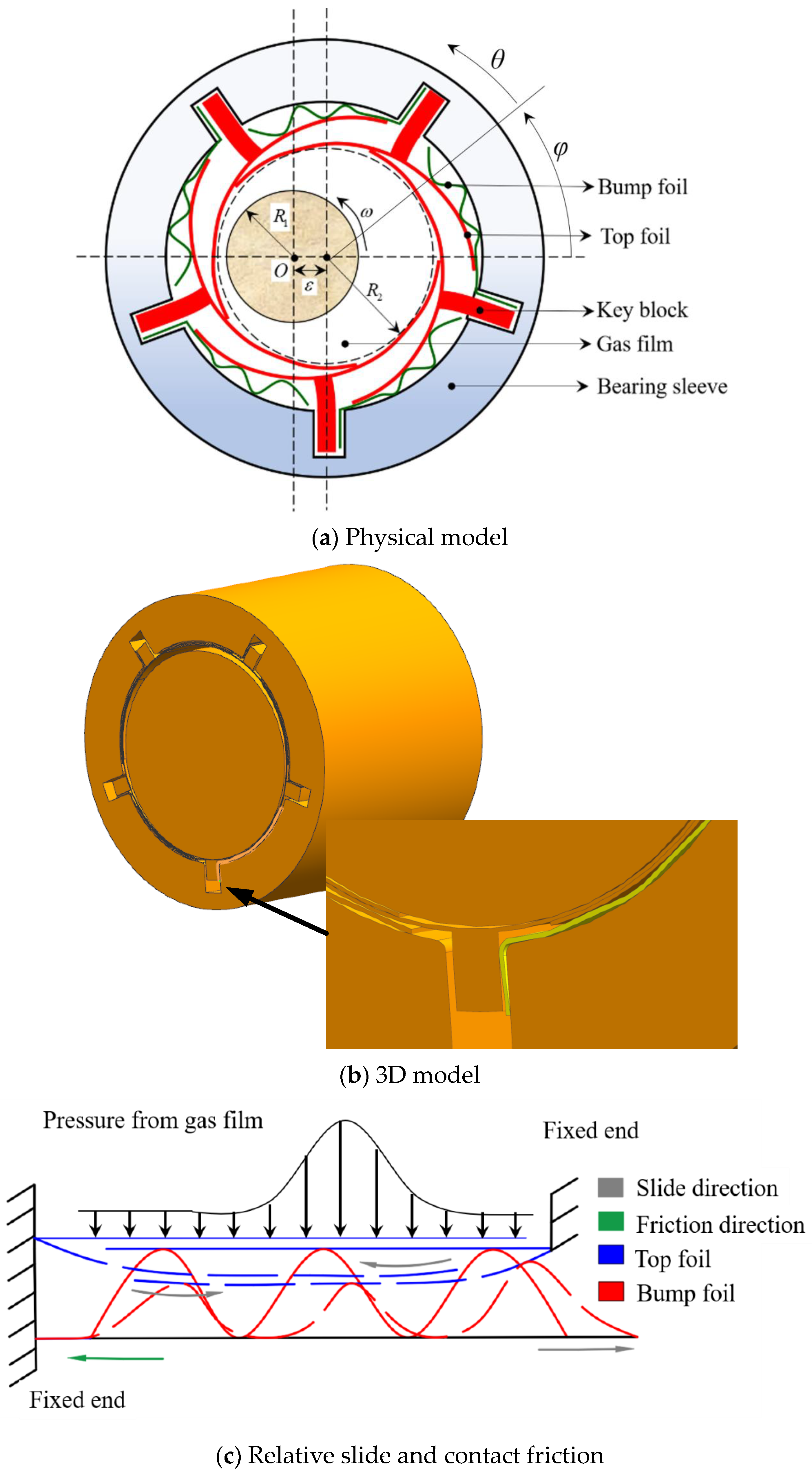
2.1. Physical Model
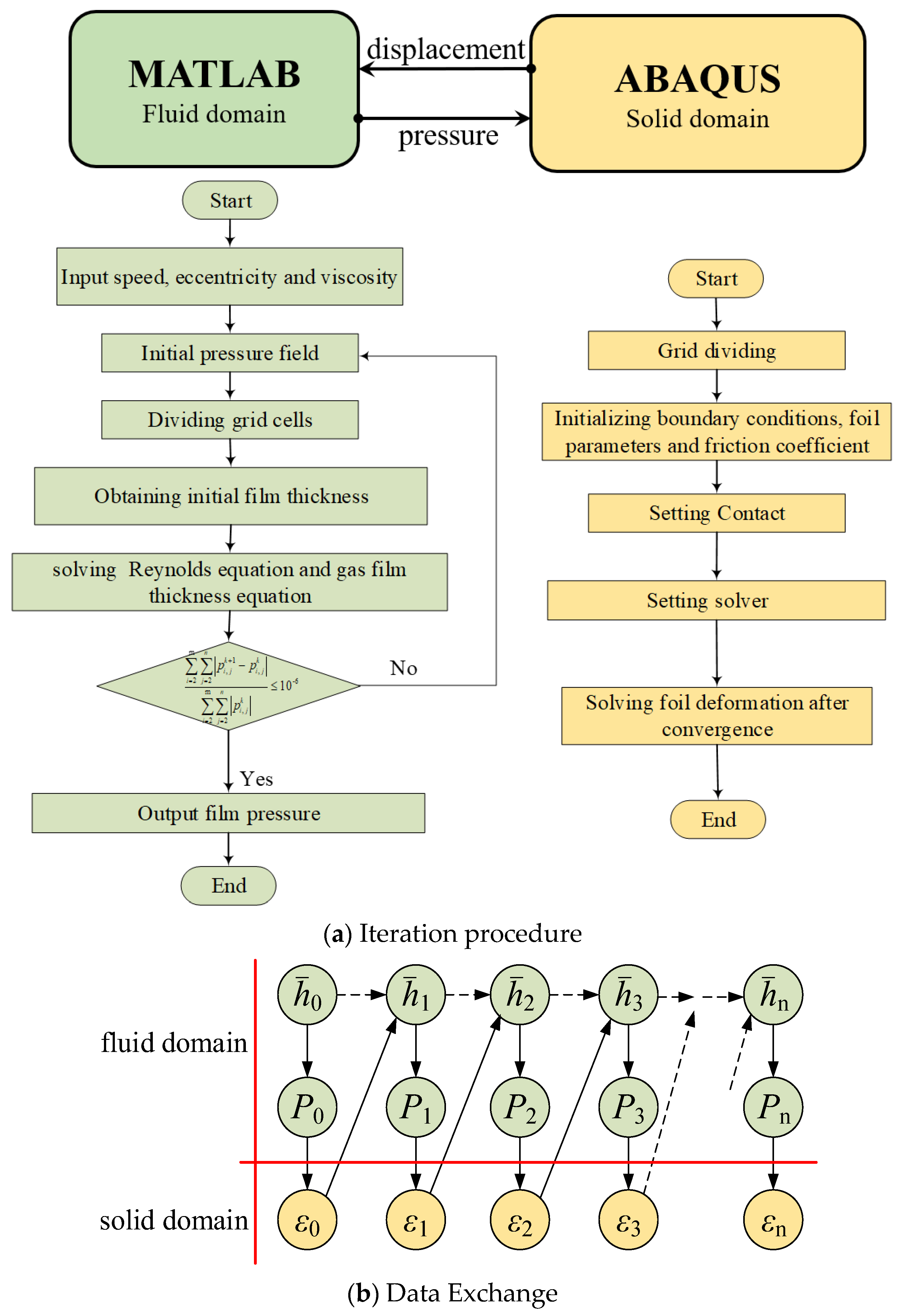
2.2. Aerodynamic–Elastic Coupling
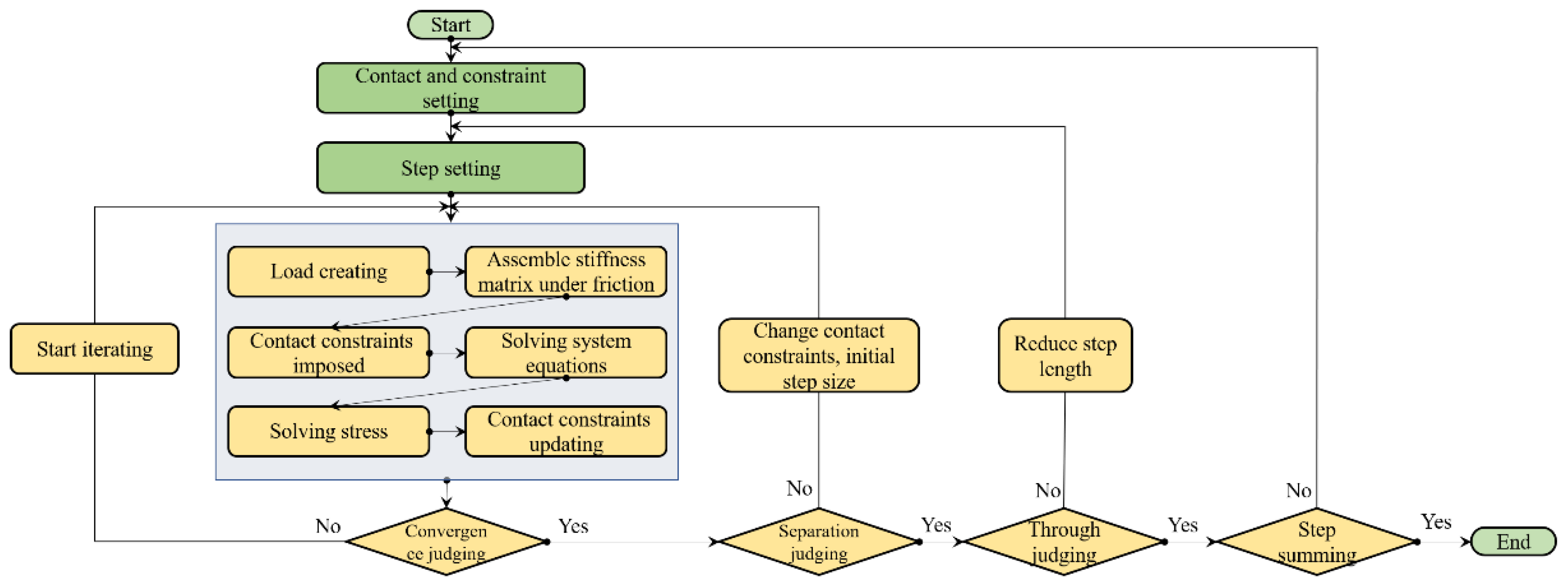
2.3. Realization of Contact Friction
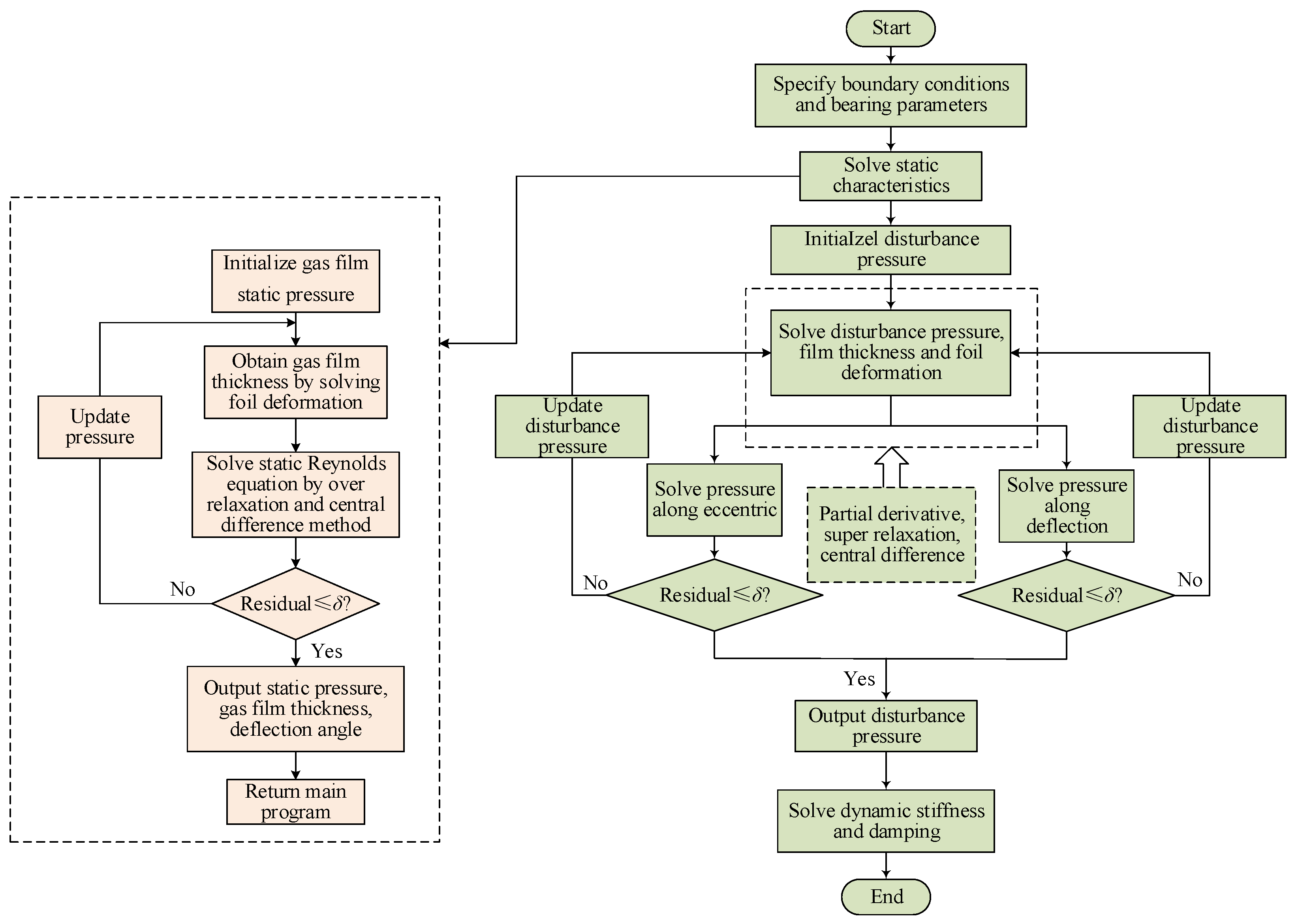
2.4. Mathematical Description
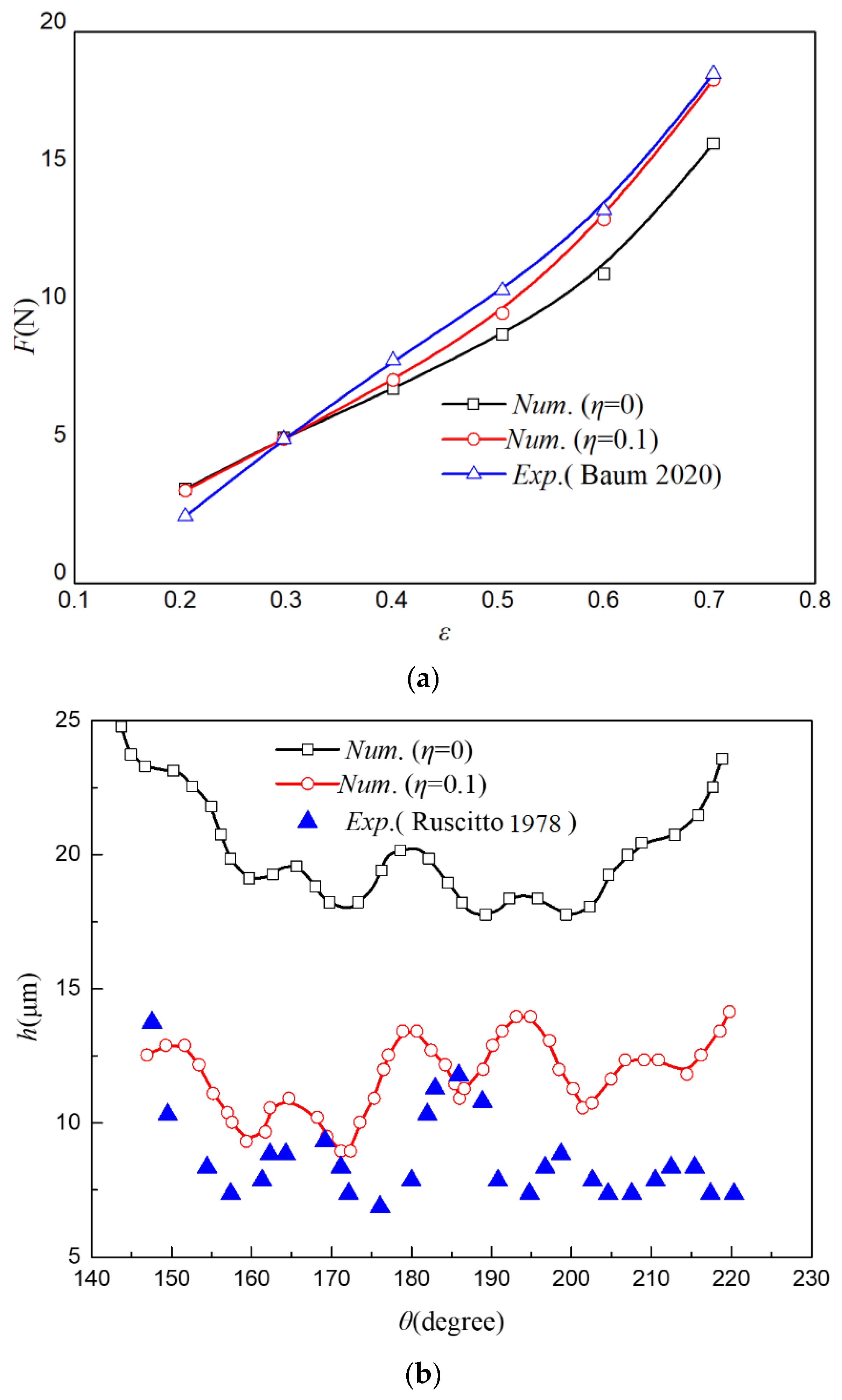
2.5. Validations of Computational Method
3. Results and Discussion
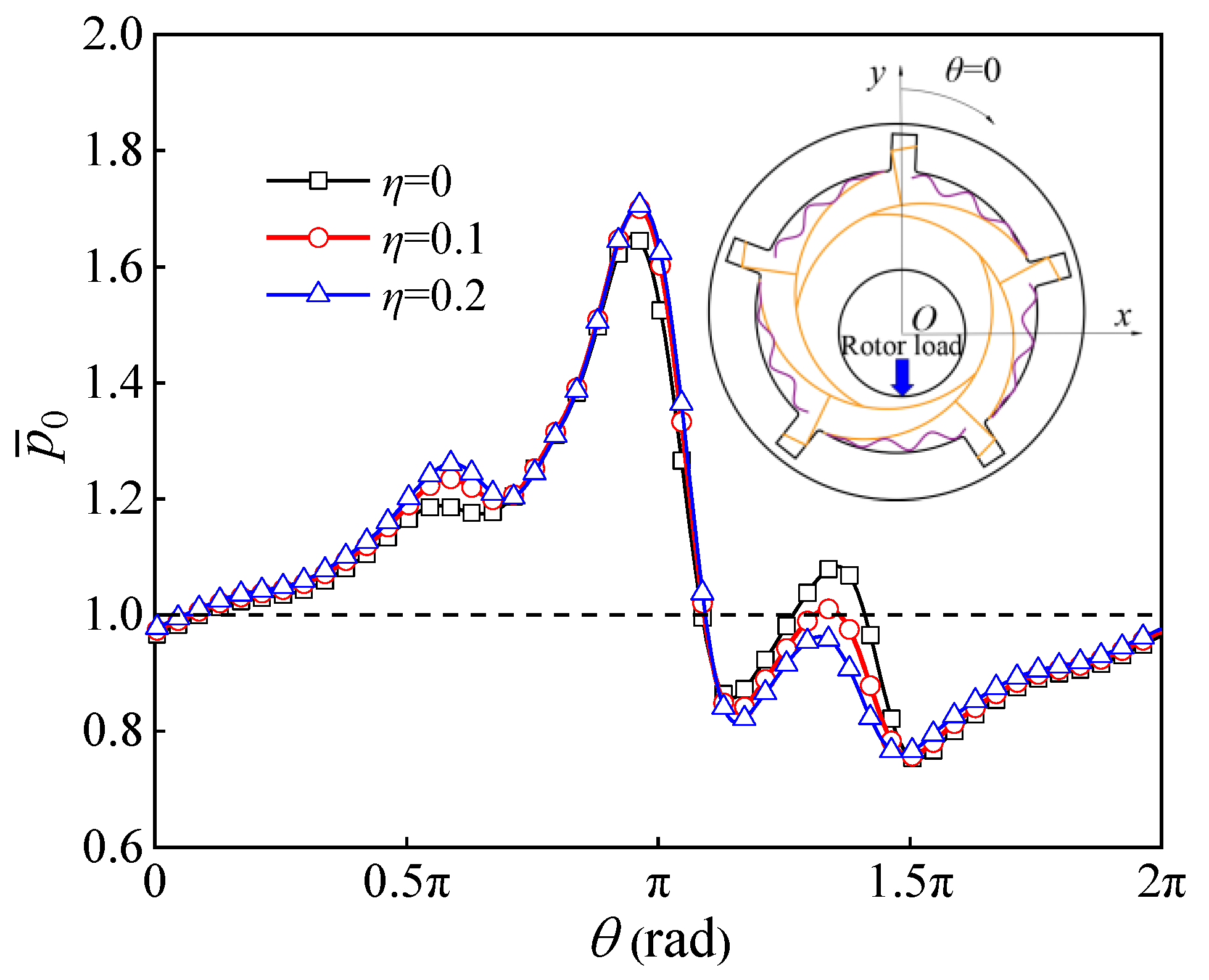
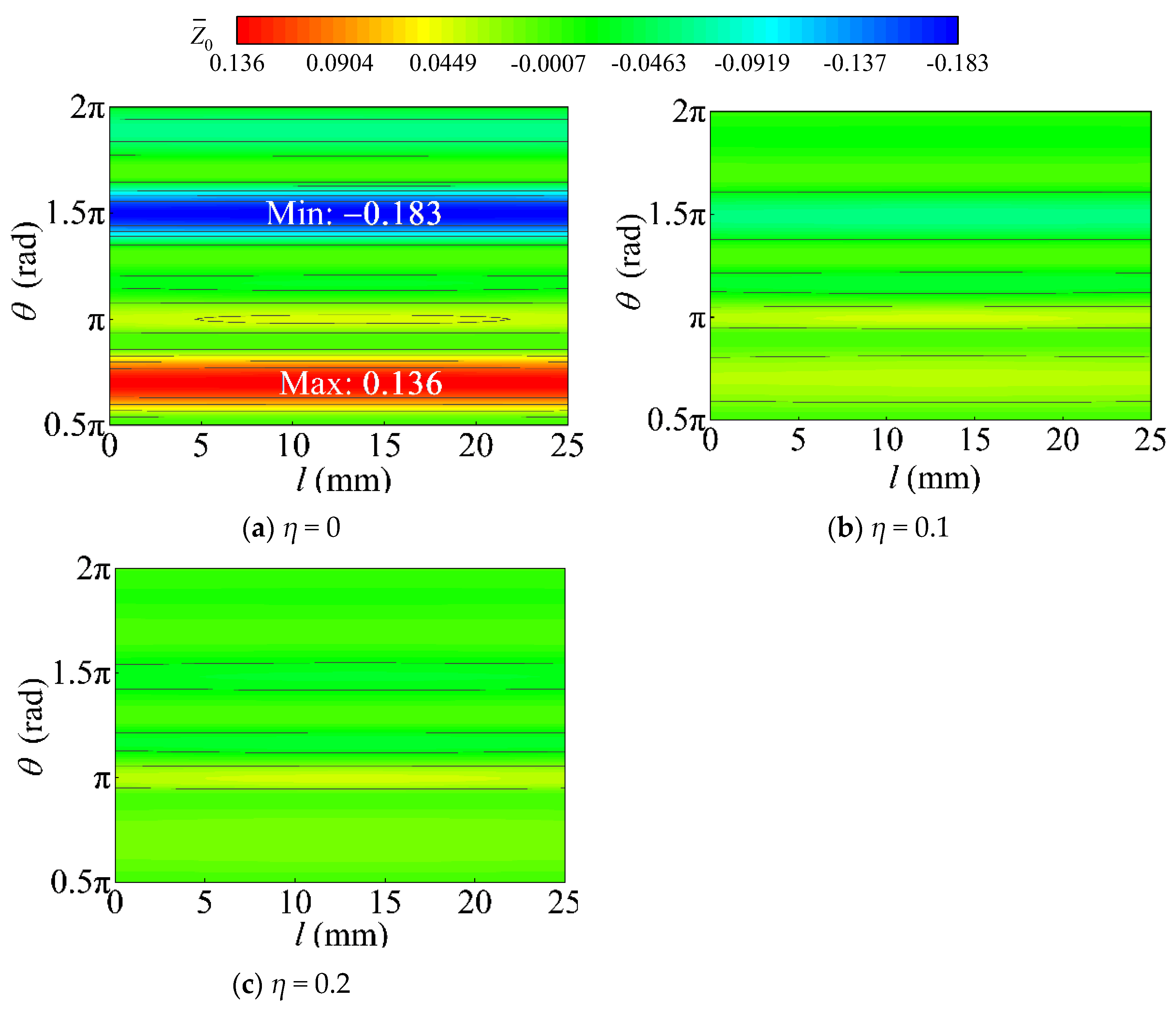
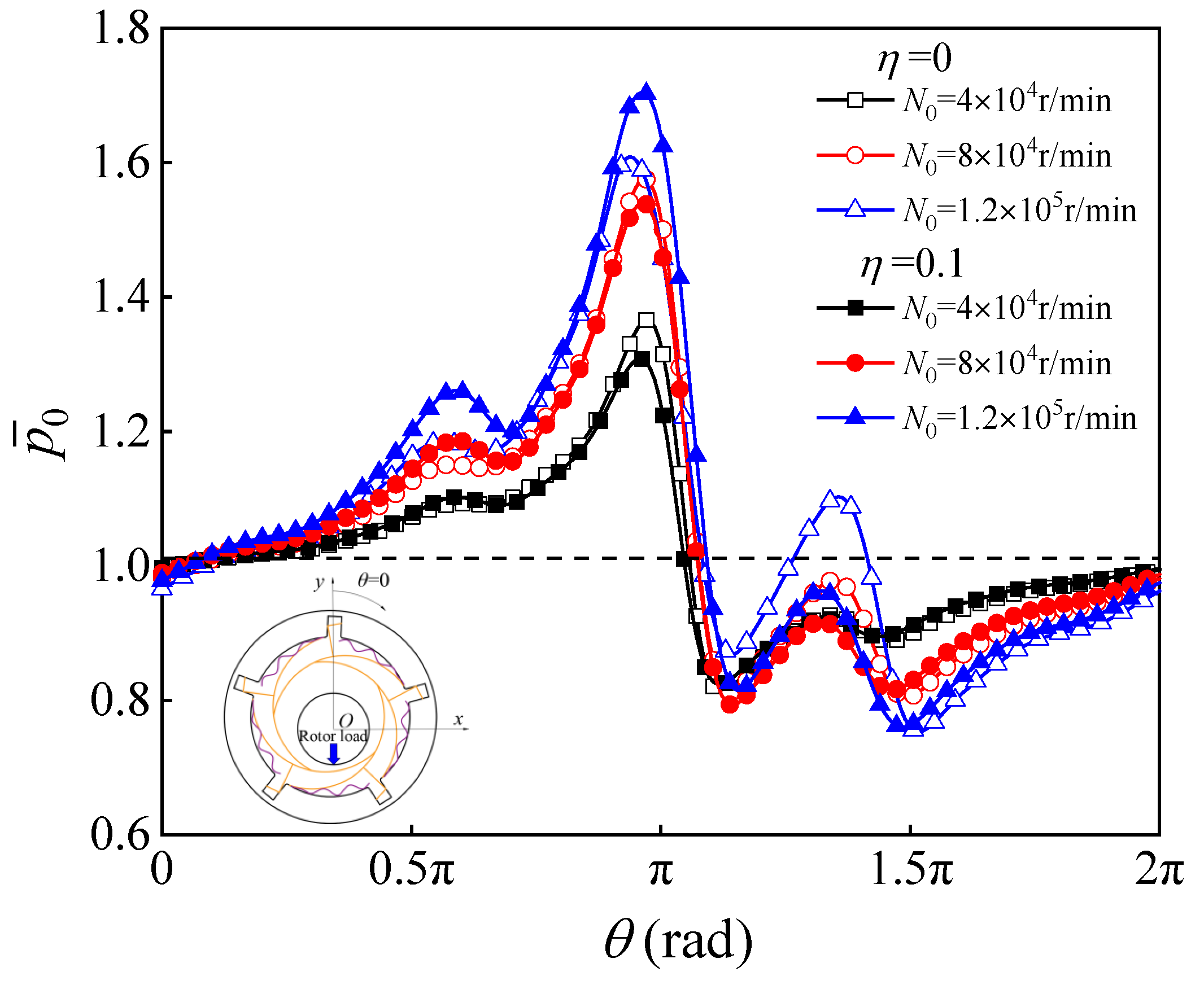
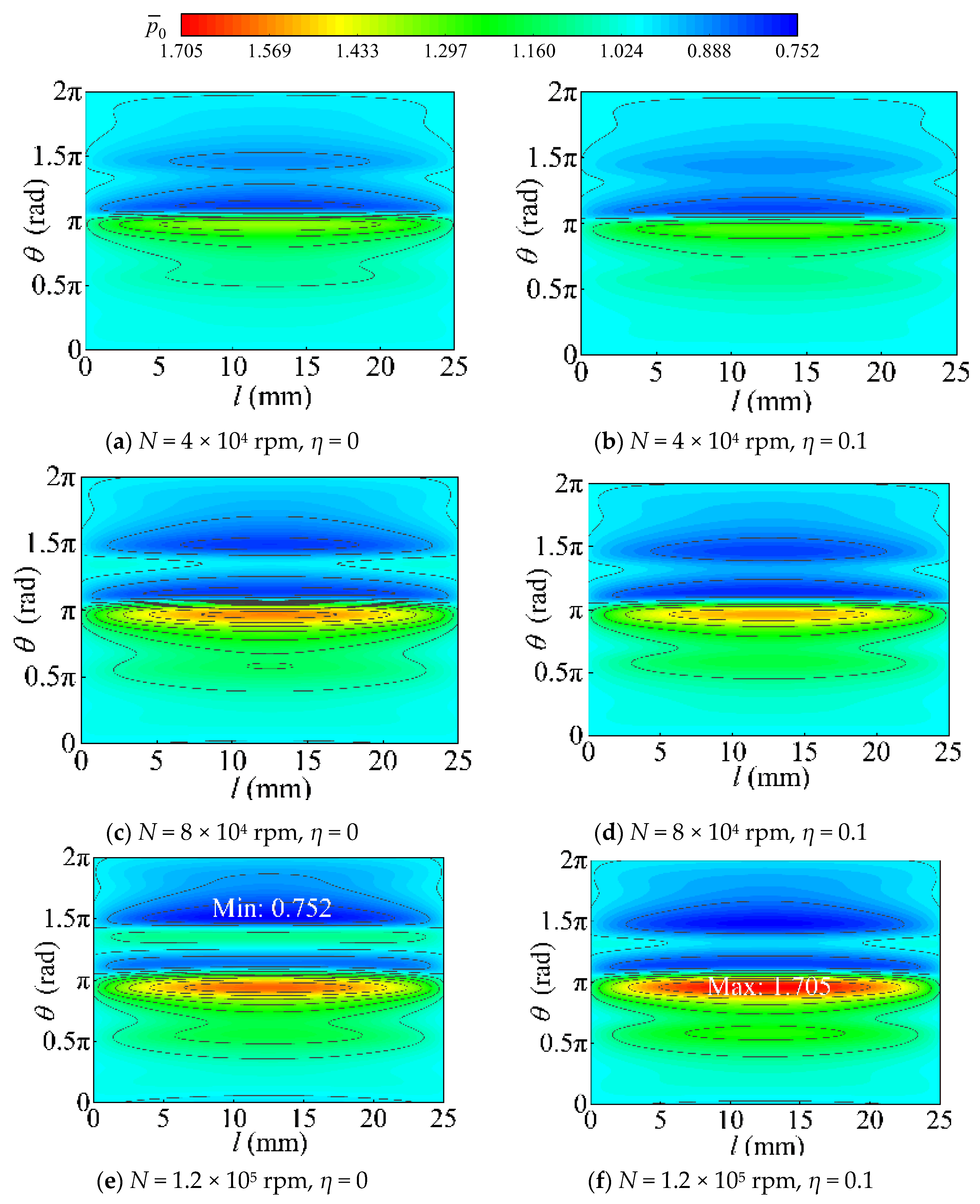
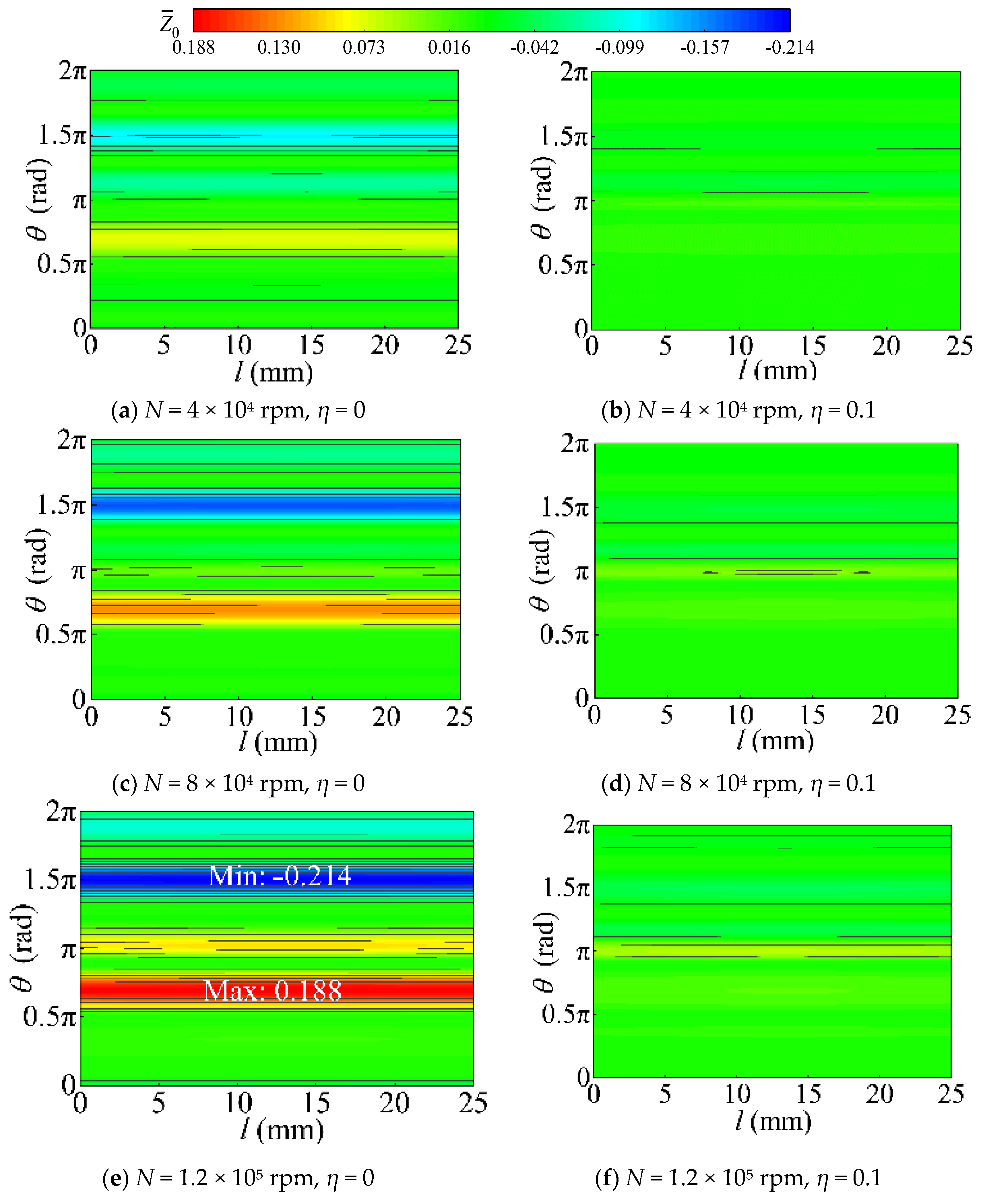
3.1. Static Characteristics
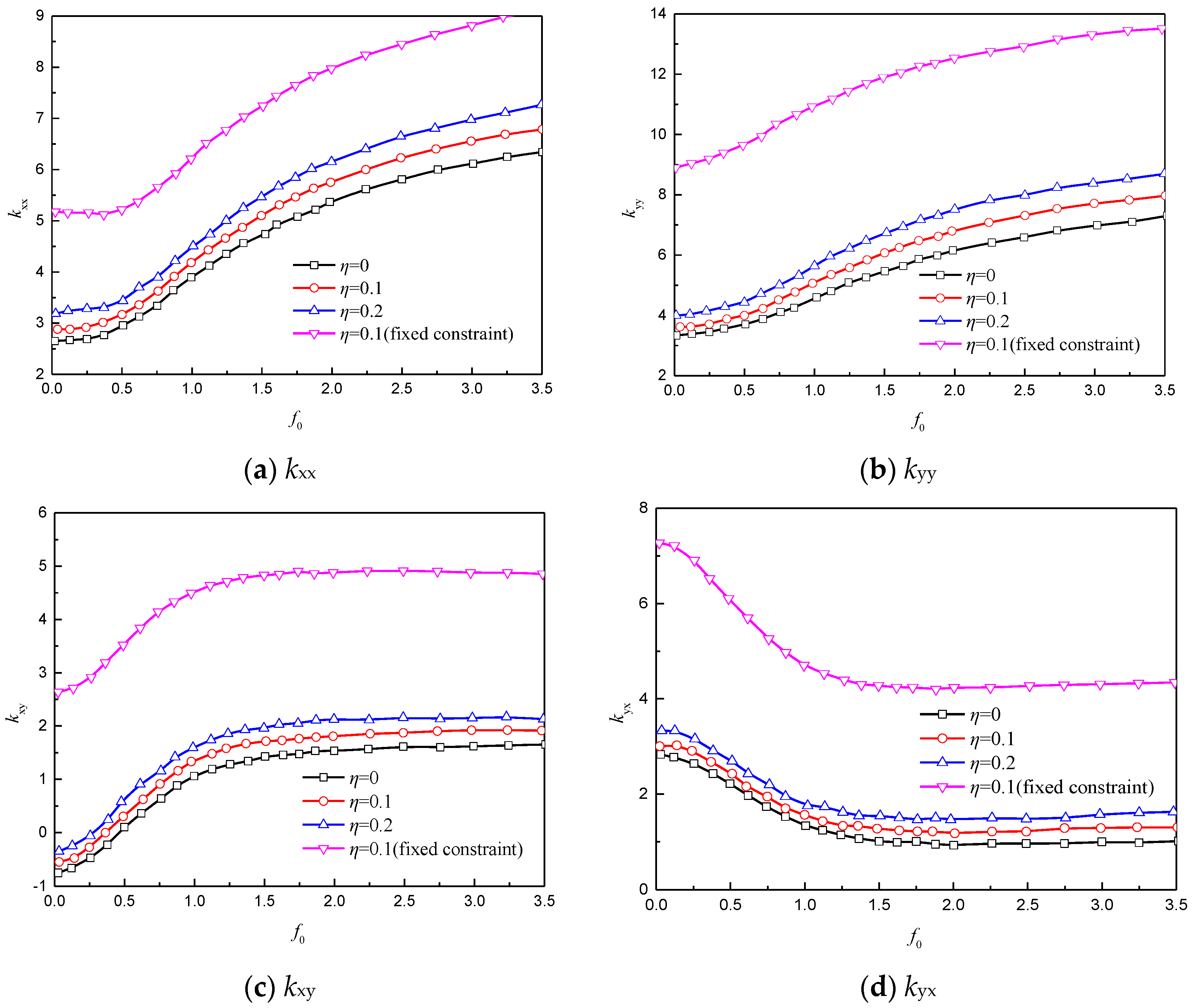
3.1.1. Static Stiffness
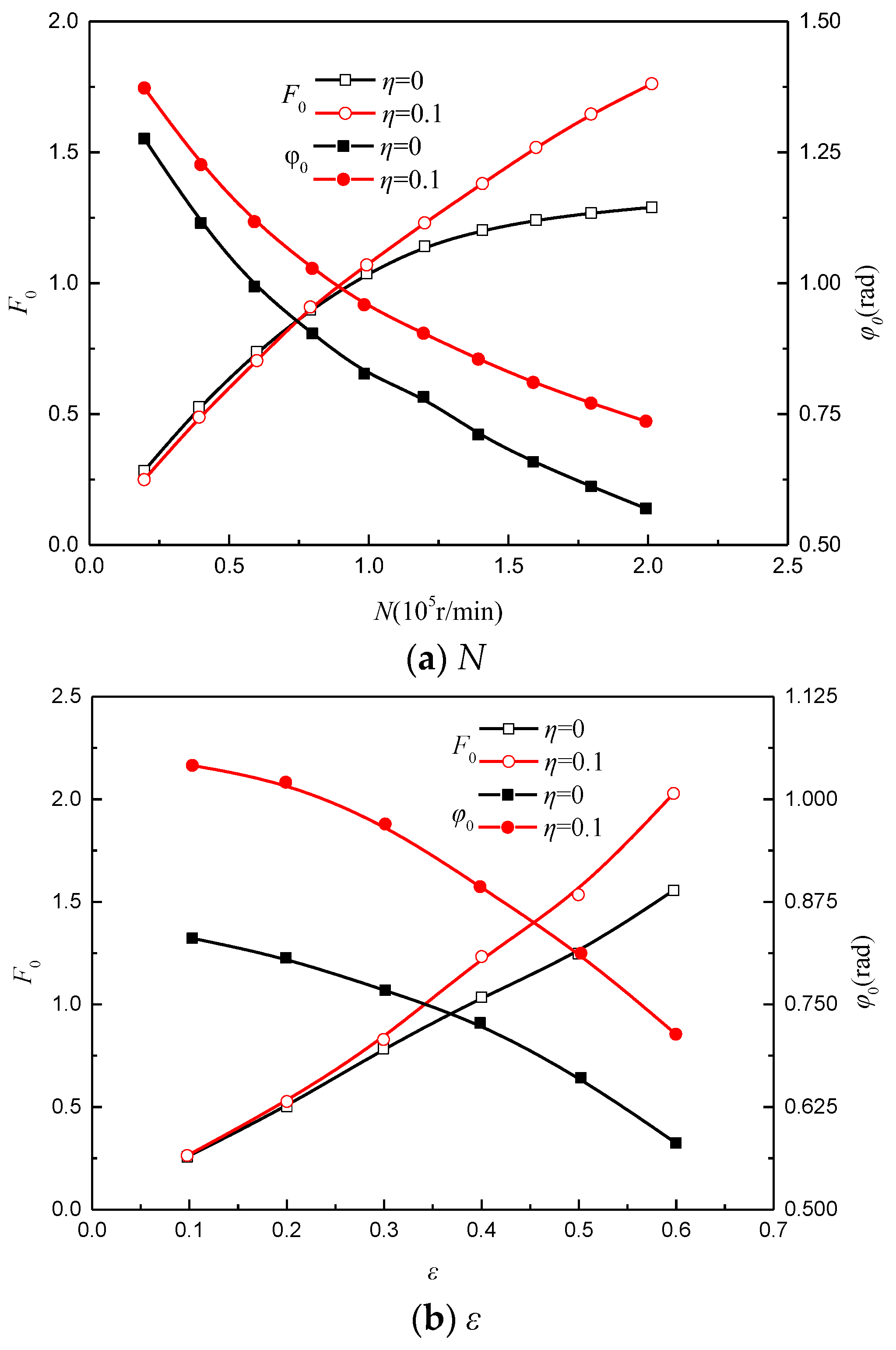
3.1.2. Load Capacity and Deflection Angle
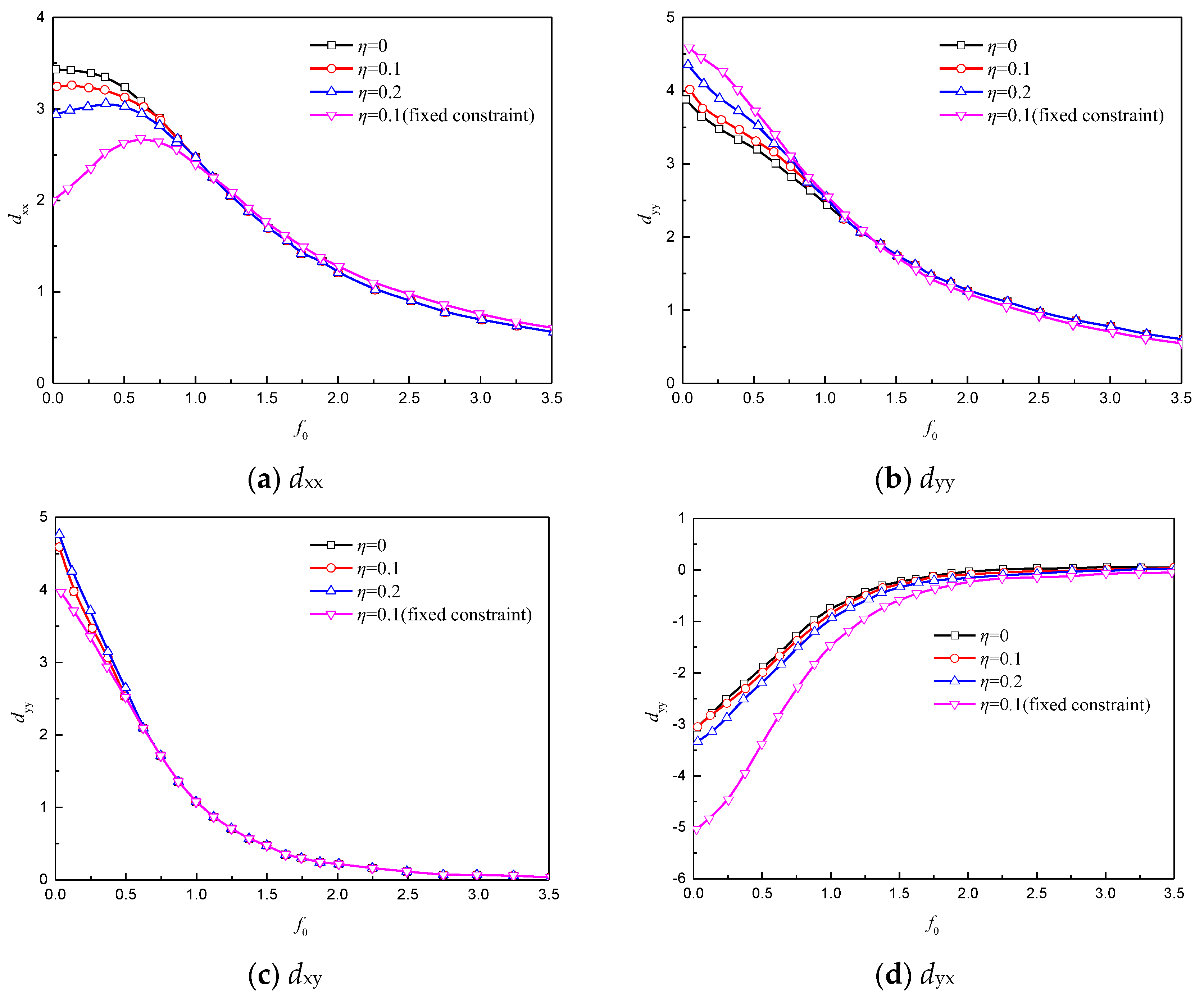
3.1.3. Dependent Factors
3.2. Dynamic Response
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Λ | Bearing number | |
| h | Thickness of the gas film (m) | |
| ε | Journal eccentricity | |
| θ | Angular coordinates | |
| hz | Radial deformation of the inner surface (m) | |
| Radial dimensionless displacement | ||
| Dimensionless distance between the top foil and rotator | ||
| Dimensionless | ||
| p | Pressure (Pa) | |
| H | Dimensionless clearance height H = h/c | |
| R | Journal radius (m) | |
| Pa | Environmental pressure (Pa) | |
| c | Nominal bearing clearance | |
| K | Nominal static stiffness | |
| η | Coefficient of friction | |
| Kn | Static stiffness of K(i,j) | |
| v | Disturbance frequency (Hz) | |
| amplitude of disturbance eccentricity | ||
| Amplitude of disturbance deflection angle | ||
| Dimensionless rotor disturbance frequency ) | ||
| Dimensionless time | ||
| Dimensionless static pressure | ||
| Dimensionless static thickness | ||
| Dimensionless disturbed pressure | ||
| Dimensionless disturbed thickness | ||
| Amplitude of the dimensionless disturbed pressure | ||
| Amplitude of the dimensionless disturbed thickness | ||
| Greek Letters | ||
| ρ | Density (kg/m3) | |
| θ | Angular coordinate | |
| λ | Axial coordinate | |
| β | Top foil opening angle | |
| μ | Dynamic viscosity (Pa·s) | |
| μt | Turbulent dynamic viscosity (Pa·s) | |
| Subscripts | ||
| b | Bump | |
| f | Fluid | |
| s | Solid | |
| t | Top |
References
- Michael, B.; David, G.; Christopher, G. Compliant gas foil bearings and analysis tools. J. Eng. Gas Turbines Power 2016, 138, 054001. [Google Scholar]
- Samanta, P.; Murmu, N.; Khonsari, M. The evolution of foil bearing technology. Tribol. Int. 2019, 135, 305–323. [Google Scholar] [CrossRef]
- DellaCorte, C. Oil-free shaft support system rotor synamics: Past, present and future challenges and opportunities. Mech. Syst. Signal Process. 2012, 29, 67–76. [Google Scholar] [CrossRef]
- Andrés, L.S.; Ryu, K.; Diemer, P. Prediction of gas thrust foil bearing performance for oil-free automotive turbochargers. In Proceedings of the ASME Turbo Expo: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Bensouilah, H.; Lahmar, M. Elastic-aerodynamic lubrication analysis of a self-acting air foil journal bearing. Lubr. Sci. 2012, 24, 95–128. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Zhao, X.R.; Chang, H.P.; Fang, H. Effects of sliding boundary on static characteristics of aerodynamic compliant foil bearing. J. Propuls. Technol. 2018, 39, 388–395. [Google Scholar]
- Andres, L.; Kim, T.H. Analysis of gas foil bearings integrating FE top foil models. Tribol. Int. 2009, 42, 111–120. [Google Scholar] [CrossRef]
- Lehn, A.; Mahner, M.; Schweizer, B. Elasto-gasdynamic modeling of air foil thrust bearings with a two-dimensional shell model for top and bump foil. Tribol. Int. 2016, 100, 48–59. [Google Scholar] [CrossRef]
- Somaya, K.; Kishino, T.; Miyatake, M. Static characteristics of small aerodynamic foil thrust bearings operated up to 350,000 rpm. J. Eng. Tribol. 2014, 228, 928–936. [Google Scholar]
- Walowit, J.A.; Anno, J.N.; Hamrock, B.J. Modern developments in lubrication mechanics. Tribol. Int. 1977, 9, 90. [Google Scholar] [CrossRef]
- Heshmat, H.; Walowit, J.A.; Pinkus, O. Analysis of gas-lubricated foil journal bearings. J. Lubr. Technol. 1983, 105, 647–655. [Google Scholar] [CrossRef]
- Heshmat, H.; Walowit, J.A.; Pinkus, O. Analysis of gas-lubricated complaint thrust bearings. ASME J. Lubr. Technol. 1983, 105, 638–646. [Google Scholar] [CrossRef]
- Heshmat, H. An analysis of gas-lubricated, multi-leaf foil journal bearings with backing springs. J. Tribol. 1995, 117, 437–443. [Google Scholar] [CrossRef]
- Peng, Z.C.; Khonsari, M.M. Hydrodynamic analysis of compliant foil bearings with compressible air flow. J. Tribol. 2004, 126, 542–546. [Google Scholar] [CrossRef]
- Carpino, M.; Talmage, G. Prediction of rotor dynamic coefficients in gas lubricated foil journal bearings with corrugated sub-foils. Tribol. Trans. 2006, 49, 400–409. [Google Scholar] [CrossRef]
- Matute, J.; Ruiz, R.; Diaz, S. A View to the Energy Dissipation Mechanism of a Gas Foil Bearing’s Structure due to Dry Friction. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012. [Google Scholar]
- Lee, D.H.; Kim, Y.C.; Kim, K.W. The effect of Coulomb friction on the static performance of foil journal bearings. Tribol. Int. 2010, 43, 1065–1072. [Google Scholar] [CrossRef]
- Peng, J.P.; Carpino, M. Coulomb friction damping effects in elastically supported gas foil bearings. Tribol. Trans. 1994, 37, 91–98. [Google Scholar] [CrossRef]
- Peng, J.P.; Carpino, M. Finite element approach to the prediction of foil bearing rotor dynamic coefficient. J. Tribol. 1997, 119, 85–90. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, G.; Sun, Y. The effect of coulomb friction in foil structure on the static and dynamic performance of bump foil journal bearings. In Turbo Expo: Power for Land, Sea, and Air, Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014; Volume 45776, p. V07BT32A001. [Google Scholar]
- Xu, F.; Sun, Y.; Zhang, G. Effect of bump structural friction on the performance of bump foil bearing and rotor dynamic behavior: Experimental study. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 233, 702–711. [Google Scholar] [CrossRef]
- Zhou, R.; Gu, Y.; Ren, G. Modeling and stability characteristics of bump-type gas foil bearing rotor systems considering stick-slip friction. Int. J. Mech. Sci. 2022, 5, 219–240. [Google Scholar] [CrossRef]
- Gu, Y.; Lan, X.; Ren, G. An efficient three-dimensional foil structure model for bump-type gas foil bearings considering friction. Friction 2021, 6, 9–18. [Google Scholar] [CrossRef]
- Brenkacz, L.; Baginski, P.; Zywica, G. Experimental Research on Foil Vibrations in a Gas Foil Bearing Carried Out Using an Ultra-High-Speed Camera. Appl. Sci. 2021, 11, 564–577. [Google Scholar] [CrossRef]
- Zhao, X.; Xiao, S. A finite element model for static performance analysis of gas foil bearings based on frictional contacts. Tribol. Trans. 2020, 64, 275–286. [Google Scholar] [CrossRef]
- Guo, Z.; Kai, F.; Liu, T. Nonlinear dynamic analysis of rigid rotor aupported by gas foil bearings: Effects of gas film and foil structure on subsynchronous vibrations. Mech. Syst. Signal Process. 2018, 107, 549–566. [Google Scholar] [CrossRef]
- Lai, T.; Guo, Y.; Wang, W. Experimental study on multi-decked protuberant foil thrust bearing with different number of thrust pads. J. Adv. Mech. Des. Syst. Manuf. 2016, 10, 106–116. [Google Scholar] [CrossRef]
- Lai, T.; Guo, Y.; Wang, W. Elastro-hydrodynamic lubrication model of multi-decked foil thrust bearing with copper wire support. J. Mech. Sci. Technol. 2017, 31, 4371–4379. [Google Scholar] [CrossRef]
- Fatu, A.; Arghir, M. Numerical analysis of the impact of manufacturing errors on the structural stiffness of foil bearings. J. Eng. Gas Turbines Power 2017, 140, 1235–1250. [Google Scholar]
- Hou, Y.; Zheng, Y.; Chen, S. The numerical study of static and dynamic characteristics of multi-layer protuberant foil bearing. J. Adv. Mech. Des. Syst. Manuf. 2015, 9, 58–64. [Google Scholar] [CrossRef]
- Liu, J.; Du, F.R. Simulation of compliant bump foil journal bearing using coupled Reynolds equation and finite element model method. Adv. Mater. Res. 2012, 479, 2499–2503. [Google Scholar] [CrossRef]
- Zywica, G.; Bagiński, P. Investigation of gas foil bearings with an adaptive and non-linear structure. Acta Mech. Autom. 2019, 13, 5–10. [Google Scholar]
- Zywica, G.; Baginski, P.; Bogulicz, M. Experimental and numerical evaluation of the damping properties of a foil bearing structure taking into account the static and kinetic dry friction. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 7. [Google Scholar] [CrossRef]
- Zywica, G.; Kiciński, J.; Bogulicz, M. Analysis of the rotor supported by gas foil bearings considering the assembly preload and hardening effect. In Proceedings of the International Conference on Rotor Dynamics, Rio De Janeiro, Brazil, 23–27 September 2018; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Duan, W.; Sun, Y.; Geng, H.; Ding, C.; Yang, W.; Yu, L. Static performance of multi-leaf compliant gas foil journal bearings with assembly preload. In Proceedings of the International Conference on Mechatronics and Automation, Takamatsu, Japan, 4–7 August 2013. [Google Scholar]
- Khamari, D.S.; Kumar, J.; Behera, S.K. Numerical investigation of influence sensitivity of a gas foil bearing parameters on the dynamic coefficients. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 167. [Google Scholar] [CrossRef]
- Baum, C.; Hartmut, H.; Schrders, S.; Leister, T.; Seemann, W. A computationally efficient nonlinear foil air bearing model for fully coupled, transient rotor dynamic investigations. Tribol. Int. 2020, 153, 106434. [Google Scholar] [CrossRef]
- Ruscitto, D.; Mccormick, J.; Gray, S. Hydrodynamic air lubricated compliant surface bearing for an automotive gas turbine engine. 1: Journal bearing performance. Automobiles 1978, 523, 181–187. [Google Scholar]
- Stickan, B.; Dillinger, J.; Schewe, G. Computational aeroelastic investigation of a transonic limit-cycle-oscillation experiment at a transport aircraft wing model. J. Fluids Struct. 2014, 49, 223–241. [Google Scholar] [CrossRef]
- Jaiman, R.; Geubelle, P.; Loth, E.; Jiao, X. Transient fluid–structure interaction with non-matching spatial and temporal discretization. Comput. Fluids 2011, 50, 120–135. [Google Scholar] [CrossRef]
- Zhou, Y.; Shao, L.; Zhang, C. Numerical and experimental investigation on dynamic performance of bump foil journal bearing based on journal orbit. Chin. J. Aeronaut. 2021, 34, 586–600. [Google Scholar] [CrossRef]
- Hu, H.; Feng, M.; Ren, T. Study on the performance of gas foil journal bearings with bump-type shim foil. Arch. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 509–552. [Google Scholar] [CrossRef]


| Parameters | Scale |
|---|---|
| Radius of rotator /mm | 10.95 |
| Number of foils | 5 |
| Radius of stator /mm | 11.51 |
| Length of bearing /mm | 25 |
| Thickness of top foil /mm | 0.1 |
| Thickness of bump foil /mm | 0.13 |
| Number of bumps of bump foil | 3 |
| Elastic modulus of top foil /Gpa | 213.7 |
| Elastic modulus of bump foil /Gpa | 207 |
| Poisson’s ratio of top foil | 0.29 |
| Poisson’s ratio of bump foil | 0.344 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Wang, Z.; Lyu, Y.; Zhang, J.; Xu, B. Numerical Investigation of Gas Dynamic Foil Bearings Conjugated with Contact Friction by Elastic Multi-Leaf Foils. Aerospace 2023, 10, 585. https://doi.org/10.3390/aerospace10070585
Yang C, Wang Z, Lyu Y, Zhang J, Xu B. Numerical Investigation of Gas Dynamic Foil Bearings Conjugated with Contact Friction by Elastic Multi-Leaf Foils. Aerospace. 2023; 10(7):585. https://doi.org/10.3390/aerospace10070585
Chicago/Turabian StyleYang, Changbao, Zhisheng Wang, Yuanwei Lyu, Jingyang Zhang, and Ben Xu. 2023. "Numerical Investigation of Gas Dynamic Foil Bearings Conjugated with Contact Friction by Elastic Multi-Leaf Foils" Aerospace 10, no. 7: 585. https://doi.org/10.3390/aerospace10070585
APA StyleYang, C., Wang, Z., Lyu, Y., Zhang, J., & Xu, B. (2023). Numerical Investigation of Gas Dynamic Foil Bearings Conjugated with Contact Friction by Elastic Multi-Leaf Foils. Aerospace, 10(7), 585. https://doi.org/10.3390/aerospace10070585






