You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Aerospace
Download PDF
  • Article
  • Open Access

24 February 2023

Decision Science Driven Selection of High-Temperature Conventional Ti Alloys for Aeroengines

and
1
Weldaloy Specialty Forgings, Warren, MI 48089, USA
2
Department of Mechanical Engineering, University of Michigan-Dearborn, Dearborn, MI 48128, USA
*
Authors to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Aerospace2023, 10(3), 211;https://doi.org/10.3390/aerospace10030211
This article belongs to the Topic Microstructure and Properties in Metals and Alloys
Version Notes
Order Reprints

Abstract

Near-α Ti alloys find themselves in advanced aeroengines for applications of up to 600 °C, mainly as compressor components owing to their superior combination of ambient- and elevated-temperature mechanical properties and oxidation resistance. We evaluated, ranked, and selected near-α Ti alloys in the current literature for high-temperature applications in aeroengines driven by decision science by integrating multiple attribute decision making (MADM) and principal component analysis (PCA). A combination of 12 MADM methods ranked a list of 105 alloy variants based on the thermomechanical processing (TMP) conditions of 19 distinct near-α Ti alloys. PCA consolidated the ranks from various MADMs and identified top-ranked alloys for the intended applications as: Ti-6.7Al-1.9Sn-3.9Zr-4.6Mo-0.96W-0.23Si, Ti-4.8Al-2.2Sn-4.1Zr-2Mo-1.1Ge, Ti-6.6Al-1.75Sn-4.12Zr-1.91Mo-0.32W-0.1Si, Ti-4.9Al-2.3Sn-4.1Zr-2Mo-0.1Si-0.8Ge, Ti-4.8Al-2.3Sn-4.2Zr-2Mo, Ti-6.5Al-3Sn-4Hf-0.2Nb-0.4Mo-0.4Si-0.1B, Ti-5.8Al-4Sn-3.5Zr-0.7Mo-0.35Si-0.7Nb-0.06C, and Ti-6Al-3.5Sn-4.5Zr-2.0Ta-0.7Nb-0.5Mo-0.4Si. The alloys have the following metallurgical characteristics: bimodal matrix, aluminum equivalent preferably ~8, and nanocrystalline precipitates of Ti3Al, germanides, or silicides. The analyses, driven by decision science, make metallurgical sense and provide guidelines for developing next-generation commercial near-α Ti alloys. The investigation not only suggests potential replacement or substitute for existing alloys but also provides directions for improvement and development of titanium alloys over the current ones to push out some of the heavier alloys and thus help reduce the engine’s weight to gain advantage.

1. Introduction and Background

The selection of materials for aeroengine applications to meet the stringent requirements of high specific strength, good creep and fatigue resistance, high fracture toughness, oxidation and corrosion resistance, and so forth, is a challenge. To explore suitable materials for applications, including compressor blades, at temperatures of up to ~500 °C, an effort to select materials using Cambridge Engineering Selector (CES) software was attempted by maximizing several material performance indices, such as resistance to bending, fatigue, specific stiffness, and so on [1]. The analysis revealed titanium (Ti) alloys provide the best performance in temperatures of up to ~500 °C considering the cost and other trade-offs among the other competing alloy systems, viz., low alloy steels, stainless steels, nickel-based superalloys, etc. However, once the selection is zoomed down to Ti alloys, as per the analyses in [1], it is imperative to focus on the choice of apt Ti alloys for applications where strength-efficient structures and corrosion resistance are immanent, including aeroengines [2].
Since the beginning of the historical evolution in 1954, the high-temperature conventional Ti alloys, also known as near-α Ti alloys [3,4,5,6,7,8], are the choice class among the five different categories of Ti alloys for applications in compressor components in temperatures of up to ~600 °C in aeroengines [9,10]. The most advanced current commercial near-α Ti alloys are IMI834 and Ti-1100, with the capability for applications up to ~600 °C [11,12]. However, several investigations have shown that low tensile ductility at room temperature is a concern, which is attributed to various reasons, such as the precipitation of silicides, silicides aided by Ti3Al, Ti3Al aided by silicides, Ti3Al, etc. [3]. Therefore, alternative thermomechanical processing (TMP) and stability of the microstructures in service conditions are currently being investigated to mitigate the low tensile ductility at room temperature (that is designer specific) in near-α Ti alloys, which is critical for compressor components in aeroengines. The standard processing condition for the most current commercial alloy (IMI 834), suitable for up to ~600 °C, is typically considered the benchmark. However, generating creep, fatigue, fracture toughness, etc., obtaining data for the intended application/s on every one of those alternatives and variations become time-consuming, tedious, and expensive. Thus, to advance research and perform testing in a limited, faster, less expensive, and more sensible way, it is necessary to sort and select a few alloys, among the several alternative alloys available in the current literature, based on the important and easy to obtain room temperature tensile properties, by adopting decision science driven methods.
Material selection, a holistic approach of selecting an optimal material from a list of materials that is best suited for a given design and application, typically involves compromises between various material properties (mechanical, physical, chemical, etc.), cost, availability, environmental effects, to name a few [13]. The most common approach to material selection is Ashby’s material-selection approach—popularly referred to as the materials property chart approach [13,14,15]. The less common techniques include multiple attribute decision making (MADM) [16,17,18,19,20,21,22,23], cost per unit property method [15,24], Pareto-optimal solutions [15], and artificial intelligence methods (e.g., neural networks) [15,25,26]. MADM refers to making preference decisions over the available alternatives (list of materials) characterized by multiple, usually conflicting attributes (i.e., properties) [22,23]. MADM techniques find applications widely in various industries, including but not limited to logistics, management, manufacturing, and so on [27]. In this paper, we compile, evaluate, sort, and select near-α Ti alloys in the current literature for high-temperature applications in aeroengines, driven by decision science integrating MADM and principal component analysis (PCA). A combination of 12 MADM methods ranks a list of 105 alloy variants based on the TMP conditions of 19 different near-α Ti alloys (the majority are ‘research’ alloys). PCA, a powerful tool that transforms a multi-dimensional dataset into two dimensions [28,29,30], consolidates the ranks from various MADMs and identifies the ten top-ranking alloy variants for the intended applications.

2. Methods

Figure 1 presents a flowchart of the decision science driven selection of near-α Ti alloys from the literature for applications in compressor parts in aeroengines. The literature data comprises 105 variants (based on the TMP routes) of 19 distinct near-α Ti alloys. The method consists of three key routines: (i) Literature data (compilation of the near-α Ti alloys), (ii) Ranking (ranking by MADM methods), and (iii) Analyses (rank consolidation by PCA and interpretation).
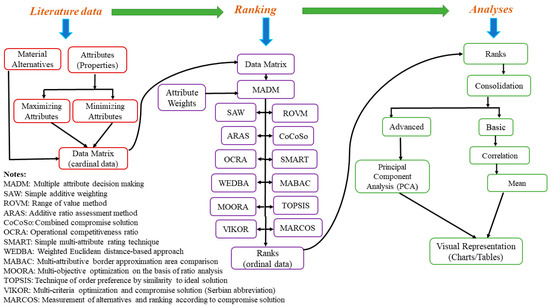
Figure 1. The flowchart of decision science driven analyses of the near-α Ti alloys. It comprises three routines: literature data, ranking, and analyses.

2.1. Literature Data

We compiled a list of near-α Ti alloys (alternatives) and their room-temperature mechanical properties (attributes) from the literature. Table A1 (in Appendix A) presents the alternatives, the near-α Ti alloys, screened for the current study primarily from peer-reviewed journals and conference proceedings [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52]. The table presents the nominal chemistry, processing conditions, and imminent microstructure. Eleven of the above 19 alloys are ‘research’ alloys (viz., WJZ-Ti, KIMS, JZ1, JZ2, JL, LD-Ti423, TMC-Ti213, TKT-1, TKT-2, TKT-3, and PC), implying they were fabricated and processed on a laboratory scale (under development) followed by characterization and testing. Eight of the 19 are current commercial alloys (IMI685, IMI829, IMI834, Ti-1100, Ti6242S, TA19, TA29, and Ti60). We identified room temperature % elongation (%EL), yield strength (YS), and ultimate tensile strength (UTS) as the properties (attributes) for the current investigation. For a targeted application, such as the compressor blade, the material needs to satisfy the desired room-temperature attributes (i.e., %EL, YS, and UTS) before examining the other important attributes, namely, the high-temperature properties, including creep resistance, oxidation resistance, and corrosion resistance to optimize the alloy. In the parlance of MADM, all of the identified attributes (%EL, YS, and UTS) are maximizing (or beneficial) attributes, suggesting, for most applications, that the alloys ought to have the following combination: high %EL, high YS, and high UTS. Table A2 (in Appendix A) is the decision matrix comprising the alternatives (near-α Ti alloys) and attributes (properties %EL, YS, and UTS) in the literature [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52].

2.2. Ranking

We evaluated the decision matrix (Table A2) by several multiple MADM methods. MADM refers to making preference decisions by evaluating and prioritizing alternatives on multiple attributes [22,23]. Distinct components of the MADM are (i) the decision matrix, which comprises the alternatives and the attributes, and (ii) attribute weights: the priorities of attributes are expressed quantitatively according to the MADM theory—they quantify the relative importance of each of the attributes [22,23,53]. The attribute weights are typical of three types [53]: (a) objective weights—based on the decision matrix utilizing mathematical models without considering the decision maker’s preferences (e.g., mean weighing, standard deviation method, entropy, etc.), (b) subjective weights, based on the preference derived from the evaluations of the experts (from their previous experience) or designers (constraints of design), or both, and (c) integrated weights, as the name suggests, both objective and subjective weighting are combined to determine the weights. We adopted objective and subjective attribute weights in this investigation.
We evaluated the weights by assigning equal weights (1/3) for each of the attributes based on the understanding of these materials and their intended application. We identified twelve MADM methods to evaluate the data matrix and rank the alloys, including the simple additive weighting (SAW) [22,23,53,54,55], range of value method (ROVM) [56,57], additive ratio assessment method (ARAS) [58,59,60], combined compromise solution (CoCoSo) [61,62,63], operational competitiveness ratio (OCRA) [64,65,66], simple multi-attribute rating technique (SMART) [22,53,67,68], weighted Euclidean distance-based approach (WEDBA) [23,69,70], multi-attributive border approximation area comparison (MABAC) [71,72], multi-objective optimization on the basis of ratio analysis (MOORA) [73,74], technique of order preference by similarity to ideal solution (TOPSIS) [22,53,75,76], multi-criteria optimization and compromise solution (VIKOR)—the Serbian name is VIse Kriterijumska Optimizacija Kompromisno Resenje—method [77,78,79], and measurement of alternatives and ranking according to compromise solution (MARCOS) [80,81]. Each MADM approach comprises a unique mathematical aggregation procedure to rank the alternatives. The MADMs identified were diverse. Applying such distinct aggregation procedures is likely to generate a robust set of ranks of the alternatives. The ranks produced by each method, as would be expected, are likely to deviate from one another; nevertheless, the correlation among the various techniques is expected to strengthen the reliability of the results. The modus operandi was soft coded in Microsoft Excel, as formulated in the respective references of MADMs.

2.3. Analyses

The ranks obtained by various MADMs were correlated. We evaluated Spearman’s correlation coefficients [82,83] among the ranks obtained from the 12 MADMs. We consolidated the ranks from various MADMs by estimating their mean and by principal component analysis (PCA). PCA, a multivariate technique, reduces the dimensionality of a dataset consisting of several interrelated variables by transforming to a new set of variables termed the principal components (PCs), which are uncorrelated and are ordered so that the first few PCs (typically one or two) retain most of the variation present in the original data [28,29]. The score plot presents a visual representation of the rank evaluation. The analyses were carried out using the commercial software Minitab® 20.

3. Results and Discussions

Figure 2 presents the ranks of the near-α Ti alloys from the literature evaluated by the 12 MADMs. The ranks of the alloys represented as points in the figure by nature are discrete; thin dotted lines for a better visual effect connect the ranks assessed by each of the MADMs. Despite the unique mathematical aggregation procedures in various MADMs, the peaks and troughs of several MADMs somewhat coincide. For example, several MADMs assign similar ranks to WJZ-Ti-2, TKT-2, WJZ-Ti-1, PC-IMDF4, and KIMS-2 (green-shaded). Moreover, the rank assigned by various MADMs to most alloys differs significantly, for instance, as in the alloys designated as Ti-1100-5, IMI834-5 and JZ2-3 (pink shaded). Table 1 presents the Spearman rank (Sρ) that correlates ranks evaluated by the 12 MADMs. For example, the Sρ between CoCoSo and ROVM, MABAC and WEDBA, or MARCOS and TOPSIS is >0.95, which indicates strong correlations. On the contrary, Sρ between ARAS and SMART or TOPSIS and SMART is less than <0.3, which is expected owing to the distinct mathematical aggregation formulation in various MADMs. Out of the 66 combinations of MADM pairs, ~72% have rank correlations equal to or above 0.70, which elicits the robustness and validity of the ranking of the near-α Ti alloys. Therefore, it is imperative to consolidate the ranks obtained from various MADMs. Based on Sρ among all various combinations of MADMs, it is practical to consolidate the rankings evaluated by the 12 different MADM evaluations. Accordingly, the mean-based (arithmetic mean) rank consolidation of Figure 2 is shown in Figure 3. The ranks of the top ten data points are WJZ-Ti-2, WJZ-Ti-1, TKT-2, TA19-2, TKT-6, TKT-1, TA19-1, KIMS-2, IMI834-2, and PC-IMDF4 in that order.
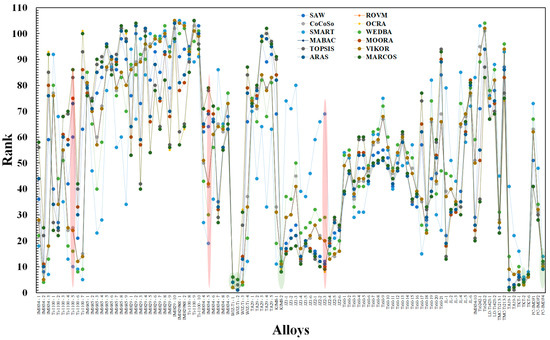
Figure 2. The ranks of the near-α Ti alloys from the literature evaluated by the 12 multiple attribute decision making (MADM) methods. Several MADMs assign relatively similar ranks (green shaded) to WJZ-Ti-2, TKT-2, WJZ-Ti-1, PC-IMDF4, and KIMS-2, while Ti-1100-5, IMI834-5, and JZ2-3 are assigned diverse set of ranks (pink shaded).
Table 1. The Spearman rank (Sρ) correlation of the near-α Ti alloys ranks from the literature evaluated by the 12 multiple attribute decision-making (MADM) methods.
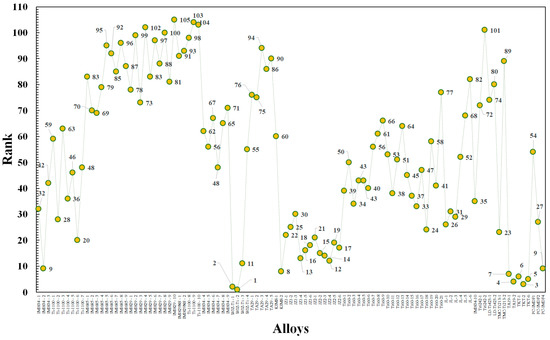
Figure 3. The arithmetic mean-based rank consolidation of the near-α Ti alloys from the literature evaluated by the 12 multiple attribute decision making (MADM) methods. The ranks of the top 10 data points are WJZ-Ti-2, WJZ-Ti-1, TKT-2, TA19-2, TKT-6, TKT-1, TA19-1, KIMS-2, IMI834-2, and PC-IMDF4 in that order.
Figure 4 is the score plot that presents the consolidated rank by PCA, of the near-α Ti alloys. It is the plot of the first two components (PC1 and PC2), post-reduction of the data dimensionality (i.e., ranks from 12 MADMs) into a two-dimensional space. Table 2 presents the eigenvalues (and their proportion) that capture the variation of the distribution of each principal component. The first principal component (PC1) captures ~82% of the variation or scatter in the original data, while the second principal (PC2) describes ~17% of the variation. Since PC1 captures nearly 82% of the variation in the initial 12 dimensions (sets of ranks), it approximates the rank of near-α Ti alloys. An imaginary reference line perpendicular to PC1 traversing from left to right (−6 to 6) indicates the overall ranks of the near-α Ti alloys. The alloy grades WJZ-Ti, TKT-2, TA19, TKT-6, TKT-1, KIMS, IMI834, and PC top the list, followed by JZ1, JZ2, Ti-1100, and so on. The ranks of the top ten data points are WJZ-Ti-2, WJZ-Ti-1, TKT-2, TA19-2, TKT-6, TKT-1, TA19-1, KIMS-2, IMI834-2, and PC-IMDF4 in that order (the data points within the box in Figure 4), while certain variants of WJZ-Ti, JZ1, and JZ2 also appear promising (the data points close to the box). The top-ranked alloys by PCA-based consolidation are strikingly similar to the top-ranked alloys evaluated by mean-based consolidation. Specifically, the PCA-based consolidation refines the IMI834-2 (rank#9) and PC-IMDF4 (rank#9) assigned by mean-based consolidation to rank#9 and #10, respectively. Therefore, it is logical to label the score plot of PCA-based consolidated ranks as a ‘rank chart’.
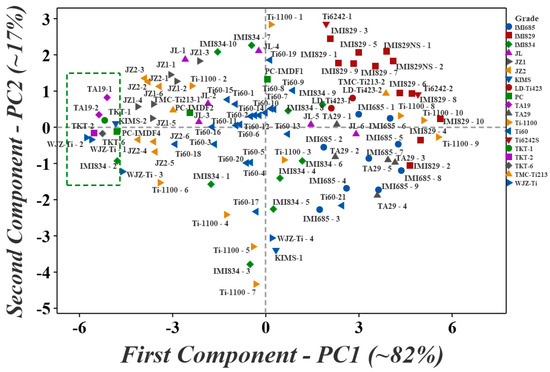
Figure 4. Score plot by principal component analysis (PCA) of the ordinal data, i.e., PCA-based rank consolidation of the near-α Ti alloys evaluated by the 12 MADM methods. The top-ranked alloy variants evaluated by PCA-based consolidation are strikingly similar to the top-ranked alloy variants evaluated by the mean-based consolidation. Specifically, the PCA-based consolidation refines the IMI834-2 (rank#9) and PC-IMDF4 (rank#9) assigned by the mean-based consolidation to rank#9 and #10, respectively.
Table 2. The eigenvalues and their proportion by the principal component analysis (PCA) of the ranks of the near-α Ti alloys from the literature by the 12 multiple attribute decision making (MADM) methods.
For deeper insight into the rank chart (Figure 4) of near-α Ti alloys, Figure 5a–d presents the score plots through the lens of various categories. Here, the region of interest (green box) corresponds to the top 10 alloy variants. Key inferences from the figures are as follows: (i) majority (seven out of 10) of the data points in the area of interest have aluminum equivalent to 8 (Figure 5a), (ii) all of the data points in the region of interest have a bimodal matrix, i.e., primary α + transformed β (Figure 5b), (iii) among the top ten data points, five (WJZ-Ti-1, TKT-2, TKT-1, TA19-2, and TA19-1) have no precipitates; one of them, WJZ-Ti-2, has precipitates Ti3Al in αp-1 (inside primary α); one of them (TKT-6) has germanide precipitates; one has silicide precipitates (KIMS-2—Hf in silicide and no Zr); and two (IMI834-2 and PC-IMDF4) have no information regarding the precipitates (Figure 5c) based on the chemistry, thermomechanical processing and the thermal treatments, these two variants would highly likely have Ti3Al and silicides; and lastly (iv) among the top 10 data points, five have no precipitates, four of them have nanocrystalline precipitates, and one has no information about any precipitate (Figure 5d). These analyses suggest guidelines for developing next-generation commercial near-α Ti alloys. The alloy design strategy for near-α Ti alloys for high-temperature applications with a combination of high YS, high UTS, and high %EL has two distinct options: (i) a combination of the aluminum equivalent to 8 and a bimodal matrix (primary α + transformed β) with no precipitates, (ii) a combination of the aluminum equivalent to 8, bimodal matrix, and nanocrystalline Ti3Al or germanide or silicide (no Zr, but Hf, as the silicides containing Hf, do not reduce ductility, however, Hf provides solid solution strengthening [3]) precipitates in α.
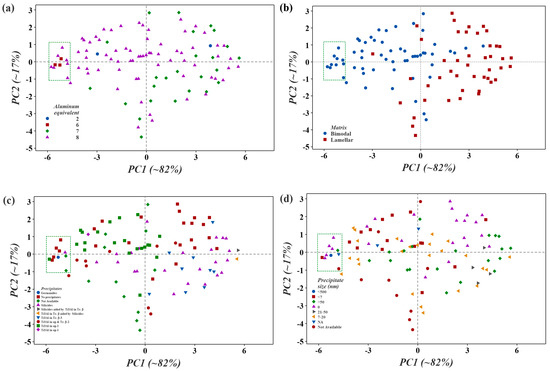
Figure 5. Score plots by the principal component analysis (PCA) of the ordinal data, i.e., PCA-based rank consolidation of the near-α Ti alloys evaluated by the 12 MADM methods through the lens of, i.e., categorized based on (a) aluminum equivalent, (b) matrix, (c) precipitates, and (d) precipitate size. The region of interest (green box) shows the top-ranked ten alloy variants.
In this investigation, we compile, evaluate, sort, and select near-α Ti alloys in the current literature for high-temperature applications in aeroengines, driven by decision science, by integrating MADM and principal component analysis (PCA). The evaluation provided valuable insight into potential existing materials (‘research alloys’) to focus on further research and development for commercialization. Among the top-ranked ten alloy variants (WJZ-Ti-2, WJZ-Ti-1, TKT-2, TA19-2, TKT-6, TKT-1, TA19-1, KIMS-2, IMI834-2, and PC-IMDF4), seven variants belong to the six ‘research grade’ alloys (WJZ-Ti, TKT-2, TKT-6, TKT-1, KIMS, and PC), while the data point IMI834-2 is a variant of an existing commercial alloy IMI834. Thus, all of these alloys appear to be strong contenders for large-scale development and testing. Additionally, in the future, newly discovered novel high-temperature Ti alloys (conventional and high-entropy alloys) can be included in the list and evaluated to assess their relative position in the rank chart and infer their potential to replace existing materials. In the near future, we plan to expand the decision science driven material selection by including several other relevant mechanical properties as they become available. Lastly, this effort (i) validates the decision science driven MADM coupled with PCA for sorting, ranking, and material selection, (ii) weeds out the alloys that need not be pursued further with time-consuming experimental studies to generate data on additional attributes that are required for use for the intended application/s, and (iii) provide directions for advancing alloys that are under development or suggest some critical improvements for possible newer alloys by providing metallurgical perspectives. Developing a methodology that applies decision science principles to compile and sort a relatively large literature data, select or identify top-ranked alloys, unearth metallurgical patterns, and recommend guidelines for developing next-generation commercial near-α Ti alloys for aeroengines is the novelty of the investigation.

4. Summary and Conclusions

We compiled, evaluated, ranked, and selected near-α Ti alloys in the current literature for high-temperature applications in aeroengines, driven by decision science by integrating MADM and principal component analysis (PCA). A combination of 12 MADM methods ranked a list of 105 alloy variants based on the thermomechanical processing (TMP) conditions of 19 different near-α Ti alloys. PCA consolidated the ranks from various MADMs and identified ten top-ranked alloy variants for the intended application/s. The ten top-ranked alloy variants are WJZ-Ti-2, WJZ-Ti-1, TKT-2, TA19-2, TKT-6, TKT-1, TA19-1, KIMS-2, IMI834-2, and PC-IMDF4 in that order and they correspond to the following eight alloys: Ti-6.7Al-1.9Sn-3.9Zr-4.6Mo-0.96W-0.23Si, Ti-4.8Al-2.2Sn-4.1Zr-2Mo-1.1Ge, Ti-6.6Al-1.75Sn-4.12Zr-1.91Mo-0.32W-0.1Si, Ti-4.9Al-2.3Sn-4.1Zr-2Mo-0.1Si-0.8Ge, Ti-4.8Al-2.3Sn-4.2Zr-2Mo, Ti-6.5Al-3Sn-4Hf-0.2Nb-0.4Mo-0.4Si-0.1B, Ti-5.8Al-4Sn-3.5Zr-0.7Mo-0.35Si-0.7Nb-0.06C, and Ti-6Al-3.5Sn-4.5Zr-2.0Ta-0.7Nb-0.5Mo-0.4Si. The top-ranked alloys evaluated by PCA-based consolidation are strikingly similar to the top-ranked alloys evaluated by mean-based consolidation. The top-ranked alloys suggest the following metallurgical characteristics: bimodal matrix (primary α + transformed β), aluminum equivalent preferably up to 8, and nanocrystalline precipitates of Ti3Al, germanides, or silicides. The analyses driven by decision science made metallurgical sense. It provides guidelines for developing next-generation commercial near-α Ti alloys. The alloy design strategy for near-α Ti alloys for high-temperature applications with a combination of high YS, high UTS, and high %EL has two distinct options: (i) a combination of the aluminum equivalent to 8 and a bimodal matrix with no precipitates, or (ii) a combination of the aluminum equivalent to 8, bimodal matrix, and nanocrystalline Ti3Al or germanide or silicide (not Zr, but Hf, as the silicides containing Hf do not reduce ductility, to the contrary, Hf provides solid solution strengthening) precipitates in α. Thus, novel alloys could be developed based on these directions for the future. A similar analysis could include data from newer exotic experimental materials, such as composites, for compressor parts.

Author Contributions

Conceptualization, T.V.J. and R.C.; Methodology, T.V.J.; Software, T.V.J.; Validation, R.C. and T.V.J.; Formal Analysis, T.V.J. and R.C.; Investigation, T.V.J. and R.C.; Data Curation, R.C.; Writing—Original Draft Preparation, T.V.J.; Writing—Review & Editing, T.V.J. and R.C.; Visualization, T.V.J.; Supervision, R.C. and T.V.J.; Project Administration, R.C. and T.V.J.; Funding Acquisition, R.C. and T.V.J. All authors have read and agreed to the published version of the manuscript.

Funding

Weldaloy Specialty Forgings (Research and Development Account# 8860.00) Institute of Advanced Vehicle Systems (grant# 052349), University of Michigan-Dearborn.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The data used in the analyses is presented in Table A1 and Table A2.

Acknowledgments

The author R. Canumalla thanks the Weldaloy Specialty Forgings management for all their support; the author T. V. Jayaraman, thanks the Department of Mechanical Engineering, College of Engineering and Computer Science, University of Michigan-Dearborn for all their support.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table A1. The alternatives, a list of 105 variants of 19 distinct near-α Ti alloys identified for the investigation, chemistry (nominal composition), fabrication and processing conditions, and microstructure; alloy designation is the unique identifier assigned to the variants.
Table A1. The alternatives, a list of 105 variants of 19 distinct near-α Ti alloys identified for the investigation, chemistry (nominal composition), fabrication and processing conditions, and microstructure; alloy designation is the unique identifier assigned to the variants.
Sl#AlloyChemistry (Nominal)Processing Step 1Processing Step 2Microstructure DescriptionAlloy
Designation		Ref.
1IMI834Ti-5.8Al-4Sn-3.5Zr-0.7Mo-0.35Si-0.7Nb-0.06C834-(α + β)ST1025 °C OQ700 °CMicro 1-Bimodal-αp (15 vol.%/15–20 µm) & Tr.βIMI834-1[31]
2IMI834Ti-5.8Al-4Sn-3.5Zr-0.7Mo-0.35Si-0.7Nb-0.06C834-TMT-(α + β)ST1000WQ600 °C-4 hMicro 2-Bimodal-higher amount of αp than Micro1IMI834-2
3IMI834Ti-5.8Al-4Sn-3.5Zr-0.7Mo-0.35Si-0.7Nb-0.06C834-TMT-βST1080 °C WQ600 °C-4 hMicro 3-Lamellar-Tr.βIMI834-3
4Ti-1100Ti-5.8Al-2.7Sn-4Zr-0.4Mo-0.45SiTi-1100 °C Forged at 980 °C AQUnagedMicro A-Bimodal-αp (15 vol.%/15–20 µm) & Tr.βTi-1100-1
5Ti-1100Ti-5.8Al-2.7Sn-4Zr-0.4Mo-0.45SiTi-1100 °C (α + β) ST940 °C WQ600 °C-4 hMicro B-Bimodal and finer than Micro ATi-1100-2
6Ti-1100Ti-5.8Al-2.7Sn-4Zr-0.4Mo-0.45SiTi-1100 °C (α + β) ST980 °C WQ600 °C-4 hMicro C-Bimodal coarse compared to Micro B but comparable to Micro-ATi-1100-3
7Ti-1100Ti-5.8Al-2.7Sn-4Zr-0.4Mo-0.45SiTi-1100 °C-βST1020 °C WQ600 °C-4 hMicro D-Lamellar-Prior β grain size 200 µmTi-1100-4
8Ti-1100Ti-5.8Al-2.7Sn-4Zr-0.4Mo-0.45SiTi-1100 °C-βST1060WQ600 °C-4 hMicro E-Lamellar-Prior β grain size 500 to 600 µmTi-1100-5
9Ti-1100Ti-5.8Al-2.7Sn-4Zr-0.4Mo-0.45SiTi-1100 °C-TMT-(α + β) ST1000 °C WQ600 °C-4 hMicro F-Bimodal-finer compared to Micro CTi-1100-6
10Ti-1100Ti-5.8Al-2.7Sn-4Zr-0.4Mo-0.45SiTi-1100 °C-TMT-βST1060 °C WQ600 °C-4 hMicro G-Lamellar-finer compared to Micro ETi-1100-7
11IMI685Ti-6.18Al-5.27Zr-0.5Mo-0.28Si685-βST1050 °C-WQUnagedLamellar α’—No precipitatesIMI685-1[32]
12IMI685Ti-6.18Al-5.27Zr-0.5Mo-0.28Si685-βST1050 °C-WQ550 °C-24 hLamellar α’—No precipitatesIMI685-2
13IMI685Ti-6.18Al-5.27Zr-0.5Mo-0.28Si685-βST1050 °C-WQ650 °C-24 hLamellar-Silicides S1 & S2—NO Ti3AlIMI685-3
14IMI685Ti-6.18Al-5.27Zr-0.5Mo-0.28Si685-βST1050 °C-WQ700 °C-24 hLamellar-Silicides S2—NO Ti3AlIMI685-4
15IMI685Ti-6.18Al-5.27Zr-0.5Mo-0.28Si685-βST1050 °C-WQ800 °C-24 hLamellar~0.1µm Silicides S2—NO Ti3AlIMI685-5
16IMI685Ti-6.18Al-5.27Zr-0.5Mo-0.28Si685-βST1050 °C-WQ700 °C-24 hLamellar-finer Silicides S2/41.2 nm—NO Ti3AlIMI685-6[33]
17IMI685Ti-6.18Al-5.27Zr-0.5Mo-0.28Si685-βST1050 °CWQ6CR700 °C-24 hLamellar-finer Silicides S2/38.6 nm—NO Ti3AlIMI685-7
18IMI685Ti-6.18Al-5.27Zr-0.5Mo-0.28Si685-βST1050 °CWQ12CR700 °C-24 hLamellar-finer Silicides S2/33.4 nm—NO Ti3AlIMI685-8
19IMI685Ti-6.18Al-5.27Zr-0.5Mo-0.28Si685-βST1050 °CWQ15CR700 °C-24 hLamellar-finer Silicides S2/28.5 nm-NO Ti3AlIMI685-9
20IMI829Ti-6.1Al-3.3Sn-3.2Zr-1Nb-0.5Mo-0.32Si829-βST1050 °C-WQUnaged Lamellar α’—No precipitatesIMI829-1[34]
21IMI829Ti-6.1Al-3.3Sn-3.2Zr-1Nb-0.5Mo-0.32Si829-βST1050 °C-WQ625 °C-24 hLamellar—Silicides S2 only-No Ti3AlIMI829-2
22IMI829Ti-6.1Al-3.3Sn-3.2Zr-1Nb-0.5Mo-0.32Si829-βST1050 °C-OQUnagedLamellar α’—No precipitatesIMI829-3
23IMI829Ti-6.1Al-3.3Sn-3.2Zr-1Nb-0.5Mo-0.32Si829-βST1050 °C-OQ625 °C-24 hLamellar-Silicides S2 only-No Ti3AlIMI829-4
24IMI829Ti-6.1Al-3.3Sn-3.2Zr-1Nb-0.5Mo-0.32Si829-βST1050 °C-ACUnagedLamellar/Widmanstatten- No precipitates-No Silicides or Ti3AlIMI829-5
25IMI829Ti-6.1Al-3.3Sn-3.2Zr-1Nb-0.5Mo-0.32Si829-βST1050 °C-AC625 °C-24 hLamellar/Widmanstatten-Silicides S2 only-No Ti3AlIMI829-6
26IMI829Ti-6.1Al-3.3Sn-3.2Zr-1Nb-0.5Mo-0.32Si829-βST1050 °C-FCUnagedAligned alpha/Lamellar—No precipitatesIMI829-7
27IMI829Ti-6.1Al-3.3Sn-3.2Zr-1Nb-0.5Mo-0.32Si829-βST1050 °C-FC625 °C-24 hAligned alpha/LamellarS2—Ti3AlIMI829-8
28IMI829Ti-5.54Al-3.48Sn-2.95Zr-0.97Nb-0.34Mo-0.28Si829-βST1050 °C-ACUnagedLamellar- No pecipitatesIMI829-9[35]
29IMI829Ti-5.54Al-3.48Sn-2.95Zr-0.97Nb-0.34Mo-0.28Si829-βST1050 °C-AC625 °C-2 h-AC-575 °C-1000 h-ACLamellar—Ti3Al (5 nm)IMI829-10
30IMI829Ti-5.51Al-3.48Sn-3.04Zr-0.99Nb-0.33Mo < 0.02Si829NS-βST1050 °C-ACUnagedLamellar-No precipitatesIMI829NS-1
31IMI829Ti-5.51Al-3.48Sn-3.04Zr-0.99Nb-0.33Mo < 0.02Si829NS-βST1050 °C-AC625 °C-2 h-AC-575 °C-1000 h-ACLamellar—Ti3Al (5 nm)IMI829NS-2
32Ti-1100Ti-6Al-2.8Sn-4Zr-0.4Mo-0.45SiTi1100-βST1093 °C-ACUnaged (593C-8 h-AC)Lamellar-No precipitatesTi-1100-8[36]
33Ti-1100Ti-6Al-2.8Sn-4Zr-0.4Mo-0.45SiTi1100-βST1093 °C-ACOveraged (Unaged + 593C-180 K min-AC)Lamellar-13 nm Ti3Al in Tr β and 175 × 35 nm SilicidesTi-1100-9
34Ti-1100Ti-6Al-2.8Sn-4Zr-0.4Mo-0.45SiTi1100-βST1093 °C-ACPAHT (Unaged + 593C-60 K min + 750C-4 h-AC)Lamellar-only Silicides (~100 nm)-NO Ti3AlTi-1100-10
35IMI834Ti-5.07Al-3.08Sn-3.45Zr-0.31Mo-0.2Si-0.66Nb-0.04C834-βST1080 °C-cooled to (α + β)1010 °C-1 h-WQUnagedLamellar-No precipitatesIMI834-4[37]
36IMI834Ti-5.07Al-3.08Sn-3.45Zr-0.31Mo-0.2Si-0.66Nb-0.04C834-βST1080 °C-cooled to (α + β)1010 °C-1 h-WQ700 °C-2 h-ACLamellar—Ti3Al (5 nm) in Tr. β and SilicidesIMI834-5
37IMI834Ti-5.07Al-3.08Sn-3.45Zr-0.31Mo-0.2Si-0.66Nb-0.04C834-βST1080 °C-cooled to (α + β)1010 °C-1 h-WQ825 °C-2 h-WQLamellar—100 to 175 nm Silicides (Ti3Al dissolved at 825 °C)IMI834-6
38IMI834Ti-5.78Al-4.54Sn-4.05Zr-0.70Nb-0.52Mo-0.44Si-0.055C834-(α + β)ST1020 °C-2 h-OQ (12-15%αp)600 °C-4 hBimodal-Ti3Al in only αpIMI834-7[38]
39IMI834Ti-5.78Al-4.54Sn-4.05Zr-0.70Nb-0.52Mo-0.44Si-0.055C834-(α + β)ST1020 °C-2 h-OQ- (12-15%αp)650 °C-4 hBimodal-Ti3Al in αp & Tr. β and Silicides S2IMI834-8
40IMI834Ti-5.78Al-4.54Sn-4.05Zr-0.70Nb-0.52Mo-0.44Si-0.055C834-(α + β)ST1020 °C-2 h-OQ- (12-15%αp)700 °C-4 hBimodal-Ti3Al in αp & Tr. β and Silicides S2IMI834-9
41WJZ-TiTi-6.7Al-1.9Sn-3.9Zr-4.6Mo-0.96W-0.23Si834-(α + β)ST940 °C-2 h-ACUnagedBimodal-No precipitatesWJZ-Ti-1[39]
42WJZ-TiTi-6.7Al-1.9Sn-3.9Zr-4.6Mo-0.96W-0.23Si834-(α + β)ST940 °C-1 h-AC600 °C-2 hBimodal-6 nm Ti3Al in αpWJZ-Ti-2
43WJZ-TiTi-6.7Al-1.9Sn-3.9Zr-4.6Mo-0.96W-0.23Si834-(α + β)ST940 °C-1 h-AC750 °C-2 hBimodal-7 nm Ti3Al in αp & Tr.βWJZ-Ti-3
44WJZ-TiTi-6.7Al-1.9Sn-3.9Zr-4.6Mo-0.96W-0.23Si834-(α + β)ST940 °C-1 h-AC750 °C-12 hBimodal-15 nm Ti3Al in αp & Tr.βWJZ-Ti-4
45TA29Ti-5.8Al-4Sn-4Zr-0.7Nb-1.5Ta-0.4Si-0.06CTA29-βST (at > 1050 °C)750 °C-2 hLamellar—~100 nm Silicides -small number at IPBTA29-1[40]
46TA29Ti-5.8Al-4Sn-4Zr-0.7Nb-1.5Ta-0.4Si-0.06CTA29-βST (at > 1050 °C) + 750 °C-2 h650 °C-8 hLamellar—~100 nm Silicides at IPB & Ti3Al (<5 nm)TA29-2
77TA29Ti-5.8Al-4Sn-4Zr-0.7Nb-1.5Ta-0.4Si-0.06CTA29-βST (at > 1050 °C) + 750 °C-2 h650 °C-100 hLamellar—~100 nm-Silicides at IPB and some inside &Ti3Al in Tr. β (~8 nm)TA29-3
48TA29Ti-5.8Al-4Sn-4Zr-0.7Nb-1.5Ta-0.4Si-0.06CTA29-βST (at > 1050 °C) + 750 °C-2 h650 °C-500 hLamellar—~100 nm Silicides at IPB and inside-IPB & Ti3Al in Tr. β (26 nm L x13 nm thk.)TA29-4
49TA29Ti-5.8Al-4Sn-4Zr-0.7Nb-1.5Ta-0.4Si-0.06CTA29-βST (at > 1050 °C) + 750 °C-2 h650 °C-1000 hLamellar—~100 nm Silicides at IPB and inside & Ti3Al in Tr. β (~20 nm dia.)TA29-5
50KIMSTi-6.5Al-3Sn-4Hf-0.2Nb-0.4Mo-0.4Si-0.1BKIMS-(α + β)ST-1 h-WQ650 °C-5 hBimodal—Ti3Al αp & Tr.β uniformly and Silicides-~80 nmKIMS-1[41]
51KIMSTi-6.5Al-3Sn-4Hf-0.2Nb-0.4Mo-0.4Si-0.1BKIMS-(α + β)ST-1 h-WQ700 °C-2 h-ACBimodal—150 nm Silicides-IPBKIMS-2
52JZ1Ti-5.6Al-4.8Sn-2Zr-1Mo-0.35SiJZ1-(α + β)ST-1005 °C-2 h-AC700 °C-2 h-ACBimodal—No precipitatesJZ1-1[42]
53JZ1Ti-5.6Al-4.8Sn-2Zr-1Mo-0.35SiJZ1-(α + β)ST-1005 °C-2 h-AC700 °C-5 h-ACBimodal—Ti3Al in αp + Silicides (~100 nm)JZ1-2
54JZ1Ti-5.6Al-4.8Sn-2Zr-1Mo-0.35SiJZ1-(α + β)ST-1005 °C-2 h-AC700 °C-15 h-ACBimodal—Ti3Al in αp + Silicides (~100 nm)JZ1-3
55JZ1Ti-5.6Al-4.8Sn-2Zr-1Mo-0.35SiJZ1-(α + β)ST-1005 °C-2 h-AC700 °C-2 h-AC-600 °C-100 hBimodal—Ti3Al in αp + Silicides JZ1-4
56JZ1Ti-5.6Al-4.8Sn-2Zr-1Mo-0.35SiJZ1-(α + β)ST-1005 °C-2 h-AC700 °C-5h-AC-600 °C-100 hBimodal—Ti3Al in αp + Silicides (~100 nm)JZ1-5
57JZ1Ti-5.6Al-4.8Sn-2Zr-1Mo-0.35SiJZ1-(α + β)ST-1005 °C-2 h-AC700 °C-15h-AC-600 °C-100 hBimodal—Ti3Al in αp + Silicides (~100 nm)JZ1-6
58JZ2Ti-6Al-4.8Sn-2Zr-1Mo-0.35SiJZ2-(α + β)ST-1015 °C-2 h-AC760 °C-2 h-ACBimodal—Ti3Al in αp + Silicides JZ2-1
59JZ2Ti-6Al-4.8Sn-2Zr-1Mo-0.35SiJZ2-(α + β)ST-1015 °C-2 h-AC760 °C-5h-ACBimodal—Ti3Al in αp + Silicides (~100 nm)JZ2-2
60JZ2Ti-6Al-4.8Sn-2Zr-1Mo-0.35SiJZ2-(α + β)ST-1015 °C-2 h-AC760 °C-10 h-ACBimodal—Ti3Al in αp + SilicidesJZ2-3
61JZ2Ti-6Al-4.8Sn-2Zr-1Mo-0.35SiJZ2-(α + β)ST-1015 °C-2 h-AC760 °C-2 h-ACBimodal—Ti3Al in αp & Tr.β + SilicidesJZ2-4
62JZ2Ti-6Al-4.8Sn-2Zr-1Mo-0.35SiJZ2-(α + β)ST-1015 °C-2 h-AC760 °C-5h-AC-600 °C-100 hBimodal—Ti3Al in αp & Tr.β + Silicides (~100 nm)JZ2-5
63JZ2Ti-6Al-4.8Sn-2Zr-1Mo-0.35SiJZ2-(α + β)ST-1015 °C-2 h-AC760 °C-10 h-AC-600 °C-100 hBimodal—Ti3Al in αp & Tr.β + SilicidesJZ2-6
64Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-(α + β)ST1010 °C-2 h-OQUnagedBimodal—No precipitates Ti60-1[43]
65Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-(α + β)ST1010 °C-2 h-OQ650 °C-2 h-ACBimodal-No Ti3Al+ small number of Silicides 100 nm-Stage 1Ti60-2
66Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-(α + β)ST1010 °C-2 h-OQ650 °C-4 h-ACBimodal-No Ti3Al+ small number of Silicides-100 nm-Stage 1Ti60-3
67Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-(α + β)ST1010 °C-2 h-OQ650 °C-8 h-ACBimodal-No Ti3Al + Silicides—100 nm-Stage 1Ti60-4
68Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-(α + β)ST1010 °C-2 h-OQ650 °C-16 h-ACBimodal-No Ti3Al + Silicides—100 nm —Stage 1Ti60-5
69Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-(α + β)ST1010 °C-2 h-OQ700 °C-2 h-ACBimodal-No Ti3Al + Silicides 100 nm Stage 1Ti60-6
70Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-(α + β)ST1010 °C-2 h-OQ700 °C-4 h-ACBimodal-Ti3Al in αp + SilicidesTi60-7
71Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-(α + β)ST1010 °C-2 h-OQ700 °C-8 h-ACBimodal-Ti3Al in αp + SilicidesTi60-8
72Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-(α + β)ST1010 °C-2 h-OQ700 °C-16 h-ACBimodal-Ti3Al in αp + Silicides Ti60-9
73Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-(α + β)ST1010 °C-2 h-OQ700 °C-24 h-ACBimodal-Ti3Al in αp + SilicidesTi60-10
74Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-(α + β)ST1010 °C-2 h-OQ700 °C-48 h-ACBimodal-Ti3Al in αp + Silicides Ti60-11
75Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-(α + β)ST1010 °C-2 h-OQ750 °C-2 h-ACBimodal-Silicides-Ti3Al in αp Ti60-12
76Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-(α + β)ST1010 °C-2 h-OQ750 °C-4 h-ACBimodal-Ti3Al in αp + SilicidesTi60-13
77Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-(α + β)ST1010 °C-2 h-OQ750 °C-8 h-ACBimodal-Ti3Al in αp + Silicides Ti60-14
78Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-(α + β)ST1010 °C-2 h-OQ750 °C-16 h-ACBimodal-Ti3Al in αp + Silicides—100 nm Ti60-15
79Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-1035C-near β forged-(α + β)ST1010 °C-2 h-AC700 °C-2 h-ACBimodal-No Ti3Al + Silicides-~100 nm Ti60-16[44]
80Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-1035C-near β forged-(α + β) ST1010 °C-2 h-AC700 °C-2 h-AC-600C-100 h-ACBimodal-Ti3Al in αp + Silicides ~200 nm Ti60-17
81Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-1035C-near β forged-(α + β)ST1010 °C-2 h-AC700 °C-2 h-A -700 °C-100 h-ACBimodal-only Silicides possibly (dissolution of Ti3Al)Ti60-18
82Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-1035C-near β forged-(α + β)ST1010 °C-2 h-AC700 °C-2 h-AC-750 °C-100 h-ACBimodal-only Silicides possibly (dissolution of Ti3Al)Ti60-19
83Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-1070C- β forged-(α + β)ST1010 °C-2 h-AC700 °C-2 h-ACLamellar + No Ti3Al + Silicides ~100 nm Ti60-20
84Ti60Ti-5.8Al-4Sn-3.5Zr-0.4Mo-0.4Nb-1Ta-0.4Si-0.06CTA60-1070C-β forged-(α + β)ST1010 °C-2 h-AC700 °C-2 h-AC-600 °C-100 h-ACLamellar-Ti3Al in Tr. β + Silicides ~100 nm Ti60-21
85JLTi-5.6Al-4.3Sn-3Zr-1Mo-0.8Nd-0.34SiJL-(α + β) forged- (α + β)ST1010 °C-2 h-ACUnagedBimodal—No precipitates (αp is ~10% vf.;~150 nm)JL-1[45]
86JLTi-5.6Al-4.3Sn-3Zr-1Mo-0.8Nd-0.34SiJL-(α + β) forged- (α + β)ST1010 °C-2 h-AC700 °C-2 h-ACBimodal—Ti3Al in αp + Silicides ~125 nmJL-2
87JLTi-5.6Al-4.3Sn-3Zr-1Mo-0.8Nd-0.34SiJL-(α + β) forged- (α + β)ST1010 °C-2 h-AC700 °C-12 h-ACBimodal—Ti3Al in αp & Tr. β + Silicides ~125 nmJL-3
88JLTi-5.6Al-4.3Sn-3Zr-1Mo-0.8Nd-0.34SiJL-(α + β) forged- βST1030 °C-2 h-ACUnagedLamellar—No precipitates (colony size; ~350 nm)JL-4
89JLTi-5.6Al-4.3Sn-3Zr-1Mo-0.8Nd-0.34SiJL-(α + β) forged- βST1030 °C-2 h-AC700 °C-2 h-ACLamellar—Ti3Al in Tr. β + Silicides ~125 nmJL-5
90JLTi-5.6Al-4.3Sn-3Zr-1Mo-0.8Nd-0.34SiJL-(α + β) forged- βST1030 °C-2 h-AC700 °C-12 h-ACLamellar—Ti3Al in Tr. β + Silicides ~125 nmJL-6
91IMI834Ti-5.8Al-4Sn-3.5Zr-0.7Mo-0.35Si-0.7Nb-0.06C834-(α + β) ST1020 °C-2 h-AC700 °C-2 h-ACBimodal—Ti3Al in αp + Silicides ~125 nmIMI834-10[46]
92Ti6242STi-5.7Al-1.9Sn-3.7Zr-1.9Mo-0.09SiTi6242S-(α + β) Hot rolled βST1052 °C-1 h-CCUnagedLamellar-No precipitatesTi6242-1[47]
93Ti6242STi-5.7Al-1.9Sn-3.7Zr-1.9Mo-0.09SiTi6242S-(α + β) Hot rolled β ST1052 °C-1 h-CC760 °C-600 h-ACLamellar-Silicides (>100 nm)Ti6242-2
94LD-Ti423Ti-8Al-1Cr-1V-0.5Fe-0.1SiVIM-Open die forged at (β)1100 °C-Hot rolled at (α + β)1000 °C-50%Reduction (Rolled plate) or HRNAHeterogenous microstructure/similar to bimodal (major equiaxed αp 11 µm and small amount of acicular αs and β phases in the interstices of equiaxed α)LD-Ti423-1[48]
95LD-Ti423Ti-8Al-1Cr-1V-0.5Fe-0.1SiVIM-Open die forged at (β)1100 °C-Hot rolled at (α + β)1000 °C-50%Reduction (Rolled plate)HR +(α + β) ST at 1000 °C-1 h-AC-Aged at 560 °C-4 h-AC (STA)Heterogenous microstructure/similar to bimodal (major equiaxed αp 20µm and small amount of acicular αs and β phases in the interstices of equiaxed α)LD-Ti423-2
96TMC-Ti213Ti-2Al-1.3VThermomechanical consolidation (TMC) of TiH2 and Ti6Al4V at a mass ratio of 2:1, and extruded to produce Ti-2Al-1.3V at 16 to 1 ratio at around 1200 °CTMC-Vac Anneal 700 °C-6 h-FClamellar α/β (lamellae of 0.9µm thk and ave. lamellar colony size of 15.4 µm)TMC-Ti213-1[49]
97TMC-Ti213Ti-2Al-1.3VThermomechanical consolidation (TMC) of TiH2 and Ti6Al4V at a mass ratio of 2:1, and extruded to produce Ti-2Al-1.3V at 16 to 1 ratio at around 1200 °CTMC-Vac Anneal 700 °C-6 h-FC-980 °C-1 h-ACequiaxed α grains and α/β lamellar structured domains (βt or β transformed structure) TMC-Ti213-2
98TA19Ti-6.6Al-1.75Sn-4.12Zr-1.91Mo-0.32W-0.1Siα-β field rolled plate, tempered in the α-β field970 °C-1 h-AC (for equiaxed structure (EM))equiaxed α grains (42%Vol.; 12 µm dia) and α/β lamellar (αs 10 µm length × 400 nm width); g.b α 420 nm width TA19-1 [50]
99TA19Ti-6.6Al-1.75Sn-4.12Zr-1.91Mo-0.32W-0.1Siα-β field rolled plate, tempered in the α-β field1015 °C-35s-cooled at 20 °C/s (for semi equiaxed structure (S-EM))Semi-equiaxed α grains (41%Vol.; 13 µm dia) and α/β lamellar (αs 11 µm length × 410 nm width); g.b α 850 nm widthTA19-2
100TKT-1Ti-4.8Al-2.3Sn-4.2Zr-2MoDouble melted; β forged qt 1100 °C-groove rolled to 50% reduction at (α + β) 960 °C to rods of 14mm diaAnnealed at 950 °C-1 h-AC-aged at 590 °C-8 h-ACBimodal microstructure comprising primary equiaxed α and α-β lamellar (transformed β) structuresTKT-1[51]
101TKT-2Ti-4.8Al-2.2Sn-4.1Zr-2Mo-1.1GeDouble melted; β forged qt 1100 °C-groove rolled to 50% reduction at (α + β) 960 °C to rods of 14mm diaAnnealed at 950 °C-1 h-AC-aged at 590 °C-8 h-ACBimodal microstructure comprising primary equiaxed α and α-β lamellar (transformed β) structuresTKT-2
102TKT-6Ti-4.9Al-2.3Sn-4.1Zr-2.1Mo-0.1Si-0.8GeDouble melted; β forged qt 1100 °C-groove rolled to 50% reduction at (α + β) 960 °C to rods of 14mm diaAnnealed at 950 °C-1 h-AC-aged at 590 °C-8 h-ACBimodal microstructure comprising primary equiaxed α and α-β lamellar (transformed β) structures with (TiZr)6(SiGe)3 precipitatesTKT-6
103PCTi-6Al-3.5Sn-4.5Zr-2.0Ta-0.7Nb-0.5Mo-0.4SiInduction skull melted ingot 80mm dia × 120mm length and then 1100 °C β upset forged to a total height reduction of 75% (reduction ratio of 4 to 1)ONE-Isothermal Multidirectional Forging (IMDF) at 1020 °C-annealed at 650 °C-6 hMainly α laths (lamellar mainly—mean size 2.13 µm) with small amount of equiaxed α PC-IMDF1[52]
104PCTi-6Al-3.5Sn-4.5Zr-2.0Ta-0.7Nb-0.5Mo-0.4SiInduction skull melted ingot 80 mm dia × 120 mm length and then 1100C β upset forged to a total height reduction of 75% (reduction ratio of 4 to 1)TWO-IMDFs at 1020 °C-annealed at 650 °C-6 hprior β boundaries start to disappear and α laths transform to spheroidal α grains (equiaxed α—mean size 1.85 µm)PC-IMDF2
105PCTi-6Al-3.5Sn-4.5Zr-2.0Ta-0.7Nb-0.5Mo-0.4SiInduction skull melted ingot 80 mm dia × 120 mm length and then 1100 °C β upset forged to a total height reduction of 75% (reduction ratio of 4 to 1)FOUR-IMDFs at 1020 °C-annealed at 650 °C-6 hlarge number of spheroidal α grains transformed from lamellaePC-IMDF4
Note: ST: solution treated; h: hours; AC: air cooled; OQ: oil quenched; WQ: water quenched; αp: primary alpha; Tr. β: transformed beta; bimodal matrix: primary α + transformed β; and lamellar matrix: completely transformed β.
Table A2. Database of 105 variants of 19 distinct near-α Ti alloys identified from the literature, which form the decision matrix comprising the alternatives and their attributes.
Table A2. Database of 105 variants of 19 distinct near-α Ti alloys identified from the literature, which form the decision matrix comprising the alternatives and their attributes.
Alloy Desig.GradeAl.eq.MatrixPrecipitatesSizeYSUTS%ElRef.
IMI834-1IMI8348BimodalNANA104011259[31]
IMI834-2IMI8348BimodalNANA1200125513
IMI834-3IMI8348LamellarNANA111012204
Ti-1100-1Ti-11007BimodalNANA90096513.5
Ti-1100-2Ti-11007BimodalNANA965105014
Ti-1100-3Ti-11007BimodalNANA99510908
Ti-1100-4Ti-11007LamellarNANA105011607.5
Ti-1100-5Ti-11007LamellarNANA108011905
Ti-1100-6Ti-11007BimodalNANA1100120010
Ti-1100-7Ti-11007LamellarNANA115012502.5
IMI685-1IMI6857LamellarNP091910587.2[32]
IMI685-2IMI6857LamellarNP096610907.3
IMI685-3IMI6857LamellarSilicides>50102011324.7
IMI685-4IMI6857LamellarSilicides>50100511024.8
IMI685-5IMI6857LamellarSilicides>5095410383.75
IMI685-6IMI6857LamellarSilicides21–50917.510215.55[33]
IMI685-7IMI6857LamellarSilicides21–5098010644.9
IMI685-8IMI6857LamellarSilicides21–5097810602.5
IMI685-9IMI6857LamellarSilicides21–501025.510672.65
IMI829-1IMI8298LamellarNP088697010[34]
IMI829-2IMI8298LamellarSilicides>50100510232
IMI829-3IMI8298LamellarNP086395111
IMI829-4IMI8298LamellarSilicides>5096010053
IMI829-5IMI8298LamellarNP086794210
IMI829-6IMI8298LamellarSilicides>508589757
IMI829-7IMI8298LamellarNP08669469
IMI829-8IMI8298LamellarSilicides>508519536.5
IMI829-9IMI8297LamellarNP0861977.59.6[35]
IMI829-10IMI8297LamellarSilicides aided by Ti3Al in Tr.β>50881.59533.1
IMI829NS-1IMI8297LamellarNP08009049.4
IMI829NS-2IMI8297LamellarTi3Al in Tr.β-3<7819.5891.59.05
Ti-1100-8Ti-11008LamellarNP091510005.5[36]
Ti-1100-9Ti-11008LamellarTi3Al in Tr.β aided by Silicides7–209559820.18
Ti-1100-10Ti-11008LamellarSilicides>508959804.15
IMI834-4IMI8347LamellarNP098711287.5[37]
IMI834-5IMI8347LamellarTi3Al in Tr.β-3<7102811346.5
IMI834-6IMI8347LamellarSilicides>5098010987.5
IMI834-7IMI8348BimodalTi3Al in αp-1<7905103713[38]
IMI834-8IMI8348BimodalTi3Al in αp & Tr.β-27–2095310759.5
IMI834-9IMI8348BimodalTi3Al in αp & Tr.β-27–2093310608.7
WJZ-Ti-1WJZ-Ti8BimodalNP01195130018[39]
WJZ-Ti-2WJZ-Ti8BimodalTi3Al in αp-1<71325145018
WJZ-Ti-3WJZ-Ti8BimodalTi3Al in αp & Tr.β-27–201230125012
WJZ-Ti-4WJZ-Ti8BimodalTi3Al in αp & Tr.β-27–20110011205
TA29-1TA298LamellarSilicides>5099510627.5[40]
TA29-2TA298LamellarTi3Al in Tr.β-3<799010756.5
TA29-3TA298LamellarTi3Al in Tr.β-37–2097510603
TA29-4TA298LamellarTi3Al in Tr.β-37–20101810852.5
TA29-5TA298LamellarTi3Al in Tr.β-37–2097510603.5
KIMS-1KIMS8BimodalTi3Al in αp & Tr.β-27–201113.81133.94.07[41]
KIMS-2KIMS8BimodalSilicides>501032.61124.616.94
JZ1-1JZ18BimodalNP0965103015.5[42]
JZ1-2JZ18BimodalTi3Al in αp-1<7965104015
JZ1-3JZ18BimodalTi3Al in αp-1<7940103015
JZ1-4JZ18BimodalTi3Al in αp-1<71000106016
JZ1-5JZ18BimodalTi3Al in αp-1<71000107014.5
JZ1-6JZ18BimodalTi3Al in αp-17-20990106015
JZ2-1JZ28BimodalTi3Al in αp-1<7965106015.5
JZ2-2JZ28BimodalTi3Al in αp-17–20960106016.5
JZ2-3JZ28BimodalTi3Al in αp-17–20960105017
JZ2-4JZ28BimodalTi3Al in αp & Tr.β-27–201040111014
JZ2-5JZ28BimodalTi3Al in αp & Tr.β-27–201040111012.5
JZ2-6JZ28BimodalTi3Al in αp & Tr.β-27–201030110013
Ti60-1Ti608BimodalNP0960108011[43]
Ti60-2Ti608BimodalSilicides>50962108210
Ti60-3Ti608BimodalSilicides>501000110010
Ti60-4Ti608BimodalSilicides>50100011009
Ti60-5Ti608BimodalSilicides>50100011009
Ti60-6Ti608BimodalSilicides>50982108210
Ti60-7Ti608BimodalTi3Al in αp-1<7970106010
Ti60-8Ti608BimodalTi3Al in αp-1<7960107010
Ti60-9Ti608BimodalTi3Al in αp-17–20940106010
Ti60-10Ti608BimodalTi3Al in αp-17–20960108010
Ti60-11Ti608BimodalTi3Al in αp-17–20980108510
Ti60-12Ti608BimodalTi3Al in αp-1<7960108210
Ti60-13Ti608BimodalTi3Al in αp-17–2097010809
Ti60-14Ti608BimodalTi3Al in αp-17–20965108010
Ti60-15Ti608BimodalTi3Al in αp-17–20955107711.5
Ti60-16Ti608BimodalSilicides>501010106011[44]
Ti60-17Ti608BimodalTi3Al in αp-17–20105011207
Ti60-18Ti608BimodalSilicides>501021109012
Ti60-19Ti608BimodalSilicides>50950101811.5
Ti60-20Ti608LamellarSilicides>50102010809
Ti60-21Ti608LamellarTi3Al in Tr.β-37–20104011004
JL-1JL8BimodalNP0944102915.6[45]
JL-2JL8BimodalTi3Al in αp-1<7985105712.2
JL-3JL8BimodalTi3Al in αp & Tr.β-2<7994106612
JL-4JL8LamellarNP0933102012.4
JL-5JL8LamellarTi3Al in Tr.β-37–2098110528.4
JL-6JL8LamellarTi3Al in Tr.β-37–2097010426.5
IMI834-10IMI8348BimodalTi3Al in αp-1<7945101214.5[46]
Ti6242-1Ti6242S7LamellarNP083794612[47]
Ti6242-2Ti6242S7LamellarSilicides>508759255.8
LD-Ti423-1LD-Ti4238BimodalNP094810468.3[48]
LD-Ti423-2LD-Ti4238BimodalNP092310138
TMC-Ti213-1TMC-Ti2132LamellarNP0996105913.9[49]
TMC-Ti213-2TMC-Ti2132BimodalNP 08769947.4
TA19-1TA198BimodalNP 0984106723.9[50]
TA19-2TA198BimodalNP01022111322.8
TKT-1TKT-16BimodalNP0980117520[51]
TKT-2TKT-26BimodalNP01075128519
TKT-6TKT-66BimodalGermanides<5001060125518
PC-IMDF1PC8LamellarNANA982102010.6[52]
PC-IMDF2PC8BimodalNANA1004104312.7
PC-IMDF4PC8BimodalNANA1072111815.6
Note: NA: not available; NP: no precipitates.

References

  1. Ikpe, E.; Ikechukwu, O.; Ebunilo, P.O.; Ikpe, E. Material selection for high pressure (HP) compressor blade for an aircraft engine. Int. J. Adv. Mater. Res. 2016, 2, 59–65. [Google Scholar]
  2. Foltz, J.; Gram, M. Introduction to titanium and its alloys. In ASM Handbook, Heat Treating of Nonferrous Alloys, Volume 4E; Totten, G.E., MacKenzie, D.S., Eds.; ASM International: Materials Park, OH, USA, 2016. [Google Scholar]
  3. Canumalla, R. On the low tensile ductility at room temperature in high temperature titanium alloys. SCIREA J. Metall. Eng. 2020, 4, 16–51. [Google Scholar]
  4. Williams, J.C.; Boyer, R.R. Opportunities and issues in the application of titanium alloys for aerospace components. Metals 2020, 10, 705. [Google Scholar] [CrossRef]
  5. Rao, M.N. Materials for gas turbines—An overview. In Advances in Gas Turbine Technology; Intechopen: Rijeka, Croatia, 2011; pp. 293–314. [Google Scholar]
  6. Gogia, K. High-temperature titanium alloys. Def. Sci. J. 2005, 55, 149–173. [Google Scholar] [CrossRef]
  7. Singh, K.; Ramachandra, C. Characterization of silicides in high temperature titanium alloys. J. Mater. Sci. 1997, 32, 229–234. [Google Scholar] [CrossRef]
  8. Ramachandra, C.; Singh, V.; Rao, P.R. On silicides in high temperature Ti alloys. Def. Sci. J. 1986, 36, 207–220. [Google Scholar] [CrossRef]
  9. Zhang, T.; Liu, C.-T. Design of titanium alloys by additive manufacturing: A critical review. Adv. Powder Mater. 2022, 1, 100014. [Google Scholar] [CrossRef]
  10. Tshephe, S.T.; Akinwamide, S.O.; Olevsky, E.; Olubambi, P.A. Additive manufacturing of titanium-based alloys—A review of methods, properties, challenges, and prospects. Heliyon 2022, 8, e09041. [Google Scholar] [CrossRef]
  11. TIMETAL 834 Datasheet; Titanium Metals Corporation: Warrensville Heights, OH, USA, 2000.
  12. TIMETAL 1100 Datasheet; Titanium Metals Corporation: Warrensville Heights, OH, USA, 2008.
  13. Ashby, M.F. Materials and the Environment Eco-Informed Material Choice, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
  14. Ashby, M.F. Materials Selection in Mechanical Design, 5th ed.; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
  15. Jahan, A.; Ismail, M.Y.; Sapuan, S.M.; Mustapha, F. Materials screening and choosing methods—A review. Mater. Des. 2010, 31, 696–705. [Google Scholar] [CrossRef]
  16. Anojkumar, L.; Ilangkumaran, M.; Sasirekha, V. Comparative analysis of MCDM methods for pipe material selectionin sugar industry. Expert Syst. Appl. 2014, 41, 2964–2980. [Google Scholar] [CrossRef]
  17. Zhou, C.; Yin, G.F.; Hu, X.B. Multi-objective optimization of material selection for sustainable products: Artificial neural networks and genetic algorithm approach. Mater. Des. 2009, 30, 1209–1215. [Google Scholar] [CrossRef]
  18. Rao, R.V.; Davim, J.P. A decision-making framework model for material selection using a combined multiple attribute decision-making method. Int. J. Adv. Manuf. Technol. 2008, 35, 751–760. [Google Scholar] [CrossRef]
  19. Gupta, N. Material selection for thin-film solar cells using multiple attribute decision making approach. Mater. Des. 2011, 32, 1667–1671. [Google Scholar] [CrossRef]
  20. Shanian, A.; Savadogo, O. A material selection model based on the concept of multiple attribute decision making. Mater. Des. 2006, 27, 329–337. [Google Scholar] [CrossRef]
  21. Chauhan, A.; Vaish, R. Magnetic material selection using multiple attribute decision making approach. Mater. Des. 2012, 36, 1–5. [Google Scholar] [CrossRef]
  22. Tzeng, G.H.; Huang, J.J. Multiple Attribute Decision Making Methods and Applications; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
  23. Rao, R.V. Decision Making in the Manufacturing Environment, Using Graph Theory and Fuzzy Multiple Attribute Decision Making Methods; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
  24. Farag, M.M. Materials and Process Selection in Engineering; Elsevier Science and Technology: Amsterdam, The Netherlands, 1979. [Google Scholar]
  25. Cherian, R.P.; Smith, L.N.; Midha, P.S. A neural network approach for selection for powder metallurgy materials and process parameters. Artif. Intell. Eng. 2000, 14, 39–44. [Google Scholar] [CrossRef]
  26. Perez-Benitez, J.A.; Padovese, L.R. Feature Selection and Neural Network for analysis of microstructural changesin magnetic materials. Expert Syst. Appl. 2011, 38, 10547–10553. [Google Scholar] [CrossRef]
  27. Zavadskas, K.; Turskis, Z.; Kildiene, S. State of art surveys of overviews on MCDM/MADM methods. Technol. Econ. Dev. Econ. 2014, 20, 165–179. [Google Scholar] [CrossRef]
  28. Rajan, K. Materials Informatics. Mater. Today 2005, 8, 38–45. [Google Scholar] [CrossRef]
  29. Cadima, J.; Jolliffle, I.T. Principal Component Analysis: A review and recent developments. Phil. Trans. R. Soc. A 2016, 374, 20150202. [Google Scholar]
  30. George, L.; Hrubiak, R.; Rajan, K.; Saxena, S.K. Principal component analysis on properties of binary and ternary hydrides and a comparison of metal versus metal hydride properties. J. Alloys Compd. 2009, 478, 731–735. [Google Scholar] [CrossRef]
  31. Peters, M.; Lee, Y.T.; Grundhoff, K.J.; Schurmann, H.; Welsch, G. Influence of processing on microstructure and mechanical properties of Ti-1100 and IMI 834. In Proceedings of the Minerals and Metals Society Fall Meeting, Detroit, MI, USA, 7–11 October 1991; pp. 533–548. [Google Scholar]
  32. Ramachandra, C.; Singh, V. Effect of silicides on tensile properties and fracture of alloy Ti-6Al-5Zr-0.5Mo-0.25Si from 300 to 823 K. J. Mater. Sci. 1988, 23, 835–841. [Google Scholar] [CrossRef]
  33. Ramachandra, C.; Singh, V. Effect of thermomechanical treatments on size and distribution of silicides and tensile properties of alloy Ti-6AI-5Zr-0.5Mo-0.25Si. Metall. Trans. A 1988, 19, 389–391. [Google Scholar] [CrossRef]
  34. Sridhar, G.; Sarma, D.S. Structure and properties of a near-alpha titanium alloy after beta solution treatment and aging at 625 °C. Metall. Trans. A 1988, 19, 3025–3033. [Google Scholar] [CrossRef]
  35. Woodfield, P.; Postans, P.J.; Loretto, M.; Smallman, R. The effect of long-term high temperature exposure on the structure and properties of the titanium alloy Ti-5331S. Acta Metall. 1988, 36, 507–515. [Google Scholar] [CrossRef]
  36. Madsen, A.; Ghonem, H. Separating the effects of T3Al and silicide precipitates on the tensile and crack growth behavior at room temperature and 593 °C in a near-alpha titanium alloy. J. Mater. Eng. Perform. 1995, 4, 301–307. [Google Scholar] [CrossRef]
  37. Srinadh, K.V.S.; Nidhi, S.; Singh, V. Role of Ti3Al/Silicides on tensile properties of Timetal 834 at various temperatures. Bull. Mater. Sci. 2007, 30, 595–600. [Google Scholar] [CrossRef]
  38. Cope, M.T.; Hill, M.J. The influence of aging temperature on the mechanical properties of IMI 834. In Proceedings of the 6th World Conference on Titanium, Cannes, France, 6–9 June 1988. [Google Scholar]
  39. Zhang, W.J.; Song, X.Y.; Hui, S.X.; Ye, W.J.; Yu, Y.; Li, Y.F. α2 phase precipitation behavior and tensile properties at room temperature and 650 °C in an (α + β) titanium alloy. Rare Met. 2019, 40, 3261–3268. [Google Scholar] [CrossRef]
  40. Li, J.; Cai, J.; Xu, Y.; Xiao, W.; Huang, X.; Ma, C. Influences of thermal exposure on the microstructural evolution and subsequent mechanical properties of a near-α high temperature titanium alloy. Mater. Sci. Eng. A 2020, 774, 138934. [Google Scholar] [CrossRef]
  41. Narayana, P.; Kim, S.W.; Hong, J.K.; Reddy, N.; Yeom, J.T. Tensile properties of a newly developed high-temperature titanium alloy at room temperature and 650 °C. Mater. Sci. Eng. 2018, 718, 287–291. [Google Scholar] [CrossRef]
  42. Zhang, J.; Peng, N.; Wang, Q.; Wang, X. A new aging treatment way for near α high temperature titanium alloys. J. Mater. Sci. Technol. 2009, 25, 454–458. [Google Scholar]
  43. Jia, W.; Zeng, W.; Yu, H. Effect of aging on the tensile properties and microstructures of a near-alpha titanium alloy. Mater. Des. 2014, 58, 108–115. [Google Scholar] [CrossRef]
  44. Jia, W.; Zeng, W.; Liu, J.; Zhou, Y.; Wang, Q. Influence of thermal exposure on the tensile properties and microstructures of Ti60 titanium alloy. Mater. Sci. Eng. A 2011, 2011, 511–518. [Google Scholar] [CrossRef]
  45. Liu, J.; Li, S.; Li, D.; Yang, R. Effect of aging on fatigue-crack growth behavior of a high temperature titanium alloy. Mater. Trans. 2004, 5, 1577–1585. [Google Scholar] [CrossRef]
  46. Singh, N.; Gauthama; Singh, V. Low cycle fatigue behavior of Ti alloy IMI 834 at room temperature. Mater. Sci. Eng. A 2002, 325, 324–332. [Google Scholar] [CrossRef]
  47. Allison, J.E.; Cho, W.; Jones, J.W.; Donlon, W.T.; Lasecki, J.V. The influence of elevated temperature on the mechanical behavior of alpha/beta titanium alloys. In Proceedings of the Sixth World Conference on Titanium, Cannes, France, 6–9 June 1988. [Google Scholar]
  48. Zhu, S.; Zhu, C.; Luo, D.; Zhang, X.; Zhou, K. Development of a Low-Density and High-Strength Titanium Alloy. Metals 2023, 13, 251. [Google Scholar] [CrossRef]
  49. Zhang, Y.; Wu, X.; Zhang, B.; Zhang, Y.; Zhang, D. Microstructure and mechanical properties of a novel PM Ti–2Al–1.3V alloy in different heat treatment conditions. Heat Treat. Surf. Eng. 2022, 4, 43–53. [Google Scholar] [CrossRef]
  50. Luo, M.; Lin, T.; Zhou, L.; Li, W.; Liang, Y.; Han, M.; Liang, Y. Deformation Behavior and Tensile Properties of the Semi-Equiaxed Microstructure in Near Alpha Titanium Alloy. Materials 2021, 14, 3380. [Google Scholar] [CrossRef]
  51. Kitashima, T.; Suresh, K.S.; Yamba-Mitarai, Y. Effect of germanium and silicon additions on the mechanical properties of a near-α titanium alloy. Mater. Sci. Eng. A 2014, 597, 212–218. [Google Scholar] [CrossRef]
  52. Zhang, J.; Guo, C.X.; Zhang, S.Z.; Feng, H.; Chen, C.Y.; Zhang, H.Z.; Cao, P. Microstructural manipulation and improved mechanical properties of a near α titanium alloy. Mater. Sci. Eng. A 2020, 771, 138569. [Google Scholar] [CrossRef]
  53. Jahan, A.; Edwards, K.L.; Bahraminasab, M. Multi-Criteria Decision Analysis—For Supporting the Selection of Engineering Materials in Product Design, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
  54. Memariani, A.; Amini, A.; Alinezhad, A. Sensitivity analysis of simple additive weighting method (SAW): The results of change in the weight of one attribute on the final ranking alternatives. J. Ind. Eng. 2009, 4, 13–18. [Google Scholar]
  55. Afshari, A.; Mojaahed, M.; Yusuff, R.M. Simple additive weighting approach to personal selection problem. Int. J. Innov. Mgt. Technol. 2010, 1, 511–515. [Google Scholar]
  56. Madic, M.; Radovanovic, M.; Manic, M. Application of the ROV method of selection of cutting fluids. Decis. Sci. Lett. 2016, 5, 245–254. [Google Scholar] [CrossRef]
  57. Jha, G.K.; Chatterjee, P.; Chatterjee, R.; Chakraborty, S. Suppliers selection in a manufacturing environment using a range of value method. J. Mech. Eng. 2013, 3, 16–22. [Google Scholar] [CrossRef]
  58. Zavadskas, K.; Turskis, Z.; Vilutiene, T. Multiple criteria analysis of foundation installment alternatives by applying additive ratio assessment (ARAS) method. Arch. Civil Mech. Eng. 2010, 10, 123–141. [Google Scholar] [CrossRef]
  59. Zavadskas, K.; Turskis, Z. A new additive ratio assessment (ARAS) method in multicriterial decision making. Technol. Econ. Dev. Econ. 2010, 16, 159–172. [Google Scholar] [CrossRef]
  60. Stanujic, S.; Jovanovic, R. Measuring a quality of faculty website using ARAS method. Contemp. Issues Bus. Manag. Educ. 2012, 2012, 545–554. [Google Scholar]
  61. Yazdabi, M.; Zavadskas, E.K.; Turskis, Z. A combined compromise solution (CoCoSo) method for multi-criteria decision-making problems. Manag. Desicion 2019, 57, 2501–2519. [Google Scholar]
  62. Qiyas, M.; Naeem, M.; Khan, S.; Abdullah, S.; Botmart, T.; Shah, T. Decision support system based on CoCoSo method with the picture fuzzy information. J. Math. 2022, 2022, 1476233. [Google Scholar] [CrossRef]
  63. Mefgouda, B.; Idoudi, H. A novel MADM based netwrok interface selection approach with rank reversal avoidance in HWNs. In Proceedings of the 2022 IEEE Wireless Communications and Networking Conference, Austin, TX, USA, 10–13 April 2022. [Google Scholar]
  64. Chatterjee, P.; Chakraborty, S. Material selection using preferential ranking methods. Mater. Des. 2012, 35, 384–393. [Google Scholar] [CrossRef]
  65. Erdogan, S.; Aydin, S.; Balki, M.K.; Sayin, C. Operational evaluation of thermal barrier coated diesel engine fueled with biodiesel/diesel blend by using MCDM method base on engine performance, emission and combustion characteristics. Renew. Energy 2020, 151, 698–706. [Google Scholar] [CrossRef]
  66. Darji, V.P.; Rao, R.V. Intelligent multi-criteria decision making methods for material selection in sugar industry. Procedia Mater. Sci. 2014, 5, 2585–2594. [Google Scholar] [CrossRef]
  67. Siregar, D.; Arisandi, D.; Usman, A.; Irwan, D.; Rahim, R. Research of simple multi-attribute rating technique for decision support. J. Phys. Conf. Ser. 2017, 930, 012015. [Google Scholar] [CrossRef]
  68. Patel, M.R.; Vashi, M.P.; Bhatt, B.V. SMART-Multi-criteria decision-making technique for use in planning activities. In Proceedings of the New Horizons in Civil Engineering, Surat, India, 25–26 March 2017. [Google Scholar]
  69. Rao, R.V.; Singh, D. Evaluating flexible manufacturing systems using euclidean distance-based integrated approach. Int. J. Risk Manag. 2012, 3, 32–53. [Google Scholar] [CrossRef]
  70. Rao, R.V.; Singh, D. Weighted Euclidean distance-based approach as a multiple attribute decision making method for plant or facility layout design selection. Int. J. Ind. Eng. Comput. 2012, 3, 365–382. [Google Scholar]
  71. Alinezhad, A.; Khalili, J. New Methods and Applications of Multiple Attribute Decision Making (MADM); Springer Nature: Berlin/Heidelberg, Germany, 2019; p. 193. [Google Scholar]
  72. Tesic, D.; Radovanovic, M.; Bozanic, D.; Pamucar, D.; Milic, A.; Puska, A. Modification of the DIBR and MABAC methods by applying rough numbers and its application in making decisions. Information 2022, 13, 353. [Google Scholar] [CrossRef]
  73. Chakraborty, S. Applications of the MOORA method for decision making in manufacturing environment. Int. J. Adv. Manuf. Technol. 2011, 4, 1155–1166. [Google Scholar] [CrossRef]
  74. Dominguez, L.P.; Mojica, K.Y.S.; Pabon, L.C.O.; Diaz, M.C.C. Application of the MOORA method for the evaluation of the industrial maintenance system. J. Phys. Conf. Ser. 2018, 1126, 012018. [Google Scholar] [CrossRef]
  75. Triantaphyllou, E.; Shu, B.; Sanchez, S.N.; Ray, T. Multi-criteria decision making: An operations research approach. In Encyclopedia of Electrical and Electronics Engineering; Webster, H.G., Ed.; John Wiley & Sons: New York, NY, USA, 1998; Volume 15, p. 175. [Google Scholar]
  76. Deng, H.; Yeh, C.H.; Willis, R.J. Inter-company comparison using modified TOPSIS with objective weights. Comput. Oper. Res. 2000, 27, 963–973. [Google Scholar] [CrossRef]
  77. Gul, M.; Celik, E.; Aydin, N.; Gumus, A.T.; Guneri, A.F. A state of the art literature review of VIKOR and its fuzzy extensions on applications. Appl. Soft Comput. 2016, 46, 60–89. [Google Scholar] [CrossRef]
  78. Sayadi, M.M.; Heydari, M.; Shahanaghi, K. Extension of VIKOR method for decision making problem with interval numbers. Appl. Math. Model. 2009, 33, 2257–2262. [Google Scholar] [CrossRef]
  79. Mohanty, P.P.; Mahapatra, S.S. A compromise solution by VIKOR method for ergonomically designed product with optimal set of design characteristics. Procedia Mater. Sci. 2014, 6, 633–640. [Google Scholar] [CrossRef]
  80. Trung, D. Multi-criteria deciison making under MARCOS method and weighting methods: Applied to milling, grinding, and turning processes. Manuf. Rev. 2022, 9, 3. [Google Scholar]
  81. Stevic, Z.; Pamucar, D.; Puska, A.; Chatterjee, P. Sustainable supplier selection in healthcare insudtries using a new MCDM method: Measurement Alternatives and Ranking according to Compromise Solution (MARCOS). Int. J. Appl. Eng. Res. 2020, 140, 106231. [Google Scholar]
  82. Levine, M.; Ramsey, P.P.; Smidt, R.K. Applied Statistics for Engineers and Scientists; Prentice-Hall: Upper Saddle, NJ, USA, 2001. [Google Scholar]
  83. Navidi, W. Statistics for Engineers and Scientists, 3rd ed.; McGraw-Hill Science/Engineering: New York, NY, USA, 2010. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Aero-Engine Modeling and Control Method with Model-Based Deep Reinforcement Learning
Previous
Innovative Integration of Severe Weather Forecasts into an Extended Arrival Manager
Next