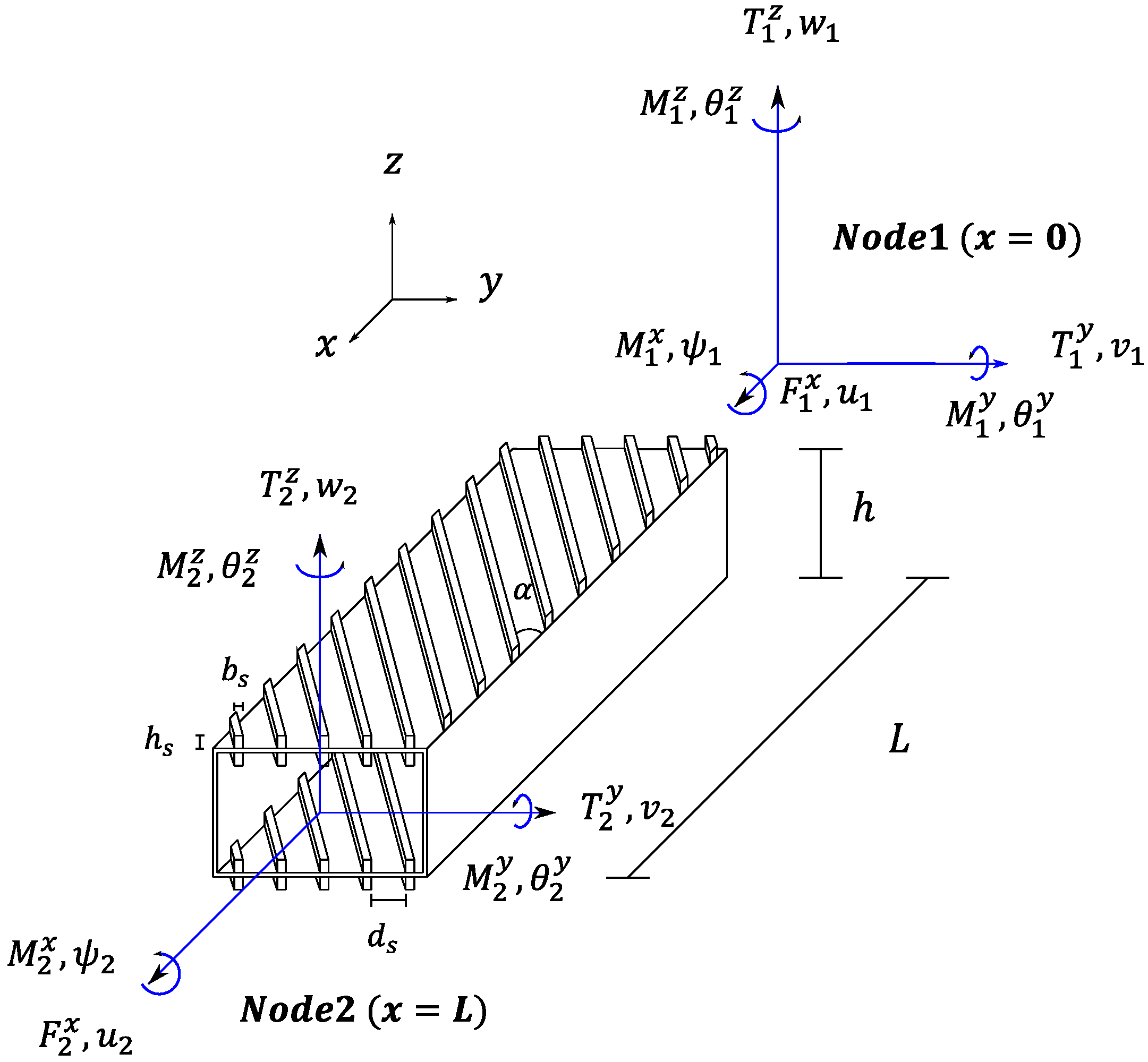
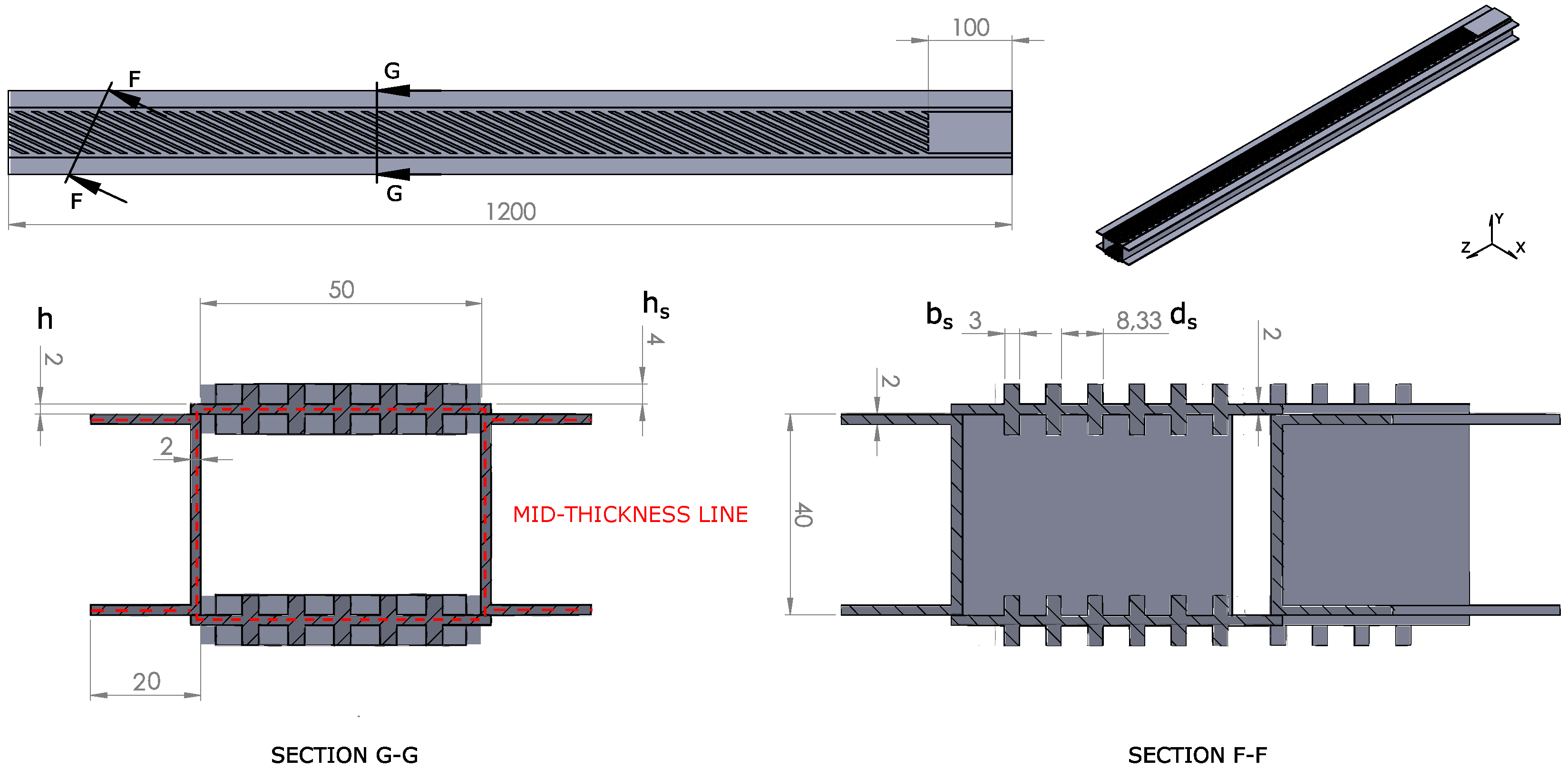
The results of the analysis described are reported in this section. The deformation along the z-axis and the torsion computed for the static analysis of Test Case 1 are reported in
Figure 7,
Figure 8 and
Figure 9 for each load case, while the relative differences for nodal displacements and torsion angles are summarized in
Table 8. The results of the modal analysis for the BTCE model of the aluminum beam are reported in
Figure 10 while the natural frequencies obtained have been compared with analytical, numerical and experimental results in
Table 9,
Table 10 and
Table 11 respectively. A converge study on the natural frequency is reported in
Figure 11. Numerical and experimental mode shapes are reported in
Figure 12,
Figure 13,
Figure 14,
Figure 15,
Figure 16 and
Figure 17, while MAC matrices for the mode shapes comparison are reported in
Figure 18. The comparison of BTCE model results for Test Case 2 and for Test Case 3 are reported in
Table 12 and
Table 13 respectively.
5.1. Static Analysis Results
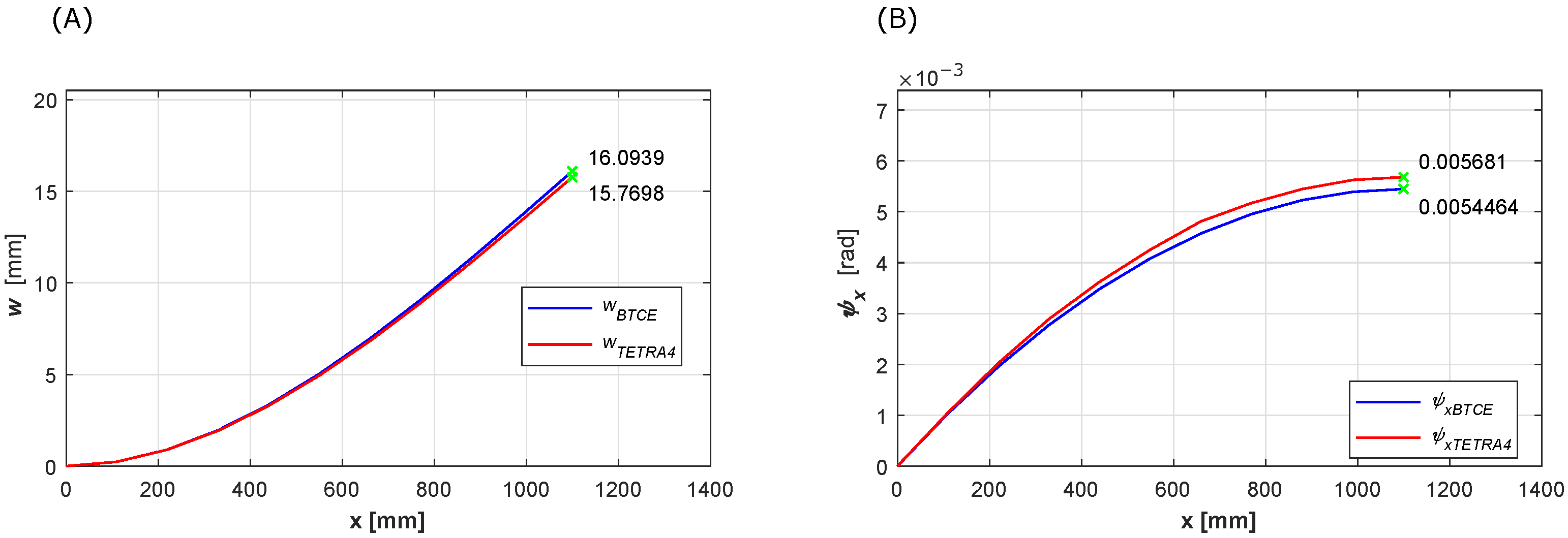
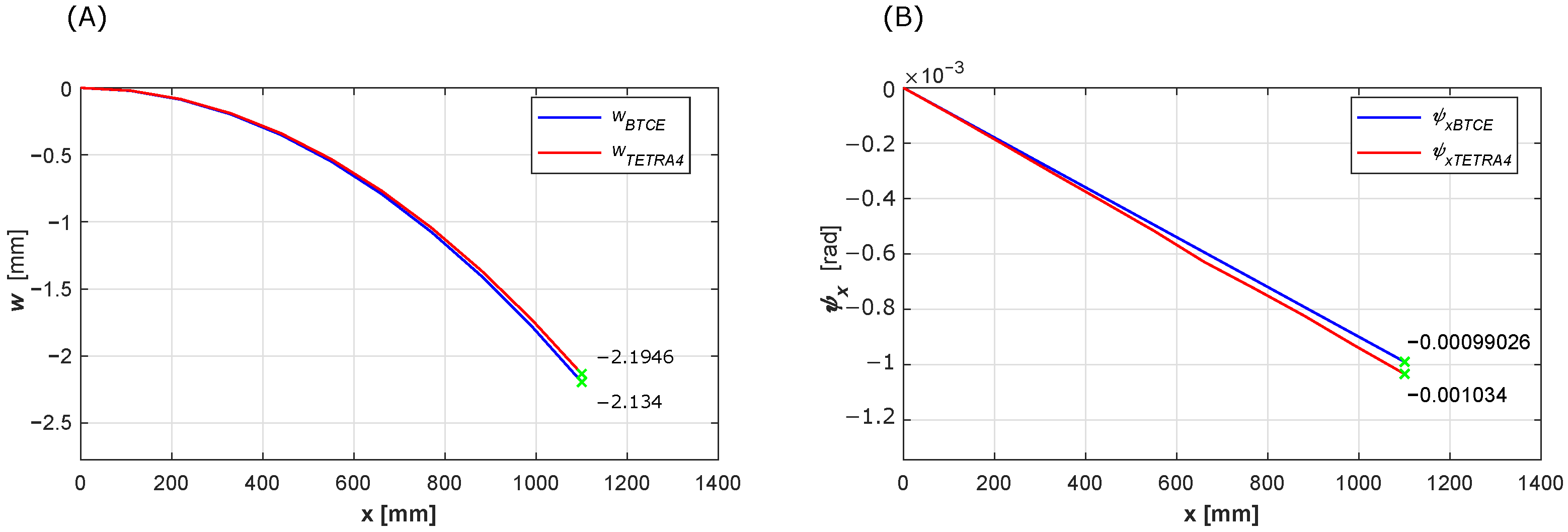
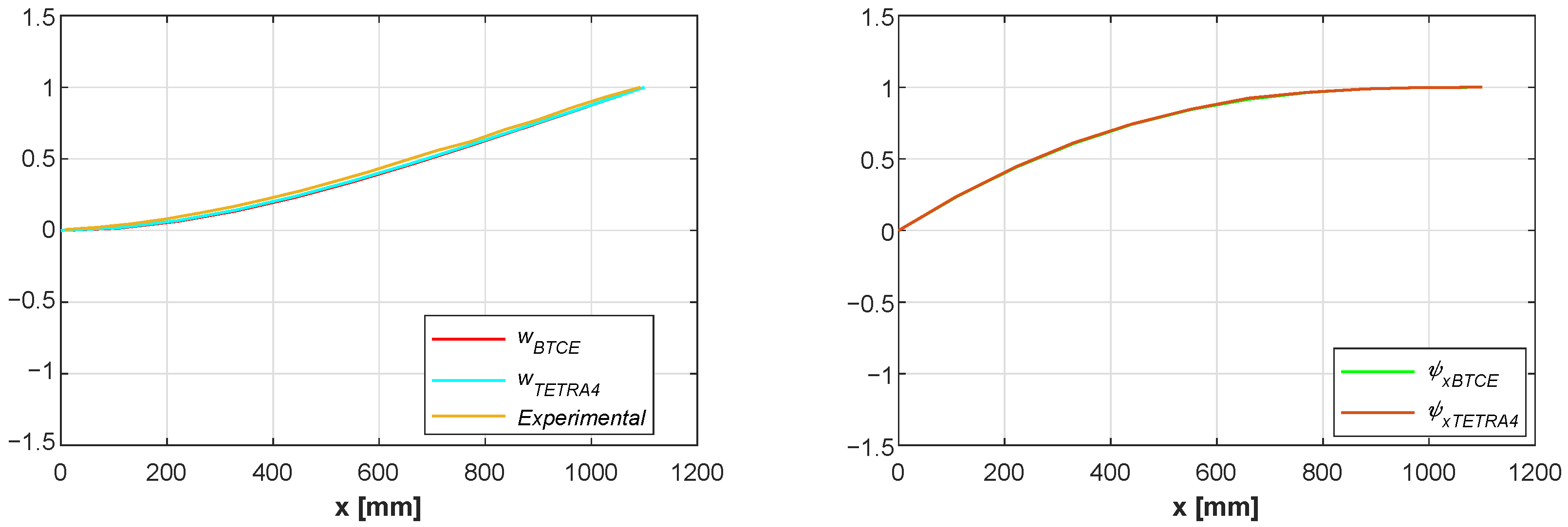
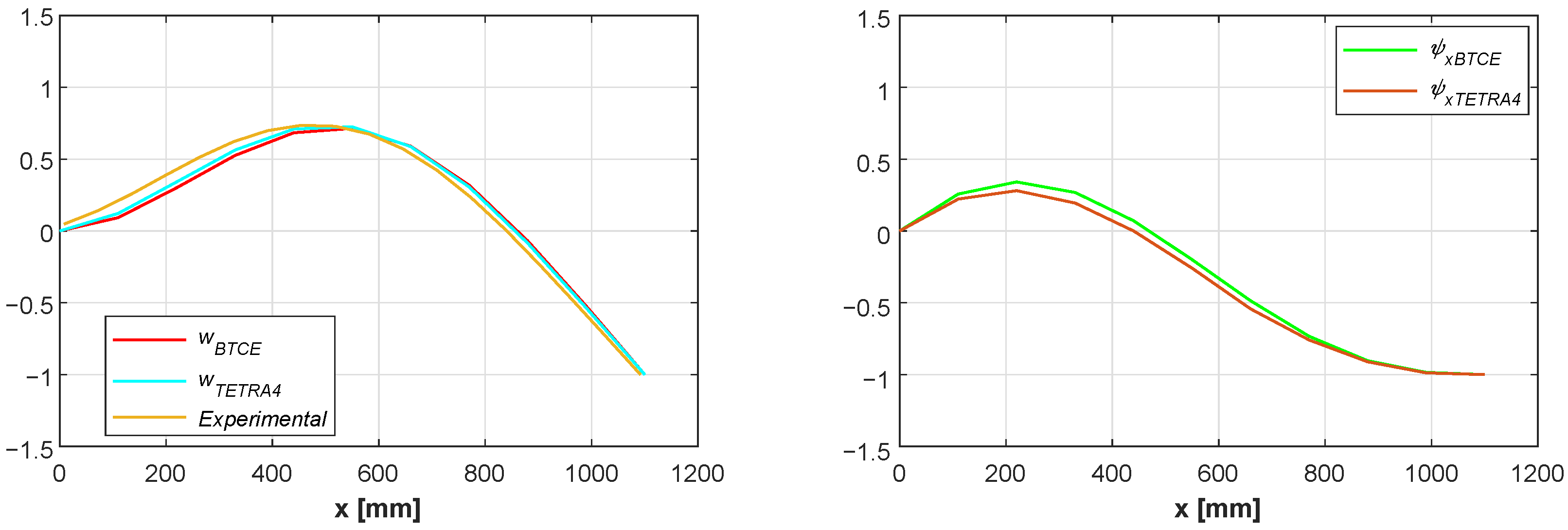
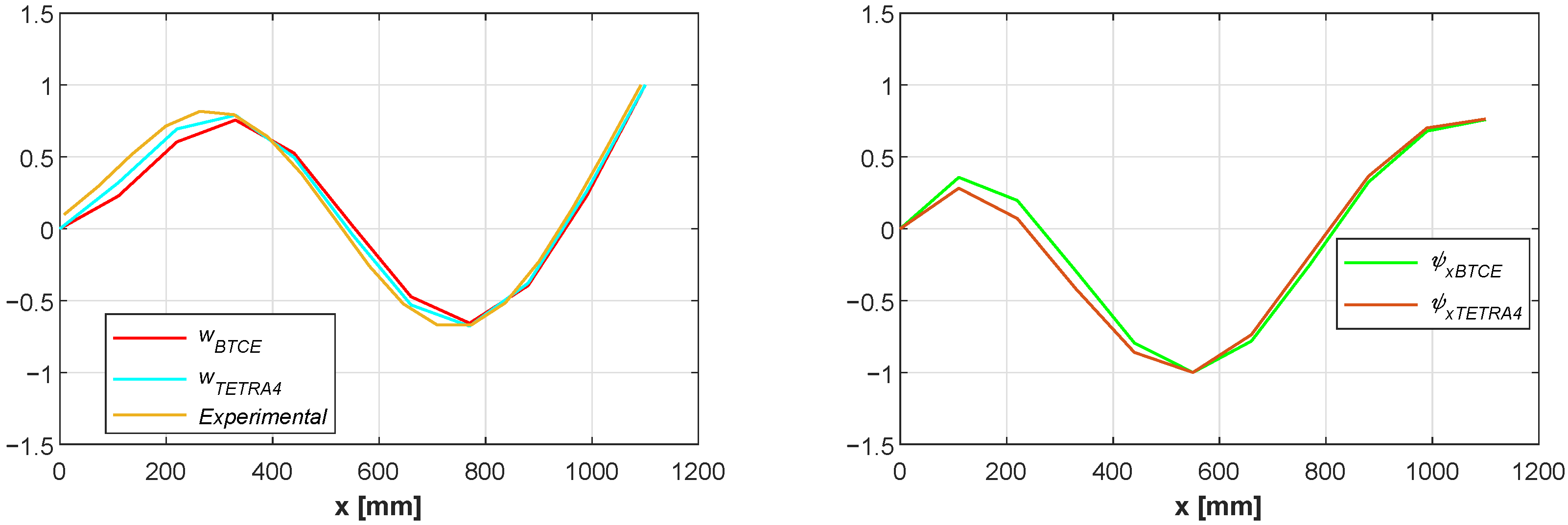
The results of the linear static analysis for the load cases presented in
Table 7 obtained for the BTCE model here derived have been compared with the numerical results of a TETRA4 FE model with the same load configuration for Test Case 1. Vertical deflection and torsion angle results have been collected and represented in
Figure 7,
Figure 8 and
Figure 9. The results reveal a good correlation between the two numerical model considered for each load case, showing the capability of the BTCE to correctly represent the bending-torsion coupling effect given by the stiffeners in presence of a static load.
The values of the deformations at the free end of the beam are reported in
Table 8, the relative difference is computed with Equation (
22) considering the result of the TETRA4 model as reference value. The relative difference is computed also for each node along the beam and the mean value is reported in the last column of
Table 8. In the same table also the results of the deformation at the free end of the beam for the uncoupled case (
) are reported, the reference values for the comparison are computed with the PVW. The comparison shows a difference lower than
for the load cases considered with a slightly higher value for the torsion angle computed for load case 3. This could be caused by an overestimation of the torsional stiffness
computed with Equation (
1). The approximation introduced when the cross section of the beam is reduced to its mid thickness line can affect the final stiffness of the beam. The results for the uncoupled configuration are in line with the analytical formulation.
5.2. Modal Analysis Results
The results of the modal analysis for Test Case 1 obtained with the procedure described in the previous section have been compared with experimental, numerical and analytical results. The frequencies computed considering the bending and torsion uncoupled (
) are reported in
Table 9 while the frequencies obtained with the TETRA4 FE model are reported in
Table 10. The experimental results have been acquired by Patuelli et al. [
18] with a laser Doppler vibrometer according to the procedure described in [
35] and reported in
Table 11 for a comparison. The second and fourth mode do not present experimental frequency value or mode shape. Due to the nature of the acquisition, the experimental modal analysis did not include the in-plane modes since the focus was on the bending-torsion coupling effect which does not affects the neglected modes.
The comparison with the analytical frequencies confirmed the consistency of the model for the uncoupled case with a negligible relative difference. Moreover, the comparison with numerical results revealed that there is good agreement between the present theory and the TETRA FE model, with relative error lower than for most of the natural frequencies computed. The natural frequency of the 6th mode present an higher relative difference of .
The correlation with experimental results is generally good, with a relative error around or lower for the 1st and the 5th mode, but with a considerably higher difference for the 3rd and the 6th mode. There are mainly two reason for the difference in natural frequencies values. As already stated before, the approximation introduced when the cross section of the beam is reduced to its mid thickness line affect the stiffness coefficients, but also the inertia properties of the beam. Moreover, the experimental results are affected by a constraint condition impossible to replicate for the beam element. The beam was clamped between two steel blocks applying pressure on the upper and lower face of the first 100 mm of the beam. With this configuration, the first section of the beam was not fully constrained which is the condition applied to the BTCE section when imposing all the degrees of freedom equals to zero for the first node.
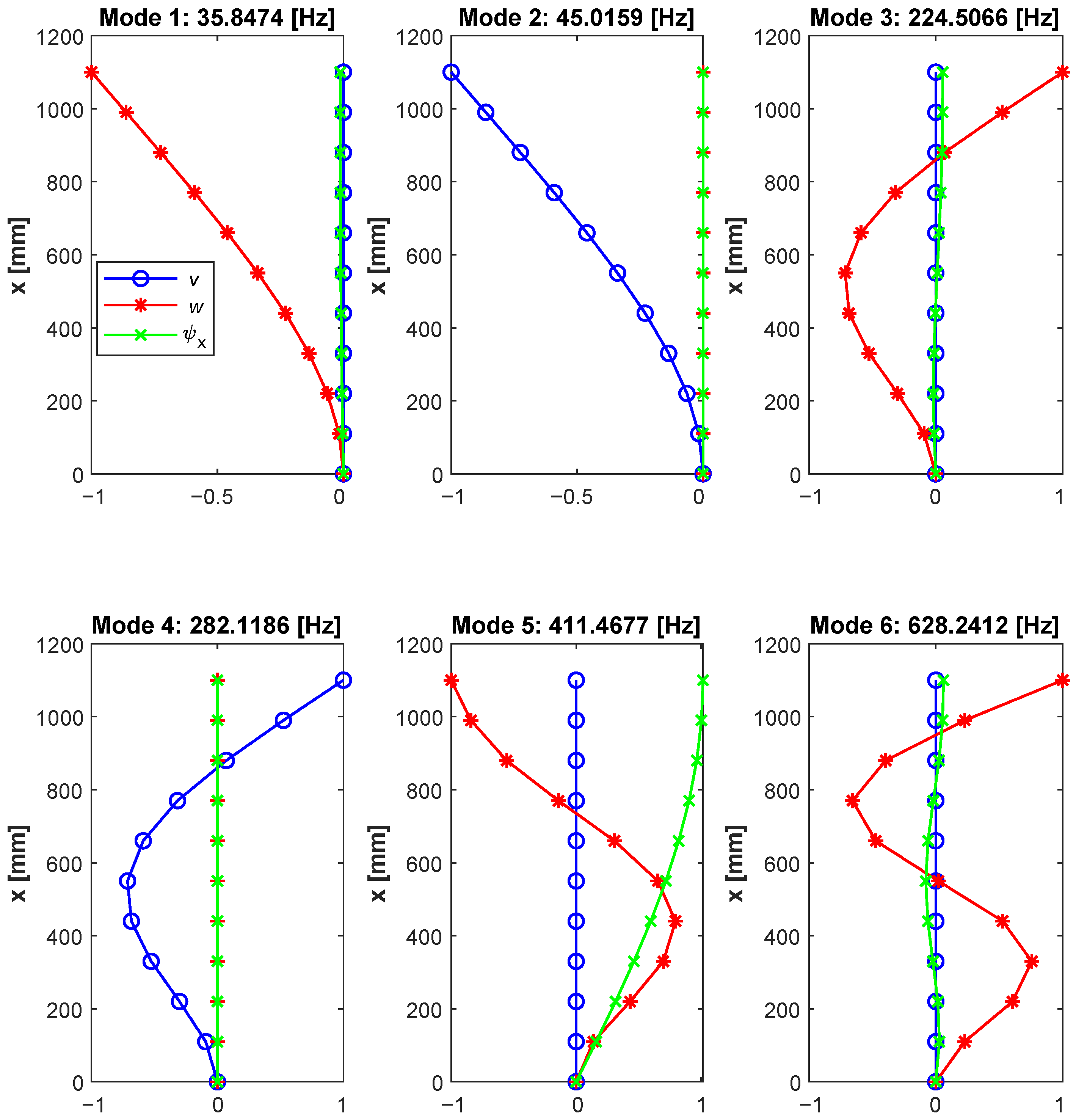
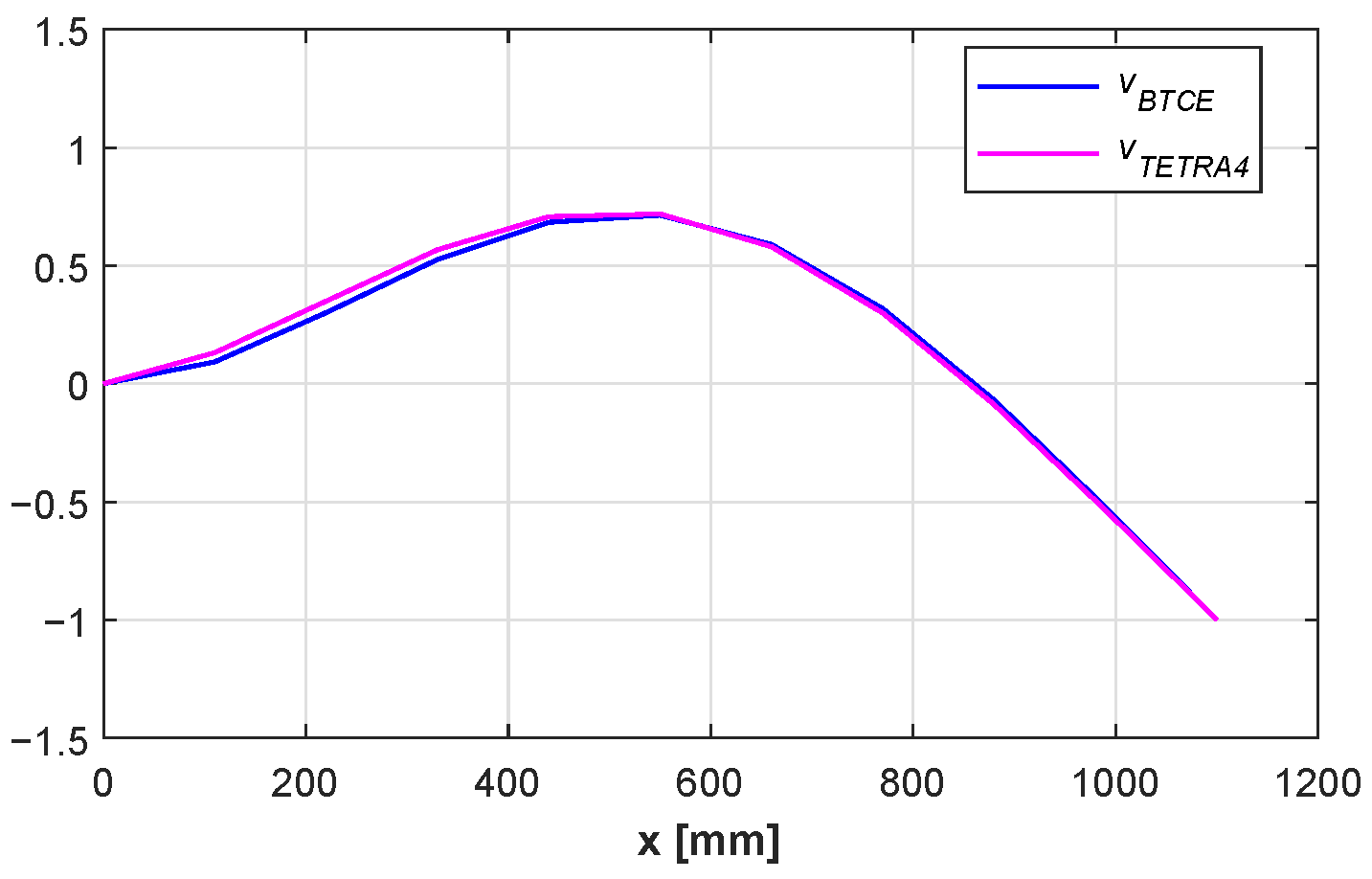
The eigenvectors solution of Equation (
24) for the BTCE model are graphically represented in
Figure 10. Only the three components of the eigenvectors involved in the modes investigated are represented, the in-plane component
v, the out-of-plane component
w, and the torsional component
. The eigenvectors components have been normalized with respect to the maximum value present among all the degrees of freedom for a given mode.
The eigenvectors depicted in
Figure 10 highlight the coupling effect for the 1st, 3rd, 5th and 6th mode where the 1st, 3rd and 6th mode are mainly bending modes with respect to the y-axis and the 5th is mainly a torsional mode around x-axis. It is worth noting that the 2nd and 4th mode which are the bending modes with respect to the z-axis are correctly not influenced by the coupling term
and result uncoupled. Similar observation can be made for the comparison reported in
Figure 12,
Figure 13,
Figure 14,
Figure 15,
Figure 16 and
Figure 17, where the mode shapes and the coupling effects are in accordance with the results obtained for the TETRA4 model. Furthermore, the mode shapes are in good agreement with experimental results for the z component of the eigeinvectors reported in [
18].
A convergence study on the computed natural frequencies has been performed considering a number of elements varying from 3 to 50. The results are represented in
Figure 11 in terms of natural frequency normalized with respect to the convergence value. It is possible to observe that the first three natural frequencies converge rapidly with the increase in the number of elements and their curves result coincident in
Figure 11, while the fourth, fifth and sixth mode require more elements to converge. However, the natural frequency computed for Mode 6 with 10 elements is only
greater than the convergence value.
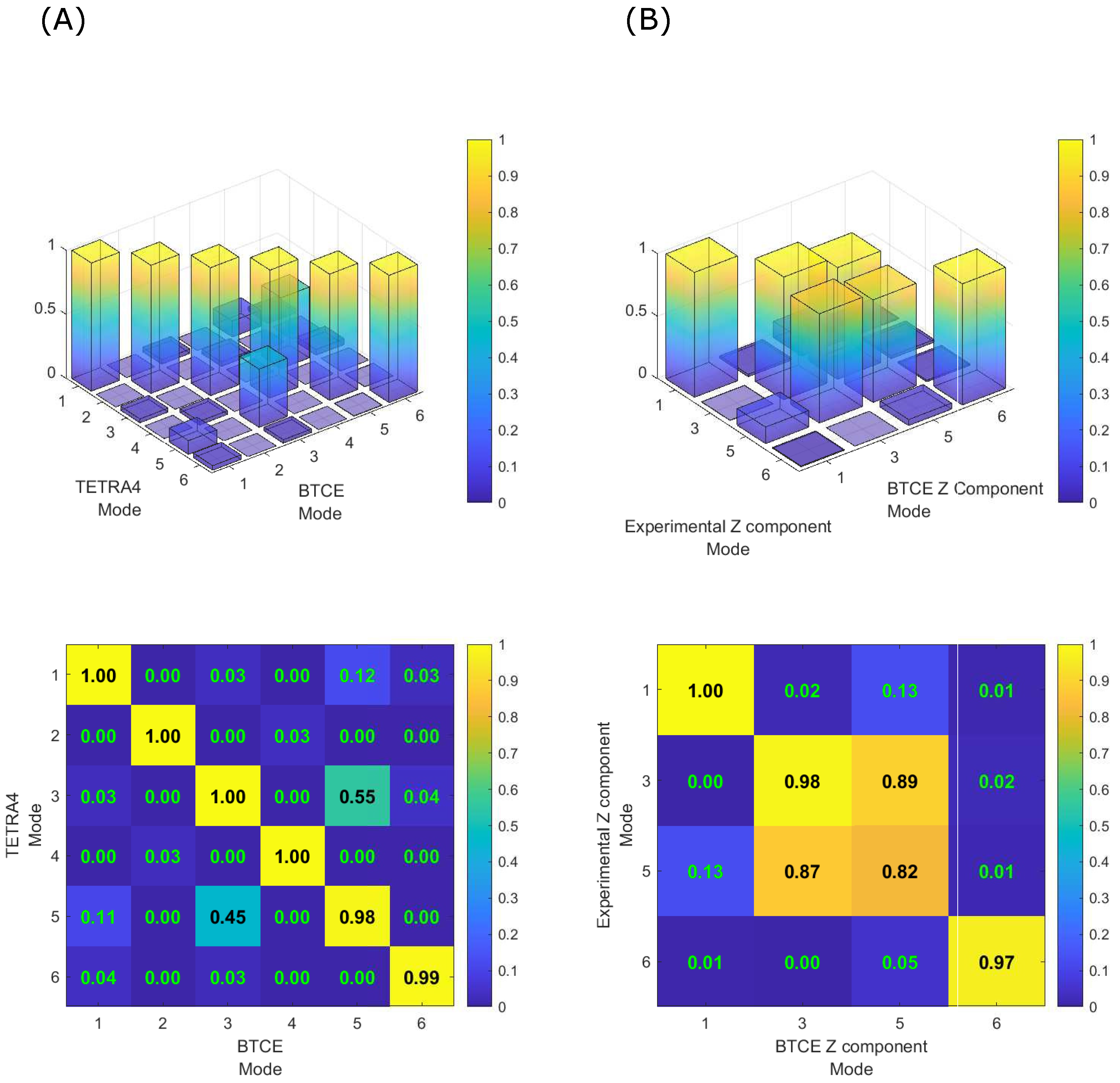
The MAC matrices computed for the mode shape comparisons are reported in
Figure 18. The BTCE model showed an excellent accordance with the TETRA4 model as reported in
Figure 18A. The results revealed a similarity between the 3rd and the 5th mode, which was expected because the torsional mode (Mode 5) is coupled with bending through the coupling term
in the stiffness matrix. This coupling effect generate a component along z-axis for the 5th mode which is similar to the same component for the second bending mode (Mode 3) as can be observed in
Figure 14 and
Figure 16. The same coupling effects are observable in the comparison with experimental results (
Figure 18B), this is testified by the off diagonal values related to the 3rd and the 5th mode. The similarity is higher because in this case only the component of the eigenvectors along z-axis is considered. The relatively low similarity between the 5th BTCE mode and the corresponding experimental mode is probably related to the reduced number of acquisition points along the beam axis during the physical test.
The results of the modal analysis performed on the BTCE model of the NREL 5MW HAWAT blade described in [
19] are reported in
Table 12. The results have been compared with the natural frequency obtained with Rayleigh theory, with Timoshenko theory and with Bernoulli theory reported in [
32]. The values computed with the BTCE model have been compared also with the results obtained with two software developed by NREL [
32], B-Modes and FAST, with the results obtained by Jeong et al. [
34] using BEM-ABAQUS commercial software and with the results obtained by Li et al. [
33] where a geometrically exact beam theory was used.
The BTCE model showed great accordance with other beam theories and commercial software results, with a relative difference below 5% for the computed natural frequencies. The error is considerably higher when the BTCE model is compared to the Bernoulli theory, however the natural frequency computed with the Bernoulli theory for the third and the fifth frequencies are not in accordance with the other theories or commercial solvers.
The results of the modal analysis performed on the CAS graphite/epoxy box beam are reported in
Table 13. The natural frequency have been compared with numerical results from [
20] and experimental data reported in [
21] computing the relative differences with Equation (
22).
The results are in good agreement with numerical and experimental results with a relative difference with the BTCE model natural frequencies mostly lower than 7% for both layups. Minor discrepancies can be observed for the for the first horizontal bending mode frequency where the relative difference with the experimental result is equal to 13.81%