Numerical Study on the Unusual Vibration Load Characteristics and Mechanisms of the Front Landing Gear Compartment

Abstract

Civilian aircraft can experience noticeable vibrations in the cockpit and cabin due to mechanical faults during flight. To address this issue, a hybrid approach was utilized to investigate fluid-induced vibration load characteristics in the front landing gear compartment under different hatch opening angles. The results reveal that the root mean square (RMS) of cumulative pressure loads on both small and large hatches under different opening angles is largest at a 15°. For all the simulated cases (0°, 5°, 10°, 15°, 20°), the power spectral density (PSD) results of the chosen monitoring points on the inner wall of the large hatch exhibit broadband frequency characteristics, and the peak PSD values for the chosen monitoring points on the outer wall of the small hatch exhibit a significant concentration of energy at approximately 75 Hz. The peak PSD values for the selected monitoring points on the inner wall of the small hatch demonstrate a more uniform distribution of energy. Utilizing the iso-surface of Q-criterion, spatial streamlines, and streamlines at different cross-sections to analyze flow characteristics, the study investigates the fluctuating load mechanisms of the compartments. The results indicate that unsteady loads stem from the blunt edges of the hatches, which induce unsteady flow and spanwise flow. Geometric gaps between different locations cause flow separation, and the flows inside the compartment exhibit characteristics similar to those of a clean cavity. Furthermore, the mutual interference can be described using circulating flow and spanwise flow, resulting in flow unsteadiness. The flow separation zones enlarge and vortex intensity increases with the increase of the hatch opening angle from 0° to 15°; then, their values decrease as the hatch opening angle increases from 15° to 20°. These variations explain the maximum RMS of cumulative pressure loads at 15°.

1. Introduction

Civilian aircraft might experience noise and vibrations perceptible to the cockpit and cabin crew during flights, such as fluid-induced vibrations of the front landing gear hatch [1,2,3] or the failure of air pressure seals [4,5]. These vibrations not only affect the overall comfort of the flight but also create psychological pressure on both the pilot and passengers. In severe cases, they can pose safety risks such as structural fatigue damage, seal failure, and even casualties [6,7,8]. When such vibrations occur under fluid-induced conditions, it is crucial for the ground crew to identify and rectify the source of the fault promptly. This is necessary to ensure flight safety, enhance aircraft comfort, and alleviate any psychological concerns for the pilot.

One key factor contributing to fluid-induced vibrations is the improper closing of the front landing gear hatch during retraction, which sometimes happens accidentally. The resulting fluctuating loads are unexpected and different from the commonly experienced unsteady aerodynamic loads such as those caused by a gust, rudder control, etc. The unwanted hatch opening leads to airflow flowing in and out through the gap between the hatch and the landing gear compartment, as well as between the hatches. These disturbances interact with various components within the main landing gear compartment, including the landing gear itself and the tires, resulting in complex flow patterns. Therefore, a detailed model of the front landing gear compartment, including the cavity, hatch, landing gear, and other relevant components, is needed to accurately study the load characteristics and mechanisms. The following sections will provide an overview of the research on the cavity, cavity + hatch, cavity + landing gear, and other related aspects.

Many research studies have been conducted on cavity noise, and over the past decades, numerous review papers have summarized and evaluated the progress in this field. For instance, S.J. Lawson [9] et al. reviewed the numerical simulation methods for cavity flow under high-speed incoming flow conditions, highlighting the promising application prospects of DES (Detached Eddy Simulation) and LES (Large Eddy Simulation) methods in the aerospace domain. This review provided valuable insights into the computational aeroacoustics problem raised by Christopher K.W. Tam [10]. Furthermore, the influence of key parameters such as shape and structural vibration on cavity-induced noise in compressible flow was elucidated, and the research status and limitations of cavity noise control technology were summarized. The review papers also addressed the challenges and future trends in dealing with cavity-induced noise. Mojtaba Sadeghian et al. [11], for instance, reviewed the feasibility of aircraft noise reduction technology in the industrial sector and discussed the subsequent trends and challenges in this area. Given the extensive coverage and comprehensive analysis provided by these review papers, this article refrains from duplicating the research progress concerning cavities.

Regarding the landing gear compartment (cavity) + hatch model, Xu Jinjin et al. [12] utilized the finite element method to analyze the impact of the airtightness of the landing gear hatch structure on the transmission stiffness. They provided a formula to determine the axial preload of the tie rod that satisfies the required airtightness. Zhang Haitao et al. [13] conducted load measurements on a landing gear hatch of a specific aircraft type and developed a strain-based method to measure the hatch load under flight conditions. This served as a basis for subsequent hatch response analysis and design optimization of the landing gear hatch and its retractable mechanism. Tao Liuyuan et al. [14] employed the finite element method to analyze the causes of cracks in the landing gear cabin’s skin. They identified that the static load resulting from aircraft maneuvering overload, along with the dynamic load generated by vibration, particularly in the triangle area of the landing gear cabin, was the main factor contributing to crack formation. Mou Yongfei et al. [4] simulated two models of the high-fidelity nose landing gear of a civilian aircraft, one with hatches and one without hatches. They investigated the flow field and far-field radiation noise characteristics, comparing and analyzing the interference-blocking effect of the nose landing gear hatch on the flow field and the noise of the landing gear. They also examined the influence of the hatch on far-field radiation noise. Their findings highlighted that the flow field in the nose gear cabin + landing gear structure differed from that of a pure cavity flow field, with stronger pressure waves. The landing gear hatch exhibited a noise-shielding effect on the side, and the area between the hatches experienced sound wave interference. Hu Chenying et al. [15] utilized an acoustic–solid coupling analysis method to study the vibration–acoustic radiation characteristics of a typical hatch structure. They emphasized that resonance noise is significantly amplified when the vibration modal frequency of the hatch structure coincides with the acoustic modal frequency of the cabin. They proposed the addition of a constrained damping layer to the hatch as a means of noise reduction. Li Xiaodong et al. [16] conducted numerical simulations to study the influence of a moving hatch on the unsteady flow field of the buried bomb bay (cavity) and the noise characteristics in the cabin. They found that the noise distribution of the moving buried bomb bay hatch was similar to that of a clean cavity, but the second-order Rossiter modal noise value was higher than that of a clean cavity. Liu Yu et al. [17] analyzed the aerodynamic noise characteristics of the cavity with and without the hatch using numerical simulation methods. They observed that adding the hatch significantly increased the SPL (sound pressure level) inside the cavity, particularly for the second-order dominant mode, which increased by up to 15 dB. S. Redonnet [18] reviewed the work conducted by ONERA over the past decade, focusing on their use of the hybrid method to calculate overall noise. They also introduced several reliable aeroacoustics calculation techniques developed by ONERA during that period. Garret C. Y. Lam et al. [19] studied the aerodynamic noise characteristics of the NACA0018 airfoil with a cavity using numerical simulations. They noted that opening the cavity in the airfoil resulted in a change in the lift-to-drag ratio from 0 to 5.3 at a 0° angle of attack, reducing the aerodynamic noise by 1.2 to 2.6 decibels.

For the landing gear compartment (cavity) + landing gear model, Li Yongbin et al. [20] conducted a study using numerical simulation methods to optimize and topologically optimize the main landing gear compartment structure. Their objective was to distribute materials effectively and reduce the structural weight. Guo [21] proposed a semi-empirical method to predict landing gear noise based on Fink’s work. This method enables the separate prediction of low-frequency, intermediate-frequency, and high-frequency noise. It is utilized by the Aircraft Noise Prediction Project (ANOPP) for landing gear noise prediction. Yi Jiang et al. [22] presented a comprehensive prediction method for landing gear noise in traditional passenger aircraft, incorporating the radiated noise from various components, including the landing gear compartment. They validated their method using Airbus A320, Boeing 737, and 777 aircraft models and achieved good agreement with the test results. Philippe R. Spalart et al. [23] calculated the aerodynamic noise of the landing gear compartment + landing gear model using the DES + FW-H (Detached Eddy Simulation with Ffowcs Williams and Hawkings) method. They emphasized the effectiveness of the DES and FW-H methods in predicting the surface noise variations and noted that the noise should be proportional to the seventh to eighth power of the incoming flow. Gareth J. Bennett et al. [24] investigated the aerodynamic noise of a full-scale nose/nose gear compartment/landing gear model through wind tunnel tests. They identified multiple peak frequencies within the 400 Hz range and highlighted the proportional relationship between the noise and the seventh power of the incoming flow velocity. Hu Ning et al. [25] utilized the numerical simulation method DDES (Delayed Detached Eddy Simulation) to examine the influence of wind tunnel blockage on the measurement of landing gear aerodynamic noise. They concluded that the aerodynamic noise characteristics of the model were closely related to the average flow characteristics under different degrees of blockage. Tulio R. Ricciardi et al. [26] employed the DES method to simulate the noise of the LAGOON landing gear. They successfully reproduced the noise generation process and utilized the POD (Proper Orthogonal Decomposition) method to identify the causes of peak noise.

The research mentioned above provides valuable technical references for the study of vibration load characteristics induced by fluid during hatch retraction, and it establishes a foundation for mechanistic research. The complex geometric shape of landing gear and its interaction with aerodynamics present challenges for theoretical and experimental studies on landing gear noise. Furthermore, fluid-induced vibrations resulting from hatch retraction involve complex interactions between the forward landing gear compartment, hatch, and landing gear, leading to intricate flow behaviors. Therefore, further research is needed to understand the characteristics and mechanisms of vibration excitation. Previous research has mainly focused on noise and vibration analysis of partial models; our model includes all components of the forward landing gear compartment, resulting in more complex flow characteristics and flow interactions between components. The NLAS method used in this paper demonstrates significantly higher computational efficiency when compared to URANS and DES + FW-H simulation methods. Through numerical simulation of the unsteady flow field after hatch retraction, we analyze pressure–time history data extracted from each component, study load characteristics, and discuss potential load mechanisms.

2. Numerical Solution and Verification of Nonlinear Acoustic Equations

2.1. Nonlinear Acoustic Equations and Their Numerical Solutions

Based on the literature review conducted by S.J. Lawson [9], S. Redonnet [18], Wang Xiansheng [27], Sun Zhenxu [28], and Xiao-dong LI et al. [29], this paper will employ a hybrid method to compute the unsteady loads resulting from the retraction of the landing gear hatch under fluid-induced conditions.

The nonlinear acoustic solver (NLAS) proposed by Batten et al. [30] is employed due to its ability to predict both broadband and tonal noise. This solver has several advantages over traditional CFD methods, such as unsteady RANS or hybrid RANS/LES in acoustic simulations. The NLAS sub-grid treatment is less diffusive than traditional LES and provides a mechanism to extract acoustic signals from unresolvable eddy footprints (i.e., footprints in the sub-grid scale). NLAS also can use a reduced mesh relative to conventional LES or hybrid RANS/LES. Its near-wall requirements are less stringent since a set of grid-converged RANS statistics can be assumed to be available from the acoustics initializations. In addition, the acoustics initialization file contains data on the RANS-mean flow, which can provide far-field absorbing boundary conditions much closer to the region of interest than would typically be the case with a single-valued dataset for the far-field conditions.

Additionally, NLAS has its limitations. In the hybrid approach, the computations of the flow field and acoustic field are decoupled. It is assumed that unsteady flow generates sound, though this sound is not deemed to exert a substantial influence on the flow dynamics. Consequently, drawing upon the tenets of acoustic analogy theory, the acoustic field’s characteristics can be extracted via post-processing, building upon the foundational computations of the flow field. The hybrid computational methodology efficiently economizes the computational resources requisite for predicting sound propagation in distant regions, rendering it particularly well-suited for addressing intricate challenges in aerodynamic acoustics within engineering applications. Nonetheless, when dealing with highly compressible flow scenarios, the computational intricacy undergoes a marked escalation, and the research inquiry must meet the precondition of a partial, rather than complete, coupling between the flow and acoustic fields.

The basic principle of the NLAS method is that the noise generated by large-scale vortices can be directly obtained by solving the nonlinear disturbance equation (NLDE), whereas the small-scale turbulence contributing to the sound source should be modeled to a certain extent. Unlike the DES method, the modeling of sub-grid scale turbulence is not based on the traditional effective eddy viscosity but on the calculation results of the RANS equation based on the statistical average, which is used to synthesize the sub-grid scale turbulence. The noise caused by the initial statistical average turbulence can be solved using RANS, and the NLAS is primarily used to simulate the generation and propagation of noise. The statistical average solution not only provides the basic characteristics of the average flow field but also presents a statistical description of the forced turbulence pulsation. Based on this statistical result, the NLAS reconstructed the acoustic source and simulated the propagation of pressure pulsation with high accuracy.

Solving aeroacoustics problems using the NLAS method can be divided into three steps: (1) solving the RANS equation to obtain the steady flow field, such as solving the closed NS equations based on the nonlinear k-ε turbulence model [31]; (2) synthesizing the sub-grid scale turbulence based on the calculation results of the RANS equation; and (3) solving the NLDE and obtaining the sound field. Therefore, there are two key steps in the NLAS method: the establishment of the NLDE and the synthesis of sub-grid scale turbulence based on the results of the RANS equation.

The NLAS method has low dissipation and can calculate noise generation at the sub-grid scale. The basic idea is that, in the three-dimensional Cartesian coordinate system, assuming that a disturbance is added to the Navier–Stokes equations, each original variable is decomposed into statistical average and random disturbance variables, that is, φ = φ + φ’. The nonlinear disturbance equation can be obtained by substituting it into the N–S equation and reorganizing the N–S equation [32]:

$$\frac{\partial q^{\prime }}{\partial t}+\frac{\partial F_i{}^{\prime }}{\partial x_i}-\frac{\partial {\left(F_i{}^v\right)}^{\prime }}{\partial x_i}=-\frac{\partial \overline{q}}{\partial t}-\frac{\partial {\overline{F}}_i}{\partial x_i}+\frac{\partial {\overline{F}}_i{}^v}{\partial x_i}$$

(1)

where $q^{\prime }$ is the transient disturbance; $\overline{q}$ is the transient average; $F_i{}^{\prime }$ is the linear inviscid perturbation; ${\overline{F}}_i$ is the inviscid average (i = 1, 2, and 3, representing the x-, y-, and z-axis directions, respectively); ${\left(F_i{}^v\right)}^{\prime }$ is the viscous disturbance; ${\overline{F}}_i{}^v$ is the viscous average; and x_i is the distance in the direction of three coordinate axes: the x-axis, the y-axis, and the z-axis. The solution for each item is shown in Equations (2)–(7).

$$q^{\prime }=\left[\begin{array}{c}{\rho }^{\prime }\\ \overline{\rho }{u}_j^{\prime }+{\rho }^{\prime }{\overline{u}}_j+{\rho }^{\prime }{u}_j^{\prime }\\ e^{\prime }\end{array}\right]$$

(2)

$${\left(F_i^{\nu }\right)}^{\prime }=\left[\begin{array}{c}0\\ {\tau }_{ij}^{\prime }\\ -{\theta }_i^{\prime }+u_k^{\prime }{\overline{\tau }}_{ki}+{\overline{u}}_k{\tau }_{ki}^{\prime }\end{array}\right]$$

(3)

$$F_i^{\prime }=\left[\begin{array}{c}\overline{\rho }{u}_i^{\prime }+{\rho }^{\prime }{\overline{u}}_i\\ {\rho }^{\prime }{\overline{u}}_i{\overline{u}}_j+\overline{\rho }{\overline{u}}_i{u}_j^{\prime }+\overline{\rho }{u}_i^{\prime }{\overline{u}}_j+p^{\prime }{\delta }_{ij}\\ u_i^{\prime }\left(\overline{e}+\overline{p}\right)+{\overline{u}}_i\left(e^{\prime }+p^{\prime }\right)\end{array}\right]+\left[\begin{array}{c}{\rho }^{\prime }{u}_i^{\prime }\\ \overline{\rho }{u}_i^{\prime }{u}_j^{\prime }+{\rho }^{\prime }{u}_i^{\prime }{\overline{u}}_j+{\rho }^{\prime }{\overline{u}}_i{u}_j^{\prime }+p^{\prime }{u}_i^{\prime }{u}_j^{\prime }\\ u_i^{\prime }\left(e^{\prime }+p^{\prime }\right)\end{array}\right]$$

(4)

$$\overline{q}={\left[\begin{array}{ccc}\overline{\rho }& \overline{\rho }{\overline{u}}_j& \overline{e}\end{array}\right]}^{\mathrm{T}}$$

(5)

$${\overline{F}}_i=\left[\begin{array}{c}\overline{\rho }{\overline{u}}_i\\ \overline{\rho }{\overline{u}}_i{\overline{u}}_{j+}\overline{p}{\delta }_{ij}\\ {\overline{u}}_i\left(\overline{e}+\overline{p}\right)\end{array}\right]$$

(6)

$${\overline{F}}_i^v=\left[\begin{array}{c}0\\ {\tau }_{ij}^{\prime }\\ -{\overline{\theta }}_i+{\overline{u}}_k{\overline{\tau }}_{ki}\end{array}\right]$$

(7)

where the values of i, j, and k are 1, 2, and 3, respectively (1, 2, and 3 represent the x-axis, y-axis, and z-axis directions, respectively); $\rho$ is the incoming flow density; $u_i$ ($u_j$, $u_k$) is the velocity of the disturbance along the x-axis (y-axis, z-axis); $\rho$ is the pressure; $e$ is the unit volume energy; ${\delta }_{ij}$ is the Kronecker function; ${\tau }_{ij}$ is the shear stress term; and $\theta$ is the heat conduction term. Neglecting density fluctuations and taking time averages of the evolution terms and all flux terms linear in the perturbations to vanish, results in:

$$\overline{LHS}=\overline{RHS}=\frac{\partial R_i}{\partial x_i}$$

(8)

with

$${\mathrm{R}}_i=\left[\begin{array}{c}0\\ \overline{\rho }\overline{u_i^{\prime }{u}_j^{\prime }}\\ C_p\overline{\rho T^{\prime }{u}_i^{\prime }}+\overline{\rho }\overline{u_i^{\prime }{u}_k^{\prime }}{\overline{u}}_k+\frac{1}{2}\overline{\rho }\overline{u_k^{\prime }{u}_k^{\prime }{u}_i^{\prime }}+\overline{u_k^{\prime }{\tau }_{ki}}\end{array}\right]$$

(9)

where $LHS$ and $RHS$ represent the left and right terms of Equation (8), respectively; $R_{\mathrm{i}}$ is the correlation between the standard Reynolds stress tensor and turbulent heat flux; $C_p$ is the pressure coefficient; $T$ is the temperature; and $\overline{\ast }$ denotes averaging $\ast$.

To solve the NLDE, the values of these unknowns must be obtained, which can typically be acquired by solving the RANS equation. A small size that cannot be solved can be obtained via the artificial reconstruction method of turbulence and used to generate the sub-grid source term. After calculating the average statistical variable, the nonlinear disturbance equation can be advanced. Kraichnan [33] proposed the earliest synthetic turbulence method in 1969; however, it only applies to isotropic turbulence. In 2001, Smirnov et al. [34] proposed a method based on the tensor scale, so that the synthetic turbulence method could be applied to non-isotropic turbulence. Batten et al. [30] proposed a variant of the Smirnov method in 2002, where the reconstruction formula for turbulent fluctuating velocity is as follows:

$$u_i\left(x_j,t\right)=a_{ik}\sqrt{\frac{2}{N}}{\displaystyle \sum _{n=1}^N\left[P_k^n\cos \left({\widehat{d}}_j^n{\widehat{x}}_j+{\omega }^n\widehat{t}\right)+q_k^n\sin \left({\widehat{d}}_j^n{\widehat{x}}_j+{\omega }^n\widehat{t}\right)\right]}$$

(10)

with

$$\begin{array}{l}{\widehat{x}}_j=\frac{2\pi x_j}{l},\widehat{t}=\frac{2\pi t}{\tau },{\widehat{d}}_j^n=d_j^n\frac{l}{\tau c^n},\\ p_i^n={\epsilon }_{ijk}{\eta }_j^n{d}_k^n,\\ q_i^n={\epsilon }_{ijk}{\xi }_j^n{d}_k^n,\\ {\eta }_i^n,{\xi }_i^n~N\left(0,1\right),\\ {\omega }^n~N\left(1,1\right),d_j^n~(0,0.5),\end{array}$$

where $l$ is the turbulence length, $\tau$ is the time scale, ${\epsilon }_{ijk}$ is the permutation tensor of the vector product operation, $C^n$ is the velocity scale of the n-order mode, $N\left(\alpha ,\beta \right)$ is the Gaussian normal distribution function with average $\alpha$ and standard deviation $\beta$, and ${\alpha }_{ij}$ is the Cholesky decomposition of the Reynolds stress tensor. For the symmetric positive definite Reynolds stress tensor $\overline{u_i{u}_j},$$a_{ij}$ can be solved using Equation (11):

$$a_{ij}=\left[\begin{array}{ccc}\sqrt{\overline{u_1^{\prime }{u}_1^{\prime }}}& 0& 0\\ \overline{\frac{u_1^{\prime }{u}_2^{\prime }}{a_{11}}}& \sqrt{\overline{u_2^{\prime }{u}_2^{\prime }}-a_{21}^2}& 0\\ \frac{\overline{u_1^{\prime }{u}_3^{\prime }}}{a_{11}}& \frac{\overline{u_2^{\prime }{u}_3^{\prime }}-a_{21}{a}_{31}}{a_{22}}& \sqrt{\overline{u_3^{\prime }{u}_3^{\prime }}-a_{31}^2-a_{32}^2}\end{array}\right]$$

(11)

The solvable-scale vortex structure can be solved directly; the synthetic turbulence only provides non-solvable-scale information, so the large-scale vortex can be omitted; that is, Equation (10) should be filtered once. The filtering method ignores those modes that meet the conditions of $L>\left|d^n\right|L^{\mathrm{\Delta }}$ ($L^{\mathrm{\Delta }}$ is the scale of the Nyquist grid), which also reduces the amount of calculation required to solve Equation (10) and saves computing resources.

In the unsteady calculation, the dual time-stepping method was used; that is, the virtual time term was introduced into the control equation, and the physical time step was set according to the accuracy to solve the real solution. In each physical time step, convergence was achieved through iteration in virtual time, and multi-grid technology was applied to accelerate the convergence of the internal iteration step. The convection flux adopted the second-order accuracy Harten–Lax–van Leer–Contact (HLLC) scheme [35], which has a total variation diminishing property and small numerical dissipation. The diffusion flux was solved using a central difference scheme.

2.2. Method Verification

The NLAS method for near-wall noise calculation employed in the present research is compared and validated by using the M219 cavity experimental results from reference [36]. The ARA TWT (Transonic Wind Tunnel), with test section dimensions 9 ft × 8 ft, was used for cavity noise measurement. The cavity for the wind tunnel test is an all-metal flat model, and the specific size is L × W × D: 20” × 4” × 4”, and the length–depth ratio of the cavity is five. Several kulite transducers were arranged at the ceiling of the cavity. The cavity experimental model, kulite transducer positions, and pressure sensors are shown in Figure 1a–c, respectively. The longitudinal positions of the relative cavity length are listed in

Table 1. Relative position of sensors [36].

Point	1	2	3	4	5	6	7	8	9	10
Longitudinal x/L	0.05	0.15	0.25	0.35	0.45	0.55	0.65	0.75	0.85	0.95

for the Ma = 0.85 case conducted by M J [36], and the longitudinal and vertical positions of the relative cavity length and depth are listed as presented in

Table 2. Relative position of sensors [37].

Point	1	2	3	4	5	6	7	8	9	10	11	12	13
Longitudinal x/L	0.2	0.4	0.5	0.6	0.7	0.8	0.9
Vertical y/D								0.143	0.286	0.429	0.571	0.714	0.857

for the Ma = 3.0 case conducted by Ming [37].

The experimental research primarily includes the flow characteristics of the cavity when Ma = 0.85 and Ma = 3.0 from [36,37]. In this experiment at Ma = 0.85 [36], the sampling frequency of the fluctuating pressure acquisition system was 6 kHz, the block size was 1024, the block period was 0.17067 s, and the number of averages was 20. In contrast, for the Ma = 3.0 test case [37], the sampling frequency of the fluctuating pressure acquisition system was 40 kHz, the sampling time was 5 s, the sampling was performed twice, the sample length was 4096, the number of samples was 48, the frequency resolution was 9.766 Hz, and the upper limit frequency was 20 kHz. The data signal acquisition system obtained the time domain information from the wind tunnel test and performed the Fourier transformation after the Hanning window correction to obtain the frequency domain information of the noise signal.

The cavity calculation domain and structured grid model are shown in Figure 2. In order to comprehensively assess the impact of the leading-edge shape on the aerodynamic characteristics of the cavity model [38], the complete model of the M219 cavity is utilized in this study rather than using an intercepted version. In terms of the NS equations used for initializing the nonlinear acoustic equations, the thickness of the first-layer grid on the wall is set to 1 × 10⁻⁶ m, resulting in a corresponding y+ value of approximately 1. For the range of fluctuating load frequencies (0 Hz to 5000 Hz), considering that the shortest acoustic wavelength is computed using 5 to 6 grid units, the minimum grid size adopted is 0.01 m, and the thickness of the first layer of the mesh is 0.002 mm. The far-field boundary conditions for the NS solver were set as the far-field Riemann invariant condition, while for the NLAS solver, they were set to acoustic far-field boundary conditions.

The statistical average value of large pressure fluctuations on the cavity ceiling at Ma = 0.85 was tested and compared with both the experimental results [36] and LES results [39], as plotted in Figure 3a, respectively. The results indicate that the Prms trends agree well with test results and LES simulation results. The maximum deviation occurs at the x/L range [0.55, 0.75], but the deviation is relatively small.

Besides the statistical average value of large pressure fluctuations, the aerodynamic loads asserted on the cavity surface are usually depicted through SPL to exhibit peak values as well as peak frequencies. In order to examine the effectiveness of the NLAS method in capturing different peak frequency noises, the test results [37] of the M219 cavity under the condition of Ma = 3.0 were also utilized for comparison and validation. The spectrum data of measuring points No. 1, No. 7, and No. 13 were analyzed and compared, as shown in Figure 3. It can be observed from the figure that the NLAS method can effectively capture the amplitude–frequency characteristics of the noise.

Additionally, the numerical results calculated using Improved Delayed Detached Eddy Simulation (IDDES) were also employed for comparison. In the IDDES simulation, the cavity wall was set as the adiabatic and non-slip wall, and according to the grid scale, the calculation time step was 2.5 × 10⁻⁶ s.

The peak value of the SPL, and the frequency corresponding to the peak value, were consistent with the experimental results, as shown in Figure 3b–d, respectively, indicating the effectiveness of the NLAS method in calculating supersonic near-wall noise. The SPL calculated through the IDDES method decayed with an increase in frequency. Moreover, the frequency corresponding to the peak value of SPL was consistent with the test results, but the peak values of SPL deviated from the test data for IDDES results. Consequently, the calculation using the NLAS method is more accurate, and the obtained noise amplitude is closer to the actual physical value. In addition, the NLAS method has lower requirements for computational grids and physics time steps, which can save more computational resources and improve computational efficiency (as shown in

Table 3. Efficiency (at Ma = 3.0), advantages, and disadvantages of different calculation methods.

	Number of CPU Cores	Time Step	Number of Grid Cells	Calculation Time	Advantages	Disadvantages
IDDES	64	2.5 × 10−6 s	7.5 million	25 days	High accuracy of subsonic calculation. Unsteady state conditions can be calculated.	Low accuracy of supersonic calculation. Low efficiency.
NLAS	64	5 × 10−6 s	3.2 million	6 days	High accuracy of subsonic and supersonic calculations. High efficiency, suitable for engineering applications.	Calculating based on the RANS equation and dynamic unsteady conditions cannot be performed.

). Accordingly, to predict aircraft surface noise by combining the advantages and disadvantages of the two methods, this study adopted the NLAS method in the cruise state.

The NLAS method requires significantly fewer grids than IDDES, improving computational efficiency. Therefore, the grid division parameters and numerical solutions of the mixed equations used in this paper can be applied in subsequent calculation studies.

3. Results and Discussion

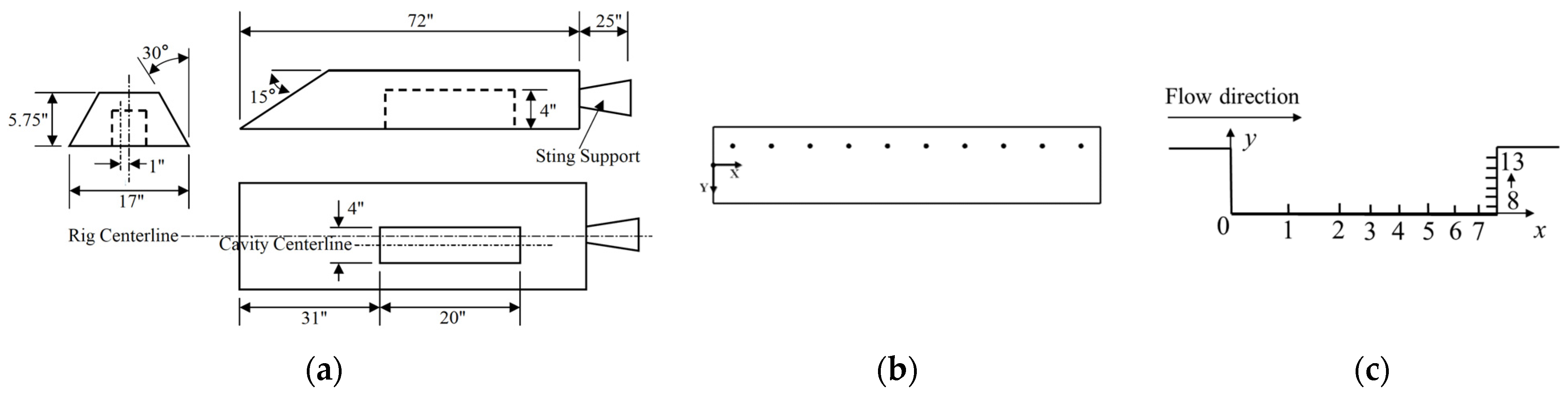
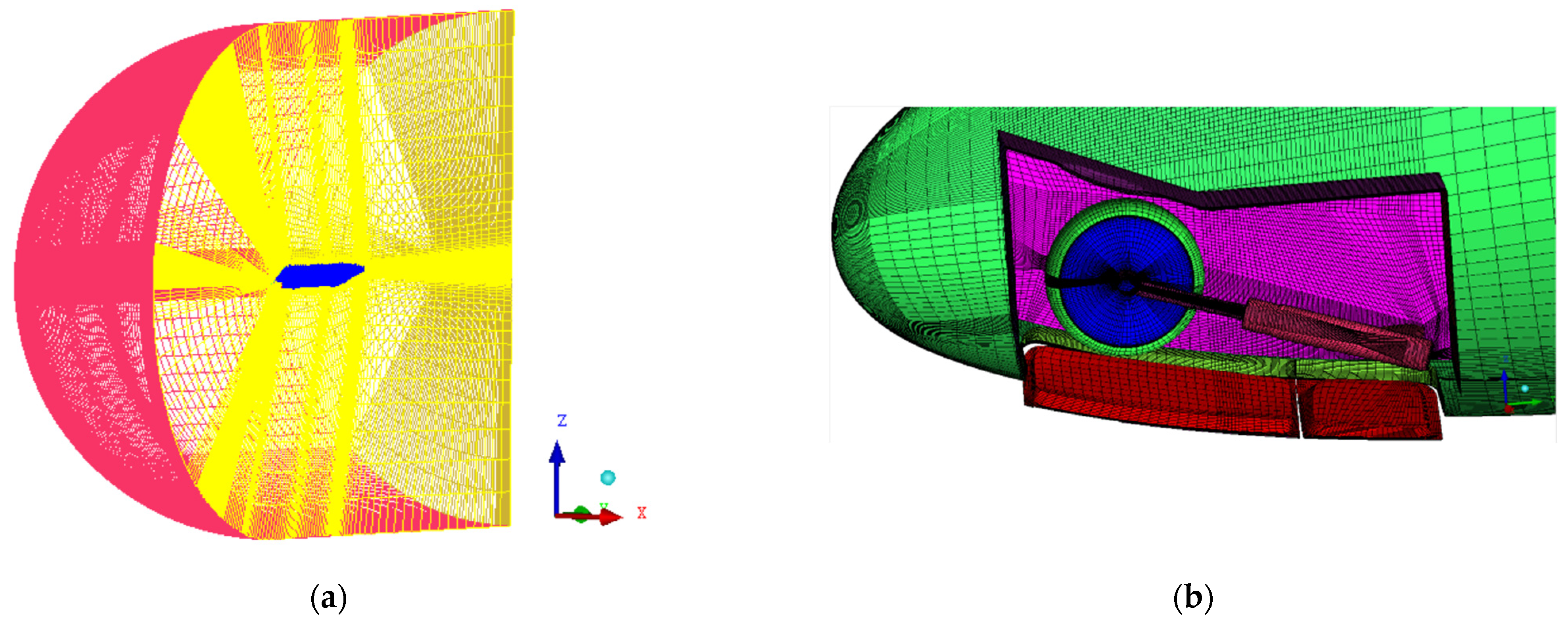
Since fluid-induced vibration occurs during the aircraft’s cruising state, it is important to focus on the front landing gear compartments as the source of the fluid-induced vibration load. As the front landing gear compartments are located upstream of the wing, it is necessary to optimize the computational efficiency by reducing the computational workload. This can be achieved by excluding components such as the wing, vertical tail, horizontal tail, and engine nacelle from the calculation domain. Thus, only the fuselage is retained, as well as the landing gear compartments. Then, multiple structured grids are generated, as depicted in Figure 4.

For various components (as shown in Figure 5a), specific monitoring points were established (Figure 5b). Due to the extensive number of monitoring points and space limitations, this paper focuses on presenting the number of monitoring points on the inner and outer walls of the large and small hatches, as depicted in Figure 6.

To address the issue of unsteady aerodynamic loads causing vibration, the hatch gap is characterized by the hatch opening angle, and its impact on the load is investigated. Specifically, the hatch opening angles considered in this study are 0°, 5°, 10°, 15°, and 20°. The load time history data for each monitoring point is computed by solving the NLAS equation.

In the structural response analysis, the RMS of the fluid-induced vibration load “Prms” is used to characterize the statistical average behavior of the fluctuating load. The Prms values of the monitoring points on the right hatch are calculated under different opening angle conditions. From Figure 7, it is seen that, as the hatch opening angle increases from 0° to 15°, the RMS of cumulative pressure loads on both the small and large hatches under different opening angles continuously increases. However, as the hatch opening angle increases from 15° to 20°, the RMS of cumulative pressure loads decreases. Hence, the peak value of the fluctuating load occurs at a hatch opening angle of 15°, whereas excessively small or large opening angles do not result in significant fluid-induced vibration loads.

The Prms of fluid loads is influenced and determined by variation of aerodynamic geometry. As shown in Figure 5 and Figure 6, a sharp variation of hatch thickness can be seen at their ends in both the body axis direction and spanwise direction of both hatches, respectively. Also, the gaps between these hatches, and the gaps between hatches and strip, can be respectively discerned. To examine the variation of RMS of pressure loads with the hatch opening angle, these monitoring points in Figure 6 are categorized into three groups for both the inner and outer wall (namely, the “Streamwise_inner wall_*”, and “Streamwise_outer wall_*”, where “*” can be 1, 2, 3.) in a streamwise direction, respectively. In the names of the six figures from Figure 8a–f, the number “1” indicates that these points are close to the symmetry plane of the airplane, while the number “3” means that these points are near to the sidewall of the landing gear compartment. The monitoring points in each categorized group are presented in

Table 4. Monitoring points in each group.

Group Names	Monitoring Point Numbers
Streamwise_inner wall_1	1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37
Streamwise_inner wall_2	2, 5, 8, 11, 14, 17, 20, 23, 26, 29, 32, 35, 38
Streamwise_inner wall_2	3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39
Streamwise_outer wall_1	40, 43, 46, 49, 52, 55, 58, 61, 64, 67, 70
Streamwise_outer wall_2	41, 44, 47, 50, 53, 56, 59, 62, 65, 68, 71
Streamwise_outer wall_3	42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72

.

In Figure 8, the horizontal axis denoted by “Y(m)” is the coordinate in the airplane body axis. For these two hatches, the y coordinate ranges from 0.953 m to 2.698 m. The large hatch ends at y = 2.094 m; the small hatch begins at y = 2.112 m. In the body axis direction, the distance from the minimum large hatch coordinate to the strip, and from the maximum small hatch coordinate to the strip, are 0.0198 m and 0.0193 m, respectively.

The Prms result plotted in Figure 7 gives the RMS of cumulative pressure loads. To examine the detailed RMS distribution of pressure loads in streamwise direction, the pressure load RMS of six groups of monitoring points are shown in Figure 8a to Figure 8f, respectively. For the inner wall, as shown in Figure 8a–c, with the thickness increase at the leading edge of the large hatch (at about y = 1.05 m), the Prms increases obviously; then, the Prms values decrease for each group at each hatch opening angle. In the geometrically central zone of the inner wall of the small hatch, the decrease in Prms values for each group at different hatch opening angles can be discerned.

Besides similar trends for these three group points, differences can also be found. At the streamwise location near the trailing edge of the large hatch, the differences are as follows: The Prms variations shown a sharp increase–decrease variation for the monitoring points near the symmetry plane, as shown in Figure 8a. This is due to the gap attributed to the hatch opening, where the flow in the gap influences the flow behavior obviously. In Figure 8b, the Prms variation is relatively small, and this is due to the fact that this group of monitoring points reside nearly on the geometrical center line in a spanwise direction of the small hatch; thus, the influence of gap flow around the symmetry plane and cavity sidewall is relatively small. In Figure 8c, as the hatch opening angle increases, the gap between the hatch and strip decreases; thus, the Prms value shows decreased variation. Then, with the sharp increase of thickness at the leading edge of the small hatch, the Prms value increases.

At the streamwise location near the trailing edge of the small hatch, the differences are as below: In Figure 8a, Prms decreases at the trailing edge. And with the increase in hatch opening angle, the Prms decreases more sharply. This is due to the fact that the air flows out of the cavity at this location; thus, the flow becomes less unsteady, inducing weaker pressure loads. The same reason is applicable to the Prms decrease with the increase of the hatch opening angle in Figure 8b. In Figure 8b, when the hatch opening angle is small (0°, 5°), the Prms variation is small, for little flow separation occurs on the inner wall of the small hatch. In Figure 8c, the Prms increases with the increase of the hatch opening angle in the angle range [0°, 15°], and this is due to the strength increase of vortices in the separation zone. When the hatch opening angle increases to 20°, the strength of vortices decreases, resulting in a decrease in Prms.

For the outer wall, as shown in Figure 8d–f, the Prms increases obviously at the leading edge of the large hatch (in the y range [0.95 m, 1.30 m]); then, the Prms values decrease for each group at each hatch opening angle. Then, at the streamwise zone between the trailing edge of the large hatch and the leading edge of the small hatch, the Prms exhibit increase–decrease variation. In the geometrically central zone of the outer wall of the small hatch, the decrease in Prms values for each group at different hatch opening angles can be seen. The differences between these three group of RMS results occur at the trailing edge of the small hatch, as depicted below: for the monitoring points near the symmetry plane (Figure 8d), the Prms decreases for a hatch opening angle [0°, 15°], while it increases at the hatch opening angle 20°. This increase is due to much more air outflow from the landing gear cavity, causing severe flow separation at this outer wall zone. As monitoring points move to the centerline of the small hatch outer wall in a spanwise direction (Figure 8e), the air outflow from the landing gear cavity causes evident flow separation in the hatch opening angle range [10°, 20°], thus resulting in a sharp increase in Prms. For the monitoring points near the sidewall of the landing gear cavity, evident flow separation occurs at a hatch opening angle range [0°, 20°]; thus, the Prms increases for all angles.

In these six figures, an increase in the RMS of cumulative pressure loads can be observed with a hatch opening angle from 0° to 15°. As the hatch opening angle increases from 15° to 20°, the RMS of cumulative pressure loads from the inner wall does not vary obviously, while the RMS of cumulative pressure loads from the outer wall evidently decreases, explaining the variation in Prms in Figure 7 within the hatch opening angle range [15°, 20°].

From Figure 8a–c, it can be seen that the Prms of the “Streamwise_Inner_Wall_1” curve exhibit locally the largest values at the inner wall leading edge of the large hatch; hence, monitoring points 4 and 7 (as shown in Figure 6) are selected to examine the amplitude–frequency distribution characteristics of fluid-induced vibration loads using PSD (power spectral density). Meanwhile, for the Prms results of monitoring points on the small hatch surface (from Figure 8a,d), the No. 22 and 55 points are locally the largest ones compared to other point results; hence, they are selected to depict the amplitude–frequency distribution characteristics of fluid-induced vibration loads at the leading edge of the small hatch. Figure 9a plots the No. 4 and No. 7 PSD results, and Figure 9b plots the No. 22 and No. 55 PSD results. For convenience of comparison, the PSD range of these two figures is set the same.

From Figure 9a, it can be seen that the PSD results exhibit broadband characteristics, whose energy is primarily concentrated below 150 Hz. In the frequency range [0 Hz, 75 Hz], the pulsating energy of the No. 4 point is larger than that of No. 7 point. This is due to the fact that sharp aerodynamic geometry variation can cause accelerated flow with separation, inducing pulsating loads with large amplitude. At the No. 7 location, the inner wall surface of the large hatch is smooth; thus, separated flow generates relatively smaller-amplitude pulsating loads. From Figure 9b, it is observed that the fluid-induced vibration loads of the No. 55 point distribute a large amount of energy at about 75 Hz, which is the largest value in all these four monitoring point PSD results. This is caused by the flow separation at the outer surface leading edge of the small hatch, which is depicted by streamlines in the following discussion. The PSD results of fluid-induced vibration loads of the No. 22 point show relatively evenly distributed energy in the frequency range [0 Hz, 300 Hz]. This is caused by the complex flow interference between different parts as discussed below.

To examine the reason for the variation in RMS of cumulative pressure loads with hatch opening angles, the iso-surfaces of Q = 100,000 based on Q-criterion [40] are extracted and rendered by vorticity magnitude. To have a clear examination, only the right parts of the iso-surfaces inside the cavity are plotted, as shown in Figure 10. In Figure 10a, it is seen that flow separation is relatively small from the inner surface of both large and small hatches. Small vortices are generated from both the symmetry gap and the gap between the hatches and strip. With the increase in the hatch opening angle, flow separations from the inner wall obviously become more intensive, e.g., at a hatch opening angle 5° (Figure 10b), flow separation can be seen at the leading edge of the large hatch and small hatch, and the trailing edge of the small hatch, respectively. The separated flow attaches to the surface of the landing gear tire. Meanwhile, the vortices generated from both the symmetry gap and the gap between the hatches and strip also become stronger. In Figure 10c, the separation zones enlarge themselves with the increase in the hatch opening angle, and the attached zone on the surface of the landing gear tire also becomes larger. The intensity of vortices from the symmetry gap and the gap between the hatches and strip continuously increases. In Figure 10d, the intensity of separation and vortices reaches their maxima, resulting in the peak value of RMS of cumulative pressure loads. Then, as the hatch opening angle increases to 20° (Figure 10e), the size of the vortices from the symmetry gap and the gap between the hatches and strip decreases, indicating a descent in intensity, which induces a drop in RMS of cumulative pressure loads.

To further analyze the origin of the fluctuating loads, both spatial streamlines in the landing gear compartment and streamlines on different cross-sections are presented, as shown in Figure 11, Figure 12 and Figure 13, respectively. In these figures, the legend “P” is the static pressure in “Pa”, “V” is the velocity component along the y axis in “m/s”, and “W” denotes the velocity component along the z axis in “m/s”.

Figure 11 shows the spatial streamlines in the landing gear compartment to give a global perspective of the flow characteristics. In Figure 11a, air flows into the landing gear compartment from the gap between the strip and the leading edge of the large hatch. The inflow air travels downstream near the inner wall of both the large and small hatches, then flows out from the gaps, which are the gaps between the small hatches and strips, the gap between small hatches, etc., respectively. The downstream-flowing air shears the air in the landing gear compartment, forming the principal vortex in the landing gear compartment. The principal vortex reaches the landing gear tires. In Figure 11b, the downstream-flowing air travels out from the landing gear compartment at a location just upstream of the trailing edge of the large hatch, from the gaps between the large hatches, and the gaps between the large hatch and the sidewall. In Figure 11c, the spanwise flow is depicted at the gap between the large hatch and the small hatch on the right side. In the zone upstream of the sharp increase in hatch thickness in the small hatch, the air flows toward the sidewall when the height is below the thickness; while, when the height exceeds the inner wall of the small hatch, the air flows to the symmetrical plane. In Figure 11d, spatial streamlines at the gap between the large hatch and the small hatch on the left side are plotted, and similar flow characteristics can be found compared to that of Figure 11c at the gap between the large and small hatches. The streamlines differ from those in Figure 11c due to the sidewall being half empty and the air being able to flow into the cavity on the left of the sidewall with a very low-velocity magnitude compared to the downstream flow in Figure 11b. The spatial streamlines in these four figures exhibit complex flow interference between different parts, as depicted by circulating flow, spanwise flow, etc.

Figure 12 illustrates the streamlines on different X cross-sections to examine the details of the flow characteristics. Figure 12a shows the streamlines on the symmetrical plane at X = 0.00 m. The downward-flowing air is seen to shear the air in the compartment and flows out of it from gaps. The shear effect establishes the principal vortex in the compartment, and flow with characteristics comparable to the cavity is formed. Due to the presence of tires, as shown in Figure 12b, a vortex is formed above the undercarriage. In Figure 12b, the hatches are cut, and the airflow accelerates into the compartment at the gap between the strip and the leading edge of the large hatch. Air also flows into the compartment from the gap between the large and small hatches. The incoming air then flows out of the compartment from the gap between the strip and the trailing edge of the small hatch. These two hatches act similarly to flat plates arranged in a line. The tire acts similarly to a small length-to-diameter ratio circular cylinder. The vortex near the tire becomes larger. The flow characteristics of the streamlines in Figure 12c are similar to that in Figure 12b, with the vortex continuously expanding. In Figure 12d, the vortex forms flow characteristics similar to that of a clean cavity. Meanwhile, the air flows into and out of the compartment.

Figure 13 shows the streamlines at different Y cross-sections in the landing gear compartment. In Figure 13a, the flow enters the compartment at the mid-span of the large hatch, while going out of it spanwise from the gaps between the sidewall and the large hatch and the gap between large hatches. In Figure 13b, it is found that the air leaves the compartment. The circular cylinder baffles the airflow, and asymmetrical flow is formed at this cross-section because air flows into the compartment from the portside cavity. The vortex beneath the circular cylinder is the wake vortex behind the tire. In Figure 13c, the sidewall on the portside is present, and flow asymmetry becomes weaker. At the leading edge of the small hatches, air flows to the sidew all near the inner wall. The limit streamlines occur nearby the thick inner wall. By referring to the special streamlines in Figure 11, it can be determined that the air above the limit streamlines goes to the compartment’s back wall, similar to that of clean cavity flow. In Figure 13d, the flow streamlines are nearly symmetrical due to the wall confinement of the sidewall on the portside. The flow goes out of the compartment from all gaps. Meanwhile, the air flows upward, forming the cavity flow in the compartment.

4. Conclusions

In this study of the amplitude–frequency characteristics and mechanisms of fluid-induced vibration loads generated by the hatch-opening of the landing gear compartment during cruising, a hybrid method comprising a steady NS solver and an unsteady NLAS solver is employed. It is compared and validated using transonic and supersonic test results of the M219 cavity. Numerical results with different hatch opening angles from 0° to 20° are computed. The numerical results show that hatches exhibit significantly greater amplitudes of fluctuating pressure in comparison to other components. The RMS of cumulative pressure loads from the hatch elements reaches its peak when the hatch opening angle is set to 15°. Four representative monitoring points with higher RMS values are chosen to examine energy distribution characteristics of pulsating loads. The PSD results of monitoring points on the inner wall of the large hatch exhibit broadband frequency characteristics; the peak PSD values corresponding to the monitoring points on the outer wall of the small hatch concentrates a significant concentration of energy at approximately 75 Hz. The peak PSD values for the selected monitoring points on the inner wall of the small hatch, on the other hand, demonstrate a more uniform distribution of energy. Flow characteristics depicted using iso-surfaces of Q-criterion, spatial streamlines, and streamlines on different cross-sections reveal that the flow across the hatches is similar to a blunt-edged plate with a spanwise flow; the tires induce flows similar to those of a small length-to-diameter circular cylinder; the landing gear compartment exhibits flows comparable to a clean cavity. These unsteady flows together form the unsteady load characteristics. The flow separation zones become wider and vortex intensity increases with the increase of the hatch opening angle from 0° to 15°; then, their values decrease as the hatch opening angle increases from 15° to 20°. These variations contribute to a peak value in RMS of cumulative pressure loads at 15°.

In this paper, the model employed encompasses all components within the forward landing gear compartment. We delve into more intricate flow characteristics and explore the interactions between these components, providing a deeper understanding compared to previous research, which predominantly concentrated on the noise and vibration analysis of partial models. Moreover, we employ the highly efficient NLAS method, ensuring accurate numerical computations when compared to URANS and DES + FW-H simulation methods. The limitations of the present study are that a rigid model is employed in numerical analysis, without including the aeroelastic effects. Additionally, the wings, nacelles, horizontal tails, and vertical tail are omitted. Their influence on fluctuating load characteristics may be further determined. Finally, the source for different frequencies of fluctuating loads can be further studied and quantified using POD or DMD (Dynamic Mode Decomposition).