Experimental and Numerical Investigations on the Dynamic Response of Blades with Dual Friction Dampers

Abstract

Friction dampers are widely employed to reduce blade resonance vibration amplitude in turbomachinery. In this paper, a study was performed on the forced response of two blades with dual friction dampers. Numerical simulation and experimental testing were conducted. Firstly, the dynamics of the blade and dual friction damper system assembly are modeled. A nonlinear code based on the multi-harmonic balance method was developed to calculate the resonance response. In this analysis, both the blade and the damper are modeled with the finite element and the matrices reduced with the component mode synthesis method, while the contact forces are modeled with a one-dimensional variable normal load array element. Secondly, a test rig made of two blades and dual friction dampers, the material of which was steel, was established to measure the nonlinear frequency response function curves of the blade system. The results indicate that when a dual friction damper is applied, superior vibration reduction characteristics are demonstrated, with the system exhibiting an average 21% reduction in the response amplitude levels and an increase of 3% in the frequency shifting range compared to a single damper. Dampers positioned at relatively higher locations contribute significantly to the vibration reduction process. In the end, the numerical predictions match very well with the experimental ones.

1. Introduction

Nowadays, the increasing demand for higher efficiency and lower fuel consumption has led to the operation of gas turbines under a critically high rotation speed at high temperatures and pressures. This makes the vibration of the bladed disk a critical problem. Furthermore, due to the wide spectrum of aerodynamic excitation, it is practically impossible to avoid all critical resonances in the operating frequency range [1,2,3]. Reducing the vibration levels at these resonant frequencies and thus reducing the high cycle fatigue failures [4,5] due to resonant stresses is the main option to ensure the durability and reliability of gas turbines. One approach to reduce the vibration levels of the blade disk is through the implementation of material damping. This involves considering the inherent characteristics of the material. Advancements in composite material development and a thorough investigation into their dynamic properties will play a crucial role in facilitating their prospective application [6]. Another common method is the introduction of dry friction damping, which contains shroud coupling, underplatform damper, lacing wire, snubber, ring damper, etc. [7,8,9,10]. Among them, the underplatform damper (UPD) has been more widely used due to its numerous advantages. A UPD is a metal device that is typically placed in a groove underneath two adjacent blade platforms and remains in contact with the platforms during operation by centrifugal loading. When the blades vibrate, the relative displacement between the platform and the damper creates friction on the contact surfaces, which leads to large energy dissipation and reduces the resonance amplitude. The energy dissipation is closely related to the frictional hysteresis characteristics between the contact surfaces [11]. Due to the friction-related nature of the problem, the dynamic response of the blade with UPDs is strongly nonlinear, with both the vibration levels and resonance frequencies being amplitude-dependent [12].

While achieving precise modeling of frictional contact and accurate prediction of nonlinear forced response presents inherent complexities, the underlying physical mechanisms governing friction-induced energy dissipation remain fundamentally straightforward. A large amount of numerical and experimental research has been performed over the years to characterize friction damping. The most basic conceptualization emerges in the form of the one-dimensional macroscopic slip element proposed by Griffin [13]. This model serves as a foundation, enabling a comprehensive investigation into the vibrational characteristics of a single Degree of Freedom (DOF) representation of a turbine blade. Yang et al. developed more sophisticated contact models and applied them to three DOF oscillators [14], shroud contacts [15], and wedge damper models [16,17]. Significant contributions have additionally been advanced by Menq [18], introducing a one-dimensional contact model with variable normal loads. Notably, this model factors in the pivotal consideration that the tangential orientation of the contact surface does not align with the direction of vibration. Yang [19] deduced in detail the state transition criteria when sticking, slipping, and separation of the contact surface states occur in this model and calculated the frequency response function (FRF) curves of the two DOF systems. Sanliturk [20] developed a time-discrete frictional contact model for two-dimensional planar motion, tracking the friction and trajectory of the contact point in the plane in two tangential directions. Yang [14] comprehensively considered the tangential relative motion in the plane and the variable normal load to establish a more refined three-dimensional contact model. When applying higher-dimensional contact models, Borrajo [21] and Petrov [22,23] developed a form of analytical formulation of the Jacobian matrix, which significantly enhanced the nonlinear calculation speed. Subsequent researchers have calculated the effects of a shroud contact and an asymmetric UPD on the vibration characteristics of the system [24,25,26].

Most test rigs employed by many researchers to test the numerical code share the same architecture. A set of cables press the damper against the platforms of two blades, simulating the centrifugal force acting in a real rotating bladed disk assembly. Sanliturk [27] and Pesaresi [28] test a wedge damper on pairs of dummy blades. The motion patterns of the dampers were investigated when the blade system showed in-phase (IP) and out-of-phase (OOP) bending modes. Firrone [29] and Gastaldi [30] applied an asymmetric damper to a real turbine blade and performed vibration response tests to measure the FRF curves at different centrifugal forces. Zhang [31] has made improvements. They built a test rig with three blades and two UPDs, simulated the centrifugal force using preloaded springs, and measured the vibration response for different damper materials, weights, and related variables.

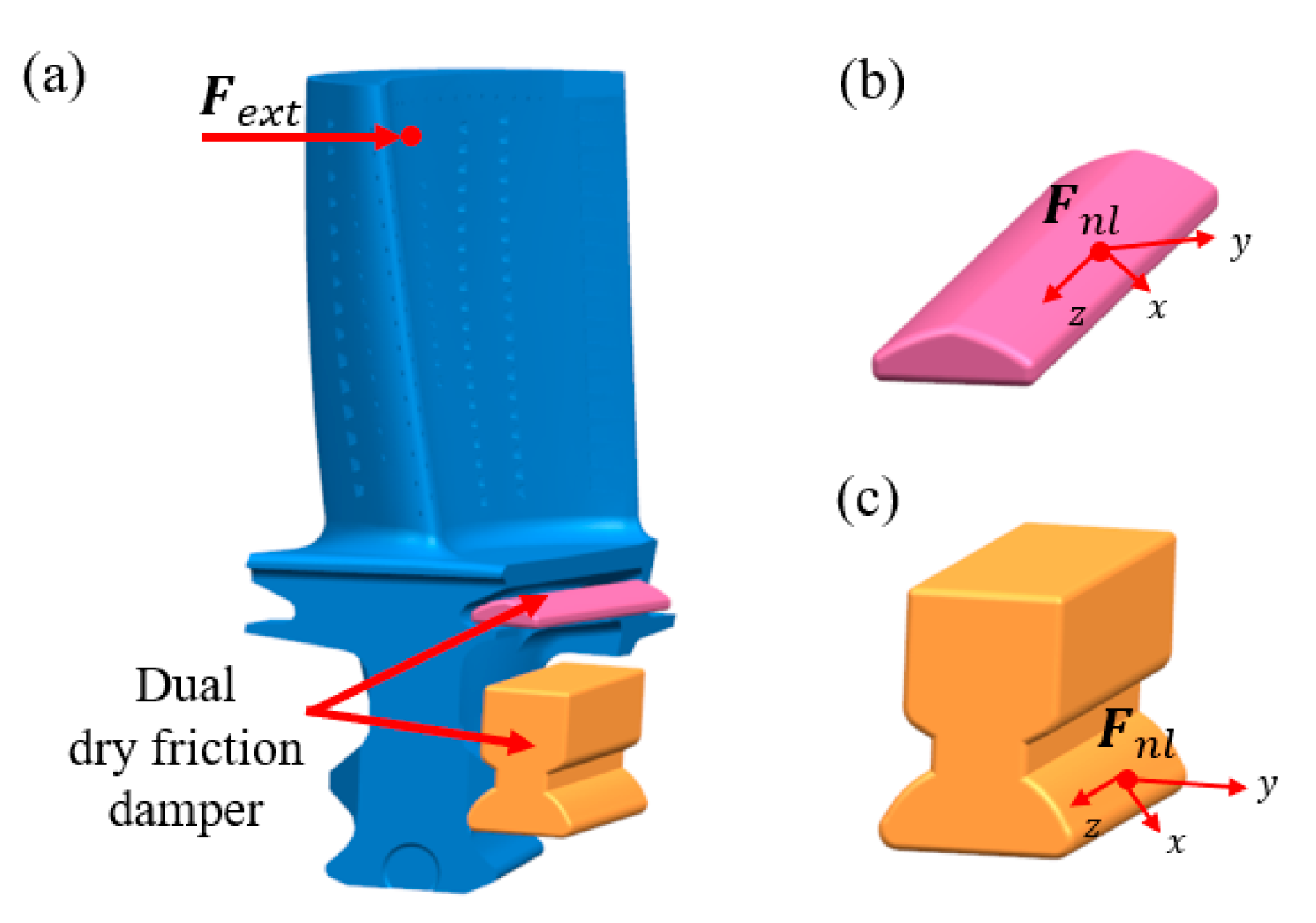
The references cited so far have considered only the dry friction-damping effect in the form of a single contact surface. A detailed study, both numerical and experimental, is carried out in this paper for the high-pressure turbine blade of a gas turbine with a dual dry friction damper. The explicit implementation of the dual dry friction damper, as detailed in Section 2, is visually expounded upon in Figure 1. The underlying principle governing this dual dry friction damper closely aligns with that of the UPD, yet it distinguishes itself by being situated at disparate locations within the system. In this work, the response of the blades with a dual dry friction damper was then simulated with a nonlinear code based on the multi-harmonic balance method (MHBM) in the frequency domain [10,32]. The periodical contact forces are modeled with a one-dimensional variable normal load array element. To enhance the robustness and precision of the experiment, the real turbine blade underwent a process of selective simplification while retaining its core structural attributes, as discussed in Section 4. The experimental rig is similar to that of several previous researchers [27,29], but the novelty lies in the experimentation of simulated components with dual dry friction damper characteristics. This innovative approach allows gauging the damping impact across varied blade neck lengths and diverse distributions of centrifugal forces, thereby offering fresh insights into the underlying dynamics. Finally, to validate the numerical code, the numerical response curves were compared with the experimental results.

The paper is organized as follows: In Section 2, we present an exhaustive dynamic model of a blade system featuring dual dry friction dampers. Section 3 introduces the frictional contact model, which is employed to describe the contact problem. Subsequently, in Section 4, a comprehensive methodology is expounded upon. Particular emphasis is placed on model reduction and the utilization of continuation techniques to ensure solution stability. Section 5 outlines the setup of the experimental test rig and details the testing process. Lastly, in Section 6, we apply the proposed methodology to solve the model involving dual dry friction dampers. We then conduct a comparative analysis of numerical simulation results against experimental data, elucidating the functional characteristics of the dual dry friction dampers.

2. Blade with Dual Dry Friction Damper

In this paper, the high-pressure turbine rotor blade with a dual dry friction damper is shown in Figure 1. It can be seen that, notably distinct from a typical UPD, this configuration introduces a friction device at the groove of the platform (called a UP damper). As the turbine blades engage in rotation, the resultant centrifugal forces prompt contact between the damper’s friction surfaces, giving rise to frictional damping. Another friction device (called a LOW damper) is applied in the raised position of the blade root. It not only acts as a damping device but can also rely on the sealing structure at the rear position for gas sealing. Owing to its lower aspect ratio, the first-order bending frequency surpasses 2000 Hz. To streamline the experimental procedures, a simplification approach is undertaken about the real blade. In this streamlined representation, only the main structural attributes are preserved, a comprehensive depiction of which is furnished in Section 4.

In the blade–damper system, the blade acts as the main structure, and the damper is a separate structure. The damper is not elastically connected to the bladed disk, and it interacts with the blade only through the nonlinear contact forces. Therefore, the dynamic models of the blade and the dual dry friction damper are created separately. For a case of steady-state forced response analysis, the dynamic equation for the blade and dual dry friction damper is

$$M_b{\ddot{Q}}_b\left(t\right)+C_b{\dot{Q}}_b\left(t\right)+K_b{Q}_b\left(t\right)=F_{ext}\left(t\right)-F_{nl}\left(t\right)$$

(1)

$$M_d{\ddot{Q}}_d\left(t\right)+C_d{\dot{Q}}_d\left(t\right)+K_d{Q}_d\left(t\right)=F_{nl}\left(t\right)$$

(2)

where $\mathbf{M}, \mathbf{C}, \mathbf{K}$ and $\mathbf{Q}$ are the mass, damping, stiffness, and displacement matrices, respectively. The subscript $b,d$ stands for the blade and damper, respectively. And $Q$ is the displacement vector of each node in the entire system, including contact surface nodes and other nodes. $F_{ext}$ is the excitation force. $F_{nl}$ is the nonlinear friction force generated between the contact surfaces. The dot above $\stackrel{·}{\left(\right)}$ indicates the time derivative, and $t$ is natural time.

In a steadily rotating machine, the excitation of the blade and the contact displacements due to the excitation are periodic, so they can be represented by a restricted $N_h$ Fourier series as follows:

$$F_{ext}\left(t\right)\approx \mathrm{Re}\left({\displaystyle \sum _{h=0}^{N_h}{\widehat{F}}_{ext}^{\left(h\right)}{e}^{ih\omega t}}\right)$$

(3)

$$Q\left(t\right)\approx \mathrm{Re}\left({\displaystyle \sum _{h=0}^{N_h}{\widehat{Q}}_{}^{\left(h\right)}{e}^{ih\omega t}}\right)$$

(4)

where ${\widehat{F}}_{ext}^{\left(h\right)}$ and ${\widehat{Q}}^{\left(h\right)}$ are the $h\mathrm{th}$$\left(h=0,1,2,\dots N_h\right)$ complex Fourier coefficients of the excitation force and displacement, respectively, $\omega$ is the angular velocity of the rotor, and $i$ is the imaginary unit. Typically, a single excitation frequency is analyzed during the simulation. However, nonlinear contact forces generate higher-order harmonics in the nonlinear force spectrum. Therefore, the usual value $N_h>1$ is required in nonlinear analysis. The total number of harmonics $N_h$ needed in the expansion is determined by solution accuracy and the harmonics of the computed nonlinear contact force spectrum that can contribute significantly to the force response. Thus, nonlinear friction can also be expanded into the form of $N_h$ order Fourier coefficients:

$$F_{nl}\left(t\right)\approx \mathrm{Re}\left({\displaystyle \sum _{h=0}^{N_h}{\widehat{F}}_{nl}^{\left(h\right)}{e}^{ih\omega t}}\right)$$

(5)

where ${\widehat{F}}_{nl}^{\left(h\right)}$ is the $n\mathrm{th}$ complex Fourier coefficients of the nonlinear forces. Inserting Equations (3)–(5) into Equations (1) and (2) and applying Fourier Galerkin’s method [10], the equation for the blade in the frequency domain is

$${\widehat{D}}_b{\widehat{Q}}_b-{\widehat{F}}_{ext}+{\widehat{F}}_{nl}=0$$

(6)

and for the dual dry friction damper is

$${\widehat{D}}_d{\widehat{Q}}_d-{\widehat{F}}_{nl}=0$$

(7)

where $\widehat{Q}={\left[{\widehat{Q}}_0^T,{\widehat{Q}}_1^T,\cdots {\widehat{Q}}_{N_h}^T\right]}^T$ is an assembly of all the Fourier coefficients of the displacement vector of the system as a column vector, and $T$ represents the transpose of the matrix. In addition, a similar expression holds for ${\widehat{F}}_{ext}^{}$ and ${\widehat{F}}_{nl}^{}$. ${\widehat{D}}_b$ and ${\widehat{D}}_d$ are the dynamic stiffness matrices for the blade and the damper, respectively. They are in a diagonal matrix from where each diagonal element represents a submatrix of $n\mathrm{th}$ harmonic and takes the following form:

$${\widehat{D}}_{b,n}=K_{b,n}-{\left(h\omega \right)}^2{M}_{b,n}+ih\omega C_{b,n}$$

(8)

$${\widehat{D}}_{d,n}=K_{d,n}-{\left(h\omega \right)}^2{M}_{d,n}+ih\omega C_{d,n}$$

(9)

By giving the specific order of the $n\mathrm{th}$ harmonic, the specific expressions of Equations (6) and (7) can be obtained to gain a solution in the frequency domain of the system.

3. Contact Model

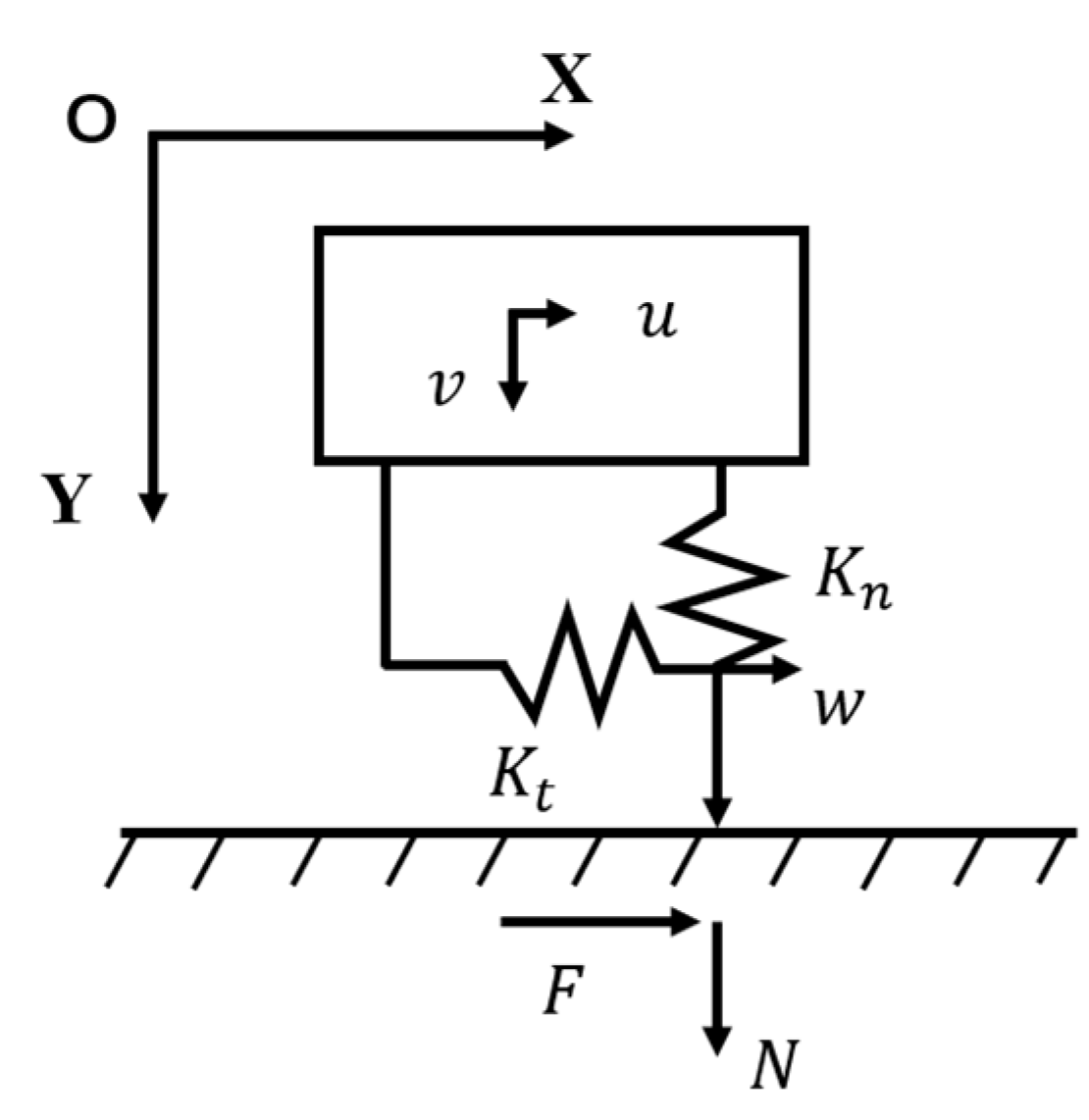
The contact model is described by the contact law between the contacting interfaces that determine the contact force. Different forms of contact models can be found in the research literature on interfaces with frictional contacts [20,22,33,34,35,36]. In this paper, a one-dimensional variable normal load model is applied, as shown in Figure 2, and its constitutive model can be found in the corresponding literature [19]. In the friction contact model, the x-direction signifies the tangential orientation of the damper contact surface, while the y-direction denotes the normal orientation of the damper contact surface, in accordance with the depiction in Figure 1.

The contact model is characterized by the following: 1. Relative tangential displacement $u(t)$ and relative normal displacement $v(t)$. 2. Normal and tangential contact stiffness $K_t$ and $K_n$. 3. Variable normal load $N(t)$. 4. Possible contact–separation–recontact of the contact surface. 5. Coulomb friction law.

The normal contact force is related to the normal contact stiffness and the normal relative displacement, which can be expressed in the form of the following form:

$$N\left(t\right)=N_0+K_{n}v\left(t\right), \mathrm{if} N_0+K_{n}v\left(t\right)>0,contact$$

(10a)

$$N\left(t\right)=0, \mathrm{if}{N}_0+K_{n}v\left(t\right)\le 0,separation$$

(10b)

The normal force is set to zero when the contact surfaces are completely separated.

The friction force is described by Coulomb friction law. The tangential force is linear with the tangential relative displacement when the contact is in stick condition. The tangential force is the friction coefficient multiplied by the normal force while the contact is in slip condition. Crucially, in the event of separation occurring between the contacting surfaces, the tangential force is immediately reduced to zero, precisely reflecting the cessation of frictional interactions.

$$F\left(t\right)=F_0+K_t\left(u\left(t\right)-u_0\right), \mathrm{if}\left|F\left(t\right)\right|<\mu N\left(t\right),stick$$

(11a)

$$F\left(t\right)=\mu N\left(t\right), \mathrm{if} \left|F\left(t\right)\right|=\mu N\left(t\right),slip$$

(11b)

$$F\left(t\right)=0, \mathrm{if} N\left(t\right)=0,separation$$

(11c)

Transitions between sliding, sticking, and separating states occur when specific conditions are met. A detailed description can be obtained from the reference [14], while a succinct representation is offered here, as presented in

Table 1. Contact state transition criteria.

Initial State	Final State	Criteria
Stick	Slip	$\left|F(t)\right|=\mu N(t),and \left|\dot{F}(t)\right|>\mu \dot{N}(t)$
	Separation	$N(t)=0,and \dot{N}(t)<0$
Slip	Stick	$\dot{w}(t)=0$
	Separation	$N(t)=0,and \dot{N}(t)<0$
Separation	Slip	$N(t)=0, N(t)>0, and \left|\dot{F}(t)\right|>\mu \dot{N}(t)$
	Stick	$N(t)=0, N(t)>0, and \left|\dot{F}(t)\right|<\mu \dot{N}(t)$

.

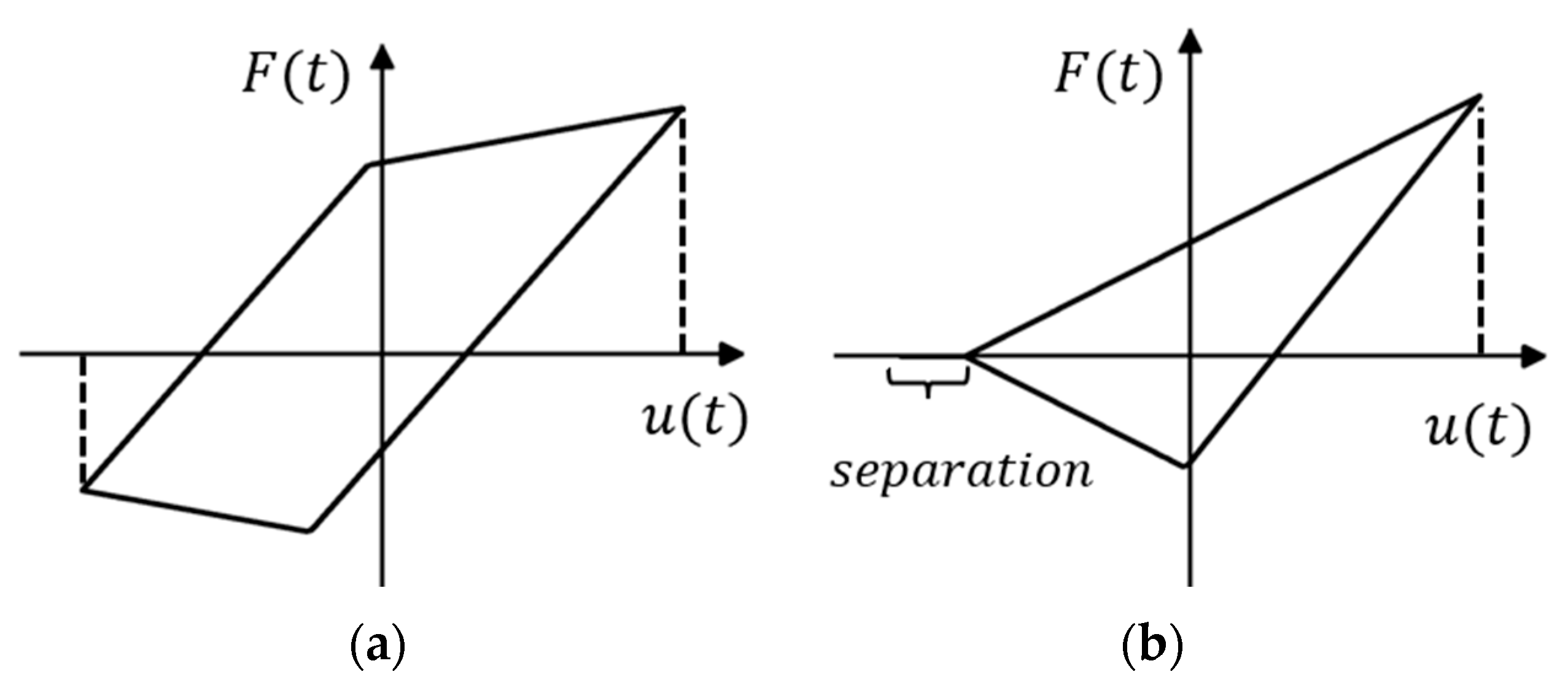
The hysteresis curves due to several specific state transitions are shown here, as illustrated in Figure 3. When there is a variation in $N(t)$, the shape of the hysteresis loop curve ceases to be entirely symmetrical. Nevertheless, it still exhibits an alternating stick–slip phenomenon, as illustrated in Figure 3a. In this case, the normal relative displacement $v(t)$ reduces to zero and the contact surfaces separate, leading to $F(t)=0$. In this context, the hysteresis curve takes on a triangular form, as illustrated in Figure 3b.

4. Solution Method

The numerical code calculates the dynamic response of the system. A specific description of the solution of numerical codes is developed below.

4.1. Finite Element Model

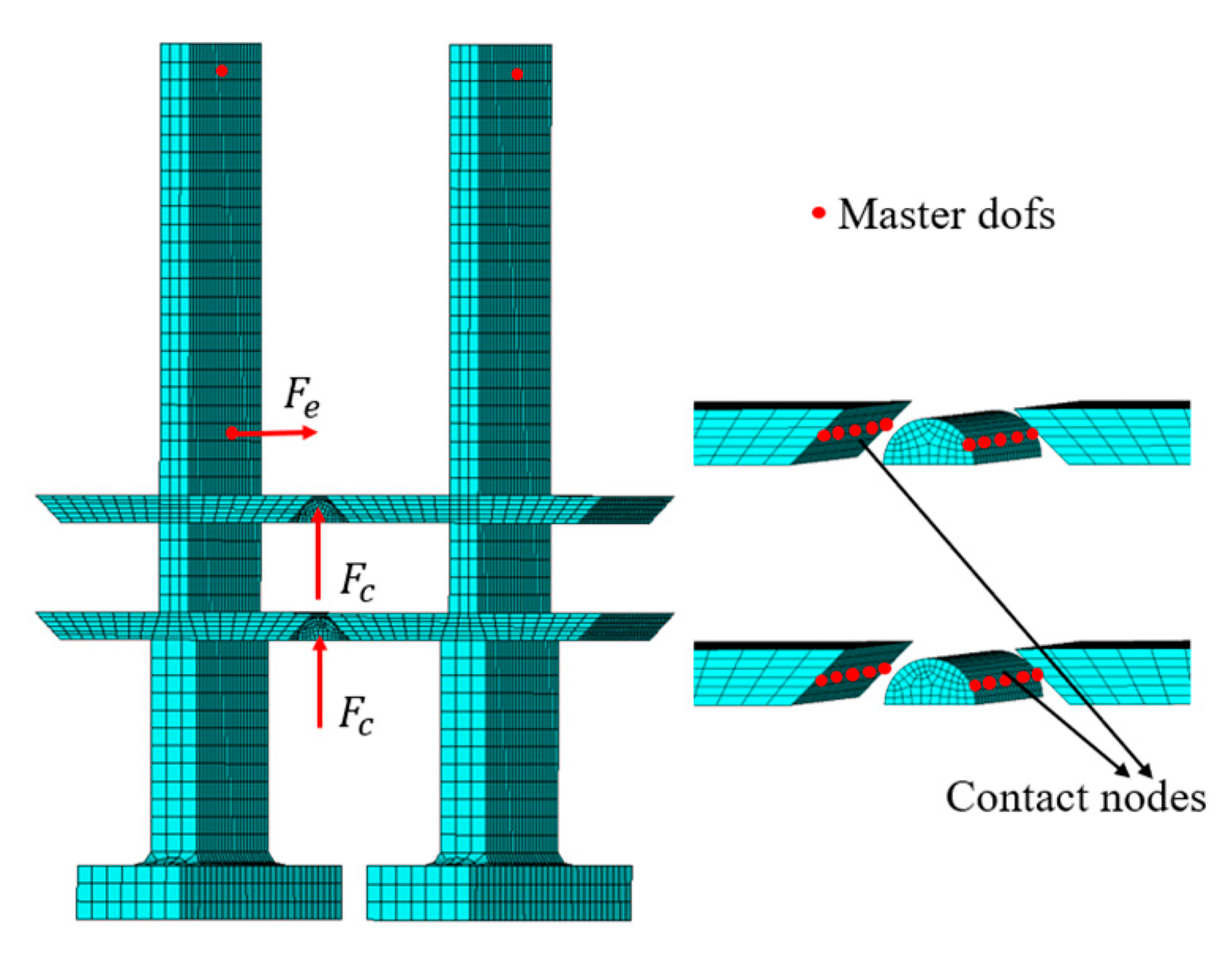
Initially, a three-dimensional solid finite element model for the blades and dampers was constructed, aiming to avoid any assumption about the damper kinematics. To control system variables, a uniform simplification of the dual dry friction damper was applied, rendering it in the form of semi-cylindrical dampers. This approach ensures a consistent and focused exploration of the damping characteristics. The blade was simplified to flat blades to facilitate subsequent experiments. The material utilized for both the damper and flat blades is steel, characterized by a density of 7800 kg/m³, a modulus of elasticity of 197 GPa, and a Poisson’s ratio of 0.3. The bottom of the blade is fully constrained, the blade body is excited by the harmonic excitation force $F_e$, and the damper is subjected to centrifugal force $F_c$.

The simplified finite element model of the blade and dual dry friction damper is shown in Figure 4. The damper is in the form of a semi-cylinder for a certain line contact. At the same time, the contact surfaces between the blades and the damper meshed with a regular and perfectly matching mesh to meet the requirement of perfectly matching contact elements implemented to couple the contacting bodies.

4.2. Model Reduction

In any case, in industrial applications, the size of the model is so large (despite the simplifications that have been made for real blades) that it is necessary to apply the reduction technique to the finite element model to obtain acceptable computational times. Therefore, the Craig–Bampton (CB) component mode synthesis method is used here to reduce the calculation matrix of blades and dampers. The physical DOFs are necessary for analysis are retained as master DOFs in the reduced model, while the other DOFs are modeled by superposition of linear normal modes with the fixed interface.

The main point of model reduction is the coordinate transformations:

$$Q_c=\Psi Q$$

(12)

where $\Psi$ is the transformation matrix, and the DOFs of $Q_c$ are much smaller than that of $Q$. For the CB method, the columns of the matrix $\Psi$ represent the constrained mode, which includes both static and dynamic vectors. In a physical context, the nth static vector is defined as the static mode induced by a unit amplitude of the nth master DOF. Therefore, the corresponding part of the column static vector of the matrix is as follows:

$${\Psi }_G=\left[\begin{array}{c}{\rm I}\\ -K_{SS}{}^{-1}{K}_{SM}\end{array}\right]$$

(13)

where ${\rm I}$ is the identity matrix, with dimensions matching those of the master DOFs. $K_{SS}$ and $K_{SM}$ are respective submatrices of the overall matrix K, corresponding to the slave and master DOFs:

$$K=\left[\begin{array}{cc}{K}_{MM}& K_{MS}\\ K_{SM}& K_{SS}\end{array}\right]$$

(14)

The corresponding part of the column dynamic vector of the matrix is composed of the modal vibration shapes, obtained from the solution of the eigenvalue problem after fixing all master DOFs:

$$\left(K-{\omega }^{2}M\right){\Psi }_S=0$$

(15)

where $\omega$ represents eigenvalues and ${\Psi }_S$ represents eigenvectors, in accordance with the CB method, the resulting coordinate transformation matrix $\Psi$ is as follows:

$$\Psi =\left[\begin{array}{cc}{\rm I}& 0\\ -K_{SS}{}^{-1}{K}_{SM}& {\Psi }_S\end{array}\right]$$

(16)

In the analysis of blades with a dual dry friction damper, the master DOFs depicted in Figure 4 are marked as red dots, as follows:

• DOFs of the blade contact point $q_{b,l}$ and $q_{b,r}$.
• DOFs of the damper contact point $q_{d,l}$ and $q_{d,r}$.
• DOF of the excitation force applied point $q_{fe}$.
• DOFs of the response picked point $q_{res}$, where the eddy current displacement is placed in the test rig to measure the response.
• Several DOFs including the first bending mode showing an IP and OOP vibration of the blade (the first 20 orders of the modes shapes ${\eta }_s$ were selected here).

The reduced mass, stiffness, and damping matrices are $M_c,K_c,C_c$. The displacement vector and excitation vector are $Q_c$ and $F_{c,ext}$, respectively. Their specific representations are as follows:

$$\begin{array}{c}{M}_c={\Psi }^{T}M\Psi ;C_c={\Psi }^{T}C\Psi ;K_c={\Psi }^{T}K\Psi ;{\widehat{F}}_{c,ext}={\Psi }^T{\widehat{F}}_{ext}\\ {\widehat{Q}}_c=\left[q_{b,l},q_{b,r},q_{d,l},q_{d,r},q_{fe},q_{res},{\eta }_s\right]\end{array}$$

(17)

4.3. Path Following Continuation Technique

The solution of Equations (6) and (7) can be carried out by substituting reduced matrix (17) into Equations (8) and (9). The solution is often written in the form of residuals, so that the equations become the following:

$${\widehat{R}}_c({\widehat{Q}}_c)={\widehat{D}}_c{\widehat{Q}}_c+{\widehat{F}}_{c,nl}-{\widehat{F}}_{c,ext}$$

(18)

where ${\widehat{R}}_c={\left[\begin{array}{cc}{\widehat{R}}_{b,c}& {\widehat{R}}_{d,c}\end{array}\right]}^T$ contains the reduced residua equations for the blades and the damper. A similar expression holds for ${\widehat{D}}_c,{\widehat{Q}}_c,{\widehat{F}}_{c,nl}$ and ${\widehat{F}}_{c,ext}$. The nonlinear factor is introduced by the nonlinear force ${\widehat{F}}_{c,nl}$, so an iterative solution scheme is necessary for solving Equation (18). The Newton–Raphson method is conventionally employed, though directly applying it to solve equations frequently encounters convergence challenges, preventing the attainment of complete FRF curves. This predicament becomes particularly pronounced when the interface undergoes a separation process, giving rise to what is commonly referred to as the “jump” phenomenon.

To overcome this limitation, a predictor–corrector procedure based on the pseudo-arc length continuation method [37] is applied. The brief process is shown in Figure 5.

The results of the first response step of the equation are calculated using the classical Newton–Raphson method, and the continuation is started. Then, given the $i\mathrm{th}$ solution ${\widehat{Q}}_i$, the $(i+1)th$ solution ${\widehat{Q}}_{i+1}^0$ is predicted by means of a tangent predictor. The corrector step is implemented searching for the solution ${\widehat{Q}}_{i+1}^n$ in a direction orthogonal to the predictor step, until the final solution ${\widehat{Q}}_{i+1}$ is found. The expanded set of equations solved in the corrector step includes the equations of equilibrium as well as the equations used to define the step direction of the corrector [38]. In addition, the vector of unknown quantities, such as the excitation frequency, is added according to the requirements of the continuation method.

4.4. Alternating Frequency/Time Scheme of Friction Force

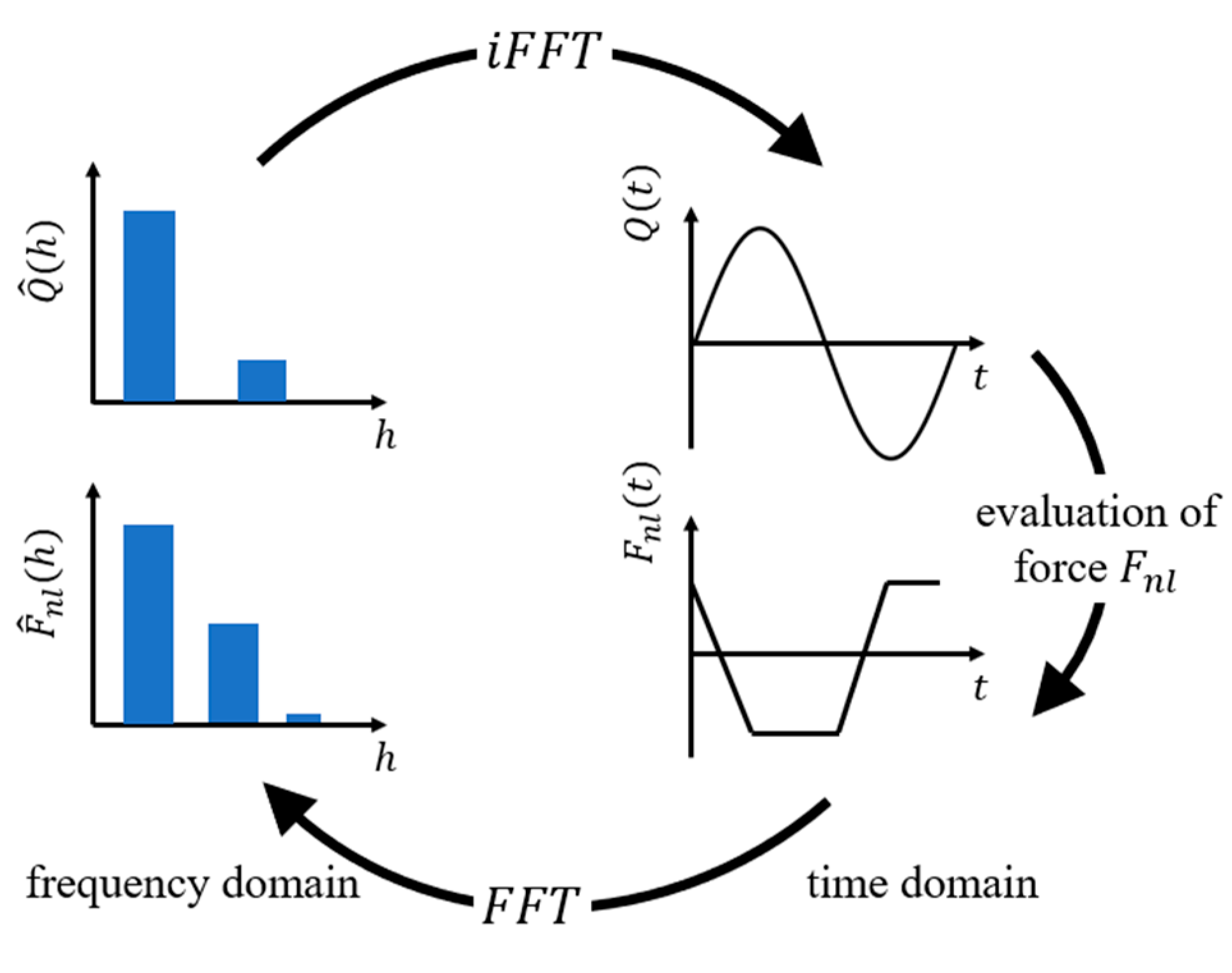
Nonlinear force is dependent on contact displacement and exhibits time-dependent characteristics, making it challenging to estimate prior. To deal with this issue, the alternating frequency/time scheme (AFT) [38] may be employed. The specific process is illustrated in Figure 6, where the inverse Fast Fourier Transform (iFFT) is employed to convert the $\widehat{Q}$ from the frequency domain into the time domain. The frictional contact model in Section 3 is utilized to resolve the frictional force $F_{nl}$ within the time domain, and eventually, the frictional force results are reverted to the frequency domain as ${\widehat{F}}_{nl}$ using the Fast Fourier Transform (FFT) for subsequent iterative calculations.

In the time domain, and $F_{nl}$ are evaluated by $N$ time steps, $t_n=\frac{2\pi n}{\omega N}$ for $n\in \left\{0,\dots ,N-1\right\}$, evenly distributed over one period $T$:

$$\begin{array}{l}Q={\left[Q_1,\dots Q_{N-1}\right]}^T\\ F_{nl}={\left[F_{nl,1},\dots F_{nl,N-1}\right]}^T\end{array}$$

(19)

Time domain displacement can be converted to frequency domain through FFT:

$$\widehat{Q}=\Gamma Q$$

(20)

where $\Gamma$ is the FFT matrix, and $\omega t_n=2\pi n/N$:

$$\Gamma =\frac{2}{N}\left[\begin{array}{ccc}\begin{array}{c}1/2\\ \cos (\frac{2\pi (0)}{N})\\ ⋮\\ \sin (\frac{2\pi h(0)}{N})\end{array}& \begin{array}{l}\cdots \\ \cdots \\ \\ \cdots \end{array}& \begin{array}{c}1/2\\ \cos (\frac{2\pi (N-1)}{N})\\ ⋮\\ \sin (\frac{2\pi h(N-1)}{N})\end{array}\end{array}\right]\otimes {\rm I}$$

(21)

On the contrary, frequency domain displacement can be transformed into time domain through iFFT:

$$Q={\Gamma }^{-1}\widehat{Q}$$

(22)

where ${\Gamma }^{-1}$ is the iFFT matrix:

$${\Gamma }^{-1}=\left[\begin{array}{cccc}\begin{array}{c}1\\ ⋮\\ 1\end{array}& \begin{array}{c}\cos (\frac{2\pi (0)}{N})\\ ⋮\\ \cos (\frac{2\pi (N-1)}{N})\end{array}& \begin{array}{l}\cdots \\ \\ \cdots \end{array}& \begin{array}{c}\sin (\frac{2\pi h(0)}{N})\\ ⋮\\ \sin (\frac{2\pi h(N-1)}{N})\end{array}\end{array}\right]\otimes {\rm I}$$

(23)

Within the above steps of the numerical scheme, the following solution procedure is obtained:

• The absolute displacement of the blade is unknown and requires an initial guess (for the first iteration step, using the sticking state of the system as the initial solution yields more stable convergence results) or is calculated from the results of the previous step.
• Absolute displacements of the blade and dual friction damper in the frequency domain are calculated, and the results of the displacements in global coordinates are transformed to the local coordinate of the contact surface. The nonlinear force can be updated using the AFT scheme.
• The harmonic order retained by the nonlinear friction force is selected (taking into account the solution rate and accuracy of the calculation, the third-order harmonic is selected here for the solution), and the system of equations is assembled to completion using the MHBM method.
• Residuals of the set of nonlinear equations are computed.

If the residuals computed at step 4 are lower than the prescribed tolerance, the procedure ends and the next iteration step continues the computation from step 1. Otherwise, the Jacobian matrix of the system is computed and another iteration is performed, following the Newton–Raphson iteration method.

5. Experiment Set Up

The experiment rig is shown in Figure 7. The two flat blades were held in place on the test rig through the installation base. The connection is made through the bolt holes reserved at the bottom of the flat blade, simplifying the form of the blade root joint.

The left blade is excited by an electromagnetic exciter, designating it as the directly excited blade. Conversely, the other blade is termed the indirectly excited blade. A force sensor plays a pivotal role as it establishes a connection between the excitation rod and the directly excited blade. Stepped sine frequency response testing is carried out using a constant input force level, which is measured with the force sensor, and kept constant through software control. The response level of both blades is measured through eddy current displacement sensors positioned at the tip of each respective blade.

The UP and LOW damper of the dual friction damper is loaded with centrifugal force using a similar form. The head and end of the damper axial direction are connected to the tensiometer using a wire rope (Figure 8 and Figure 9), and two wires were chosen instead of one to distribute the load along the damper axis more uniformly. The opposite terminus of the tensiometer is linked to a turnbuckle, and fine-tuning the turnbuckle’s tension allows for a linear adjustment of the centrifugal force exerted on the damper. The wire rope possesses a degree of flexibility to facilitate the vertical movement of the damper. Although there exists a slight deviation angle of less than 3° between the wire rope and the vertical axis, the resultant error stemming from this aspect is of negligible magnitude.

The response level of the blade is measured to determine the vibration characteristics of the system with a dual friction damper by applying a constant magnitude step sinusoidal sweeping excitation to the directly excited blade. For each constant level of excitation force, $F_c$, different centrifugal forces were applied to the dual dry friction damper, and the experiment was performed as follows:

• Install the UP damper separately and pull it through the wire rope.
• The response of the blade was measured by tightening the turnbuckle to increase the centrifugal force in sequence from small to large, and the frequency range included the first bending mode of the blades, i.e., the IP and OOP mode.
• Disassemble the damper from the blade, and clean the damper.
• Repeat steps 1–3. At this time, the centrifugal force is changed to be applied from large to small.
• Iterate through steps 2–4 for the individual installation of the LOW damper, and subsequently, for the concurrent installation of both the UP and LOW dampers. Procure the response data for the system in each configuration.

6. Result and Discussion

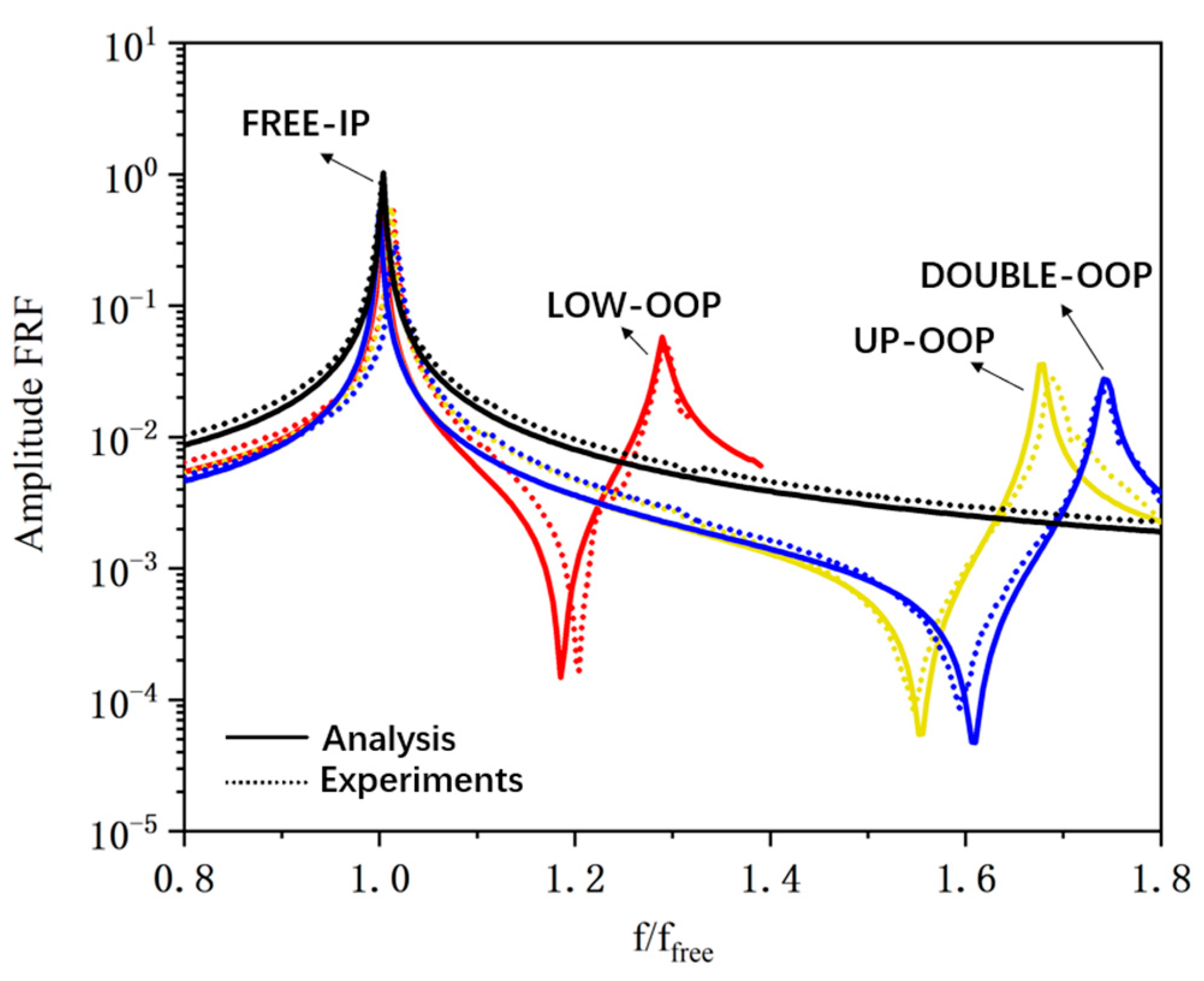
Experimental results corresponding to different centrifugal force levels of dual dry friction dampers were available. Figure 10 shows the experimental (dashed line) and numerical (solid line) FRF results of the directly excited blade for the fully stuck state of the damper with an excitation force $F_e$ of 1 N. FREE represents blade-free, UP represents the upper damper in the dual dry friction damper acting separately, LOW represents the lower damper in the dual dry friction damper acting separately, and DOUBLE represents both the UP and LOW dampers in the dual dry friction damper acting at the same time. The horizontal axis is the normalized frequency, which is the sweep frequency divided by the FREE state resonance frequency. The vertical axis is the normalized amplitude, which is the sweep amplitude divided by the FREE state resonance amplitude. It is notable that in the case of the other three conditions (LOW-IP, UP-IP, and DOUBLE-IP), the IP modes exhibit comparatively minor frequency shifts when contrasted with the FREE condition. Consequently, the curves corresponding to these conditions closely align with the FREE-IP mode and have been omitted from labeling due to their overlapping characteristics. This is due to the fact that for the semi-cylindrical damper, more rolling than sliding occurs between the damper and platform contact surfaces during the IP mode, and thus no additional friction is generated, as described in detail in [39].

On the contrary, there is a significant frequency shift in the OOP mode. The stiffening effect produced by the damper for the two modes is different; this is visible by looking at the relevant difference in frequency. Since the LOW damper acts independently, the system reaches a full stick condition as the $F_c$ of 260 N. The OOP mode experiences a significant frequency shift of 27%, with its amplitude reaching the highest value. Additionally, when the UP damper operates independently with a $F_c$ of 300 N, keeping the system in a fully stick condition, the OOP mode encounters a frequency shift of 69%, with a slightly lower amplitude compared to the UP damper. Finally, when both the UP and the LOW dampers of the dual dry friction damper come into play, the combined effect results in a maximum frequency shift of 75% and a minimum amplitude level.

One of the main difficulties in precisely predicting the response of a structure with a friction damper is that the additional stiffness provided by the damper depends on the value of the contact stiffness and the actual contact conditions at the damper surface. In addition, the contact results are related to the mesh quality and the contact algorithm when computed using conventional finite element methods. These inherent limitations often hinder the attainment of precise contact calculations. Thus, the calculations outlined in this study incorporate a tuning strategy aimed at determining the optimal number of contact elements needed to accurately describe the contact state of the contact surfaces. Figure 10 is the resulting linear tuning calculation for FRF curves.

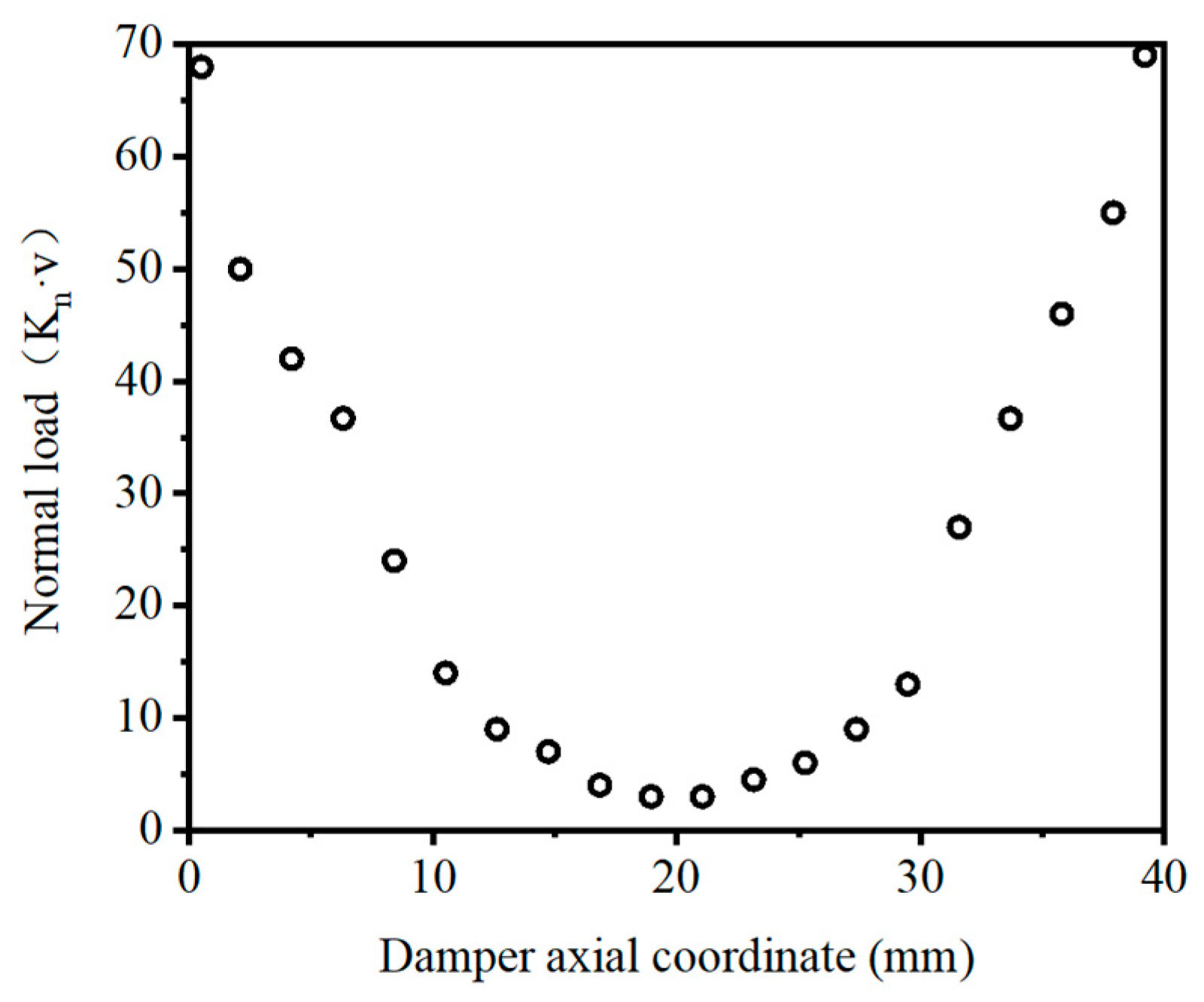
A distribution load, as illustrated in Figure 11, is employed to scrutinize the contact condition along the length of the damper. Meanwhile, the normal load is ascertained through a nonlinear static analysis. As depicted in Figure 12, the normal load on the damper surface was produced by the normal contact stiffness times the static normal relative displacement. Remarkably, it is evident that the distribution of the static normal load is far from uniform. Specifically, the loads at the front and rear ends of the damper exhibit higher values, while the normal loads within the inner region are comparatively lower. Moreover, this non-uniform distribution also leads to instances of separation occurring within the system.

Building upon the insights garnered from both experimental data and static analysis, a tuning strategy is implemented as follows: Commencing from the midpoint of the damper surface, the contact elements are progressively detached until the resonance frequency obtained in the full-stick condition matches the resonance frequency derived from experimental curves (as shown in Figure 8). The optimal alignment is achieved when a total of six contact elements are present at each end of the damper. The position of the contact elements is shown in Figure 13 (red dots represent contact elements). At this time, the contact stiffness of the contact surface is calculated utilizing the numerical contact model developed by Allara [40]. Subsequently, this calculated contact stiffness is uniformly distributed across the activated contact nodes. The static normal load on both sides of the damper is computed by solving the decoupled static balance equation of the damper in the context of frictional contact [24]. This systematic tuning approach enables the accurate representation of the contact conditions, enhancing the reliability of the analysis.

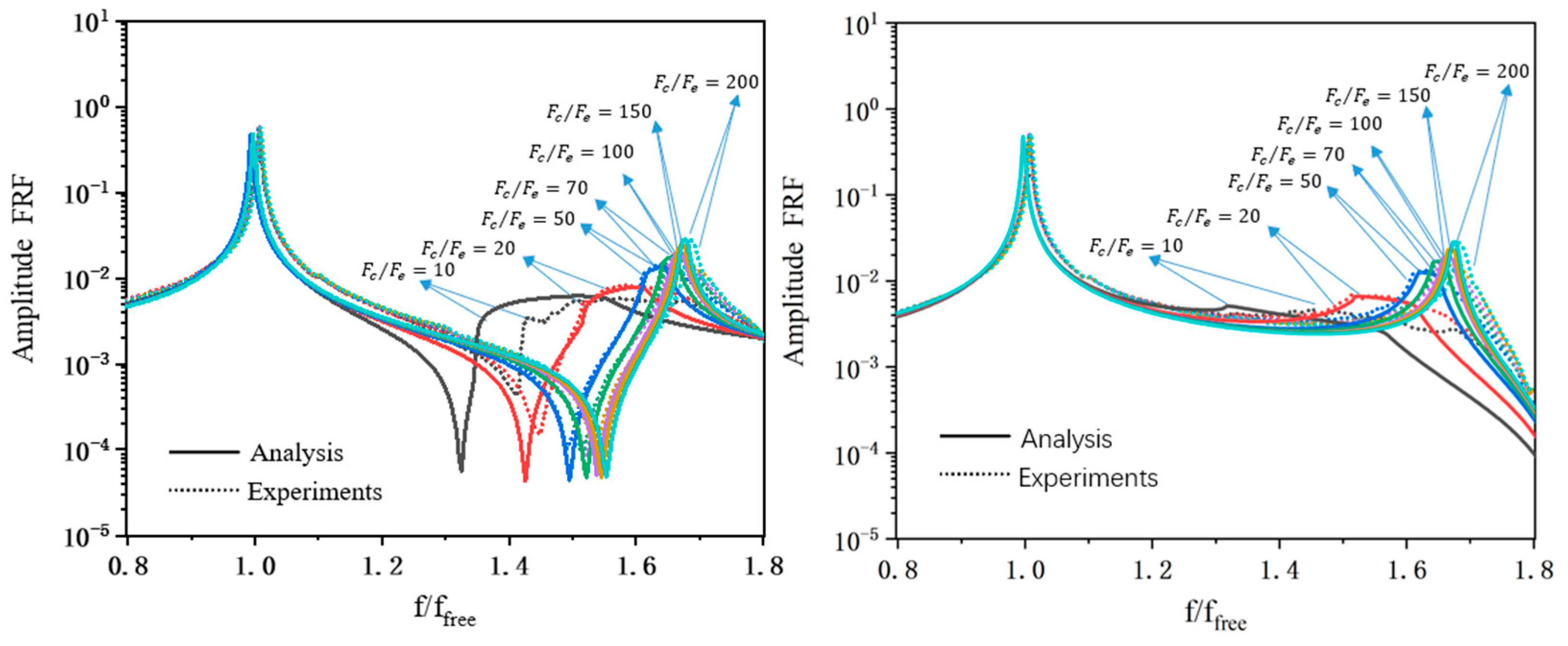
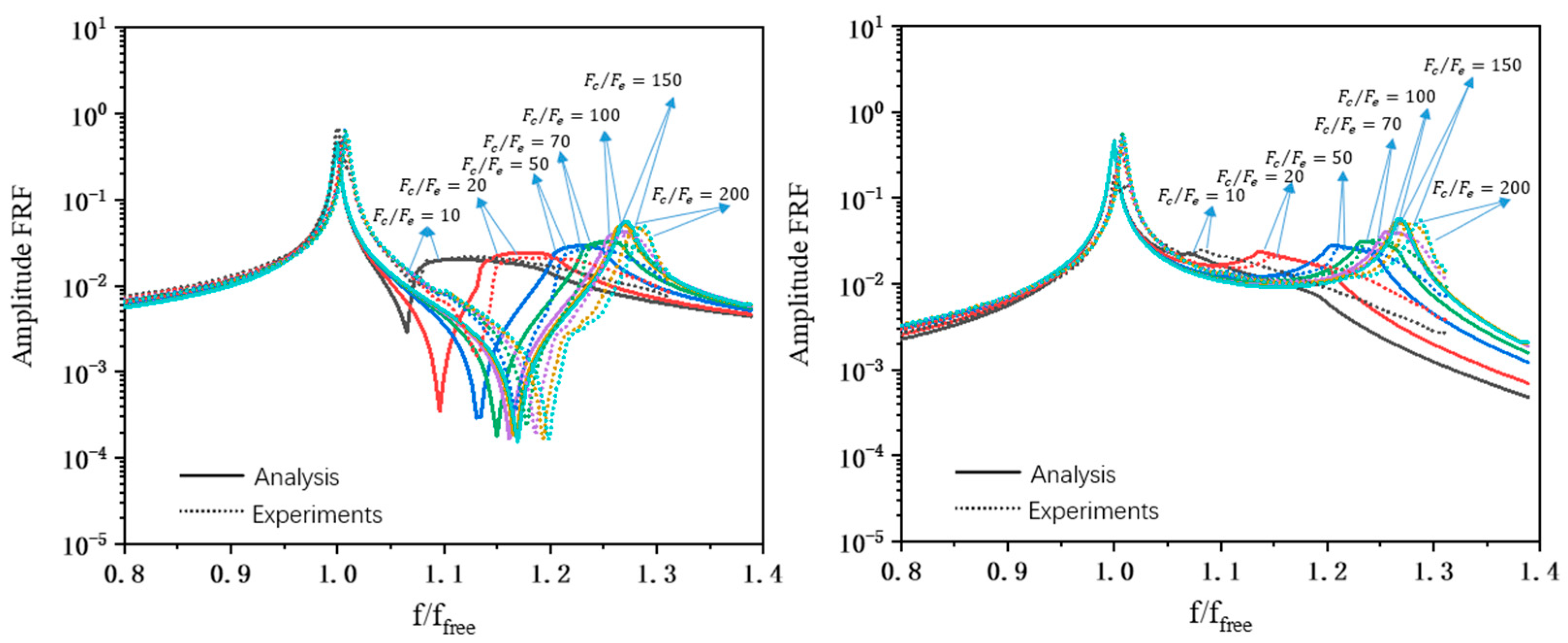
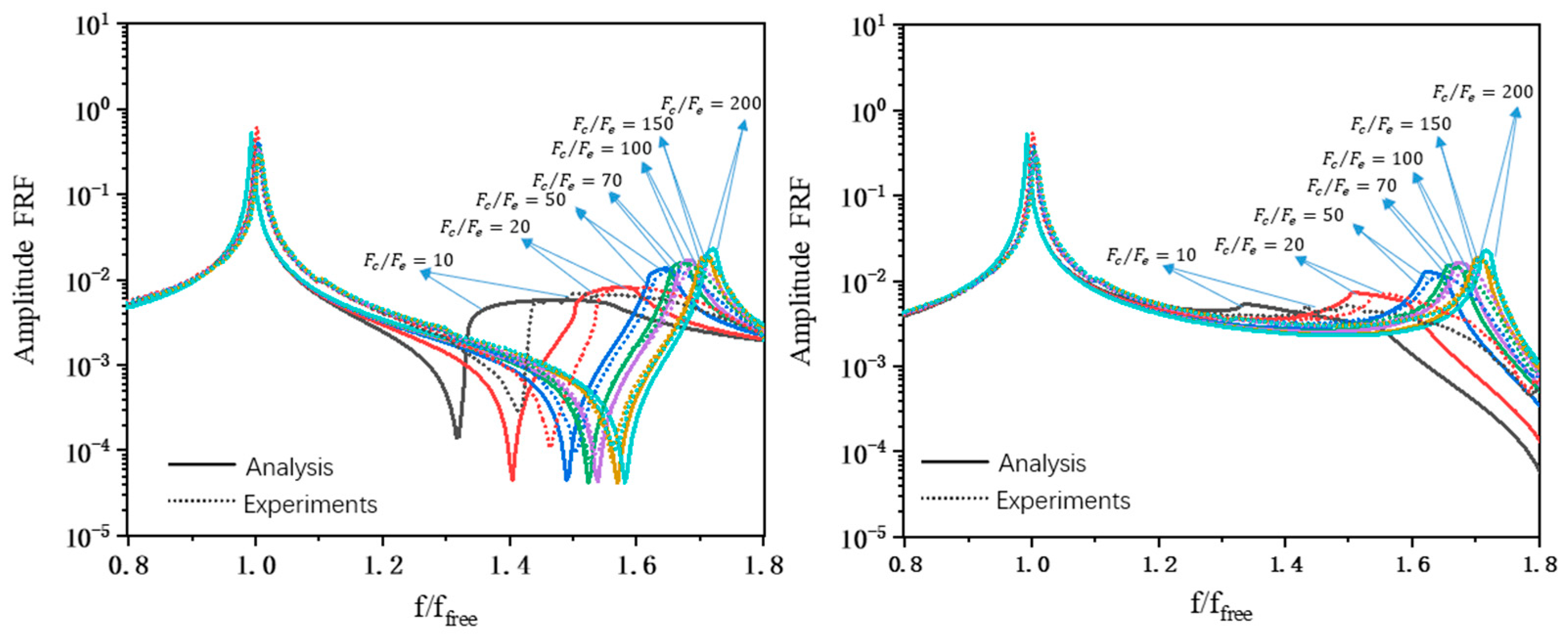
Subsequent analyses are conducted in accordance with the established tuning strategy. The excitation force $F_e$ was kept at 1N during the test. The centrifugal force on the damper is varied to measure the vibration response of the system. In Figure 14, Figure 15 and Figure 16, the experimental FRF curves for different $F_c/F_e$ ratios are compared to the corresponding numerical FRF curves for the directly and indirectly excited blades of UP, LOW, and DOUBLE dampers.

The congruence between experimental and simulation results is readily apparent; although there is a slight disparity wherein the numerical frequency shift falls below the measured value, the overall agreement remains strong. It is found that the damper will not slide in the IP mode, as should be expected, and the value of the contact parameter will not influence the response [39], as shown in the above figures. Therefore, the comparison of results focused on the OOP mode. 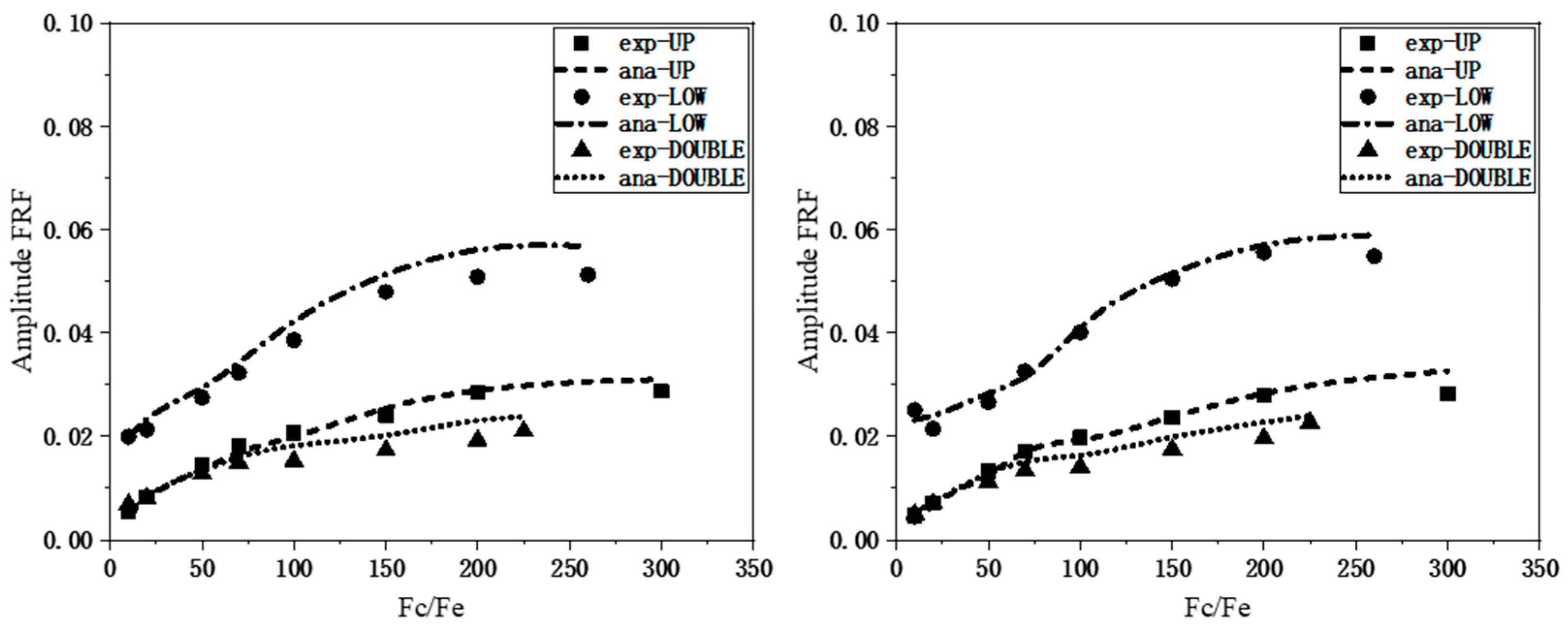The results of different response curves are plotted on the same graphs to present so-called “performance curves” of the damper in analogy with similar curves in the literature [13,14,28]. The resonance amplitudes and frequencies are plotted versus the ratio $F_c/F_e$ both for the directly and indirectly excited blades for the OOP mode, as shown in Figure 17 and Figure 18.

The performance curves of the damper provide insightful observations. It is notably evident that the damper exhibits great damping performance within the OOP mode, as illustrated in Figure 17. In this mode, both the directly and indirectly excited blades experience a remarkable reduction in amplitude, surpassing 90% compared to the FREE condition. This efficacy arises from the damper’s optimal performance during the OOP mode, characterized by substantial relative displacements between the damper and the blade. Furthermore, as depicted in the resonant frequency performance curve (Figure 18), the calculated frequencies fall on the softer side compared to the measured frequencies. This is a limitation intrinsic to the numerical simulation method employed. Specifically, the simulation applies contact elements to a finite number of contact pairs rather than comprehensively covering the entire contact surface. Lastly, Figure 17 and Figure 18 highlight an intriguing trend: the system exhibits the largest resonance amplitude when the LOW damper operates independently. Conversely, when the UP damper functions in isolation, the resonance amplitude diminishes. However, the most noteworthy advantage lies with the DOUBLE damper configuration. In this case, the system registers the lowest resonance amplitude and enjoys the broadest frequency shift range, illustrating the significant benefits of employing a dual friction damper setup.

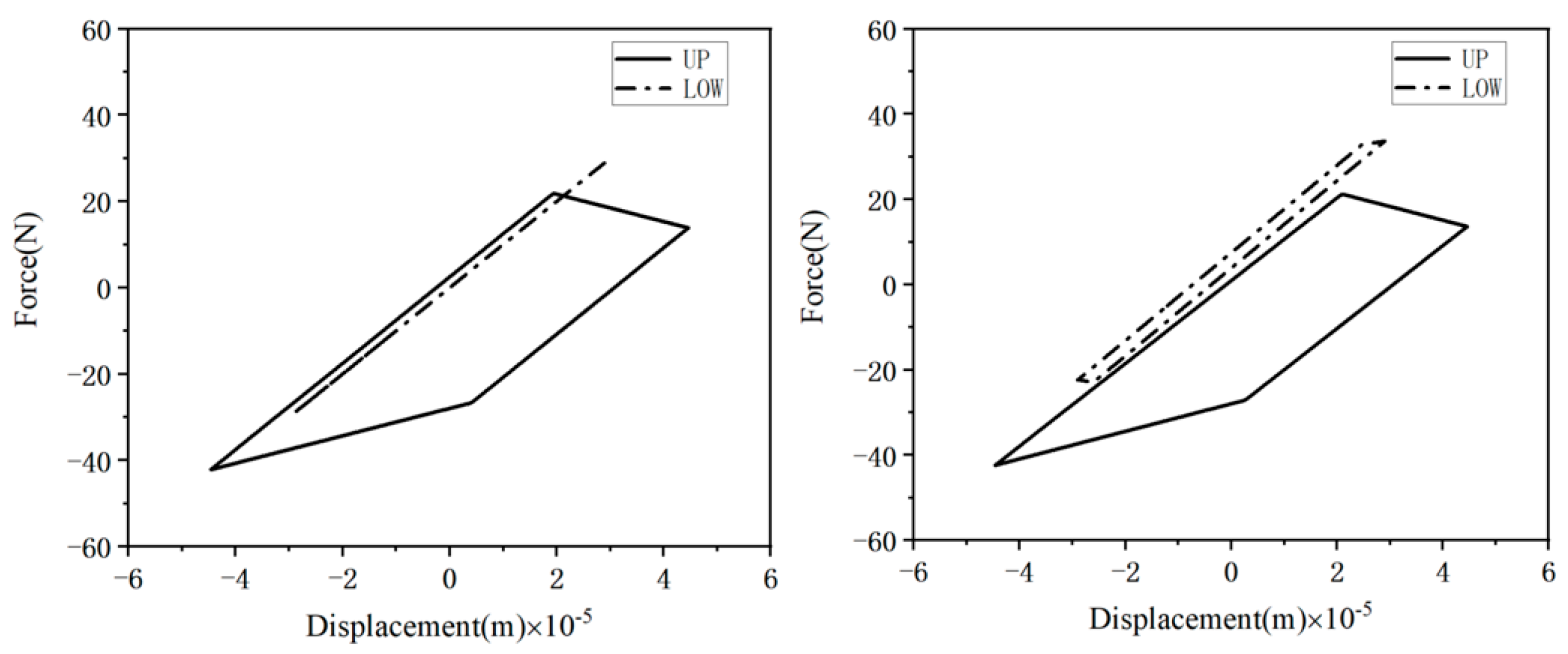
In addition, the damper performance curves when the UP damper is acting are close to those when the DOUBLE damper is acting. Therefore, when the ratio $F_c/F_e$ is 100, the frequency f = 435 Hz is chosen to analyze when the DOUBLE damper acts. The hysteresis curves of the left and right contact surfaces when the UP and LOW dampers act at this time are shown in Figure 19, where the dashed line represents the LOW damper and the solid line represents the UP damper.

In contrast to the LOW damper, the UP damper exhibits a notably larger area within its hysteresis curve when it is in operation. This observation substantiates that when the damper’s geometry and the applied centrifugal force on its surface are held constant, the UP damper contributes a larger proportion to the damping processes.

7. Conclusions

In this paper, the dynamics of the blade with a dual friction damper have been investigated experimentally and numerically.

The dual friction dampers were simplified to the same semi-cylindrical shape to obtain a line of contact between the dampers and the blades. Moreover, it was also to maintain a single variable to facilitate the investigation of the vibration characteristics when the dual dampers act separately.

A numerical code of the assembly with a dual dry friction damper was then performed to predict the response levels at multiple centrifugal force levels of the test rig.

The damper and the blade were modeled by means of three-dimensional solid finite elements in order to avoid any assumptions about either the damper kinematics or the influence of damper bulk stiffness on the damper dynamics. The frequency response function curves of the system with a dual friction damper were solved based on the Newton–Raphson method and continuation technique. A comparison with the experimental data was performed, and the numerical simulation shows good agreement with the experimental results.

The friction damping effects generated by the dual dry friction damper on resonance amplitude and frequency are investigated for directly and indirectly excited blades. For the first-order bending OOP mode, the dual dry friction dampers exhibit excellent damping performance compared to the single damper. The system has an average 21% reduction in response amplitude levels and an increase of 3% in the frequency shifting range. Meanwhile, with the same centrifugal force, the UP damper in the dual friction damper has a larger hysteresis curve area and better damping performance. Thus, it plays a more significant role in influencing the damping characteristics of the dual friction damper.

In future investigations, the utilization of real blades should be prioritized to garner more meaningful results for engineering applications, building upon the insights gained from this experiment. Furthermore, exploring the realms of damper wear and temperature variations presents a promising avenue. Subsequent studies can delve deeper into understanding the implications of wear and temperature changes on the vibration characteristics of the entire system, particularly those arising from the frictional contact of the dual friction damper.