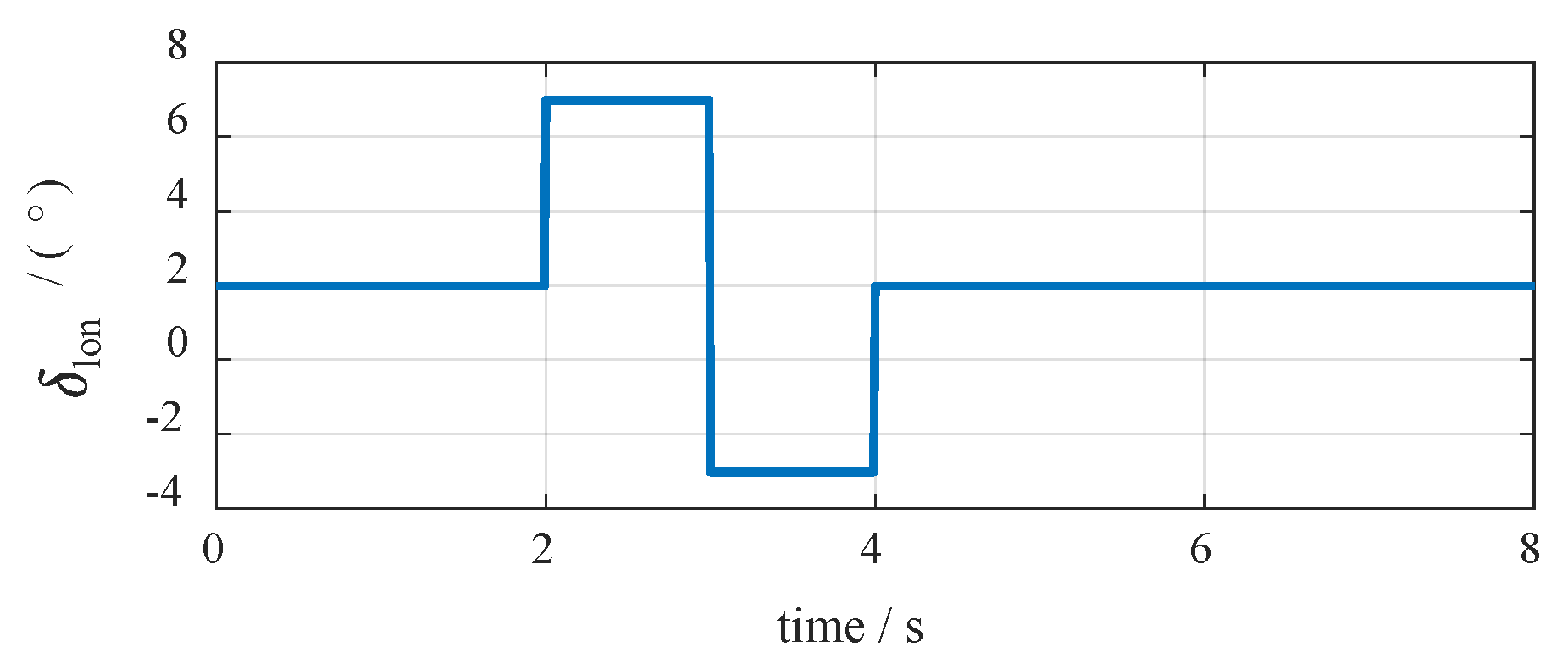1. Introduction
In the controller design of rotorcrafts, especially in that of the configurations that have varying flight dynamic characteristics and multiple controls on the same axis like tiltrotor aircrafts, time-varying features, nonlinearities, and model uncertainties are of major concern for the development personnel. With the process of development and exploration, neural networks (NNs) have shown their merits in approximating nonlinear functions with arbitrarily small errors under the condition of a sufficient number of neurons. This advantage has been adopted by authors in the development of nonlinear controllers along with the techniques of feedback linearization control since the end of the last century. The approach was then developed for systems of multi-input multi-output (MIMO) with unmodeled dynamics. A network of a single hidden layer was adopted to cancel modeling errors. For approaches buttressed by similar principles, the offline-trained NN plays a central role as an inverse model for the cancellation of the dynamics of the original model, thus linearizing and decoupling the system. A network-based model reference adaptive control scheme has been utilized in control problems of the rotorcrafts under situations of saturations [
1]. Regarding the Mars rotorcraft blade design, a neural network was also adopted with the optimization of a genetic algorithm [
2]. For helicopters in vertical flight, robust NN improved flight control was provided, with a flight dynamic of the nonlinear nonaffine model, to ensure tracking accuracy [
3]. NNs are also capable of combining several modern control techniques of adaptive schemes, such as adaptive sliding mode control, model reference adaptive control (MRAC), and model prediction control (MPC), mainly applied to compensate the specific modeling, unmodeled dynamics, and nonlinearity. In [
4], an adaptive sliding mode controller was presented for attitude control and position control of the quadrotors. The NN was used for the adaptive tuning of the slide manifold parameters. A hybrid controller of MRAC and MPC for tiltrotors was provided in [
5] with a compensational NN to cancel the error between a linear reference model and the nonlinear plant.
Besides the application of controller synthesis, NNs have also been utilized extensively as a surrogate model in structural and aerodynamic design and optimization. Yu and Hesthaven [
6] presented a novel approach to reconstructing the flow field using an artificial NN. To improve the training effectiveness of an NN surrogate model of high-fidelity and high-dimension, an adaptive sampling method based on the Gaussian process was proposed and applied in the aerodynamic design of the prediction of the airfoil lift-to-drag ratio [
7]. For structural designs, a deep convolutional NN-based surrogate model was proposed to perform topological optimization for two dimensional and three dimensional structures [
8]. Other works considering the optimization of the design of rotorcrafts and propeller-driven aircrafts include handling-quality-enhancement-oriented PID optimizations [
9] and rotorcraft configuration optimization [
10]. Studies on the analysis of aerodynamics and the performance of the helicopters and rotorcrafts also involved the high-fidelity flight dynamics model of the vehicle [
11,
12,
13].
For the application of a specific NN, either as an inverse model for flight controller implementation or as a surrogate model for complicated system optimization, as long as an offline-trained network is involved, the requirement of a proper training set is of undoubted necessity. In this case, the demand for the optimization of the training set will emerge on a natural basis. Generally, the behavior of the process of the network training effectiveness (considering training time, computational memory required, and training error) under different data sets will be nonconvex and of great complexity, which makes the problem usually very hard to be solved by a parametric deterministic algorithm. With the recent boost of metaheuristic algorithms, swarm intelligence algorithms have been adopted for problems of this category. Mimicking the behavior of a large population or the evolution of some natural phenomena, recent metaheuristic algorithms can be classified into several categories: (1) the imitation of the group behavior of animal foraging or the evolutionary process of a plant, such as the Sparrow Search Algorithm (SSA) [
14], the Mayfly Optimization Algorithm (MA) [
15], Bald Eagle Search (BES) [
16], and Hybrid Rice Optimization (HRO) [
17]; (2) the inspiration by human cognition, decision, and biogenetics processes, for instance, the Brain Storm Optimization (BSO) [
18], the Collective Decision Optimization Algorithm (CDOA) [
19], and the Volleyball Premier League Algorithm (VPLA) [
20]; (3) the simulation of natural phenomena, such as the Equilibrium Optimizer (EO) [
21] and the Thermal Exchange Optimization (TEO) [
22]. These algorithms involve swarm intelligence and all have incorporated some stochastic operators, thus making them capable of not being trapped by the local minima in nonconvex optimization tasks.
As was summarized above, a wide class of NNs is used either to approximate the system dynamic or as a surrogate model of a complicated model. These cases can be addressed as an issue of the universal approximation of a multivariable function. With the increasing number of function input variables, the scale of the specific NN will grow considerably. For tiltrotor aircraft, there are much more states and controls than a traditional fixed-wing aircraft or a helicopter. If an NN is adopted to represent to tiltrotor aircraft flight dynamics model, a huge amount of data will be needed to obtain a desirable NN with adequate precision. To solve this issue practically and thus make the usage of NNs more feasible in engineering practices, a novel approach is presented in this work. The basic idea is to exploit the limited number of training sets to a better degree by finding a certain optimized sample pattern of the training set. This paper, driven by the above purpose, is organized as follows. The nonlinear flight dynamics model of the tiltrotor aircraft is presented first. The radial basis function neural network (RBFNN) approximation of the plant is addressed. The problem is then parameterized as finding a training set distribution pattern by which an RBFNN with minimized mean square error can be trained. An improved differential evolutionary particle swarm optimizer based on the fourth-order Runge–Kutta algorithm is adopted to solve for the optimum pattern. The presented optimization scheme is applied to an example case of the approximation of a relatively complicated nonlinear function to show the principle and effectiveness of the methodology. The provided scheme is then generalized to the application of the tiltrotor aircraft model approximation. Early and late stages of its conversion mode, represented by the tiltrotor nacelle angle of 30 deg and 70 deg, respectively, are considered in this work. The longitudinal model of the aircraft, i.e., the field of the derivative of pitching angular velocity with respect to the helicopter rotor control and fixed-wing control surface deflection, is studied as the objective of the RBFNN. Results of both the example case and the application to tiltrotors show the applicational readiness, effectiveness, and high performance of the approximation accuracy of the presented method.
2. Approximation of Flight Dynamics Model
2.1. Flight Dynamics Model of a Small-Scaled Tiltrotor Aircraft
The flight dynamics model of the aircraft is of great importance in its flying quality analysis, control design, and flight simulation, especially in the domain of rotorcraft design. In this work, model fidelity is improved by adopting a set of 6 degree-of-freedom (DoF) nonlinear motion equations, a blade element theory (BET)-based rotor aerodynamics model with non-uniform rotor inflow, and quasi-steady blade flapping. The airframe aerodynamics is implemented by table-lookup of the wind tunnel data.
2.1.1. Rotor Aerodynamic Forces and Moments
The Euler angle representation of the 6 DoF nonlinear model of the tiltrotor aircraft is adopted as the object of research of this paper. The two main rotors verified both experimentally and computationally in [
23] are modeled by BET with a truncated quasi-steady version of the Pitt–Peters dynamic inflow model. The rotor aerodynamic forces and moments can be represented as follows:
in which
T,
H,
S,
L,
M, and
Q denote the rotor thrust, in-plane forces pair, aerodynamic rolling and pitching moments, and aerodynamic torque, respectively. The
Nb,
K,
r0, and
r1 are the number of blades, azimuth stations, blade root cutout, and tip loss, respectively. Angles
and
are blade flapping and azimuth angles. Components d
Fp and d
Ft are the blade element perpendicular and tangential force elements, which can be represented by the element lift and drag as
in which
Up and
Ut denote the velocity in-plane and normal components seen by the rotor. These components can be evaluated by the advance ratio and inflow ratio. The rotor inflow ratio (i.e., dimensionless induced velocity) is governed by the quasi-steady version of the Pitt–Peters’ dynamic in-flow model. The inflow ratio at each station of the rotor disk is expanded as the base and first harmonic term as follows:
and the governing equation is
The
Lnl is related to the rotor wake angle
, the hub total velocity
VT, the advancing ratio
, and the resultant inflow
as follows:
The rotor blade flapping motion is governed by the following equation:
in the above equation,
denotes the derivative with respect to the azimuth angle, variables with a bar denote the normalization by the blade tip speed
. The
and
are dimensionless quantities of the hub rolling and pitching angular velocity components in the hub-wind axis. The rotor flapping motion caused by its gyroscopic acceleration is also taken into consideration by the first term on the right side of the above equation. This equation is then transformed into Multi-Blade Coordinates (MBC) by defining the variables in the MBC (i.e., the collective flap
, the longitudinal flap
, and the lateral flap
) according to the following relations:
in which flapping angles in each coordinate are
and
. The transformation matrix
is obtained by the definition of the collective and first harmonic flapping angles. By concatenating the flapping motion equations of each blade, the rotor flapping equation in MBC takes the following form:
Again, due to flapping angular velocity and accelerations being less significant in nature for flight dynamics analysis and to reduce the number of system states, the derivative terms are truncated from the equation, and only quasi-steady flapping motion is considered. This leaves the above equation as
in which
is affected mainly by the rotor rotational centripetal acceleration and center-spring stiffness, while
is the result of the aerodynamics and hub motion.
Rotor aerodynamic forces and moments are then converted to the airframe body axis by the rotor nacelle tilting angle . The total rotor aerodynamic forces and moments on the airframe center of gravity are the sums of those produced by the left and right rotors.
2.1.2. Airframe Forces and Moments
The airframe forces and moments are computed in the wind axis by the corresponding dimensionless coefficients:
in which the longitudinal forces and moments coefficients (
CD,
CL,
Cm) and the lateral forces and moments coefficients (
CY,
Cl,
Cn) are functions of the fuselage states and controls, which can be written as
The fuselage states and controls are
Forces and moments acting on the airframe center of gravity are obtained by converting the above relations to the body axis.
2.1.3. Nonlinear Equations of Motion
The total forces and moments are obtained by adding those produced by the rotors and the fuselage. When incorporated in the 6-DoF Euler angle-based representations, the equations governing the aircraft motion are
where
are the airframe body axis velocities,
are the body axis angular velocities, and
are the Euler angles.
denotes the components of the airframe inertia tensor.
2.2. Aircraft Model Approximation Using a Neural Network
Mathematical representations of nonlinear dynamic systems, in general, are intrinsically a set of nonlinear ordinary differential equations. By the analysis of the above sections, the nonlinear system of the tiltrotor aircraft can be represented in the following form:
in which the state vector containing nine fuselage stats is
, the control vector is
, including rotor controls (i.e., collective pitch, differential collective pitch, lateral cyclic pitch, longitudinal cyclic pitch, and differential longitudinal cyclic pitch), fixed-wing control surface deflections (i.e., aileron, elevator, and rudder deflection), and the nacelle tilting angle, the output vector y is often a selection of state variables of particular interest, and the matrix
C is of proper size and time-invariant.
Surrogate models are widely used throughout the aircraft design procedure, from parametric design and optimization and aerodynamic interference modelling to flight control law design. Specifically, extensively adopted methodologies in rotorcraft control law synthesis including dynamic inversion control often utilize the help of an inverse model of the plant to cancel out the modeled dynamic nonlinearities. The use of the inverse model is of a certain form of a surrogate model. Under this circumstance, neural networks come into play with their universal approximation property.
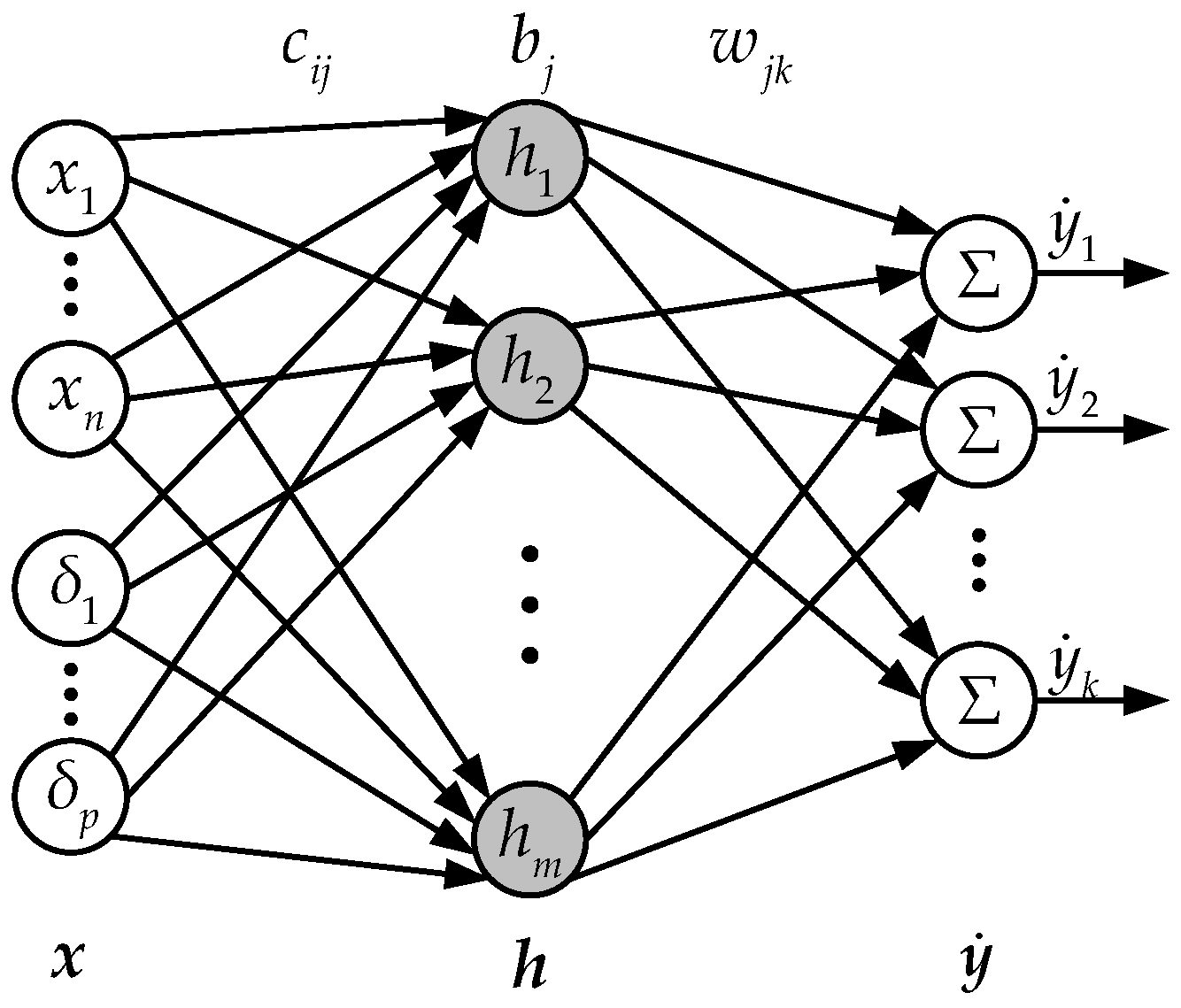
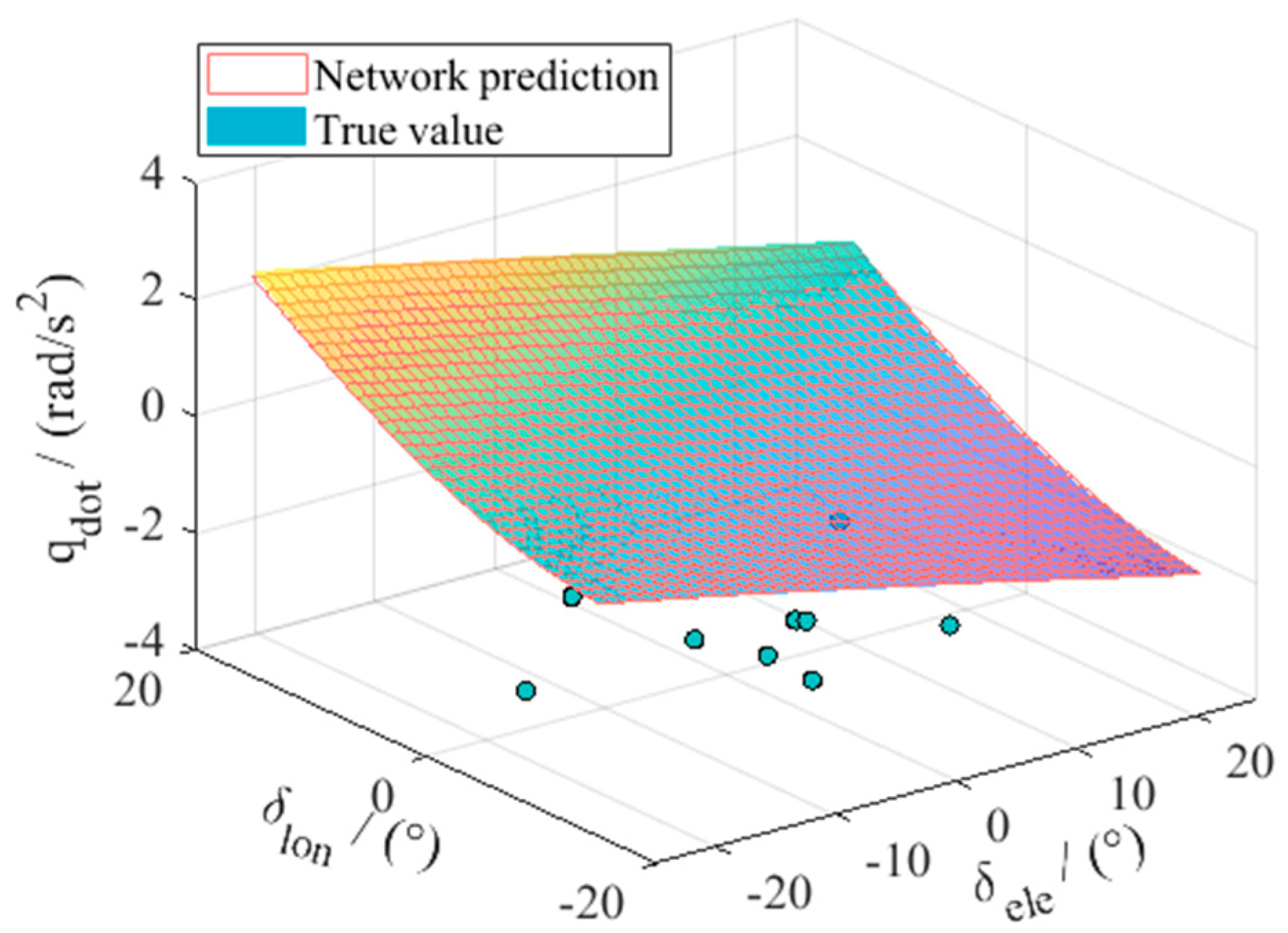
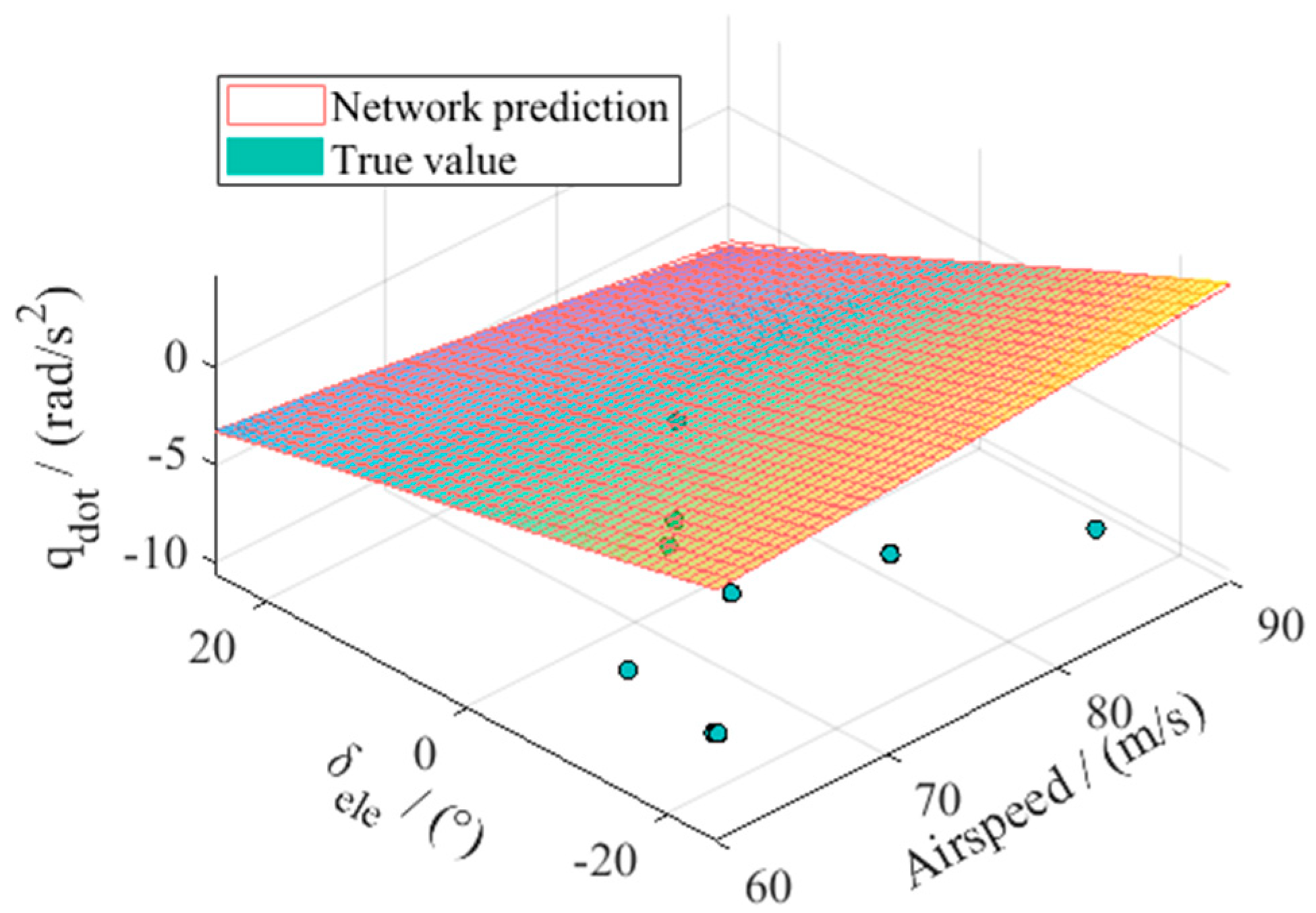
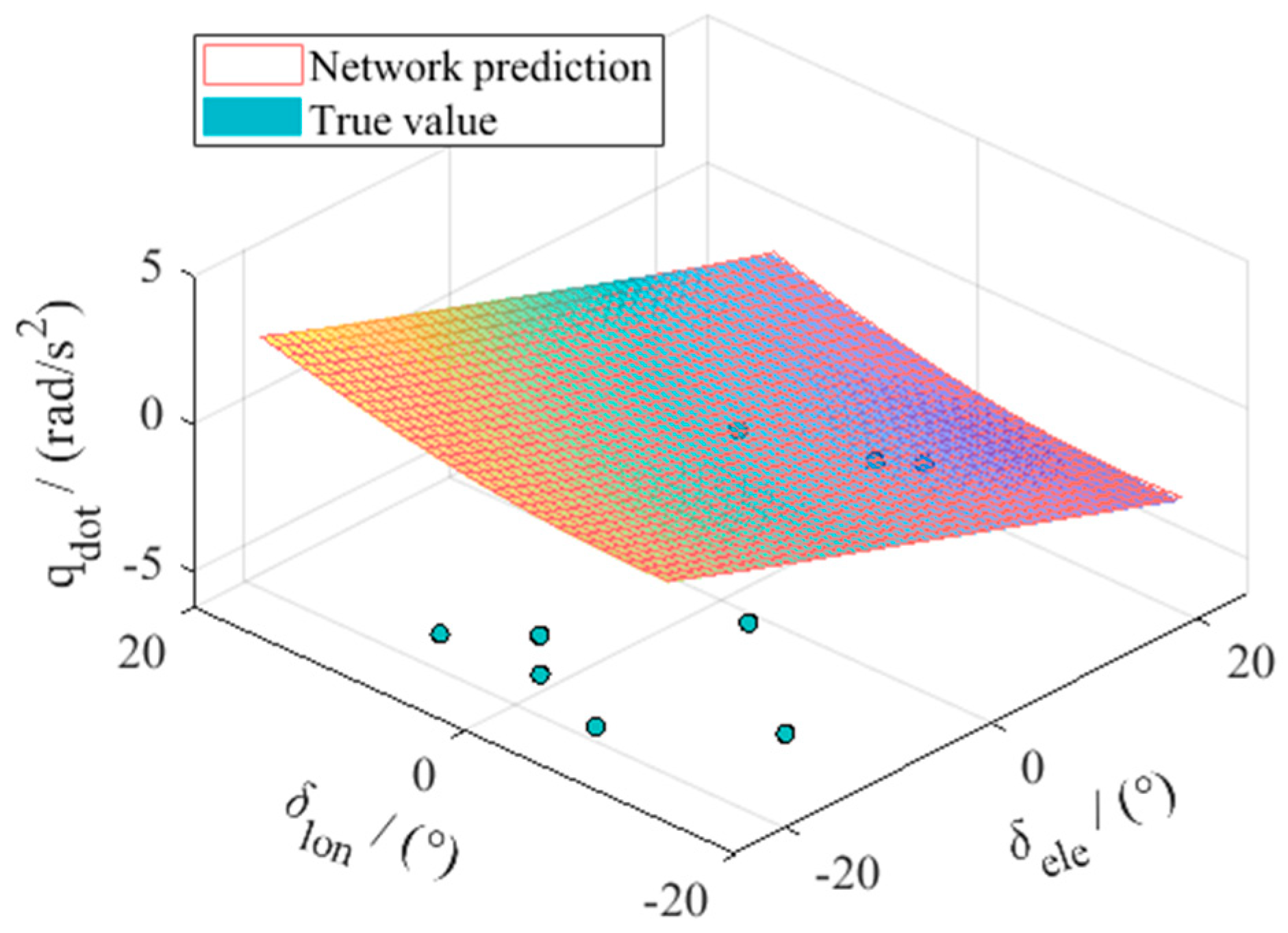
In this work, the nonlinear mapping to be approximated by the network is the mapping from the state and control vector pair to the state time derivatives, i.e., the mapping F of Equation (14). A radial basis function neural network (RBFNN) is adopted to accomplish the work in this paper. The network structure is shown in
Figure 1.
The network can be represented as
in which the network input is the state-control vector pair
, and the network output is the selected state variables of particular interest, which in the application of inner-loop RCAH controller design is the angular rate derivatives
. The
hj is the output of the
j’s Gaussian basis function,
and
are the respective center coordinates and the width of the
j’s basis function, and
is the time-invariant network weight matrix. The network should be trained offline by the data covering the desired flight envelope derived from the flight dynamics model of the tiltrotor aircraft obtained from previous sections. It is worth noting that the training data should cover all of the valid ranges of each control deflection.
In this work, to study the model approximation of a tiltrotor aircraft during conversion mode, the dynamic tilting of the rotor nacelles is of great importance. In this case, two typical nacelle angles will be selected. Considering the dynamic tilting, although these two cases are fixed nacelle angles, the model to be approximated is by no means static. The training data of the network are obtained from the dynamics models rather than trimmed static models. This can be explained by the non-zero state derivatives, i.e., the output of the network contains all possible values of the pitching rate. In the meantime, under practical applications, the input of the actual network will not contain only discrete points of nacelle angles but rather a continuous range from 0 deg to 90 deg. The choice of these two angles is for the convenience of illustrating the basic idea of the article.
3. Optimization of the Neural Network Sample Distribution Pattern
With a uniformly distributed sample pattern, the total number of training set data points would be as many as 95 for each network output under the condition that only five points are selected for each flight state and control. This would be challenging for both the computer memory size and the total training time. As a result, in order to save computational resources and reduce the total CPU time, it is desirable to exploit the limited number of sample points.
On closer inspection of the resultant mapping of
Section 2.2, one can find the characteristics of the ‘response surface’, which is the curvature of the surface that is often not identical throughout the domain. This resulted in the fact that each aerodynamic component of the aircraft is modelled with a different mathematical complexity. For example, helicopter rotor forces and moments intrinsically nonlinearly depend on its rotor controls, while forces and moments produced by the fixed-wing control deflections are linearly modelled by factors of control effectiveness. This, under a point of view of regarding the aircraft model as its state-derivative field (i.e.,
in Equation (14)) in a vector space of its state-control pair, will lead to the fact that the gradient field of F is non-uniform. Under this circumstance, in order to obtain an optimum result of network training, sample points should be distributed densely in the region where
varies drastically. In the region where the gradient is nearly uniform, fewer sample points should be adequate to obtain a desirable network Mean Square Error (MSE).
3.1. Problem Formularization and Methodology
Through the above statement, the subject can be considered to find the optimum distribution pattern of the sample points, that is to say, the best combination of network input variables through which one can obtain a trained network with a minimized MSE, and this can be formulated by a non-convection optimization problem as follows:
in which the optimization objective is the MSE of the trained network provided by the training algorithm
, D is the set of training samples of size N,
x(n) and
u(n) are the sampled network inputs, and
is the corresponding output.
The particle swarm optimization (PSO) algorithm proposed by Eberhart and Kennedy [
24], as one of the most well-regarded swarm intelligence algorithms, was inspired by the foraging of bird flocks. With the following rules, i.e., (1) each bird flies toward the individual closest to itself and avoids collision; (2) the flock flies toward a food source; and (3) every bird tends to the center of the flock, the PSO algorithm searches the global optimum of every iteration. Like other metaheuristic algorithms, this scheme avoids being trapped by the local optima through a stochastic operator on each individual’s velocity vector, specifically by randomly altering the ratio of its social learning and self-recognition factors (
CSR and
CSL, respectively):
In this work, instead of the standard PSO algorithm, an improved differential evolutionary particle swarm optimizer based on the fourth-order Runge–Kutta algorithm (DPSORK) is adopted to accomplish the above sample pattern optimization task. The scheme is derived from the general differential PSO model:
In the above model,
and
are the velocity and position of the ith individual at the current time (iteration),
CIW,
CSR, and
CSL are the respective inertia weight, self-recognition, and social learning factors, rand is the uniformly distributed random number between [0,1], and
Pib and
Pgb are the optima encountered by the individual itself and by the flock in history (global optimum). Viewed as ordinary differential equations, the above model can be solved by several different numerical methods, which results in variants of schemes. A fourth-order Runge–Kutta method is adopted for its relatively high order of truncation error. Thus, the scheme with a step size of h can be represented as
In the above scheme, for a better and rapid convergence, parameters
CIW,
CSR, and
CSL of the optimizer are incorporated with the following time-varying form:
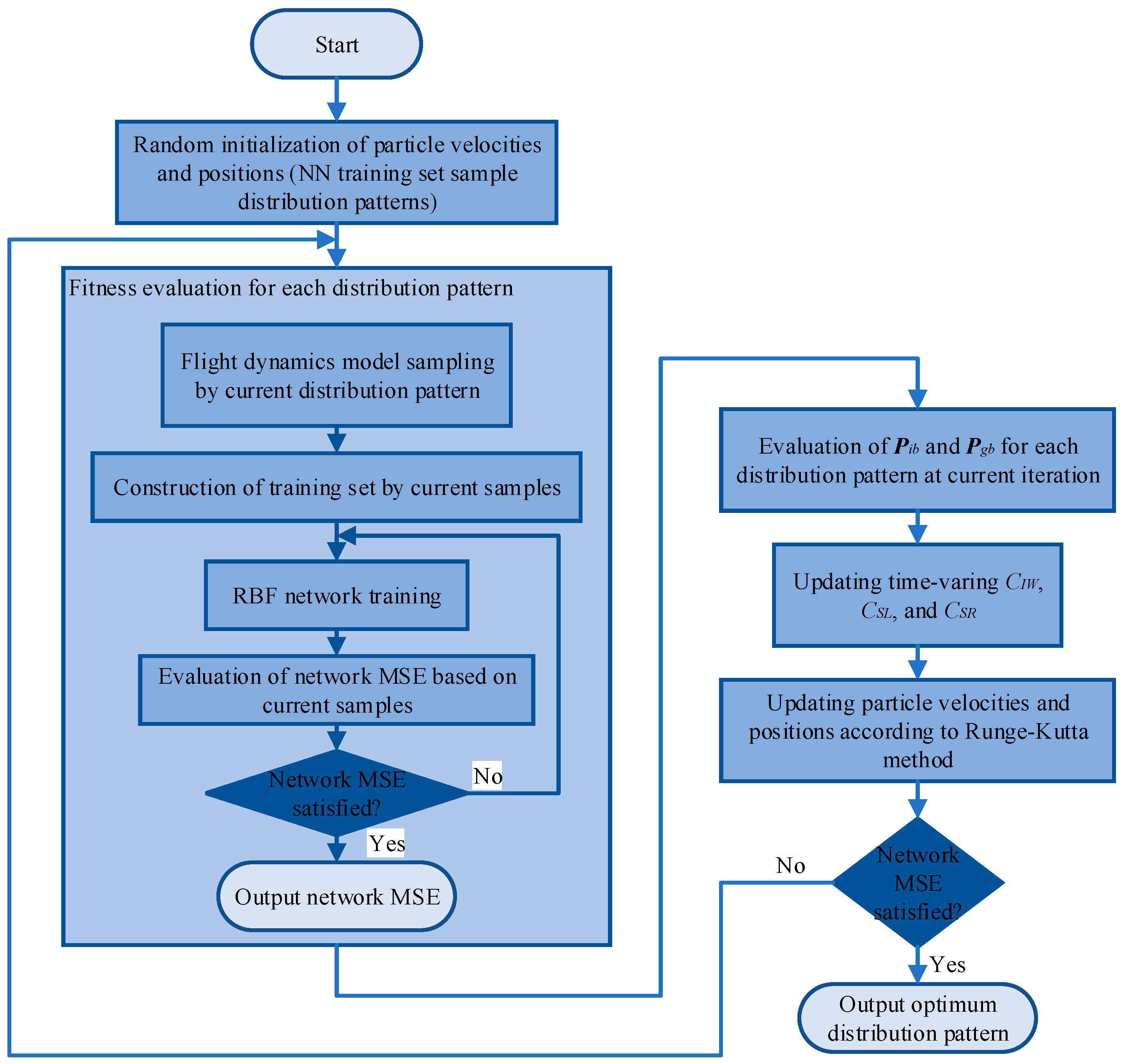
The procedure of optimization of the network training set sample distribution pattern is shown as
Figure 2.
3.2. Case Studies
3.2.1. Approximation of a Nonlinear Function
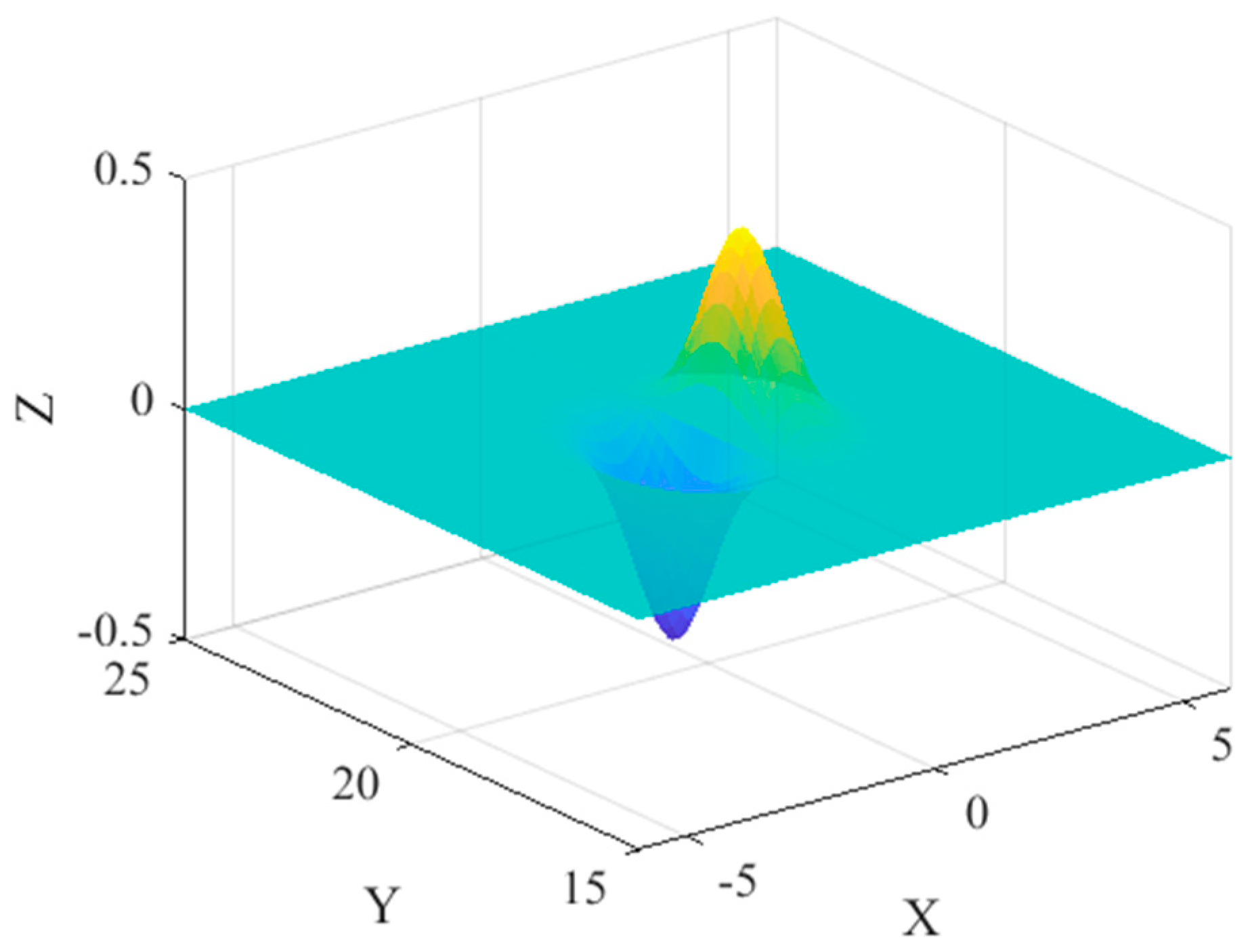
To further explain the principle of the methodology presented in the previous section, an example case is discussed by the approximation of the objective function:
The function plot is shown in
Figure 3. The neighborhoods of its two maxima (the two ‘spikes’ on the function plot) are the primary concern indicating the optimization results where the distribution pattern should condense its samples. A total sample number is confined to 40 points in this task. The parameters of the optimizer are summarized in
Table 1.
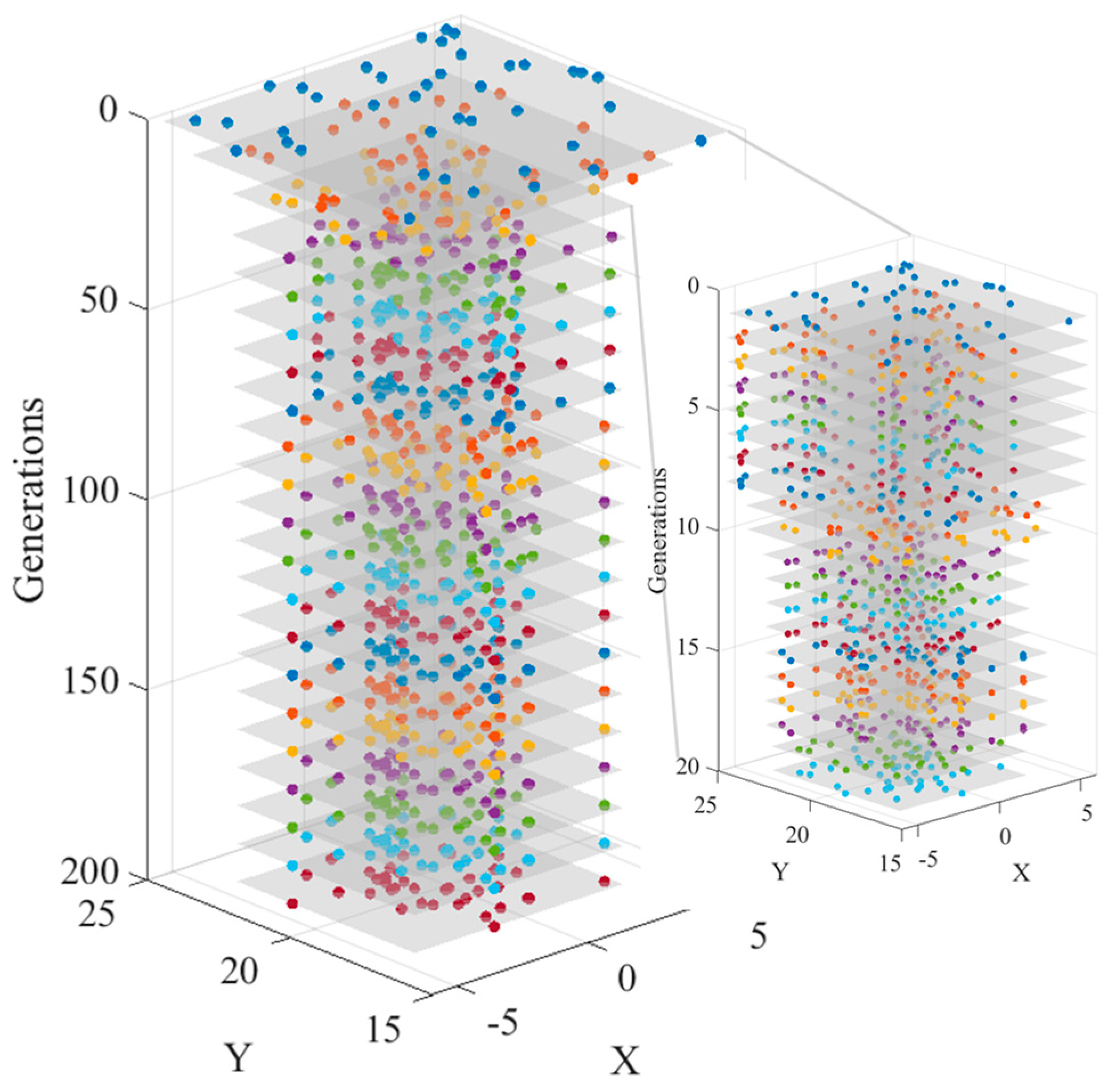
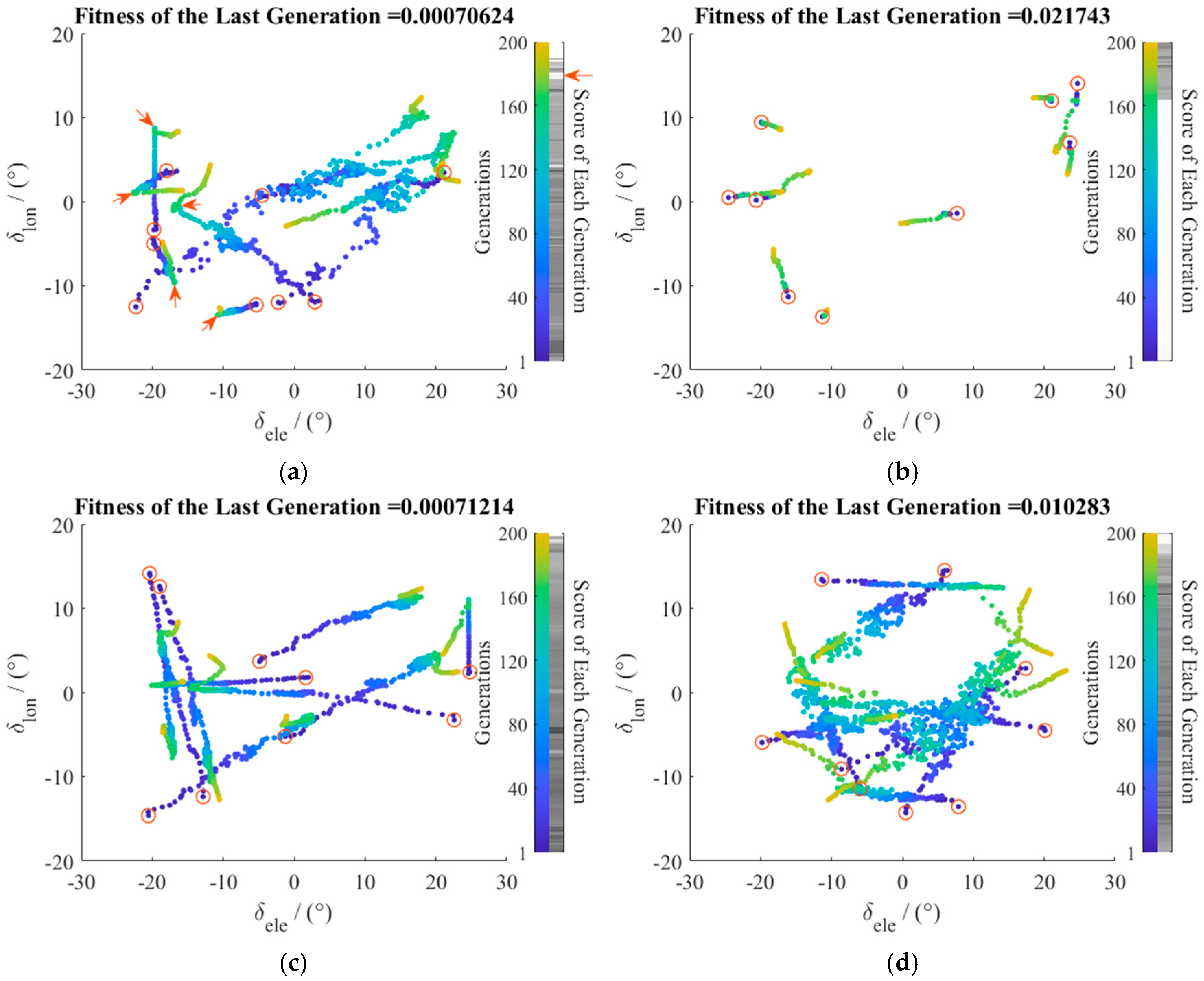
The convergence history of the elite from each generation is presented in
Figure 4. Colored dots on the shaded plane denote the best sample points of each generation. From the right-sided details of the first twenty generations, one can find from the evolution process that the distribution pattern indicates an obvious tendency of the concentration of sample points from a uniformly random distribution on the XY plane to the two ‘spikes’ of the objective function. These ‘spikes’ are exactly where the gradient varies drastically. On the contrary, from the region where the surface is relatively ‘flat’, fewer sample points are selected.
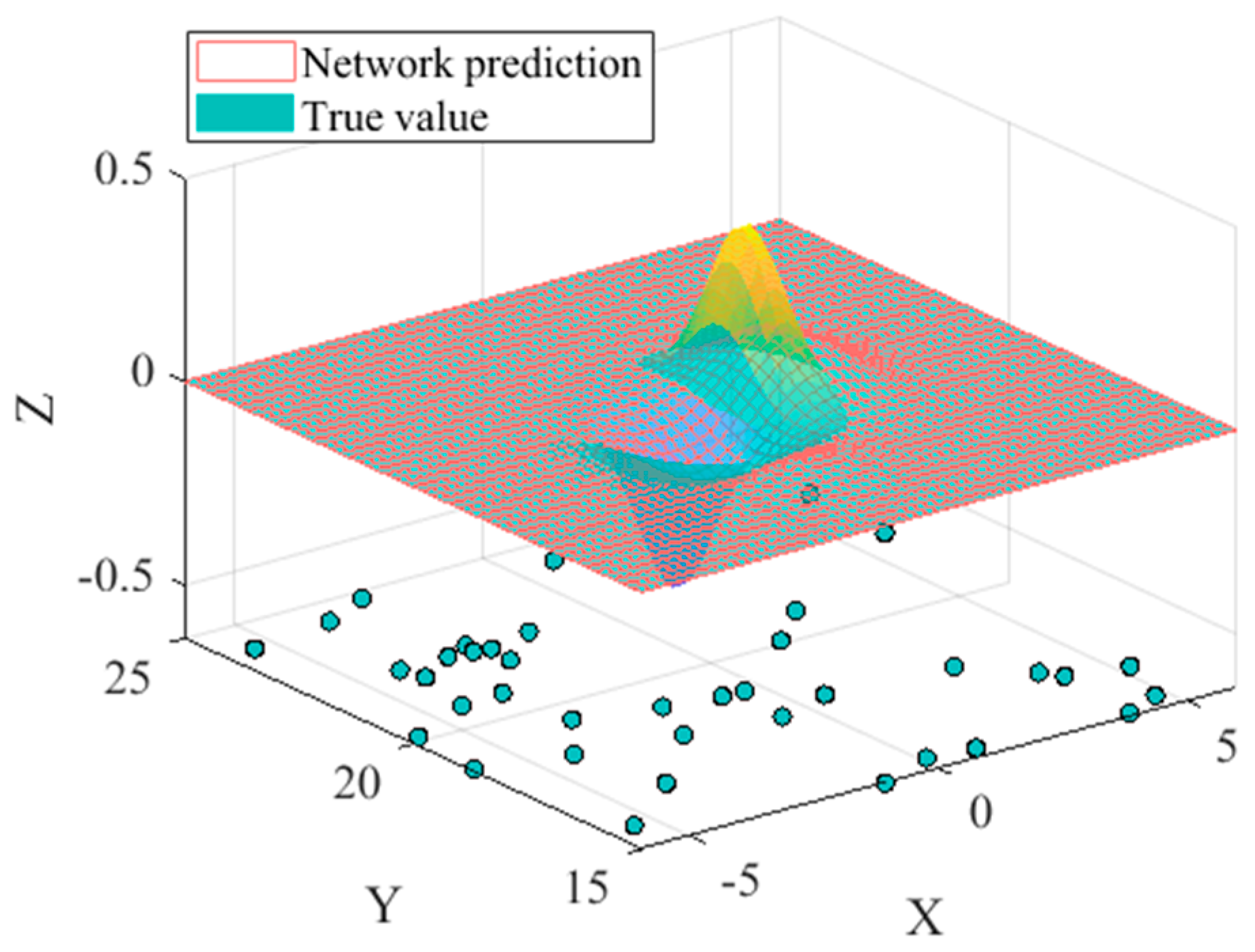
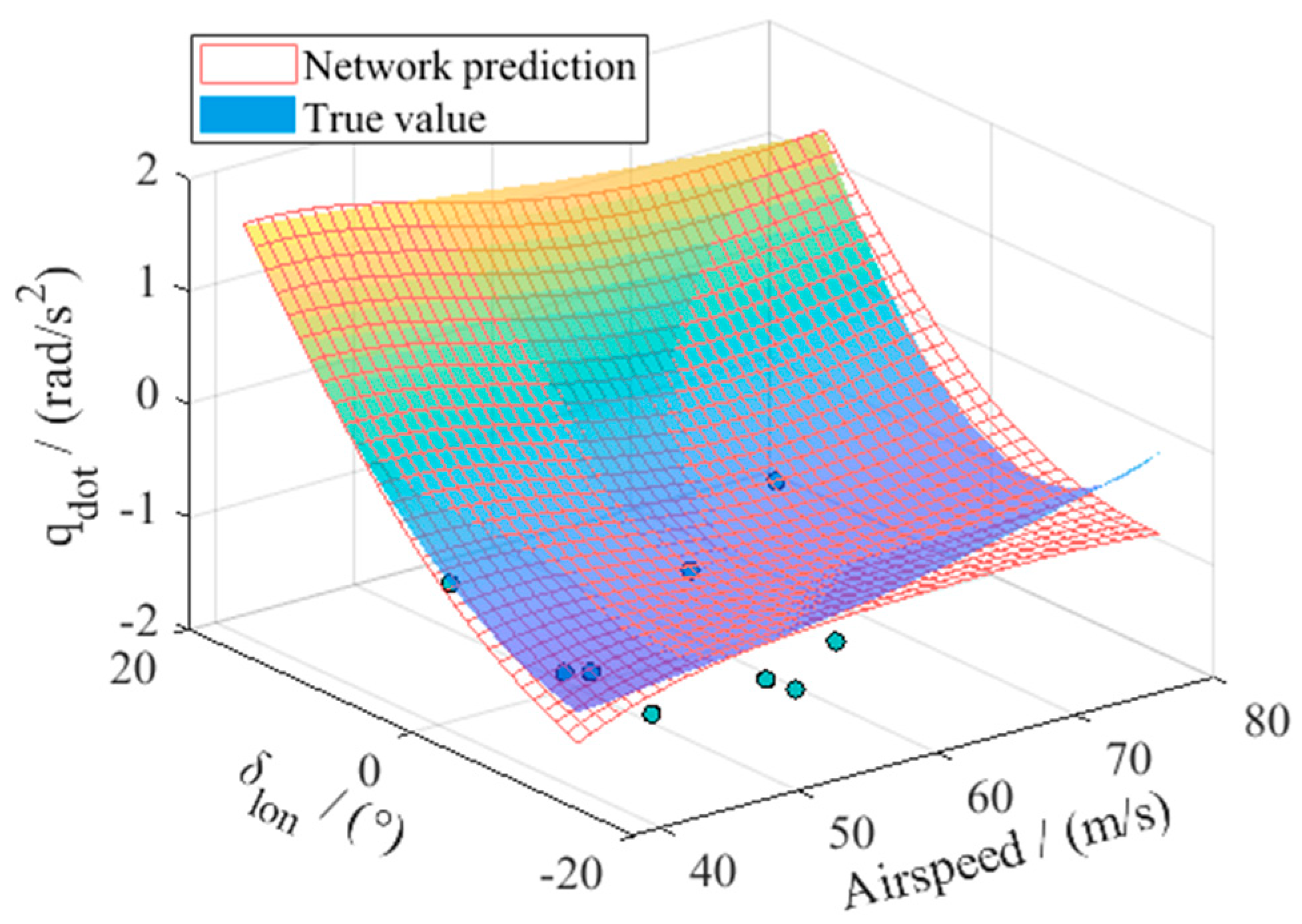
The network trained from the optimum sample pattern was simulated, and the result is shown by
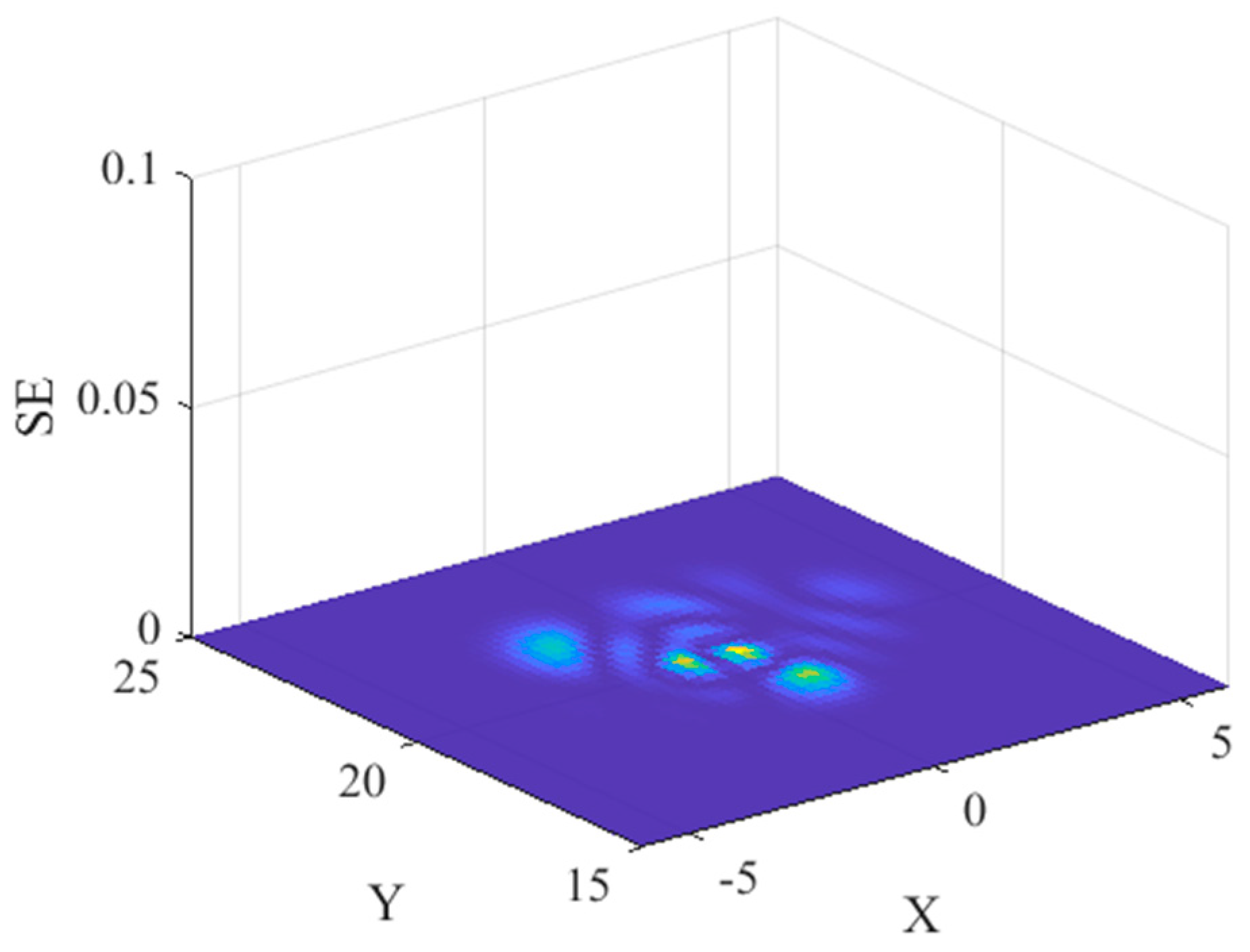
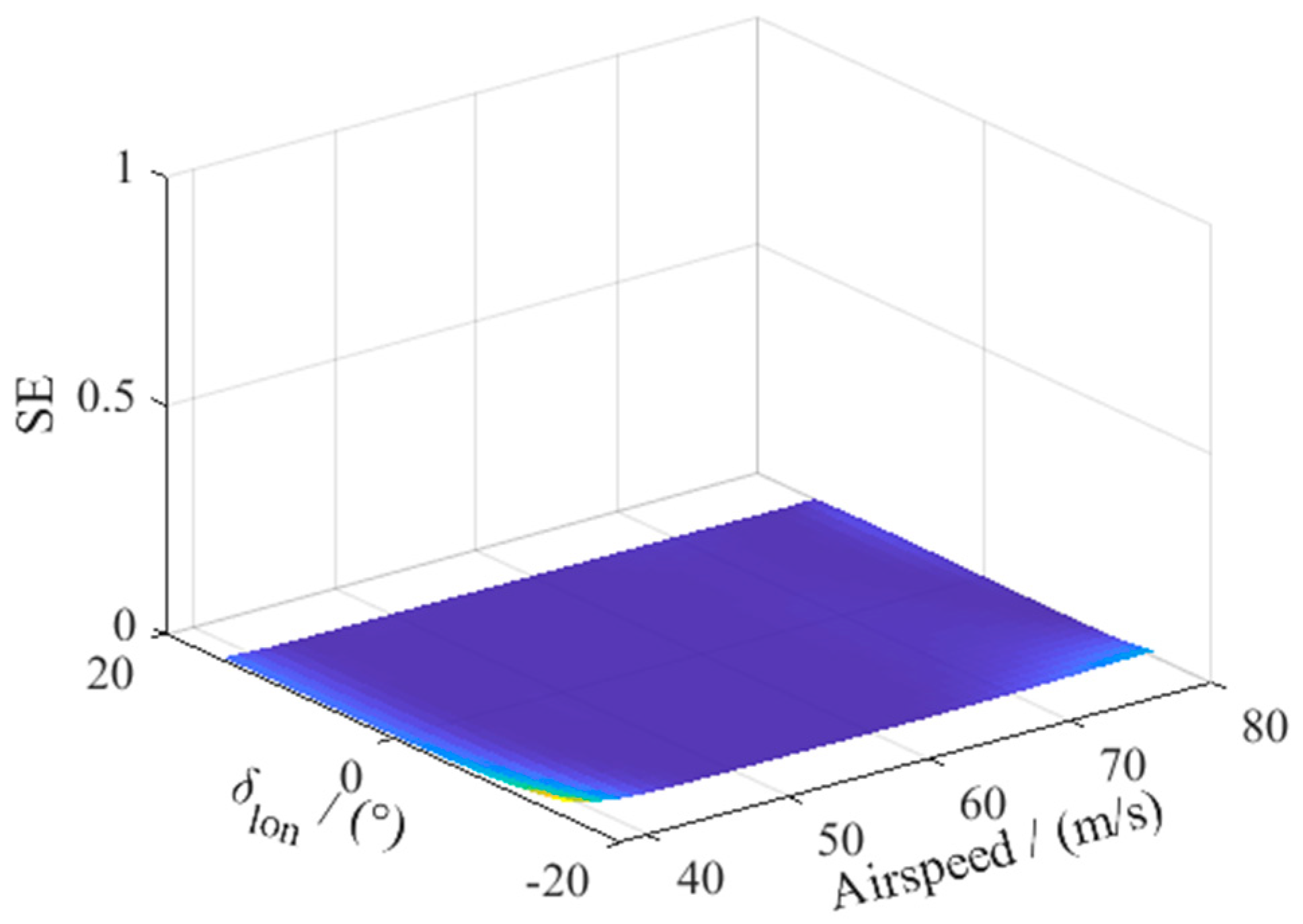
Figure 5. The true values obtained by sampling the objective function are shown by the colored surface, while the network prediction at the same sample points is shown by the mesh grid. As a result, the pattern optimized by DPSORK can be used to obtain an RBF network approximating the example function with relatively high accuracy. The global network square error (SE) distribution is shown in
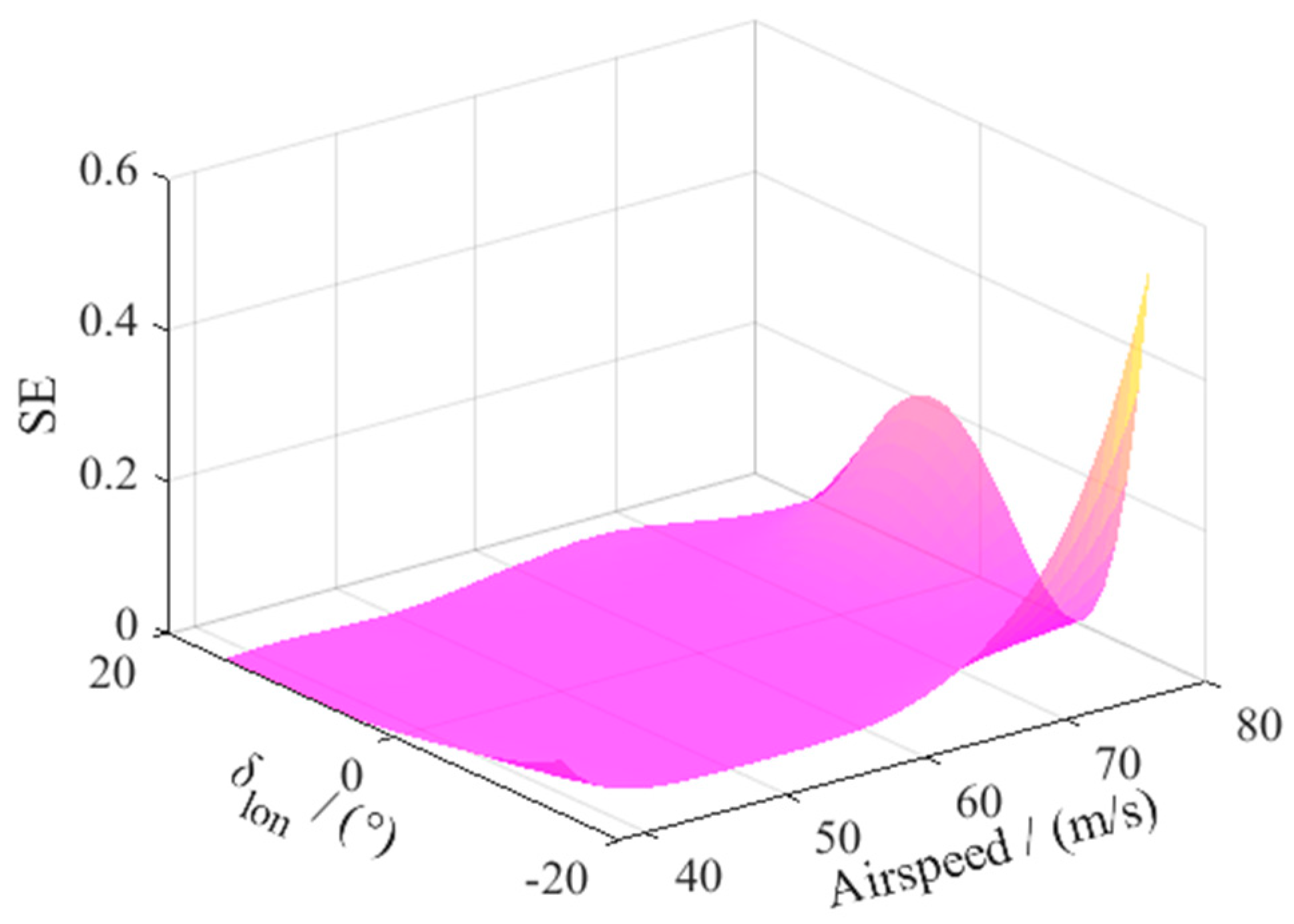
Figure 6.
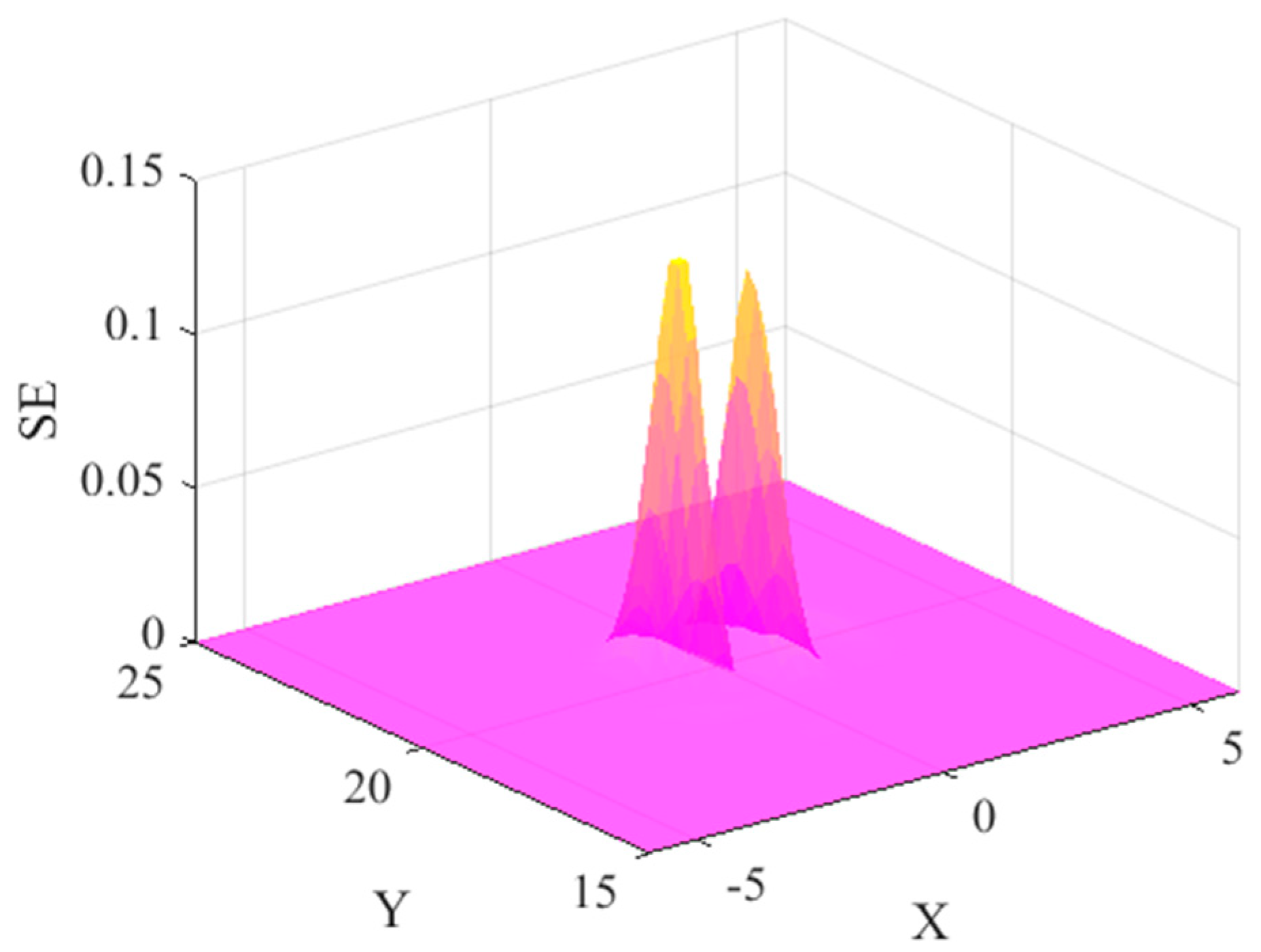
In the meantime, a comparative network trained by randomly selected samples uniformly distributed on the problem domain is simulated in
Figure 7. Obvious error can be seen between the predicted value and true value. From the global SE distribution shown in
Figure 8, one can find that the large values of SE are primarily around the two ‘spike’ regions of the objective function domain because of a lack of adequate amount of sample points allocated to these regions.
3.2.2. Parameter Analysis for Searching the Particle Number and Sample Number
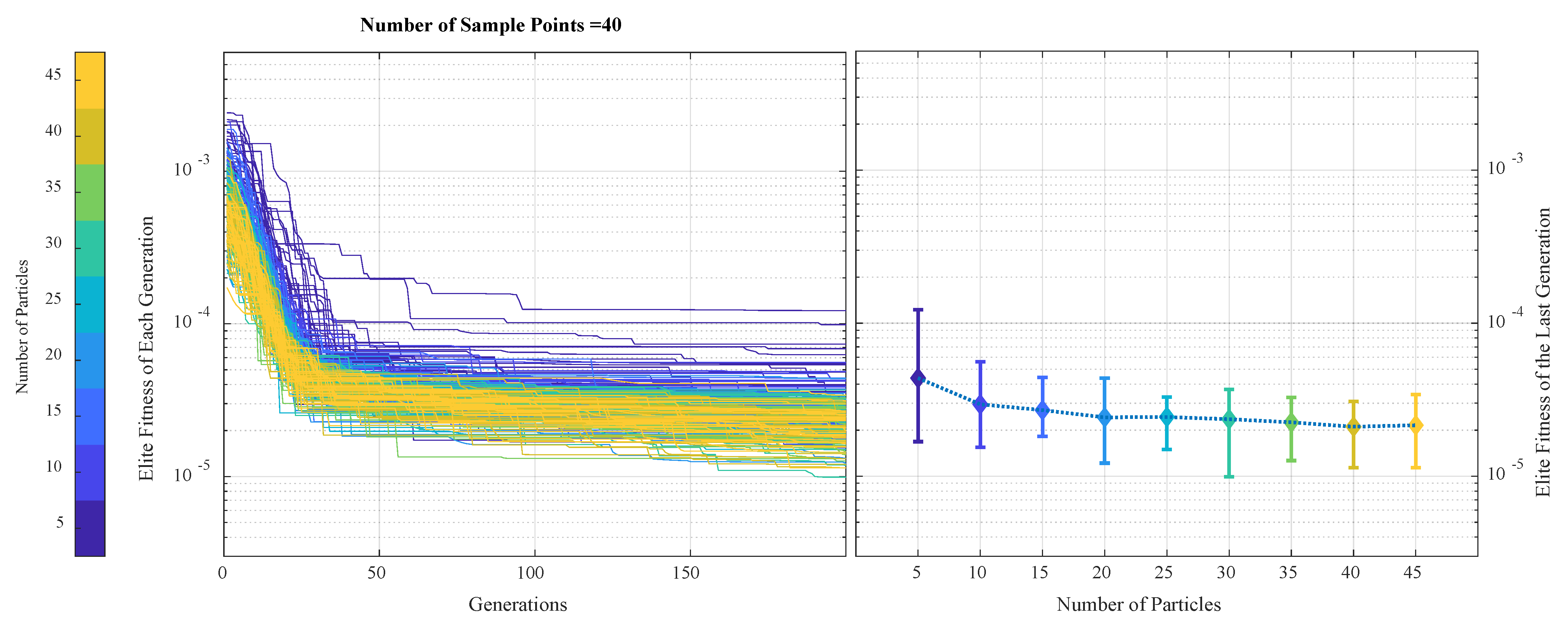
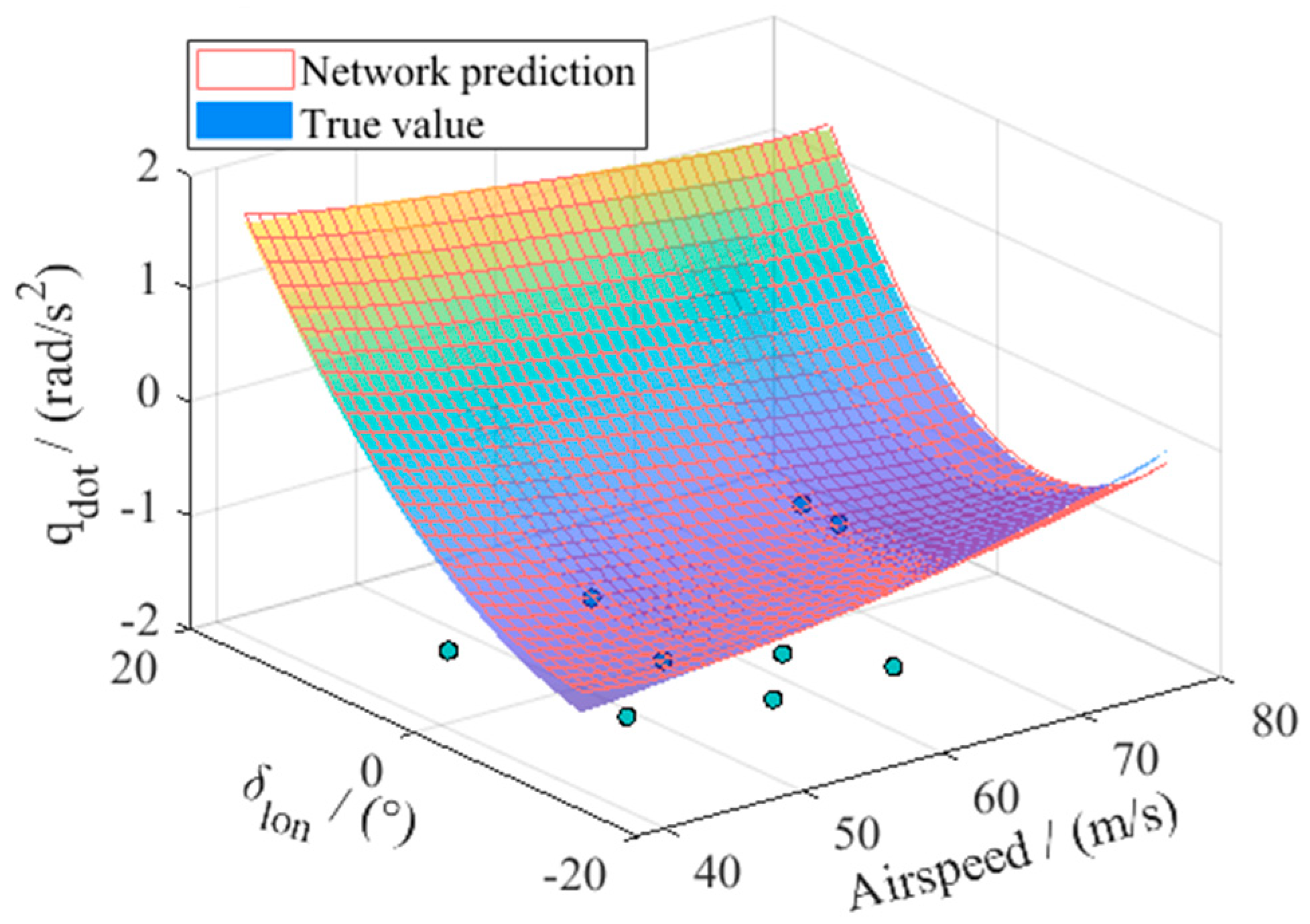
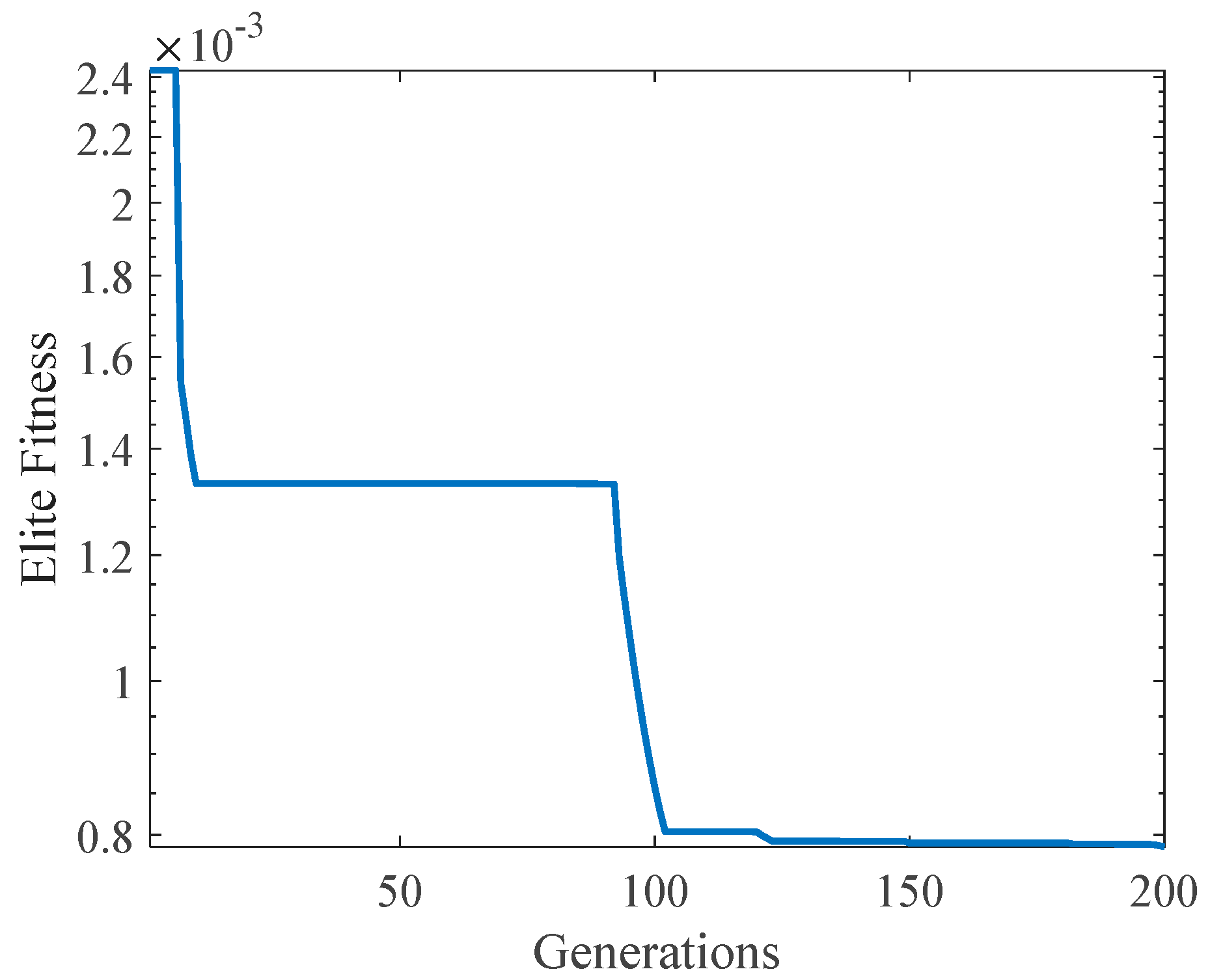
To reveal the impact of algorithm parameters including searching the particle number and sample number, repeated averaging simulations were performed. First, the particle number was fixed at 20, and the sample points increased from 10 samples to 140 samples. Every case was repeated 30 times to exclude the randomness of performance. The results are shown in
Figure 9. The left part indicates the convergence history of the elite population of each generation. Different colors indicate result from different sample point numbers on the graph. The right part of the figure is the average and dispersion of the elite fitness of the last generation, and the averages are indicated by the diamond marker while the error bars showed the maximum and minimum values of the 30-repeated simulations. As a result, under the same amount of searching particles, the sample point number has a major impact on the convergence performance, and after 40 samples, the influence of the sample point number can be regarded as negligible.
Secondly, the sample point number was fixed at 40 to study the impact of searching particle numbers. With the same procedure, the searching particle number increased from 5 to 45, and each case (the same number of particles) was repeated 30 times. The results are shown in
Figure 10. From the convergence history below, one can find that the searching particle number has a minor influence on the overall precision after convergence. Both average fitness and dispersion are affected weakly by the particle number, especially for those cases with a particle number greater than 10. As a result, a combination of 40 sample points with 20 searching particles was selected in this work.
3.2.3. Time Domain Response Performance
To illustrate the approximation performance of the presented optimization algorithm for an unstable nonlinear multi-variable dynamic system, this subsection selects a Van der Pol oscillator as the example, and the time-response of the system is shown. The Van der Pol oscillator is a representative nonlinear autonomous dynamic system with two states. The system equations can be written as
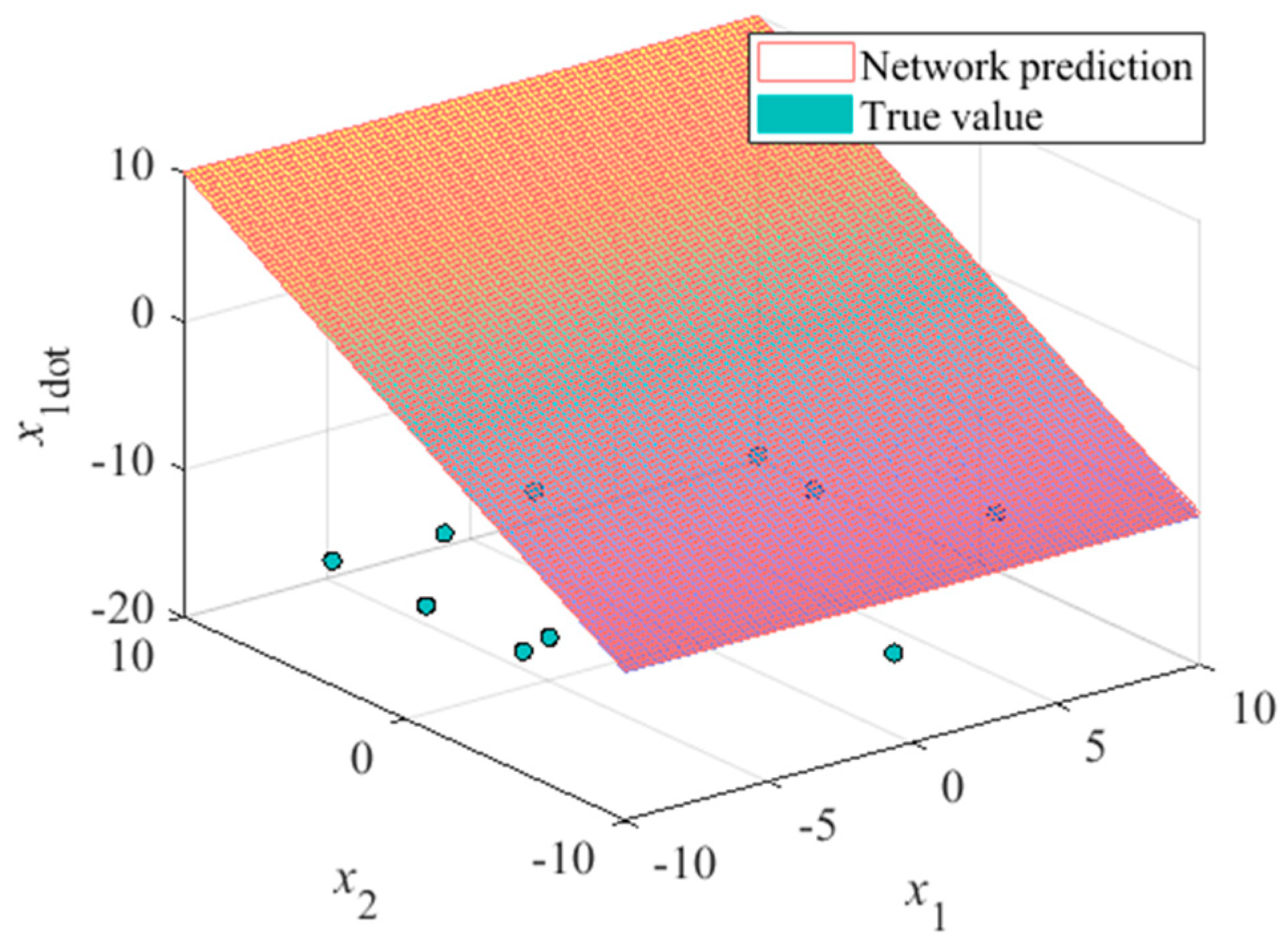
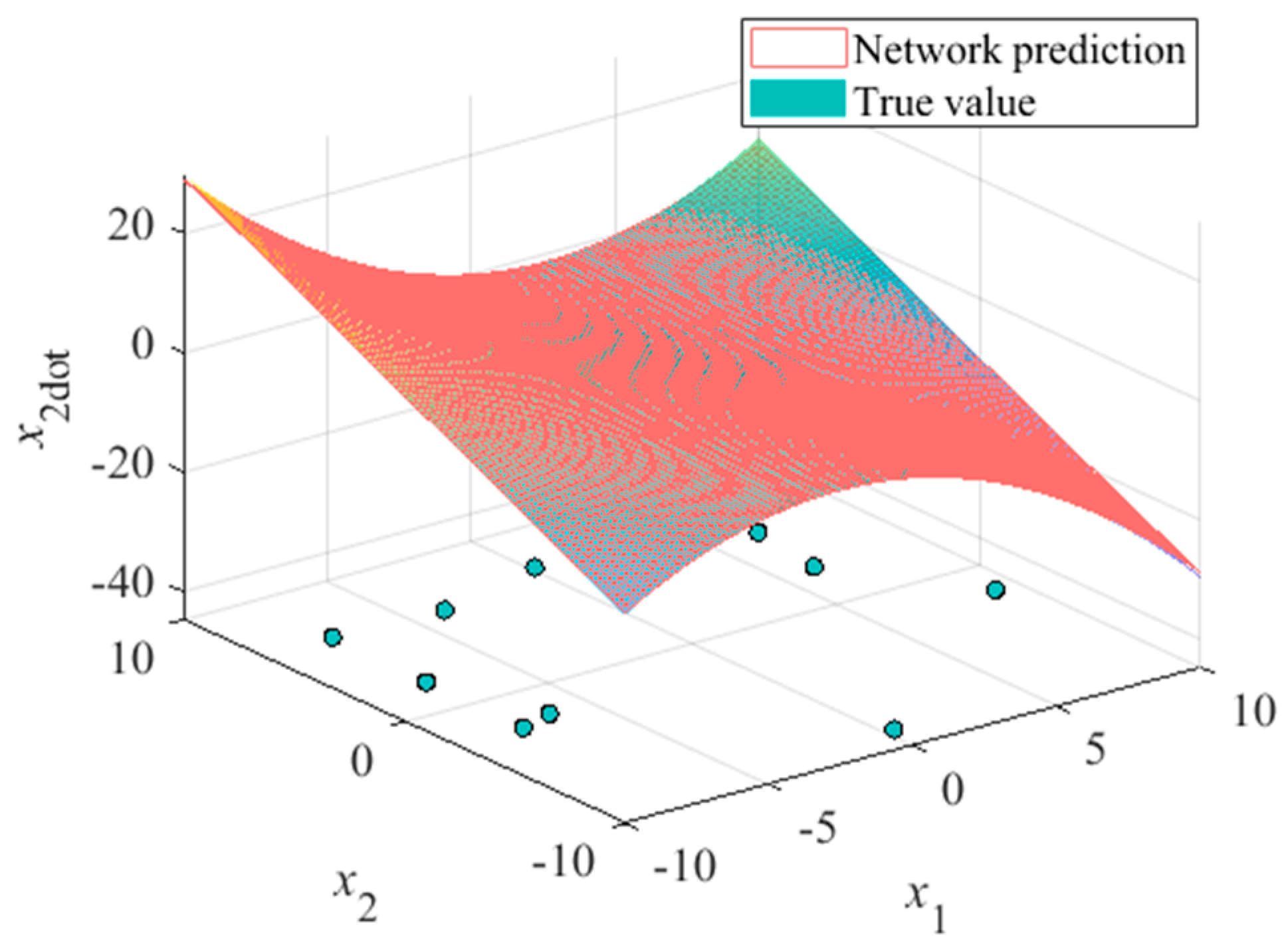
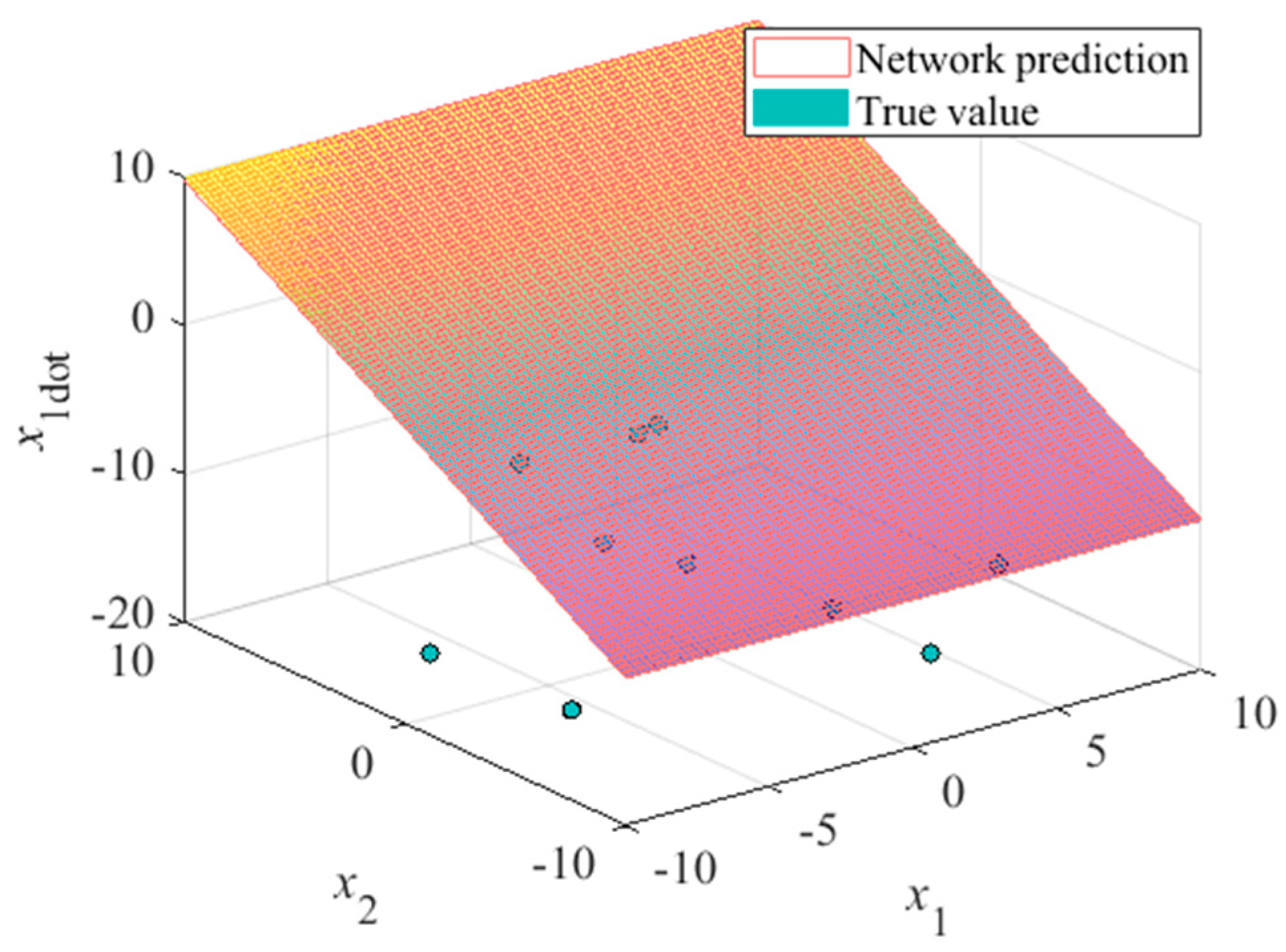
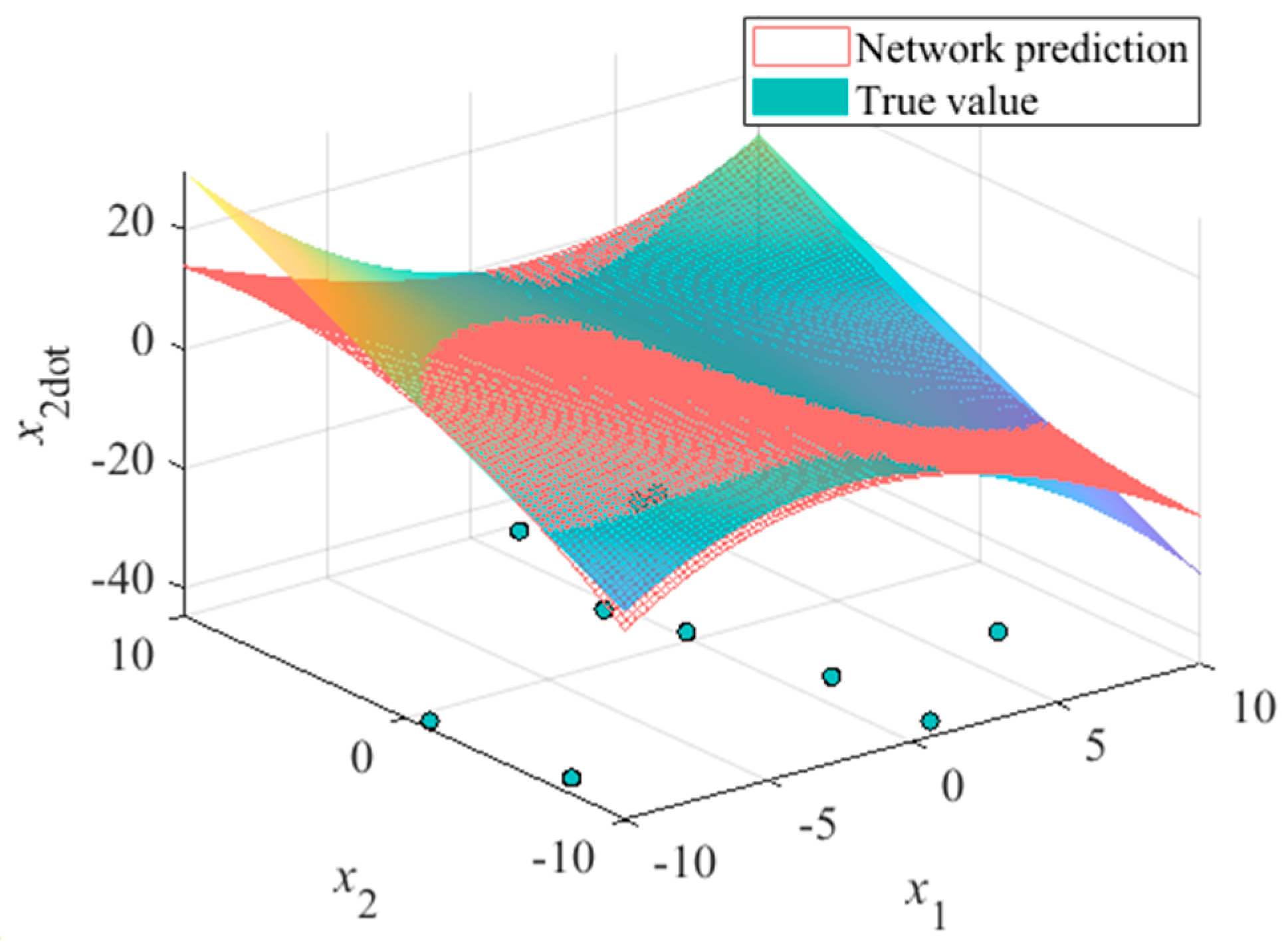
A total number of 10 sample points on the state space was restricted to this task. The comparative results of the network-approximated Van der Pol system derivatives are shown in
Figure 11,
Figure 12,
Figure 13 and
Figure 14. The global MSE of these networks with multiple outputs is the sum of all outputs, i.e., state derivatives. The
field of the Van der Pol oscillator is a flat surface with respect to its two states, which can be seen from the system equation, so the approximation precision can be relatively high even under the random sample case (seen in
Figure 13). The approximation of the
field, however, shows a low performance if the training set has not been optimized (see
Figure 12 and
Figure 14).
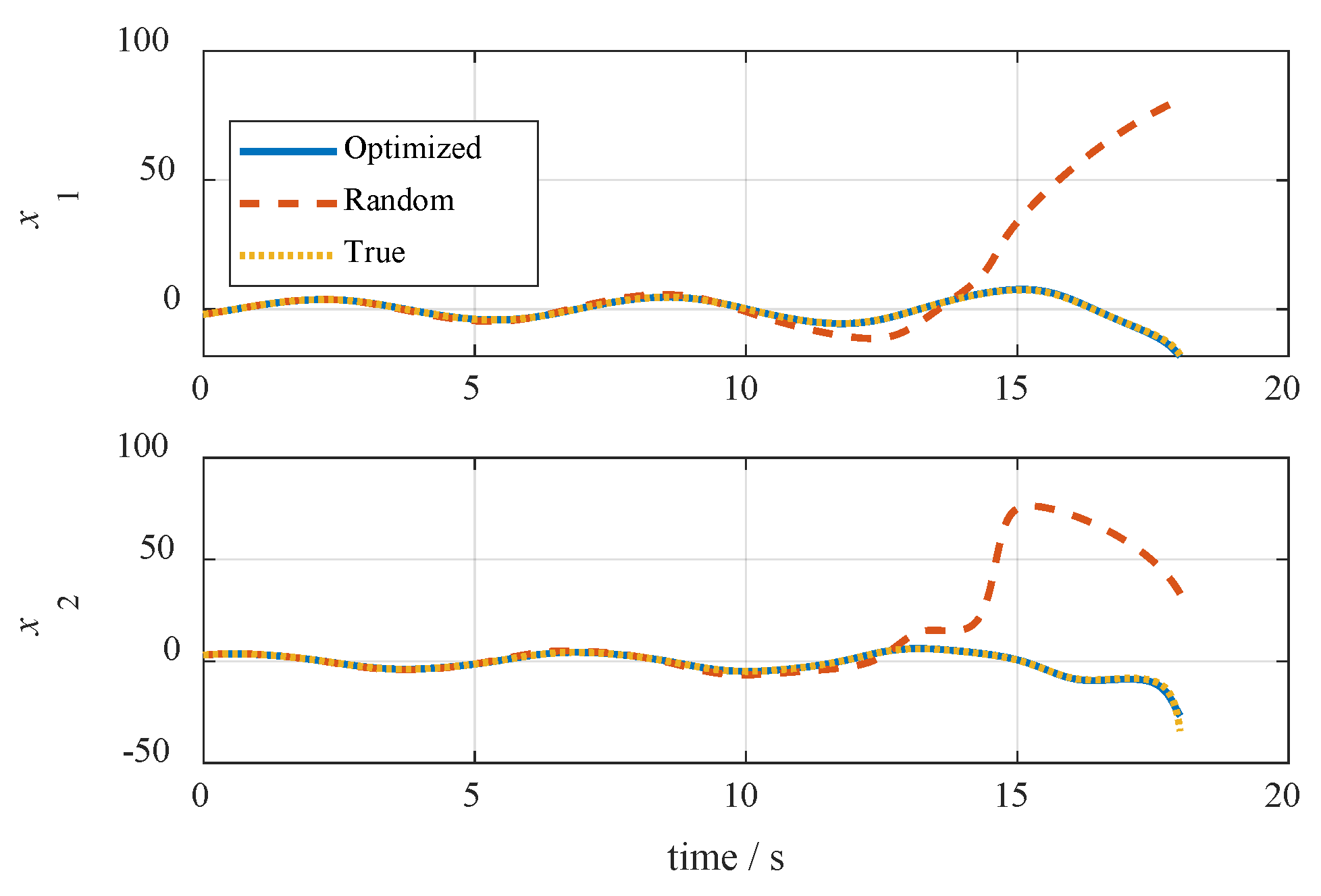
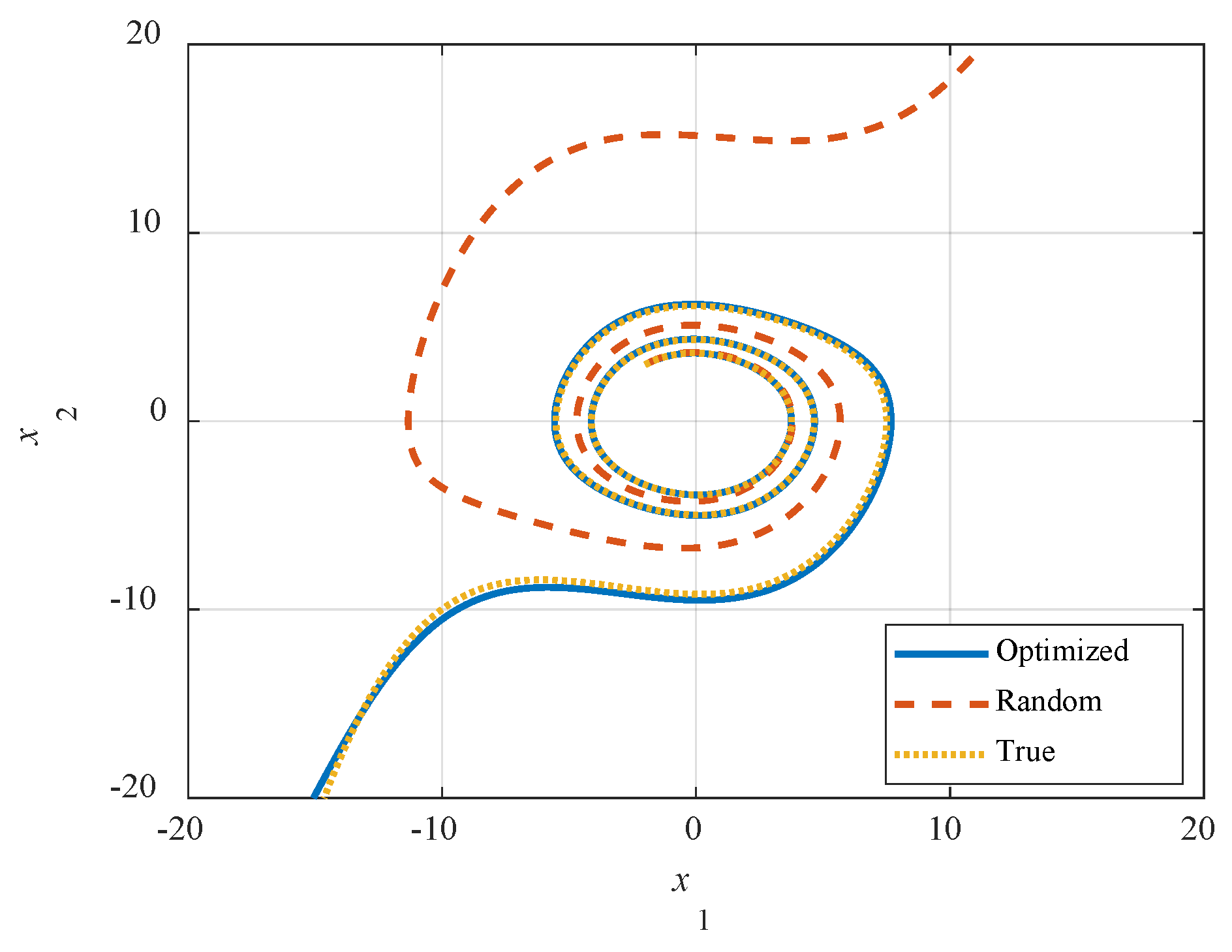
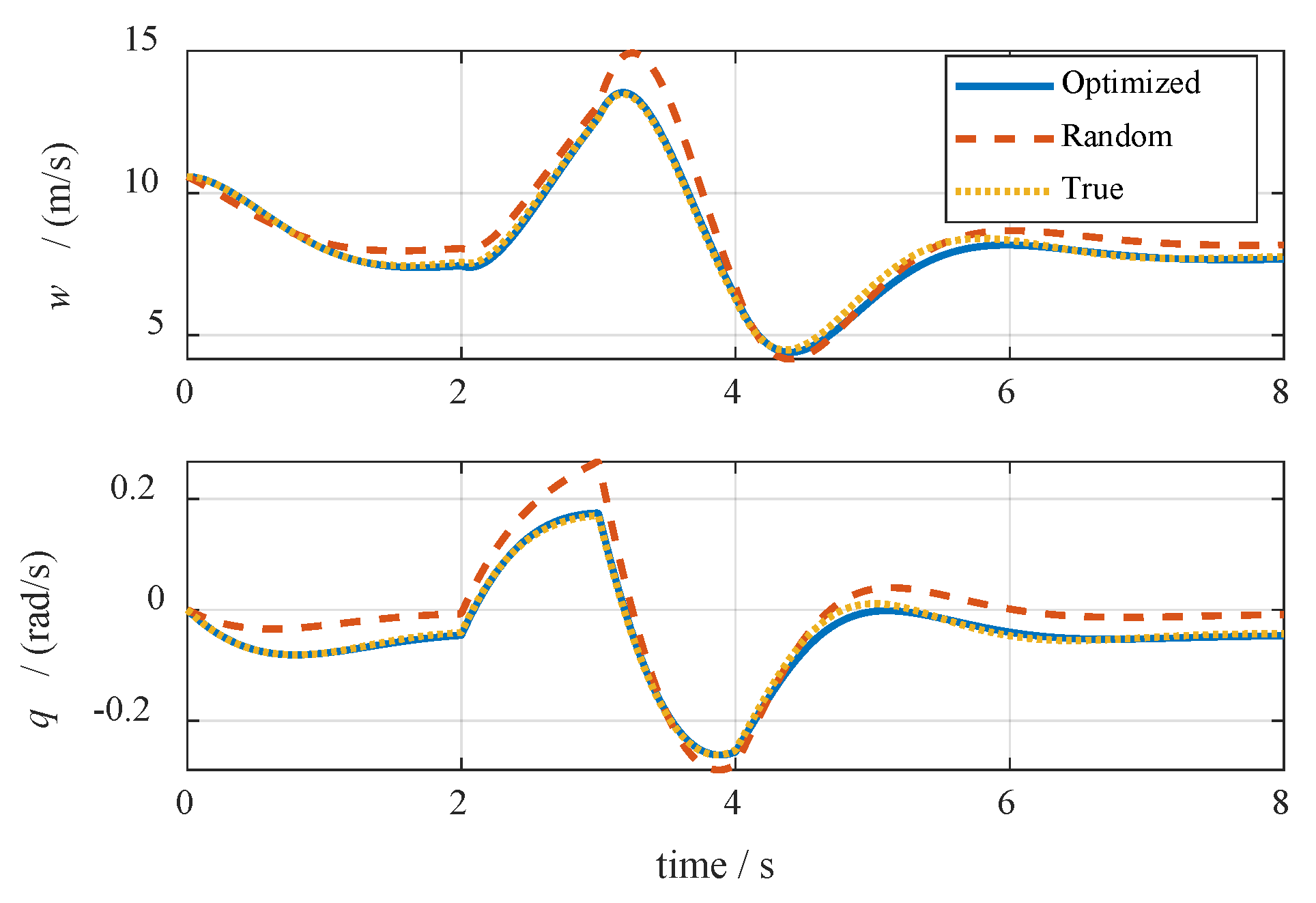
Simulation was performed on the optimum network obtained by the presented algorithm, the random set-trained network, and the true system, and a fixed-step Runge–Kutta solver with a 0.01 s time step was adopted. Results are shown in
Figure 15 and
Figure 16;
Figure 15 depicts the time response of the two state variables, and the system phase portraits are shown in
Figure 16. From these results, the optimized approximation system coincided with the actual system, and the nonlinearity and unstableness were reconstructed well by the optimized neural network.