Abstract
Unmanned aerial vehicles (UAVs) are becoming popular in various applications. However, there are still challenging issues to be tackled, such as effective obstacle avoidance, target identification within a crowd, and specific target tracking. This paper focuses on dynamic target following and obstacle avoidance to realize a prototype of a quadcopter drone to serve as an autonomous object follower. An adaptive target identification system is proposed to recognize the specific target in the complicated background. For obstacle avoidance during flight, we introduce an idea of space detection and use it to develop a so-called contour and spiral convolution space detection (CASCSD) algorithm to evade obstacles. Thanks to the low architecture complexity, it is appropriate for implementation on onboard flight control systems. The target prediction is integrated with fuzzified flight control to fulfill an autonomous target tracker. When this series of technical research and development is completed, this system can be used for applications such as personal security guard and criminal detection systems.
1. Introduction
Over the past few years, various innovative applications of unmanned aerial vehicles (UAVs) have emerged due to lower cost in hardware and appearance of powerful onboard microcomputers.
UAVs can conquer topographic barrier so that they are appropriate for conducting missions in dangerous zones, replacing manpower to transport goods, or even serving as a personal standby assistant.
Recently, artificial intelligence (AI)-based automatic control technology has received attention attributed to the significant improvement such as the generalization capability of deep learning. Deep learning drives many AI applications that improve automation, performing analytical and physical tasks without human intervention. For instance: the robot “pepper” in [1] is used for domestic and navigation purposes; the biped robot is used to replace soldiers [2]; there are medical hospitality robots [3], autonomous cars [4,5], and much more. In addition to land vehicles, there are various aerospace vehicles developed for specific purposes, such as the delivery UAVs [6,7,8], disaster relief UAVs, and multi-machine protocol flying UAVs [9].
UAVs that track targets need to adapt to various environments to fly. In [10], the authors proposed a robust adaptive recursive sliding mode attitude control, which can make the quadrotor effectively resist unknown interference. The work of [11] proposed an anti-jamming control scheme based on multi-observers to counteract multiple interferences so that the quadrotor can resist strong wind and load interference.
Focusing on the technical issues, while research efforts in target following and obstacle avoidance techniques have been quite mature in the field of robotics, the two issues are still challenging for the operational scenarios of miniature UAVs such as quadcopter drones because of the relatively limited hardware resources available and the resulting neutral instability [12].
Improving the reliability of UAVs is one of the challenging issues in the market. Crash events of UAVs are not unusual. Moreover, static or dynamic target identification in a crowd is also a difficult issue for miniature UAV development due to the limited computational resources and budget cameras used [13]. In the academic research field, while there are research efforts dedicated to investigating target tracking [14,15,16] and obstacle avoidance [17,18,19,20], further improvement on functional enhancement, especially in target identification and tracking, is still highly demanded. For example, the proposed target tracking in [15] requires the target to be identified wearing a special T-shirt with a QR code on it. The study of [16] relies on color features to identify the specific target. The rough obstacle avoidance method adopted in [19] might cause the UAV to collide with obstacles when the sensor is not in parallel with the obstacles. Although the research tasks of [21,22] have combined the capability of target tracking and obstacle avoidance, their results were only verified via simulation study. The common difficulty of various research efforts is that the extremely large computational resources were unsuitable for implementation on the onboard microprocessor.
Considering the general weaknesses of the current approaches, this research task proposes the methods developed for target identification and movement prediction, the adaptive cruise control (ACC) system, and the Kalman filtering navigation to fulfill a mission-oriented flight control system. Our research motivations are listed as follows:
- The tracking capability of the commercial miniature UAV is still immature [12,13]. The methods developed in the papers might not be applicable in real-world applications [14,15]. These methods are feasible, but are slightly restricted from the viewpoint of practical applications. For human target following, this research proposes an adaptive target identification system to resolve the problem when the specific target is in a crowd.
- The current UAV obstacle avoidance algorithms revealed in the papers were difficult to implement in the small-scale embedded system because of the large computational sizes. Here, we propose a novel contour and spiral convolution space detection (CASCSD) algorithm to tackle the issue. Through the emulated expansion and etching of the image processing, we can filter out noises while enlarging imaging signals to indicate that if the obstacles might interfere with the flight path. This algorithm consumes less computational resources and is appropriate to be used in the current miniature UAV applications.
- Intelligent mobile assistants have recently become popular; however, UAVs moving inside a building, on stairs, or in rugged areas is still a challenge. A miniature UAV drone is one of the potential substitutes for work under these scenarios.
In addition, in order to improve the research quality, we also refer to other UAV and tracking-related literature, such as [23], which mainly discusses the deep learning application of UAVs in Internet of Things applications and investigates the related applications of UAVs in detail. Ref. [24] discusses the issues related to the bionic control of UAVs, which can provide more ideas for the control of UAVs in this paper. In the research of tracking, [25] uses a UAV to track the landing point on the roof of a car and allows the UAV to safely land at the target point. Ref. [26] proposed an adaptive lightweight UAV tracking algorithm, which allows UAVs to track various targets at high altitudes. Ref. [27] proposed a distance estimation method based on hybrid stereo vision, which can accurately calculate the distance between the robot and the object and can provide more ideas for this research on obstacle avoidance. Ref. [28] used deep learning, simulated tracking, and obstacle avoidance with multiple UAVs, and the results showed the algorithm’s effectiveness. Synthesizing various research ideas, this study found that the ability of UAVs to fly indoors and outdoors is still lacking, and this research intends to complete a personal security guard system. The overall system of UAVs needs to have identification, tracking, and obstacle avoidance at the same time. The three functions and the algorithm need to be as lightweight as possible. Only by fulfilling these demands can the experimental purpose of the research be achieved.
2. System Description
The dynamics of the UAV directly affect flight stability [29]; to enable the UAV to have intelligent tracking and obstacle avoidance functions, we first need to establish a quadrotor flight dynamic model and control equations. Secondly, the image and the entire coordinate system must be convertible so that we can import the image information and various algorithms into the flight control perform tasks.
2.1. Architecture
Figure 1 illustrates the quadcopter architecture implemented in this research task. The miniature UAV drone is designed to be a vision-based autonomous target follower. The functions of the key modules include the following modules: a flight control system including an inertial navigation system (INS), gyroscope, optical flow sensor using ground texture and visible features for indoor positioning, and barometer for attitude determination; an onboard AI processor is responsible for intelligent target identification and tracking, flight path computation with obstacle avoidance, and realization of all supporting algorithms; and a depth camera is responsible for transmitting external images to the AI processor. It also provides information of the relative distance between the target and the environment.
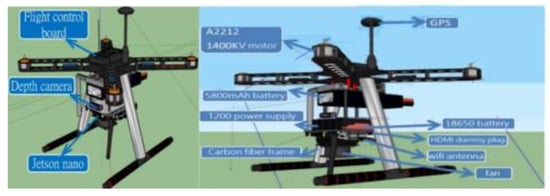
Figure 1.
Architecture of the miniature quadcopter drone implemented in this research.
2.2. Modeling
The four-rotor mathematical model of the miniature quadcopter for the purpose of target identification and tracking is given in Appendix A.
Flight Dynamics Model (FDM) Description
The world frame and the quadcopter body frame of this study are shown in Figure 2, where is the inertial coordinate system, is the origin of the inertial coordinate, and is the unit vector along the inertial coordinate axis. is the rigid body coordinate system of the quadcopter body, is the origin of the rigid body coordinate, and is the unit vector along the rigid body coordinate axes.
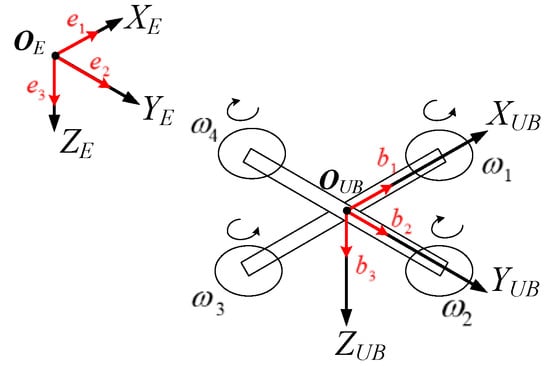
Figure 2.
The world and body frames.
Proceeding to the development given in the Appendix A, we have the acceleration and angular acceleration equations of the quadcopter as:
To proceed, we perform coordinate transformation from the body frame to the world frame along the yaw, roll, and pitch axes:
where denote the angles of pitch, roll, and yaw respectively (see Figure 3). For completeness, the coefficients of the air resistance and coefficients of the rotary resistance are considered. It can then be further transferred into the state space representation by considering the gyro effect:
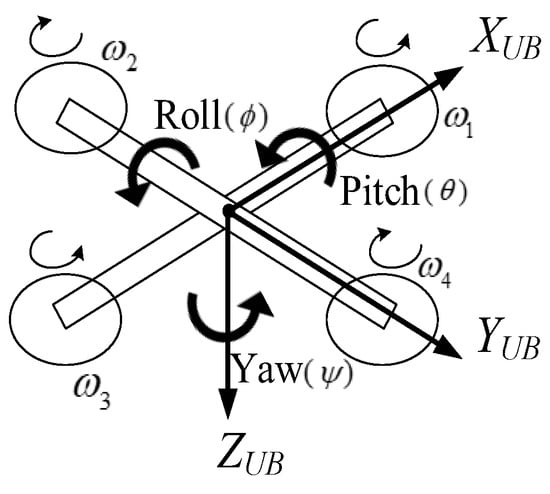
Figure 3.
Schematic diagram illustrating the respective attitude angles.
3. Target Tracking and Obstacle Avoidance
A depth camera is utilized to detect the target and surrounding objects. Before conducting target identification, image calibration is conducted.
3.1. Calibration and Coordinate Conversion
The pinhole imaging model [30,31] is used to describe this process, and it is corrected by the principle of similar triangles (see Figure 4).
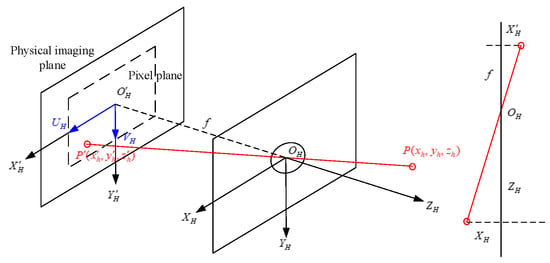
Figure 4.
The pinhole photo picturing model.
Suppose that the camera coordinate system is denoted by with the origin . The pixel coordinates are and the origin is , as shown in Figure 4. Furthermore, there is a targeted point in reality, and its new coordinate mapped to the pixel plane is . Let the focal length f be the distance from the pinhole to the pixel coordinate plane. This gives rise to the following ratio formula:
We define the origin of the pixel coordinate system as being located at the upper left corner of the image; the axis is parallel to the axis, and the axis is parallel to the axis and is at the same plane as the pixel coordinate system. Thus, there is a two-axis difference between the two-pixel coordinates.
Assume that the and axes are zoomed in by and times, respectively, and the origin is linearly shifted by the base unit . One obtains:
Let and , then
Transforming this into a matrix representation gives
where is the camera’s inner parameter matrix. It is used to compute the camera’s outer parameter matrix.
Let be the point P from the camera coordinate to the world coordinate, where R and t are the rotation and translation of the camera, respectively.
Performing normalization gives
The point P is at the normalized plane at the point . The normalized coordinate that multiplies the camera intrinsic parameters results in the modified pixel coordinate.
3.2. Dynamic Target ID and Locking
The traditional YOLO model [32] can only identify objects that are already trained, it would be insufficient while being applied to the current objective. We updated the function of specific target identification by considering the limited onboard resources.
At first, the results , , , of the bounding boxes generated by the modified YOLO network given in [33] are used to determine the centroid position of the targeted person. The coordinates of the four vertices of each bounding boxes are , and . To be realized on the onboard computer, the modified YOLO is only used to frame possible objects in the image frame.
To track the specific object with the limited computational resources, a lightweight algorithm is proposed in this research task for dynamic target identification. The algorithm involves three parts which are calculated per video frame, including: the color scores of the target’s clothes, pants, and hair; the respective length-to-width ratio scores; and the tracking error of the dynamic target. The equations are described as follows:
where component color denotes the ith colored component with a Boolean value (“1” for matched and “0” for unmatched), component length denotes the ith length-to-width ratio component (“1” for matched and “0” for unmatched), and represent the total number of colored components and length-to-width ratio components, respectively, and and are the ith weighted exponents. After obtaining scores of CS and LS, the position score is calculated according to the target locking schematic illustrated in Figure 5 with the score
where , PA refers to the accuracy of calculating the target position of each frame. and are the offset and slope of the sigmoid function, respectively, with their respective equations being as follows: , where denotes the position of the current target frame, denotes the position of the previous frame, and , where represents the number of targets locked within the image space , with L and W being the image length and width, respectively. The bias is used to adjust the maximum error size of the position and filter out the surrounding noise. For the value of , when the target position falls within the gray area as shown in Figure 5, it means that the target position is not located in the central focused region. The closer the position is to the edge, the lower the score. It is designed by , where represents the number of people locked within the reconnaissance space with the semi-major axis of length and semi-minor axis of length and . The rules are summarized as follows:
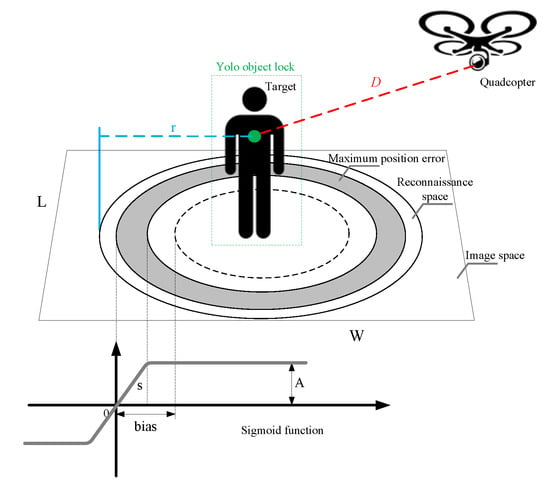
Figure 5.
Target locking schematic framework.
- There are many people that appear in the image. The bias is increased to reflect the noisy background.
- There are few people in the image, but they are tightly crowded. The bias is decreased and s is increased by increasing to rise discriminative sensitivity.
- There are many people, but they are widely dispersed. The bias is decreased to aid highlighting the target.
- There are few people and they are widely dispersed. The bias is set to zero and a large s is suggested to boost the discriminative effect.
After obtaining , , and , the target ID score is characterized by
where the normalized individual scores , , and correspond to , , and , respectively, and are the respective weighting factors satisfying .
Figure 6 illustrates the operational flow of the adaptive target identification system.
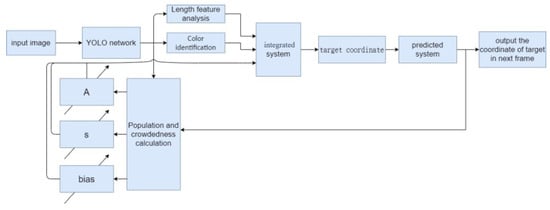
Figure 6.
Operational flow of the adaptive target identification system.
3.3. Target Positioning in 3D Space
Once the target position in the pixel coordinates is obtained, it is transferred to the Cartesian plane. In addition, the relative distance D with respect to the target provided by the depth lens is integrated with the pixel coordinate representation to yield the target position in the spherical coordinates, as shown in Figure 7.
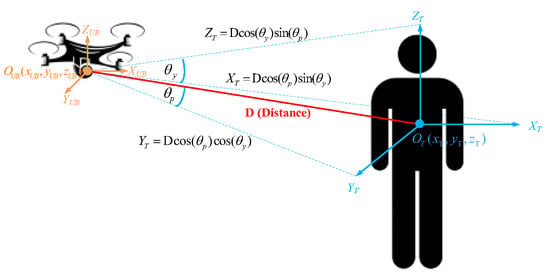
Figure 7.
Coordinate transformation.
For the current experiment, the camera’s field of view (FOV) is 69.4 × 42.5 × 77 degrees with 640 × 480 p (4:3) pixel resolutions. It is used to compute the degree of the pixels within a frame. We end up with the following equations to transform the spherical coordinate system to the Cartesian coordinates:
where and are the pitch and yawing plane line-of-sight (LOS) angles, respectively. The quadcopter rotates its body to move; thus, we have
where is the quadcopter position after performing rotation and R is the coordinate rotational matrix.
3.4. Target Movement Estimation
Let the target state vector be , including the target position p, the velocity v, and the acceleration a, which is random and conformed to the Gaussian distribution with mean and variance . Consider external interference and measurement so that the prediction of measurement statistics is characterized by the estimated measurement , with the error covariance of estimation and t denoting the current time step and the real measurement characterized by , where is the measurement noise covariance.
The prediction equations of the state and error covariance are given by
where the process noise covariance and the system matrix given by
where is the sampling period. Including the two Gaussian distribution terms provides the state update equations:
where and , with being a small positive constant.
3.5. Flight Path Planning
The imaging processing system uses an embedded microcomputer to realize deep learning and Kalman filtering computation. We first propose a contour and spiral convolution space detection algorithm (CASCSD) to handle obstacle avoidance and plan an appropriate flight path to track the target with its center of mass located at .
Using the flyable space detection process, the image is divided into two types of blocks, denoted by “1” or “0”, which refer to the safe-to-fly (STF) and non-STF regions, respectively. We use the infrared of the depth camera to measure the relative distance. As it is easily affected by environmental light, the image processing system first slightly erodes the scope of the space, that is, the expanded scope of the obstacle, which is performed to prevent smaller obstacles from being filtered. Next, it enhances the dilated space range to filter out the light pollution or other noise that infrared ray cannot measure. Then, the space is eroded back to its original size; see Figure 8 for the process. A safety buffering range to prevent the UAV from drifting is reserved at the edge of each detected obstacle.
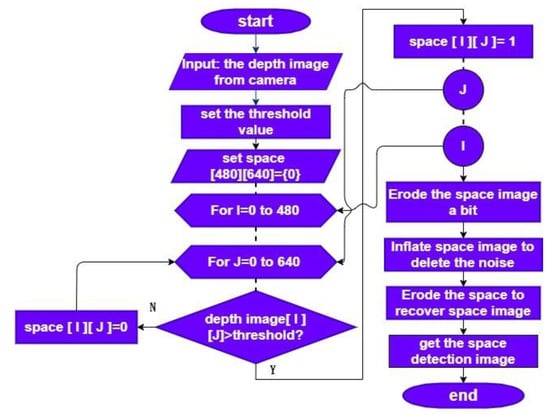
Figure 8.
Noise removal and spatial detection flow.
To ensure that the target can be tracked with the shortest path, the two-dimensional pixel coordinates are inversely derived from the predicted coordinates generated by the Kalman filter. Let the predicted coordinates of the Kalman filter be . The line-of-sight (LOS) angles and can be deduced from
where . Based on the current camera’s FOV, the center position of the target measured from the image are .
The spiral convolution from the centroid position outwards determines whether there is available space for the quadcopter to fly forward. The spiral convolution means that the filter matrix rotates from inside to outside and convolves the spatial detection feature map. The size of the filter depends on the coverage of the boundary on the imaging plane, as illustrated in Figure 9.
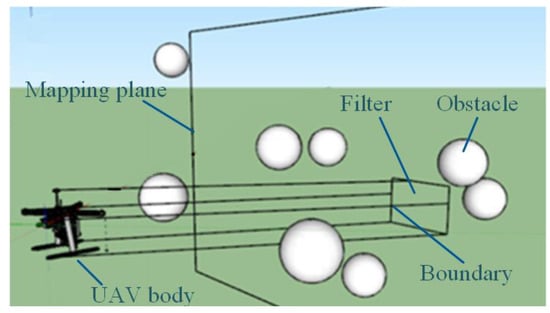
Figure 9.
Graphical explanation of the CACSD distinguishing the safety zone.
As shown in Figure 9, the image projection will be zoomed in. Therefore, it is necessary to set up a threshold of the mapping frame from the FOV. For the current system, the lengths of and axes per pixel are determined by and .
The control system measures the distance between the camera and the global positioning system (GPS), the left and right wings, and the feet and the ratio between them, and calculates the size of the quadcopter on the imaging plane at the critical distance.
For the spiral convolution, it starts from the target mass center on the pixel coordinates to find the space to move from the inside to the outside. If the target is not found, the next process is completed. Because the space around the target has already been searched during the process of spiral convolution, there is no need to continue searching for the shortest path around the target. Instead, it directly starts searching for the remaining part.
4. Adaptive Cruise Control (ACC)
The adaptive cruise control system aims at the distance between the quadcopter drone and the target by adaptive adjusting the speed of target tracking.
4.1. Thrust Force
The acceleration of the quadcopter is determined by the body inclination angle . As the moment of inertia , arm length , and motor coefficient are all constants, thus the rotational speed of the motor is a major concern. The thrust force is computed by , where length is the propeller diameter, pitch denotes the propeller pitch angle, and denote the voltage per revolution of the motor. The thrust force of the motor is gram-force. With the obtained thrust force, propeller diameter, and moment of inertia, the inclination is .
4.2. Fuzzy Control Implementation
Figure 10 illustrates the scenario of the target follower. When the quadcopter is far away from the target, the flight control command increases the angle of the pitch axis to speed up the task.
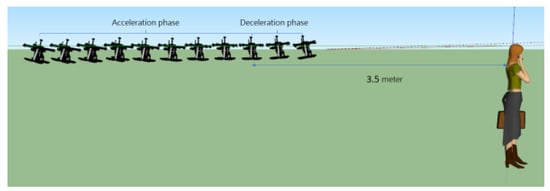
Figure 10.
Graphical explanation of the target follower.
As the quadcopter drone gradually approaches the target with higher speed, the relative distance between the target and quadcopter would be gradually decreasing. When the quadcopter decelerates but the target person starts to move forward, the quadcopter would respond by speeding up again. The faster the target walks, the faster the quadcopter will follow.
Figure 11 displays the schematic diagram of the overall control system where the motor mixing algorithm (MMA) transfers the roll, yaw, and pitch control commands to the driving commands of four DC brushless motors.
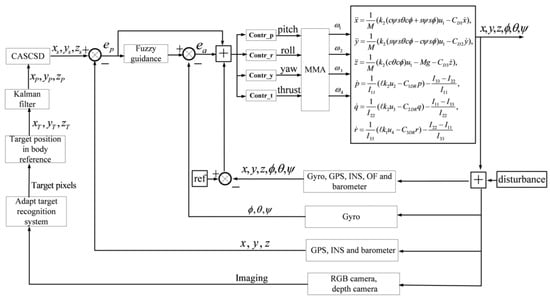
Figure 11.
The flight control system.
To cope with the high nonlinearity of the quadcopter flight dynamics, a fuzzy logic control is incorporated here as the core of the ACC system. A fuzzy guidance controller with two inputs and one output is implemented. The adopted membership functions are shown in Figure 12, Figure 13 and Figure 14, where the fuzzified inputs are and and the fuzzified output is , with representing the degree of membership of fuzzification; and V are the relative distance and speed between the quadcopter and the target, respectively, and is the acceleration output. Each group of the membership functions possesses seven fuzzy sets. The membership functions in Figure 12 specify the relative distance between the quadcopter and the target. Considering the capability of the camera, the fixed relative distance is set to be 3.5 m. This corresponds to the linguistic variable .
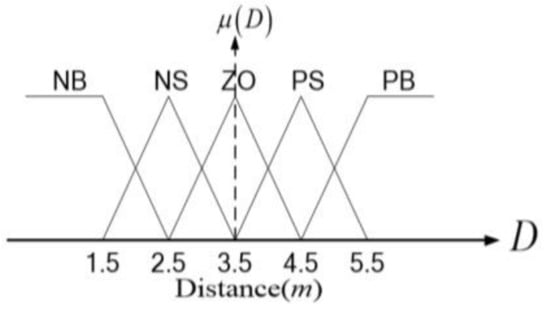
Figure 12.
Membership functions for characterizing the target–quadcopter relative distance.
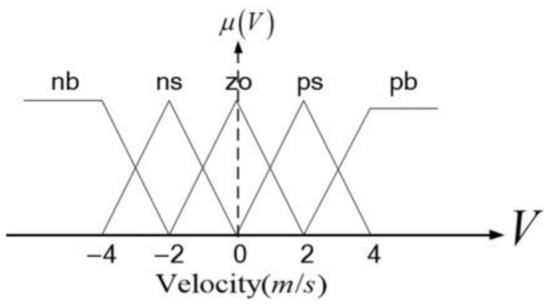
Figure 13.
Membership functions for characterizing the target–quadcopter relative speed.
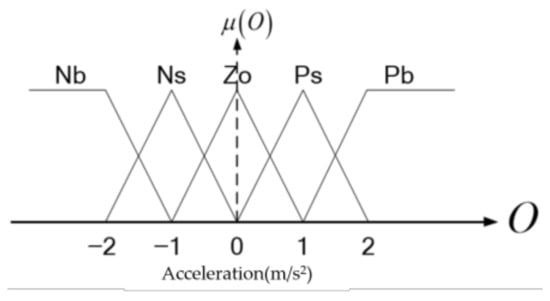
Figure 14.
Membership functions for characterizing control command.
The membership functions in Figure 13 are used to fuzzify the relative speed. In the universe of discourse, zero means that the target and the quadcopter are in still status or they are synchronously moving; the interval from zero to two refers to the walking status of the target, and the interval from two to four refers to the running status. Refined fuzzification of the variables is achievable by increasing the number of membership functions.
Figure 14 shows the membership functions characterizing the acceleration command. The goal is for the quadcopter to maintain a certain distance and quadcopter speed and LOS between to the target.
There are 25 guidance rules in total that are sorted in Table 1. The guidance law adopts proportional navigation guidance (PNG) commonly adopted by homing air target missiles based on the fact that the target and quadcopter are on a contact course when their direct LOS does not significantly change direction as the range closes. The guidance rules here are to keep a constant relative distance between the target and the quadcopter. The center of gravity method is adopted for the defuzzification of the inferred results.

Table 1.
Fuzzy guidance rule base.
5. Experimental Verification
In order to prove the feasibility of the theory, we conducted experiments such as outdoor tracking targets, indoor tracking targets, ladder tracking targets, and intelligent obstacle avoidance. The results are shown and explained as follows, and one can also refer to the following video URL: https://www.youtube.com/watch?v=ko9BaSFTcwA (accessed on 21 November 2021).
5.1. Autonomous Flight
Firstly, to examine the capability of a fundamentally stable flight, a 3D rectangular flight for the performance validation of the ACC was conducted. The real-world experimental results are shown in Figure 15 for the autonomous flight. The green solid line shows the planned flight path, the blue dotted line shows the flight result estimated by the extended Kalman filter (EKF), and the red dotted line presents the GPS measurement result. It verifies that under the interference of strong wind, the offset of the UAV flight path and the planned path is satisfactorily less than 0.2 m under the help of the real-time kinematic positioning (RTK) technique [23].
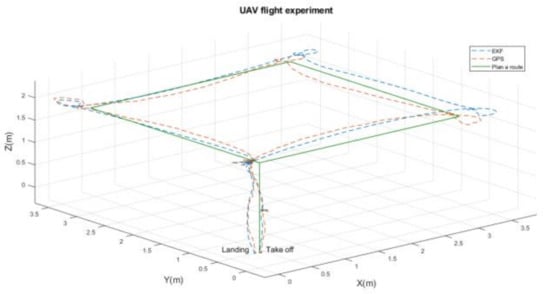
Figure 15.
The experimentally autonomous rectangular flight.
5.2. Target Identification
A demonstrative image for locating the object based on the proposed YOLO algorithm is shown in Figure 16, where the matching scores are shown corresponding to the target feature, human face, clothing, and shorts.
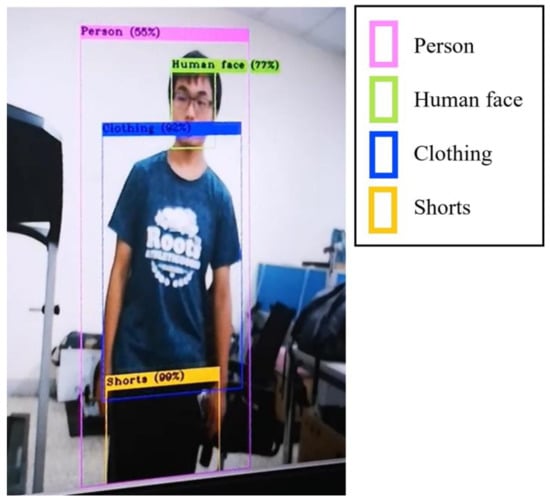
Figure 16.
Demonstration of the locking the target.
The setting of weighting factors for target features is . IS is set to 4 × 3, a = 0.8, and b = 0.6. The position accuracy is normalized via the sigmoidal function, and are the prediction coordinates from the previous frame of the target. It is based on the prediction of the position from the last frame compared with the measured position in the current frame. If the target achieves a high score with an accuracy level higher than, for example, 70%, the subject is recognized. We aimed to track the target with an orange jacket, blue trousers, and short black hair, as illustrated in Figure 17. The experimental result of the recognition rate (RR) of each subject within the video frame is listed in Table 2.

Figure 17.
Experimental test of the adaptive target identification.

Table 2.
RR of the objects that appear in Figure 17.
5.3. Estimation of Target Movement
Figure 18 illustrates the experimental result of the estimated target trajectory. The specific scenario is an inclined stair. The red line denotes the target trajectory and the green line denotes the predicted trajectory. This scenario represents a kind of extremal situation for the quadcopter drone during flight. When the target moves back and forth along the stair, the Kalman filter can still accurately predict the moving target trajectory.
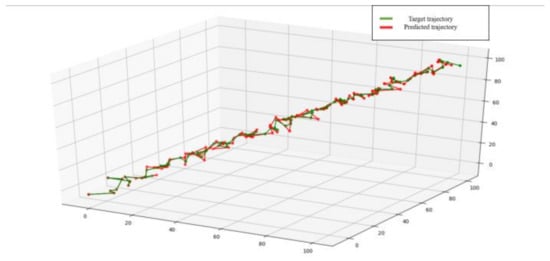
Figure 18.
Kalman filtering estimation of the moving target movement along an inclined stair.
Figure 19 displays the real-world experimental results, which shows that even when the target is walking past a shelter, the state estimator can keep tracking the target. In the photo, the red dot denotes the human target center and the green dot shows the predicted point generated by the Kalman filter.

Figure 19.
The experimental results of the target trajectory estimation.
5.4. Dynamic Target Tracking
The test environment includes outdoor grass, indoor corridors, and staircase. Figure 20 demonstrates the outdoor tracking test where the image tracking system, based on the deep learning algorithm proposed, has precisely locked target and started tracking.

Figure 20.
Front tracking of the target from the view of the quadcopter.
As shown in Figure 21, there are two difficulties when the quadcopter is tracking the target under a windy environment. It is difficult for a lightweight quadcopter to maintain a stable altitude because the air pressure sensor might be affected by the environmental disturbance. The second is that the quadcopter itself is susceptible to the influence of wind, which always destabilizes the body attitude. The fuzzy control tuning proposed here has reserved a margin for tracking performance under the severe operating environments.

Figure 21.
UAV tracking target test outdoors (The sequence of target movement and UAV tracking is shown in 1–4).
Figure 22 demonstrates the quadcopter tracking a target who is climbing the stairs. The difficulty in this case is that the target may simultaneously move horizontally and vertically. Thus, the quadcopter speed has to be accurately controlled to avoid the loss of locking.

Figure 22.
UAV tracking target test on stairs (The sequence of target movement and UAV tracking is shown in 1–3).
The case of target tracking in a narrow corridor is shown in Figure 23. This scenario tests the stability of the quadcopter without GPS assistance. For this kind of constricted environment, the quadcopter may suffer from the self-generated wind turbulence while the propelled air rebounds from the wall. Moreover, the indoor sharp corner movement becomes another critical issue to challenge the quadcopter’s capability in space detection and agility of attitude control.

Figure 23.
UAV tracking target test at the corridor (The sequence of target movement and UAV tracking is shown in 1–5).
5.5. Feature Comparison
The smart tracking and obstacle avoidance functions of this study are mainly based on the UAV personal security guard system. In order to prove the significance of the research, we cite several documents to show that the functions do not meet the research requirements. The comparison is as follows in Table 3.

Table 3.
Feature comparison table.
6. Conclusions
This paper proposes a lightweight and intelligent UAV tracking and obstacle avoidance system. First, we used the YOLO model with fewer layers to recognize humanoid objects. Secondly, we proposed a lightweight adaptive target identification algorithm, which can extract personal clothing features and filter out complex image backgrounds other than the targets for target identification among crowds. Next, it was necessary to determine the movable space of the UAV, so we proposed the contour and spiral convolutional space detection (CASCSD) algorithm to search the moving area with the shortest distance between the UAV and the object and combine it with the Kalman filter, which estimates the displacement path when obstacles block the tracked object. Finally, a fuzzy adaptive cruise control (ACC) system keeps the drone at an optimal distance while tracking targets. As the selected experimental sites of this study are indoors, outdoors, and in stairwells, it can be applied to the personal security guard scenario.
Because the YOLO model is used for human recognition, it accounts for most of the computing power of the embedded system, resulting in only about ten frames of images during tracking, so the tracking efficiency is not good. However, we have also tested the sum of the other algorithms; it only takes 0.03 s to complete all calculations. We believe that more experts and scholars will propose more lightweight human recognition algorithms in the future. By then, with the lightweight algorithm of this research, the personal security guard system will have higher flexibility and stability.
Author Contributions
Conceptualization, W.-C.C. and C.-L.L.; methodology, W.-C.C. and Y.-Y.C.; software, W.-C.C.; validation, Y.-Y.C., C.-L.L. and H.-H.C.; formal analysis, W.-C.C.; investigation, Y.-Y.C.; resources, C.-L.L.; data curation, H.-H.C.; writing—original draft preparation, W.-C.C.; writing—review and editing, Y.-Y.C.; visualization, W.-C.C.; supervision, C.-L.L.; project administration, C.-L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Ministry of Science and Technology, Taiwan under the grant MOST 110-2221-E-005-084-MY2.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The following development for quadcopter dynamics is standard in [34], in which necessary modifications been considered to fit in the current purpose. Firstly, for the upward thrust force of four motors shown in Figure 2, we define
where is the rotational speed of each motor and is a proportional constant.
The quadcopter heads move in the direction of . The four propellers generating downward thrust are standard and given by
Assume that the magnitude of the generated torque is proportional to the square of the rotation speed. That is,
where is a positive gain. The torques of the four motors can then be written as
One can obtain the relationship between the above-mentioned motor thrusts – and the arm length of the quadcopter. The induced torque generated by the outer product of the force arm vector and the thrust is given by
where refers to the arm length and denotes the ith force arm vector. The induced torques of four motors are, respectively, given by
The rigid body momentum and angular momentum are described by
where is the rigid body momentum, denotes the angular momentum, and the subscript ex represents the external force applied to the rigid body.
Lagrangian mechanics are adopted for the analysis. The configuration space of the quadcopter is denoted as , where and refer to the position and direction of the quadcopter and motor frames, respectively. Because the four motors on the quadcopter are fixed on the frame and can only rotate around their respective axis, this means that they have only one degree of freedom relative to the quadcopter frame. Therefore, it can be further simplified to .
The quadcopter movement is controlled by the motor rotational speed. is in the group. It has the following property:
Next, define the angular speed matrix , where and denotes the antisymmetric matrix operation.
The kinetic energy of the quadcopter is given by
where the translational kinetic energy is
with being the quadcopter mass and the rotational kinetic energy:
where is the standard inner product in and is the inertia tensor, is the atmospheric density, is each mass point on the quadcopter, , is the center of mass, and is the position of the small mass in the coordinate system.
Let . We calculate the kinetic energy metric for the manifold by the following equation:
where are the velocity parameters of on the manifold. That is,
where denotes the moment of inertia of the corresponding axis and are the respective linear speed of the center of mass along the corresponding axes. As is the smooth function, it is a pseudo-Riemannian manifold because of its characteristics. Therefore, one can use a tensor to derive the Levi-Civita connection coordinate and adopt the Christoffel symbols in the holonomic equation:
As G is a constant matrix, it represents a flat manifold.
Lagrangian Mechanics
Recalling (A4)–(A6) and (A14), those are the conditions for the Newtonian mechanics that transfer to the Lagrangian mechanics. Let be the element in the tangent bundle of the manifold of (8). is the dual vector in the dual tangent space, is the Lagrangian force, and
where , was defined in (A3) and and are the velocity and angular speed, respectively. One can expand by linear projection:
Substituting (A1)–(A6) into (18) gives
where is the gravitational constant.
References
- Karar, A.S.; Said, S.; Beyrouthy, T. Pepper Humanoid Robot as A Service Robot: A Customer Approach. In Proceedings of the 2019 3rd International Conference on Bio-engineering for Smart Technologies (BioSMART), Paris, France, 24–26 April 2019. [Google Scholar]
- Cuthbertson, A. Watch: Is Google’s New Two-Legged Robot the Soldier of the Future? In Newsweek; IBT Media: NY, USA, 2016. [Google Scholar]
- Ou, S.Q. Vision-based Path Planning and Control of a Mobile Robot Based on DNN Object Recognition and ORB-SLAM2. Master’s Thesis, National Chiao Tung University, Taiwan, 2019. [Google Scholar]
- Kiss, G. External Manipulation of Autonomous Vehicles. In Proceedings of the 2019 IEEE Smartworld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computing, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation, Leicester, UK, 19–23 August 2019. [Google Scholar]
- NTU. Singapore and Volvo Unveil World’s First Full Size, Autonomous Electric Bus. 2019. Available online: https://www.volvobuses.com/en/news/2019/mar/volvo-and-singapore-university-ntu-unveil-world-first-full-size-autonomous-electric-bus.html (accessed on 8 June 2020.).
- Jeong, H.Y.; Song, B.D.; Lee, S. The Flying Warehouse Delivery System: A Quantitative Approach for the Optimal Operation Policy of Airborne Fulfillment Center. IEEE Trans. Intell. Transp. Syst. 2020, 22, 7521–7530. [Google Scholar] [CrossRef]
- Palmer, A. Amazon Wins FAA Approval for Prime Air Quadcopter Delivery Fleet. In Consumer News and Business Channel; NBC Universal: Englewood Cliffs, NJ, USA, 2020. [Google Scholar]
- Yang, N.K.; San, K.T.; Chang, Y.S. A Novel Approach for Real Time Monitoring System to Manage UAV Delivery. In Proceedings of the 2016 5th IIAI International Congress on Advanced Applied Informatics, Kumamoto, Japan, 10–14 July 2016. [Google Scholar]
- Mechali, O.; Xu, L.; Xie, X.; Iqbal, J. Theory and practice for autonomous formation flight of quadrotors via distributed robust sliding mode control protocol with fixed-time stability guarantee. Control Eng. Pract. 2022, 123, 105150. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Z.; Gao, H. Robust adaptive recursive sliding mode attitude control for a quadrotor with unknown disturbances. ISA Trans. 2022, 122, 114–125. [Google Scholar] [CrossRef] [PubMed]
- Guo, K.; Jia, J.; Yu, X.; Guo, L.; Xie, L. Multiple observers based anti-disturbance control for a quadrotor UAV against payload and wind disturbances. Control Eng. Pract. 2020, 102, 104560. [Google Scholar] [CrossRef]
- Qin, X.; Wang, T. Visual-based Tracking and Control Algorithm Design for Quadcopter UAV. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019. [Google Scholar]
- Zhang, W.; Song, K.; Rong, X.; Li, Y. Coarse-to-Fine UAV Target Tracking with Deep Reinforcement Learning. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1522–1530. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Z.; Wang, D.; Wang, S.; Qi, Y.; Lu, H. Online Single Person Tracking for Unmanned Aerial Vehicles: Benchmark and New Baseline. In Proceedings of the ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing, Brighton, UK, 12–17 May 2019. [Google Scholar]
- Vasconcelos, F.; Vasconcelos, N. Person-Following Uavs. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Lake Placid, NY, USA, 7–10 March 2016. [Google Scholar]
- Shen, Q.; Jiang, L.; Xiong, H. Person Tracking and Frontal Face Capture with UAV. In Proceedings of the IEEE 18th International Conference on Communication Technology, Chongqing, China, 8–11 October 2018. [Google Scholar]
- Singla, A.; Padakandla, S.; Bhatnagar, S. Memory-Based Deep Reinforcement Learning for Obstacle Avoidance in UAV with Limited Environment Knowledge. IEEE Trans. Intell. Transp. Syst. 2019, 22, 107–118. [Google Scholar] [CrossRef]
- Hou, J.; Zhang, Q.; Zhang, Y.; Zhu, K.; Lv, Y.; Yu, C. Low Altitude Sense and Avoid for MUAV Based on Stereo Vision. In Proceedings of the 2016 35th Chinese Control Conference, Chengdu, China, 27–29 July 2016. [Google Scholar]
- Li, B.W. Obstacle Detection and Collision Avoidance for Multicopters; National Central University: Taichung, Taiwan, 2017. [Google Scholar]
- Han, D.; Yang, Q.; Wang, R. Three-Dimensional Obstacle Avoidance for UAV Based on Reinforcement Learning and RealSense. J. Eng. 2020, 13, 540–544. [Google Scholar] [CrossRef]
- Zheng, Z.; Yao, H. A Method for UAV Tracking Target in Obstacle Environment. In Proceedings of the 2019 Chinese Automation Congress, Hangzhou, China, 22–24 November 2019. [Google Scholar]
- Wang, Y.; Wang, H.; Lun, Y. Shortest Path Planning of UAV for Target Tracking and Obstacle Avoidance in 3D Environment. In Proceedings of the Chinese Control Conference, Shenyang, China, 27–30 July 2020. [Google Scholar]
- Heidari, A.; Navimipour, N.J.; Unal, M.; Zhang, G. Machine Learning Applications in Internet-of-Drones: Systematic Review, Recent Deployments, and Open Issues. ACM Comput. Surv. 2022. [Google Scholar] [CrossRef]
- Tanaka, S.; Asignacion, A.; Nakata, T.; Suzuki, S.; Liu, H. Review of Biomimetic Approaches for Drones. Drones 2022, 6, 320. [Google Scholar] [CrossRef]
- Guo, K.; Tang, P.; Wang, H.; Lin, D.; Cui, X. Autonomous Landing of a Quadrotor on a Moving Platform via Model Predictive Control. Aerospace 2022, 9, 34. [Google Scholar] [CrossRef]
- Tian, X.; Jia, Y.; Luo, X.; Yin, J. Small Target Recognition and Tracking Based on UAV Platform. Sensors 2022, 22, 6579. [Google Scholar] [CrossRef]
- Solak, S.; Bolat, E.D. A new hybrid stereovision-based distance-estimation approach for mobile robot platforms. Comput. Electr. Eng. 2018, 67, 672–689. [Google Scholar] [CrossRef]
- Li, B.; Wu, Y. Path Planning for UAV Ground Target Tracking via Deep Reinforcement Learning. IEEE Access 2020, 8, 29064–29074. [Google Scholar] [CrossRef]
- Henkel, P.; Lamm, M.; Mittmann, U.; Fritzel, T.; Strauß, R.; Steinert, H.-J.; John, M. Verification of RTK Positioning of UAVs with High-Precision Laser Tracker. In Proceedings of the 2022 16th European Conference on Antennas and Propagation (EuCAP), Madrid, Spain, 27 March–1 April 2022. [Google Scholar]
- Gao, S.; Zhang, T. 14 Lectures on Visual SLAM; Publishing House of Electronics Industry: Beijing, China, 2017. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. Yolov3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Chen, W.C. Design and Implementation of an Intelligent UAV. Master’s Thesis, National Chung Hsing University, Taiwan, 2021. [Google Scholar]
- Huang, Q. Mathematical Modeling of Quadcopter Dynamics; Rose-Hulman Scholar: Terre Haute, IN, USA, 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).