1. Introduction
The Intergovernmental Panel on Climate Change [
1] (IPCC) has estimated the likely range of equilibrium climate sensitivity (ECS) to be between 1.5 and 4.5 K. The ECS, which is widely used in assessments of anthropogenic climate change, is defined as the asymptotic temperature increase following an instantaneous CO
doubling. In Earth system models (ESMs), the ECS is generally estimated via the so-called Gregory plots [
2], where the response in the top-of-the-atmosphere radiation
N is plotted against the global mean surface temperature (GMST) anomaly
during the equilibration following an instantaneous doubling or quadrupling of the atmospheric CO
concentration. The assumption is that the adjustment in radiation depends linearly on the surface temperature increase,
so that the feedback parameter
and the forcing
F can be determined via linear regression. The ECS is hence
, where
is the forcing associated with a CO
doubling. The Gregory plots show that the linearity assumption is only approximate, and in particular, there are slow feedbacks in the models that reduce the feedback parameter as the planet warms [
3]. A state dependence is also observed in the so-called paleo sensitivity [
4,
5,
6,
7]. Nevertheless, the usefulness of ECS and its estimation still relies on the linearity assumption in Equation (
1). Satellite observations of the top-of-the-atmosphere radiation are available through the Clouds and the Earth’s Radiant Energy System (CERES), but unfortunately, the data only covers the years 2000-present. The state-of-the-art ECS estimates based on the satellite data gives a wide likely range (in this case a 17–83% confidence interval) of 2.4–4.5 K [
8].
A different approach, which can be used when the top-of-the-atmosphere radiation is unknown, is to combine model results with the instrumental temperature record. Recently Cox et al. claimed that ECS can be constrained to a “likely range” (in this paper specified to be the 66% confidence interval) of 2.2 to 3.4 K, with a best estimate of 2.8 K [
9]. They propose a metric
characterizing the correlation structure of the internal variability of the GMST in both the instrumental temperature record in the period 1880 to 2016 and in the corresponding historical runs in the Coupled Model Intercomparison Project Phases 5 (CMIP5) ensemble. By exploring a so-called emergent relationship between ECS and
, they estimate a distribution
for the Gregory estimate of ECS conditioned on
, and using the law of total probability in conjunction with Bayes Theorem, they obtain a probability density function
constrained by the instrumental record. However, it has been demonstrated that their estimated metric depends on the response to the strong anthropogenic forcing in the time period after year 1950, and hence one has to take into account that the historical forcing times series used in different models in the ensemble are not exactly the same [
10]. Another problem is that the emergent relationship was derived from an oversimplified one-box stochastic energy balance equation (Equation (
7) described in
Section 2.1). This model does not take into account the memory effects in the response due to heat exchange between the ocean mixed layer and the deep ocean. Models that do incorporate such memory effects are briefly reviewed in
Section 2.2 and
Section 2.3.
A method of constraining ECS from the instrumental record that does not draw on a simplified physical model is to include data for historical forcing, with its uncertainties, and to estimate response functions that describe the relationship between global radiative forcing and the observed GMST. If one adopts a hypothesis of a linear and stationary response, then the temperature anomaly
can be written as a convolution of the forcing
F with a response function
:
where the term
is the known (deterministic) forcing and
represents a white-noise random forcing that gives rise to the internal variability. Equation (
2) only assumes linearity and stationarity of the response, and it is only the functional form of
that depends on the particular physical modeling of this response. As discussed in
Section 2.2, such a linear response can be derived from a multi-layer energy balance model, where the response function is a sum of exponential functions with decay rates that are given by the real and negative eigenvalues of the system of differential equations. Fredriksen and Rypdal [
11] have shown that three exponential terms are sufficient to obtain a model that simultaneously displays responses to historical and reconstructed forcing that are consistent with the instrumental temperature record and the reconstructed last millennium global mean temperature, respectively. In addition, it correctly describes the statistical properties of the internal variability on time scales from months to centuries [
12]. The constructed response function corresponds to an ECS estimate of 3.0 K, obtained by using the forcing
in Equation (
2), where
is the unit step function. Defining the ECS as
, Equation (
2) yields
The forcing
is well approximated by a logarithmic dependence of the CO
concentration, with a best estimate of 3.7 W/m
found by the IPCC [
1]. Uncertainties associated with the radiative transfer calculations are small [
13]. However, forcing estimates from CMIP5 models often include rapid adjustments of the atmosphere, resulting in larger uncertainties [
14]. The more serious issues are the uncertainty of the estimate of the response function, the uncertainty of the adjusted forcing data, and the validity of the linearity assumption.
The uncertainty of the response function estimates can be assessed in several ways, for instance using an ensemble of runs of the same experiment in one ESM. The uncertainty of the forcing presents a significant challenge, which is not addressed by Cox et al. [
9]. In the present paper, we take part of this uncertainty into account by analyzing the spread of the adjusted forcing over the CMIP5 ensemble. We shall also consider the order of magnitude of uncertainty that can be attributed to our limited knowledge about the forcing from volcanic aerosols. In model runs with historical forcing, the adjusted forcing is obtained from Equation (
1) by comparing the time series of
and the top-of-the-atmosphere radiation
for a fixed estimate of the feedback parameter
[
15]. The resulting time series
is an estimate of the forcing experienced by the ESM. However, the construction of
from the assumed linear relationship between
and
results in forcing signals where some short-scale internal climate variability, including the El Niño Southern Oscillation (ENSO), are clearly observable in the forcing signal. Consequently, these forcing data are not suitable for statistical estimation of response functions
from Equation (
2). The alternative, which is used in this paper, is to fix a forcing time series, for instance the time series provided by Hansen et al. [
16], and to modify it for each model so that the trend (or low-frequency variability) is equal to the adjusted forcing for the model. This approach serves two purposes; we ensure that when we fit a response function to a model the increasing trend in the forcing is consistent with the forcing in the model run, and it provides an ensemble of forcing time series with different trends. The estimates of the response function from the observed temperature record can be repeated across this ensemble of forcing time series and provide an estimate of the uncertainty in the response function that is associated with the uncertainty in the forcing trend.
If one derives the response function from a multibox energy balance model it will take the form (see
Section 2.2),
In
Section 3 it is described how to obtain statistical estimates
and
of the parameters
and
from historical runs of each of the ESMs in the CMIP5 ensemble, as well as for the instrumental temperature record. For each model, this estimate corresponds to an estimate of ECS through Equation (
3), which in this case reads
If the estimate
correlates strongly with the Gregory estimate of ECS over the CMIP5 ensemble, then the estimate
obtained from the instrumental temperature record can be used to constrain the distribution of ECS in the ensemble. Unfortunately, such an analysis will show a very weak correlation between the two estimates, and this apparently indicates that response function estimates are useless for constraining ECS. On the other hand, the reason for the low correlation is that the instrumental temperature record is too short to provide useful information about the slow response of the climate system, and the general form of the response function leads to statistical over-fitting. The method can be improved by reducing the number of free parameters. A naïve approach is to reduce the response function to one characteristic time scale (which is what comes out of using the one-box model employed by Cox et al. [
9]). This gives a model that is unable to accurately describe the temporal structure of the temperature response, and would lead to a systematic underestimation of the ECS. A better alternative is to use the emergent property of temporal scale invariance.
Rypdal and Rypdal [
12] have demonstrated that a scale-invariant response model, i.e., Equation (
2) with
where
km
J
is a factor needed to give
the right physical dimension, provides a parsimonious and accurate model on time scales from months to several centuries, although not on longer time scales. In fact, it will be argued in
Section 4 that the power-law dependence (at least in the models) is invalid on time scales substantially longer than a millennium. The existence of a cut-off in this dependence on very long time scales is obvious, since the ECS according to Equation (
3) would be infinite otherwise [
12]. We don’t have to worry about this cut-off when we estimate the model parameters from historical data since the temperature records and the forcing time series we have for the industrial period are relatively short compared to this cut-off time, which corresponds to the time it takes for global surface temperature to relax to a new equilibrium after an abrupt CO
doubling in ESMs. This large separation of the two time scales (observation time and relaxation time) is also the main reason why it is so difficult to provide accurate estimates of ECS from observational data. The fact that a response model with infinite ECS can perform well when tested on observation data suggests that these time series are too short for ECS assessment and that ECS may not be the most useful measure of climate sensitivity in the face of anthropogenic climate change. It may be more useful to study the scale-dependent (or frequency-dependent) sensitivity;
where
is the Fourier transform of the response function. However, as the main results of this paper will show, the scale dependent sensitivity evaluated at
y
correlates strongly with the Gregory estimate of ECS. Hence, this technique can be used to constrain the ECS in the model ensemble on the instrumental temperature record. It is evident from the results presented in this paper that uncertainty in the historical forcing data is the main obstacle for more accurate assessment of ECS.
The paper is structured as follows. In
Section 2 we discuss stochastic linear response models for global surface temperature variability to motivate the analyses presented in
Section 4. We also discuss some dissipation-response relations that follow from this modeling framework. Details on data employed and the statistical analyses are presented in
Section 3. In
Section 4 we present the main results, and in
Section 5 we discuss and conclude our findings.
4. Results
For each ESM in the CMIP5 ensemble we modify the forcing data of Hansen et al. [
16] such that its 17-year moving average becomes identical to the the moving average of adjusted forcing provided by Forster et al. [
15] for that model. This is done by adding the difference between the moving average of the adjusted model forcing and the Hansen forcing to the raw Hansen forcing time series. The idea is to construct forcing time series for each model that retain a common structure on time scales that resolve volcanic forcing, the solar cycle and ENSO variability, but exhibit the overall trend on multi-decadal time scales of the forcing time series used in the respective models. A 17-year moving average window is found to be the optimum choice to achieve that goal. For the model given by Equation (
2) with response function given by Equation (
5) we fit parameters
and
to the global surface temperature of the historical run of the given ESM, using the modified Hansen forcing as input. The parameters are estimated using a technique described in
Section 3.
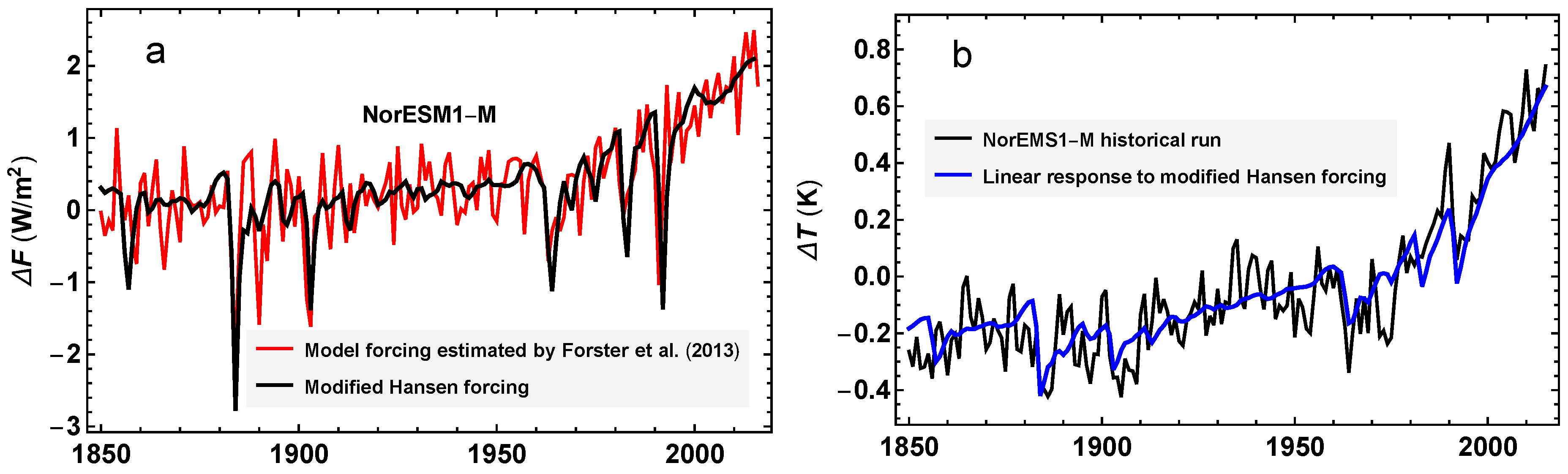
Figure 1a shows the adjusted forcing and the modified Hansen forcing for the NorESM1-M model, and
Figure 1b shows the response to the modified Hansen forcing according to the fitted linear response model together with the global surface temperature in the historical run of the NorESM1-M model.
When parameters
and
are estimated for the historical runs of each ESM, the estimated scale dependent sensitivity
can be computed for each model using Equation (
6). The factor
is taken individually for each model based on the Gregory estimates in [
1]. A scalar metric
R is obtained by evaluating the functions
at the frequency
y
. The results are presented in
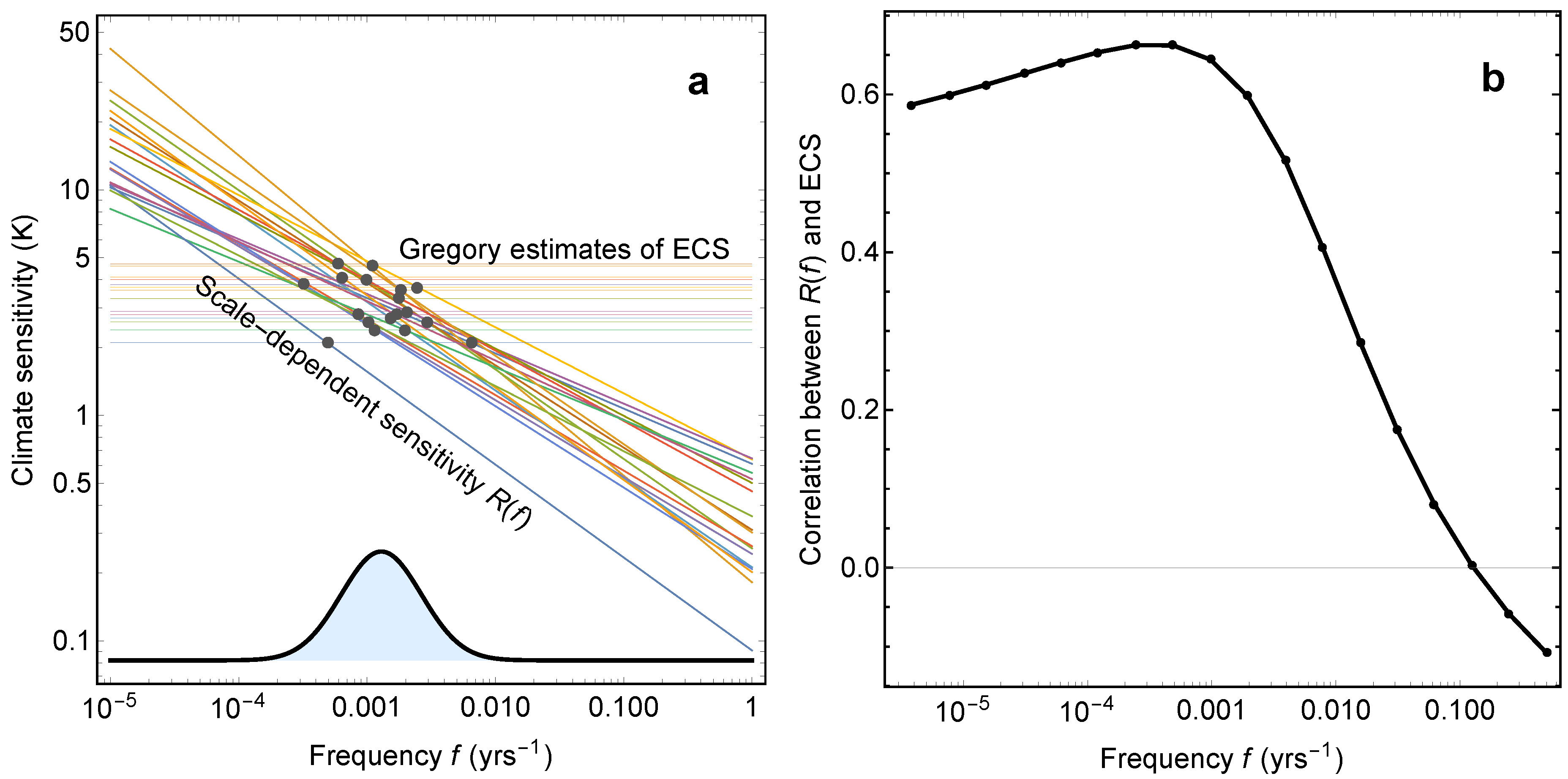
Table 1. The choice of frequency is based on how well the corresponding scalar metric correlates with the Gregory estimates of ECS. The scale-dependent sensitivities are computed from Equation (
6) under the assumption that the response function is scaling and given by Equation (
5). Hence the
-curves are power-laws and displayed as the straight, sloping lines in the double-logarithmic plot in
Figure 2a. The figure shows that over the model ensemble,
typically equals the Gregory estimate of ECS for frequencies
y
, and
Figure 2b shows that the correlation (over the model ensemble) between
and the Gregory estimate of ECS has its maximum for
y
. The falling correlation for lower
f suggests that the power-law assumption for
fails for time scales much longer than a millennium.
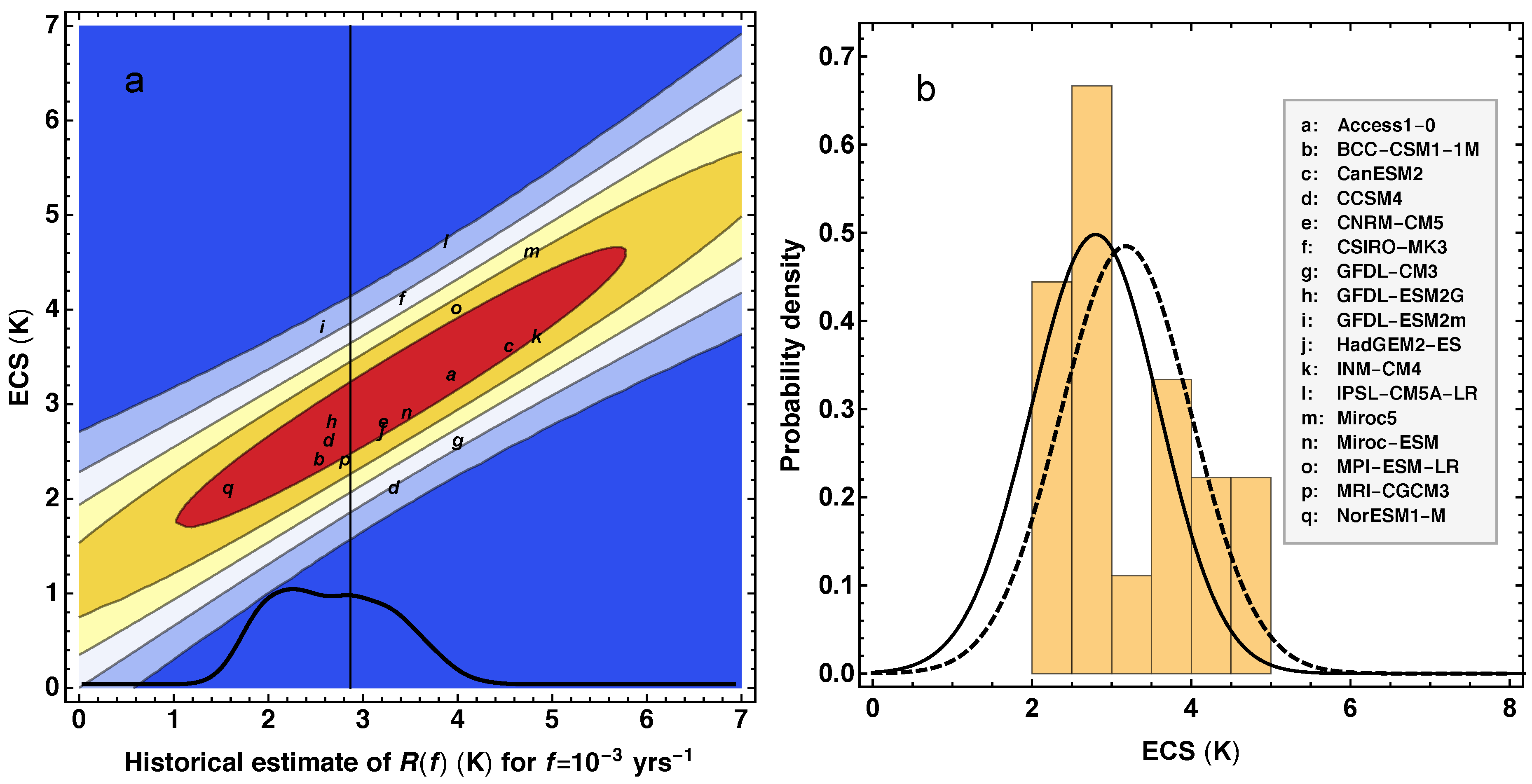
Figure 3a shows a plot of the
R, i.e.,
evaluated at
y
, versus the Gregory estimate of ECS. The points (letters) represent the different ESMs in the model ensemble, and the contour plot shows the conditional probability density function (PDF)
estimated from the seventeen data points corresponding to the seventeen ESMs in the ensemble. The method used to estimate
is the same as prescribed by Cox et al. (2018) [
9], with the obvious weakness that it is based on the assumption that the deviation among the models from an emergent linear relationship
between ECS and
R has a Gaussian distribution.
The vertical black line in
Figure 3a is
K. This value of
R is obtained from the parameters
and
y
, which are estimated from the instrumental temperature record using the Hansen-forcing. We have used
W/m
, which is the value for the GISS-E2-R model given in
Table 1. Hence this value for
R is the one estimated for the effective forcing used in this particular model and applied to the observed temperature time series. Similar estimates are made for the adjusted forcing in all the other models, using the values of
for those models given in
Table 1. The black curve in the lower part of
Figure 3a is a PDF
for the metric
R estimated this way. The PDF is obtained by considering two sources of uncertainty in the
R-estimates. One is the spread in parameter estimates when we vary the forcing. The forcing is varied over the set of modified Hansen forcing time series, where each modification corresponds to a historical run of an ESM in the ensemble. The parameter estimates for the instrumental temperature record, and the resulting value of
R, for varying forcing data is shown in
Table 2. Another source of uncertainty is the spread in the parameters
and
across repeated historical runs of the same model, i.e., runs where the known forcing is the same, but where chaotic dynamics create random components that vary among realizations.
Table 3 shows a set of parameter estimates for repeated historical runs of the CSIRO model, which is the model in the CMIP5 ensemble that provides the largest number of runs with identical forcing. The total variability from these two sources is obtained by a simple mixture model, and the plotted PDF is computed by a smooth kernel method. The black, full curve in
Figure 3b shows the PDF for ECS computed from the formula
where
is the PDF shown in
Figure 3a. The histogram in
Figure 3b is the distribution of ECS in the model ensemble, and the dotted curve is a Gaussian fit to the distribution of ECS in the model ensemble. The figure demonstrates that when constrained by the scale-dependent sensitivity of the instrumental temperature record, the best estimate of ECS in the model ensemble is reduced by approximately
K. The PDF
shown in
Figure 3a, also shows that, with the uncertainties taken into account, models with ECS larger than 4 K are inconsistent with the instrumental temperature record.
From
Figure 3a and Equation (
14) we observe that the uncertainty represented by
in
Figure 3b is formed by a combination of the range of
R-values
R represented by the black curve for
in
Figure 3a and the width of the conditional PDF represented by the contour lines in that panel. The latter represents the uncertainty associated with the deviation from the emergent linear relation between ECS and
R among the models, which is the main source of uncertainty found by Cox et al. (2018) [
9]. In our approach, however, the wide range of the metric
R represented by
that we have found by using the adjusted forcing of each model to estimate
R is a major contribution to the uncertainty in
.
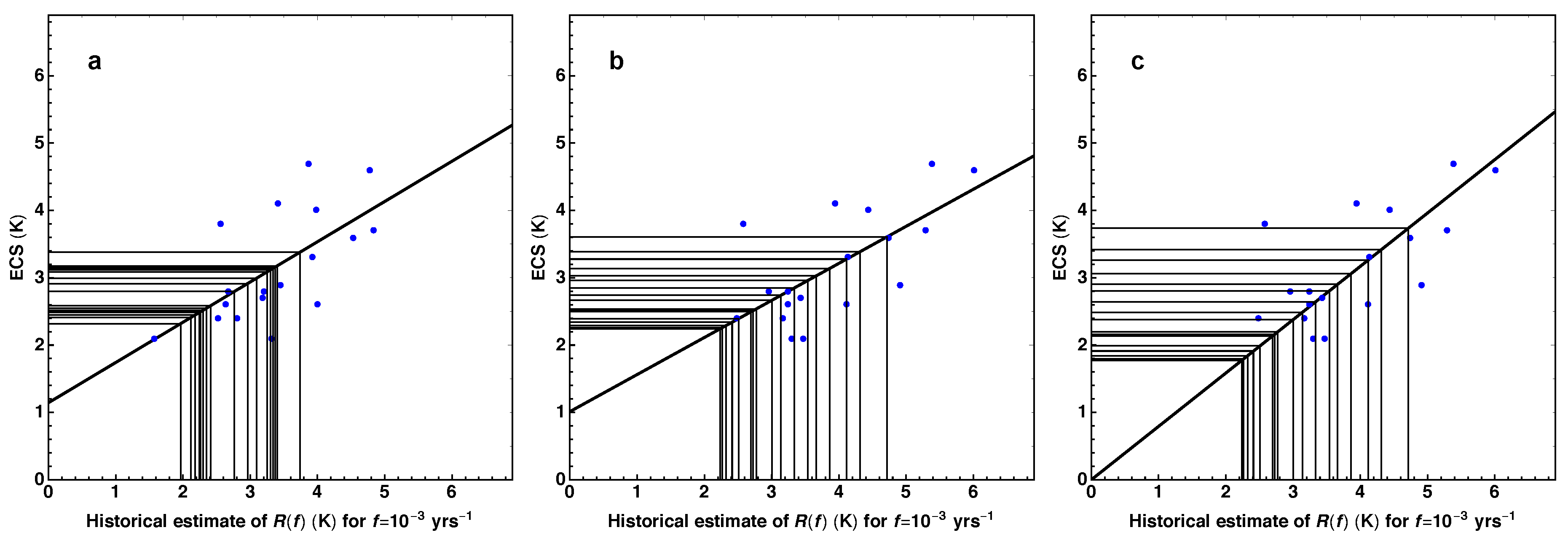
One can explore the effect of uncertainty of adjusted forcing among models on the uncertainty of ECS by neglecting the uncertainty associated with deviations from the emergent linear relation. From the scatter plot in
Figure 3a we can fit a linear relationship
, and in
Table 2 we have a set of estimates of
R for the instrumental temperature record. The linear fit maps each of the
R-estimates to an ECS-value, which can be interpreted as the best estimate of ECS based on the corresponding forcing data. This mapping is shown in
Figure 4a. The range of these best estimates of ECS are between 2.3 and 3.4 K. Note that these are the best estimate of
R for each model and that the uncertainty of each estimate arising from uncertainty in estimates of
and
is not taken into account. For this reason, we don’t plot PDFs, but only indicate the range of best estimates of
R.
The effect of uncertainty in the forcing on the estimated ECS can be explored further by varying the various forcing components within plausible ranges of uncertainty. As an example we consider the forcing from volcanic aerosols, which are subject to considerable controversy. In
Figure 4b we have made the same plot as in
Figure 4a, but with the volcanic component of the Hansen forcing reduced by 50 percent. The effect on the spread in the estimated ECS is considerable. Another source of uncertainty is the choice of regression model for the emergent relation between ECS and
R. From a physical viewpoint, vanishing ECS should correspond to vanishing
R, so if one sticks to a linear model it could be reasonable to choose the model
rather than
. The result for such a model, keeping the low volcanic forcing, is shown in
Figure 4c, with a range of best estimates for ECS between 1.8 and 3.7 K.
5. Discussion
The PDF for the ECS shown in
Figure 3b is similar to the one presented by Cox et al. [
9]. However, there are important differences in methodology that must be pointed out. Cox et al. use a pure dissipation-response relationship to constrain ECS in the model ensemble. They propose a metric
, which plays a similar role as the metric
R proposed in this work, and claim that estimates of
are independent of the forcing. This claim has been demonstrated to be false [
10]. In our framework, an approach in the spirit of Cox et al. would be to use Equation (
10), and to seek estimates of the correlation function (or equivalently the PSD) of the climate noise
that are independent of the forcing. Such an approach would lead to the same problems as those in [
9], namely that the estimates would be influenced by the strong anthropogenic forcing in the instrumental period. This is our motivation for developing a method that employs forcing data in the estimation of our metric
R, and as a consequence we have to take the uncertainty in the forcing into account. We have done this by using a fixed data set for historical forcing (the Hansen-forcing) and varied its low-frequency variability over the ensemble of adjusted forcing time series provided by Forster et al. [
15]. Clearly, this does not represent the full uncertainty in the historical forcing, and hence the spread in the distribution of ECS (the black, full curve in
Figure 3b) is narrower than what we expect to find if we were to model the full forcing uncertainty. We conclude that accurate estimates of the uncertainty in historical forcing is a key factor for establishing constraints on ECS in ESM ensembles.
The modeling of the relationship between
R and ECS is also a source of uncertainty. It is evident from
Figure 4a that the coefficient
a in the linear map
is less than one. In fact, its estimated value is
. As a consequence the mapping from
R to ECS is contracting, so that the spread in ECS-values is smaller than the spread in
R-values. The same is true for the analysis presented in
Figure 3, since the conditional PDF
is constructed from the fitted line
. We note that for a model without the intercept term
b, and lower volcanic forcing, the estimated coefficient is
, and the range of the best estimates of ECS becomes 1.8–3.7 K. Other assumptions about the functional relationship between
R and ECS will lead to yet different ranges of best estimates.
Apart from the constraints on ECS, an important result presented in this paper is that scale-dependent climate sensitivity provides a good proxy for ECS. Moreover, despite having infinite ECS, scale-invariant linear response models are useful for estimating ECS from observational data. The advantage over multi-layer energy balance models is that the scale-invariant models have few free parameters and are less prone to statistical overfitting. The accuracy of the models is associated with the scaling nature of climate variability, an emergent property of the complex climate system.