Clustering Indian Ocean Tropical Cyclone Tracks by the Standard Deviational Ellipse
Abstract
1. Introduction
2. Data and Methodology
2.1. Data
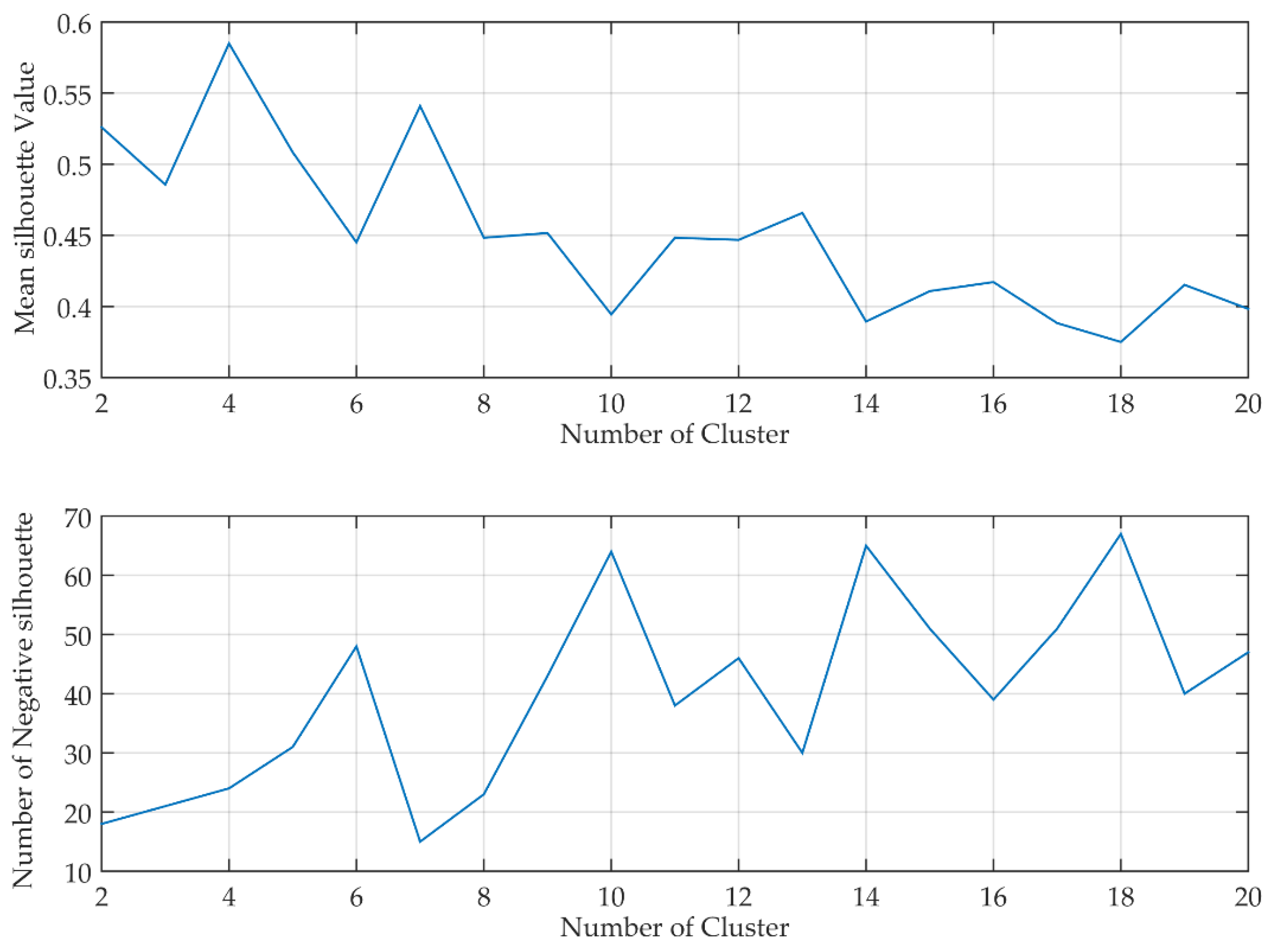
2.2. Clustering Process
2.3. Analysis of Large-Scale Climate Variabilities
2.4. Statistical Significance Test
3. Results and Discussion
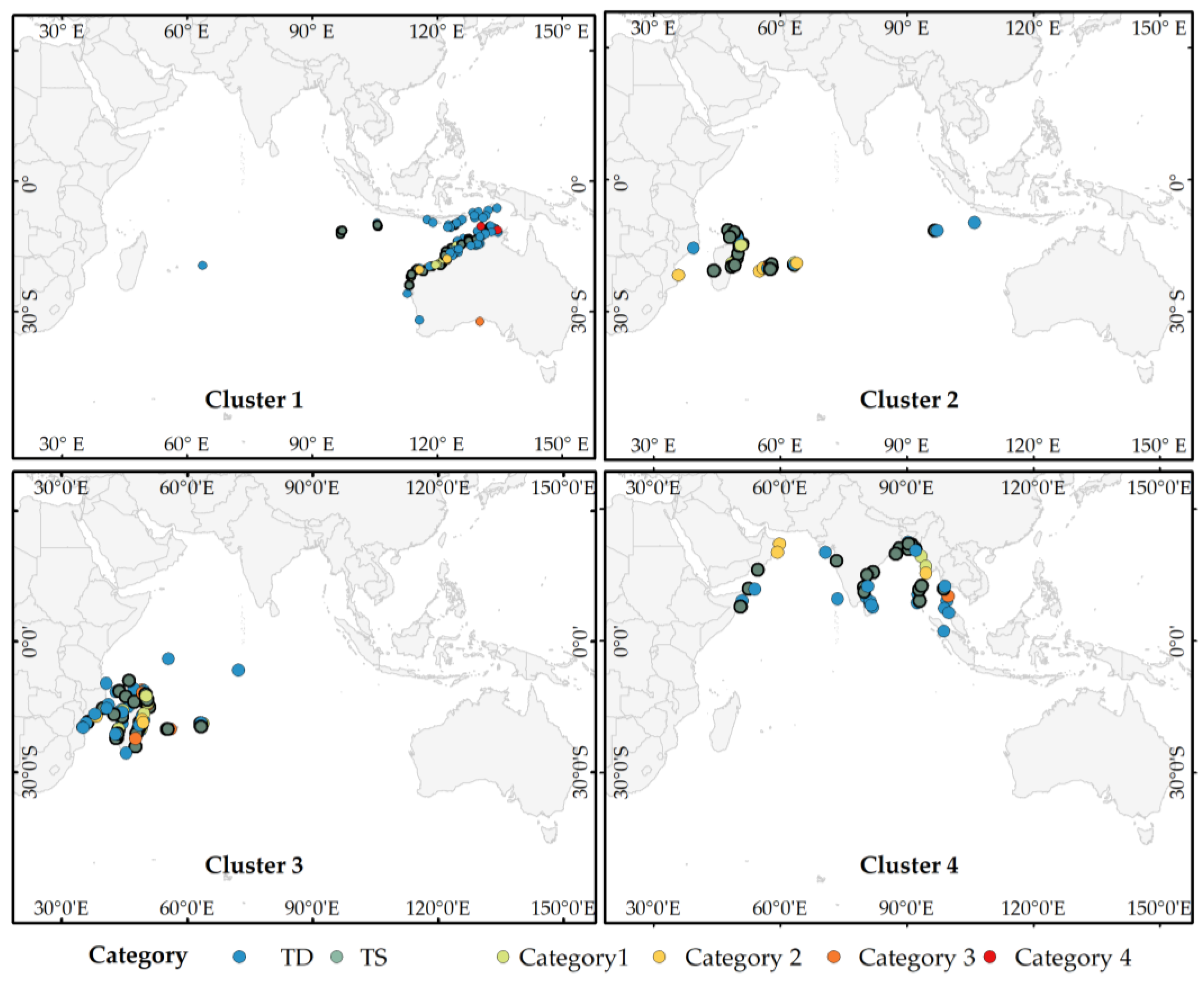
3.1. Genesis Location and Track Shape
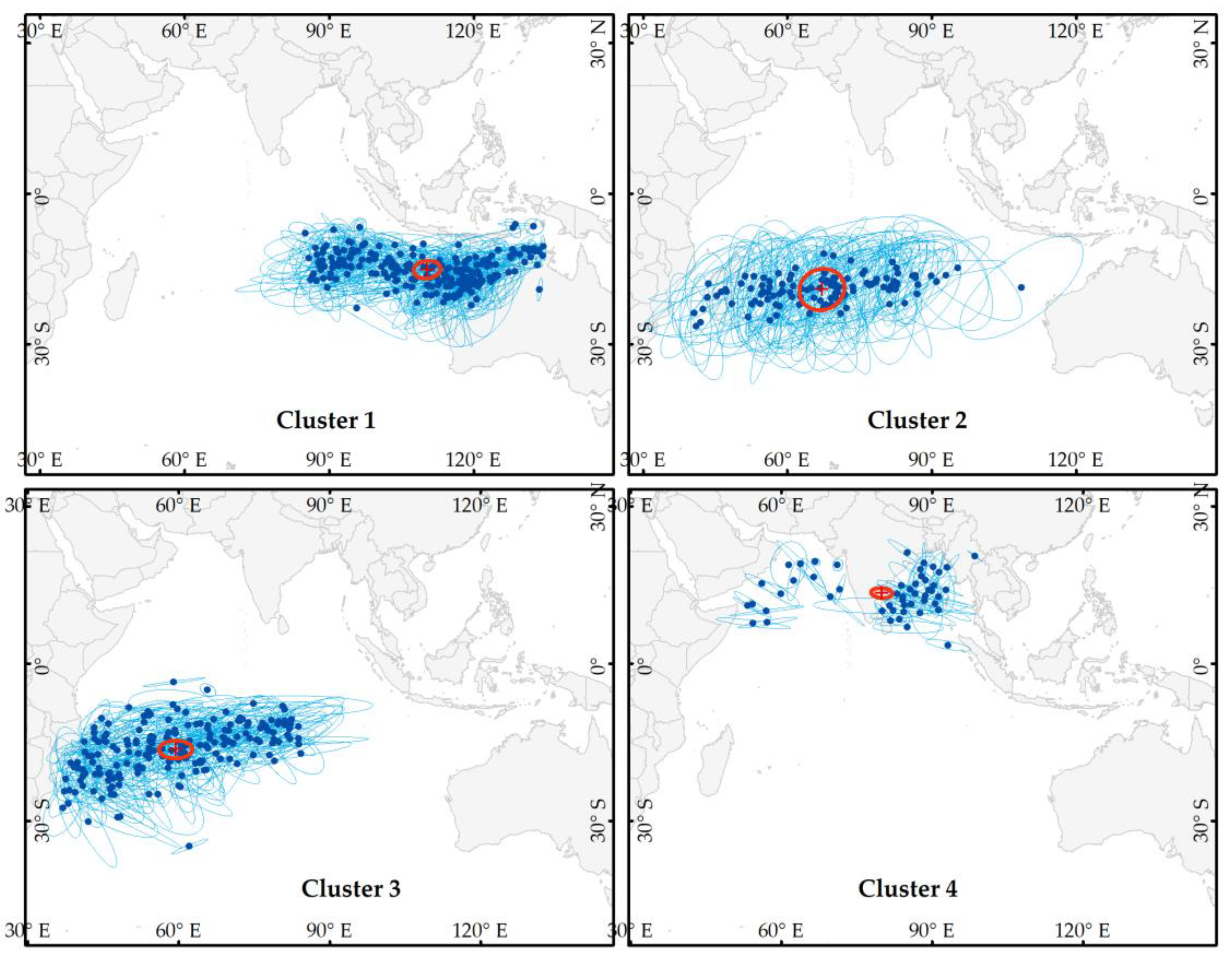
3.2. Cluster Centroids and Properties
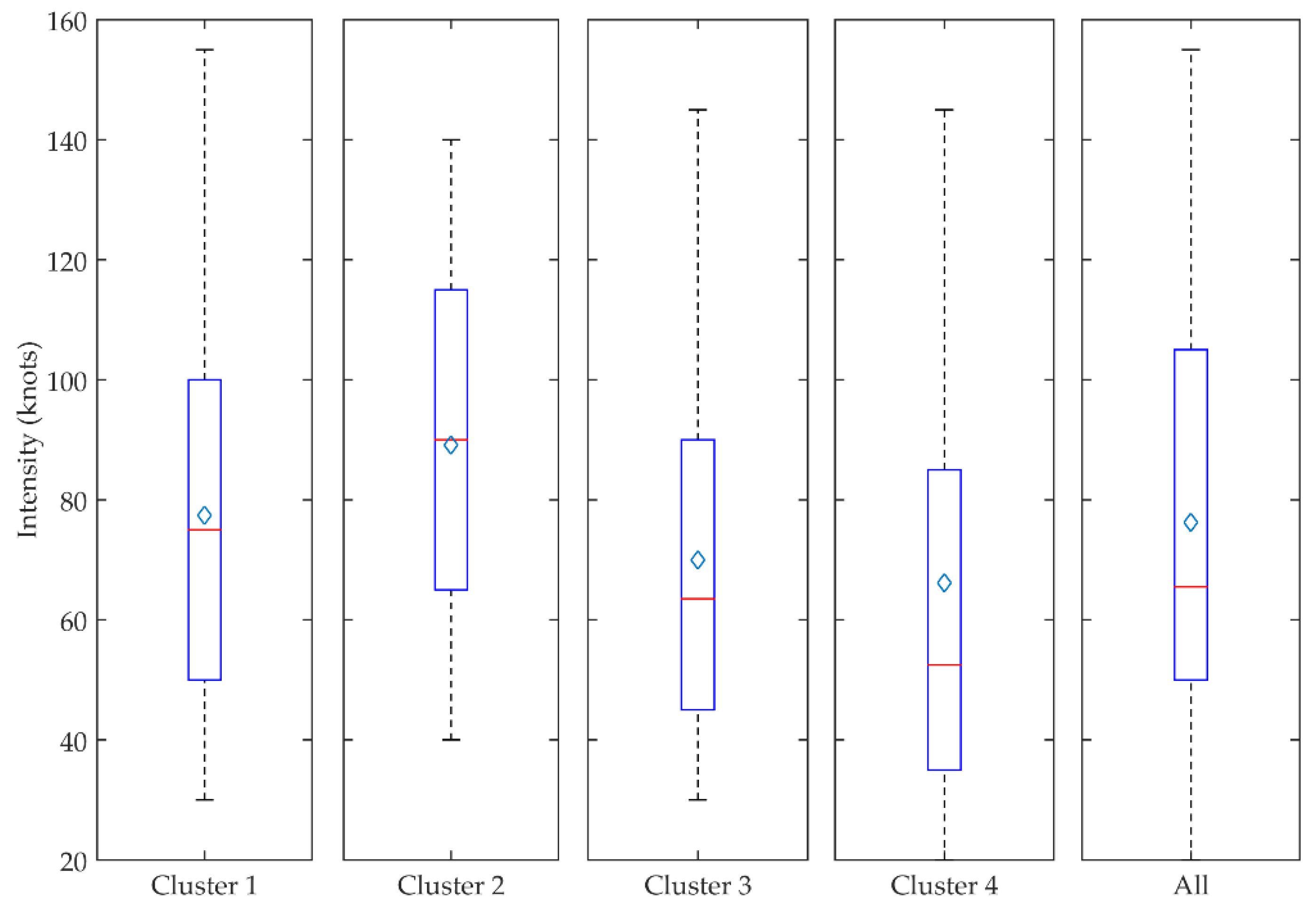
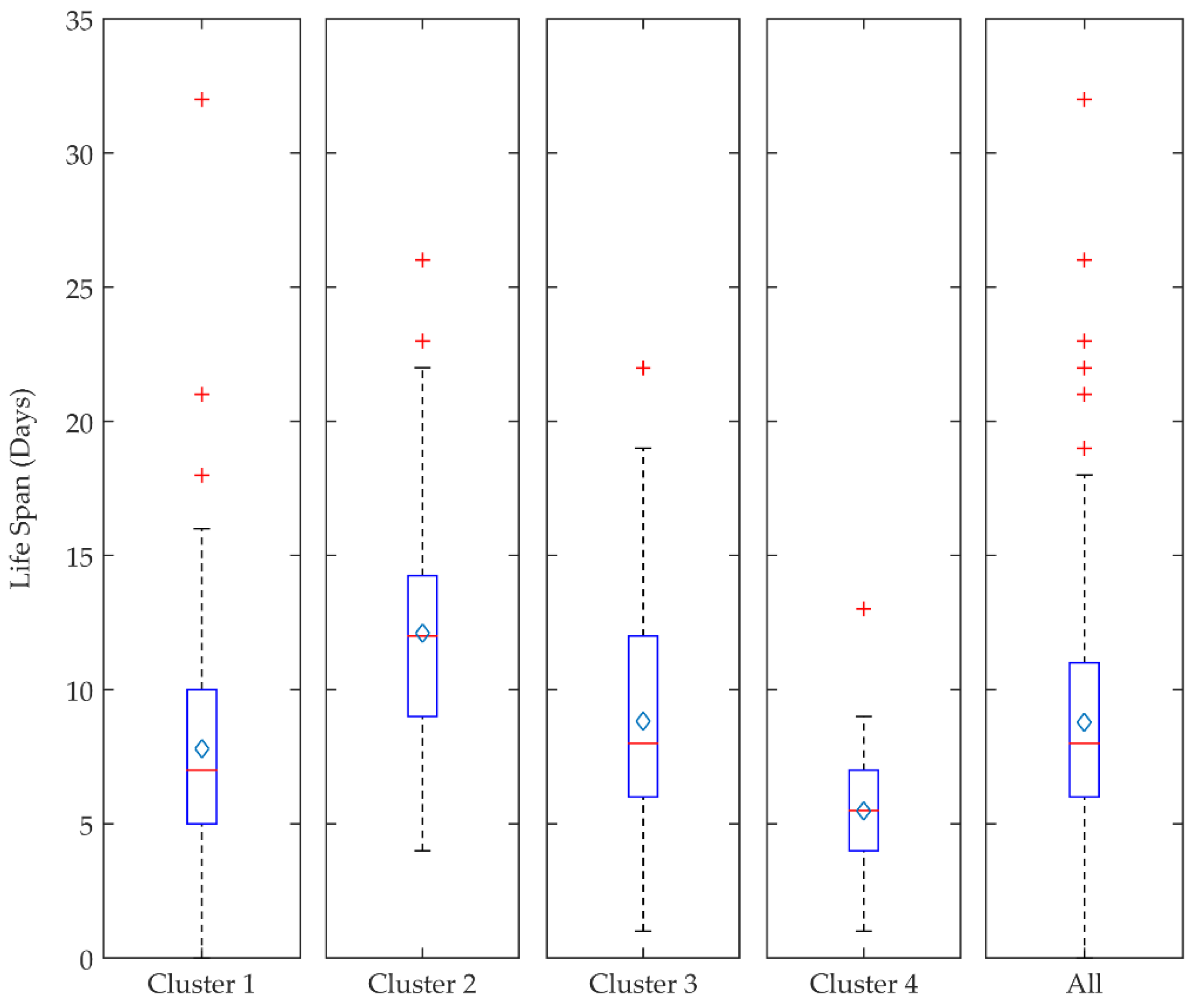
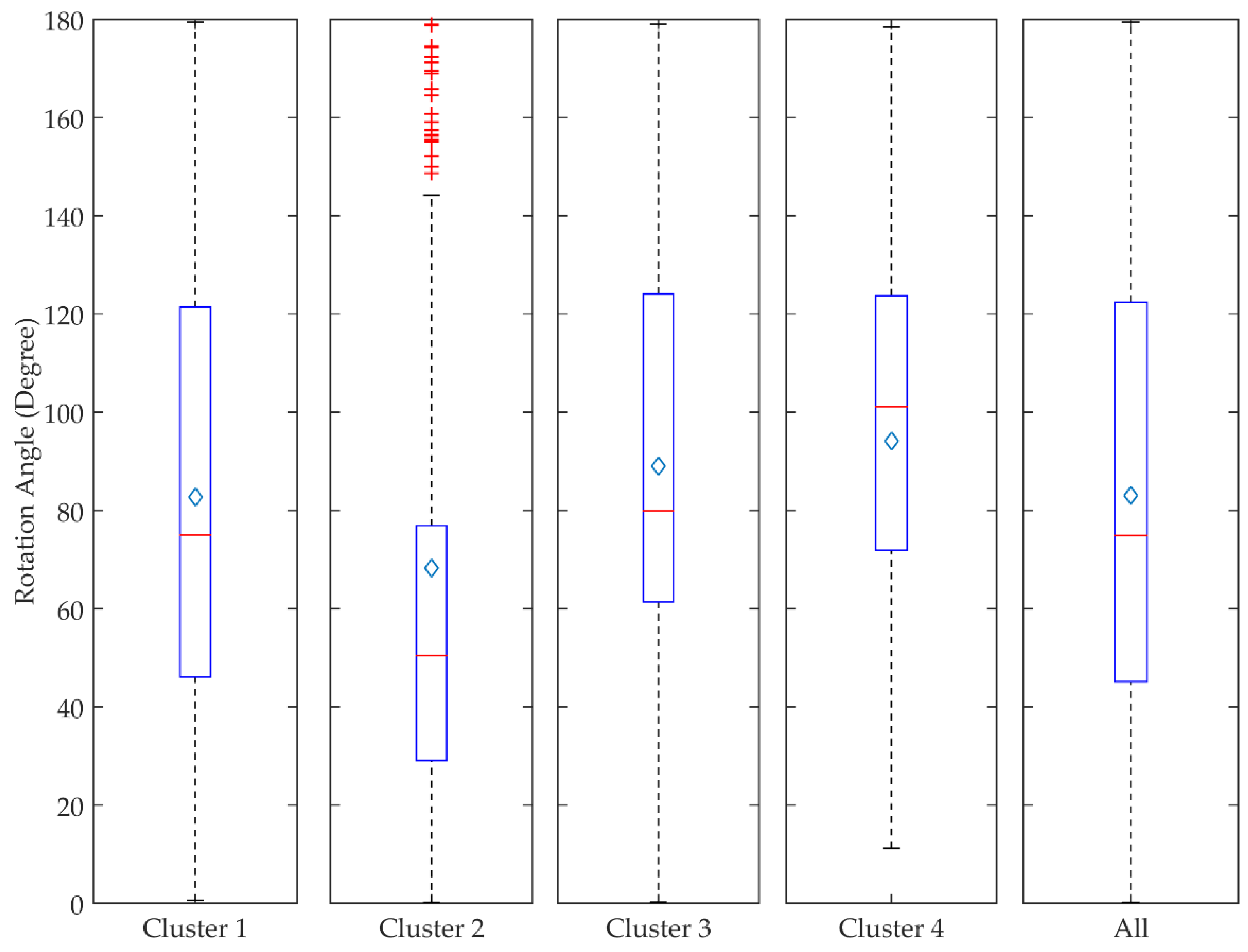
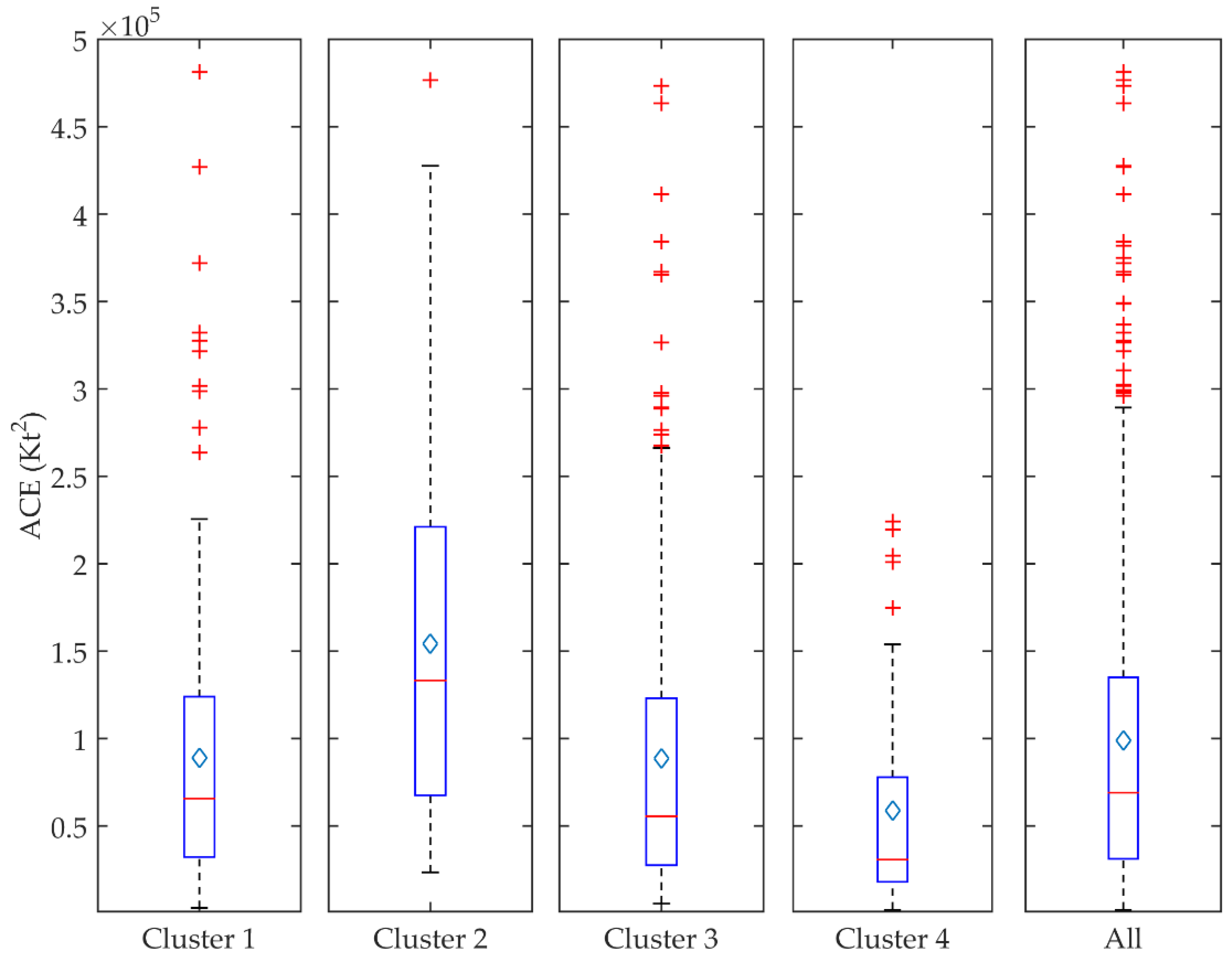
3.3. Cyclone Intensity, Track Length, Rotation, and Lifespan
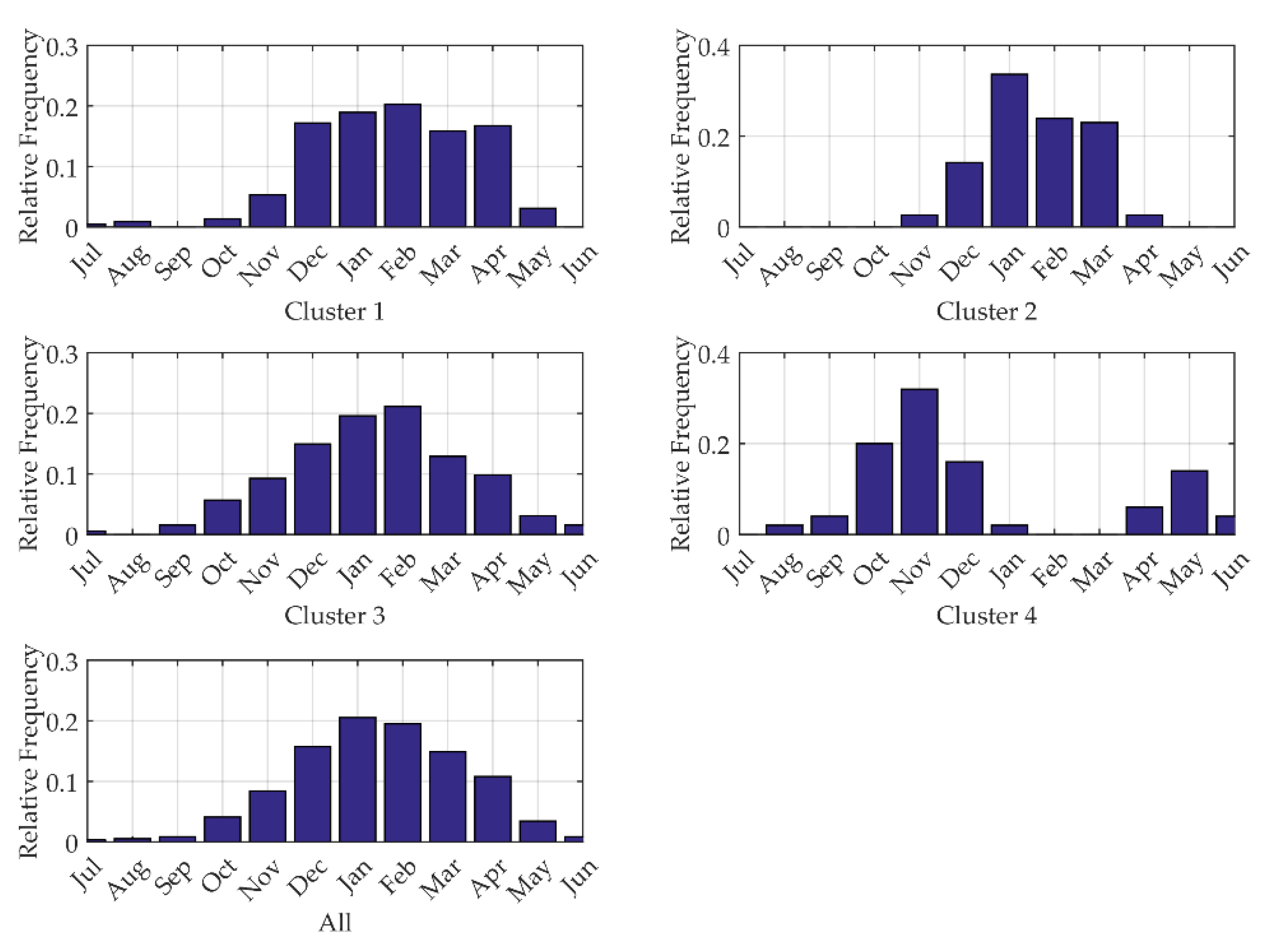
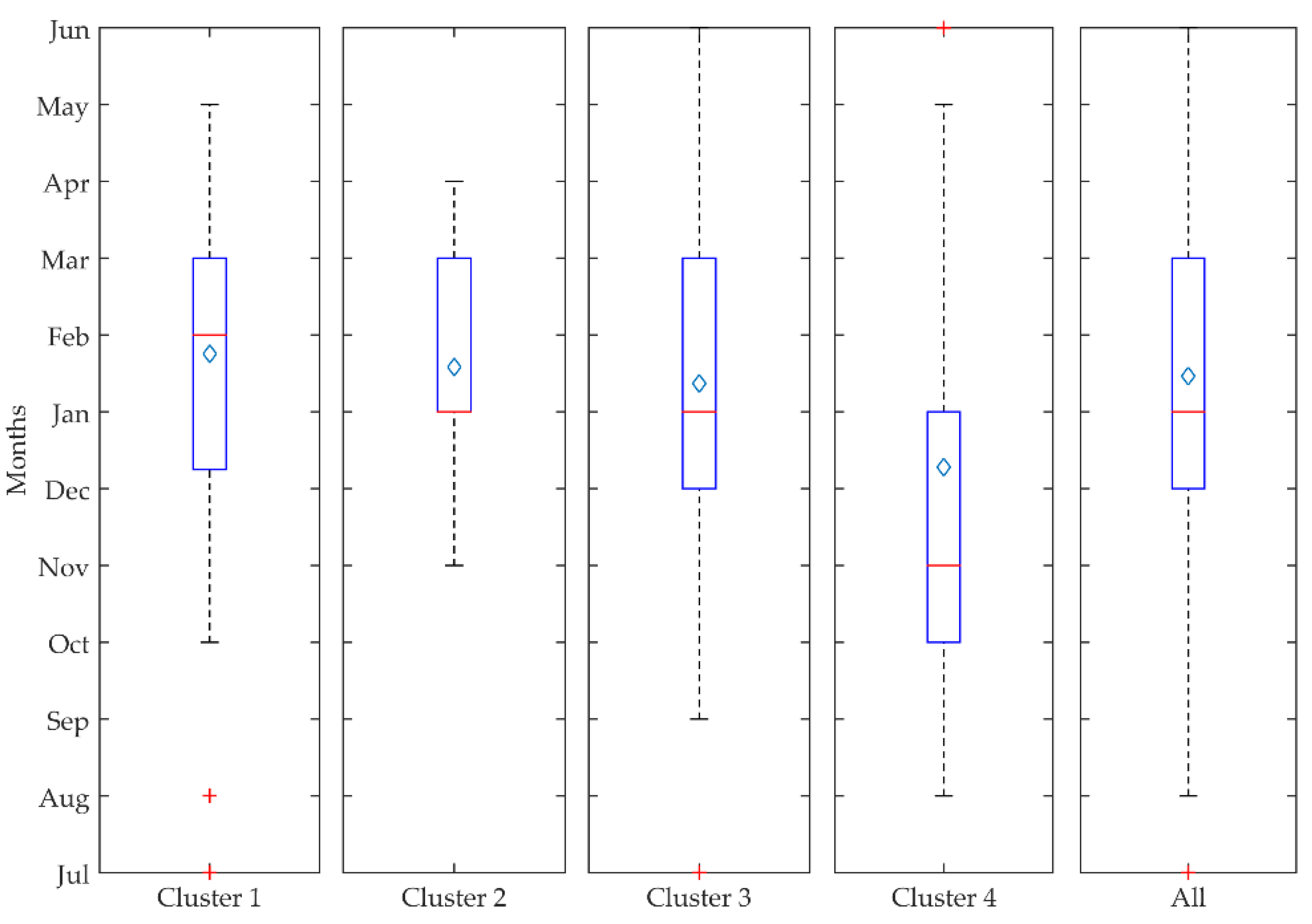
3.4. Seasonality
3.5. Landfall
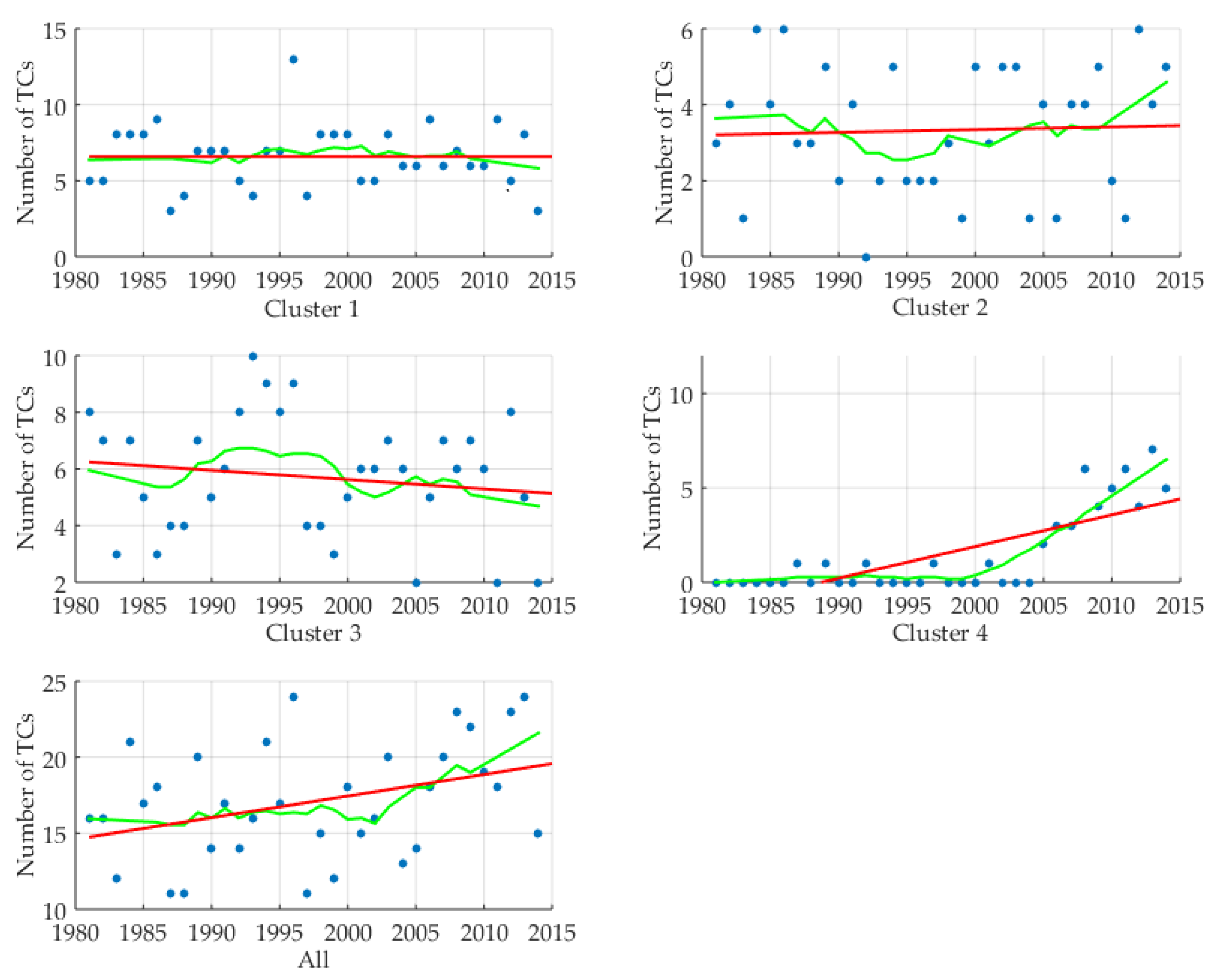
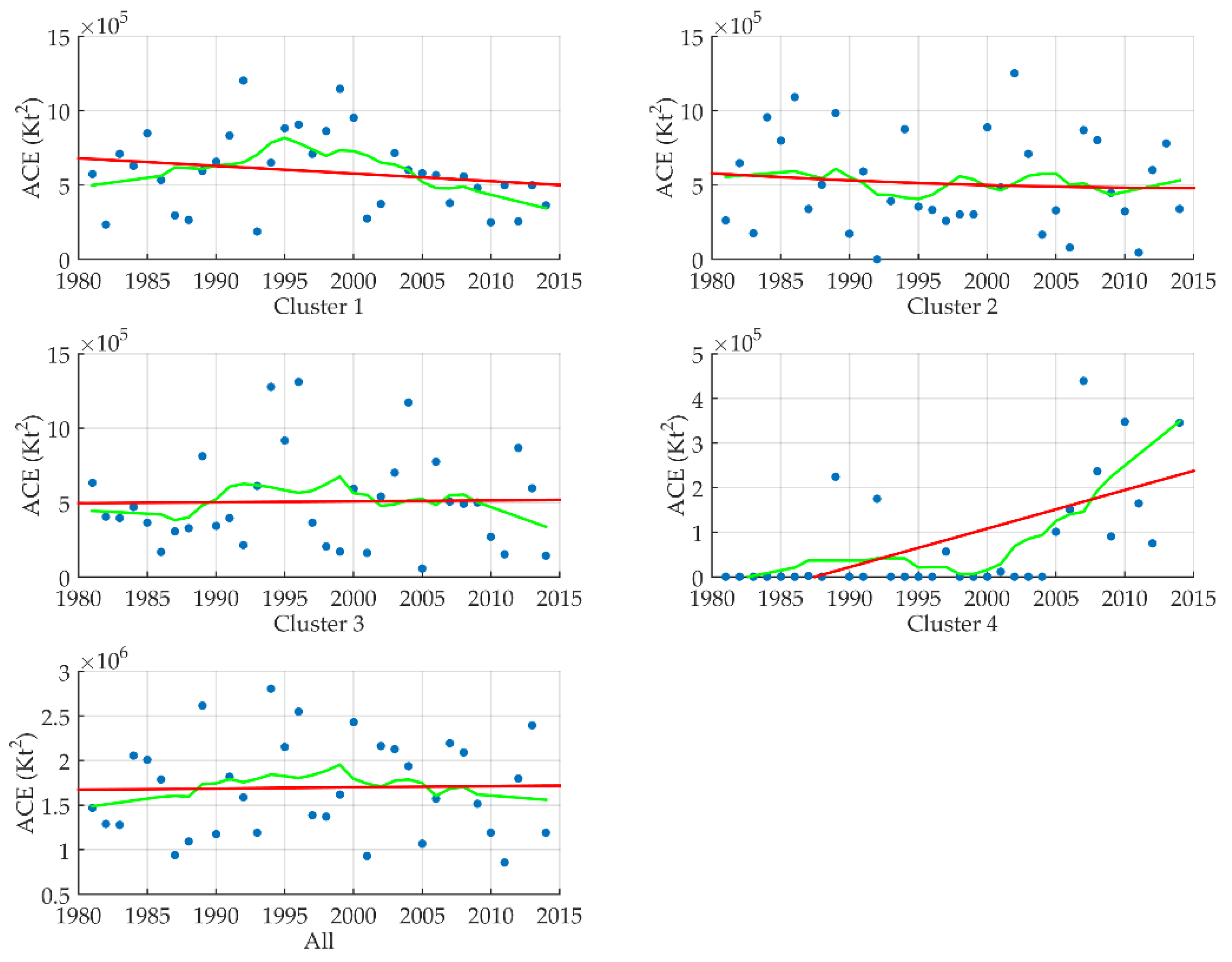
3.6. Trend Analysis
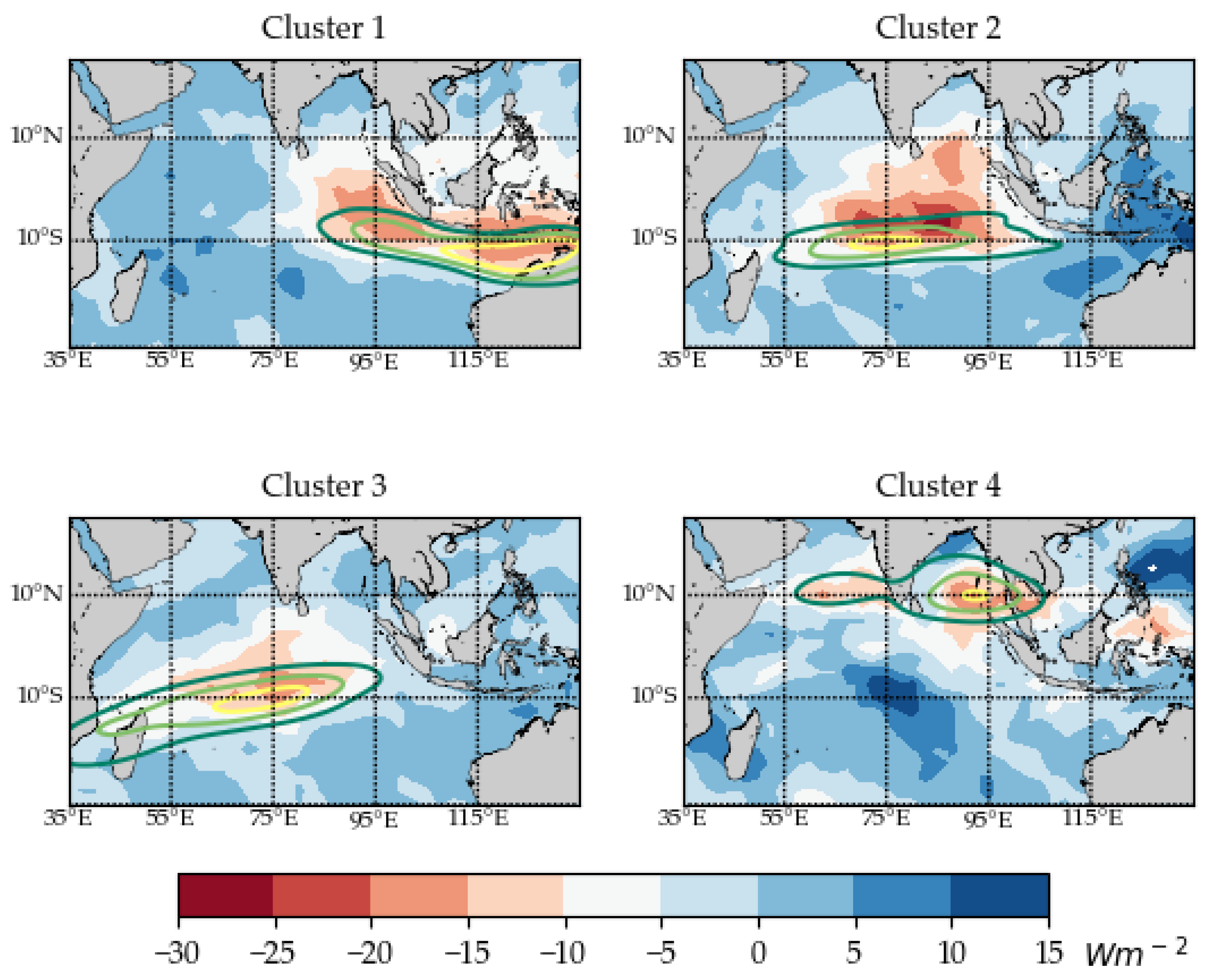
3.7. Large-Scale Environmental Variabilities and TC Genesis
3.8. Statistical Significance of the Clusters
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Mu, M.; Zhou, F.; Wang, H. A Method for Identifying the Sensitive Areas in Targeted Observations for Tropical Cyclone Prediction: Conditional Nonlinear Optimal Perturbation. Mon. Weather Rev. 2009, 137, 1623–1639. [Google Scholar] [CrossRef]
- Rahman, M.S.; Di, L. The state of the art of spaceborne remote sensing in flood management. Nat. Hazards 2017, 85, 1223–1248. [Google Scholar] [CrossRef]
- Rahman, M.S.; Ahmed, B.; Di, L. Landslide initiation and runout susceptibility modeling in the context of hill cutting and rapid urbanization: A combined approach of weights of evidence and spatial multi-criteria. J. Mt. Sci. 2017, 14, 1919–1937. [Google Scholar] [CrossRef]
- Nakamura, J.; Lall, U.; Kushnir, Y.; Camargo, S.J. Classifying North Atlantic Tropical Cyclone Tracks by Mass Moments. J. Clim. 2009, 22, 5481–5494. [Google Scholar] [CrossRef]
- Ahmed, B.; Kelman, I.; Fehr, H.K.; Saha, M. Community resilience to cyclone disasters in coastal Bangladesh. Sustainability 2016, 8, 805. [Google Scholar] [CrossRef]
- Hoque, M.A.-A.; Phinn, S.; Roelfsema, C.; Childs, I. Modelling tropical cyclone risks for present and future climate change scenarios using geospatial techniques. Int. J. Digit. Earth 2018, 11, 246–263. [Google Scholar] [CrossRef]
- Rahman, M.S.; Kausel, T. Coastal community resilience to Tsunami: A study on planning capacity and social capacity, Dichato, Chile. IOSR J. Humanit. Soc. Sci. 2013, 12, 55–63. [Google Scholar] [CrossRef]
- Paul, B.K. Why relatively fewer people died? The case of Bangladesh’s Cyclone Sidr. Nat. Hazards 2009, 50, 289–304. [Google Scholar] [CrossRef]
- Bangladesh, G. Cyclone Sidr in Bangladesh: Damage, Loss and Needs Assessment for Disaster Recovery and Reconstruction; Government of Bangladesh: Dhaka, Bangladesh, 2008.
- Fritz, H.M.; Blount, C.D.; Thwin, S.; Thu, M.K.; Chan, N. Cyclone Nargis storm surge in Myanmar. Nat. Geosci. 2009, 2, 448. [Google Scholar] [CrossRef]
- Webster, P.J. Myanmar’s deadly daffodil. Nat. Geosci. 2008, 1, 488. [Google Scholar] [CrossRef]
- Probst, P.; Proietti, C.; Annunziato, A.; Paris, S.; Wania, A. Tropical Cyclone ENAWO Post-Event Report; Joint Research Centre (JRC), The European Commission’s Science and Knowledge Service: Brussels, Belgium, 2017. [Google Scholar]
- Impact Forecasting. February 013 Global Catastrophe Recap; Aon Benfield: Chicago, IL, USA, 2013. [Google Scholar]
- Belanger, J.I.; Webster, P.J.; Curry, J.A.; Jelinek, M.T. Extended prediction of North Indian Ocean tropical cyclones. Weather Forecast. 2012, 27, 757–769. [Google Scholar] [CrossRef]
- Samson, G.; Masson, S.; Lengaigne, M.; Keerthi, M.G.; Vialard, J.; Pous, S.; Madec, G.; Jourdain, N.C.; Jullien, S.; Menkès, C. The NOW regional coupled model: Application to the tropical Indian Ocean climate and tropical cyclone activity. J. Adv. Model. Earth Syst. 2014, 6, 700–722. [Google Scholar] [CrossRef]
- Ramsay, H.A.; Camargo, S.J.; Kim, D. Cluster analysis of tropical cyclone tracks in the Southern Hemisphere. Clim. Dyn. 2012, 39, 897–917. [Google Scholar] [CrossRef]
- Frank, W.M. Tropical cyclone formation. In A Global View of Tropical Cyclones; University of Chicago Press: Chicago, IL, USA, 1987; pp. 53–90. [Google Scholar]
- Shay, L.K.; Goni, G.J.; Black, P.G. Effects of a warm oceanic feature on Hurricane Opal. Mon. Weather Rev. 2000, 128, 1366–1383. [Google Scholar] [CrossRef]
- Leipper, D.F.; Volgenau, D. Hurricane heat potential of the Gulf of Mexico. J. Phys. Oceanogr. 1972, 2, 218–224. [Google Scholar] [CrossRef]
- Gray, W.M.; Brody, L.R. Global View of the Origin of Tropical Disturbances and Storms; Colorado State University: Collins, CO, USA, 1967. [Google Scholar]
- Schade, L.R.; Emanuel, K.A. The ocean’s effect on the intensity of tropical cyclones: Results from a simple coupled atmosphere–ocean model. J. Atmos. Sci. 1999, 56, 642–651. [Google Scholar] [CrossRef]
- Matyas, C.J. Tropical cyclone formation and motion in the Mozambique Channel. Int. J. Climatol. 2015, 35, 375–390. [Google Scholar] [CrossRef]
- Malan, N.; Reason, C.J.C.; Loveday, B.R. Variability in tropical cyclone heat potential over the Southwest Indian Ocean. J. Geophys. Res. 2013, 118, 6734–6746. [Google Scholar] [CrossRef]
- Knapp, K.R.; Kruk, M.C.; Levinson, D.H.; Diamond, H.J.; Neumann, C.J. The International Best Track Archive for Climate Stewardship (IBTrACS): Unifying Tropical Cyclone Data. Bull. Am. Meteorol. Soc. 2010, 91, 363–376. [Google Scholar] [CrossRef]
- TCFAQ. E25) Which Countries Have Had The Most Tropical Cyclones Hits? Available online: http://www.aoml.noaa.gov/hrd/tcfaq/E25.html (accessed on 14 February 2018).
- Gray, W.M. Hurricanes: Their formation, structure and likely role in the tropical circulation. Meteorol. Trop. Oceans 1979, 77, 155–218. [Google Scholar]
- Rahman, M.S.; Kausel, T. Disaster as an Opportunity to Enhance Community Resilience: Lesson Learnt from Chilean Coast. J. Bangladesh Inst. Plan. ISSN 2012, 5, 1–11. [Google Scholar]
- Kossin, J.P.; Camargo, S.J.; Sitkowski, M. Climate modulation of North Atlantic hurricane tracks. J. Clim. 2010, 23, 3057–3076. [Google Scholar] [CrossRef]
- Colbert, A.J.; Soden, B.J. Climatological variations in North Atlantic tropical cyclone tracks. J. Clim. 2012, 25, 657–673. [Google Scholar] [CrossRef]
- Balaguru, K.; Taraphdar, S.; Leung, L.R.; Foltz, G.R. Increase in the intensity of postmonsoon Bay of Bengal tropical cyclones. Geophys. Res. Lett. 2014, 41, 3594–3601. [Google Scholar] [CrossRef]
- Camargo, S.J.; Wheeler, M.C.; Sobel, A.H. Diagnosis of the MJO modulation of tropical cyclogenesis using an empirical index. J. Atmos. Sci. 2009, 66, 3061–3074. [Google Scholar] [CrossRef]
- Jury, M.; Gadgil, S.; Meyers, G.; Ragoonaden, S.; Reason, C.; Sribimawati, T.; Tangang, F. Applications of An Indian Ocean Observing System to Climate Impacts and Resource Predictions in Surrounding Countries in the Context of ENSO-Monsoon Teleconnections; OceanDocs: Paris, France, 2000. [Google Scholar]
- Kuleshov, Y.; Qi, L.; Fawcett, R.; Jones, D. On tropical cyclone activity in the Southern Hemisphere: Trends and the ENSO connection. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Liebmann, B.; Hendon, H.H.; Glick, J.D. The relationship between tropical cyclones of the western Pacific and Indian Oceans and the Madden-Julian oscillation. J. Meteorol. Soc. Jpn. 1994, 72, 401–412. [Google Scholar] [CrossRef]
- Jury, M.R.; Pathack, B. A study of climate and weather variability over the tropical southwest Indian Ocean. Meteorol. Atmos. Phys. 1991, 47, 37–48. [Google Scholar] [CrossRef]
- Suzuki, R.; Behera, S.K.; Iizuka, S.; Yamagata, T. Indian Ocean subtropical dipole simulated using a coupled general circulation model. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Terry, J.P.; Gienko, G. Developing a new sinuosity index for cyclone tracks in the tropical South Pacific. Nat. Hazards 2011, 59, 1161–1174. [Google Scholar] [CrossRef]
- Terry, J.P.; Kim, I.-H.; Jolivet, S. Sinuosity of tropical cyclone tracks in the South West Indian Ocean: Spatio-temporal patterns and relationships with fundamental storm attributes. Appl. Geogr. 2013, 45, 29–40. [Google Scholar] [CrossRef]
- Leroy, A.; Wheeler, M.C. Statistical prediction of weekly tropical cyclone activity in the Southern Hemisphere. Mon. Weather Rev. 2008, 136, 3637–3654. [Google Scholar] [CrossRef]
- Nakamura, J.; Lall, U.; Kushnir, Y.; Rajagopalan, B. HITS: Hurricane intensity and track simulator with North Atlantic Ocean applications for risk assessment. J. Appl. Meteorol. Climatol. 2015, 54, 1620–1636. [Google Scholar] [CrossRef]
- Camargo, S.J.; Robertson, A.W.; Gaffney, S.J.; Smyth, P.; Ghil, M. Cluster Analysis of Typhoon Tracks. Part I: General Properties. J. Clim. 2007, 20, 3635–3653. [Google Scholar] [CrossRef]
- Villarini, G.; Vecchi, G.A.; Smith, J.A. US landfalling and North Atlantic hurricanes: Statistical modeling of their frequencies and ratios. Mon. Weather Rev. 2012, 140, 44–65. [Google Scholar] [CrossRef]
- McCloskey, T.A.; Bianchette, T.A.; Liu, K.-B. Track patterns of landfalling and coastal tropical cyclones in the Atlantic basin, their relationship with the North Atlantic Oscillation (NAO), and the potential effect of global warming. Am. J. Clim. Chang. 2013, 2, 12. [Google Scholar] [CrossRef]
- Ho, C.-H.; Kim, J.-H.; Kim, H.-S.; Choi, W.; Lee, M.-H.; Yoo, H.-D.; Kim, T.-R.; Park, S. Technical note on a track-pattern-based model for predicting seasonal tropical cyclone activity over the western North Pacific. Adv. Atmos. Sci. 2013, 30, 1260–1274. [Google Scholar] [CrossRef]
- Camargo, S.J.; Robertson, A.W.; Barnston, A.G.; Ghil, M. Clustering of eastern North Pacific tropical cyclone tracks: ENSO and MJO effects. Geochem. Geophys. Geosyst. 2008, 9. [Google Scholar] [CrossRef]
- Mohapatra, M.; Bandyopadhyay, B.K.; Tyagi, A. Best track parameters of tropical cyclones over the North Indian Ocean: A review. Nat. Hazards 2012, 63, 1285–1317. [Google Scholar] [CrossRef]
- Free, M.; Bister, M.; Emanuel, K. Potential intensity of tropical cyclones: Comparison of results from radiosonde and reanalysis data. J. Clim. 2004, 17, 1722–1727. [Google Scholar] [CrossRef]
- Neumann, C.J. Tropical Cyclones of the North Atlantic Ocean, 1871–1986; US National Oceanic and Atmospheric Administration, National Weather Service: Washington, DC, USA, 1981.
- Reynolds, R.W.; Rayner, N.A.; Smith, T.M.; Stokes, D.C.; Wang, W. An improved in situ and satellite SST analysis for climate. J. Clim. 2002, 15, 1609–1625. [Google Scholar] [CrossRef]
- Liebmann, B.; Smith, C.A. Description of a complete (interpolated) outgoing longwave radiation dataset. Bull. Am. Meteorol. Soc. 1996, 77, 1275–1277. [Google Scholar]
- Wong, D.W.-S.; Lee, J. Statistical Analysis of Geographic Information with ArcView GIS and ArcGIS; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005; ISBN 978-0-471-46899-8. [Google Scholar]
- Friendly, M.; Monette, G.; Fox, J. Elliptical insights: Understanding statistical methods through elliptical geometry. Stat. Sci. 2013, 28, 1–39. [Google Scholar] [CrossRef]
- MacQueen, J. Others some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Oakland, CA, USA, 1967; Volume 1, pp. 281–297. [Google Scholar]
- Gaffney, S.J. Probabilistic Curve-Aligned Clustering and Prediction with Regression Mixture Models; University of California, Irvine: Irvine, CA, USA, 2004. [Google Scholar]
- Moertini, V. Introduction to Five Data Clustering Algorithm; Integral: Bonn, Germany, 2002; pp. 87–96. [Google Scholar]
- Harr, P.A.; Elsberry, R.L. Large-scale circulation variability over the tropical western North Pacific. Part I: Spatial patterns and tropical cyclone characteristics. Mon. Weather Rev. 1995, 123, 1225–1246. [Google Scholar] [CrossRef]
- Elsner, J.B. Tracking Hurricanes. Bull. Am. Meteorol. Soc. 2003, 84, 353–356. [Google Scholar] [CrossRef]
- Elsner, J.B.; Liu, K. Examining the ENSO-typhoon hypothesis. Clim. Res. 2003, 25, 43–54. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Bowman, A.W.; Azzalini, A. Applied Smoothing Techniques for Data Analysis: The Kernel Approach with S-Plus Illustrations; Oxford University Press: Oxford, UK, 1997; Volume 18. [Google Scholar]
- Burt, J.E.; Barber, G.M.; Rigby, D.L. Elementary Statistics for Geographers, 3rd ed.; Guilford Press: New York, NY, USA, 2009; ISBN 978-1-60918-093-5. [Google Scholar]
- Ash, K.D.; Matyas, C.J. The influences of ENSO and the subtropical Indian Ocean Dipole on tropical cyclone trajectories in the southwestern Indian Ocean. Int. J. Climatol. 2012, 32, 41–56. [Google Scholar] [CrossRef]
- Box Plot. MATLAB Boxplot. Available online: https://www.mathworks.com/help/stats/boxplot.html (accessed on 21 April 2018).
- Bell, G.D. The 1999 North Atlantic hurricane season: A climate perspective. State of the Climate in 1999. Bull. Am. Meteorol. Soc. 2000, 81, S1–S50. [Google Scholar] [CrossRef]
- Singh, O.P.; Khan, T.A.; Rahman, M.S. Changes in the frequency of tropical cyclones over the North Indian Ocean. Meteorol. Atmos. Phys. 2000, 75, 11–20. [Google Scholar] [CrossRef]
- Webster, P.J.; Holland, G.J.; Curry, J.A.; Chang, H.-R. Changes in tropical cyclone number, duration, and intensity in a warming environment. Science 2005, 309, 1844–1846. [Google Scholar] [CrossRef] [PubMed]
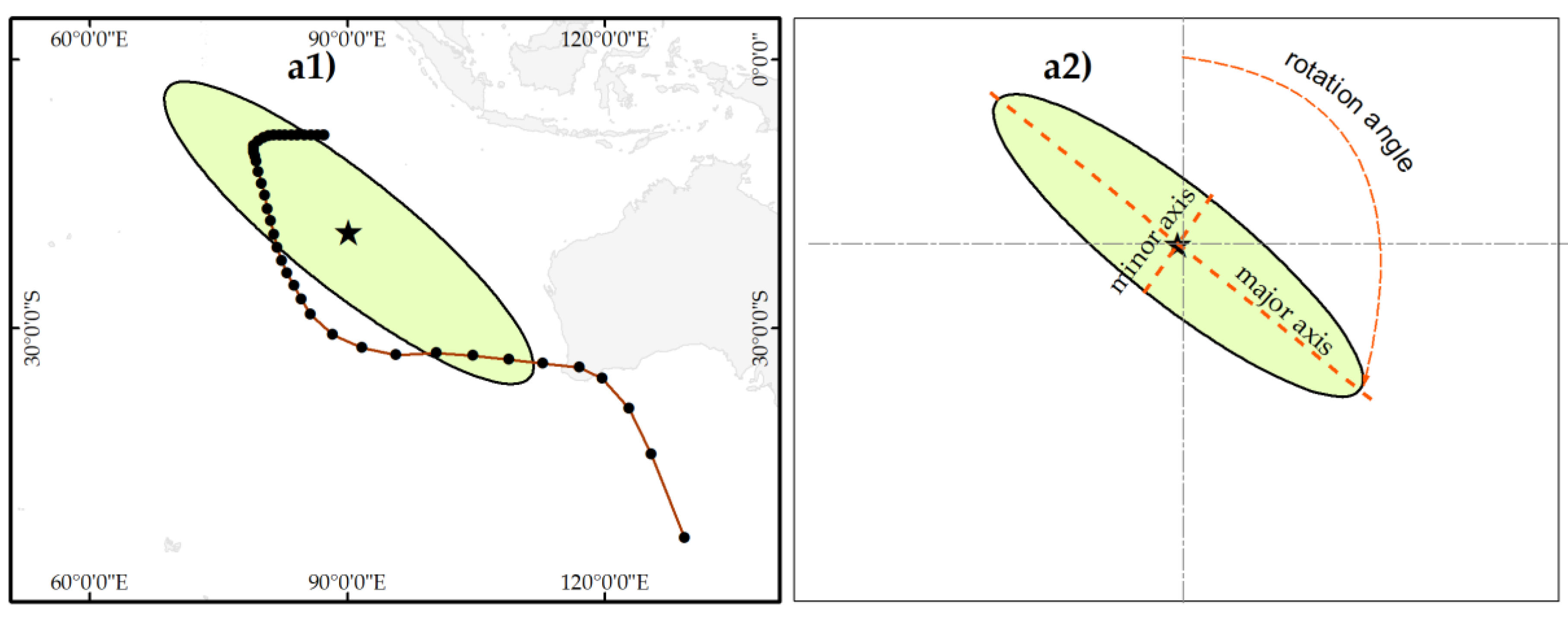
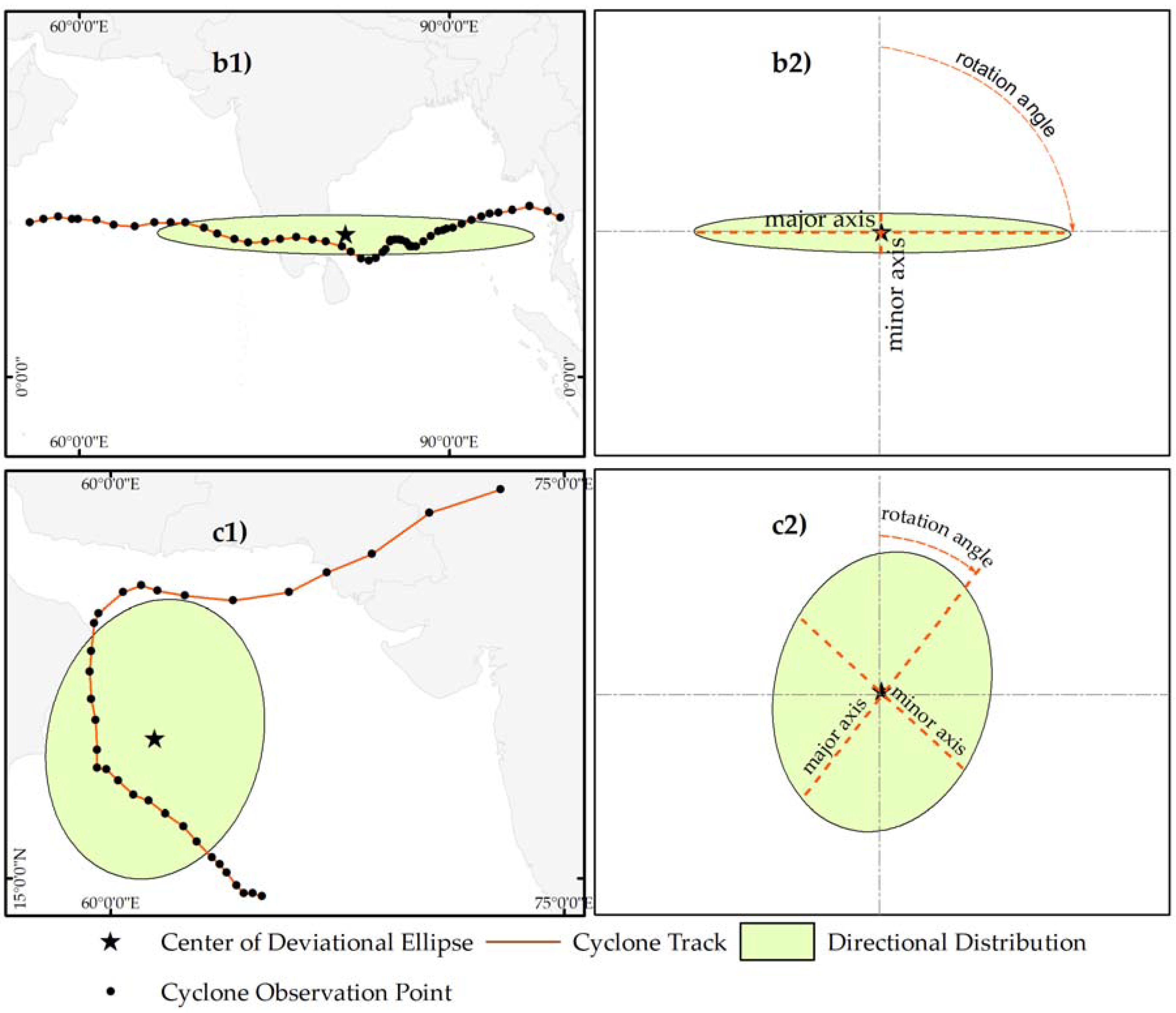
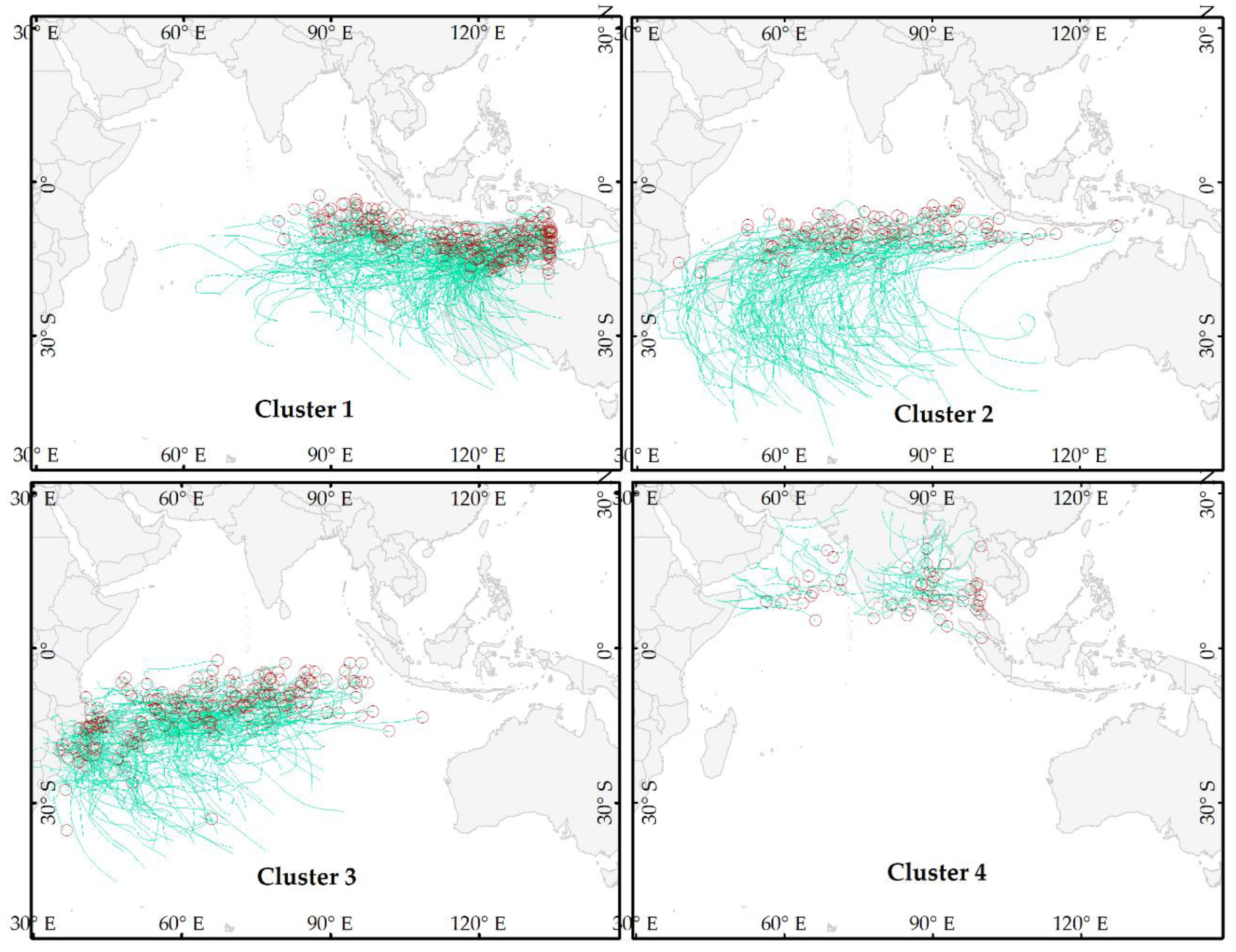
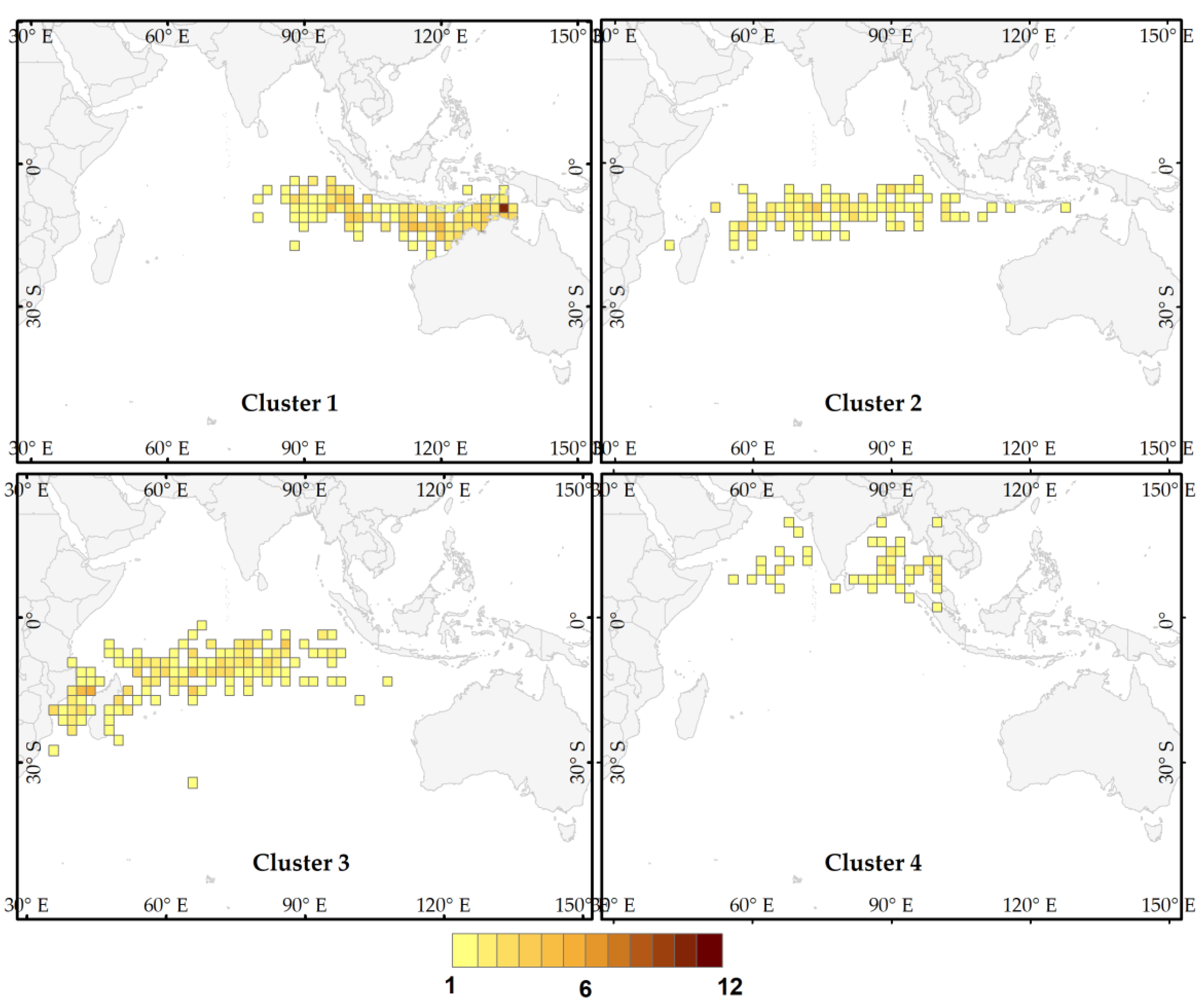

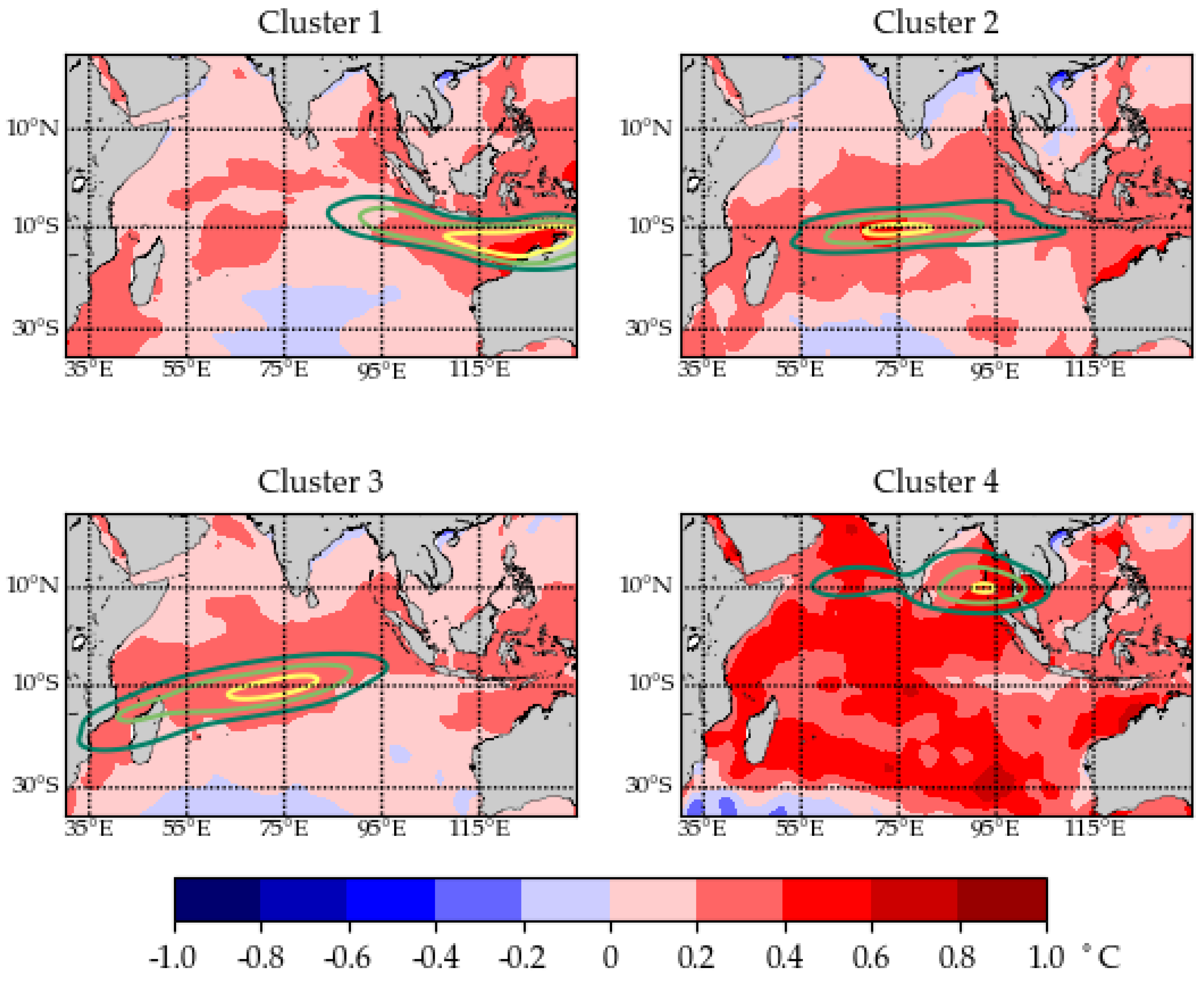
| Clusters | Mean X Genesis | Mean Y Genesis | Genesis X Range | Genesis Y Range | Number of Tracks |
|---|---|---|---|---|---|
| 1 | 115.0° E | 11.4° S | 79.4° E–134.9° E | 2.8° S–19.1° S | 230 |
| 2 | 78.3° E | 10.5° S | 38.0° E–127.0° E | 4.4° S–18.2° S | 116 |
| 3 | 64.7° E | 12.5° S | 35.1° E–108.6° E | 2.5° S–34.7°S | 195 |
| 4 | 84.6° E | 8.6° N | 56.5° E–100.0° E | 2.0° N–20.2° N | 51 |
| Cluster No. | Centroid X (° E) | Centroid Y (° N/° S) | Variance X (°) | Variance Y (°) | Variance XY (°) | Number of Tracks |
|---|---|---|---|---|---|---|
| 1 | 110.34° E | 15.58° S | 23.86 | 10.01 | 3.15 | 230 |
| 2 | 67.10° E | 19.40° S | 50.69 | 40.1 | 17.33 | 116 |
| 3 | 59.40° E | 16.77° S | 29.92 | 9.19 | 3.08 | 195 |
| 4 | 79.87° E | 14.01° N | 11.81 | 4.39 | −1.95 | 51 |
| Cluster | N | Landfalls | Landfall Percentage | Category 1 | Category 2 | Category 3 | Category 4 | Cat 1–4 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | % | N | % | N | % | N | % | N | % | ||||
| 1 | 230 | 119 | 51.73 | 8 | 6.72 | 4 | 3.36 | 2 | 1.68 | 3 | 2.52 | 17 | 14.28 |
| 2 | 116 | 39 | 33.62 | 6 | 15.38 | 6 | 15.38 | 1 | 2.56 | 1 | 2.56 | 14 | 35.89 |
| 3 | 195 | 91 | 46.67 | 11 | 12.09 | 5 | 5.49 | 8 | 8.79 | 1 | 1.1 | 25 | 27.47 |
| 4 | 51 | 43 | 84.31 | 2 | 4.65 | 3 | 6.98 | 1 | 2.33 | 0 | 0.00 | 6 | 13.95 |
| All | 592 | 292 | 49.32 | 27 | 9.25 | 18 | 6.16 | 12 | 4.11 | 5 | 1.71 | 62 | 21.23 |
| Variables | Unit | Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | H | p-Value |
|---|---|---|---|---|---|---|---|
| Intensity | knots | 75 | 90 | 63.5 | 52.5 | 39.45 | 0.0001 |
| Rotation angle | Degree | 74.98 | 50.45 | 79.93 | 101.12 | 26.02 | 0.00009 |
| Life span | Days | 7 | 12 | 8 | 5.5 | 121.24 | 0.00000 |
| Track Length | km | 2863 | 5373 | 3245 | 1702 | 183.43 | 0.00000 |
| ACE | Kt2 | 65,652 | 133,247 | 55,550 | 30,737 | 75.57 | 0.00000 |
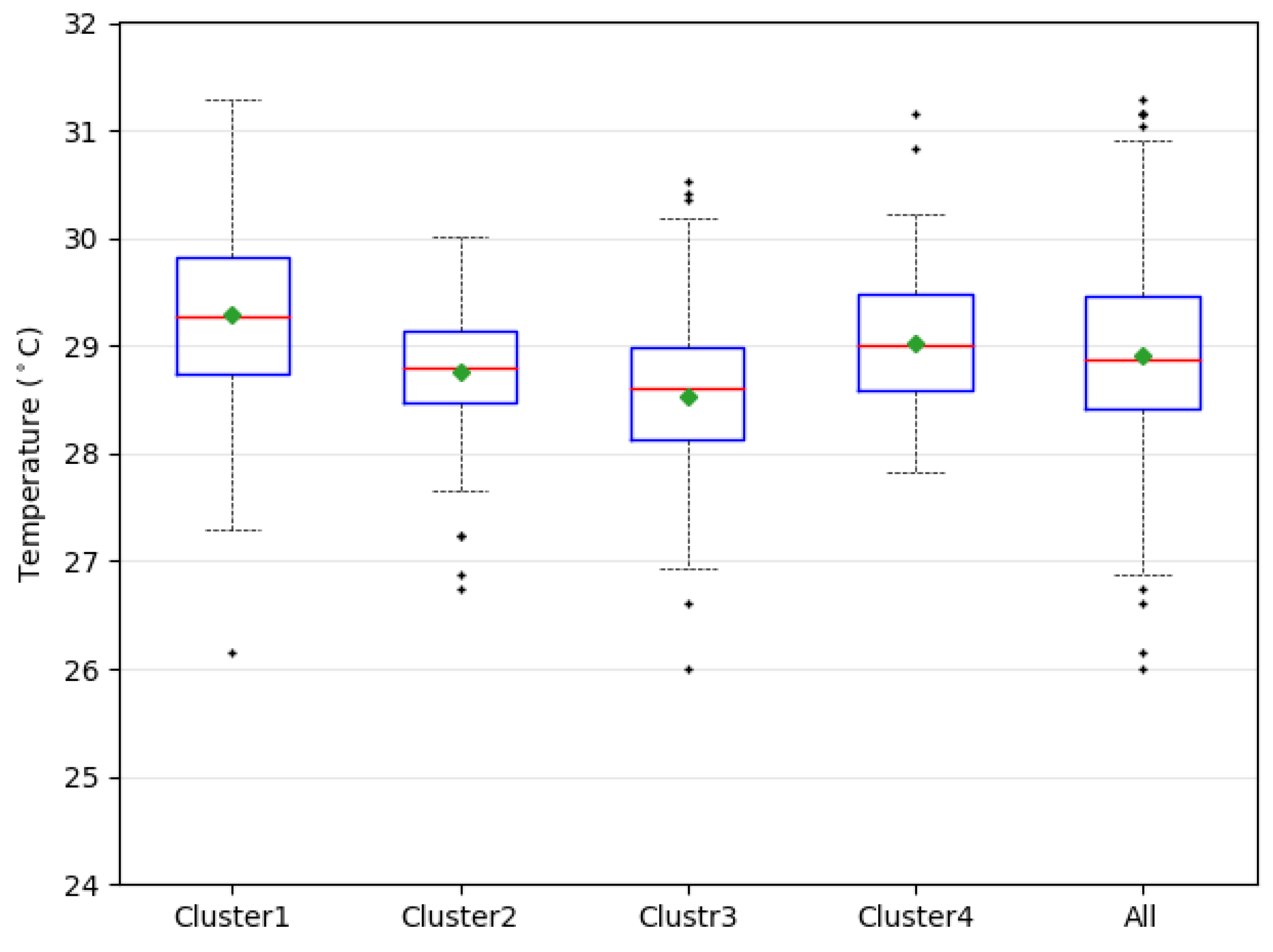
| SST | °C | 29.27 | 28.78 | 28.61 | 29.00 | 84.59 | 0.00000 |
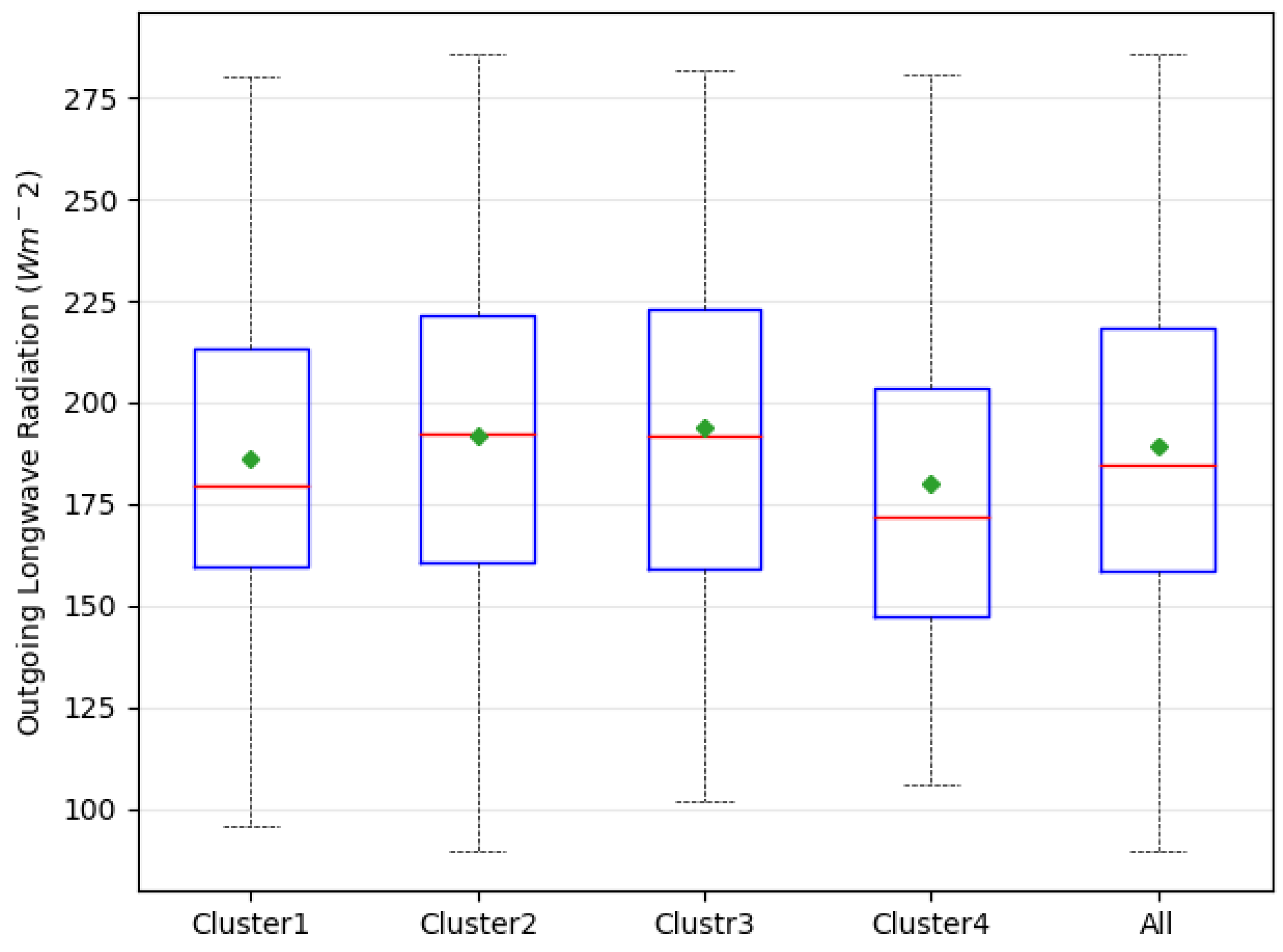
| OLR | Wm−2 | 179.5 | 192.4 | 192 | 171.9 | 11.73 | 0.0577 |
| Clusters | C1 | C2 | C2 | C3 | C3 | C4 | C1 | C3 | C1 | C4 | C2 | C4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| U | p | U | p | U | p | U | p | U | p | U | p | ||
| Variables | Intensity | 9772 | 0.000 | 6827 | 0.00 | 4121 | 0.079 | 18,516 | 0.002 | 4197 | 0.001 | 1590 | 0.00 |
| Rotation angle | 9965 | 0.000 | 7256 | 0.00 | 4277 | 0.099 | 19,717 | 0.046 | 4699 | 0.029 | 1985 | 0.00 | |
| Life span | 5043 | 0.000 | 6172 | 0.00 | 2376 | 0.000 | 18,690 | 0.004 | 3320 | 0.000 | 319 | 0.00 | |
| Track Length | 3210 | 0.000 | 3578 | 0.00 | 2163 | 0.000 | 19,671 | 0.030 | 2829 | 0.000 | 69 | 0.00 | |
| Seasonality | 9679 | 0.000 | 8361 | 0.00 | 2448 | 0.000 | 21,692 | 0.395 | 2556 | 0.000 | 917 | 0.00 | |
| ACE | 7011 | 0.000 | 5689 | 0.00 | 3649 | 0.004 | 20,503 | 0.112 | 3907 | 0.000 | 933 | 0.00 | |
| SST | 7622 | 0.000 | 8779 | 0.007 | 3234 | 0.000 | 10,800 | 0.000 | 4566 | 0.011 | 2308 | 0.02 | |
| OLR | 12,023 | 0.067 | 11,188 | 0.437 | 4034 | 0.019 | 20,006 | 0.028 | 5221 | 0.110 | 2406 | 0.03 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, M.S.; Yang, R.; Di, L. Clustering Indian Ocean Tropical Cyclone Tracks by the Standard Deviational Ellipse. Climate 2018, 6, 39. https://doi.org/10.3390/cli6020039
Rahman MS, Yang R, Di L. Clustering Indian Ocean Tropical Cyclone Tracks by the Standard Deviational Ellipse. Climate. 2018; 6(2):39. https://doi.org/10.3390/cli6020039
Chicago/Turabian StyleRahman, Md. Shahinoor, Ruixin Yang, and Liping Di. 2018. "Clustering Indian Ocean Tropical Cyclone Tracks by the Standard Deviational Ellipse" Climate 6, no. 2: 39. https://doi.org/10.3390/cli6020039
APA StyleRahman, M. S., Yang, R., & Di, L. (2018). Clustering Indian Ocean Tropical Cyclone Tracks by the Standard Deviational Ellipse. Climate, 6(2), 39. https://doi.org/10.3390/cli6020039







