Abstract
It has been widely predicted that Southeast Asia is among the regions facing the most severe climate change impacts. Despite this forecast, little research has been published on the potential impacts of climate change on soil erosion in this region. This study focused on the impact of climate change on spatial and temporal patterns of soil erosion in the Laos–Vietnam transnational Upper Ca River Watershed. The Soil and Water Assessment Tool (SWAT) coupled with downscaled global climate models (GCMs) was employed for simulation. Soil erosion in the watershed was mostly found as “hill-slope erosion”, which occurred seriously in the upstream area where topography is dominated by numerous steep hills with sparse vegetation cover. However, under the impact of climate change, it is very likely that soil erosion rate in the downstream area will increase at a higher rate than in its upstream area due to a greater increase in precipitation. Seasonally, soil erosion is predicted to increase significantly in the warmer and wetter climate of the wet season, when higher erosive power of an increased amount and intensity of rainfall is accompanied by higher sediment transport capacity. The results of this study provide useful information for decision makers to plan where and when soil conservation practice should be focused.
1. Introduction
As more evidence on human-induced climate change has accumulated, rapidly increasing attention of researchers around the world has been paid to its potential impacts on the environment. Soil erosion is one of the environmental phenomena most affected by climate change. There is a general consensus in previous research that increases in the amount and intensity of rainfall will lead to greater rates of soil erosion unless protection measures are taken. According to Parry et al. [1], soil erosion rates can be affected by changes in climate for a wide variety of reasons: changes in plant canopy due to shifts in plant biomass production caused by changes in moisture regime; changes in litter cover on the ground due to changes in plant residue decomposition rates, moisture-dependent soil microbial activity, and plant biomass production rates; changes in surface runoff ratios due to changes in soil moisture caused by shifting precipitation regimes and evapotranspiration rates; changes in soil erodibility caused by a decrease in soil organic matter concentrations; a shift from non-erosive snow to erosive rainfall due to temperature rise; melting of permafrost, which induces an erodible soil state from a previously non-erodible one; and changes in land use to adapt to new climatic regimes.
A number of studies have been conducted to examine the change of soil erosion in response to changing climate conditions, especially change in rainfall under different global climate models (GCMs). For example, Nearing [2] used the output from two GCMs (HadCM3 and CGCM1) and relationships between monthly precipitation and rainfall erosivity to assess potential changes in rainfall erosivity in the USA. The study found that the changes were significant, but results from the two models differed both in magnitude and regional distributions. Zhang et al. [3] used HadCM3 to assess potential changes in rainfall erosivity in the Huanghe River Basin of China, projecting increases in rainfall erosivity by as much as 11% to 22% by 2050. Pruski and Nearing [4] used HadCM3 to simulate erosion under maize and wheat cropping systems at eight locations in the USA for the 21st century, with consideration of the primary physical and biological mechanisms affecting erosion. The study found that where precipitation was projected to increase, estimated erosion increased by 15% to 100%. However, the results were more complex where precipitation was projected to decrease, due largely to interactions between plant biomass, runoff, and erosion, and either increases or decreases in overall erosion could occur. Zhang and Nearing [5] predicted the potential impacts of climate change on soil erosion in central Oklahoma State of the USA, while the HadCM3-predicted mean annual precipitation during 2070–2099 decreased by 6.2%, 13.6%, and 7.2%, for GGa1, A2, and B2, respectively, the predicted erosion increased by 67%–82% for GGa1, increased by 18%–30% for A2, and remained similar for B2. The larger increase in erosion in the GGa1 scenario was attributed to larger variability in monthly precipitation and an increased frequency of large storms in the model simulation. According to Parry et al. [1], extreme rainfall events contribute a disproportionate amount of soil erosion relative to the total rainfall contribution, and this effect will be exacerbated if the frequency of such events increases in the future.
In Southeast Asia, climate change is widely projected to severely hit the region in coming decades. Despite this forecast, little research has been published on the potential impacts of climate change on soil erosion in this region. Research focusing on transnational watersheds is especially scarce due to the lack of collaboration and data sharing among riparian states. This study aimed to predict the impact of climate change on spatial and temporal patterns of soil erosion in the Laos–Vietnam transnational Upper Ca River Watershed (UCRW). The UCRW is a large agricultural watershed playing an important role in the economic development of both countries, but it is severely affected by soil erosion due to its hilly-slope topography, high intensity of rainfall, and other climate and land cover characteristics. Identifying spatial and temporal patterns of soil erosion under the impact of climate change could therefore provide useful information about where and when soil conservation practice should be focused in order to protect the soil for long-term agricultural cultivation.
2. Materials and Methods
2.1. The Study Area and Data
The Ca River Watershed is situated in north-central Vietnam and north-east Laos. In Laos, the watershed covers an area of more than 9000 km2 of the Provinces of Houaphanh and Xiangkhouang. In Vietnam, it covers the entire area of the Provinces of Nghe An and Ha Tinh and a part of Thanh Hoa Province. The Upper Ca River Watershed defined in this study is the upper part of the watershed which has its outlet at Yen Thuong Hydrological Station of Vietnam (105°23′ E, 18°41′ N), draining an area of approximately 22,800 km2. Geographic location and detailed information of the UCRW are shown in Figure 1.
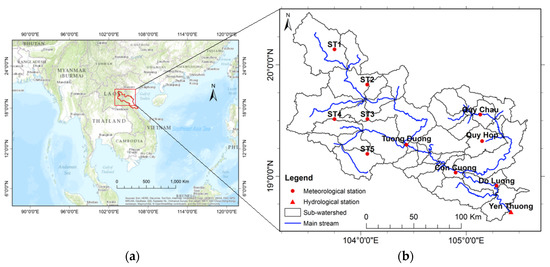
Figure 1.
Geographic location of the entire Ca River Watershed in (a) Southeast Asiaand; (b) the Upper Ca River Watershed (UCRW).
In the UCRW, precipitation is abundant, but is spatially and seasonally uneven in its distribution. Average annual precipitation observed varies from 1200 mm to 2100 mm depending on the weather station, with an average of approximately 1700 mm, of which the rainy season accounts for more than 80%. The UCRW is dominated by rugged terrain with approximately 70% of the watershed area having a slope of greater than 15 degrees and 20% having a slope of greater than 30 degrees. Highly steep areas are mostly located in the middle part of the watershed, where high mountains are alternated by low and narrow strips along streams. Soils in the UCRW include mostly Humic Acrisols (strongly weathered acid soil, with generally low inherent soil fertility) and Plinthic Ferralsols (deeply weathered red or yellow soil, dominated by low activity clays including mainly kaolinite and sesquioxides). Except for the alluvial soils in the low valleys, soils in the area are generally acidic, poor in nutrients, and highly susceptible to erosion. The natural land cover is mostly evergreen and semi-deciduous tropical moist forest, although mixed forest can be found throughout the watershed. Anthropogenic land-cover in the UCRW includes annual rain-fed crops (e.g., corn, groundnuts, beans, and upland rice), irrigated rice, perennial crops (e.g., banana, sugarcane), orchards, pastures, bare soil, and residential areas. Maps presenting climate, topography, and ground cover of the UCRW are shown in Figure 2.
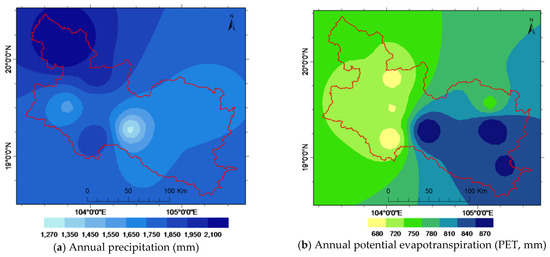
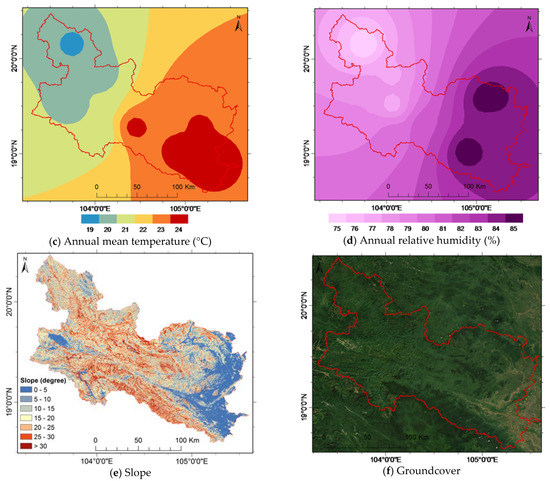
Figure 2.
Spatial pattern of climate data, slope, and groundcover of the UCRW.
In this study, daily weather data including precipitation, temperature, potential evapotranspiration (PET), and relative humidity was collected from the Hydro-Meteorological Data Center of Vietnam. In addition, five points where weather data was available from the National Centers for Environmental Prediction (NCEP) Climate Forecast System Reanalysis (CFSR) were used for simulation by the SWAT model. A digital elevation model (DEM) with 3 arc-second resolution covering the entire Ca River Watershed was obtained from the NASA Shuttle Radar Topographic Mission. Land use data and soil data were collected from multiple sources; and were then reclassified in accordance with the SWAT model input requirement.
2.2. Prediction of Future Climate Change
In the present study, future climate projections under three emission scenarios B1, B2, and A2 from the Fourth Assessment Report (AR4) of the Intergovernmental Panel on Climate Change (IPCC)—which respectively represent low, medium, and high greenhouse gas emission levels—were generated using the MAGICC/SCENGEN model [6]. The model contains output of 20 GCMs of the Coupled Model Intercomparison Project Phase 3 (CMIP3) archive. A list of the 20 GCMs can be found in Wigley [6]. The result from the model display changes in monthly precipitation, temperature, etc. relative to the baseline period on each prediction grid cell. The baseline period defined in this study was 1980–1999. Then, downscaling methods were used to downscale these data to at-site daily data. First, a statistical downscaling method with conversion functions was used to transfer the large-scale monthly climate data to site-scale monthly data at local stations, and downscaled data from these local stations was then used to estimate average data for other areas in the watershed by the Inverse Distance Weighting (IDW) interpolation method [7]. The conversion function is a linear regression equation y = ax + b; where y is monthly temperature (or precipitation) observed at a local station, x is predicted monthly temperature (or precipitation) in the grid cell at the coordinates of the local station, and a and b are constants. The statistical downscaling for climate stations in Vietnam can be referred to in IMHEN [8]. Spatial interpolation is a process which can estimate or predict values at unsampled points based on values of sampled points. It is widely used to predict unknown values for various climatic data such as precipitation, temperature, humidity, and evaporation, etc. IDW is an interpolation method that estimates cell values by averaging the values of measured points surrounding each processing cell. The assumption of IDW is that the variable being mapped decreases in influence with distance from its sampled locations. In other words, the closer a point is to the center of the cell being estimated, the more weight, or influence [9,10,11]. The general equation of IDW is as follows:
where:
- is the value of temperature (or precipitation) being predicted for location ;
- N is the number of measured sample points around the prediction location that will be employed in the prediction;
- is the weight assigned to measured point i. The weight will decrease when distances increase.
- is the the observed value at the location .
The weights are determined by the following equation:
where:
As the distance becomes larger, the weight is reduced by a factor of p.
The quantity di0 are the distance between the prediction location (s0) and each of the measured locations (si).
The power parameter p influences the weighting of the measured location’s value on the value of prediction location; that is, as the distance between the measured sample locations and the prediction location increases, the influence (or weight) that the measured point will have on the prediction will exponentially decrease. The weights for the measured sample locations that will be employed in the prediction are scaled, their sum is therefore equal to 1 [11,12]. In this study, to consider the effect of topography on temperature/precipitation, observed baseline temperature/precipitation was used as the “Weight Field”, and optimal p values were identified based on root mean square error (RMSE) of the prediction. The optimal p value is the value that produces the lowest RMSE.
Next, the downscaled monthly data at the local stations were downscaled again to daily data using the MODAWEC weather generator model [13]. The daily data for precipitation and temperature at the local stations were then employed for the simulation by the SWAT model. More detailed methodology for the generation of future climate change scenarios in this study can be referred to Pham et al. [14]
2.3. Simulation of Soil Erosion
In the present study, a soil erosion simulation was performed using the SWAT model [15]. SWAT was developed for the computation of runoff and sediment and agricultural chemical yields in large complex watersheds with varying soils and land use management conditions over long time periods [15,16,17]. In this model, a watershed is divided into multiple sub-watersheds that are then further subdivided into unique soil/land-use characteristics called hydrologic response units (HRUs).
SWAT calculates soil erosion within each HRU using the Modified Universal Soil Loss Equation (MUSLE) [18], which is shown in Equation (3).
where:
- Sed is the sediment yield in a given day (metric tons);
- Qsurf is the surface runoff volume (mm/ha);
- qpeak is the peak surface runoff rate (m3/s);
- areahru is the area of the HRU (ha);
- K is the Universal Soil Loss Equation (USLE) soil erodibility factor, which is available from the Soil Survey Geographic (SSURGO) data;
- C is the USLE cover and management factor and can be derived from land cover data;
- P is the USLE support practice factor, which is a field specific value;
- CFRG is the coarse fragment factor.
- LS is the topographic factor. It is a function of the land slope length (Lhill), the angle of slope (αhill), and the exponential term m in the equation below:
Parameters including K, C, P, LS, and CFRG are to be adjusted in the calibration process. The use of a physically-based hydrology model such as SWAT when coupled with the MUSLE may reduce uncertainty in soil erosion prediction when compared to the original USLE-based calculations of long-term sediment yields that are highly sensitive to topographic factors [19].
The peak runoff rate (qpeak) is the maximum runoff flow rate occurring with a given rainfall event. It is an indicator of the erosive power of the rainfall event, and in SWAT, it is calculated as follows:
where:
- αtc is the fraction of daily rainfall that occurs during the time of concentration (time of concentration is the amount of time from the beginning of a rainfall event until the entire sub-basin area is contributing to flow at the sub-basin outlet) [17];
- Qsurf is the surface runoff (mm H2O);
- Area is the area of sub-basin (km2);
- 3.6 is a unit conversion factor;
- tconc is the time of concentration for the sub-basin (h).
2.4. SWAT Model Calibration and Validation
Model calibration and validation are necessary and critical steps in any model application. Calibration is an iterative procedure of parameter adjustment and refinement, as a result of comparing simulated and observed values of interest. Validation is a process to ensure that the calibrated model properly assesses all the variables and conditions which can affect model results and demonstrate the ability of the calibrated model to predict field observations for periods separate from the calibration effort [20,21]. SWAT input parameters must be held within a realistic range of uncertainty. The first step in the calibration in SWAT is to determine the most sensitive parameters for the investigated watershed. The method of sensitivity analysis in the SWAT model combines Latin Hypercube (LH) [22] and one-factor-at-a-time (OAT) sampling [23]. During sensitivity analysis, SWAT runs (p + 1) ×m times, where p is the number of parameters being evaluated and m is the number of LH loops. For each loop, a set of parameter values is selected such that a unique area of the parameter space is sampled. That set of parameter values is used to run a baseline simulation for that unique area. Then, using OAT, a parameter is randomly selected, and its value is changed from the previous simulation by a user-defined percentage. SWAT is run on the new parameter set, and then a different parameter is randomly selected and varied. After all the parameters have been varied, the LH algorithm locates a new sampling area by changing all the parameters [24,25].
Two types of analysis are available in the sensitivity analysis tool in SWAT. The first type of analysis uses only simulated data to identify the impact of adjusting a parameter value on some specific model outputs, such as average streamflow. The second type of analysis uses observed data to provide an overall “goodness of fit” estimation between the simulated and the observed time series. The first type of analysis may help to identify parameters that improve a particular process or characteristic of the model, while the second type of analysis identifies the parameters that are affected by the characteristics of the study watershed [24,25]. In this study, the selection of parameters for stream discharge and sediment calibration was carried out based on the sensitivity analysis, following the guidelines reported by Veith and Ghebremichael [24] and Van Liew and Veith [25].
SWAT model calibration and validation were performed using observed data of sediment yield recorded at the watershed outlet during 40 years (1971–2010), in which 25 years (1971–1995) were used for calibration and 15 years (1996–2010) were used for validation. To evaluate the model predictions for both time periods, four statistical indicators, including the coefficient of determination (R2), Nash–Sutcliffe simulation efficiency (Nash), and Percent Bias (PBIAS), and root mean square error—observation standard deviation ratio (RSR) were used. R2 was used as an indicator to measure the strength of the linear relationship between simulated data and observed data, meanwhile the Nash indicator was used to indicate how well the plot of observed versus simulated data fits the 1:1 line—or in other words, how close the simulated data was to the observed data. PBIAS was used to determine if the average tendency of the simulated data to be larger or smaller than their observed counterparts, which points out whether the model tends to underestimate or overestimate the simulated variable. In addition to R2, Nash, and PBIAS, RSR was used to incorporate the benefits of error index statistics (i.e., root mean square error) and a scaling/normalization factor (i.e., standard deviation—STDEV), so that the resulting statistic and reported values can be applied to various constituents. A comprehensive description of these indicators can be found in Pham et al. [14]. These indicators are calculated as in Equations (6)–(9), and their values were then compared with the guideline values introduced by Moriasi et al. [26], which recommended that for monthly time-step simulations, sediment prediction can be judged as “satisfactory” if Nash >0.50, RSR ≤ 0.70, and PBIAS ≤ ±55%, as “good” if 0.65 < NSE ≤ 0.75, 0.50 < RSR ≤ 0.60, and ±15% ≤ PBIAS ≤ ±30%, and as “very good” if 0.75 < NSE ≤ 1.00, PBIAS < ±15%, and 0.00 ≤ RSR ≤ 0.50.
where:
- and are the observed and simulated values of the variable X, respectively;
- and are the mean of the observed values and the mean of the simulated values of the variable X, respectively;
- n is the total number of observations.
In this study, X represents sediment yield.
A graphical comparison of time series observed versus simulated sediment yield in the present study can be referred to Pham et al. [27]. The results of evaluation statistics calculation show that there was a high agreement between simulated data and observed data in both calibration and validation periods, as all evaluation statistics computed for both periods were strong. Specifically, the R2 was 0.88 and 0.87 and Nash was 0.89 and 0.87 for calibration and validation periods, respectively. Meanwhile, the values of RSR were 0.34 and 0.35 and the values of PBIAS were 0.9% and 4.14%. Positive values of PBIAS indicator found in this study (0.90% for calibration and 4.14% for validation) indicate that there was an underestimation bias for both time periods, although the bias was insignificant. Comparing with the guideline of Moriasi et al. [26] described previously, the performance of the SWAT model in this study can be assessed as “very good”. This confirms that the model is applicable to the present study.
3. Results and Discussion
3.1. Projected Warming
Figure 3 presents projected monthly average temperature for the basin average. Temperature is predicted to increase in all months, with warming rates ranging from 0.6 °C to 1.2 °C by the 2030s, from 1 °C to 2.5 °C by the 2060s, and from 1.4 °C to 3.9 °C by the 2090s, depending on the emission scenario and month. The highest warming rates are expected for February and April, with 3.6 °C and 3.9 °C by the 2090s according to scenario A2. Other months with a high warming rate are June and September, which are expected to warm by as much as 3.5 °C by the 2090s compared to the baseline average. In contrast, the smallest warming rates are predicted for March and August, with 2.6 °C and 2.3 °C, respectively, by the 2090s according to the high emission scenario (A2). From a seasonal point of view, temperature is likely to rise faster in the dry season (winter and spring) than in the wet season (summer and autumn). A faster warming rate in winter and spring may cause destruction of the seasonal cycle, gradually leading summer to come earlier than normal and winter and spring to become shorter. This issue has been discussed in several recent studies [28,29].
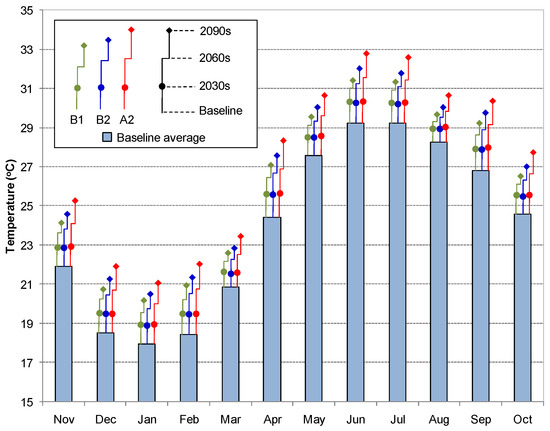
Figure 3.
Projected monthly temperature for the future periods under three emission scenarios.
Considering the temperature prediction behaviors of the three selected scenarios B1, B2, and A2, it should be noted that the difference in behavior of the three scenarios changes with time. The three scenarios give similar predictions until the near future period (2030s), and then the predictions begin to diverge: temperature increases fastest under A2, followed by B2, and then B1. This is in line with the characteristics of the emission scenarios, which evolve similarly until the middle of the 21st century, when A2 becomes more negative due to the continuous increase in greenhouse gas emissions as a result of the increase in population growth. In contrast, B1 becomes less negative due to the slowing of population growth, and therefore a reduction in greenhouse gas emissions [1,30]. Similar findings have also been reported in several recent studies using IPCC TAR or IPCC AR4 models on a regional scale [31,32,33].
3.2. Projected Change in Precipitation
The results of climate projection show that precipitation in the UCRW is likely to change, varying by months. Figure 4 shows the projected precipitation in future periods. It can be easily seen that precipitation is predicted to increase for February, and for all months from June to December, and to decrease for January, March, April, and May. Significant decreases are likely to occur in January and April, while significant increases are likely to occur from July to October. Comparing the three scenarios, the order scenarios with respect to the magnitude of precipitation change until the 2030s is A2 > B1 > B2. From the 2030s onwards, this order shifts to A2 > B2 > B1, with the difference among the scenarios growing larger throughout the century. Maps showing spatial patterns of changes in mean annual precipitation for the 2090s are presented in Figure 5.
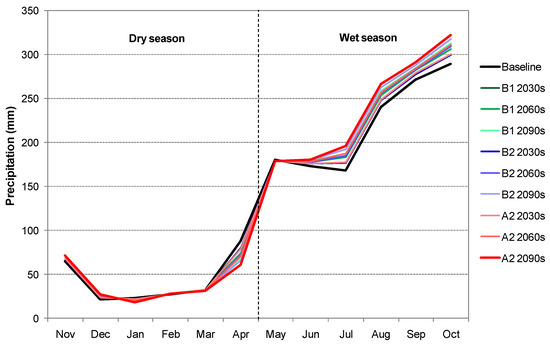
Figure 4.
Projected mean monthly precipitation. The bold black line presents data for the baseline period, whereas the bold redline presents data with the largest change compared to the baseline period.
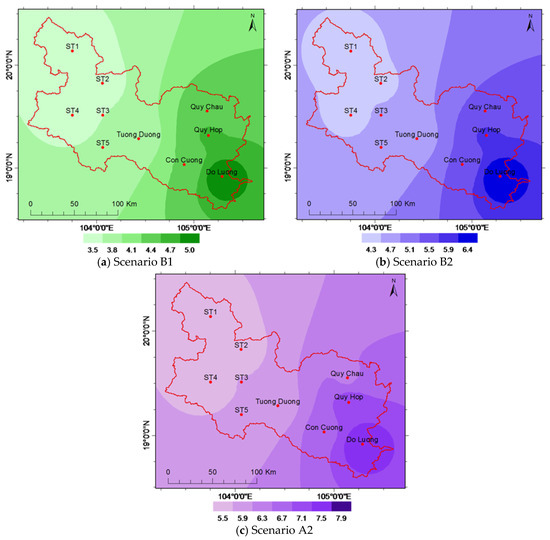
Figure 5.
Maps present increases in average annual precipitation in the 2090s compared to the baseline period, units in percent.
3.3. Spatial Pattern of Changes in Erosion Rate
Figure 6 presents spatial patterns of erosion for the UCRW during the baseline period. The erosion rate ranges from 2.7 tons/ha/year to 51.6 tons/ha/year with a mean value of 21.3 tons/ha/year. In general, the upstream areas were found to have more severe erosion than the downstream areas. Among the 39 sub-watersheds in the UCRW, upstream sub-watersheds 4, 7, 8, and 9 were identified as having the highest erosion rates (more than 40 tons/ha/year), while downstream sub-watersheds 20, 36, and 37 were found to have the lowest erosion rates (less than 5 tons/ha/year). One possible reason for this is that upstream sub-watersheds have steep slopes and receive a large amount of rainfall (Figure 2a), and are subjected to shifting cultivation, while downstream sub-watersheds are mostly flat (Figure 2e). Interestingly, although the UCRW receives a large amount of rainfall in both upstream and downstream areas and less rainfall in its middle part, erosion was found to occur severely in the middle stream sub-watersheds (for example, sub-watersheds 24 and 25). This indicates that not only surface runoff plays an important role in the movement of soil particles, but the erosion process is substantially affected by other factors. We refer to Equation (3) to examine factors causing a high erosion rate for the identified areas. Equation (3) calculates erosion rate as a result of combined effects of rainfall (through surface runoff), soil erodibility factor (K), cover and management factor (C), support practice factor (P), topographic factor (LS), and coarse fragment factor (CFRG). Since soil in the watershed is mostly Ferralsols (deeply weathered red or yellow soil, dominated by low activity clays including mainly kaolinite and sesquioxides), soil-related factors (K and CFRG) could almost have the same values for the entire watershed. The P factor is related to soil conservation practice; it reflects the effects of practices that will reduce the amount and rate of the water runoff and thus reduce the amount of erosion. In this study, we assumed that no supporting practice was applied in the watershed. The C factor is related to land surface cover. C varies from zero to one, with high values for barren land and crop land (e.g., row crops, rice), and low values for forest land and pasture. Although most of the crop land (C was set at 0.3) is located downstream, the area of crop land is small. In addition, the upstream area—and especially middle stream area—are subjected to shifting cultivation and deforestation, resulting in large areas of barren land, which is highly sensitive to erosion. The topographic factor LS is a function of the land slope length and the angle of slope Thus, the larger the slope length, and the larger the slope angle are, the larger the topographic factor will be. In other words, the longer and steeper the slope of surface, the higher the risk for erosion. Therefore, although the middle stream area receives less rainfall than other parts (Figure 2a), due to the rugged terrain with long and steep hill slopes (Figure 2e) soil erosion was found to occur severely in this area. In short, the physical meaning of the two key factors (i.e., C and especially LS) discussed above can explain the spatial patterns of soil erosion in the UCRW.
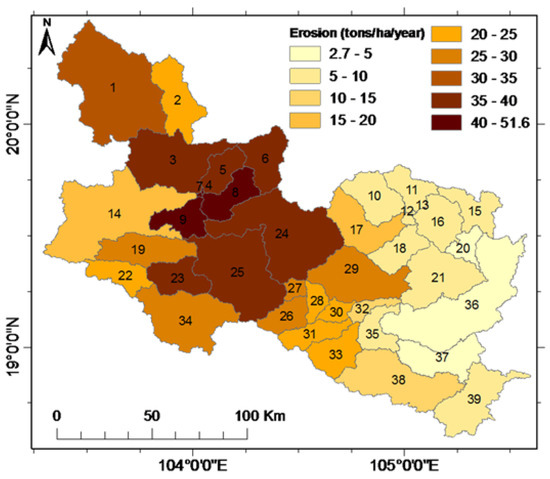
Figure 6.
Average annual erosion rate in each sub-watershed in the baseline period.
Figure 7 shows the variation in erosion rates by sub-watersheds in the future time stages under the three emission scenarios. Although erosion is predicted to change differently depending on the sub-watershed, time stage, and emission scenario, an increasing trend throughout the 21st century can be seen in all three scenarios. Erosion is likely to increase the most with scenario A2, followed by scenario B2, and the least with scenario B1. For the near future time stage (2030s) the predictions of erosion under the three emission scenarios are very similar. This is consistent with the characteristic of the increase in temperature (Figure 3) and precipitation (Figure 4). On a basin-wide average, annual erosion rate is projected to be approximately 22.5 tons/ha/year by the 2030s, 23.5–24.0 tons/ha/year by the 2060s, and 24.1–25.6 tons/ha/year by the 2090s.
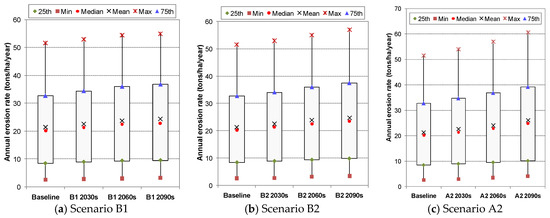
Figure 7.
Box and whisker plots showing variation of annual erosion rates in sub-watersheds of the UCRW in the future time stages.
A map showing the spatial pattern of increase in erosion rate in the UCRW by the 2090s according to the high emission scenario A2 is shown in Figure 8. All sub-watersheds are projected to experience an increase in erosion rates ranging from approximately 13.3% to approximately 32.6%. It is noticeable that middle stream and downstream areas are projected to be more sensitive to climate change than upstream areas in terms of soil erosion. This may be due to the projected precipitation and temperature, both of which are projected to increase more in the middle stream and downstream areas than in the upstream areas. In general, a larger increase in precipitation will produce a greater increase in surface runoff, which is a direct factor causing more erosion (Equation 3). Increases in temperature may to a certain extent facilitate plant growth, but temperature in the UCRW is already high, and an increase in temperature in the area may cause stress to plants, consequently leading to a reduction in plant biomass [1]. On the other hand, an increase in temperature and a resulting increase in moisture will likely cause a faster residue decomposition process due to an increase in microbial activity [1,4,34]. These would lead to a reduction in biological ground cover, making the area more exposed to the projected increasing precipitation, and ultimately lead to more erosion. Large increases in erosion rate in some middle stream sub-watersheds can also be explained by the steep topography of these sub-watersheds. The effect of increased rainfall due to climate change on erosion in steep areas has been reported previously [19].
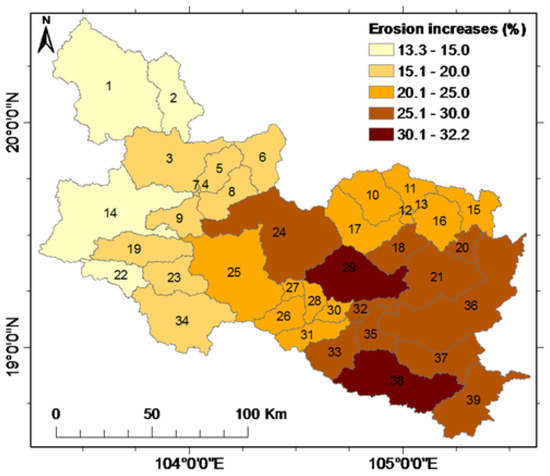
Figure 8.
Increases in soil erosion in the 2090s compared to the baseline period according to the high emission scenario A2.
3.4. Temporal Pattern of Changes in Erosion Rate
The temporal pattern of climate change impacts on erosion rate in the UCRW was investigated. The column chart in Figure 9 presents average monthly erosion rate for the baseline period, while the line chart presents projected change in erosion rate in the future time stages relative to the baseline period. Average intra-annual (monthly) erosion rate of the baseline period varies from 0.15 tons/ha (February) to 5.3 tons/ha (September), with an annual total of 21.3 tons/ha. In general, erosion rates in the wet season months are much higher than in the dry season months. The seasonal erosion rate for the dry season is 2.2 tons/ha, and for the wet season is 19.1 tons/ha. Predicted monthly change in the erosion rate ranges from a 39.5% decrease to a 33.4% increase depending on the specific month, emission scenario, and time period. From a seasonal point of view, the erosion rate is predicted to increase from mid wet season to early dry season (July to December), and to decrease from mid dry season to early wet season (January to June). Increases in the erosion rate in the months from July to December can be explained by the projected increases in precipitation in these months. When precipitation increases, its erosive power and sediment transport capacity increase, resulting in an increase of erosion. However, it should be noted that the magnitudes and patterns of the change in erosion rate are not consistent with that of the change in precipitation. This is because besides precipitation (and as a result, surface runoff), erosion rate depends on other factors such as evaporation, topography, soil, land cover, and plant growth, etc. For example, a decrease in the erosion rate during the months from January to June may be related to changes in antecedent soil water content during precipitation events under future climate conditions. Even when an increase in precipitation was predicted, an increase in evaporation (due to the warmer climate) appeared to cause a reduction in soil water content which may lead to an increase in saturation deficit. This means that more precipitation is needed to bring the soil to saturation and generate the same amount of runoff as under the current climate conditions. The role of antecedent soil water content on soil erosion in saturation excess dominated areas has been reported [19,34]. In addition, increased temperature and increased precipitation in the dry-cold months (spring) may also accelerate plant growth, which results in increased biological cover, and less erosion as a result. However, it should be noted that the decrease in erosion rate in February and June is very small, and the pattern of the decrease is complicated. While in the other months, the magnitude of changes (increase or decrease) becomes larger with time, the magnitude of decrease in these two months decreases gradually toward zero. This means that if a larger increase in precipitation was predicted, the change in erosion rate in these two months would be positive (turn to an increase, following the increasing trend of rainfall).
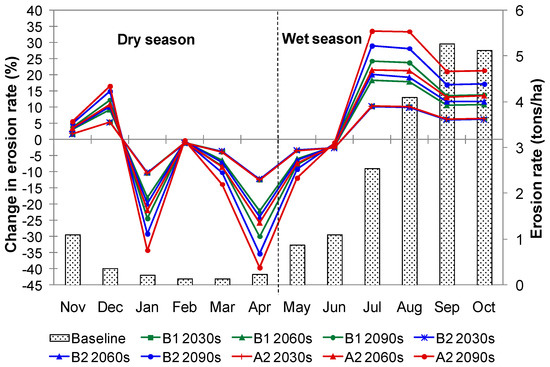
Figure 9.
Projected changes in soil erosion relative to the baseline period.
4. Conclusions
This study investigated spatial and temporal responses of soil erosion to climate change impacts in the Upper Ca River Watershed, which is shared upstream by Laos and downstream by Vietnam. Soil erosion in the study watershed was mostly found as “hill-slope erosion”, which occurred seriously in the upstream and middle stream areas, where topography is dominated by numerous steep hills with sparse vegetation cover. However, under the impact of climate change, it is likely that soil erosion rate in the downstream area will increase at a higher rate than in the upstream and middle stream areas. From a seasonal point of view, soil erosion is predicted to increase significantly in the warmer and wetter climate of the wet season, when higher sediment transport capacity is accompanied by the higher erosive power of an increased rainfall amount and intensity. These results provide useful information for decision makers and local people to plan where and when soil conservation practice should be focused. To protect the soil from erosion, countermeasures should focus on the peak months of the wet season, such as August, September and October, when erosion occurs the most seriously and is likely to increase with a high rate. For the steep upstream and middle stream areas where groundcover is mostly dominated by degraded or exploited forests and shifting cultivation land, countermeasures aiming to increase groundcover and to prevent hill-slope erosion such as reforestation, afforestation, terrace farming, and construction of check dams and retaining walls should be planned and implemented by the local governments. For the downstream area where the topography is less steep and agricultural fields are located, measures by local farmers such as crop rotation, cover cropping, and mulching should be encouraged.
Acknowledgments
The authors are grateful to the agencies of the Government of Vietnam for providing the data necessary for this study. We would like to thank the anonymous reviewers of the manuscript for their thorough review and helpful comments and suggestions.
Author Contributions
The design of study, data collection and analysis, model simulation, and manuscript writing were done by Pham Quy Giang. All authors contributed to the discussion of the study results and editing the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Parry, M.L.; Canziani, O.F.; Palutikof, J.P.; van der Linden, P.J.; Hanson, C.E. Climate Change 2007: Working Group II: Impacts, Adaptation and Vulnerability; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Nearing, M.A. Potential changes in rainfall erosivity in the United States with climate change during the 21st century. J. Soil Water Conserv. 2001, 56, 229–232. [Google Scholar]
- Zhang, G.H.; Nearing, M.A.; Liu, B.Y. Potential effects of climate change on rainfall erosivity in the Yellow River basin of China. Trans. ASAE 2005, 48, 511–517. [Google Scholar] [CrossRef]
- Pruski, F.F.; Nearing, M.A. Climate-induced changes in erosion during the 21st century for eight U.S. locations. Water Resour. Res. 2002, 38, 1298. [Google Scholar] [CrossRef]
- Zhang, X.C.; Nearing, M.A. Impact of climate change on soil erosion, runoff, and wheat productivity in Central Oklahoma. Catena 2005, 61, 185–195. [Google Scholar] [CrossRef]
- Wigley, T.M.L. MAGICC/SCENGEN 5.3: User Manual Version 2; National Center for Atmospheric Research: Boulder, CO, USA, 2008; p. 81. [Google Scholar]
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 1968 ACM National Conference, Las Vegas, NV, USA, 27–29 August 1968.
- Vietnam Institute of Meteorology, Hydrology, and Climate Change (IMHEN). Impacts of Climate Change on Water Resources and Adaptation Measure: Final Report; IMHEN: Hanoi, Vietnam, 2010; p. 120. [Google Scholar]
- Burrough, P.A. Principles of Geographical Information Systems for Land Resources Assessment; Oxford University Press: Oxford, UK, 1986; p. 194. [Google Scholar]
- Watson, D.F. Contouring: AGuide to the Analysis and Display of Spatial Data; Pergamon Press: Oxford, UK, 1992. [Google Scholar]
- Environmental Systems Research Institute (ESRI). ArcGIS 9, Using Arc Geostatistical Analyst; Environmental Systems Research Institute Inc.: Redlands, CA, USA, 2003; p. 300. [Google Scholar]
- Pham, Q.G. Effectiveness of different spatial interpolators in estimating heavy metal contamination in shallow groundwater: A case study of arsenic contamination in Hanoi, Vietnam. Environ. Nat. Resour. J. 2011, 9, 31–37. [Google Scholar]
- Liu, J.; Williams, J.R.; Wang, X.; Yang, H. Using MODAWEC to generate daily weather data for the EPIC model. Environ. Model. Softw. 2009, 24, 655–664. [Google Scholar] [CrossRef]
- Pham, Q.G.; Toshiki, K.; Sakata, M.; Kunikane, S.; Tran, Q.V. Modelling Climate Change Impacts on the Seasonality of Water Resources in the Upper Ca River Watershed in Southeast Asia. Sci. World J. 2014. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Williams, J.; Arnold, J.G. A System of Hydrologic Models. U.S.Geological Survey. Water Resources Investigations Report; U.S. Geological Survey: Reston, VA, USA, 1993; pp. 93–4018.
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation; Version 2009; Blackland Research Center: Temple, TX, Texas, USA, 2011; p. 618. [Google Scholar]
- Williams, J.R. Sediment-yield prediction with universal equation using runoff energy factor. Present and Prospective Technology for Predicting Sediment Yield and Sources. In Proceedings of the Sediment Yield Workshop, USDA Sedimentation Lab., Oxford, MS, USA, 28–30 November 1972; pp. 244–252.
- Mukudan, R.; Soni, M.P.; Elliot, M.S.; Donald, C.P.; Aavudai, A.; Mark, S.Z.; Adão, H.M.; David, G.L.; Tammo, S.S. Suspended sediment source areas and future climate impact on soil erosion and sediment yield in a New York City water supply watershed, USA. Geomorphology 2013, 183, 110–119. [Google Scholar] [CrossRef]
- Donigian, S. Watershed model calibration and validation: The HSPF experience. In Proceedings of the Water Environment Federation, St. George, UT, USA, 10–12 October 2001.
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; van Liew, M.W.; et al. SWAT: Model use, calibration and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Van Griensven, A. Sensitivity, Auto-Calibration, Uncertainty and Model Evaluation in SWAT 2005. Available online: http://biomath.ugent.be/~ann/swat_manuals/SWAT2005_manual_sens_cal_unc.pdf (accessed on 6 March 2017).
- Veith, T.L.; Ghebremichael, L.T. How to: Applying and interpreting the SWAT Auto-calibration tools. In Proceedings of the Fifth International SWAT Conference Proceedings, Boulder, CO, USA, 5–7 August 2009.
- Van Liew, M.W.; Veith, T.L. Guidelines for Using the Sensitivity Analysis and Auto-Calibration Tools for Multi-Gage or Multi-Step Calibration in SWAT. Available online: http://www.academia.edu/21601923/Guidelines_for_Using_the_Sensitivity_Analysis_and_Auto-calibration_Tools_for_Multi-gage_or_Multi-step_Calibration_in_SWAT (accessed on 6 March 2017).
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Binger, R.L.; Harmel, R.D.; Veith, T. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2006, 50, 885–900. [Google Scholar] [CrossRef]
- Giang, P.Q.; Toshiki, K.; Sakata, M.; Kunikane, S. Modelling the seasonal response of sediment yield to climate change in the Laos-Vietnam Transnational Upper Ca River Watershed. EnvironmentAsia 2014, 7, 152–162. [Google Scholar]
- Stine, A.R.; Huybers, P.; Fung, I.Y. Changes in the temperature in the phase of the annual cycle of surface temperature. Nature 2009, 457, 435–440. [Google Scholar] [CrossRef] [PubMed]
- Jacques, F.M.B.; Shi, G.; Li, H.; Wang, W. An early-middle Eocene Antarctic summer monsoon: Evidence of ‘fossil climates’. Gondwana Res. 2014, 25, 1422–1428. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Special Report on Emissions Scenarios: A Special Report of Working Group III of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2000; p. 570. [Google Scholar]
- Ribalaygua, J.; Pino, M.R.; Pórtoles, J.; Roldán, E.; Gaitán, E.; Chinarro, D.; Torres, L. Climate change scenarios for temperature and precipitation in Aragón (Spain). Sci. Total Environ. 2013, 463, 1015–1030. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Hong, Y.; Hocker, J.E.; Shafer, M.A.; Carter, L.M.; Gourley, J.J.; Bednarczyk, C.N.; Yong, B.; Adhikari, P. Analyzing projected changes and trends of temperature and precipitation in the southern USA from 16 downscaled global climate models. Theor. Appl. Climatol. 2012, 109, 345–360. [Google Scholar] [CrossRef]
- Jiang, X.; Yang, Z.L. Projected changes of temperature and precipitation in Texas from downscaled global climate models. Clim. Res. 2012, 53, 229–244. [Google Scholar] [CrossRef]
- Williams, J.R.; Nearing, M.A.; Nicks, A.; Skidmore, E.; Valentine, C.; King, K.; Savabi, R. Using soil erosion models for global change studies. J. Soil Water Conserv. 1996, 51, 381–385. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).