Ensemble Forecasts: Probabilistic Seasonal Forecasts Based on a Model Ensemble
Abstract
:1. Introduction
2. Methods
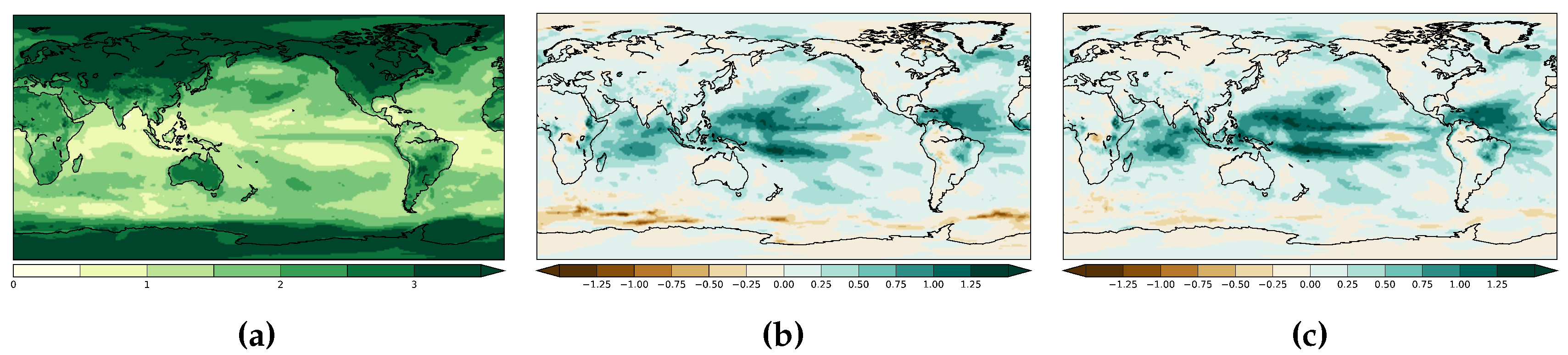
2.1. Data
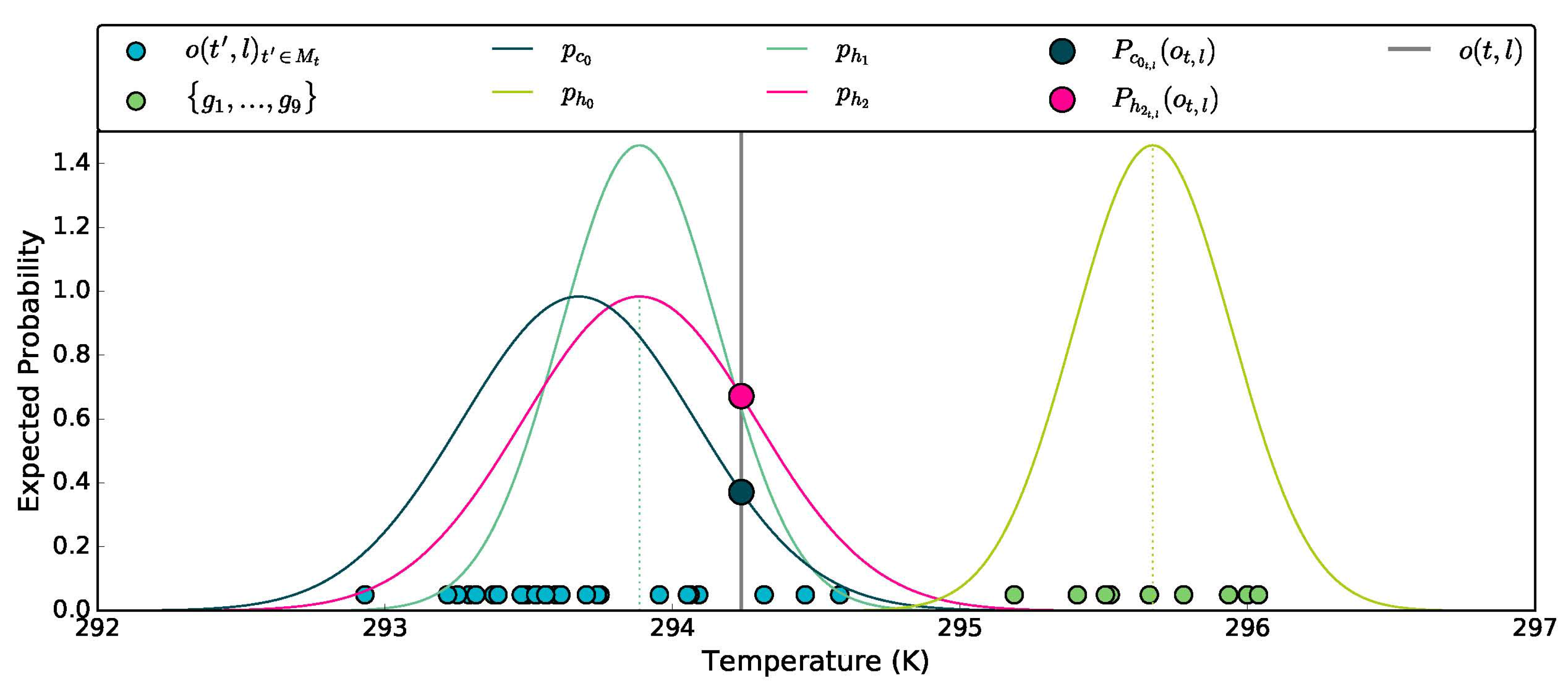
2.2. Probabilistic Models
2.2.1. A First Probabilistic Forecast Model
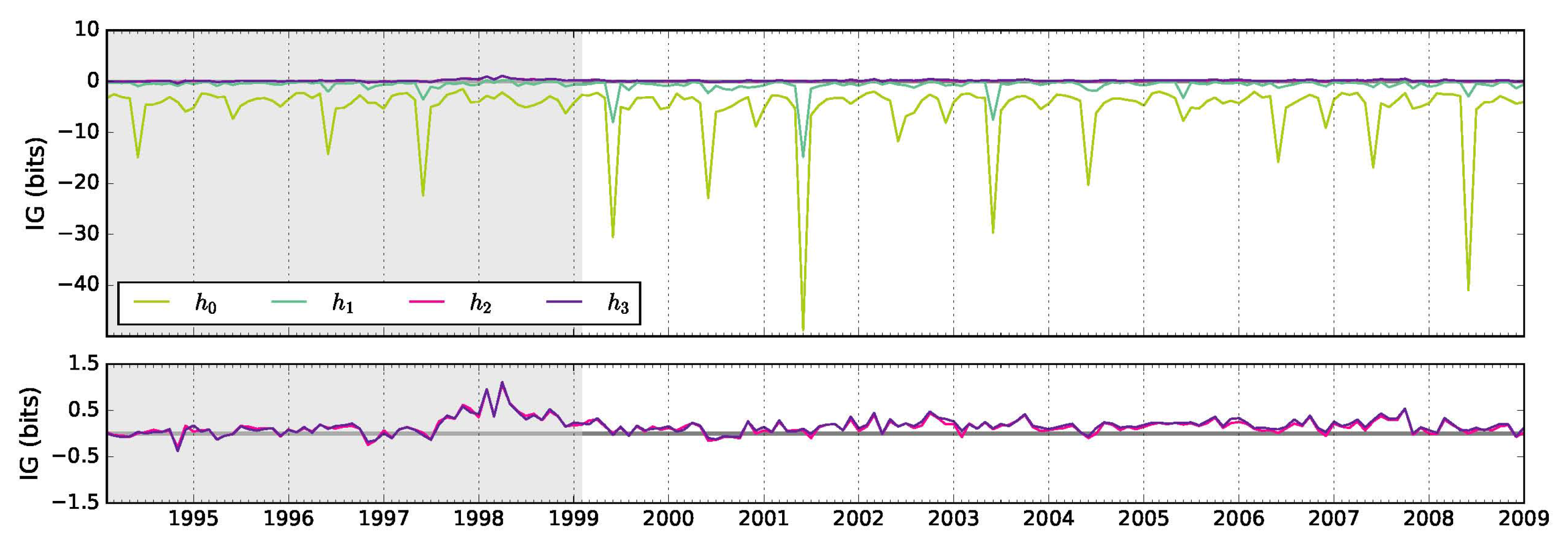
2.2.2. Information Gain Over Climatology
2.3. Improved Probabilistic Models
2.3.1. Bias-Corrected Probabilistic Model
2.3.2. Climatological Variance Adjusted Probabilistic Models
2.3.3. Mean Adjusted Forecast RMSE Adjusted Probabilistic Models
2.4. Autoregressive Models
2.4.1. Autoregressive Climatology
2.4.2. Combined GCM-Autoregressive Forecast Model
2.4.3. Auto-Regressive Weights
- computing the climatology using EWMA (, )
- updating the weights in the online regression using EWMA (, )
- combining methods 1 and 2 (, )
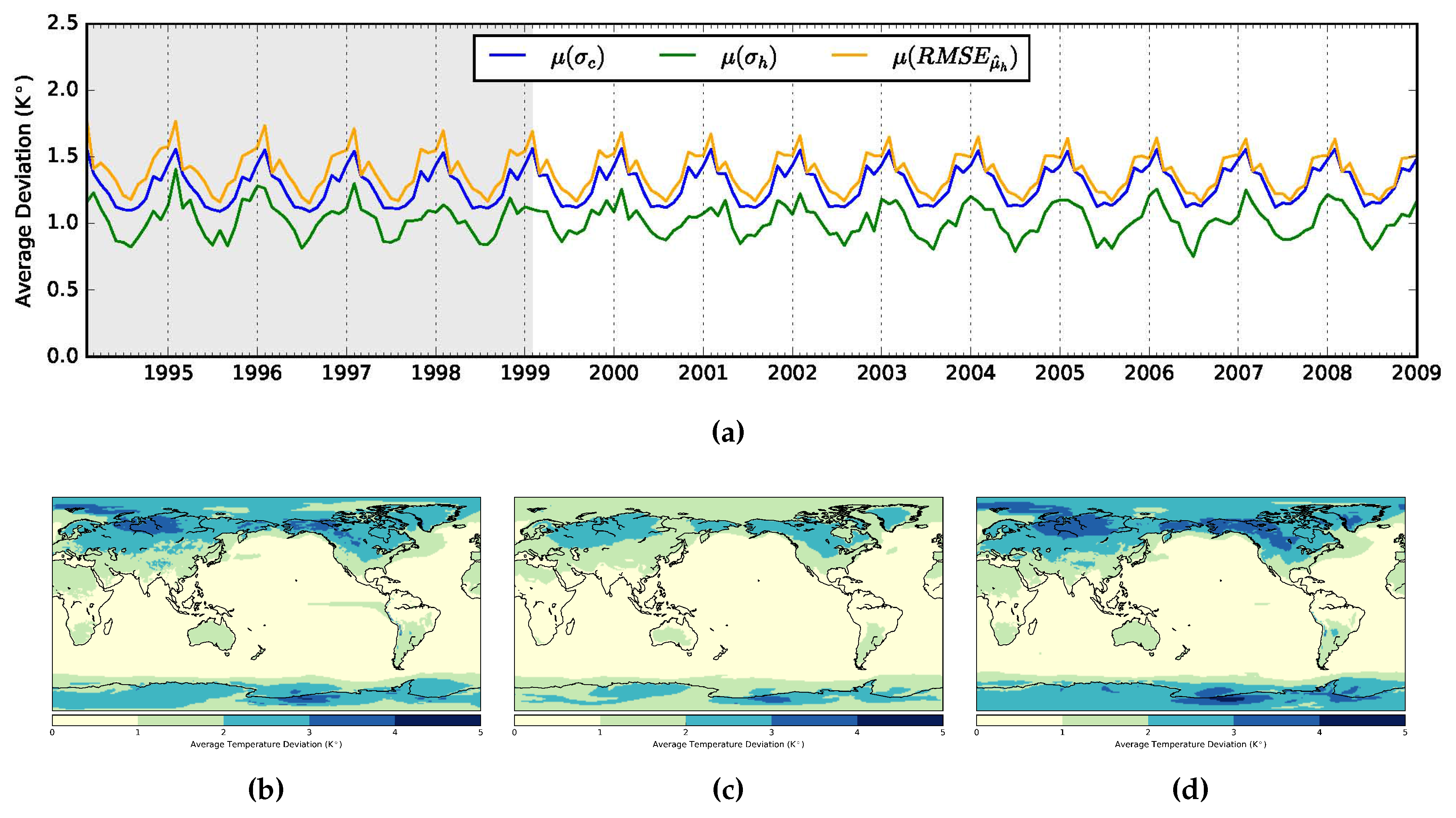
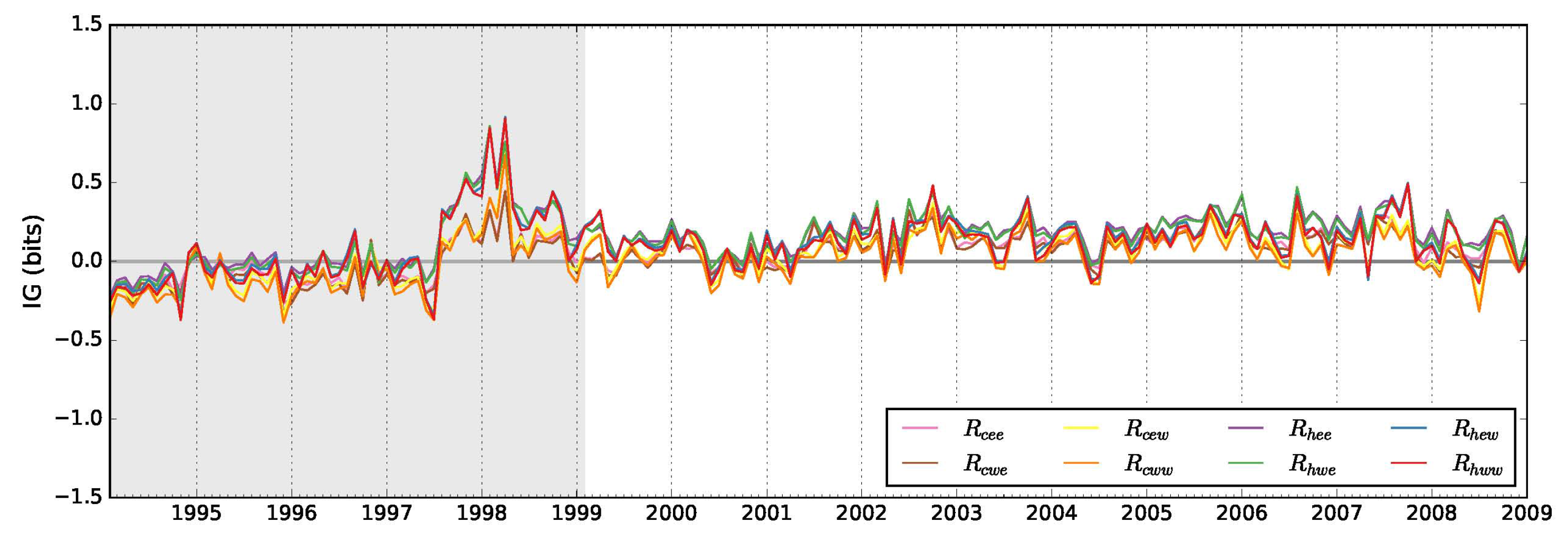
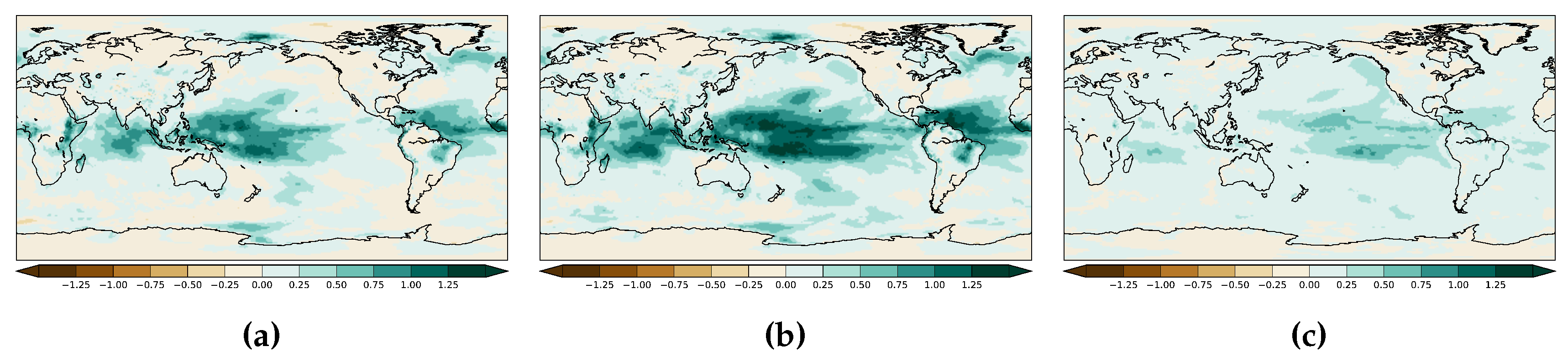
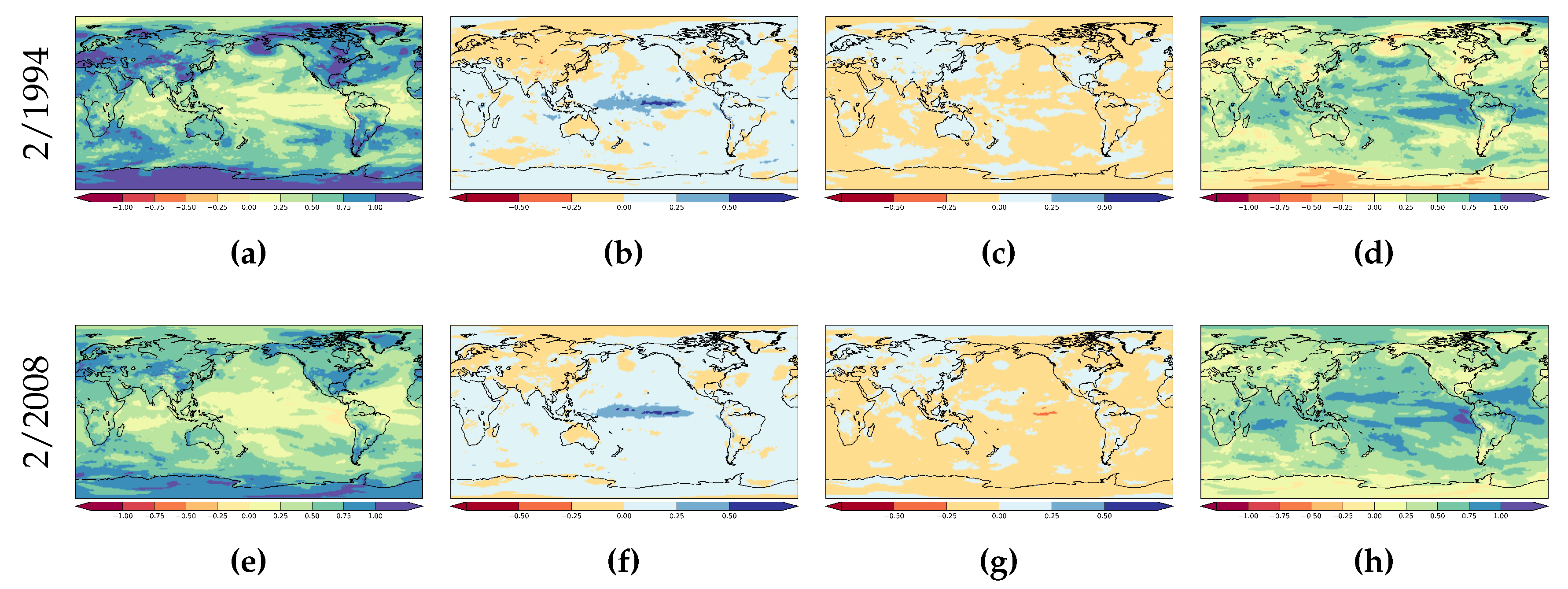
3. Results
3.1. Non-Auto-Regressive Probabilistic Models
3.2. Auto-Regressive Models
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- National Research Council. Assessment of Intraseasonal to Interannual Climate Prediction and Predictability; National Research Council: Washington, DC USA, 2010. [Google Scholar]
- Krishnamurti, T.N.; Kishtawal, C.M.; LaRow, T.E.; Bachiochi, D.R.; Zhang, Z.; Williford, C.E.; Gadgil, S.; Surendran, S. Improved weather and seasonal climate forecasts from multimodel superensemble. Science 1999, 285, 1548–1550. [Google Scholar] [CrossRef] [PubMed]
- Palmer, T.N. Predicting uncertainty in forecasts of weather and climate. Rep. Prog. Phys. 2000, 63, 71–116. [Google Scholar] [CrossRef]
- Barnston, A.G.; Mason, S.J.; Goddard, L.; Dewitt, D.G.; Zebiak, S.E. Multimodel ensembling in seasonal climate forecasting at IRI. Bull. Am. Meteorol. Soc. 2003, 84, 1783–1796. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E.; Westveld, A.H.; Goldman, T. Calibrated probabilistic forecasting using ensemble model output statistics and minimum CRPS estimation. Mon. Weather Rev. 2005, 133, 1098–1118. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian model averaging to calibrate forecast ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef]
- Johnson, C.; Swinbank, R. Medium-range multimodel ensemble combination and calibration. Q. J. R. Meteorol. Soc. 2009, 135, 777–794. [Google Scholar] [CrossRef]
- Weigel, A.P.; Liniger, M.A.; Appenzeller, C. Seasonal ensemble forecasts: Are recalibrated single models better than multimodels? Mon. Weather Rev. 2009, 137, 1460–1479. [Google Scholar] [CrossRef]
- Bundel, A.; Kryzhov, V.; Min, Y.M.; Khan, V.; Vilfand, R.; Tishchenko, V. Assessment of probability multimodel seasonal forecast based on the APCC model data. Russ. Meteorol. Hydrol. 2011, 36, 145–154. [Google Scholar] [CrossRef]
- Krakauer, N.Y.; Grossberg, M.D.; Gladkova, I.; Aizenman, H. Information content of seasonal forecasts in a changing climate. Adv. Meteorol. 2013, 2013, 480210. [Google Scholar] [CrossRef]
- Krakauer, N.Y.; Fekete, B.M. Are climate model simulations useful for forecasting precipitation trends? Hindcast and synthetic-data experiments. Environ. Res. Lett. 2014, 9, 024009. [Google Scholar] [CrossRef]
- Krakauer, N.Y.; Devineni, N. Up-to-date probabilistic temperature climatologies. Environ. Res. Lett. 2015, 10, 024014. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.T.; ya Chuang, H.; Iredell, M.; et al. The NCEP climate forecast System Version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Yuan, X.; Wood, E.F.; Luo, L.; Pan, M. A first look at Climate Forecast System version 2 (CFSv2) for hydrological seasonal prediction. Geophys. Res. Lett. 2011, 38, L13402. [Google Scholar] [CrossRef]
- Kumar, A.; Chen, M.; Zhang, L.; Wang, W.; Xue, Y.; Wen, C.; Marx, L.; Huang, B. An analysis of the nonstationarity in the bias of sea surface temperature forecasts for the NCEP Climate Forecast System (CFS) Version 2. Mon. Weather Rev. 2012, 140, 3003–3016. [Google Scholar] [CrossRef]
- Zhang, Q.; van den Dool, H. Relative merit of model improvement versus availability of retrospective forecasts: the case of Climate Forecast System MJO prediction. Weather Forecast. 2012, 27, 1045–1051. [Google Scholar] [CrossRef]
- Barnston, A.G.; Tippett, M.K. Predictions of Nino3.4 SST in CFSv1 and CFSv2: a diagnostic comparison. Clim. Dyn. 2013, 41, 1615–1633. [Google Scholar] [CrossRef]
- Luo, L.; Tang, W.; Lin, Z.; Wood, E.F. Evaluation of summer temperature and precipitation predictions from NCEP CFSv2 retrospective forecast over China. Clim. Dyn. 2013, 41, 2213–2230. [Google Scholar] [CrossRef]
- Kumar, S.; Dirmeyer, P.A.; Kinter, J.L., III. Usefulness of ensemble forecasts from NCEP Climate Forecast System in sub-seasonal to intra-annual forecasting. Geophys. Res. Lett. 2014, 41, 3586–3593. [Google Scholar] [CrossRef]
- Narapusetty, B.; Stan, C.; Kumar, A. Bias correction methods for decadal sea-surface temperature forecasts. Tellus 2014, 66A, 23681. [Google Scholar] [CrossRef]
- Silva, G.A.M.; Dutra, L.M.M.; da Rocha, R.P.; Ambrizzi, T.; Érico, L. Preliminary analysis on the global features of the NCEP CFSv2 seasonal hindcasts. Adv. Meteorol. 2014, 2014, 695067. [Google Scholar] [CrossRef]
- Weijs, S.V.; Schoups, G.; van de Giesen, N. Why hydrological predictions should be evaluated using information theory. Hydrol. Earth Syst. Sci. 2010, 14, 2545–2558. [Google Scholar] [CrossRef]
- Peirolo, R. Information gain as a score for probabilistic forecasts. Meteorol. Appl. 2011, 18, 9–17. [Google Scholar] [CrossRef]
- Tödter, J. New Aspects of Information Theory in Probabilistic Forecast Verification. Master’s Thesis, Goethe University, Frankfurt, Germany, 2011. [Google Scholar]
- Weijs, S.V.; van Nooijen, R.; van de Giesen, N. Kullback–Leibler divergence as a forecast skill score with classic reliability–resolution–uncertainty decomposition. Mon. Weather Rev. 2010, 138, 3387–3399. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Stephenson, D.B. Proper scores for probability forecasts can never be equitable. Mon. Weather Rev. 2008, 136, 1505–1510. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Stephenson, D.B. Forecast Verification; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Krakauer, N.Y.; Puma, M.J.; Cook, B.I. Impacts of soil-aquifer heat and water fluxes on simulated global climate. Hydrol. Earth Syst. Sci. 2013, 17, 1963–1974. [Google Scholar] [CrossRef]
- Cui, B.; Toth, Z.; Zhu, Y.; Hou, D. Bias correction for global ensemble forecast. Weather Forecast. 2012, 27, 396–410. [Google Scholar] [CrossRef]
- Williams, R.M.; Ferro, C.A.T.; Kwasniok, F. A comparison of ensemble post-processing methods for extreme events. Q. J. R. Meteorol. Soc. 2013. [Google Scholar] [CrossRef]
- Kirtman, B.P.; Min, D.; Infanti, J.M.; Kinter, J.L.; Paolino, D.A.; Zhang, Q.; van den Dool, H.; Saha, S.; Mendez, M.P.; Becker, E.; et al. The North American Multi-Model Ensemble (NMME): Phase-1 seasonal to interannual prediction, Phase-2 toward developing intra-seasonal prediction. Bull. Am. Meteorol. Soc. 2014, 95, 585–601. [Google Scholar] [CrossRef]
- Aizenman, H.; Grossberg, M.; Gladkova, I.; Krakauer, N. Longterm Forecast Ensemble Evaluation Toolkit. Available online: https://bitbucket.org/story645/libltf (accessed on 28 March 2016).
| IG of Relative to | ||||
|---|---|---|---|---|
| Model | Param. | Mean | Median | |
| - - - - | - - - - | |||
| –5.602 | –0.410 | |||
| –0.858 | 0.151 | |||
| 0.140 | 0.035 | |||
| 0.169 | 0.037 | |||
| IG Relative to | |||||
|---|---|---|---|---|---|
| Model | Hindcasts | EWMA Weighted | Mean | Median | |
| Climatology | Regression | ||||
| no | no | no | 0.112 | –0.053 | |
| no | yes | no | 0.095 | –0.084 | |
| no | no | yes | 0.095 | –0.056 | |
| no | yes | yes | 0.067 | –0.074 | |
| yes | no | no | 0.200 | 0.005 | |
| yes | yes | no | 0.190 | –0.011 | |
| yes | no | yes | 0.151 | –0.014 | |
| yes | yes | yes | 0.137 | –0.0033 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aizenman, H.; Grossberg, M.D.; Krakauer, N.Y.; Gladkova, I. Ensemble Forecasts: Probabilistic Seasonal Forecasts Based on a Model Ensemble. Climate 2016, 4, 19. https://doi.org/10.3390/cli4020019
Aizenman H, Grossberg MD, Krakauer NY, Gladkova I. Ensemble Forecasts: Probabilistic Seasonal Forecasts Based on a Model Ensemble. Climate. 2016; 4(2):19. https://doi.org/10.3390/cli4020019
Chicago/Turabian StyleAizenman, Hannah, Michael D. Grossberg, Nir Y. Krakauer, and Irina Gladkova. 2016. "Ensemble Forecasts: Probabilistic Seasonal Forecasts Based on a Model Ensemble" Climate 4, no. 2: 19. https://doi.org/10.3390/cli4020019
APA StyleAizenman, H., Grossberg, M. D., Krakauer, N. Y., & Gladkova, I. (2016). Ensemble Forecasts: Probabilistic Seasonal Forecasts Based on a Model Ensemble. Climate, 4(2), 19. https://doi.org/10.3390/cli4020019







