Rainy Day Prediction Model with Climate Covariates Using Artificial Neural Network MLP, Pilot Area: Central Italy

Abstract

The reconstruction of daily precipitation data is a much-debated topic of great practical use, especially when weather stations have missing data. Missing data are particularly numerous if rain gauges are poorly maintained by their owner institutions and if they are located in inaccessible areas.In this context, an attempt was made to assess the possibility of reconstructing daily rainfall data from other climatic variables other than the rainfall itself, namely atmospheric pressure, relative humidity and prevailing wind direction.The pilot area for the study was identified in Central Italy, especially on the Adriatic side, and 119 weather stations were considered.The parameters of atmospheric pressure, humidity and prevailing wind direction were reconstructed at all weather stations on a daily basis by means of various models, in order to obtain almost continuous values rain gauge by rain gauge. The results obtained using neural networks to reconstruct daily precipitation revealed a lack of correlation for the prevailing wind direction, while correlation is significant for humidity and atmospheric pressure, although they explain only 10–20% of the total precipitation variance. At the same time, it was verified by binary logistic regression that it is certainly easier to understand when it will or will not rain without determining the amount. In this case, in fact, the model achieves an accuracy of about 80 percent in identifying rainy and non-rainy days from the aforementioned climatic parameters. In addition, the modelling was also verified on all rain gauges at the same time and this showed reliability comparable to an arithmetic average of the individual models, thus showing that the neural network model fails to prepare a model that performs better from learning even in the case of many thousands of data (over 400,000). This shows that the relationships between precipitation, relative humidity and atmospheric pressure are predominantly local in nature without being able to give rise to broader generalisations.

1. Introduction

1.1. Aim of the Study and State of the Art

The reconstruction of daily precipitation data is a topic that climatologists have always tried to solve. The difficulty lies in the fact that rainfall can be extremely localised, [1] and therefore, change radically a few kilometres away from the measurement, so it is complicated to reconstruct it on the basis of nearby rain gauges or terrain topography [2]. In an attempt to solve this problem, climatologists very often rely on satellite measurements in order to quantify daily precipitation over the entire globe [3,4]. Among the tools that enable these evaluations are the IMERG (Integrate Multi-satellitE Retrievals for GPM) algorithm or the TMPA (TRMM multi-satellite precipitation analyses) or PERSIANN (Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks), etc.; however, to date, it has been shown that they are still highly inaccurate in some areas, and therefore, not always very useful for quantifying rainfall [5,6,7]. On the other hand, there remains the possibility of trying to reconstruct rainfall values with neighbouring rain gauges through geostatistics, which although probably the most accurate and reliable method, with the obvious problems described above, for reasons of time and calculation is not very useful on a daily scale [8,9]. In this context, therefore, a path remains little explored to date, that of reconstructing precipitation from other climatic variables, such as atmospheric pressure, relative humidity and the prevailing wind direction in our case.In fact, it is very rare in the literature that other climate parameters are used to reconstruct precipitation on a daily scale [10]. This reconstruction procedure is very often neglected because weather stations are more often equipped with rain gauges than with hygrometers, anemometers or barometers, so it is complicated to reconstruct rainfall data from variables that are not continuous over the territory and the individual weather station.Sometimes pressure data are used to reconstruct precipitation in very old time series, due to the lack of rainfall data, which leads to not very reliable results [11]; while precipitation reconstructions with relative humidity and wind direction as covariates are almost absent in the literature.In order to obtain the aforementioned climate variables (atmospheric pressure, relative humidity and prevailing wind direction) for each weather station whose precipitation data are available, it is necessary in some cases to reconstruct them in full.Many methods for reconstructing climate data are reported in the literature, e.g., for wind, modelling based either on digital terrain models [12] or combined with satellite data (Lidar) is very often used [13]. Relative humidity, on the other hand, is very often spatialised, especially with the use of deterministic or geostatistical techniques, however, the timescale is rarely daily and more often monthly or yearly [14,15]. The key part of reconstructing precipitation data lies in the choice of the statistical method used, i.e., modelling. There are many ways to reconstruct data on the basis of the relationships observed between the dependent variable and the supposed independent variables. The time scale is certainly an important limitation, as geostatistical methods, such as kriging with its variants are based on the interpretation of the semivariogram, so in the case of hundreds of data to reconstruct, it is very time-consuming [16]. In these cases, techniques that need to estimate fewer parameters are required, among these are the various types of regression, linear, non-linear, logistic, or even artificial neural networks including radial basis functions or multilayer perceptrons [17,18]. Previous climate research shows a greater potential of the artificial neural network than multiple regression, allowing for a reduction in error [19]. There have been approaches to the reconstruction of climate variables completely based on machine learning, combining stochastic synthesis with a multilayer perceptron; however, serious doubts remain as to the comprehensibility of the model and its repeatability due to the two hidden layers having no physical or climatic variables as input parameters [20]. In the literature, there have also been examples of machine learning models applied to the reconstruction of daily rainfall that has good results, in particular, studies have verified the reconstruction potential of the multilayer perceptron with the support vector machine and the random forest [21]. These models developed in semi-arid areas perform well in terms of RMSE and R², precisely because of the greater ease of predicting near-zero values and the resulting low variance [21]. This research aims to interpolate or reconstruct if necessary, the data of independent variables, such as relative humidity, atmospheric pressure and prevailing wind direction. Subsequently, the aim of the research is to assess the significance of the relationships between precipitation and other climatic variables, so as to be able to help explain a percentage of the variance in daily precipitation and to use this model together with other independent variables in order to obtain increasingly reliable results. At the same time, there is also the ambitious goal of understanding, by reducing precipitation to a binary variable that can always be assessed by means of multilayer perceptron analysis, how to predict a rainfall event and with what accuracy.Thus, the innovativeness of this research lies both in quantifying the relationship between variables, such as relative humidity, wind and atmospheric pressure for the prediction of daily rainfall, and in the possibility of understanding on the basis of these variables the presence or absence of a rainy day, all using neural networks as a modelling technique.In fact, there are no other examples in the literature that rely on three independent climate variables to reconstruct daily rainfall.

1.2. Geographical Framework

Central Italy is bordered by two seas, the Tyrrhenian Sea and the Adriatic Sea, arms of the Mediterranean Sea which, depending on their size, influence the climate of inland areas to a greater or lesser extent. The extent of the study area is approximately 13,400 km, and a total of 119 rain gauges are distributed over the area (Figure 1).

The study area encompasses an area that stretches from the Adriatic Sea to the Apennines with peaks over 2000 m and overlooks the Tyrrhenian slope for a few kilometres, thus it is a particularly heterogeneous area in terms of elevation

2. Materials and Methods

2.1. Weather Stations and Climate Data

Climate data were collected by four institutions: the Functional Multiple Risk Centre of the Civil Protection of the Marche Region, the hydrographic service of the Umbria Region, the national system for the processing and dissemination of climate data of the IstitutoSuperiore per la Protezione e la RicercaAmbientale (ISPRA) and the Experimental Geophysical Observatory of Macerata (OGSM). The total number of rain gauges is 119, collected from 2010 to 2021, a shorter period than the classic standard 30-year period prescribed by the WMO, which was chosen on the one hand due to the large amount of data (scale is daily), and on the other hand due to missing data not being too extensive for each weather station, what it would have been like collecting the previous 20 years. Regarding the prevailing wind direction, data were collected from 16 anemometers, while 42 weather stations in the study area are equipped with hygrometers and 12 weather stations with barometers (

Table 1. Name, name of the weather stations, Long., longitude, Lat., latitude, Alt., altitude, Sen., equipment of sensors to measure climatic variables r (rain gauge), p (barometer), w (anemometer), h (hygrometer).

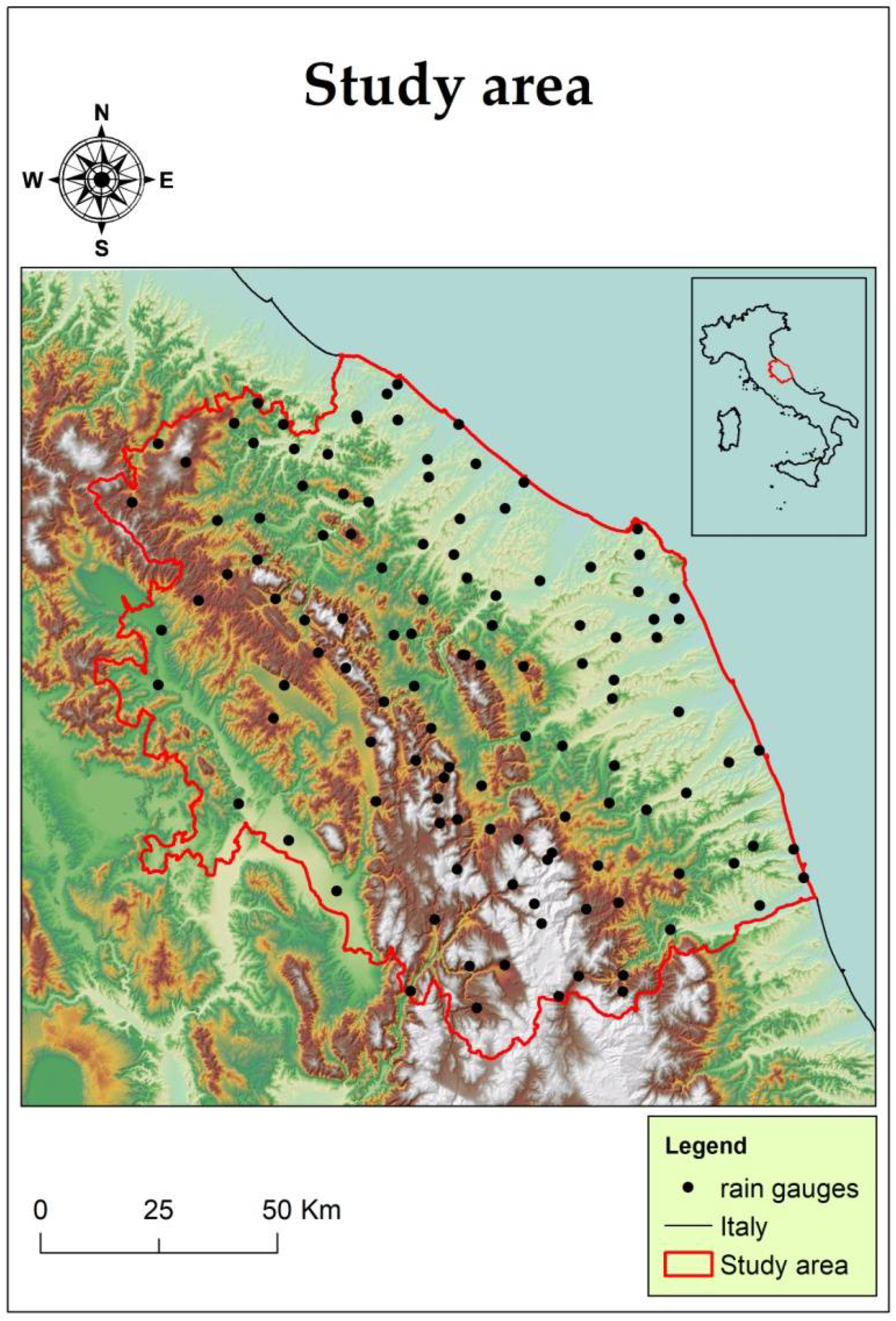
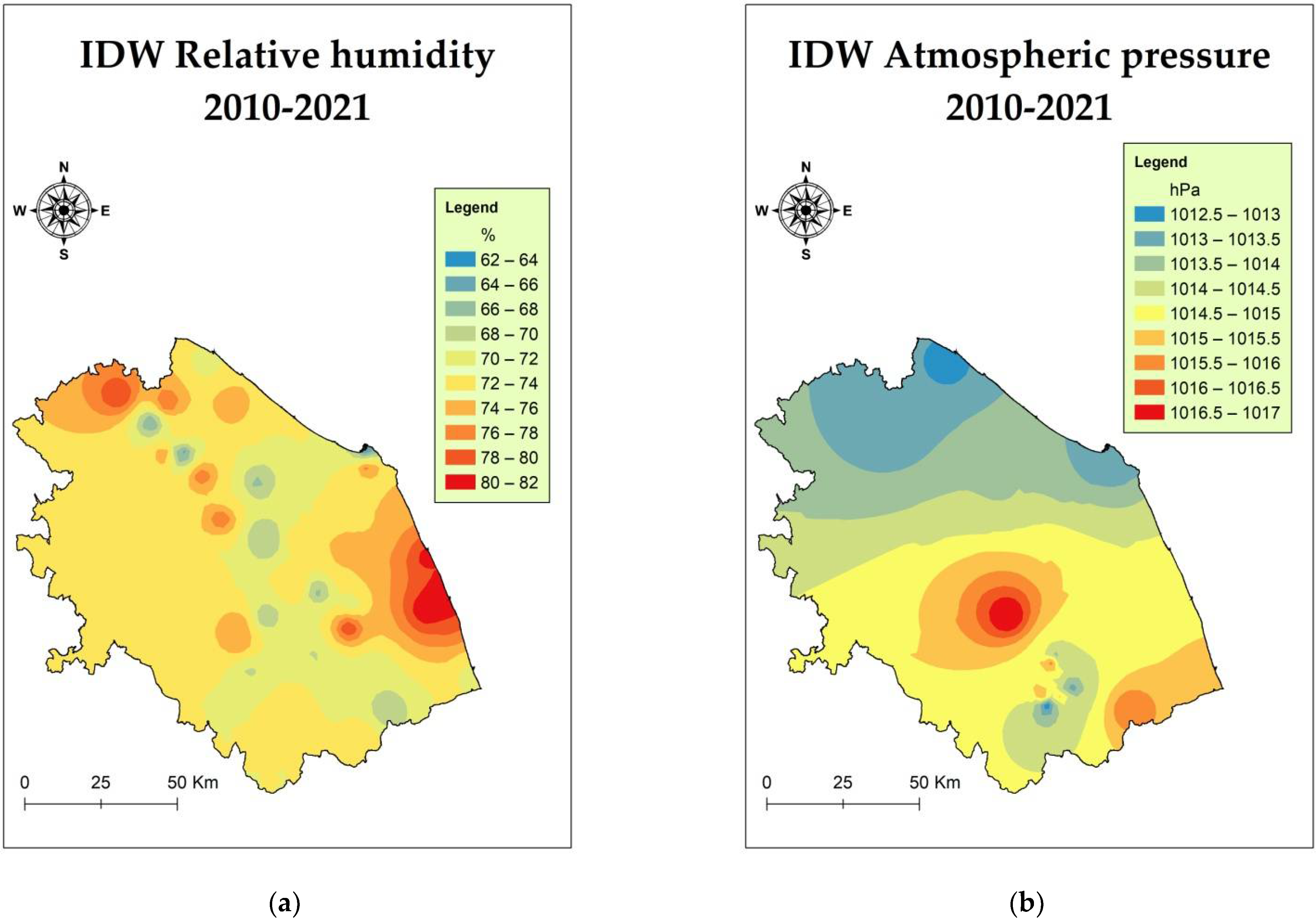
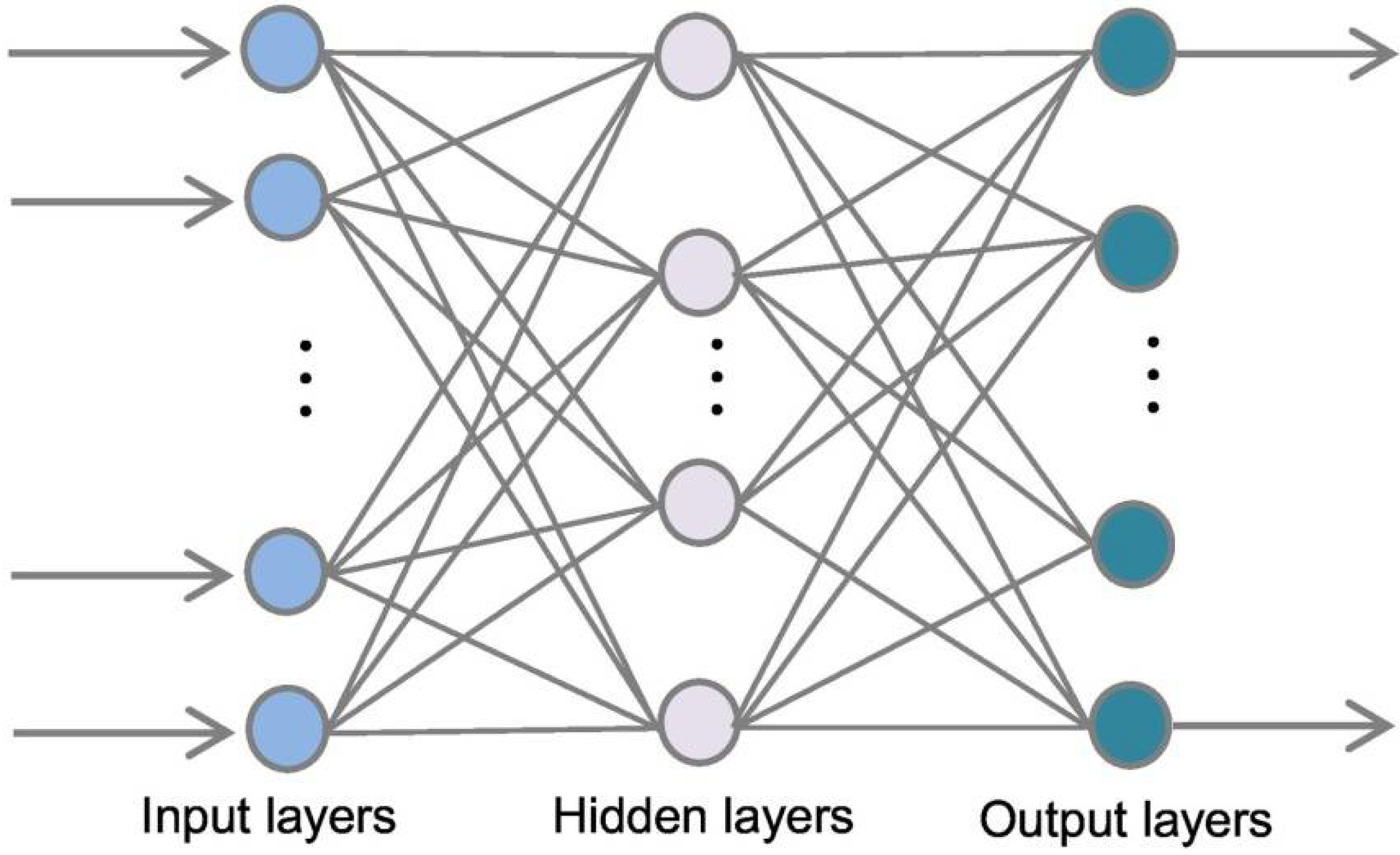
Id	Name	Long.	Lat.	Alt.	Sen.	Id	Name	Long.	Lat.	Alt.	Sen.
1	Acqualagna	12.7	43.6	193	r,h	61	Monte Grimano Terme	12.5	43.8	362	r
2	Acquasanta	13.4	42.8	392	r,h	62	Monte Paganuccio	12.8	43.6	889	r,h
3	Agugliano	13.4	43.5	170	r	63	Monte Prata	13.2	42.9	1813	r,p,w,h
4	Amandola	13.4	43.0	550	r	64	Montecchio	12.8	43.9	43	r
5	Ancona Baraccola	13.5	43.6	37	r,h	65	Montefano	13.4	43.4	215	r,h
6	Ancona Regione	13.5	43.6	91	r,p,w,h	66	Montelabbate	12.8	43.8	65	r
7	Apecchio	12.4	43.6	465	r	67	Montemonaco	13.3	42.9	987	r
8	Appignano	13.3	43.4	199	r	68	Mozzano	13.5	42.8	193	r,p,h
9	Arcevia	12.9	43.5	535	r,h	69	Nocera Umbra	12.8	43.1	535	r
10	Arquata del Tronto	13.3	42.8	720	r	70	Norcia	13.1	42.8	700	r
11	Badia Tedalda	12.2	43.7	756	r	71	Osimo Monteragolo	13.5	43.5	123	r,w,h
12	Barbara	13.0	43.6	219	r	72	Pennabilli	12.3	43.8	600	r
13	Bastia Umbra	12.6	43.1	214	r	73	Pergola	12.8	43.6	306	r,h
14	Bettolelle	13.2	43.7	26	r	74	Pesaro	12.9	43.9	9	r
15	Bocca Serriola	12.4	43.5	730	r	75	Piagge	13.0	43.7	201	r
16	Bolognola Pintura	13.2	43.0	1352	r,p,w,h	76	Pianello di Cagli	12.6	43.5	384	r,w,h
17	Bronzo	12.5	43.8	173	r,h	77	Pievebovigliana	13.1	43.1	451	r
18	Ca’Mazzasette	12.6	43.8	112	r	78	Piobbico	12.5	43.6	339	r
19	Camerino	13.1	43.1	664	r,p,w,h	79	Pioraco	13.0	43.2	441	r
20	Campodiegoli	12.8	43.3	507	r	80	Poggio San Vicino	13.1	43.4	580	r,h
21	Cantiano	12.6	43.5	360	r	81	Ponte Felcino	12.4	43.1	205	r
22	Capodacqua	13.2	42.7	817	r	82	Porto Sant’Elpidio	13.8	43.2	3	r,p,w,h
23	Carestello	12.5	43.3	523	r	83	Recanati	13.5	43.4	235	r
24	Carpegna	12.3	43.8	748	r	84	Ripatransone	13.8	43.0	494	r
25	Cascia	13.0	42.7	604	r	85	Rostighello	13.5	43.4	28	r
26	Case San Giovanni	13.0	43.4	620	r	86	Rotella	13.6	43.0	385	r
27	Cingoli	13.2	43.4	790	r,h	87	Sant’Angelo in Pontano	13.4	43.1	473	r
28	Citta di Castello	12.3	43.5	304	r	88	Sant’Angelo in Vado	12.4	43.7	359	r,h
29	Colle	13.1	43.5	350	r,p,w,h	89	San Bendetto del Tronto	13.9	42.9	6	r,p,w,h
30	Colleponi	12.9	43.4	254	r,h	90	San Giovanni	13.0	43.4	625	r
31	Corinaldo	13.0	43.6	203	r	91	San Lorenzo in Campo	12.9	43.6	209	r
32	Cupramontana	13.1	43.4	506	r	92	Santa Maria di Pieca	13.3	43.1	467	r
33	Esanatoglia Convento	12.9	43.3	608	r	93	Santa Maria Goretti	13.7	43.0	130	r
34	Fabriano	12.9	43.3	357	r,h	94	Santa Maria in Arzilla	12.9	43.8	53	r
35	Fermo	13.7	43.2	280	r	95	San Severino Marche	13.2	43.2	220	r,h
36	FiastraTrebbio	13.2	43.0	747	r,h	96	Sassofeltrio	12.5	43.9	221	r
37	Filottrano	13.3	43.4	270	r	97	Sassoferrato	12.9	43.4	312	r
38	Foligno	12.7	43.0	224	r	98	Sassotetto	13.2	43.0	1365	r,p,w,h
39	Fonte Avellana	12.7	43.5	689	r,h	99	Scheggia	12.7	43.4	688	r
40	Foresta della Cesana	12.7	43.7	640	r,h	100	Sefro	13.0	43.2	469	r
41	Forsivo	13.0	42.8	968	r	101	Sellano	12.9	42.9	608	r
42	Fossombrone	12.8	43.7	116	r	102	Senigallia	13.2	43.7	5	r,w,h
43	Gallo	12.7	43.8	122	r,h	103	Serravalle di Chienti	13.0	43.1	647	r,h
44	Gelagna Alta	13.0	43.1	711	r	104	Servigliano	13.5	43.1	215	r
45	Grottammare	13.9	43.0	4	r	105	Sorti	13.0	43.1	672	r,h
46	Grottazzolina	13.6	43.1	200	r	106	Spindoli	12.9	43.2	484	r
47	GualdoTadino	12.8	43.2	535	r	107	Spinetoli	13.8	42.9	52	r
48	Gubbio	12.6	43.3	473	r	108	Svarchi	13.6	43.5	6	r
49	Illice	13.4	42.9	760	r	109	Tavoleto	12.6	43.8	426	r
50	Jesi	13.2	43.5	96	r,h	110	Tolentino	13.3	43.2	244	r,w,h
51	Loreto	13.6	43.4	127	r,h	111	Trestina	12.2	43.4	257	R
52	Loro Piceno	13.4	43.2	435	r,h	112	Umito	13.4	42.7	646	R
53	Lucrezia	13.0	43.8	36	r,h	113	Urbania	12.5	43.7	273	R
54	Macerata	13.4	43.3	294	r,w,h	114	Urbino	12.6	43.7	451	r,p,w,h
55	Marotta	13.1	43.7	144	r	115	Ussita	13.1	43.0	744	r
56	Metaurilia	13.1	43.8	7	r	116	Villa Fastiggi	12.9	43.9	22	r,p,w,h
57	Moie	13.1	43.5	110	r	117	Villa Potenza	13.4	43.3	133	r,h
58	Monte Bove Sud	13.2	42.9	1917	r,p,w,h	118	Villa San Filippo	13.6	43.3	58	r
59	Monte Cavallo	13.0	43.0	960	r	119	Vallo di Nera	12.9	42.8	310	r
60	Monte Cucco	12.7	43.4	1092	r

).

2.2. Interpolation and Extrapolation of Climate Data

In order to obtain the climatic values for atmospheric pressure, relative humidity and prevailing wind direction, interpolative procedures were required. For both atmospheric pressure and relative humidity, an inverse distance weighting (IDW) based on the square of the distance was performed, with the following formula:

$$\widehat{z}\left(x\right)=\frac{{{\displaystyle \sum }}_i^n{w}_i{z}_i}{{{\displaystyle \sum }}_i^n{w}_i}$$

(1)

where

$$w_i={\left|x-x_i\right|}^{-2}$$

(2)

$$\left|x-x_i\right|=\mathrm{Euclidean}\mathrm{distance}$$

$\widehat{z}\left(x\right)$ = value z at location x, it is a weighted mean of nearby observations

IDW has been calculated for each day reconstructing missing values and testing errors by means of cross-correlation, which led on average to the resultsshown in

Table 2. Table of average errors in the model from 2010 to 2021; ME, mean error; RMSE, root mean square error.

Error of a Model in the Prediction	Relative Humidity	Atmospheric Pressure
ME	−0.14	−0.01
RMSE	4.86	1.79

and Figure 2.

On the other hand, for the prevailing wind direction, the situation was more complex, both because of the variability to which the direction is usually subject on uneven topographical surfaces, and because of the few weather stations equipped with an anemometer.In light of these issues, in order to obtain the most correct values possible, wind direction and wind speed modelling software, Wind Ninja, was used [22]. This software was primarily designed to assess the development of fires; however, it also performs well in the climatic field.In this way, the values of wind from the weather stations were introduced into the software and the response was evaluated by interpolating the entire surface based on the topographic obstacles encountered by the wind. This procedure then made it possible to extrapolate the values obtained inall weather stations where wind direction values were missing (Figure 3).

2.3. Predictive Modelling

The main objective of the research is to obtain a model that can best exploit atmospheric pressure, relative humidity and prevailing wind direction to predict precipitation or at least explain some of the variance. Artificial neural networks were used to do this, which have the peculiarity of simulating the functioning of the animal brain by using non-linear data modelling to discover complex relationships between data (Figure 4). In particular, the algorithm called multilayer perceptron (MLP) was used, which has input layers and output layers, and in between the two, there are hidden layers with many stacked neurons [23].

The MLP algorithm is as follows:

$$f\left(X\right)=b_2+W_2\ast \left(f_A\left(b_1+W_1\ast X\right)\right)$$

(3)

where

$W_1$ = weight matrices of the hidden layer

$W_2$ = weight matrices of the output layer

$b_1$ = bias vector of the hidden layer

$b_2$ = bias vector of the output layer

$f_A$ = activation function

The goodness of the model was assessed using the relative error [24]:

$$R{E}_v=y_{rv}-{\widehat{y}}_{rv}/y_{rv}$$

(4)

where

$y_{rv}$ = source point

${\widehat{y}}_{rv}$ = predicted point

Subsequently, the possibility of creating a model that could predict whether it would rain or not was also considered. Again, the MLP technique was used, and precipitation was transformed into a binary categorical variable, with zero indicating no precipitation and one indicating the presence of precipitation. In this case, the success rate of the model was evaluated, corresponding to the ability to correctly predict a rainy or a non-rainy day. In order to assess the importance of each individual variable in the model, an analysis was carried out to assess how much the predicted values change as the independent variables change. In particular, the effect of a perturbation introduced into the model is measured and related to the measured data. It is calculated by measuring the effect this perturbation has by computing the Root Mean Square difference between the original $\widehat{y}$ and the perturbed ${\widehat{y}}_i$. A larger Root Mean Square difference means that the variable is “more important”. Finally, to assess the reliability of the model, it was divided into 30% data subject to training and 70% data subject to testing. For each of these two categories, the correctly predicted values were evaluated, i.e., those in which the model predicts rain or no rain, in agreement with the observed data, and this generates a percentage of model reliability.

3. Results

3.1. Quantitative Rainfall Prediction Model Based on MLP Technique

The MLP technique was used on all 119 available weather stations, with precipitation as the dependent variable and relative humidity, atmospheric pressure and prevailing wind direction as covariates. From the point of view of the architecture of the neural network, two hidden layers were chosen between the input and output layersand evaluatedon the basis of the decrease in relative error. For each weather station modelled, a 70% sample was taken for model training and a 30% sample for testing the model. This percentage was chosen by analysing the best performance of the model in relation to the various percentages of data taken for training and those taken for testing as can be seen in

Table 3. Evaluation of the correct prediction percentage of rainfall and non-rainfall events with different percentages of testing and training datasets.

Training Percentage	Testing Percentage	Correct Percentage
50	50	79.7
60	40	79.8
70	30	80.0
80	20	79.9
90	10	79.9

.

The results as can be seen in

Table 4. Assessment of the relative error for the training (reTr) and for the testing (ret), for each weather station identified by the id code (Id).

Id	reTr	ret	Id	reTr	ret	Id	reTr	ret	Id	reTr	ret	Id	reTr	ret	Id	reTr	ret
1	0.83	0.83	21	0.82	0.83	41	0.89	0.89	61	0.89	0.93	81	0.86	0.81	101	0.83	0.86
2	0.89	0.85	22	0.84	0.87	42	0.87	0.84	62	0.87	0.88	82	0.90	0.87	102	0.87	0.89
3	0.83	0.86	23	0.84	0.81	43	0.86	0.82	63	0.90	0.91	83	0.83	0.84	103	0.89	0.92
4	0.93	0.89	24	0.85	0.88	44	0.86	0.84	64	0.86	0.85	84	0.89	0.89	104	0.90	0.91
5	0.84	0.88	25	0.80	0.83	45	0.81	0.87	65	0.86	0.86	85	0.87	0.83	105	0.78	0.80
6	0.86	0.87	26	0.88	0.88	46	0.76	0.84	66	0.90	0.86	86	0.81	0.73	106	0.88	0.84
7	0.85	0.86	27	0.89	0.90	47	0.90	0.89	67	0.86	0.84	87	0.91	0.90	107	0.82	0.77
8	0.83	0.82	28	0.86	0.90	48	0.83	0.82	68	0.82	0.73	88	0.89	0.88	108	0.91	0.92
9	0.90	0.91	29	0.84	0.88	49	0.84	0.83	69	0.84	0.80	89	0.88	0.96	109	0.93	0.93
10	0.86	0.91	30	0.83	0.83	50	0.85	0.84	70	0.88	0.85	90	0.82	0.78	110	0.85	0.86
11	0.88	0.87	31	0.84	0.83	51	0.88	0.88	71	0.86	0.81	91	0.92	0.94	111	0.86	0.91
12	0.87	0.84	32	0.87	0.87	52	0.86	0.86	72	0.84	0.85	92	0.85	0.84	112	0.88	0.90
13	0.89	0.86	33	0.85	0.85	53	0.87	0.87	73	0.82	0.82	93	0.88	0.88	113	0.85	0.88
14	0.85	0.85	34	0.81	0.85	54	0.86	0.85	74	0.84	0.87	94	0.93	0.91	114	0.85	0.83
15	0.89	0.90	35	0.81	0.79	55	0.86	0.83	75	0.86	0.88	95	0.81	0.88	115	0.88	0.85
16	0.86	0.89	36	0.86	0.84	56	0.93	0.90	76	0.85	0.85	96	0.73	0.90	116	0.84	0.85
17	0.91	0.87	37	0.86	0.86	57	0.81	0.83	77	0.88	0.87	97	0.85	0.90	117	0.85	0.82
18	0.91	0.91	38	0.88	0.85	58	0.89	0.92	78	0.88	0.88	98	0.86	0.90	118	0.89	0.86
19	0.84	0.82	39	0.75	0.80	59	0.80	0.82	79	0.82	0.84	99	0.87	0.88	119	0.86	0.85
20	0.85	0.82	40	0.83	0.82	60	0.82	0.83	80	0.85	0.81	100	0.85	0.84

are not such that daily precipitation can be predicted on the basis of the chosen covariates, however, some interesting indications were obtained. It was observed that especially atmospheric pressure and relative humidity possess a significant relationship with precipitation and thus could be exploited for introduction into other models together with other variables.

From Table 4, it can be seen that the model can estimate on average between 10 and 20% of the variance of the daily precipitation at each weather station.At the same time, the importance of each independent variable used in the model was tested for each weather station, and this revealed that both atmospheric pressure and relative humidity have a weight, while wind direction does not seem to influence precipitation(

Table 5. Independent variable importance for all the weather stations; Id = code to identify the weather station; V. = independent variable (p, atmospheric pressure; h, relative humidity; w, wind direction); Imp = value of the independent variable importance.

Id	V.	Imp	Id	V.	Imp	Id	V.	Imp	Id	V.	Imp	Id	V.	Imp	Id	V.	Imp	Id	V.	Imp	Id	V.	Imp
1	p	0.64	16	p	0.46	31	p	0.53	46	p	0.29	61	p	0.33		p	0.58		p	0.84		p	0.76
	h	0.34		h	0.44		h	0.44		h	0.62		h	0.61	76	h	0.34	91	h	0.10	106	h	0.15
	w	0.02		w	0.10		w	0.03		w	0.09		w	0.06		w	0.08		w	0.06		w	0.09
2	p	0.55	17	p	0.49	32	p	0.49	47	p	0.77	62	p	0.52		p	0.66		p	0.37		p	0.06
	h	0.37		h	0.43		h	0.47		h	0.04		h	0.35	77	h	0.18	92	h	0.57	107	h	0.85
	w	0.08		w	0.08		w	0.04		w	0.19		w	0.13		w	0.16		w	0.06		w	0.09
3	p	0.42	18	p	0.67	33	p	0.79	48	p	0.61	63	p	0.16		p	0.74		p	0.51		p	0.60
	h	0.49		h	0.26		h	0.11		h	0.32		h	0.59	78	h	0.13	93	h	0.45	108	h	0.38
	w	0.09		w	0.07		w	0.10		w	0.07		w	0.25		w	0.13		w	0.04		w	0.02
4	p	0.59	19	p	0.53	34	p	0.55	49	p	0.24	64	p	0.62		p	0.49		p	0.77		p	0.97
	h	0.16		h	0.45		h	0.39		h	0.72		h	0.28	79	h	0.48	94	h	0.05	109	h	0.02
	w	0.25		w	0.02		w	0.06		w	0.04		w	0.10		w	0.03		w	0.18		w	0.01
5	p	0.46	20	p	0.80	35	p	0.42	50	p	0.53	65	p	0.61		p	0.51		p	0.64		p	0.46
	h	0.42		h	0.13		h	0.53		h	0.44		h	0.32	80	h	0.38	95	h	0.32	110	h	0.51
	w	0.12		w	0.07		w	0.05		w	0.03		w	0.07		w	0.11		w	0.04		w	0.03
6	p	0.48	21	p	0.55	36	p	0.65	51	p	0.60	66	p	0.44		p	0.48		p	0.62		p	0.87
	h	0.43		h	0.39		h	0.32		h	0.37		h	0.41	81	h	0.47	96	h	0.36	111	h	0.05
	w	0.09		w	0.06		w	0.03		w	0.03		w	0.15		w	0.05		w	0.02		w	0.08
7	p	0.68	22	p	0.80	37	p	0.49	52	p	0.61	67	p	0.43		p	0.72		p	0.48		p	0.80
	h	0.18		h	0.06		h	0.46		h	0.37		h	0.51	82	h	0.23	97	h	0.47	112	h	0.02
	w	0.14		w	0.14		w	0.05		w	0.02		w	0.06		w	0.05		w	0.05		w	0.18
8	p	0.53	23	p	0.82	38	p	0.91	53	p	0.59	68	p	0.28		p	0.46		p	0.66		p	0.50
	h	0.39		h	0.08		h	0.03		h	0.39		h	0.68	83	h	0.51	98	h	0.34	113	h	0.46
	w	0.08		w	0.10		w	0.06		w	0.02		w	0.04		w	0.03		w	0.00		w	0.04
9	p	0.69	24	p	0.49	39	p	0.52	54	p	0.45	69	p	0.74		p	0.41		p	0.82		p	0.51
	h	0.24		h	0.49		h	0.36		h	0.44		h	0.08	84	h	0.57	99	h	0.03	114	h	0.41
	w	0.07		w	0.02		w	0.12		w	0.11		w	0.18		w	0.02		w	0.15		w	0.08
10	p	0.52	25	p	0.53	40	p	0.56	55	p	0.42	70	p	0.93		p	0.52		p	0.87		p	0.61
	h	0.36		h	0.42		h	0.44		h	0.52		h	0.05	85	h	0.48	100	h	0.10	115	h	0.38
	w	0.12		w	0.05		w	0.00		w	0.06		w	0.02		w	0.00		w	0.03		w	0.01
11	p	0.68	26	p	0.71	41	p	0.95	56	p	0.71	71	p	0.60		p	0.15		p	0.92		p	0.52
	h	0.20		h	0.22		h	0.02		h	0.19		h	0.35	86	h	0.84	101	h	0.04	116	h	0.42
	w	0.12		w	0.07		w	0.03		w	0.10		w	0.05		w	0.01		w	0.04		w	0.06
12	p	0.47	27	p	0.51	42	p	0.55	57	p	0.34	72	p	0.47		p	0.59		p	0.58		p	0.61
	h	0.51		h	0.37		h	0.38		h	0.64		h	0.50	87	h	0.16	102	h	0.38	117	h	0.34
	w	0.02		w	0.12		w	0.07		w	0.02		w	0.03		w	0.25		w	0.04		w	0.05
13	p	0.79	28	p	0.81	43	p	0.66	58	p	0.48	73	p	0.47		p	0.73		p	0.44		p	0.41
	h	0.18		h	0.11		h	0.32		h	0.51		h	0.44	88	h	0.21	103	h	0.41	118	h	0.48
	w	0.03		w	0.08		w	0.02		w	0.01		w	0.09		w	0.06		w	0.15		w	0.11
14	p	0.48	29	p	0.55	44	p	0.82	59	p	0.50	74	p	0.47		p	0.55		p	0.45		p	0.85
	h	0.50		h	0.37		h	0.07		h	0.33		h	0.43	89	h	0.38	104	h	0.15	119	h	0.14
	w	0.02		w	0.08		w	0.11		w	0.17		w	0.10		w	0.07		w	0.40		w	0.01
15	p	0.92	30	p	0.42	45	p	0.35	60	p	0.42	75	p	0.50		p	0.38		p	0.63		p
	h	0.03		h	0.35		h	0.62		h	0.53		h	0.43	90	h	0.54	105	h	0.23	120	h
	w	0.05		w	0.23		w	0.03		w	0.05		w	0.07		w	0.08		w	0.14		w

).In this case, the influence of each variable on precipitation was calculated through the independent variable importance, which is a measure of how much the value predicted by the model changes for different values of the independent variable(Table 5).

The most important variable in most cases is atmospheric pressure, followed by relative humidity, with wind being of little importance, although there are some weather stations for which wind is a significant variable.

3.2. Binary Forecast Model of Rainy and Non-Rainy Days Based on the MLP Technique

Observing the significance ofthe correlation between relative humidity, atmospheric pressure and precipitation, led us to draw up another model with the aim this time of predicting rainy and non-rainy days (

Table 6. Error computation based on the percentage of correctly predicted rainy or non-rainy days, testing value in percentage (test), for each weather station identified by the id code (Id).

Id	test	Id	test	Id	test	Id	test	Id	test	Id	test	Id	test	Id	test
1	81.2	16	77.6	31	79.6	46	80.2	61	77.0	76	78.9	91	78.2	106	76.6
2	76.8	17	77.6	32	83.1	47	77.6	62	76.9	77	78.7	92	75.9	107	79.0
3	78.1	18	81.2	33	76.7	48	76.9	63	76.4	78	76.3	93	74.4	108	79.3
4	75.3	19	81.2	34	80.6	49	75.0	64	79.1	79	77.2	94	79.3	109	78.8
5	83.0	20	80.3	35	76.9	50	83.7	65	82.2	80	80.1	95	81.4	110	78.6
6	81.7	21	77.0	36	76.9	51	82.3	66	78.8	81	81.3	96	81.7	111	79.3
7	76.5	22	76.7	37	75.4	52	78.8	67	73.1	82	80.2	97	76.9	112	75.9
8	83.0	23	81.3	38	81.0	53	82.4	68	82.4	83	76.2	98	77.6	113	81.5
9	82.8	24	78.2	39	82.4	54	81.4	69	82.1	84	79.5	99	79.2	114	81.0
10	78.1	25	80.2	40	77.1	55	78.9	70	78.9	85	78.8	100	79.9	115	77.8
11	75.9	26	83.3	41	76.7	56	78.8	71	80.7	86	75.9	101	81.7	116	82.6
12	78.8	27	77.7	42	83.9	57	82.2	72	79.8	87	76.8	102	82.2	117	81.4
13	84.1	28	79.0	43	82.6	58	76.3	73	82.6	88	77.2	103	80.9	118	77.3
14	79.4	29	80.3	44	78.0	59	82.7	74	80.8	89	83.1	104	75.6	119	79.1
15	77.8	30	81.5	45	81.5	60	73.5	75	81.8	90	77.0	105	81.2	120

).

In this case, the model developed with the MLP turned out to be much better when it does not have to assess the extent of rainfall but only discriminates between rainy and non-rainy days. The hyperbolic tangent was chosen as the hidden layer activation function and the softmax as the output layer activation function. In fact, the correctness of the model in the random samples chosen as tests for the model itself led to the model being considered correct, on average, in 79.7% of the cases for the training part of the data and 80% for the testing part of the data. The sensitivity and specificity of the test arealso reported in order to understand the actual validity of the model and how accurately it can reconstruct rainy and non-rainy days (

Table 7. Sensitivity and specificity of the model, in the testing part, amounting to 30% of the total data. True Positive days with rain correctly predicted by the model; True Negative days without rain correctly predicted by the model; False Negative days without rain incorrectly predicted; False Positive days with rain incorrectly predicted.

	Cases		Cases
True Positive (rain)	17,535	True Negative (no rain)	86,811
False Negative	9570	False Positive	16,574
Sensitivity	65%	Specificity	84%

).

For further confirmation, all observations were also tested simultaneously; however, this did not improve the model, which gave almost exactly the same results with a prediction accuracy of 80.1%.

For the purpose of completeness, here is the network diagram showing how wind direction has been treated as a categorical variable, while atmospheric pressure and relative humidity as numerical variables (Figure 5).

4. Discussion

This research had the absolutely innovative aim of using other climate variables as covariates to predict daily precipitation. In particular, there are many examples in the literature of multivariate analyses in which the independent variables are precipitation-related environmental variables spatialised in a GIS environment [17,25,26]. In contrast, there are no examples exploring the correlation between precipitation and other climatic variables, especially atmospheric pressure in the literature is never considered for this type of analysis, but rather is often correlated with teleconnective indices [27]. However, a good significance was observed in the correlation between daily precipitation and atmospheric pressure, so this was on average the most important variable for the model in the analysis.Regarding the prevailing wind direction, in some cases, it was used as a well-correlated variable for precipitation prediction [28,29], exactly the opposite of what was found in this analysis, where wind direction was observed to be of marginal importance compared to the other variables used.Finally, relative humidity is most often part of analyses that combine climate and pollution [30], although in this case, it shows a good correlation for precipitation prediction.From the point of view of model architecture, MLP-type artificial neural networks have been increasingly used for predictive purposes over the past 20 years, and they have also found quite interesting applications in rainfall forecasting [31]. Normally, however, predictive climate analyses of this type analyse monthly scales, whereas in this case the daily scale was evaluated. There have also been analyses that seem to be able to predict rainfall, again using machine learning techniques, but with one major difference, that these analyses were performed on arid climate zones that, therefore, do not possess the high variability of rainfall present in the pilot area that can be defined as a humid climate. This has obvious repercussions on the error of the model and it follows that it cannot be considered more correct if it is not applied to the same climate zone [21]. In the case of the present research, the input parameters were represented by threeclimate variables. The result of the quantitative analysis on the one hand made it clear that the threechosen variables are not sufficient to be able to indicate responsive precipitation values; however, they do allow us to discriminate those that could be exported into a new model by making it more refined.In particular, atmospheric pressure, relative humidity and prevailing wind direction can explain 10 to 20 percent of the variance, with a smaller role for the wind variable. On the other hand, a good model fit emerged with regard to the possibility of rain during the day, in fact, the correctness of the forecast reaches about 80 percent, which is certainly significant.

5. Conclusions

Quantitative prediction of daily precipitation is certainly not an easy subject to solve, and variables, such as atmospheric pressure, relative humidity and prevailing wind direction alone are not sufficient to guarantee a good model response. However, the relationships found, make it possible to think of developments through the addition of other variables that may have even greater weight. As far as the prediction of the possibility of daily precipitation is concerned, then in that case they show that they can result in a rather high-performance model.A final consideration must be made regarding the applicability of the relationships obtained, since having observed that a much larger number of samples does not improve the model, it is evident that the relationships between precipitation and atmospheric pressure or relative humidity are extremely local, so much so that not even in such a close and almost homogeneous environment do they lead to an improvement in the performance of the model. Therefore, a model, such as this must always be calibrated area by area and cannot be subject to extensive generalisations.