High-Resolution Estimation of Monthly Air Temperature from Joint Modeling of In Situ Measurements and Gridded Temperature Data
Abstract
:1. Introduction
2. Methods
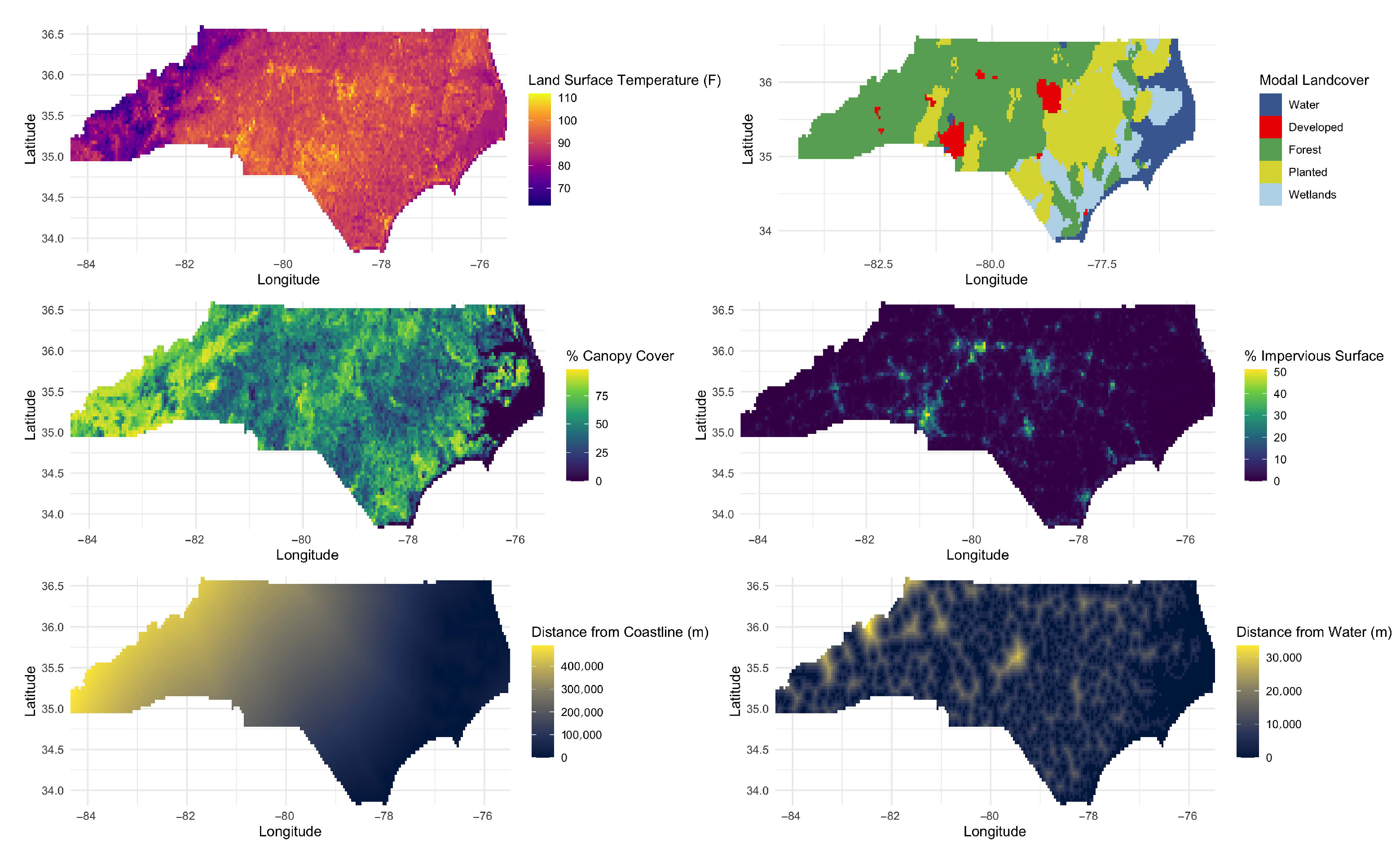
2.1. Temperature Records and Covariate Data
2.2. Model Framework
2.3. Model Specification
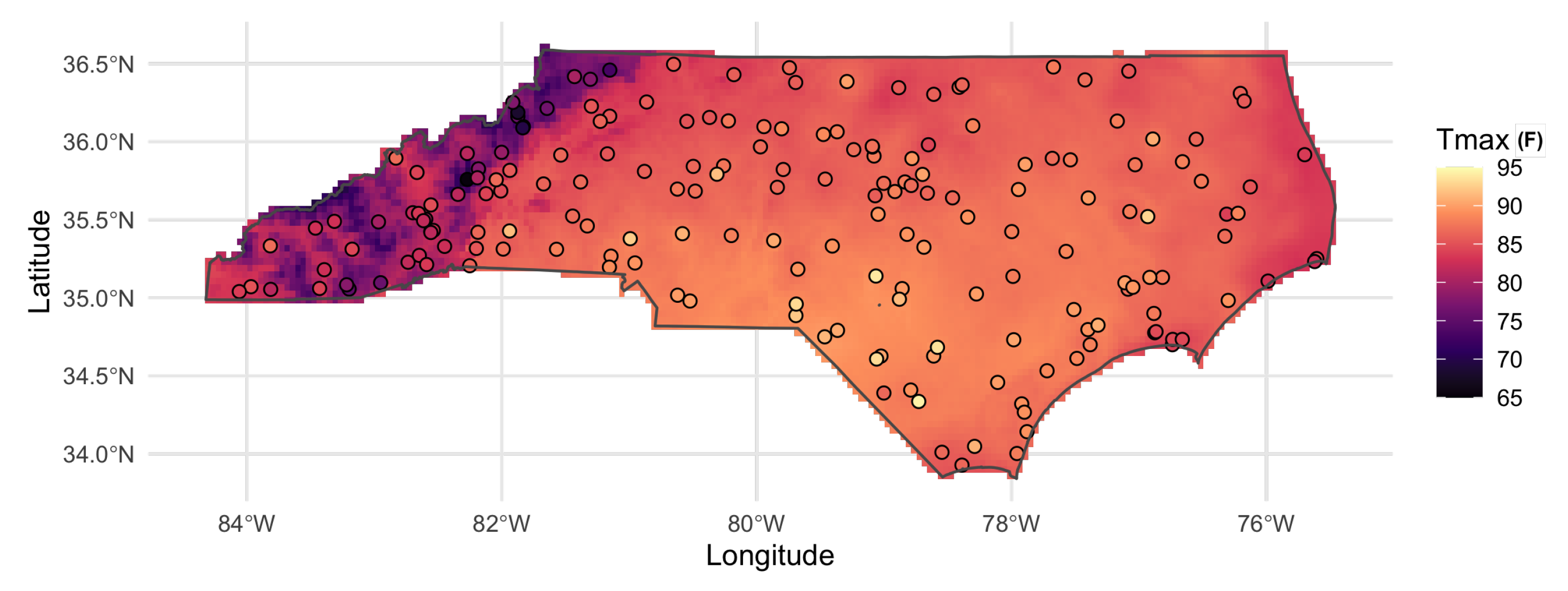
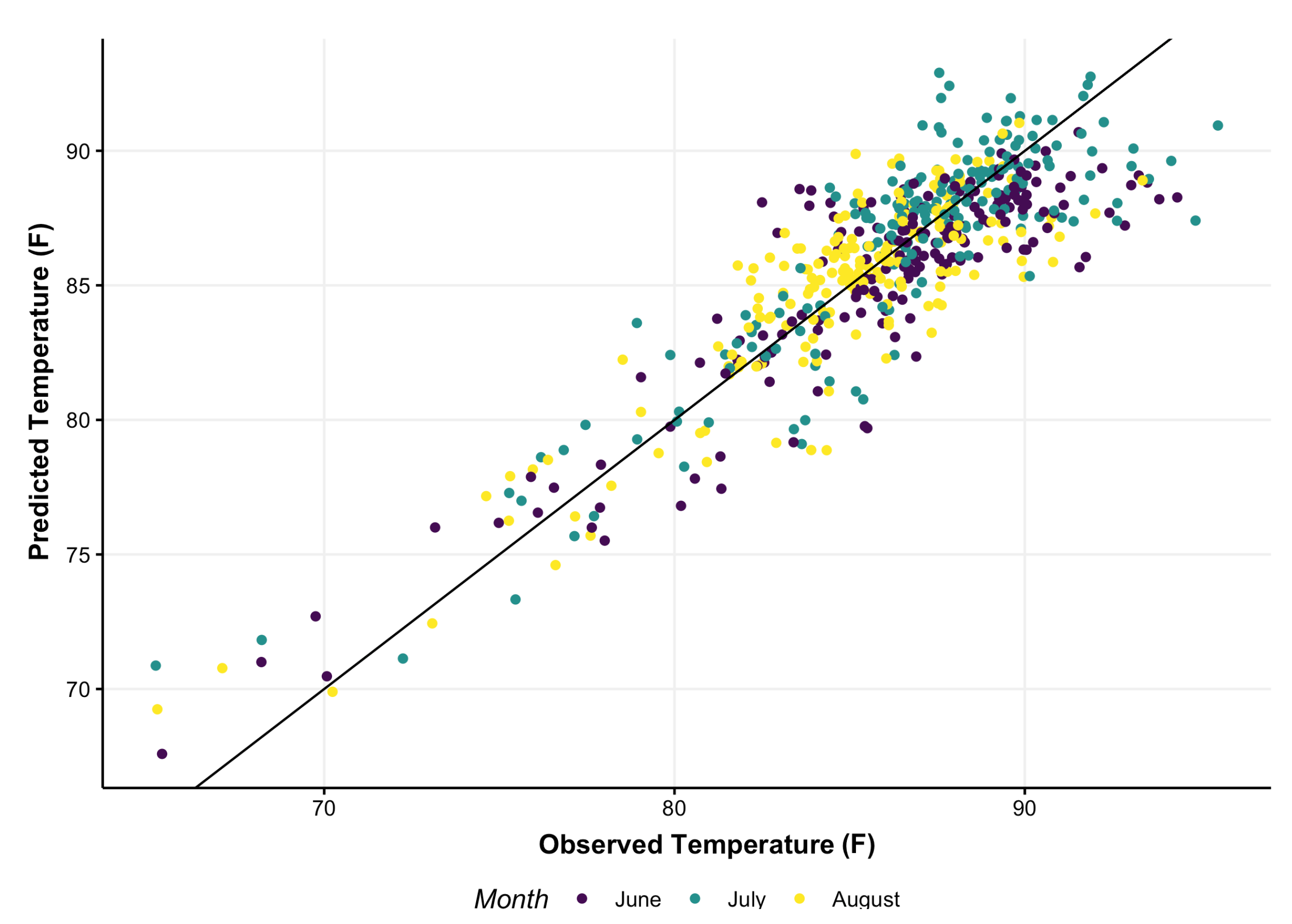
3. Results
3.1. Validation Results
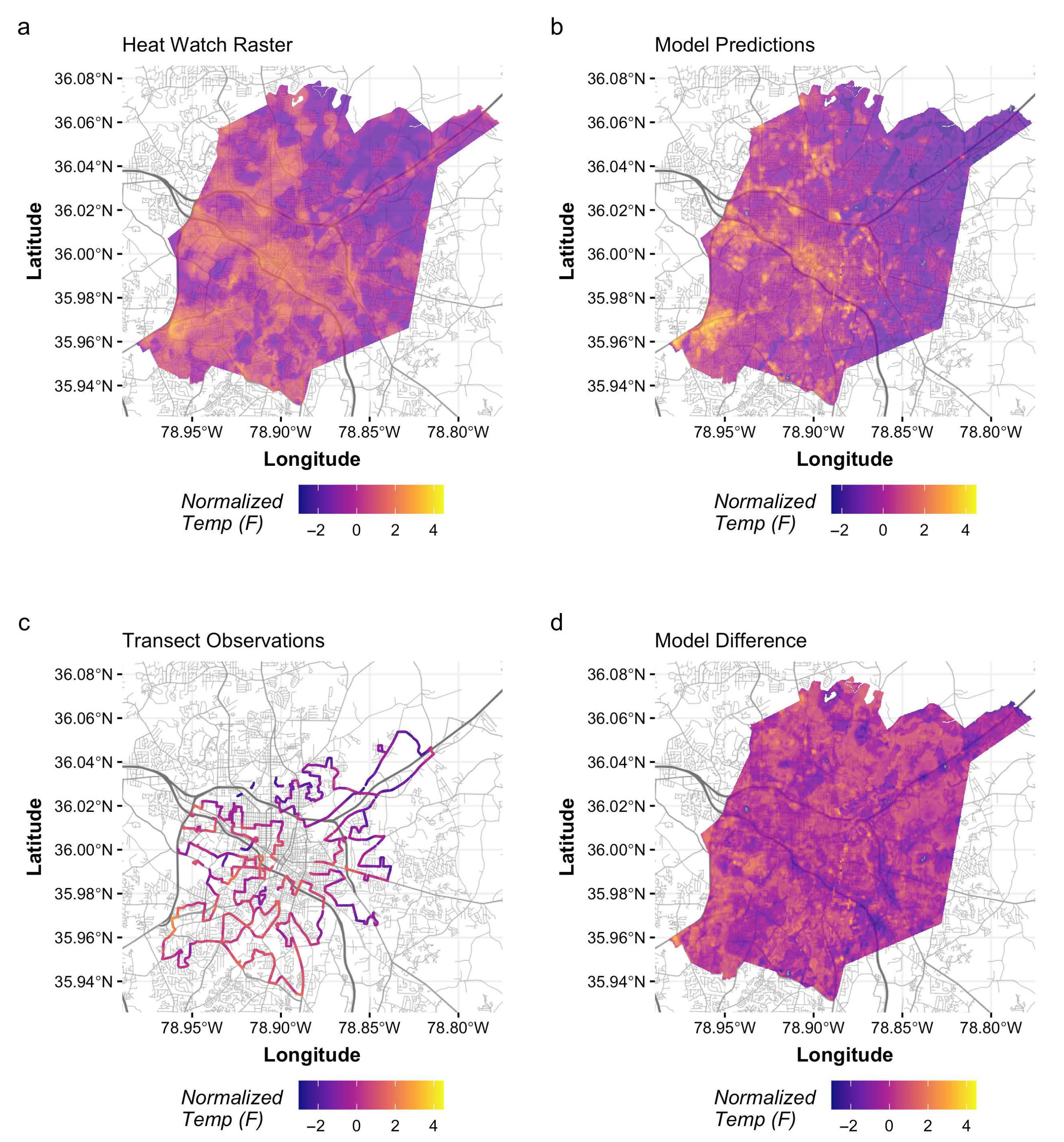
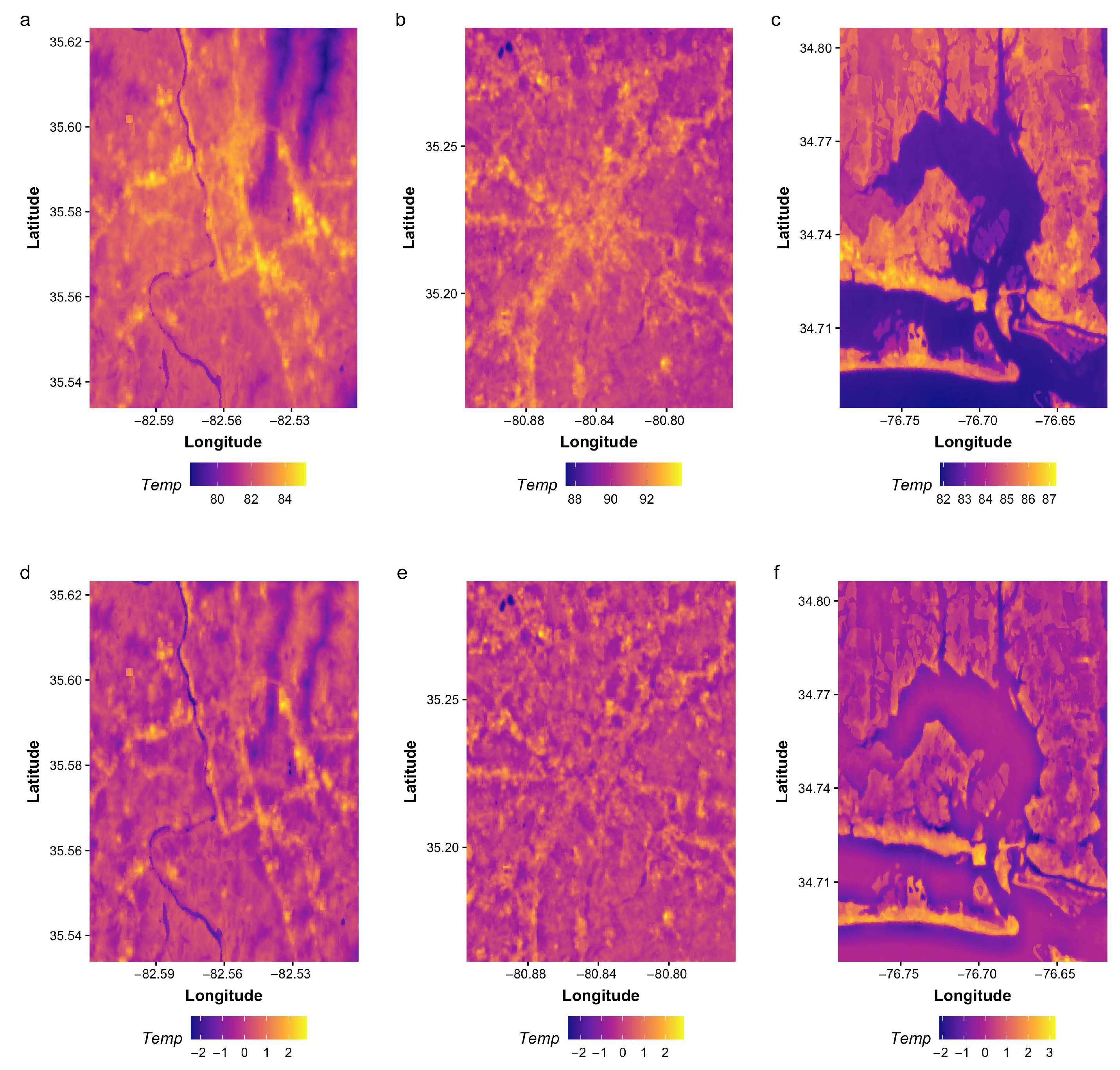
3.2. Correlation with CAPA Heat Watch Data
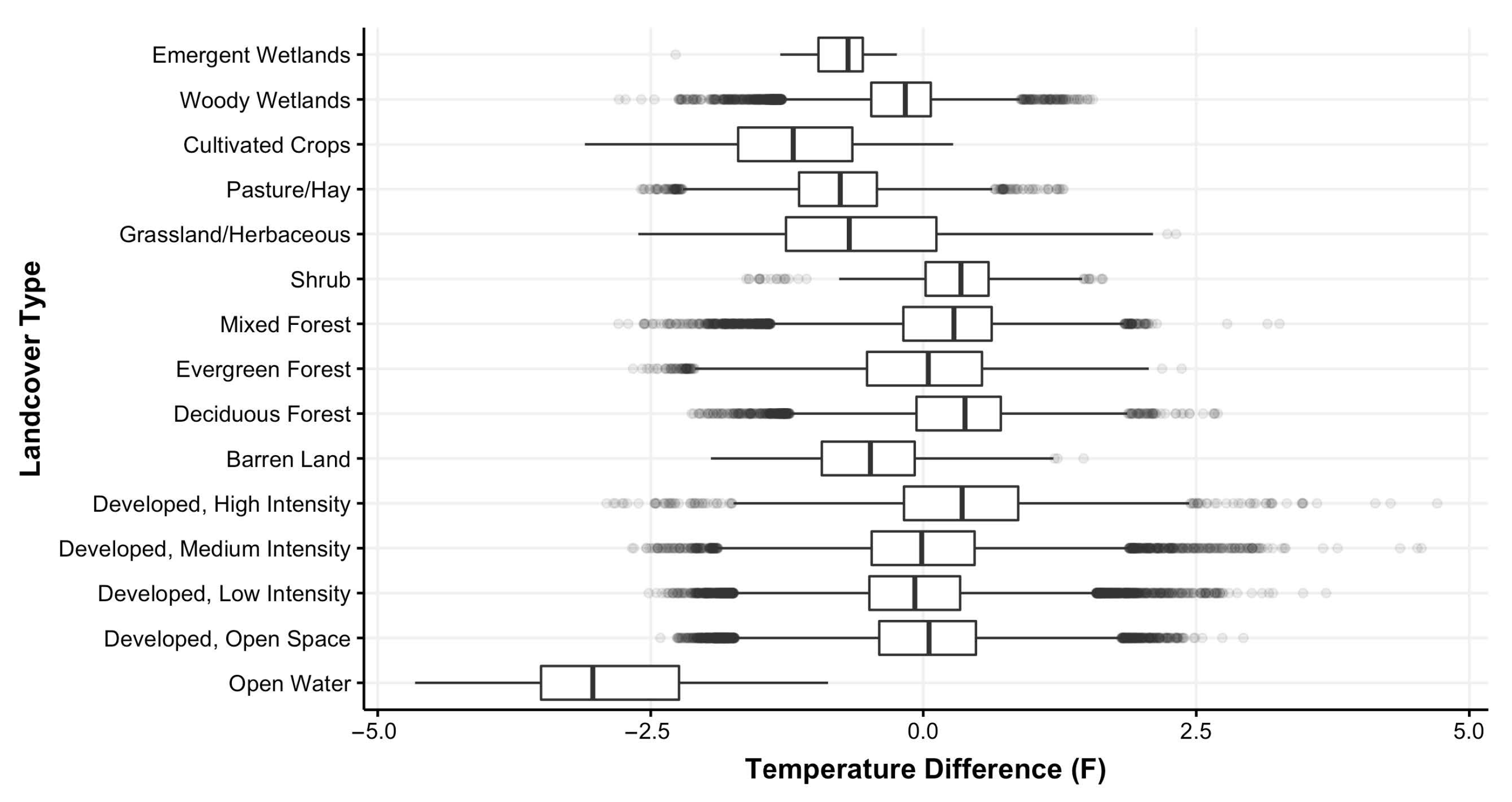
3.3. Evaluating Gridded Predictions across Geographies
4. Discussion
4.1. Limitations and Tradeoffs
4.2. Implications for Evaluating Extreme Heat Risks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Variable | Source | Resolution |
|---|---|---|
| Elevation | USGS National Elevation Database | 10 m |
| Land Cover | 2016 NLCD | 30 m |
| Canopy Cover | 2016 NLCD | 30 m |
| Impervious Surface Cover | 2016 NLCD | 30 m |
| Surface Water | JRC Global Surface Water, v1.3 | 30 m |
| Coastlines | NOAA Composite Shorelines | Vector |
| Original Class | Modified Class |
|---|---|
| Open Water | Water |
| Developed, Open Space | Developed |
| Developed, Low Intensity | Developed |
| Developed, Medium Intensity | Developed |
| Developed, High Intensity | Developed |
| Barren Land | Crops/Barren |
| Deciduous Forest | Forest/Shrub |
| Evergreen Forest | Forest/Shrub |
| Mixed Forest | Forest/Shrub |
| Shrub | Forest/Shrub |
| Grassland/Herbaceous | Forest/Shrub |
| Pasture/Hay | Crops/Barren |
| Cultivated Crops | Crops/Barren |
| Woody Wetlands | Wetlands |
| Emergent Wetland | Wetlands |
| Parameter | Mean | SD | 2.5% | 50% | 97.5% |
|---|---|---|---|---|---|
| Intercept | −0.757 | 20.844 | −41.900 | −0.779 | 40.466 |
| Elevation (km) | −9.330 | 0.039 | −9.407 | −9.330 | −9.252 |
| Canopy | 0.009 | 0.000 | 0.013 | 0.013 | 0.014 |
| LULC, developed | 78.087 | 0.445 | 77.204 | 78.088 | 78.960 |
| LULC, planted | 77.930 | 0.442 | 77.054 | 77.932 | 78.797 |
| LULC, forest | 78.195 | 0.443 | 77.318 | 78.197 | 79.063 |
| LULC, water | 77.161 | 0.438 | 76.293 | 77.162 | 78.019 |
| LULC, wetlands | 77.580 | 0.442 | 76.705 | 77.582 | 78.446 |
| log(distance coastline (km)) | 0.057 | 0.002 | 0.053 | 0.057 | 0.061 |
| log(distance water (km)) | 0.005 | 0.001 | 0.002 | 0.005 | 0.007 |
| LST | 0.112 | 0.001 | 0.087 | 0.089 | 0.092 |
| Range for spatial field | 23.53 | 3.741 | 16.92 | 23.28 | 31.60 |
| Stdev for spatial field | 16.40 | 2.580 | 11.81 | 16.24 | 21.92 |
| Random Effects | |||||
| Jun | −1.218 | 0.4062 | −2.016 | −1.220 | −0.411 |
| Impervious (Jun) | −0.001 | 0.002 | −0.006 | −0.001 | 0.003 |
| Jul | 1.854 | 0.406 | 1.057 | 1.852 | 2.661 |
| Impervious (Jul) | −0.001 | 0.002 | −0.005 | −0.001 | 0.004 |
| Aug | −0.024 | 0.002 | −0.028 | −0.024 | −0.019 |
| Impervious (Aug) | 0.012 | 0.003 | 0.0063 | 0.012 | 0.017 |
| MAE | RMSE | Bias (°F) | |
|---|---|---|---|
| All Months | 1.61 | 2.11 | 0.23 |
| June | 1.70 | 2.22 | 0.75 |
| July | 1.61 | 2.14 | −0.01 |
| August | 1.51 | 1.97 | −0.06 |
References
- Rasmussen, D.J.; Meinshausen, M.; Kopp, R.E. Probability-Weighted Ensembles of U.S. County-Level Climate Projections for Climate Risk Analysis. J. Appl. Meteorol. Climatol. 2016, 55, 2301–2322. [Google Scholar] [CrossRef] [Green Version]
- Broadbent, A.M.; Krayenhoff, E.S.; Georgescu, M. The motley drivers of heat and cold exposure in 21st century US cities. Proc. Natl. Acad. Sci. USA 2020, 117, 21108–21117. [Google Scholar] [CrossRef]
- Meehl, G.A.; Tebaldi, C. More Intense, More Frequent, and Longer Lasting Heat Waves in the 21st Century. Science 2004, 305, 994–997. [Google Scholar] [CrossRef] [Green Version]
- Dahl, K.; Licker, R.; Abatzoglou, J.T.; Declet-Barreto, J. Increased frequency of and population exposure to extreme heat index days in the United States during the 21st century. Environ. Res. Commun. 2019, 1, 075002. [Google Scholar] [CrossRef]
- Anderson, G.B.; Bell, M.L. Heat Waves in the United States: Mortality Risk during Heat Waves and Effect Modification by Heat Wave Characteristics in 43 U.S. Communities. Environ. Health Perspect. 2011, 119, 210–218. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eisenman, D.P.; Wilhalme, H.; Tseng, C.H.; Chester, M.; English, P.; Pincetl, S.; Fraser, A.; Vangala, S.; Dhaliwal, S.K. Heat Death Associations with the built environment, social vulnerability and their interactions with rising temperature. Health Place 2016, 41, 89–99. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Funk, C.; Peterson, P.; Peterson, S.; Shukla, S.; Davenport, F.; Michaelsen, J.; Knapp, K.R.; Landsfeld, M.; Husak, G.; Harrison, L.; et al. A High-Resolution 1983–2016 Tmax Climate Data Record Based on Infrared Temperatures and Stations by the Climate Hazard Center. J. Clim. 2019, 32, 5639–5658. [Google Scholar] [CrossRef]
- Verdin, A.; Funk, C.; Peterson, P.; Landsfeld, M.; Tuholske, C.; Grace, K. Development and validation of the CHIRTS-daily quasi-global high-resolution daily temperature data set. Sci. Data 2020, 7, 303. [Google Scholar] [CrossRef] [PubMed]
- Tuholske, C.; Caylor, K.; Funk, C.; Verdin, A.; Sweeney, S.; Grace, K.; Peterson, P.; Evans, T. Global urban population exposure to extreme heat. Proc. Natl. Acad. Sci. USA 2021, 118. [Google Scholar] [CrossRef]
- Manoli, G.; Fatichi, S.; Schläpfer, M.; Yu, K.; Crowther, T.W.; Meili, N.; Burlando, P.; Katul, G.G.; Bou-Zeid, E. Magnitude of urban heat islands largely explained by climate and population. Nature 2019, 573, 55–60. [Google Scholar] [CrossRef]
- Rennie, J.J.; Palecki, M.A.; Heuser, S.P.; Diamond, H.J. Developing and Validating Heat Exposure Products Using the U.S. Climate Reference Network. J. Appl. Meteorol. Climatol. 2021, 60, 543–558. [Google Scholar] [CrossRef]
- Smith, A.; Lott, N.; Vose, R. The Integrated Surface Database: Recent Developments and Partnerships. Bull. Am. Meteorol. Soc. 2011, 92, 704–708. [Google Scholar] [CrossRef]
- Menne, M.J.; Durre, I.; Vose, R.S.; Gleason, B.E.; Houston, T.G. An Overview of the Global Historical Climatology Network-Daily Database. J. Atmos. Ocean. Technol. 2012, 29, 897–910. [Google Scholar] [CrossRef]
- Daly, C.; Halbleib, M.; Smith, J.I.; Gibson, W.P.; Doggett, M.K.; Taylor, G.H.; Curtis, J.; Pasteris, P.P. Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous United States. Int. J. Climatol. 2008, 28, 2031–2064. [Google Scholar] [CrossRef]
- Abatzoglou, J.T. Development of gridded surface meteorological data for ecological applications and modelling. Int. J. Climatol. 2013, 33, 121–131. [Google Scholar] [CrossRef]
- Thornton, P.E.; Shrestha, R.; Thornton, M.; Kao, S.C.; Wei, Y.; Wilson, B.E. Gridded daily weather data for North America with comprehensive uncertainty quantification. Sci. Data 2021, 8, 190. [Google Scholar] [CrossRef]
- Jones, B.; O’Neill, B.C.; McDaniel, L.; McGinnis, S.; Mearns, L.O.; Tebaldi, C. Future population exposure to US heat extremes. Nat. Clim. Chang. 2015, 5, 652–655. [Google Scholar] [CrossRef]
- Kim, H.H. Urban heat island. Int. J. Remote Sens. 1992, 13, 2319–2336. [Google Scholar] [CrossRef]
- Stewart, I.D.; Oke, T.R. Local Climate Zones for Urban Temperature Studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
- Arnfield, A.J. Two decades of urban climate research: A review of turbulence, exchanges of energy and water, and the urban heat island. Int. J. Climatol. 2003, 23, 1–26. [Google Scholar] [CrossRef]
- Moffett, K.B.; Makido, Y.; Shandas, V. Urban-Rural Surface Temperature Deviation and Intra-Urban Variations Contained by an Urban Growth Boundary. Remote Sens. 2019, 11, 2683. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Huang, G.; Cadenasso, M.L. Does spatial configuration matter? Understanding the effects of land cover pattern on land-surface temperature in urban landscapes. Landsc. Urban Plan. 2011, 102, 54–63. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, S.; Liu, S.; Zhang, L.; Zhu, C. Surface urban heat island in China’s 32 major cities: Spatial patterns and drivers. Remote Sens. Environ. 2014, 152, 51–61. [Google Scholar] [CrossRef]
- Jenerette, G.D.; Harlan, S.L.; Buyantuev, A.; Stefanov, W.L.; Declet-Barreto, J.; Ruddell, B.L.; Myint, S.W.; Kaplan, S.; Li, X. Micro-scale urban surface temperatures are related to land-cover features and residential heat related health impacts in Phoenix, AZ USA. Landsc. Ecol. 2016, 31, 745–760. [Google Scholar] [CrossRef]
- Hoffman, J.S.; Shandas, V.; Pendleton, N. The Effects of Historical Housing Policies on Resident Exposure to Intra-Urban Heat: A Study of 108 US Urban Areas. Climate 2020, 8, 12. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Lű, A.; Jia, S. Estimation of daily maximum and minimum air temperature using MODIS land-surface temperature products. Remote Sens. Environ. 2013, 130, 62–73. [Google Scholar] [CrossRef]
- Johnson, S.; Ross, Z.; Kheirbek, I.; Ito, K. Characterization of intra-urban spatial variation in observed summer ambient temperature from the New York City Community Air Survey. Urban Clim. 2020, 31, 100583. [Google Scholar] [CrossRef]
- Shi, R.; Hobbs, B.F.; Zaitchik, B.F.; Waugh, D.W.; Scott, A.A.; Zhang, Y. Monitoring intra-urban temperature with dense sensor networks: Fixed or mobile? An empirical study in Baltimore, MD. Urban Clim. 2021, 39, 100979. [Google Scholar] [CrossRef]
- Voelkel, J.; Shandas, V. Towards Systematic Prediction of Urban Heat Islands: Grounding Measurements, Assessing Modeling Techniques. Climate 2017, 5, 41. [Google Scholar] [CrossRef] [Green Version]
- Shandas, V.; Voelkel, J.; Williams, J.; Hoffman, J. Integrating Satellite and Ground Measurements for Predicting Locations of Extreme Urban Heat. Climate 2019, 7, 5. [Google Scholar] [CrossRef] [Green Version]
- White, N.J.L.; Brines, S.J.; Brown, D.G.; Dvonch, J.T.; Gronlund, C.J.; Zhang, K.; Oswald, E.M.; O’Neill, M.S. Validating Satellite-Derived Land Surface Temperature with in Situ Measurements: A Public Health Perspective. Environ. Health Perspect. 2013, 121, 925–931. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moraga, P.; Cramb, S.M.; Mengersen, K.L.; Pagano, M. A geostatistical model for combined analysis of point-level and area-level data using INLA and SPDE. Spat. Stat. 2017, 21, 27–41. [Google Scholar] [CrossRef] [Green Version]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. (Stat. Methodol.) 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Lindgren, F.; Rue, H.; Lindström, J. An explicit link between Gaussian fields and Gaussian Markov random fields: The stochastic partial differential equation approach. J. R. Stat. Soc. Ser. (Stat. Methodol.) 2011, 73, 423–498. [Google Scholar] [CrossRef] [Green Version]
- Lawrimore, J.; Ray, R.; Applequist, S.; Korzeniewski, B.; Menne, M.J. Global Summary of the Month (GSOM), Version 1; National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 2021. [CrossRef]
- Shi, L.; Liu, P.; Kloog, I.; Lee, M.; Kosheleva, A.; Schwartz, J. Estimating daily air temperature across the Southeastern United States using high-resolution satellite data: A statistical modeling study. Environ. Res. 2016, 146, 51–58. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kloog, I.; Nordio, F.; Coull, B.A.; Schwartz, J. Predicting spatiotemporal mean air temperature using MODIS satellite surface temperature measurements across the Northeastern USA. Remote Sens. Environ. 2014, 150, 132–139. [Google Scholar] [CrossRef]
- Good, E.J.; Ghent, D.J.; Bulgin, C.E.; Remedios, J.J. A spatiotemporal analysis of the relationship between near-surface air temperature and satellite land-surface temperatures using 17 years of data from the ATSR series. J. Geophys. Res. Atmos. 2017, 122, 9185–9210. [Google Scholar] [CrossRef]
- Estes, M.G., Jr.; Insaf, T.; Crosson, W.L.; Al-Hamdan, M.Z. Evaluation of NLDAS 12-km and downscaled 1-km temperature products in New York State for potential use in health exposure response studies. In Proceedings of the AGU Fall Meeting Abstracts ADS Bibcode, New Orleans, LA, USA, 11–15 December 2017. [Google Scholar]
- Sheng, L.; Tang, X.; You, H.; Gu, Q.; Hu, H. Comparison of the urban heat island intensity quantified by using air temperature and Landsat land-surface temperature in Hangzhou, China. Ecol. Indic. 2017, 72, 738–746. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, L.; Li, D.; Huang, D.; Zhu, C. Climate–vegetation control on the diurnal and seasonal variations of surface urban heat islands in China. Environ. Res. Lett. 2016, 11, 074009. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, J.; Cadenasso, M.L. Effects of the spatial configuration of trees on urban heat mitigation: A comparative study. Remote Sens. Environ. 2017, 195, 1–12. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Oltra-Carrió, R.; Sòria, G.; Bianchi, R.; Paganini, M. Impact of spatial resolution and satellite overpass time on evaluation of the surface urban heat island effects. Remote Sens. Environ. 2012, 117, 50–56. [Google Scholar] [CrossRef]
- Cook, M.; Schott, J.R.; Mandel, J.; Raqueno, N. Development of an Operational Calibration Methodology for the Landsat Thermal Data Archive and Initial Testing of the Atmospheric Compensation Component of a Land Surface Temperature (LST) Product from the Archive. Remote Sens. 2014, 6, 11244–11266. [Google Scholar] [CrossRef] [Green Version]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Du, P.; Chen, J.; Bai, X.; Han, W. Understanding the seasonal variations of land-surface temperature in Nanjing urban area based on local climate zone. Urban Clim. 2020, 33, 100657. [Google Scholar] [CrossRef]
- Jin, S.; Homer, C.; Yang, L.; Danielson, P.; Dewitz, J.; Li, C.; Zhu, Z.; Xian, G.; Howard, D. Overall Methodology Design for the United States National Land Cover Database 2016 Products. Remote Sens. 2019, 11, 2971. [Google Scholar] [CrossRef] [Green Version]
- Bakka, H.; Rue, H.; Fuglstad, G.A.; Riebler, A.; Bolin, D.; Illian, J.; Krainski, E.; Simpson, D.; Lindgren, F. Spatial modeling with R-INLA: A review. WIREs Comput. Stat. 2018, 10, e1443. [Google Scholar] [CrossRef] [Green Version]
- CAPA/NIHHIS. Heat Watch Raleigh—Durham; OSF: Charlottesville, VA, USA, 2021. [Google Scholar]
- Murage, P.; Hajat, S.; Kovats, R.S. Effect of night-time temperatures on cause and age-specific mortality in London. Environ. Epidemiol. 2017, 1, e005. [Google Scholar] [CrossRef]
- Vanos, J.K.; Baldwin, J.W.; Jay, O.; Ebi, K.L. Simplicity lacks robustness when projecting heat-health outcomes in a changing climate. Nat. Commun. 2020, 11, 6079. [Google Scholar] [CrossRef]
- Grimmond, C.S.B.; Oke, T.R. Turbulent Heat Fluxes in Urban Areas: Observations and a Local-Scale Urban Meteorological Parameterization Scheme (LUMPS). J. Appl. Meteorol. Climatol. 2002, 41, 792–810. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Li, Y.; Bejan, A.; Wang, Y.; Yang, X. Horizontal extent of the urban heat dome flow. Sci. Rep. 2017, 7, 11681. [Google Scholar] [CrossRef] [Green Version]
- Swaid, H. Numerical Investigation into the Influence of Geometry and Construction Materials on Urban Street Climate. Phys. Geogr. 1993, 14, 342–358. [Google Scholar] [CrossRef]
- Peterson, T.C. Assessment of Urban Versus Rural In Situ Surface Temperatures in the Contiguous United States: No Difference Found. J. Clim. 2003, 16, 2941–2959. [Google Scholar] [CrossRef] [Green Version]
- Wong, K.V.; Paddon, A.; Jimenez, A. Review of World Urban Heat Islands: Many Linked to Increased Mortality. J. Energy Resour. Technol. 2013, 135. [Google Scholar] [CrossRef]
- Shi, L.; Kloog, I.; Zanobetti, A.; Liu, P.; Schwartz, J.D. Impacts of temperature and its variability on mortality in New England. Nat. Clim. Chang. 2015, 5, 988–991. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Declet-Barreto, J.; Brazel, A.J.; Martin, C.A.; Chow, W.T.L.; Harlan, S.L. Creating the park cool island in an inner-city neighborhood: Heat mitigation strategy for Phoenix, AZ. Urban Ecosyst. 2013, 16, 617–635. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilson, B.; Porter, J.R.; Kearns, E.J.; Hoffman, J.S.; Shu, E.; Lai, K.; Bauer, M.; Pope, M. High-Resolution Estimation of Monthly Air Temperature from Joint Modeling of In Situ Measurements and Gridded Temperature Data. Climate 2022, 10, 47. https://doi.org/10.3390/cli10030047
Wilson B, Porter JR, Kearns EJ, Hoffman JS, Shu E, Lai K, Bauer M, Pope M. High-Resolution Estimation of Monthly Air Temperature from Joint Modeling of In Situ Measurements and Gridded Temperature Data. Climate. 2022; 10(3):47. https://doi.org/10.3390/cli10030047
Chicago/Turabian StyleWilson, Bradley, Jeremy R. Porter, Edward J. Kearns, Jeremy S. Hoffman, Evelyn Shu, Kelvin Lai, Mark Bauer, and Mariah Pope. 2022. "High-Resolution Estimation of Monthly Air Temperature from Joint Modeling of In Situ Measurements and Gridded Temperature Data" Climate 10, no. 3: 47. https://doi.org/10.3390/cli10030047
APA StyleWilson, B., Porter, J. R., Kearns, E. J., Hoffman, J. S., Shu, E., Lai, K., Bauer, M., & Pope, M. (2022). High-Resolution Estimation of Monthly Air Temperature from Joint Modeling of In Situ Measurements and Gridded Temperature Data. Climate, 10(3), 47. https://doi.org/10.3390/cli10030047








