1. Introduction
Bayesian model averaging (BMA; see, for example,
Hoeting et al. 1999) is a way to combine different Bayesian hierarchical models that can be used to estimate highly parameterized models. By computing an average model, the uncertainty about the model choice is taken into account when estimating the uncertainty of the model parameters.
As BMA often requires fitting a large number of models, this can be time consuming when the time required to fit each of the models is large. The integrated nested Laplace approximation (INLA;
Rue et al. 2009) offers an alternative to the computationally intensive Markov chain Monte Carlo (MCMC;
Gilks et al. 1996) methods. INLA focuses on obtaining an approximation of the posterior marginal distributions of the models parameters of latent GMRF models (
Rue and Held 2005). Hence, BMA with INLA is based on combining the resulting marginals from all the models averaged.
Bivand et al. (
2014) and
Bivand et al. (
2015) used this approach to fit some spatial econometrics models by fitting conditional models on some of the hyperparameters of the original models. The resulting models are then combined using BMA to obtain estimates of the marginals of the hyperparameters of the original model.
Gómez-Rubio and Rue (
2018) embedded INLA within MCMC so that the joint posterior distribution of a subset of the model parameters is estimated using the Metropolis–Hastings algorithm (
Hastings 1970;
Metropolis et al. 1953). This requires fitting a model with INLA (conditional on some parameters) at each step, so that the resulting models can also be combined to obtain the posterior marginals of the remainder of the model parameters.
While typical BMA focuses on averaging models with various fixed and random effects, the different models that appear in the methodology of BMA with INLA presented in this paper (
Bivand et al. 2014;
Bivand et al. 2015) are due to a discretization of the parametric space of some of the hyperparameters. The models are fit conditional on some values of these hyperparameters, so that BMA with INLA accounts for the uncertainty about these parameters, but the underlying model structure is the same for all the models. However, the basic methodology for averaging models is the same as in typical BMA as weights are assigned with the different models, which are in turn used to produce an average model.
Hence, BMA with INLA relies on a weighted sum of the conditional marginals obtained from a family of conditional models on some hyperparameters. Weights are computed by using Bayes’ rule, and they depend on the marginal likelihood of the conditional model and the prior distribution of the conditioning hyperparameters. This new approach is described in detail in
Section 4. We will illustrate how this works by developing an example on spatial econometrics models described in
Section 2.
Compared to
Bivand et al. (
2014) and
Bivand et al. (
2015) we extend BMA with INLA to more than one dimension. In addition, we provide details about how to explore the parametric space of the conditioning hyperparameters, as well as how to consider the grid for numerical integration and how to define it using an internal scale to deal with unbounded parameters for computational convenience. The extent of the grid is based on maximum likelihood estimates and their standard errors of the model hyperparameters. The Delta method is used here to estimate the standard error of the transformed parameters in the internal scale. Hence, the numerical integration approach is more thorough and robust than in
Bivand et al. (
2014) and
Bivand et al. (
2015).
This paper is organized as follows. Spatial econometrics models are summarized in
Section 2. Next, an introduction to INLA is given in
Section 3. This is followed by a description of Bayesian model averaging (with INLA) in
Section 4. An example is developed in
Section 5. Finally,
Section 6 gives a summary of the paper and includes a discussion on the main results.
2. Spatial Econometrics Models
Spatial econometrics models (
LeSage and Pace 2009) are often employed to account for spatial autocorrelation in the data. Usually, these models include one or more spatial autoregressive terms.
Halleck Vega and Elhorst (
2015) proposed a model (termed the general nesting spatial model, GNS) that includes an autoregressive term on the response and another one in the error term:
Here,
is the response,
a matrix of covariates with coefficients
,
an adjacency matrix. and
lagged covariates with coefficients
. Finally,
is an error term. This error term is often modeled to include spatial autocorrelation:
Here, is a vector of independent Gaussian observations with zero mean and precision .
The previous model can be rewritten as:
with
an error term with a multivariate Gaussian distribution with zero mean and precision matrix:
Note that here, the same adjacency matrix
is used for the two autocorrelated terms, but different adjacency matrices could be used. The range of
and
is determined by the eigenvalues of
. When
is taken to be row-standardized, the range is the interval
, where
is the minimum eigenvalue of
(see, for example,
Haining 2003). In this case, the lagged covariates
represent the average value at the neighbors, which is useful when interpreting the results.
In a Bayesian context, a prior needs to be set on every model parameter. For the spatial autocorrelation parameter, a uniform in the interval will be used. For the coefficients of the covariates, a normal with zero mean and precision 1000 is used and for precision , Gamma with parameters and .
When the lagged covariates term
is dropped, the resulting model is often referred to as the spatial autoregressive combined (SAC) model (
LeSage and Pace 2009). Other important models in spatial econometrics appear when some of the terms in the GNS model are dropped (
Halleck Vega and Elhorst 2015). See, for example,
Gómez-Rubio et al. (
2017) and how these models are fit with INLA.
In spatial econometrics models, how changes in the value of the covariates affect the response in neighboring regions is of interest. These spill-over effects or impacts (
LeSage and Pace 2009) are caused by the term
that multiplies the covariates, and they are defined as:
where
n is the number of observations,
p the number of covariates, and
the value of covariate
r in region
j.
Hence, for each covariate k, there will be an associated matrix of impacts. The diagonal values are known as direct impacts as they measure the effect of changing a covariate on the same areas. The off-diagonal values are known as indirect impacts as they measure the change of the response at neighboring areas when covariate k changes. Finally, total impacts are the sum of direct and indirect impacts.
Gómez-Rubio et al. (
2017) described the impacts for different spatial econometrics models. For the SAC model, the impact matrix for covariate
k is:
In practice, average impacts are reported as a summary of the direct, indirect, and total impacts (for details, see, for example,
Gómez-Rubio et al. 2017;
LeSage and Pace 2009). In particular, the average direct impact is the trace of
divided by
n; the average indirect impact is defined as the sum of the off-diagonal elements divided by
n; and the average total impact is the sum of all elements of
divided by
n. The average total impact is also the sum of the average direct and average indirect impacts.
For the SAC model, the average total impact is , and the average direct impact is . The average indirect impact can be computed as the difference between the average total and average direct impacts, , or by computing the sum of the off-diagonal elements of divided by n.
Note that computing the impacts depends on parameters and . For this reason, the joint posterior distribution of both parameters would be required. As explained below, this is not a problem, because it can be rewritten as .
3. The Integrated Nested Laplace Approximation
Markov chain Monte Carlo algorithms (see, for example,
Brooks et al. 2011) are typically used to estimate the joint posterior distribution of the ensemble of parameters and latent effects of a hierarchical Bayesian model. However, these algorithms are often slow when dealing with high parameterized models.
Rue et al. (
2009) proposed a computationally efficient numerical method to estimate the posterior marginals of the hyperparameters and latent effects. This method is called integrated nested Laplace approximation (INLA) because it is based on repeatedly using the Laplace approximation to estimate the posterior marginals. In addition, INLA focuses on models that can be expressed as a latent Gaussian Markov random fields (GMRF;
Rue and Held 2005).
In this context, the model is expressed as follows. For each observation
in the ensemble of observations
y, its likelihood is defined as:
where
denotes the density of the likelihood function.
For each observation , its mean will be conveniently linked to the linear predictor using the appropriate function (which will depend on the likelihood used). The linear predictor will include different additive effects such as fixed effects and random effects.
Next, the vector of latent effects
is defined as a GMRF with zero mean and precision matrix
(which may depend on the vector of hyperparameters
):
Finally, the hyperparameters are assigned a prior distribution. This is often done assuming prior independence. Without loss of generality, this can be represented as:
Note that is a multivariate distribution, but that in many cases, it can be expressed as the product of several univariate (or small dimension) prior distributions.
For the GNS model, the model fit is such that the likelihood
is a univariate Gaussian distribution with the mean equal to a linear predictor
and precision
, which will be set to a very small value (as explained in
Appendix A) to remove the error term. The linear predictor of observation
i is:
The structure of GMRF is defined on the vector of latent effects:
with a vector of hyperparameters
. Precision matrix
of
is a block diagonal matrix defined according to the different latent effects in the model.
Hence, if
represents the vector of
h hyperparameters and
the vector of
l latent effects, INLA provides the posterior marginals:
and
Note that represents the observed data, and it includes response , covariates , and any other known quantities required for model fitting.
In addition to the marginals, INLA can be used to estimate other quantities of interest. See, for example,
Rue et al. (
2017) for a recent review.
INLA can provide accurate approximations to the marginal likelihood of a model, which are computed as:
Here,
is a Gaussian approximation to the distribution of
, and
is the posterior mode of
for a given value of
. This approximation seems to be accurate in a wide range of examples (
Gómez-Rubio and Rue 2018;
Hubin and Storvik 2016).
As described in
Section 4, the marginal likelihood plays a crucial role in BMA as it determines the weights, together with the prior distribution of some of the hyperparameters in the model.
As stated above, INLA approximates the posterior marginals of the parameters of latent GMRF models. Hence, an immediate question is whether INLA will work for different models.
Gómez-Rubio and Rue (
2018) introduced the idea of using INLA to fit conditional latent GMRF models by conditioning on some of the hyperparameters. In this context, the vector of hyperparameters
is split into
and
, so that models are fit with INLA conditional on
, and the posterior marginals of the elements of
and latent effects
are obtained, i.e.,
and
, respectively. Here,
represents any element in
and
any element in
.
In practice, this involves setting hyperparameters
to some value, so that the model becomes a latent GMRF that INLA can tackle.
Gómez-Rubio and Rue (
2018) provided some ideas on how these can be chosen.
Gómez-Rubio and Palmí-Perales (
2019) proposed setting these values to maximum likelihood estimates (for example) and other options, and provided examples that showed that this may still provide good approximations to the posterior marginal distributions of the remainder of the parameters in the model.
4. Bayesian Model Averaging with INLA
As stated above, fitting conditional models by setting some hyperparameters () to fixed values can be a way to use INLA to fit wider classes of models. However, this ignores the uncertainty about these hyperparameters and makes inference about them impossible. However, BMA may help to fit the complete model, even if it cannot be fit with INLA initially.
This differs from a typical use of BMA in which models with different fixed or random effects are averaged. For example, in
Bivand et al. (
2014) and
Bivand et al. (
2015), the different models appeared as a result of setting the spatial autocorrelation of the model to different values (in a discretization of its original parametric space), but otherwise, the structure of the models was the same. For the SAC model, models are fit conditional on
, so that
, and
is fixed to remove the Gaussian error term (see
Appendix A). Hence, we extend the methodology in
Bivand et al. (
2014) and
Bivand et al. (
2015) to the multivariate case.
First of all, it is worth noting that the posterior marginals (of the hyperparameters
and latent effects
) can be written as:
The first term in the integrand,
, is the conditional posterior marginal given
, while the second term is the joint posterior distribution of
, and it can be expressed as:
The first term is the conditional (on ) marginal likelihood, which can be approximated with INLA. The second term is the prior for , which is known. Hence, the posterior distribution of could be computed by re-scaling the previous expression.
Bivand et al. (
2014) showed that when
is unidimensional, numerical integration can be used to estimate the posterior marginal. This is done by using a regular grid of
K values
of a fixed step.
Hence, the posterior marginals of the remainder of the hyperparameters and latent effects can be estimated as:
with weights
defined as:
Note how the posterior marginal is expressed as a BMA using the conditional posterior marginals of all the fit models.
Inference on is based on the values and weights . For example, the posterior mean of the element in could be computed as . Other posterior quantities could be computed similarly. Note that this also allows for multivariate posterior inference on the elements of .
The former approach was used in
Bivand et al. (
2014) and
Bivand et al. (
2015) in one dimension, but it can be easily extended to higher dimensions by considering a multidimensional grid of points for
, so that each point is the center of a region of a space of equal volume. In practice, it is not necessary to consider the complete space (as it is not feasible), but the region of posterior high probability of
. This may be obtained by, for example, maximizing
, which can be easily computed with INLA or by using a maximum likelihood estimate if available (as discussed, for example, in
Gómez-Rubio and Palmí-Perales 2019).
For the SAC model, we will be dealing with dimension two as
. A regular grid about the posterior mode of
will be created for each model using the maximum likelihood estimates. The grid is defined in an internal scale to have unbounded variables using the transformation
and
. The variance of
and
can be derived using the Delta method (see
Appendix A for details), and it can be computed using the ML standard error estimate of
and
. In particular, each interval is centered at the transformed ML estimate and a semi-amplitude of three standard errors of the variables in the internal scale.
Regarding the grid, this approach may work for small dimensions of
. For large dimensions, a central composite design (CCD;
Box and Draper 2007) may be used, as INLA can do for the models that
R-INLA implements. This was explored in
Gómez-Rubio and Palmí-Perales (
2019), and the ML estimates of the model parameters could be used to define the CCD points. Note that the dimension of the grid may depend on the model and that it may be difficult to set it beforehand. Grids that are too thin will provide averaged marginals that are too wobbly, and a smaller step may be required.
5. Example: Turnout in Italy
In order to provide an example of the methodology presented in previous sections, we take the turnout dataset described in
Ward and Gleditsch (
2008), which is available from the website
http://ksgleditsch.com/srm_book.html. This dataset records the turnout in the 2001 Italian elections, as well as GDP per capita (
GDPCAP) in 1997 (in million Lire). The data are comprised of 477 areas, which represent collegi or single-member districts (SDM). Adjacency is defined so that regions whose centroids are 50 km or less away are neighbors to ensure that all regions have neighbors, contiguous regions are neighbors, and Elba is joined to the closest mainland region. In order to assess the impact of the GDP per capita in the estimation of the spatial autocorrelation parameters, two models with and without the covariate are fit. The covariate is included in the log-scale to compare to the results in
Ward and Gleditsch (
2008).
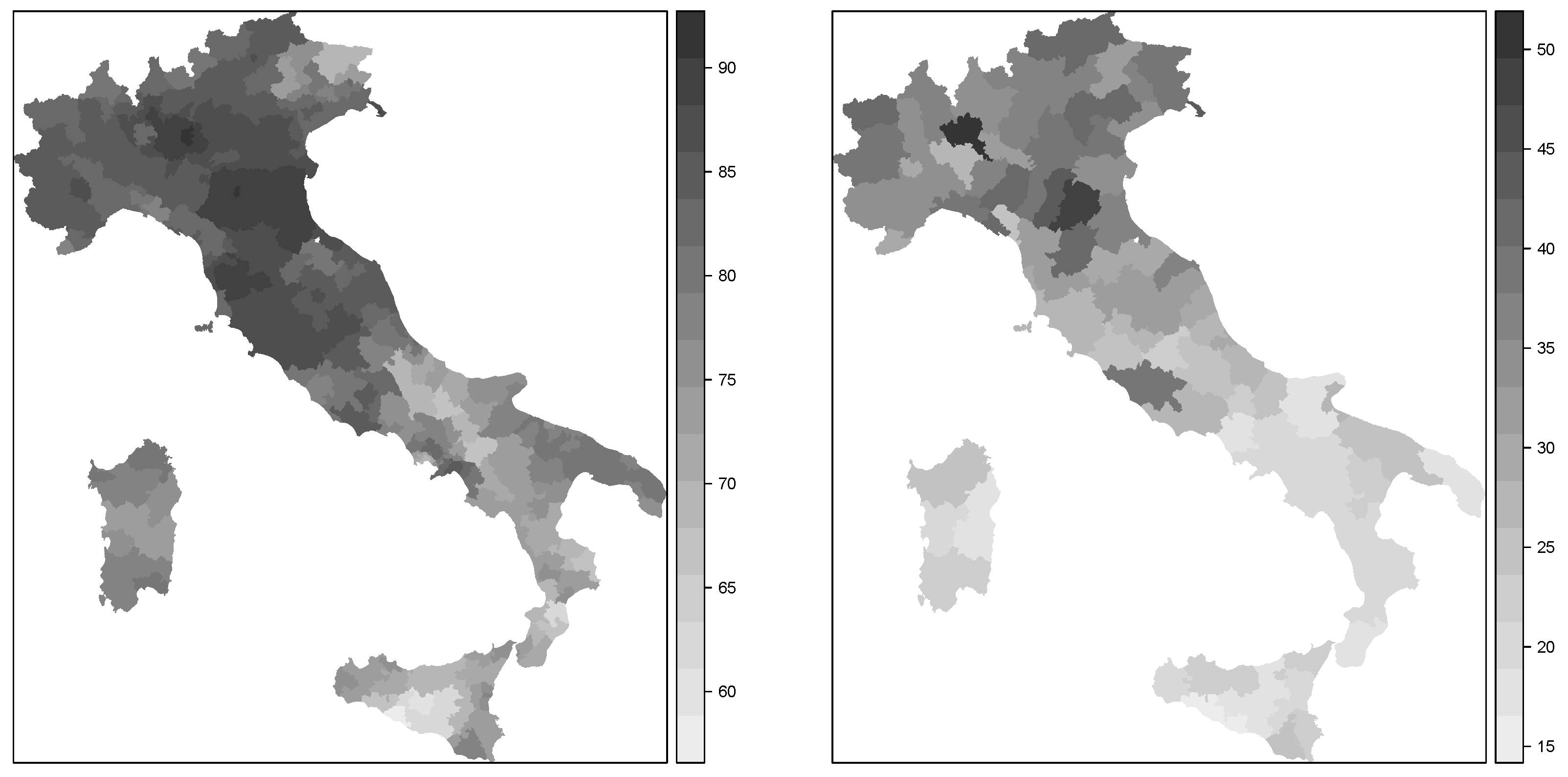
Figure 1 shows the spatial patterns of these two variables. As can be seen, there was a clear south-north pattern for both variables. Hence, we were interested in fitting spatial econometrics models on turnout in 2011 using GDP per capita in 1997 (in the log-scale) as a predictor so that residual spatial autocorrelation was captured by the two autoregressive terms in the model.
The SAC model is fit with INLA by conditioning on the values of the two spatial autocorrelation parameters. As described in
Section 2, after conditioning, the resulting model is a typical mixed-effects model with a particular matrix of covariates and a known structure for the precision matrix of the random effects. Hence, we consider
and
.
Both autocorrelation parameters are given values in the range (−1, 1). Note that, because the same adjacency matrix is used, the actual domain for both parameters is , with the minimum eigenvalue of the adjacency matrix . In this case, , so taking the range will be enough.
Maximum likelihood estimates of the models are obtained with package
spdep (
Bivand et al. 2013), and MCMC estimates are obtained with package
spatialreg (
Bivand and Piras 2015;
Bivand et al. 2013). For MCMC, we used 10,000 burn-in iterations, plus another 90,000 iterations for inference, of which only one in ten was kept to reduce autocorrelation. To speed up convergence, the initial values of
and
were set to their maximum likelihood estimates. BMA with INLA estimates was obtained as explained next.
A grid about the posterior mode of
was created as described in
Section 4 using the ML estimates and their standard errors. See
Table 1 for the actual values of the ML estimates. Furthermore, a grid of
points was used to represent the search space and fit the conditional models with
R-INLA for the model without the covariate and a grid of
for the model with
log(GDPCAP). A different grid was used because the model without the covariate required a thinner grid.
The computation times of the different models were small, and each individual model took about one second to fit on a computer with 32 cores of two Intel Xeon Gold 6130 CPUs at 2.101 GHz with more than 500 Gb of RAM. Although the number of models required to be fit was large, we fit 62 models in parallel (using a single thread each) so that the total time required to fit the model without covariates was about 2 min and less than 1 min for the model with the covariate (because it had a smaller grid). Since all the INLA models were run in parallel, the computational cost was easily distributed across a network of computers to reduce computing time. Merging the different INLA models took a few seconds only.
Table 1 provides a summary of the estimates of the model parameters using different inference methods. First of all are the maximum likelihood (ML) estimates (computed with the function
sacsarlm in the
spdep package). Next,
and
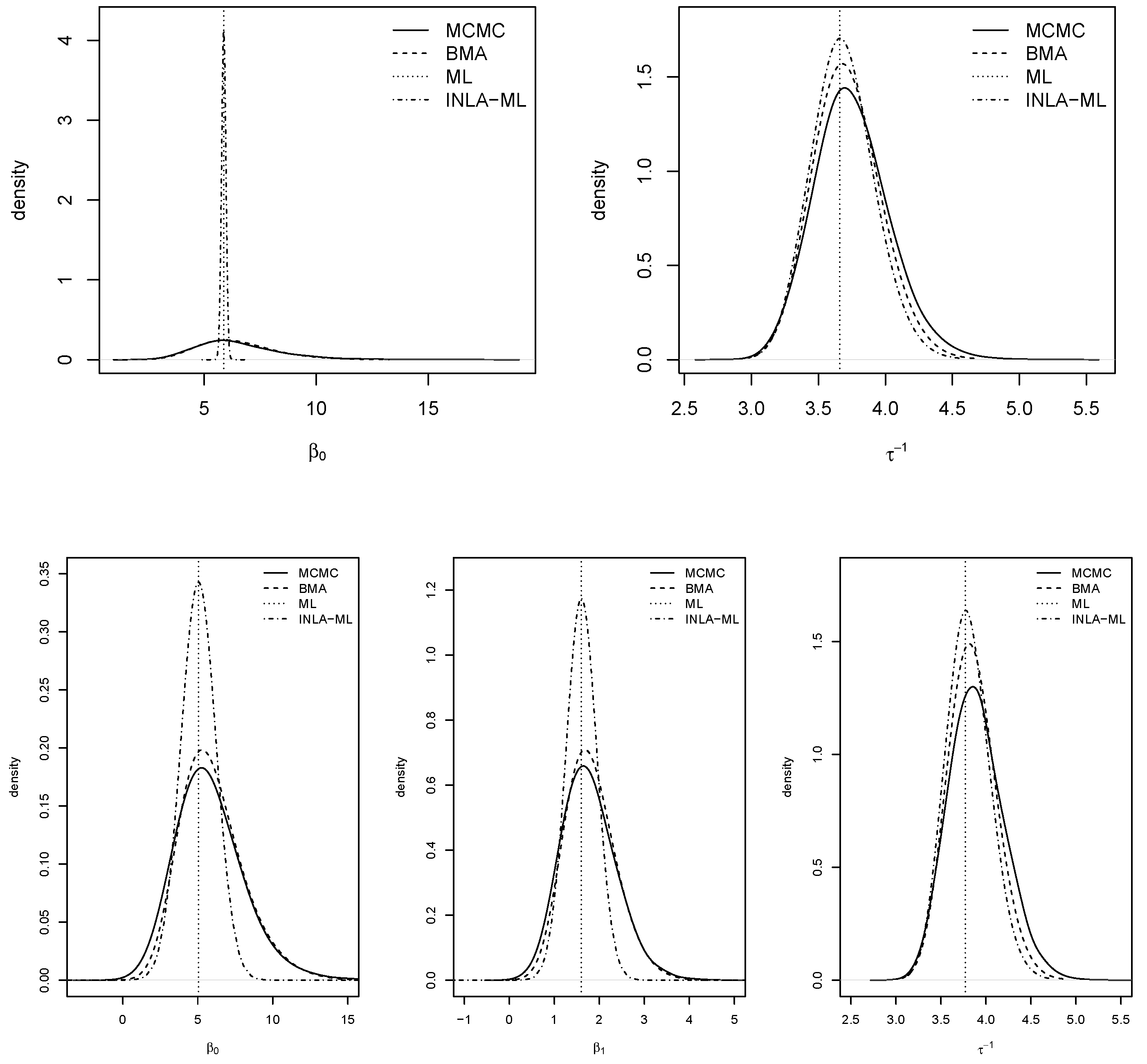
were fixed at their ML estimates, and the model was fit with INLA. Next, the posterior marginals of the model parameters using BMA with INLA and MCMC are shown. In general, point estimates obtained with the different methods provided very similar values. MCMC and maximum likelihood also provided very similar estimates of the uncertainty of the point estimates (when available for maximum likelihood). BMA with INLA seemed to provide very similar results to MCMC for both models.
Note the positive coefficient of log-GDP per capita, which meant a positive association with turnout. Furthermore, the spatial autocorrelation had a higher value than , which indicated higher autocorrelation on the response than on the error term.
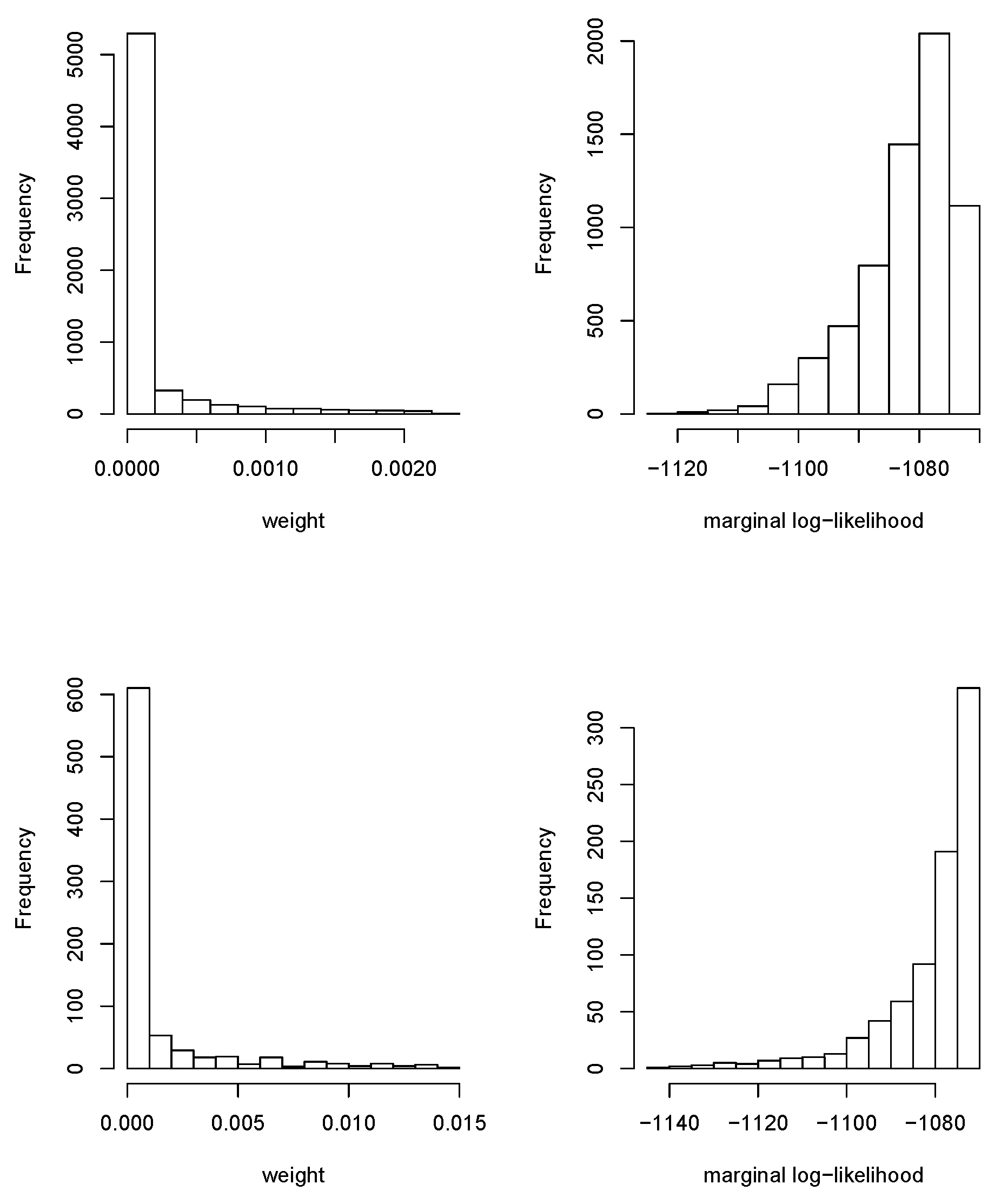
Figure 2 shows the values of the marginal log-likelihoods of all the conditional models fit, as well as the weights used in BMA. Note that the wide variability of the marginal log-likelihoods made the weights very small. Weights were almost zero for most models with a very few exceptions. Note that this was good because it indicated that the search space for
and
was adequate and that the region of high posterior density was explored because the log-posterior density decayed as the values of
moved away from the posterior mode. Note that there was an implicit assumption that the posterior of
was unimodal. Expanding the grid may help to detect other modes if we suspected this were the case. However, in this particular case, we did not believe that the SAC model produced multimodal posteriors as the plots in
Figure 1 showed a positive spatial correlation, and negative values of
and
were not likely.
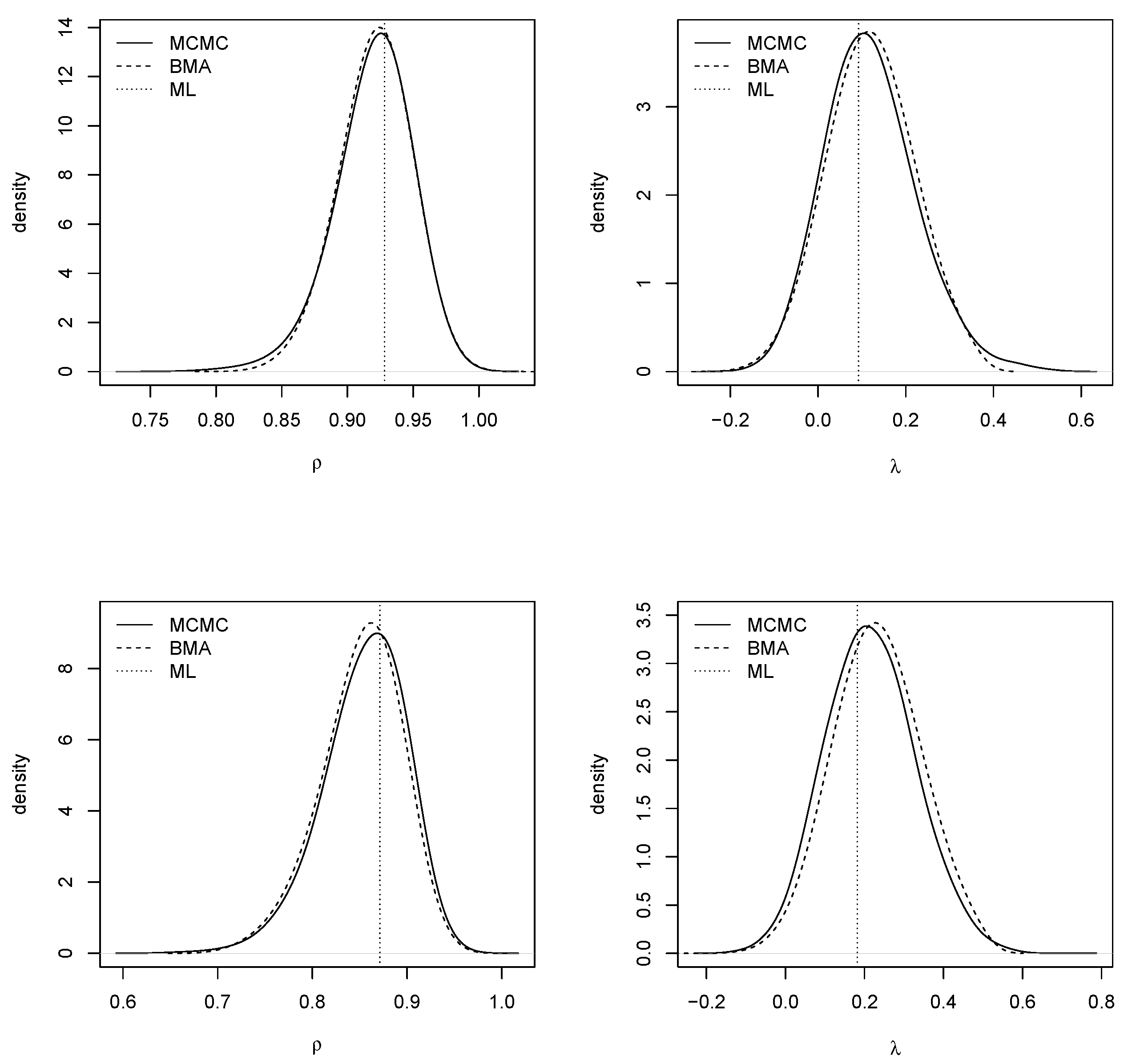
Figure 3 shows the posterior marginals of the spatial autocorrelation parameters using kernel smoothing (
Venables and Ripley 2002). For the BMA output, weighted kernel smoothing was used. In general, there was good agreement between BMA with INLA and MCMC. The ML estimates were also very close to the posterior modes.
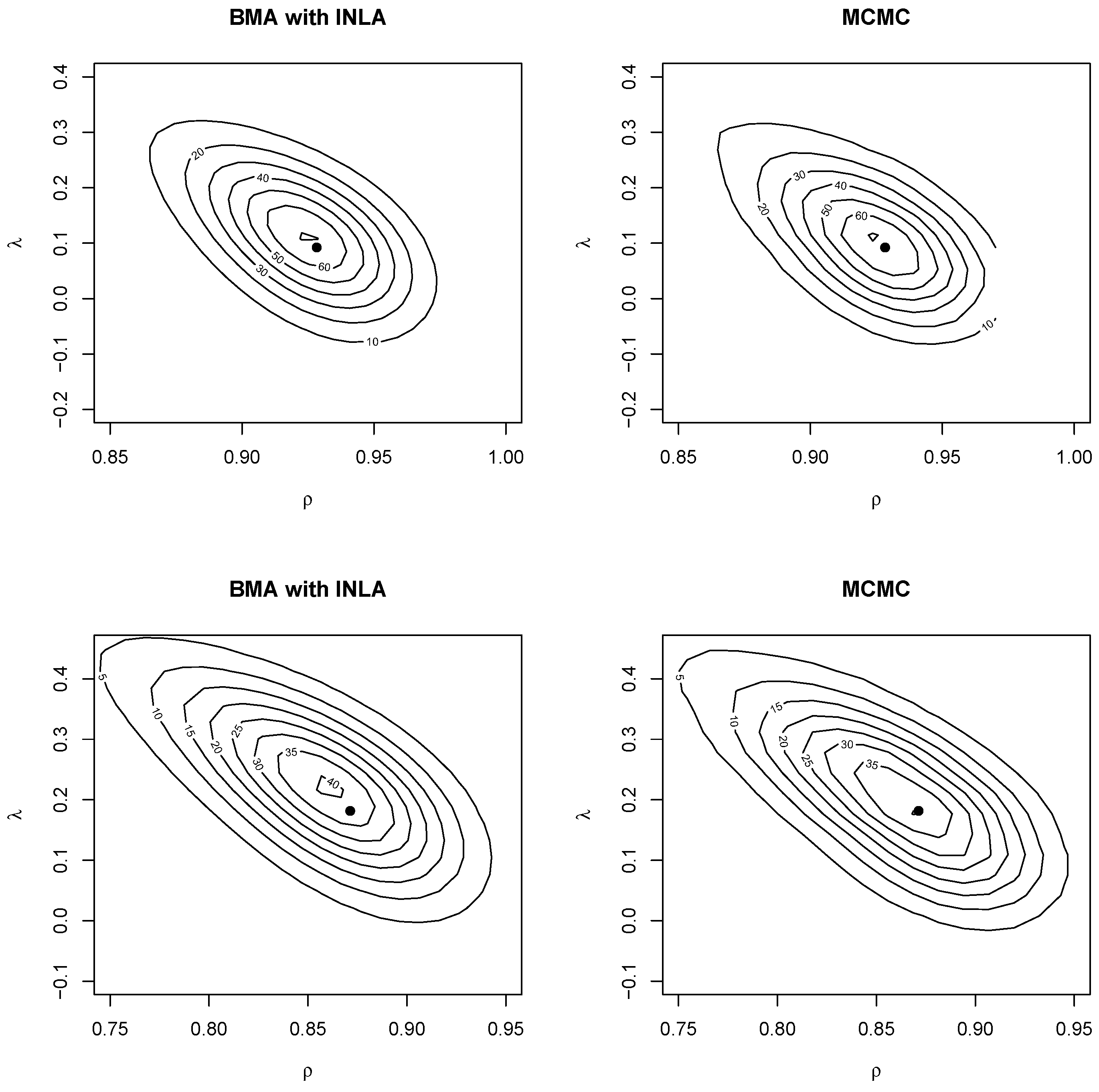
Similarly,
Figure 4 shows the joint posterior distribution of the autocorrelation parameters obtained using two-dimensional kernel smoothing. For the BMA output, this was obtained using two-dimensional weighted kernel smoothing with function
kde2d.weighted in package
ggtern (
Hamilton and Ferry 2018). The ML estimate were also added (as a black dot). As with the posterior marginals, the joint distribution was close between MCMC and BMA with INLA. The posterior mode was also close to the ML estimate. The plots showed a negative correlation between the spatial autocorrelation parameters, which may indicate that they struggled to explain spatial correlation in the data (see also
Gómez-Rubio and Palmí-Perales 2019). Furthermore, BMA with INLA was a valid approach to make joint posterior inference on a subset of hyperparameters in the model.
These results showed the validity of relying on BMA with INLA to fit highly parameterized models. This approach also accounted for the uncertainty of all model parameters and should be preferred to other inference methods based on plugging-in or fixing some of the models parameters. In our case, we relied on BMA with INLA so that conditional sub-models were fit and then combined. This had two main benefits. First of all, it allowed for full inference on all model parameters, and secondly, uncertainty about all parameters was taken into account.
Figure 5 shows the posterior marginals of the coefficients and the variance of the models. In general, BMA with INLA and MCMC showed very similar results for all parameters The posterior modes of MCMC and BMA with INLA were very close to the ML estimates. Marginals provided by INLA with ML estimates were very narrow for the fixed effects, which was probably due to ignoring the uncertainty about the spatial autocorrelation parameters.
Computation of the impacts was important because they measured how changes in the values of the covariates reflected on the changes of the response variable in the current area (direct impacts) and neighboring areas (indirect impacts). Note that impacts were only computed for the model with the covariate included.
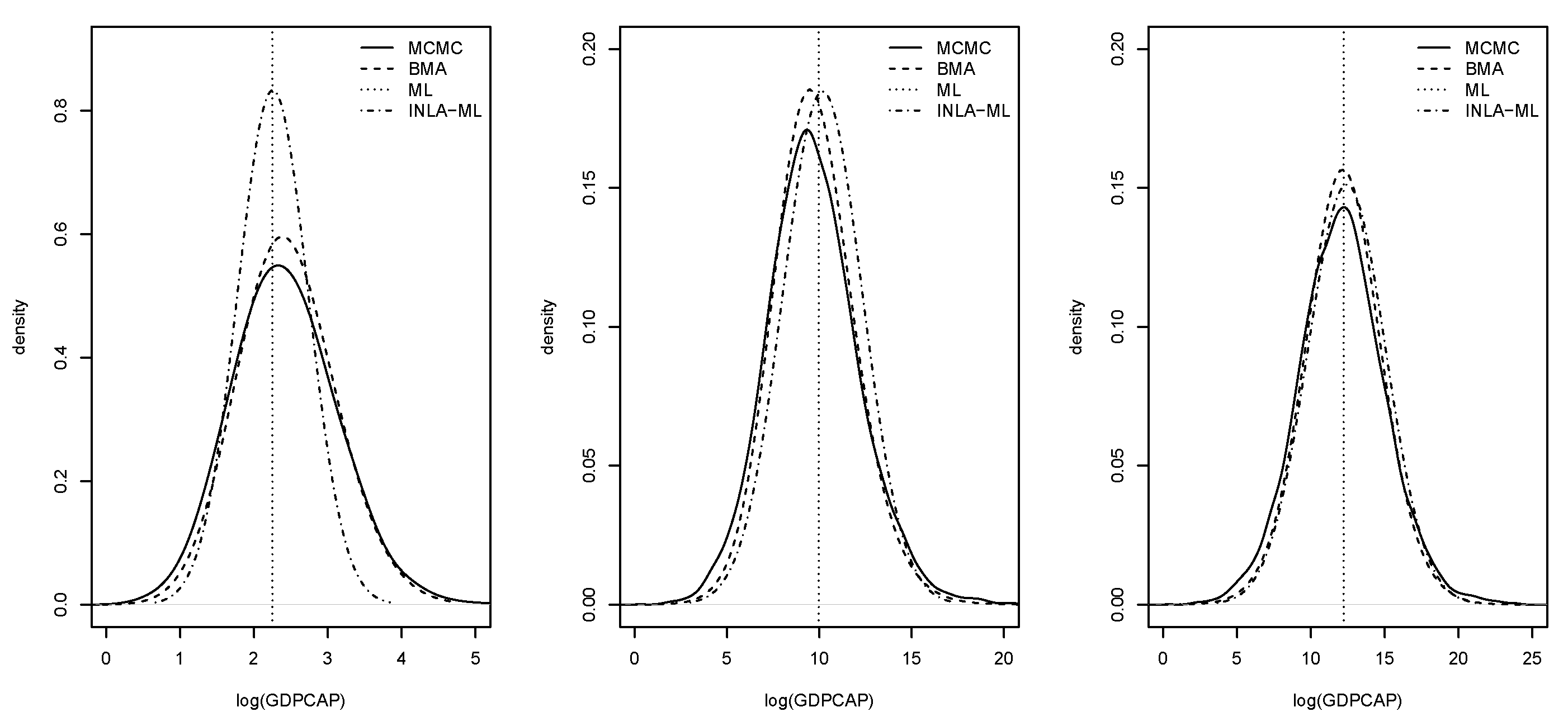
Table 2 shows the estimates of the different average impacts. In general, all estimation methods provided very similar values of the point estimates, and BMA with INLA and MCMC estimates were very close.
Figure 6 displays the posterior marginal distributions of the average impacts. Again, these estimates were very similar among estimation methods.
Finally, the two models fit to the data could also be averaged to account for the model uncertainty. Note that this resembled the typical use of BMA as the models were not exactly the same and included different terms (i.e., covariates in this case). The marginals of the common effects could be averaged by weighting their marginals as seen in
Section 4, where the weights now depended on the corresponding marginal likelihoods of the model. For the effects that only appeared in some of the models, the weights could be computed using only the models where these terms appeared. When averaging marginals for individual effects, the functions in package
INLABMA (
Bivand et al. 2015) can be used.
For this particular example, the marginal log-likelihoods for the model with no covariates and with covariates were −1121.80 and −1143.94, respectively. This made the weights be about one and zero for the common effects and one for the effect of the covariate.
6. Discussion
Bayesian model averaging with the integrated nested Laplace approximation was illustrated to make inference about the parameters and latent effects of highly parameterized models. The appeal of this methodology was that it relaxed the constraints on the model, which did not need to be latent GMRF anymore, but conditional latent GMRF. This was laid out with an example based on spatial econometrics models.
The different models that were averaged appeared because of a discretization of a subset of the hyperparameters, which were assumed fixed when the models were fit. Hence, the structure of the model did not change, but the values of some hyperparameters did. By combining the different models using BMA, these hyperparameters were integrated out and their uncertainty accounted for. However, the joint posterior of this subset of the hyperparameters could be obtained, which allowed us to make multivariate posterior inference. This was different from a typical BMA, where models with different latent effects are considered, but this was also possible with INLA once the desired models were fit.
Less expensive alternatives to BMA include setting the values of a subset of the hyperparameters to their posterior modes or maximum likelihood estimates. This could still produce accurate estimates of the posterior marginals of the remainder of the parameters in the model (
Gómez-Rubio and Palmí-Perales 2019), but ignored the uncertainty about some parameters in the model, as well as any posterior inference about them.
Although we used numerical integration methods to estimate the joint posterior distribution of the conditioning hyperparameters, this was limited to low dimensions and may not scale well. However, other approaches could be used such as MCMC algorithms (
Gómez-Rubio and Rue 2018).
Finally, BMA with INLA made inference about a small subset of hyperparameters in the model possible. This was an interesting feature as INLA focused on marginal inference, and joint posterior analysis required sampling from the internal representation of the latent field (
Gómez-Rubio 2020), which could be costly. We also showed how this could be used to compute the posterior marginal distributions of derived quantities (i.e., the impacts) that depended on a small subset of hyperparameters. Our results with BMA with INLA were very close to those obtained with MCMC, which supported the use of BMA with INLA as a feasible alternative for multivariate posterior inference.