Macroeconomic Forecasting with Factor-Augmented Adjusted Band Regression
Abstract
1. Introduction
2. Methods
2.1. Simple Linear Forecast
2.2. Selecting Factors for Prediction
2.3. Using Factors for Prediction
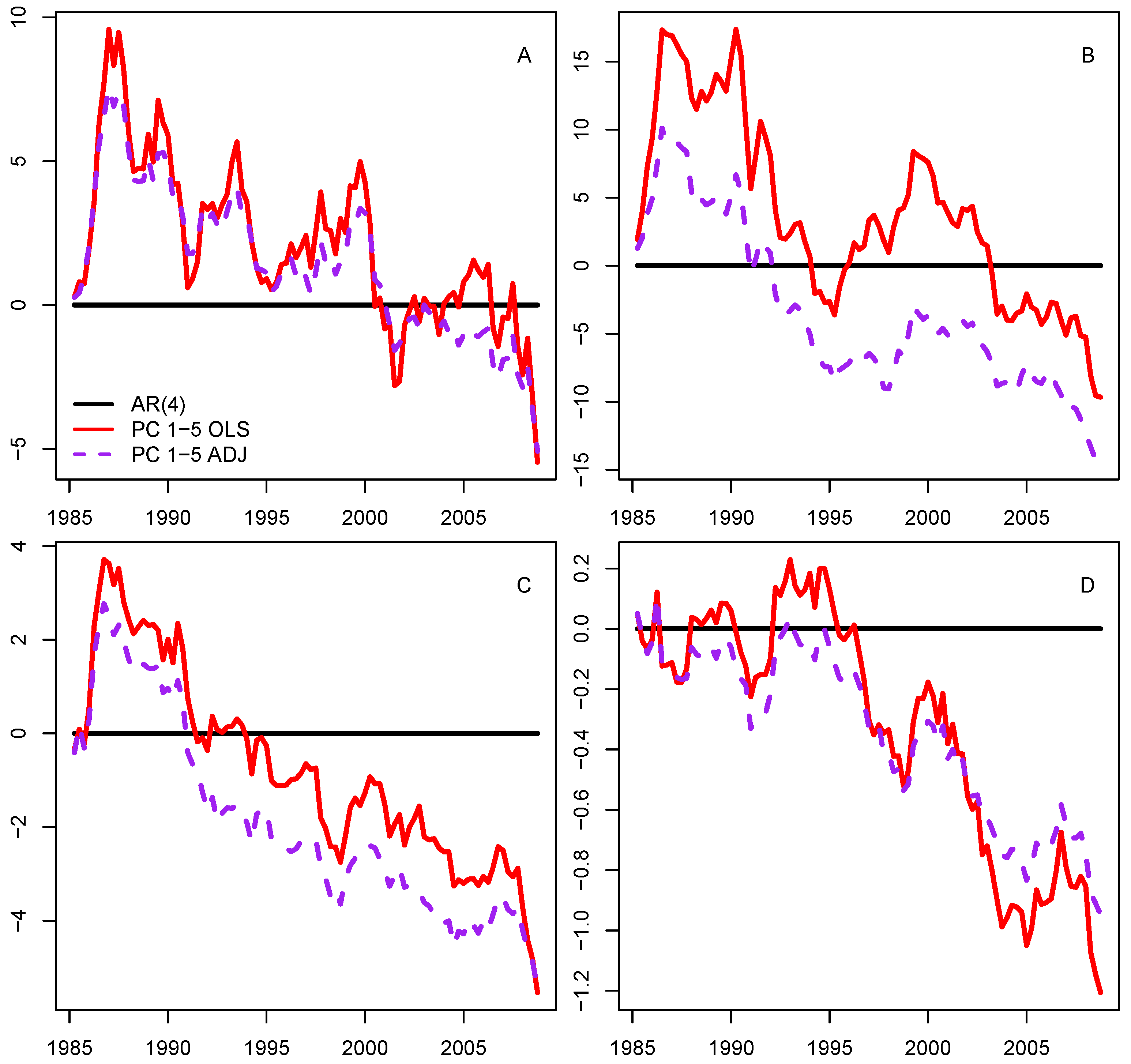
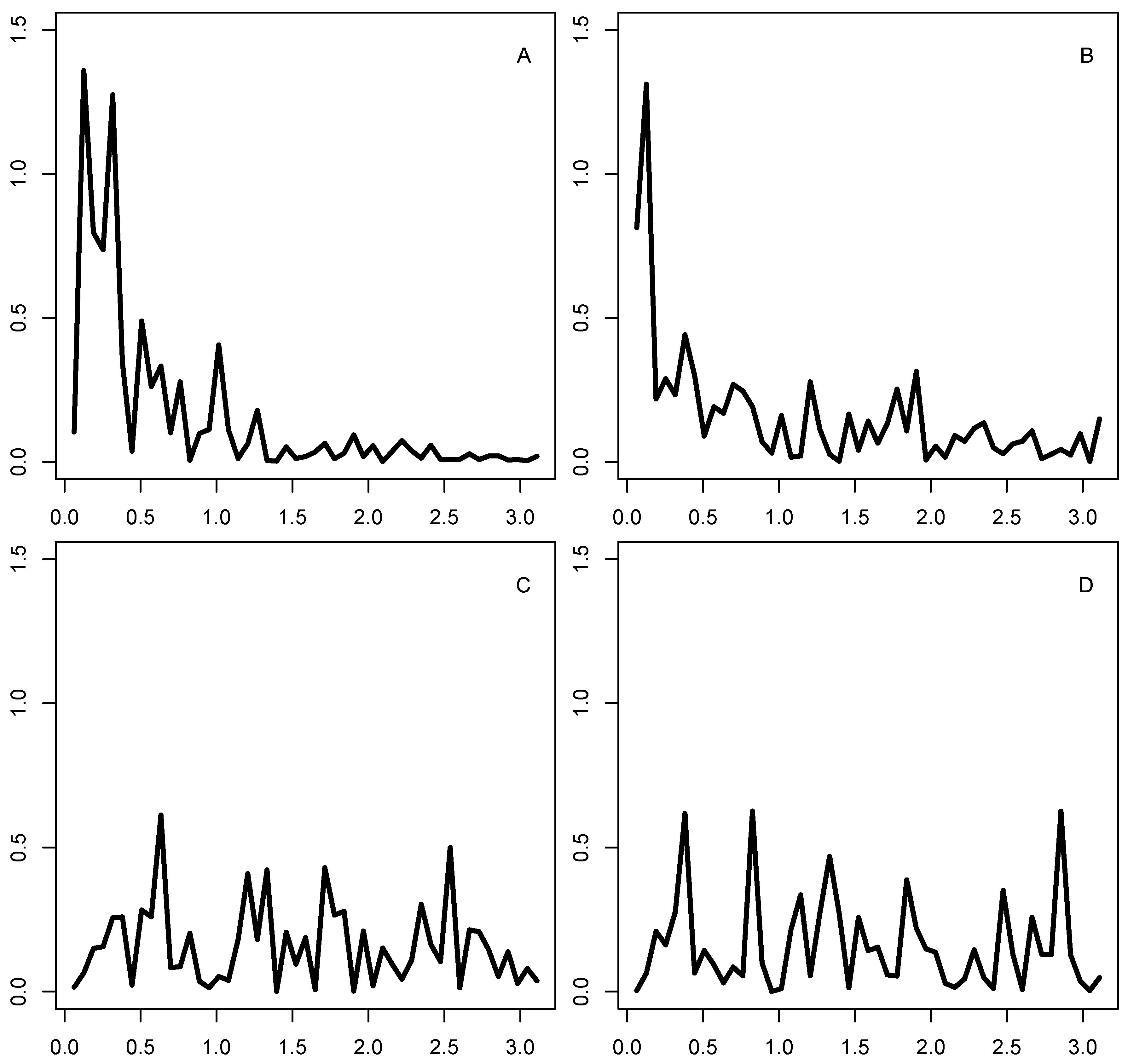
2.4. Adjusting Factor Prediction with Frequency-Band Filter
3. Empirical Results
3.1. Data and Transformations
3.2. Forecasting the Major Measures of Economic Activity
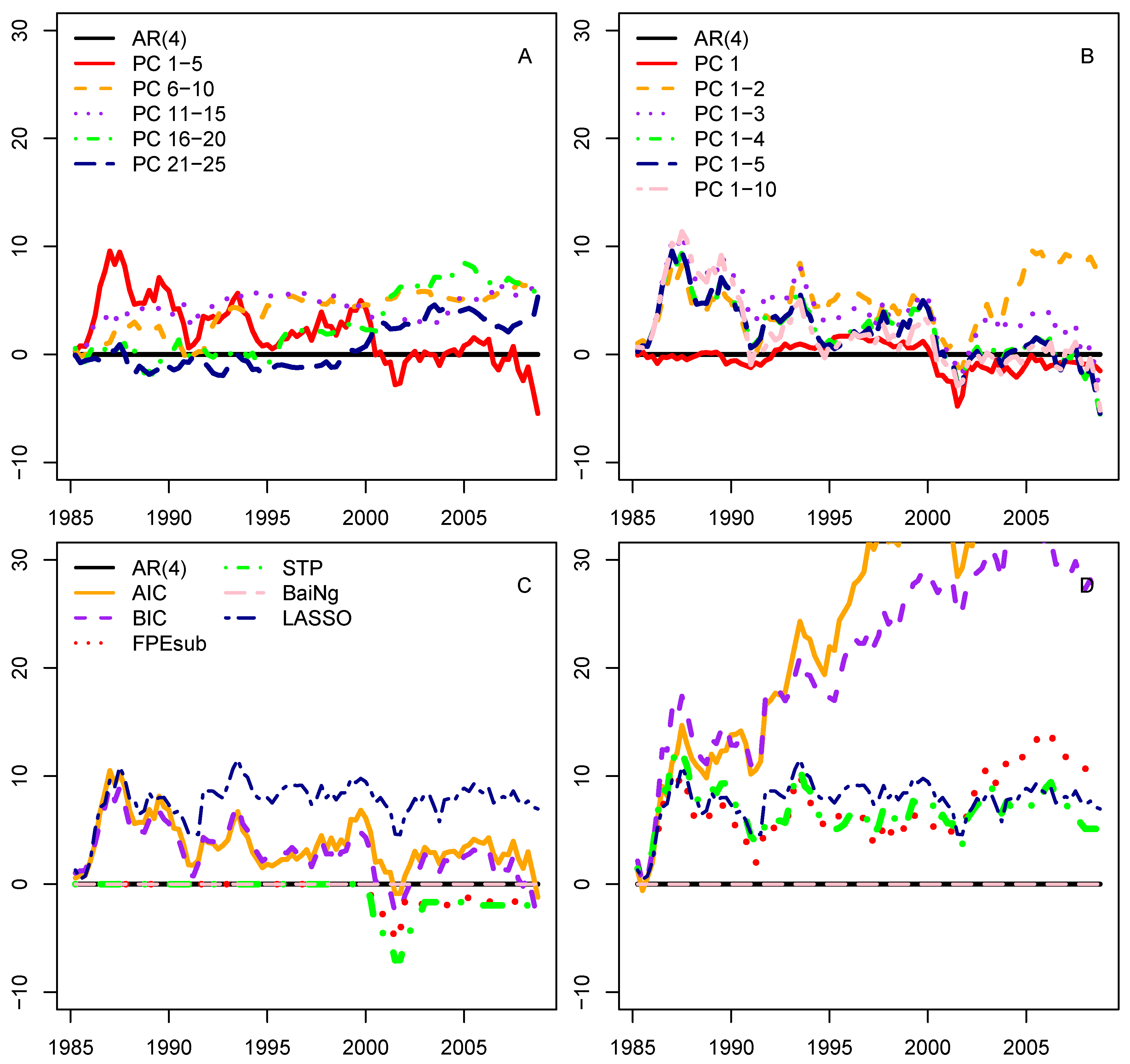
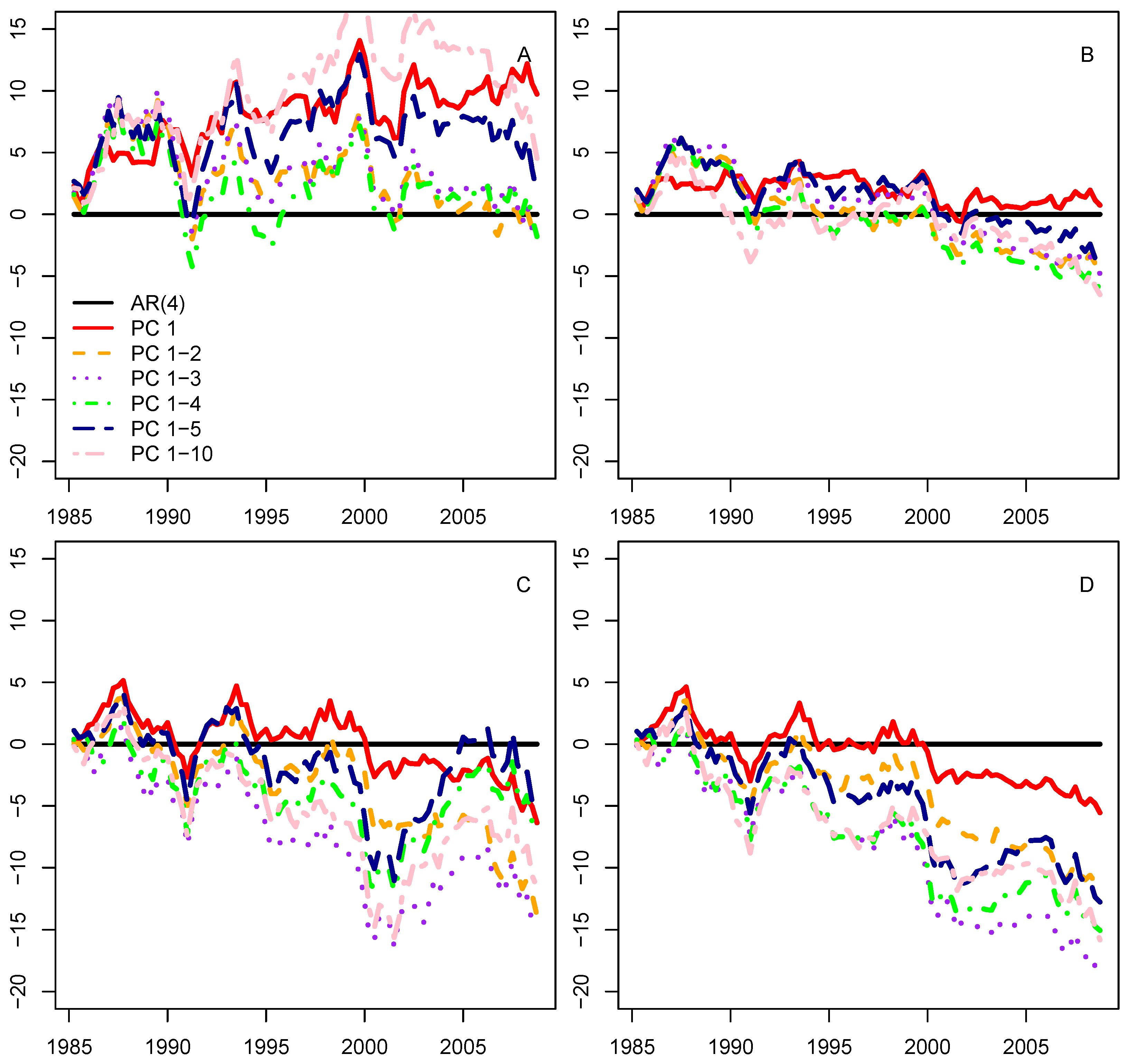
3.3. Selecting the Predictors
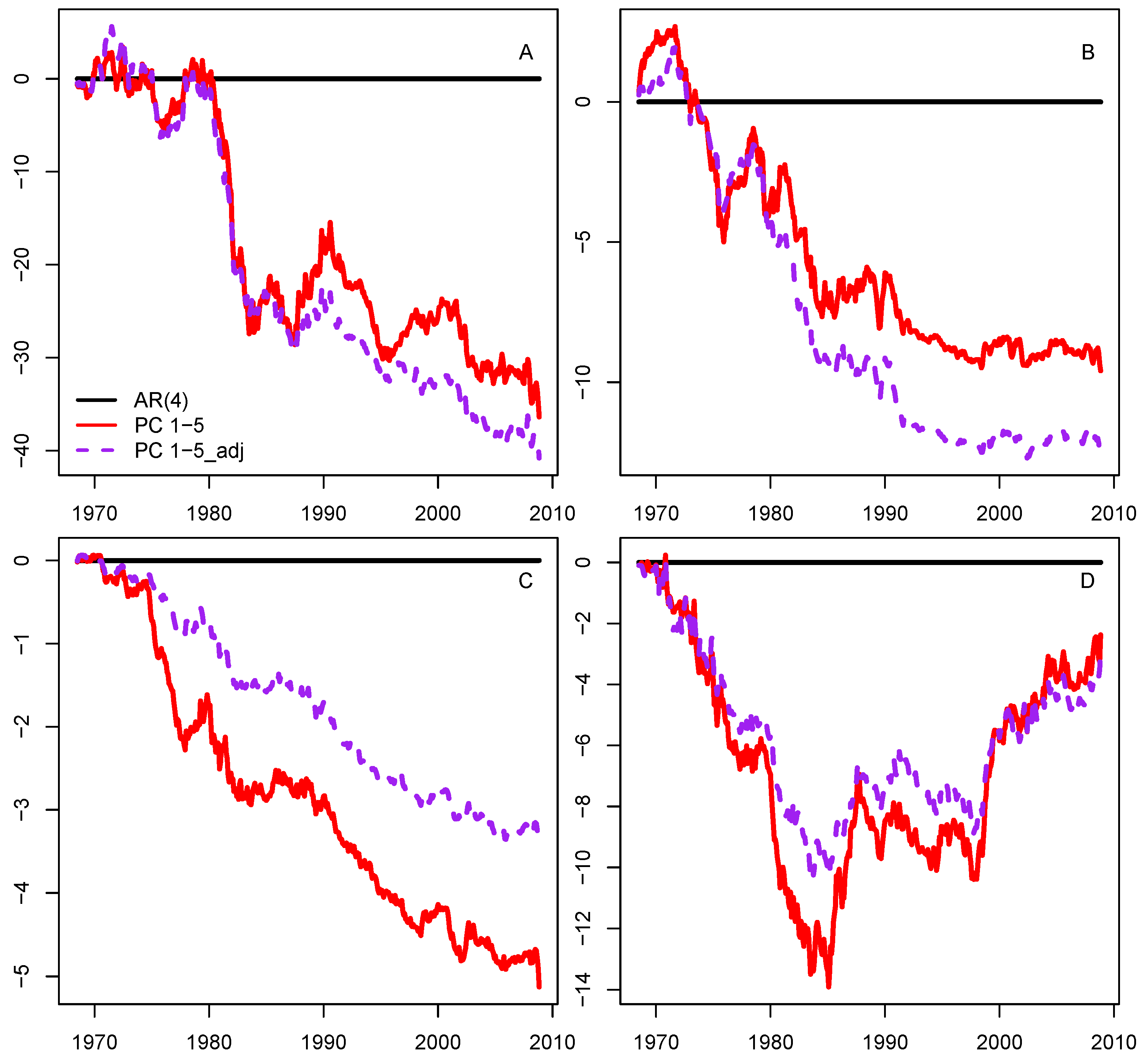
3.4. Using Frequency-Domain Information in Case of Small Subsets of Predictors
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Akaike, H. 1969. Fitting autoregressive models for prediction. Annals of the institute of Statistical Mathematics 21: 243–47. [Google Scholar] [CrossRef]
- Akaike, H. 1998. Information Theory and an Extension of the Maximum Likelihood Principle. New York: Springer, pp. 199–213. [Google Scholar]
- Altissimo, F., R. Cristadoro, M. Forni, M. Lippi, and G. Veronese. 2010. New eurocoin: Tracking economic growth in real time. The Review of Economics and Statistics 92: 1024–34. [Google Scholar] [CrossRef]
- Bai, J., and S. Ng. 2002. Determining the number of factors in approximate factor models. Econometrica 70: 191–221. [Google Scholar] [CrossRef]
- Bai, J., and S. Ng. 2006. Evaluating latent and observed factors in macroeconomics and finance. Journal of Econometrics 131: 507–37. [Google Scholar] [CrossRef]
- Bai, J., and S. Ng. 2008a. Forecasting economic time series using targeted predictors. Journal of Econometrics 146: 304–17. [Google Scholar] [CrossRef]
- Bai, J., and S. Ng. 2008b. Large dimensional factor analysis. Foundations and Trends in Econometrics 3: 89–163. [Google Scholar] [CrossRef]
- Chen, L., J. J. Dolado, and J. Gonzalo. 2014. Detecting big structural breaks in large factor models. Journal of Econometrics 180: 30–48. [Google Scholar] [CrossRef]
- Cheng, X., and B. Hansen. 2015. Forecasting with factor-augmented regression: A frequentist model averaging approach. Journal of Econometrics 186: 280–93. [Google Scholar] [CrossRef]
- Connor, G., and R. A. Korajczyk. 1993. A test for the number of factors in an approximate factor model. The Journal of Finance 48: 1263–91. [Google Scholar] [CrossRef]
- Eickmeier, S., and C. Ziegler. 2008. How successful are dynamic factor models at forecasting output and inflation? A meta-analytic approach. Journal of Forecasting 27: 237–65. [Google Scholar] [CrossRef]
- Engle, R. F. 1974. Band spectrum regression. International Economic Review 15: 1–11. [Google Scholar] [CrossRef]
- Forni, M., M. Hallin, M. Lippi, and L. Reichlin. 2000. The generalized dynamic-factor model: Identification and estimation. The Review of Economics and Statistics 82: 540–54. [Google Scholar] [CrossRef]
- Foster, D., and E. George. 1994. The risk inflation criterion for multiple regression. Annals of Statistics 22: 1947–75. [Google Scholar] [CrossRef]
- George, E., and D. Foster. 2000. Calibration and empirical bayes variable selection. Biometrika 87: 731–47. [Google Scholar] [CrossRef]
- Hannan, E. 1963. Regression for time series. In Proceedings of the Symposium on Time Series Analysis. Edited by M. Rosenblatt. New York: John Wiley and Sons Inc., pp. 14–37. [Google Scholar]
- Johnson, N. L., D. Rothman, R. G. Krutchkoff, P. A. Lachenbruch, and R. R. Hocking. 1968. Letters to the editor. Technometrics 10: 423. [Google Scholar]
- Kim, H. H., and N. R. Swanson. 2014. Forecasting financial and macroeconomic variables using data reduction methods: New empirical evidence. Journal of Econometrics 178: 352–67. [Google Scholar] [CrossRef]
- Müller, U., and M. Watson. 2016. Measuring uncertainty about long-run predictions. Review of Economic Studies 83: 1711–40. [Google Scholar] [CrossRef]
- Phillips, P. B. C. 1991. Spectral regression for co-integrated time series. In Nonparametric and Semiparametric Methods in Economics and Statistics. Edited by W. Barnett, J. Powell and G. Tauchen. Cambridge: Cambridge University Press. [Google Scholar]
- Reschenhofer, E. 2004. On subset selection and beyond. Advances and Applications of Statistics 4: 265–86. [Google Scholar]
- Reschenhofer, E. 2010. Discriminating between non-nested models. Far East Journal of Theoretical Statistics 31: 117–33. [Google Scholar]
- Reschenhofer, E. 2015. Consistent variable selection in large regression models. Journal of Statistics: Advances in Theory and Applications 14: 49–67. [Google Scholar]
- Reschenhofer, E., and M. Chudy. 2015a. Adjusting band-regression estimators for prediction: Shrinkage and downweighting. International Journal of Econometrics and Financial Management 3: 121–30. [Google Scholar]
- Reschenhofer, E., and M. Chudy. 2015b. Imposing frequency-domain restrictions on time-domain forecasts. Journal of Statistical and Econometric Methods 4: 1–16. [Google Scholar]
- Reschenhofer, E., D. Preinerstorfer, and L. Steinberger. 2013. Non-monotonic penalizing for the number of structural breaks. Computational Statistics 28: 2585–98. [Google Scholar] [CrossRef]
- Reschenhofer, E., M. Schilde, E. Oberecker, E. Payr, H. Tandogan, and L. Wakolbinger. 2012. Identifying the determinants of foreign direct investment: A data-specific model selection approach. Statistical Papers 53: 739–52. [Google Scholar] [CrossRef]
- Schwarz, G. 1978. Estimating the dimension of a model. The Annals of Statistics 6: 461–64. [Google Scholar] [CrossRef]
- Stock, J., and M. W. Watson. 2009. Forecasting in Dynamic Factor Models Subject to Structural Instability. Oxford: Oxford University Press, pp. 1–57. [Google Scholar]
- Stock, J., and M. Watson. 2012. Generalised shrinkage methods for forecasting using many predictors. Journal of Business and Economic Statistics 30: 482–93. [Google Scholar] [CrossRef]
- Stock, J., and Mark W. Watson. 2002. Forecasting using principal components from a large number of predictors. Journal of the American Statistical Association 97: 1167–79. [Google Scholar] [CrossRef]
- Tibshirani, R. 1996. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological) 58: 267–88. [Google Scholar] [CrossRef]
- Tibshirani, R., and K. Knight. 1999. The covariance inflation criterion for adaptive model selection. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 61: 529–46. [Google Scholar] [CrossRef]
| 1. | |
| 2. | The tuning parameter , which controls for the parsimonity of the LASSO procedure, is selected by leave-one-out cross validation at each rolling iteration. |
| 3. | Note that in Section 3.3, we use LASSO for selecting the factors, whereas here we use LASSO for preselecting the predictors. |
| Ordinary Least Squares | Adjusted-Band-Regression | |||
|---|---|---|---|---|
| Group | RMSPE | RMAPE | RMSPE | RMAPE |
| GDP | 0.915 | 0.965 | 0.926 | 0.968 |
| IP | 0.971 | 0.959 | 0.940 | 0.939 |
| Employment | 0.906 | 0.919 | 0.919 | 0.920 |
| Unemployment | 0.884 | 0.911 | 0.919 | 0.930 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chudý, M.; Reschenhofer, E. Macroeconomic Forecasting with Factor-Augmented Adjusted Band Regression. Econometrics 2019, 7, 46. https://doi.org/10.3390/econometrics7040046
Chudý M, Reschenhofer E. Macroeconomic Forecasting with Factor-Augmented Adjusted Band Regression. Econometrics. 2019; 7(4):46. https://doi.org/10.3390/econometrics7040046
Chicago/Turabian StyleChudý, Marek, and Erhard Reschenhofer. 2019. "Macroeconomic Forecasting with Factor-Augmented Adjusted Band Regression" Econometrics 7, no. 4: 46. https://doi.org/10.3390/econometrics7040046
APA StyleChudý, M., & Reschenhofer, E. (2019). Macroeconomic Forecasting with Factor-Augmented Adjusted Band Regression. Econometrics, 7(4), 46. https://doi.org/10.3390/econometrics7040046





