Heteroskedasticity in One-Way Error Component Probit Models
Abstract
1. Introduction
2. Heteroskedasticity and Likelihood Function
2.1. Different Sources of Heteroskedasticity
- Heteroskedasticity a la Mazodier and Trognon (1978): The heteroskedasticity is due to the individual effects. Thus, and .
2.2. Likelihood Function
3. Estimation and Tests
3.1. Estimation Requirements
3.2. Test Procedure
4. Monte Carlo Experiments
4.1. Power and Empirical Size of the Test
4.2. Bias and Mean Square Error of the Estimates
4.3. Robustness of Validity
5. Additional Robustness Checks
5.1. Application Examples and Comparisons
5.2. Quadrature Points Check
5.3. Misspecified Heteroskedasticity: Effects of Applying the Wrong Approach
6. Case Study
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. STATA Code for Computing the Marginal Effects

Appendix B. STATA Code for Generating the Dataset

Appendix C. STATA Code for Monte Carlo Experiments
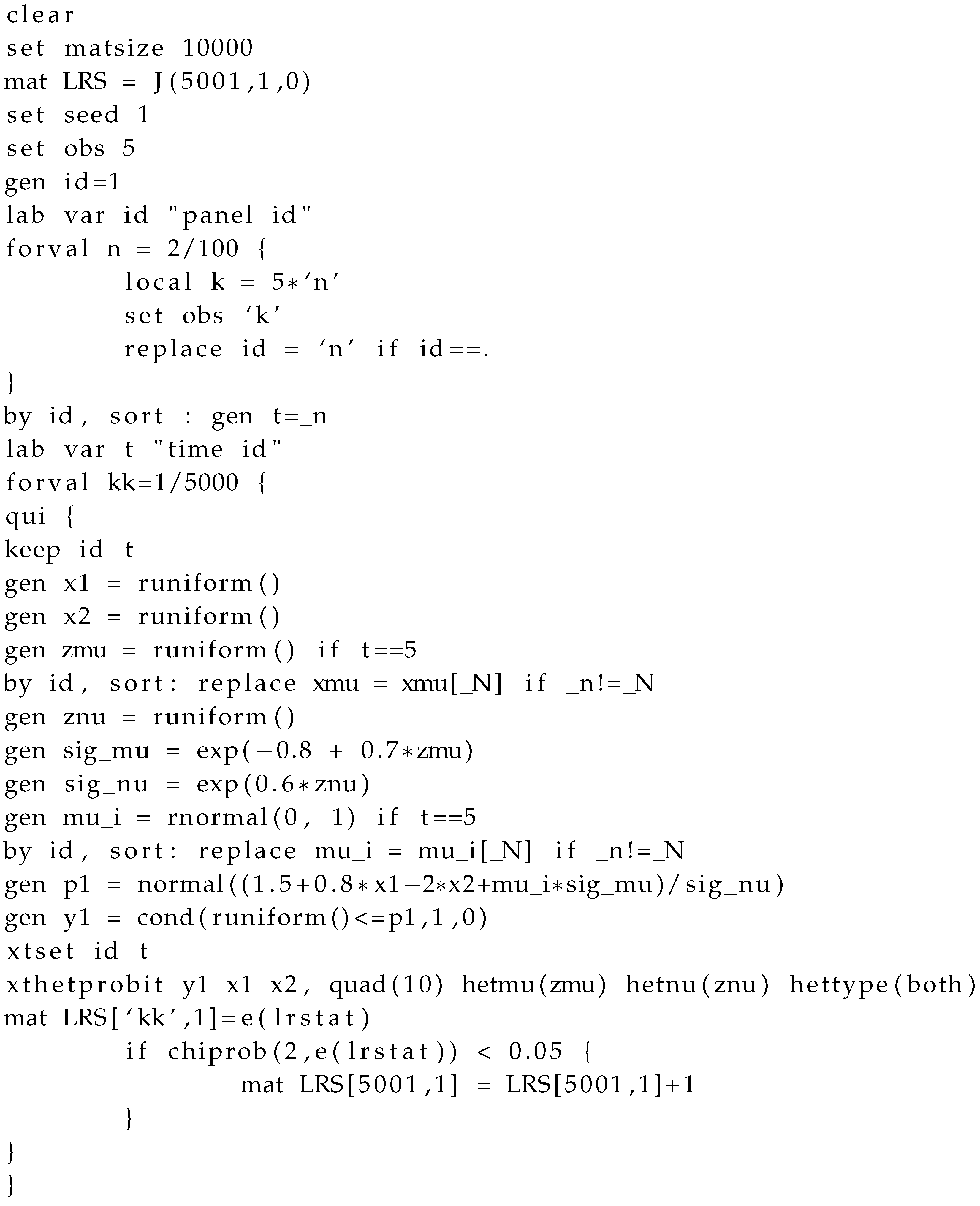
Appendix D. Power of the Test for Different Degrees of Heteroskedasticity
Appendix D.1. Testing for the Joint Hypothesis
| Setting | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 4.48 | 4.88 | 4.44 | 5.42 | 5.58 | 5.52 | 5.6 | 5.6 |
| 0 | 1 | 12.68 | 91.24 | 99.48 | 100 | 6.6 | 92.24 | 98.42 | 100 |
| 0 | 2 | 35.88 | 99.92 | 100 | 100 | 31.84 | 100 | 100 | 100 |
| 0 | 3 | 50.22 | 99.94 | 100 | 100 | 38.42 | 100 | 100 | 100 |
| 1 | 0 | 22.08 | 39.08 | 99.48 | 100 | 13.36 | 29.3 | 98.46 | 100 |
| 1 | 1 | 26.56 | 97.56 | 100 | 100 | 14.46 | 90.04 | 99.6 | 100 |
| 1 | 2 | 46.36 | 100 | 100 | 100 | 49.26 | 100 | 100 | 100 |
| 1 | 3 | 45.78 | 100 | 100 | 100 | 62.56 | 100 | 100 | 100 |
| 2 | 0 | 30.79 | 72.34 | 100 | 100 | 21.08 | 43.12 | 100 | 100 |
| 2 | 1 | 54.14 | 99.26 | 100 | 100 | 23.08 | 75.34 | 100 | 100 |
| 2 | 2 | 78.28 | 100 | 100 | 100 | 65.62 | 100 | 100 | 100 |
| 2 | 3 | 79.28 | 100 | 100 | 100 | 87.06 | 100 | 100 | 100 |
| 3 | 0 | 50.92 | 73.8 | 100 | 100 | 30.08 | 58.46 | 100 | 100 |
| 3 | 1 | 59.52 | 96.88 | 100 | 100 | 37.72 | 56.46 | 100 | 100 |
| 3 | 2 | 90.3 | 100 | 100 | 100 | 57.88 | 99.92 | 100 | 100 |
| 3 | 3 | 95.46 | 100 | 100 | 100 | 93.8 | 100 | 100 | 100 |
Appendix D.2. Testing for the Marginal Hypothesis of No Heteroskedasticity in Individual Effects Given Homoskedastic Idiosyncratic Errors
| Setting | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 5.26 | 5.46 | 5.06 | 5.02 | 4.42 | 5.08 | 4.76 | 4.72 | |
| 1 | 24.86 | 47.12 | 99.54 | 100 | 5.88 | 15.76 | 77.84 | 98.68 | |
| 2 | 35.16 | 71.7 | 100 | 100 | 6.22 | 17.68 | 90.52 | 100 | |
| 3 | 29.14 | 64.98 | 100 | 100 | 4.94 | 15.28 | 99.32 | 100 | |
| 0 | 5.26 | 5.46 | 5.06 | 5.02 | 4.42 | 5.08 | 4.76 | 4.72 | |
| 1 | 5.78 | 5.46 | 5.56 | 4.74 | 5.06 | 4.82 | 4.72 | 4.4 | |
| 2 | 5.26 | 5.06 | 5.58 | 4.46 | 5.56 | 4.62 | 5.02 | 4.42 | |
| 3 | 5.12 | 4.94 | 4.96 | 4.44 | 5.44 | 4.74 | 4.92 | 4.42 | |
| 0 | 0 | 5.26 | 5.46 | 5.06 | 5.02 | 4.42 | 5.08 | 4.76 | 4.72 |
| 0 | 1 | 5.78 | 5.46 | 5.56 | 4.74 | 5.06 | 4.82 | 4.72 | 4.4 |
| 0 | 2 | 5.26 | 5.06 | 5.58 | 4.46 | 5.56 | 4.62 | 5.02 | 4.42 |
| 0 | 3 | 5.12 | 4.94 | 4.96 | 4.44 | 5.44 | 4.74 | 4.92 | 4.42 |
| 1 | 0 | 24.86 | 47.12 | 99.54 | 100 | 5.88 | 15.76 | 77.84 | 98.68 |
| 1 | 1 | 27.2 | 53.2 | 99.6 | 100 | 15.66 | 34.26 | 96.3 | 100 |
| 1 | 2 | 23.88 | 45.78 | 97.2 | 100 | 22.56 | 42.84 | 98.64 | 100 |
| 1 | 3 | 14 | 33.56 | 79.58 | 100 | 19.08 | 31.72 | 92.44 | 100 |
| 2 | 0 | 35.16 | 71.7 | 100 | 100 | 6.22 | 17.68 | 90.52 | 100 |
| 2 | 1 | 59.46 | 91.98 | 100 | 100 | 24.76 | 59.52 | 100 | 100 |
| 2 | 2 | 67 | 94.98 | 100 | 100 | 55.48 | 89.68 | 100 | 100 |
| 2 | 3 | 52.72 | 89.16 | 100 | 100 | 55.9 | 88.36 | 100 | 100 |
| 3 | 0 | 29.14 | 64.98 | 100 | 100 | 4.94 | 15.28 | 99.32 | 100 |
| 3 | 1 | 66.46 | 95.96 | 100 | 100 | 21.56 | 59.06 | 100 | 100 |
| 3 | 2 | 88.42 | 99.8 | 100 | 100 | 65.1 | 97.06 | 100 | 100 |
| 3 | 3 | 86.9 | 99.66 | 100 | 100 | 83.36 | 99.58 | 100 | 100 |
Appendix D.3. Testing for the Marginal Hypothesis of no Heteroskedasticity in Idiosyncratic Errors Given Homoskedastic Individual Effects
| Setting | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 4.64 | 4.48 | 4.44 | 5.1 | 5.56 | 5.6 | 5.6 | 5.6 | |
| 1 | 20.5 | 95.6 | 99.8 | 100 | 11.12 | 96.62 | 99.5 | 100 | |
| 2 | 54.28 | 99.98 | 100 | 100 | 52.8 | 100 | 100 | 100 | |
| 3 | 66.18 | 99.96 | 100 | 100 | 62.46 | 100 | 100 | 100 | |
| 0 | 4.64 | 4.48 | 4.44 | 5.1 | 5.56 | 5.6 | 5.6 | 5.6 | |
| 1 | 6.6 | 8.2 | 39.06 | 43.18 | 23.96 | 23.98 | 87.02 | 96.4 | |
| 2 | 16.08 | 23.78 | 77.06 | 96.1 | 15.54 | 34.34 | 99.96 | 99.42 | |
| 3 | 25.28 | 29.19 | 97.98 | 98.72 | 24.58 | 49.7 | 99.96 | 100 | |
| 0 | 0 | 4.64 | 4.48 | 4.44 | 5.1 | 5.56 | 5.6 | 5.6 | 5.6 |
| 0 | 1 | 20.5 | 95.6 | 99.8 | 100 | 11.12 | 96.62 | 99.5 | 100 |
| 0 | 2 | 54.28 | 99.98 | 100 | 100 | 52.8 | 100 | 100 | 100 |
| 0 | 3 | 66.18 | 99.96 | 100 | 100 | 62.46 | 100 | 100 | 100 |
| 1 | 0 | 6.6 | 8.2 | 39.06 | 43.18 | 23.96 | 23.98 | 87.02 | 96.4 |
| 1 | 1 | 11.52 | 96.46 | 99.54 | 100 | 34.2 | 87.7 | 84.38 | 100 |
| 1 | 2 | 50.92 | 100 | 100 | 100 | 53.16 | 100 | 100 | 100 |
| 1 | 3 | 60.96 | 100 | 100 | 100 | 76.9 | 100 | 100 | 100 |
| 2 | 0 | 16.08 | 23.78 | 77.06 | 96.1 | 15.54 | 34.34 | 99.96 | 99.42 |
| 2 | 1 | 24.22 | 86.38 | 91.18 | 100 | 25.24 | 50.28 | 100 | 100 |
| 2 | 2 | 45.94 | 100 | 100 | 100 | 34.06 | 99.98 | 100 | 100 |
| 2 | 3 | 70.08 | 100 | 100 | 100 | 78.88 | 100 | 100 | 100 |
| 3 | 0 | 25.28 | 29.19 | 97.98 | 98.72 | 24.58 | 49.7 | 99.96 | 100 |
| 3 | 1 | 33.71 | 56.64 | 98.04 | 99.92 | 32.36 | 59.6 | 100 | 100 |
| 3 | 2 | 48.88 | 99.98 | 100 | 100 | 51.34 | 99.32 | 100 | 100 |
| 3 | 3 | 67.52 | 100 | 100 | 100 | 65.98 | 100 | 100 | 100 |
Appendix E. Application and Comparisons
Appendix E.1. Application and Comparison for Data Generated with Individual Effects Heteroskedastic
| Variables | Homoskedastic | Heteroskedastic | Heteroskedastic | |
|---|---|---|---|---|
| Panel Probit | Pooled Probit | Panel Probit | ||
| With | ||||
| *** | 6.2328 ** | |||
| The estimated index function parameters. | ||||
| *** | *** | *** | ||
| *** | *** | *** | ||
| *** | *** | *** | ||
| The variance parameters. | ||||
| *** | ** | |||
| *** | *** | |||
| 1 | 1 | 1 | 1 | |
| With | ||||
| *** | *** | |||
| The estimated index function parameters. | ||||
| *** | *** | *** | ||
| *** | *** | *** | ||
| *** | *** | *** | ||
| The variance parameters. | ||||
| *** | *** | |||
| *** | *** | |||
| 1 | 1 | 1 | 1 | |
Appendix E.2. Application and Comparison for Data Generated with Idiosyncratic Errors Heteroskedastic
| Variables | Homoskedastic | Heteroskedastic | Heteroskedastic | |
|---|---|---|---|---|
| Panel Probit | Pooled Probit | Panel Probit | ||
| With | ||||
| 5.99 ** | *** | |||
| The estimated index function parameters. | ||||
| *** | *** | *** | ||
| *** | *** | *** | ||
| *** | *** | *** | ||
| The variance parameters. | ||||
| *** | *** | |||
| *** | *** | |||
| With | ||||
| *** | *** | |||
| The estimated index function parameters. | ||||
| *** | *** | *** | ||
| *** | *** | *** | ||
| *** | *** | *** | ||
| The variance parameters. | ||||
| *** | *** | |||
| *** | *** | |||
Appendix E.3. Application and Comparison for Data Generated with Both Individual Effects and Idiosyncratic Heteroskedastic
| Variables | Homoskedastic | Heteroskedastic | Heteroskedastic | |
|---|---|---|---|---|
| Panel Probit | Pooled Probit | Panel Probit | ||
| With | ||||
| *** | *** | |||
| The estimated index function parameters. | ||||
| *** | *** | *** | ||
| *** | *** | *** | ||
| *** | *** | *** | ||
| The variance parameters. | ||||
| ** | ||||
| *** | *** | |||
| *** | *** | |||
| With | ||||
| *** | *** | |||
| The estimated index function parameters. | ||||
| *** | *** | *** | ||
| *** | *** | *** | ||
| *** | *** | *** | ||
| The variance parameters. | ||||
| * | *** | |||
| *** | *** | |||
| *** | *** | |||
Appendix F. Estimates for Different Numbers of Quadrature Points
| Variables | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| *** | *** | *** | *** | *** | *** | *** | *** | ||
| *** | *** | *** | *** | *** | *** | *** | *** | ||
| *** | *** | *** | *** | *** | *** | *** | *** | ||
| *** | *** | *** | *** | *** | *** | *** | *** | ||
| *** | *** | *** | *** | *** | *** | *** | *** | ||
| *** | *** | *** | *** | *** | *** | *** | *** | ||
| 41 | 53 | 62 | 79 | 96 | 106 | 130 | 133 |
References
- Baltagi, Badi H. 1988. An alternative heteroscedastic error component model, problem 88.2.2. Econometric Theory 4: 349–50. [Google Scholar] [CrossRef]
- Baltagi, Badi H. 2008. Econometric Analysis of Panel Data, 4th ed. Hoboken: John Wiley & Sons. [Google Scholar]
- Baltagi, Badi H., Georges Bresson, and Alain Pirotte. 2006. Joint lm test for homoskedasticity in a one-way error component model. Journal of Econometrics 134: 401–17. [Google Scholar] [CrossRef][Green Version]
- Bland, James R., and Amanda C. Cook. 2018. Random effects probit and logit: understanding predictions and marginal effects. Applied Economics Letters 26: 116–23. [Google Scholar] [CrossRef]
- Davidson, Russell, and James G. MacKinnon. 1984. Convenient specification tests for logit and probit models. Journal of Econometrics 25: 241–62. [Google Scholar] [CrossRef]
- Gould, William, Jeffrey Pitblado, and William Sribney. 2010. Maximum Likelihood Estimation With Stata, 4th ed. College Station: Stata Press. [Google Scholar]
- Greene, William H. 2012. Econometric Analysis, 7th ed. Upper Saddle Rive: Prentice Hall. [Google Scholar]
- Greene, William H. 2018. Econometric Analysis, 8th ed. New York: Pearson. [Google Scholar]
- Johnston, John, and John DiNardo. 2001. Econometric Methods, 4th ed. New York: The McGraw-Hill Companies. [Google Scholar]
- Lancaster, Tony. 2000. The incidental parameter problem since 1948. Journal of Econometrics 95: 391–413. [Google Scholar] [CrossRef]
- Lechner, Michael. 1995. Some specification tests for probit models estimated on panel data. Journal of Business and Economic Statistics 13: 475–88. [Google Scholar] [CrossRef]
- Liu, Qing, and Donald A. Pierce. 1994. A note on gauss-hermite quadrature. Biometrika 83: 624–29. [Google Scholar] [CrossRef]
- Mazodier, Pascal, and Alain Trognon. 1978. Heteroskedasticity and stratification in error components models. Annales de l’INSEE 30: 451–82. [Google Scholar]
- Montes-Rojas, Gabriel, and Walter Sosa-Escudero. 2011. Robust tests for heteroskedasticity in the one-way error components model. Journal of Econometrics 160: 300–10. [Google Scholar] [CrossRef]
- Moussa, Richard, and Eric Delattre. 2018. On the estimation of causality in a bivariate dynamic probit model on panel data with stata software. a technical review. Theoretical Economics Letters 8: 1257–78. [Google Scholar] [CrossRef]
- Naylor, Jennifer C., and Adrian F. M. Smith. 1982. Applications of a method for the efficient computation of posterior distributions. Applied Statistics 31: 214–25. [Google Scholar] [CrossRef]
- Randolph, William C. 1988. A transformation for heteroscedastic error components regression models. Economics Letters 27: 349–54. [Google Scholar] [CrossRef]
- Verbon, Harrie. 1980. Testing for heteroscedasticity in a model of seemingly unrelated regression equations with variance components. Economics Letters 5: 149–53. [Google Scholar] [CrossRef]
- Wansbeek, Tom. 1989. An alternative heteroscedastic error components model, solution 88.1.1. Econometric Theory 5: 326. [Google Scholar] [CrossRef]
- Wooldridge, Jeffrey M. 2001. Econometric Analysis of Cross Section and Panel Data. Cambridge: The MIT Press. [Google Scholar]
| 1. | A user-written Stata’s ado file is provided to deal with these purposes. This ado file is an extension of the existing Stata’s and commands that accounts for each of the types of heteroskedasticity observed in panel one-way error component models in the literature. A Stata code for computing the marginal effects after the proposed estimation procedure is given in the Appendix A. |
| 2. | The estimation procedure described above has been implemented as a Stata user-written ado file using the Stata’s procedure for maximum likelihood estimation (see Gould et al. 2010; Moussa and Delattre 2018). |
| 3. | For all others applications presented herein, is used as the number of quadrature points. |
| 4. | An example of the Stata code for the experiment of the power of the test in presence of heteroskedasticity due to both and with and is provided in the Appendix C. The Appendix B reports the Stata code used to generate the data. |
| 5. | The empirical size estimated on 5000 replications is significantly different from the nominal size of 5% if it does not range between 4.4% and 5.6%. These thresholds are calculated as . |
| Settings | ||||
|---|---|---|---|---|
| Dimensions | Obs. | % | % | % |
| Low degree of heteroskedasticity: , and | ||||
| 250 | 12.04 | 23.86 | 14.62 | |
| 500 | 19.88 | 43.32 | 31.68 | |
| 2500 | 69.54 | 97.22 | 96.74 | |
| 500 | 19.9 | 39.74 | 35.16 | |
| 1000 | 34.04 | 65.62 | 64.72 | |
| 5000 | 94.14 | 99.98 | 100 | |
| 1000 | 27.4 | 67.14 | 63.74 | |
| 2000 | 50.58 | 93.2 | 92.94 | |
| 99.26 | 100 | 100 | ||
| High degree of heteroskedasticity: , and | ||||
| 250 | 81.72 | 47.78 | 65.16 | |
| 500 | 98.44 | 85 | 96.2 | |
| 2500 | 100 | 100 | 100 | |
| 500 | 94.72 | 93.7 | 98.12 | |
| 1000 | 98.88 | 99.9 | 99.96 | |
| 5000 | 100 | 100 | 100 | |
| 1000 | 98.36 | 99.98 | 100 | |
| 2000 | 100 | 100 | 100 | |
| 100 | 100 | 100 | ||
| Settings | ||||
|---|---|---|---|---|
| Dimensions | Obs. | % | % | % |
| 250 | 4.82 | 4.98 | 4.54 | |
| 500 | 4.7 | 5.02 | 4.52 | |
| 2500 | 4.64 | 5.34 | 4.68 | |
| 500 | 5.36 | 5.46 | 4.72 | |
| 1000 | 4.54 | 4.74 | 5.14 | |
| 5000 | 4.62 | 4.48 | 4.68 | |
| 1000 | 5.08 | 5.00 | 4.94 | |
| 2000 | 4.92 | 4.48 | 5.04 | |
| 4.58 | 5.54 | 5.04 | ||
| Settings | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | DGP | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE |
| Parameters of the index function | |||||||||
| 0.0009 | 0.2435 | 0.0814 | 0.0554 | 0.0402 | 0.0225 | 0.0606 | 0.0126 | ||
| 0.0040 | 0.2474 | 0.0331 | 0.0474 | 0.0237 | 0.0221 | 0.0400 | 0.0062 | ||
| 0.0072 | 0.4323 | 0.0834 | 0.0814 | 0.0530 | 0.0388 | 0.0909 | 0.0172 | ||
| Parameters of the variances of and | |||||||||
| 0.1683 | 1.5406 | 0.0609 | 0.2058 | 0.0517 | 0.0846 | 0.0407 | 0.0177 | ||
| 0.1660 | 1.1061 | 0.0232 | 0.4044 | 0.0412 | 0.1204 | 0.0353 | 0.0316 | ||
| 0.0721 | 0.2369 | 0.0618 | 0.0447 | 0.0456 | 0.0225 | 0.0301 | 0.0119 | ||
| DGP | |||
|---|---|---|---|
| Normal | 4.82 | 4.98 | 5.54 |
| Student (3) | 6.38 | 7.86 | 8.32 |
| Exponential | 17.56 | 7.18 | 21.36 |
| Uniform | 5.74 | 7.68 | 8.7 |
| Chi-square | 3.24 | 5.8 | 4.5 |
| Case | Heteroskedastic | Heteroskedastic | and Heteroskedastic | |||
|---|---|---|---|---|---|---|
| Model | (1) | (2) | (3) | (4) | (5) | (6) |
| *** | *** | *** | *** | *** | ||
| The variance parameters. | ||||||
| *** | *** | |||||
| *** | *** | *** | *** | |||
| *** | *** | |||||
| *** | *** | *** | ||||
| Model | (1) | (2) | (3) |
|---|---|---|---|
| The variance parameters. | |||
| *** | *** | ||
| *** | |||
| Variables | Homoskedastic Model | Heteroskedastic Model | ||||
|---|---|---|---|---|---|---|
| *** | *** | *** | *** | *** | *** | |
| *** | *** | *** | *** | *** | *** | |
| *** | *** | *** | *** | *** | ||
| *** | ||||||
| The variance parameters: variance of | ||||||
| *** | ||||||
| *** | ||||||
| *** | ||||||
| The variance parameters: variance of | ||||||
| *** | ||||||
| ** | ||||||
| *** | ||||||
| *** | ||||||
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moussa, R.K. Heteroskedasticity in One-Way Error Component Probit Models. Econometrics 2019, 7, 35. https://doi.org/10.3390/econometrics7030035
Moussa RK. Heteroskedasticity in One-Way Error Component Probit Models. Econometrics. 2019; 7(3):35. https://doi.org/10.3390/econometrics7030035
Chicago/Turabian StyleMoussa, Richard Kouamé. 2019. "Heteroskedasticity in One-Way Error Component Probit Models" Econometrics 7, no. 3: 35. https://doi.org/10.3390/econometrics7030035
APA StyleMoussa, R. K. (2019). Heteroskedasticity in One-Way Error Component Probit Models. Econometrics, 7(3), 35. https://doi.org/10.3390/econometrics7030035





