Income Inequality, Cohesiveness and Commonality in the Euro Area: A Semi-Parametric Boundary-Free Analysis
Abstract
:1. Introduction
2. Income Classes and the Gini Coefficient: Inequality, Polarization and Segmentation of Subgroups
2.1. Mixture of Distribution to Identify Income Classes
2.2. The Gini Coefficient and Segmentation of Subgroups
2.3. Comparing Constituent Distributions: Polarization, Transvariation and Utopia-Dystopia Index
2.3.1. Polarization
2.3.2. Transvariation
2.3.3. Utopia-Dystopia
3. Data Issues
4. Empirical Results
4.1. Number of Classes and Estimation of Mixture Parameters in the Community Income Distribution
4.2. Inequality, Polarization and Segmentation in an Income Class Decomposition of the Eurozone Income Distribution
4.3. The Progress of Individual Constituent Nations
5. Concluding Remarks
Author Contributions
Conflicts of Interest
Appendix A
Appendix A.1. Gini Segmentation
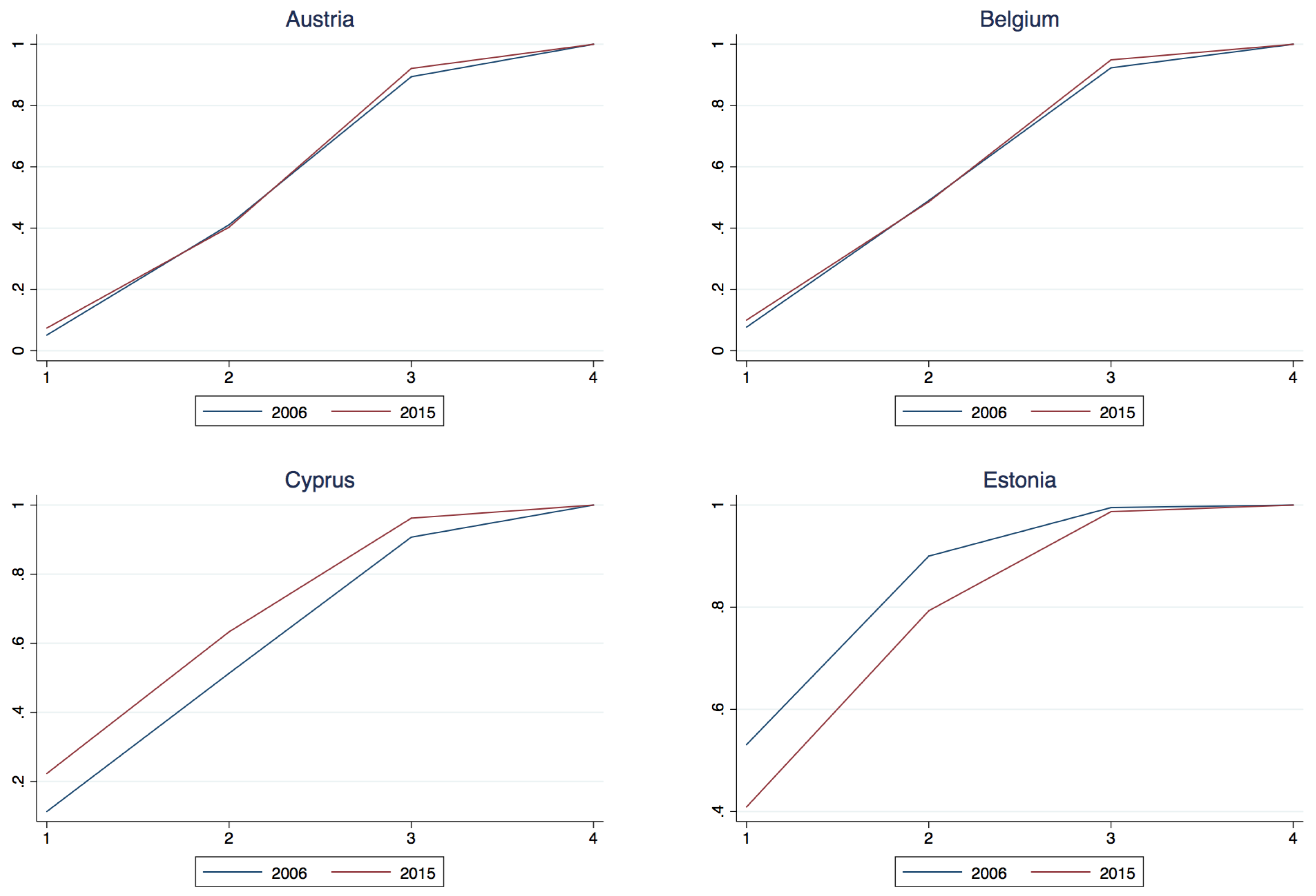
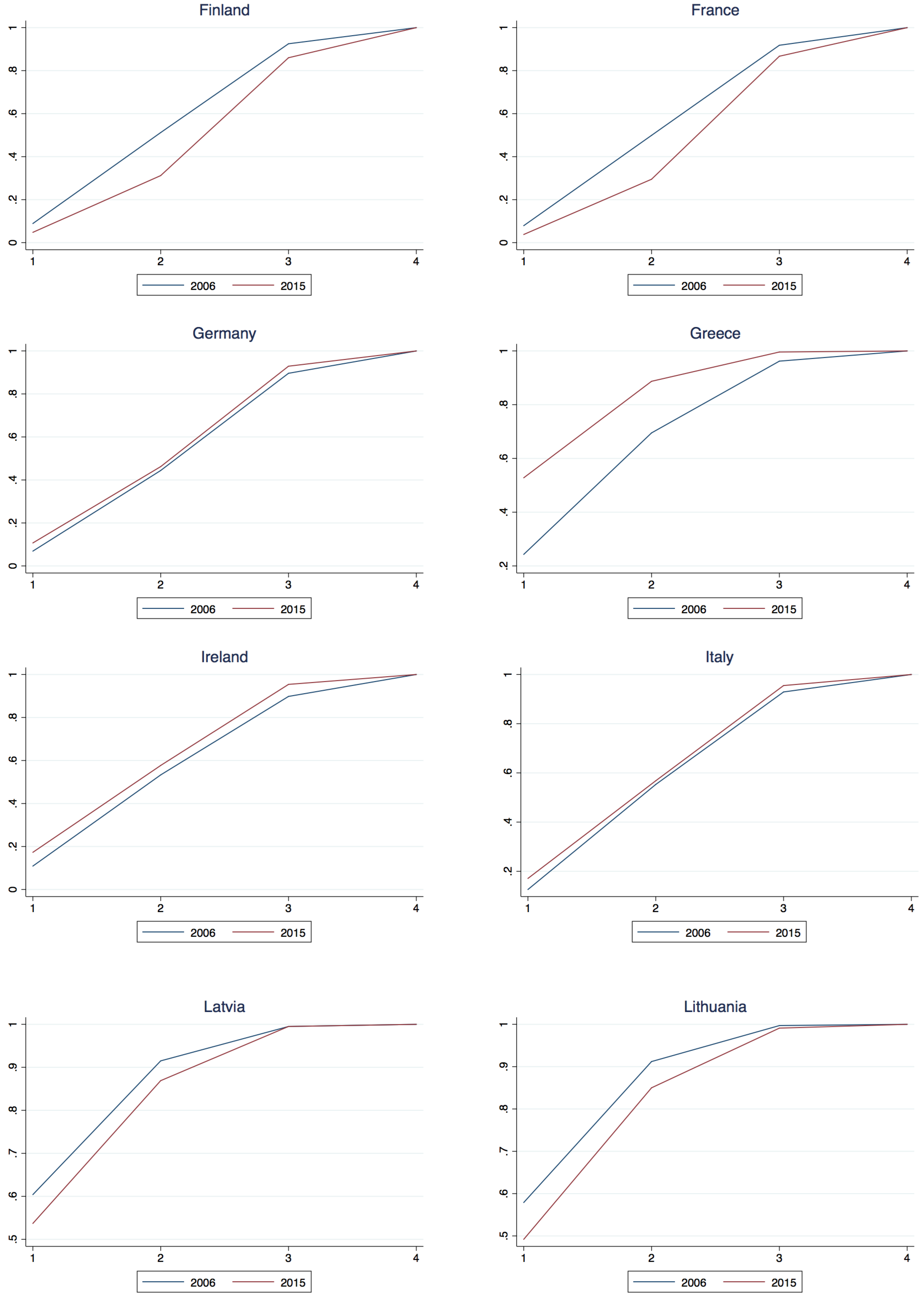
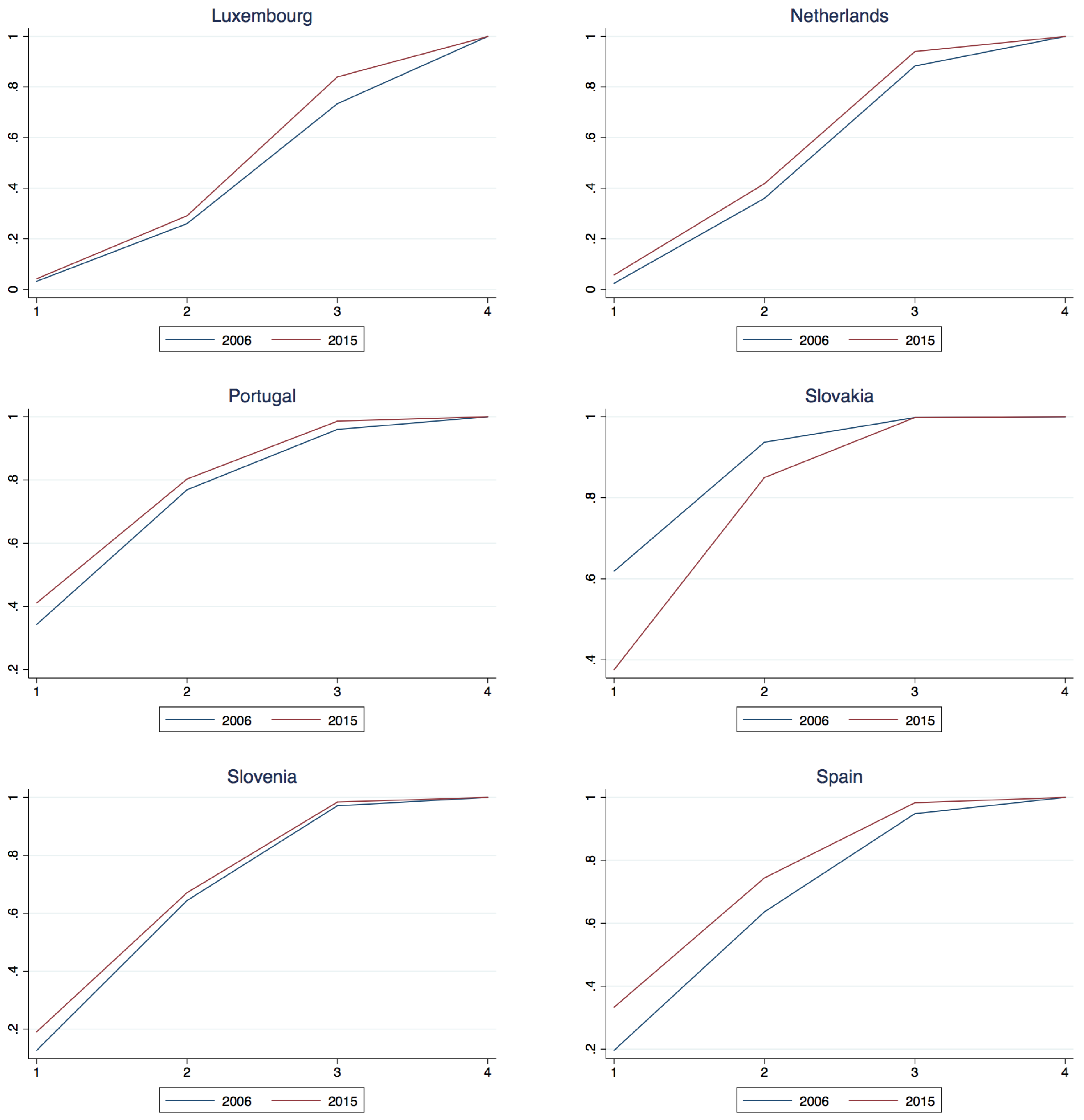
Appendix A.2. National Class Membership Cumulative Density
References
- Anderson, Gordon J. 2010. Polarization of the Poor: Multivariate Relative Poverty Measurement Sans Frontiers. Review of Income and Wealth 56: 84–101. [Google Scholar] [CrossRef]
- Anderson, Gordon J., Alessio Farcomeni, Maria Grazia Pittau, and Roberto Zelli. 2016. A new approach to measuring and studying the characteristics of class membership: The progress of poverty, inequality and polarization of income classes in urban China. Journal of Econometrics 191: 348–59. [Google Scholar] [CrossRef]
- Anderson, Gordon J., Alessio Farcomeni, Maria Grazia Pittau, and Roberto Zelli. 2017a. More equal yet less similar: Human development and the progress of nation wellbeing since 1990. A multidimensional mixture distribution analysis. Working paper. Toronto, Canada: Mimeo, University of Toronto. [Google Scholar]
- Anderson, Gordon J., Oliver Linton, and Jasmin Thomas. 2017b. Similarity, dissimilarity and exceptionality: Generalizing Gini’s transvariation to measure ‘differentness’ in many distributions. Metron 75: 161–80. [Google Scholar] [CrossRef]
- Anderson, Gordon J., and Teng Wah Leo. 2017. On Providing a Complete Ordering of Non-Combinable Alternative Prospects. Working paper. Toronto, Canada: Mimeo, University of Toronto. [Google Scholar]
- Anderson, Gordon J., Thierry Post, and Yoon-Jae Whang. 2017c. Ranking Incomparable Prospects: The Utopia Index. Working paper. Toronto, Canada: Mimeo, University of Toronto. [Google Scholar]
- Anderson, Gordon J., and Jasmin Thomas. 2017. More Unequal Yet Increasingly Similar Incomes: Polarization, Segmentation and Ambiguity in the Changing Anatomy of Constituent Canadian Income Distributions in the 21st Century. Working Paper 587. Toronto, Canada: Department of Economics, University of Toronto. [Google Scholar]
- Andrews, Rick L., and Imran S. Currim. 2003. A comparison of segment retention criteria for finite mixture logit’s models. Journal of Marketing Research 40: 235–43. [Google Scholar] [CrossRef]
- Atkinson, Anthony B., and Andrea Brandolini. 2013. On the identification of the middle class. In Income Inequality. Edited by Anet C. Gornick and Markus Jäntti. Stanford: Stanford University Press, pp. 77–100. [Google Scholar]
- Álvarez-Esteban, Pedro C., Eustasio del Barrio, Juan A. Cuesta-Albertos, and Carlos Matrán. 2016. A contamination model for the stochastic order. Test 25: 751–74. [Google Scholar] [CrossRef]
- Bourguignon, François. 1979. Decomposable Income Inequality Measures. Econometrica 47: 901–20. [Google Scholar] [CrossRef]
- Brandolini, Andrea. 2007. Measurement of income distribution in supranational entities: The case of the European Union. In Inequality and Poverty Re-Examined. Edited by Stephen P. Jenkins and John Micklewright. Oxford: Oxford University Press, pp. 62–83. [Google Scholar]
- Cowell, Frank A., and Emmanuel Flachaire. 2015. Statistical methods for distributional analysis. In Handbook of Income Distribution. Edited by Anthony B. Atkinson and François Bourguignon. North Holland: Elsevier, vol. 2A, chp. 6. pp. 359–465. [Google Scholar]
- Davidson, Russell. 2009. Reliable inference for the Gini index. Journal of Econometrics 150: 30–40. [Google Scholar] [CrossRef]
- Deaton, Angus. 2010. Price Indexes, Inequality, and the Measurement of World Poverty. American Economic Review 100: 5–34. [Google Scholar] [CrossRef]
- Dempster, Arthur P., Nard M Laird, and Donald B. Rubin. 1977. Maximum likelihood from incomplete data via EM algorithm. Journal of the Royal Statistical Society 69: 1–38. [Google Scholar]
- Duclos, Jean-Yves, Joan Esteban, and Debraj Ray. 2004. Polarization: Concepts, Measurement, Estimation. Econometrica 72: 1737–72. [Google Scholar] [CrossRef]
- Filauro, Stefano. 2017. European Incomes, National Advantages: EU-Wide Inequality and Its Decomposition by Country and Region. EERI Research Papers Series No 05/2017; Brussels, Belgium: Economics and Econometrics Research Institute (EERI). [Google Scholar]
- Giles, David E. A. 2004. Calculating a Standard Error for the Gini Coefficient: Some Further Results. Oxford Bulletin of Economics and Statistics 66: 425–33. [Google Scholar] [CrossRef]
- Gini, Corrado. 1916. Il concetto di transvariazione e le sue prime applicazioni. Giornale degli Economisti e Rivista di Statistica 52: 13–43. [Google Scholar]
- Hey, John D., and Peter J. Lambert. 1980. Relative Deprivation and the Gini Coefficient: Comment. Quarterly Journal of Economics 95: 567–73. [Google Scholar] [CrossRef]
- Kaufman, Leonard, and Peter J. Rousseeuw. 1990. Finding Groups in Data: An Introduction to Cluster Analysis. New York: Wiley. [Google Scholar]
- Keribin, Christine. 2000. Consistent estimation of the order of mixture model. Sankhya 62: 49–66. [Google Scholar]
- Konte, Maty. 2016. The effects of remittances on support for democracy in Africa: Are remittances a curse or a blessing? Journal of Comparative Economics 44: 1002–22. [Google Scholar] [CrossRef]
- Longford, Nicholas T. 2014. Statistical Studies of Income, Poverty and Inequality in Europe: Computing and Graphics in R Using EU-SILC. Boca Raton: Chapman & Hall/CRC Press. [Google Scholar]
- Marron, J. S., and M. P. Wand. 1992. Exact mean integrated squared error. The Annals of Statistics 20: 712–36. [Google Scholar] [CrossRef]
- McLachlan, Geoffret, and David Peel. 2000. Finite Mixture Models. New York: Wiley. [Google Scholar]
- Milanovic, Branko. 2011. The Haves and the Have-Nots: A Brief and Idiosyncratic History of Global Inequality. New York: Basic Books. [Google Scholar]
- Modarres, Reza, and Joseph L. Gastwirth. 2006. A cautionary note on estimating the standard error of the Gini index of inequality. Oxford Bulletin of Economics and Statistics 68: 385–90. [Google Scholar] [CrossRef]
- Mookherjee, Dilip, and Anthony Shorrocks. 1982. A decomposition analysis of the trend in UK income inequality. Economic Journal 92: 886–902. [Google Scholar] [CrossRef]
- OECD. 2011. Perspectives on Global Development 2012: Social Cohesion in a Shifting World. Paris: OECD Publishing. [Google Scholar]
- Pittau, Maria Grazia, and Roberto Zelli. 2017. At the roots of Gini’s transvariation: Extracts from ‘Il concetto di transvariazione e le sue prime applicazioni’. Metron 75: 127–40. [Google Scholar] [CrossRef]
- Pittau, Maria Grazia, Roberto Zelli, and Paul A. Johnson. 2010. Mixture Models, Convergence Clubs and Polarization. Review of Income and Wealth 56: 102–22. [Google Scholar] [CrossRef]
- Ravallion, Martin. 2010. Mashup Indices of Development. Policy Research Working Paper. No. 5432. Washington, DC, USA: World Bank. [Google Scholar]
- Ravallion, Martin. 2012. Why Don’t We See Poverty Convergence? Economic Review 102: 504–23. [Google Scholar] [CrossRef]
- Stoline, Michael R., and Hans K. Ury. 1979. Tables of the Studentized Maximum Modulus Distribution and an Application to Multiple Comparisons among Means. Technometrics 21: 87–93. [Google Scholar] [CrossRef]
- Törmälehto, V. -M. 2017. High Income and Affluence: Evidence From the European Union Statistics on Income and Living Conditions (EU-SILC). Statistical Working Papers. Luxembourg: Eurostat. [Google Scholar]
- Yitzhaki, Shlomo. 1994. Economic Distance and overlapping of distributions. Journal of Econometrics 61: 147–59. [Google Scholar] [CrossRef]
- Weymark, John. 2003. Generalized Gini Indices of Equality of Opportunity. Journal of Economic Inequality 1: 5–24. [Google Scholar] [CrossRef]
| 1 | Witness The World Bank, 2017 GNI per capita ($ US equivalent) thresholds used for classifying nation income status. These were established in 1989—based upon previously established operational criteria–and inflation updated each year, or the United Nations $1 a day or the subsequent changes in the United Nations Development goals $1 a day poverty measure. |
| 2 | Mixture distributions have also been used to deal with measurement error/data contamination problems, see Alvarez-Esteban et al. (2016). On the usefulness of mixture models for distributional analysis, see Cowell and Flachaire (2015). |
| 3 | These ideas are readily generalized to multidimensional environments (see Anderson et al. 2017a). |
| 4 | This decomposition is readily extended to the Absolute Gini (Hey and Lambert 1980; Weymark 2003) by multiplying these equations by the overall mean from whence it may be seen that the overall Absolute Gini is a weighted sum of subgroup Absolute Ginis, the between group Absolute Gini and the Absolute Non Segmentation factor. Results in Giles (2004) facilitate inference. Derivation of the decomposition in the context of continuous distributions is shown in Appendix A.1. |
| 5 | In the context of mixture distributions, these ideas can be explored by considering the component distributions to be the basic densities. |
| 6 | Note that only First Order Dominance comparisons can be made here since the ordering is not endowed with cardinal measure. |
| 7 | Namely: Austria, Belgium, Cyprus, Estonia, Finland, France, Germany, Greece, Ireland, Italy, Latvia, Lithuania, Luxembourg, Netherlands, Portugal, Slovakia, Slovenia, and Spain. |
| 8 | For a discussion on the use of PPPs in the EU income distribution see Brandolini (2007). For some recent results on the EU-wide and Eurozone income inequality using EU-SILC data, see Filauro (2017). |
| 9 | For the purpose of comparison, the variance of each component population was inflated by a factor of to match that of the kernel density, where h is the estimated bandwidth of the kernel. |
| 10 | See Pittau et al. (2010) for a discussion on polarization measurements within a normal mixture framework. |
| 11 | Inferential comparison of Gini coefficients was implemented using Giles’s (2004) simple regression technique. As Modarres and Gastwirth (2006) and Davidson (2009) both indicate, Giles (2004) overstates the magnitude of the standard error so it can be considered an upper bound. Since it turns out to be very small relative to observed differences in the Gini coefficients rendering differences significant, further more sophisticated computations were deemed to be unwarranted. |
| 12 | Similar results have been obtained adopting the alternative estimate of country membership as in Equation (5). |
| 13 | This can be thought of as avoiding data contamination issues that would be present in ordinal comparison. |
| 14 | Note that for Austria and Belgium the second class component is estimated positive, however not significantly so, that is to say one could not reject the hypothesis that the component was negative, thus taken with the significant 1st and 3rd components one could not reject the joint hypothesis that 2006 dominates 2015 for these two countries. |
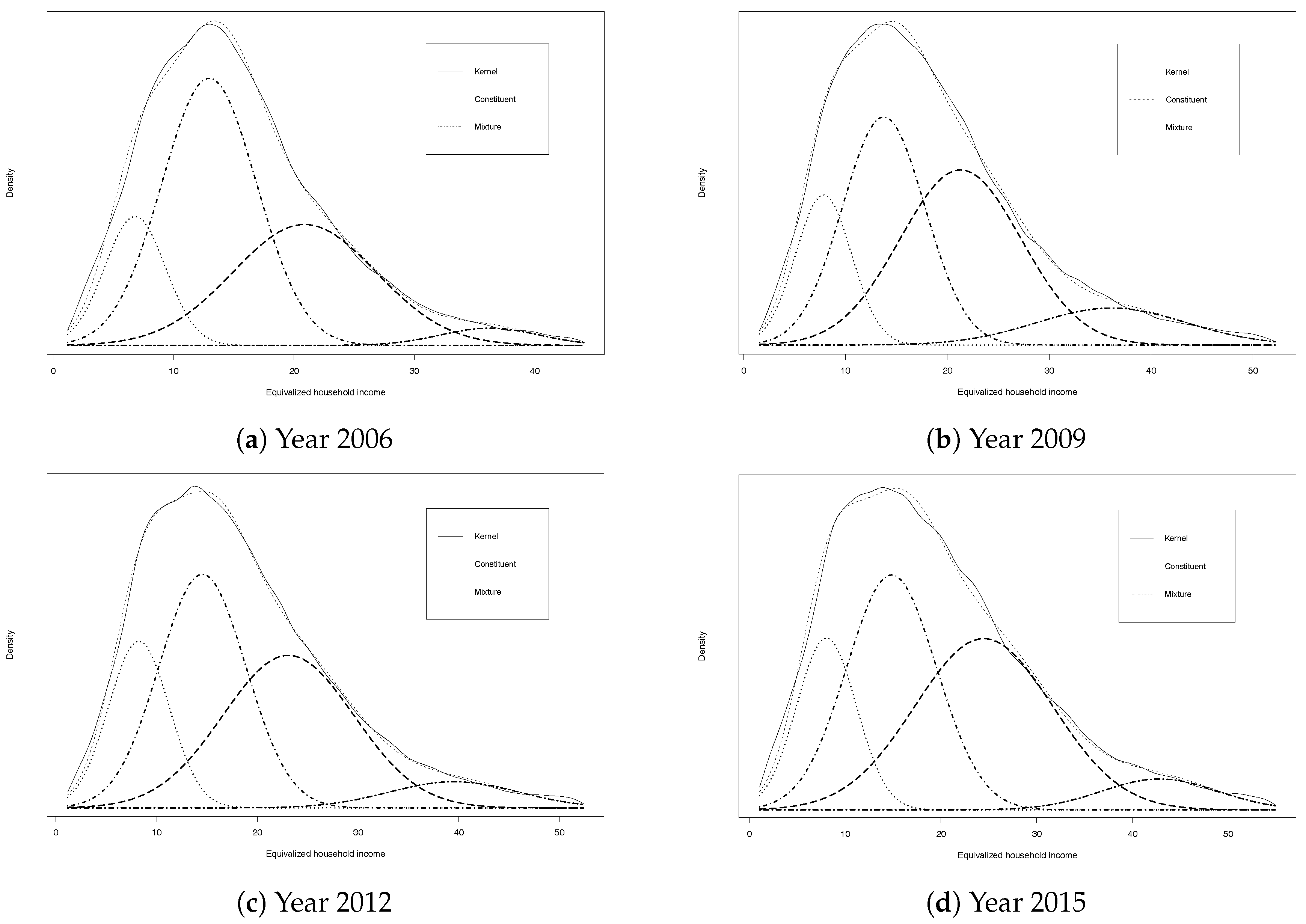
| N. of Components | Loglik | BIC | AIC | CAIC | AIC3 |
|---|---|---|---|---|---|
| 2006 | |||||
| 1 | −470,056 | 940,136 | 940,114 | 940,138 | 940,138 |
| 2 | −466,189 | 932,437 | 932,383 | 932,442 | 932,393 |
| 3 | −465,139 | 930,373 | 930,286 | 930,381 | 930,302 |
| 4 | −464,693 | 929,516 | 929,397 | 929,527 | 929,419 |
| 5 | −464,695 | 929,556 | 929,404 | 929,570 | 929,432 |
| 2009 | |||||
| 1 | −510,880 | 1,021,784 | 1,021,762 | 1,021,786 | 1,021,766 |
| 2 | −500,152 | 1,000,363 | 1,000,309 | 1,000,368 | 1,000,319 |
| 3 | −498,302 | 996,699 | 996,612 | 996,707 | 996,628 |
| 4 | −497,977 | 996,084 | 995,965 | 996,095 | 995,987 |
| 5 | −497,864 | 995,894 | 995,742 | 995,908 | 995,770 |
| 2012 | |||||
| 1 | −528,245 | 1,056,514 | 1,056,492 | 1,056,516 | 1,056,496 |
| 2 | −517,724 | 1,035,507 | 1,035,453 | 1,035,512 | 1,035,463 |
| 3 | −516,046 | 1,032187 | 1,032,100 | 1,032,195 | 1,032,116 |
| 4 | −515,655 | 1,031,441 | 1,031,321 | 1,031,452 | 1,031,343 |
| 5 | −515,636 | 1,031,438 | 1,031,286 | 1,031,452 | 1,031,314 |
| 2015 | |||||
| 1 | −562,189 | 1,124,402 | 1,124,380 | 1,124,404 | 1,124,384 |
| 2 | −552,080 | 1,104,220 | 1,104,165 | 1,104,225 | 1,104,175 |
| 3 | −550,175 | 1,100,445 | 1,100,358 | 1,100,453 | 1,100,374 |
| 4 | −549,761 | 1,099,653 | 1,099,533 | 1,099,664 | 1,099,555 |
| 5 | −549,701 | 1,099,569 | 1,099,416 | 1,099,583 | 1,099,444 |
| Year | 2006 | 2009 | 2012 | 2015 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Class | ||||||||||||
| Low (L) | 6.77 | 2.50 | 0.15 | 7.84 | 2.68 | 0.16 | 8.21 | 2.98 | 0.19 | 7.99 | 3.14 | 0.18 |
| Lower-Middle (LM) | 12.95 | 3.90 | 0.49 | 13.75 | 3.99 | 0.35 | 14.54 | 4.26 | 0.38 | 14.83 | 4.66 | 0.36 |
| Upper-Middle (UM) | 20.88 | 5.92 | 0.33 | 21.30 | 5.90 | 0.39 | 23.08 | 6.47 | 0.37 | 24.47 | 7.17 | 0.40 |
| High (H) | 36.27 | 4.01 | 0.03 | 36.11 | 7.29 | 0.10 | 39.52 | 6.36 | 0.06 | 42.85 | 5.98 | 0.06 |
| 2006 | 2009 | 2012 | 2015 | |
|---|---|---|---|---|
| 0.25 | 1.070 | 1.049 | 0.976 | 1.133 |
| 0.5 | 0.869 | 0.871 | 0.796 | 0.943 |
| 1 | 0.746 | 0.768 | 0.693 | 0.838 |
| Overall | Low | Lower-Middle | Upper-Middle | High | Non-Lower | Non-High | |
|---|---|---|---|---|---|---|---|
| 2006 | 0.385 | 0.283 | 0.239 | 0.226 | 0.088 | 0.330 | 0.343 |
| 2009 | 0.400 | 0.267 | 0.231 | 0.221 | 0.158 | 0.342 | 0.335 |
| 2012 | 0.404 | 0.281 | 0.233 | 0.224 | 0.125 | 0.338 | 0.349 |
| 2015 | 0.421 | 0.298 | 0.249 | 0.233 | 0.104 | 0.352 | 0.362 |
| Year | Within Gini | Between Gini | NSF | SI | PG | ||
|---|---|---|---|---|---|---|---|
| 2006 | 0.084 | 0.202 | 0.099 | 0.743 | 0.624 | 0.370 | 0.172 |
| 2009 | 0.068 | 0.223 | 0.109 | 0.726 | 0.636 | 0.375 | 0.297 |
| 2012 | 0.072 | 0.223 | 0.110 | 0.729 | 0.634 | 0.408 | 0.236 |
| 2015 | 0.078 | 0.231 | 0.112 | 0.734 | 0.635 | 0.396 | 0.232 |
| 2006 | 2009 | 2012 | 2015 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nation | L | LM | UM | H | L | LM | UM | H | L | LM | UM | H | L | LM | UM | H |
| Austria | 0.051 | 0.360 | 0.483 | 0.105 | 0.101 | 0.355 | 0.436 | 0.108 | 0.086 | 0.294 | 0.463 | 0.157 | 0.074 | 0.329 | 0.518 | 0.078 |
| Belgium | 0.077 | 0.413 | 0.433 | 0.077 | 0.139 | 0.395 | 0.394 | 0.072 | 0.118 | 0.365 | 0.426 | 0.092 | 0.100 | 0.386 | 0.463 | 0.052 |
| Cyprus | 0.113 | 0.400 | 0.394 | 0.093 | 0.157 | 0.360 | 0.375 | 0.108 | 0.143 | 0.355 | 0.375 | 0.126 | 0.223 | 0.410 | 0.329 | 0.038 |
| Germany | 0.069 | 0.375 | 0.452 | 0.105 | 0.115 | 0.357 | 0.421 | 0.107 | 0.099 | 0.311 | 0.447 | 0.143 | 0.107 | 0.355 | 0.467 | 0.071 |
| Estonia | 0.531 | 0.369 | 0.095 | 0.004 | 0.525 | 0.348 | 0.119 | 0.008 | 0.487 | 0.352 | 0.149 | 0.013 | 0.409 | 0.384 | 0.194 | 0.013 |
| Greece | 0.243 | 0.452 | 0.267 | 0.038 | 0.334 | 0.409 | 0.228 | 0.028 | 0.447 | 0.384 | 0.158 | 0.012 | 0.528 | 0.359 | 0.109 | 0.004 |
| Spain | 0.196 | 0.440 | 0.312 | 0.052 | 0.248 | 0.388 | 0.298 | 0.066 | 0.256 | 0.375 | 0.304 | 0.066 | 0.333 | 0.411 | 0.239 | 0.017 |
| Finland | 0.089 | 0.423 | 0.413 | 0.074 | 0.101 | 0.344 | 0.433 | 0.122 | 0.077 | 0.290 | 0.468 | 0.165 | 0.048 | 0.264 | 0.548 | 0.140 |
| France | 0.079 | 0.420 | 0.419 | 0.082 | 0.075 | 0.320 | 0.447 | 0.158 | 0.071 | 0.295 | 0.470 | 0.164 | 0.038 | 0.257 | 0.572 | 0.132 |
| Ireland | 0.109 | 0.424 | 0.365 | 0.102 | 0.160 | 0.392 | 0.355 | 0.094 | 0.179 | 0.388 | 0.350 | 0.083 | 0.173 | 0.404 | 0.377 | 0.046 |
| Italy | 0.126 | 0.427 | 0.376 | 0.071 | 0.181 | 0.387 | 0.351 | 0.081 | 0.160 | 0.351 | 0.388 | 0.102 | 0.171 | 0.397 | 0.387 | 0.044 |
| Lithuania | 0.579 | 0.333 | 0.085 | 0.003 | 0.545 | 0.326 | 0.118 | 0.011 | 0.533 | 0.329 | 0.128 | 0.009 | 0.492 | 0.358 | 0.141 | 0.009 |
| Luxembourg | 0.032 | 0.228 | 0.474 | 0.267 | 0.041 | 0.244 | 0.457 | 0.258 | 0.035 | 0.214 | 0.467 | 0.285 | 0.042 | 0.249 | 0.549 | 0.160 |
| Latvia | 0.604 | 0.311 | 0.080 | 0.005 | 0.587 | 0.297 | 0.105 | 0.011 | 0.594 | 0.291 | 0.106 | 0.009 | 0.537 | 0.332 | 0.126 | 0.006 |
| Netherlands | 0.024 | 0.336 | 0.523 | 0.118 | 0.043 | 0.320 | 0.500 | 0.137 | 0.049 | 0.314 | 0.502 | 0.135 | 0.057 | 0.361 | 0.522 | 0.060 |
| Portugal | 0.343 | 0.426 | 0.191 | 0.040 | 0.436 | 0.360 | 0.171 | 0.033 | 0.413 | 0.365 | 0.186 | 0.035 | 0.411 | 0.392 | 0.183 | 0.014 |
| Slovenia | 0.127 | 0.517 | 0.327 | 0.029 | 0.179 | 0.465 | 0.322 | 0.033 | 0.181 | 0.435 | 0.345 | 0.039 | 0.191 | 0.480 | 0.313 | 0.016 |
| Slovakia | 0.619 | 0.318 | 0.061 | 0.002 | 0.524 | 0.365 | 0.106 | 0.004 | 0.336 | 0.442 | 0.208 | 0.014 | 0.376 | 0.474 | 0.148 | 0.002 |
| Country | t Values | ||||||
|---|---|---|---|---|---|---|---|
| Austria | −0.023 | 0.008 | −0.027 | 5.14 | 0.88 | 5.05 | 2006 dominates 2015 |
| Belgium | −0.023 | 0.004 | −0.026 | 4.36 | 0.43 | 5.71 | 2006 dominates 2015 |
| Cyprus | −0.110 | −0.120 | −0.055 | 13.22 | 10.71 | 9.63 | 2006 dominates 2015 |
| Germany | −0.038 | −0.018 | −0.033 | 10.75 | 2.90 | 9.41 | 2006 dominates 2015 |
| Estonia | 0.122 | 0.107 | 0.008 | 12.99 | 15.86 | 4.48 | 2015 dominates 2006 |
| Greece | −0.285 | −0.192 | −0.034 | 39.81 | 28.49 | 12.98 | 2006 dominates 2015 |
| Spain | −0.137 | −0.108 | −0.035 | 24.37 | 18.20 | 14.88 | 2006 dominates 2015 |
| Finland | 0.041 | 0.200 | 0.065 | 11.77 | 29.93 | 15.16 | 2015 dominates 2006 |
| France | 0.041 | 0.204 | 0.051 | 12.44 | 30.38 | 11.85 | 2015 dominates 2006 |
| Ireland | −0.064 | −0.044 | −0.056 | 9.63 | 4.63 | 11.31 | 2006 dominates 2015 |
| Italy | −0.045 | −0.015 | −0.026 | 12.23 | 2.93 | 10.91 | 2006 dominates 2015 |
| Lithuania | 0.087 | 0.062 | 0.006 | 8.43 | 9.28 | 3.76 | 2015 dominates 2006 |
| Luxembourg | −0.010 | −0.031 | −0.106 | 2.16 | 2.83 | 10.65 | 2006 dominates 2015 |
| Latvia | 0.067 | 0.046 | 0.000 | 6.71 | 7.47 | 0.00 | 2015 dominates 2006 |
| Netherlands | −0.033 | −0.058 | −0.057 | 11.46 | 8.06 | 13.54 | 2006 dominates 2015 |
| Portugal | −0.068 | −0.034 | −0.026 | 7.56 | 4.39 | 7.98 | 2006 dominates 2015 |
| Slovenia | −0.064 | −0.027 | −0.013 | 11.76 | 3.82 | 5.93 | 2006 dominates 2015 |
| Slovakia | 0.243 | 0.087 | 0.000 | 25.84 | 14.83 | 0.00 | 2015 dominates 2006 |
| 2006–2009 | 2006–2012 | 2009–2012 | 2006–2015 | 2009–2015 | 2012–2015 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Country | s.e. | s.e. | s.e. | s.e. | s.e. | s.e. | ||||||
| Austria | 0.605 | 0.009 | 0.673 | 0.009 | 0.568 | 0.009 | 0.492 | 0.009 | 0.387 | 0.009 | 0.319 | 0.009 |
| Belgium | 0.614 | 0.009 | 0.611 | 0.009 | 0.497 | 0.009 | 0.495 | 0.009 | 0.381 | 0.009 | 0.384 | 0.009 |
| Cyprus | 0.618 | 0.012 | 0.627 | 0.011 | 0.509 | 0.012 | 0.610 | 0.011 | 0.492 | 0.012 | 0.483 | 0.011 |
| Germany | 0.597 | 0.006 | 0.637 | 0.006 | 0.540 | 0.006 | 0.509 | 0.006 | 0.412 | 0.006 | 0.372 | 0.006 |
| Estonia | 0.495 | 0.010 | 0.428 | 0.010 | 0.433 | 0.010 | 0.273 | 0.010 | 0.278 | 0.010 | 0.345 | 0.010 |
| Greece | 0.663 | 0.009 | 0.855 | 0.010 | 0.692 | 0.009 | 1.002 | 0.008 | 0.839 | 0.007 | 0.647 | 0.008 |
| Spain | 0.632 | 0.006 | 0.647 | 0.006 | 0.515 | 0.006 | 0.704 | 0.007 | 0.572 | 0.006 | 0.557 | 0.006 |
| Finland | 0.619 | 0.007 | 0.657 | 0.007 | 0.538 | 0.007 | 0.549 | 0.007 | 0.430 | 0.007 | 0.392 | 0.007 |
| France | 0.644 | 0.007 | 0.648 | 0.007 | 0.504 | 0.007 | 0.519 | 0.007 | 0.375 | 0.007 | 0.371 | 0.007 |
| Ireland | 0.585 | 0.010 | 0.602 | 0.010 | 0.517 | 0.010 | 0.516 | 0.010 | 0.431 | 0.010 | 0.414 | 0.010 |
| Italy | 0.630 | 0.005 | 0.629 | 0.005 | 0.499 | 0.005 | 0.537 | 0.005 | 0.407 | 0.005 | 0.408 | 0.005 |
| Lithuania | 0.448 | 0.010 | 0.421 | 0.010 | 0.473 | 0.010 | 0.338 | 0.010 | 0.390 | 0.010 | 0.417 | 0.010 |
| Luxembourg | 0.501 | 0.012 | 0.542 | 0.011 | 0.541 | 0.010 | 0.307 | 0.012 | 0.306 | 0.012 | 0.265 | 0.011 |
| Latvia | 0.478 | 0.010 | 0.488 | 0.010 | 0.510 | 0.009 | 0.367 | 0.010 | 0.389 | 0.009 | 0.379 | 0.009 |
| Netherlands | 0.577 | 0.007 | 0.585 | 0.007 | 0.508 | 0.007 | 0.451 | 0.007 | 0.374 | 0.007 | 0.366 | 0.007 |
| Portugal | 0.672 | 0.011 | 0.631 | 0.010 | 0.459 | 0.010 | 0.584 | 0.009 | 0.412 | 0.009 | 0.453 | 0.008 |
| Slovenia | 0.613 | 0.007 | 0.628 | 0.007 | 0.515 | 0.007 | 0.602 | 0.007 | 0.489 | 0.008 | 0.474 | 0.008 |
| Slovakia | 0.315 | 0.010 | −0.042 | 0.010 | 0.143 | 0.010 | 0.014 | 0.010 | 0.199 | 0.010 | 0.556 | 0.010 |
| 2006 | 2009 | 2012 | 2015 | |||||
|---|---|---|---|---|---|---|---|---|
| Country | UI | Rank | UI | Rank | UI | Rank | UI | Rank |
| Austria | 0.78 | 3 | 0.73 | 5 | 0.79 | 5.00 | 0.82 | 4 |
| Belgium | 0.69 | 5 | 0.62 | 8 | 0.65 | 7.00 | 0.71 | 7 |
| Cyprus | 0.66 | 8 | 0.65 | 7 | 0.65 | 8.00 | 0.48 | 10 |
| Germany | 0.75 | 4 | 0.71 | 6 | 0.75 | 6.00 | 0.74 | 6 |
| Estonia | 0.08 | 15 | 0.06 | 15 | 0.11 | 16.00 | 0.19 | 13 |
| Greece | 0.43 | 13 | 0.30 | 13 | 0.14 | 15.00 | 0.01 | 18 |
| Spain | 0.50 | 12 | 0.47 | 12 | 0.44 | 12.00 | 0.29 | 12 |
| Finland | 0.67 | 7 | 0.75 | 4 | 0.81 | 4.00 | 0.96 | 3 |
| France | 0.69 | 6 | 0.83 | 3 | 0.81 | 2.00 | 0.98 | 2 |
| Ireland | 0.66 | 9 | 0.61 | 9 | 0.55 | 10.00 | 0.57 | 9 |
| Italy | 0.62 | 10 | 0.57 | 10 | 0.61 | 9.00 | 0.58 | 8 |
| Lithuania | 0.04 | 16 | 0.05 | 16 | 0.06 | 17.00 | 0.07 | 16 |
| Luxembourg | 0.99 | 1 | 1.00 | 1 | 1.00 | 1.00 | 1.00 | 1 |
| Latvia | 0.03 | 17 | 0.01 | 18 | 0.00 | 18.00 | 0.02 | 17 |
| Netherlands | 0.84 | 2 | 0.86 | 2 | 0.81 | 3.00 | 0.80 | 5 |
| Portugal | 0.31 | 14 | 0.19 | 14 | 0.21 | 14.00 | 0.18 | 14 |
| Slovenia | 0.53 | 11 | 0.49 | 11 | 0.48 | 11.00 | 0.46 | 11 |
| Slovakia | 0.00 | 18 | 0.04 | 17 | 0.25 | 13.00 | 0.16 | 15 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anderson, G.; Pittau, M.G.; Zelli, R.; Thomas, J. Income Inequality, Cohesiveness and Commonality in the Euro Area: A Semi-Parametric Boundary-Free Analysis. Econometrics 2018, 6, 15. https://doi.org/10.3390/econometrics6020015
Anderson G, Pittau MG, Zelli R, Thomas J. Income Inequality, Cohesiveness and Commonality in the Euro Area: A Semi-Parametric Boundary-Free Analysis. Econometrics. 2018; 6(2):15. https://doi.org/10.3390/econometrics6020015
Chicago/Turabian StyleAnderson, Gordon, Maria Grazia Pittau, Roberto Zelli, and Jasmin Thomas. 2018. "Income Inequality, Cohesiveness and Commonality in the Euro Area: A Semi-Parametric Boundary-Free Analysis" Econometrics 6, no. 2: 15. https://doi.org/10.3390/econometrics6020015
APA StyleAnderson, G., Pittau, M. G., Zelli, R., & Thomas, J. (2018). Income Inequality, Cohesiveness and Commonality in the Euro Area: A Semi-Parametric Boundary-Free Analysis. Econometrics, 6(2), 15. https://doi.org/10.3390/econometrics6020015





