Generalized Information Matrix Tests for Detecting Model Misspecification
Abstract
:1. Introduction
1.1. Information Matrix Test Methods for Detection of Model Misspecification
1.2. Recent Developments in Information Matrix Test Theory
2. GIMT Theoretical Framework: Definitions and Assumptions
2.1. Data Generating Process
2.2. Probability Model
2.3. Hypothesis Function
2.4. Notation
2.5. Regularity Conditions
3. GIMT Theoretical Framework: Theorems and Formulas
3.1. Classical Results
3.2. GIMT Statistic Asymptotic Behavior
3.3. GIMT Covariance Matrix Estimators
3.4. Adjusted GIMT Hypothesis Functions
4. Simulation Studies
4.1. Generalized Information Matrix Tests
4.1.1. Adjusted Classical GIMT (Directional) [23]
4.1.2. Fisher Spectra GIMT (Directional)
4.1.3. Robust Log GAIC GIMT (Directional)
4.1.4. Robust Log GAIC Ratio GIMT (Directional)
4.1.5. Composite Log GAIC GIMT (Nondirectional)
4.1.6. Composite GAIC GIMT (Non-Directional)
4.2. Methods
4.2.1. Simulated Data Generating Processes
4.2.2. Estimation of Type 1 and Type 2 Error Rates
4.3. Results and Discussion
4.3.1. Type 1 Error Performance
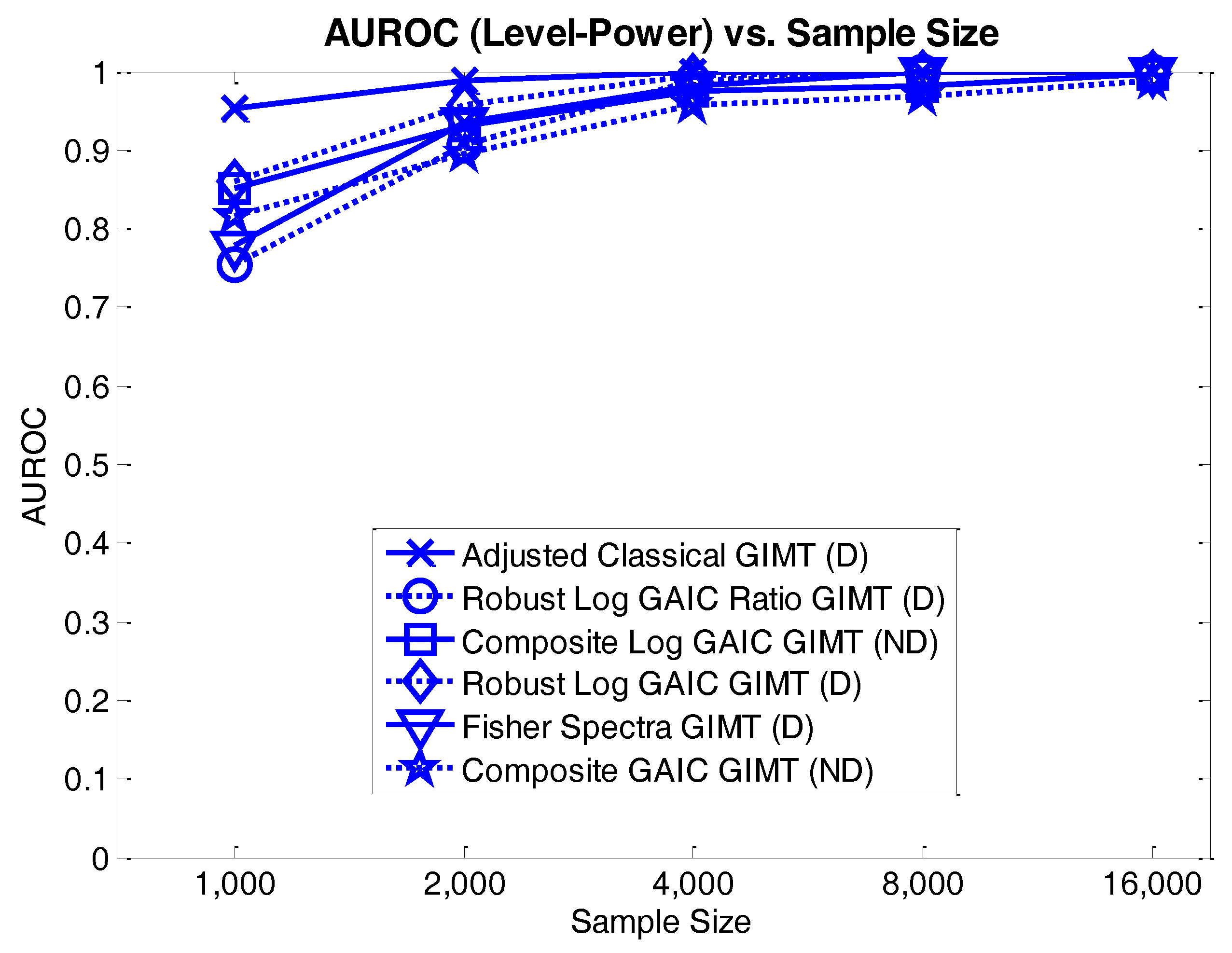
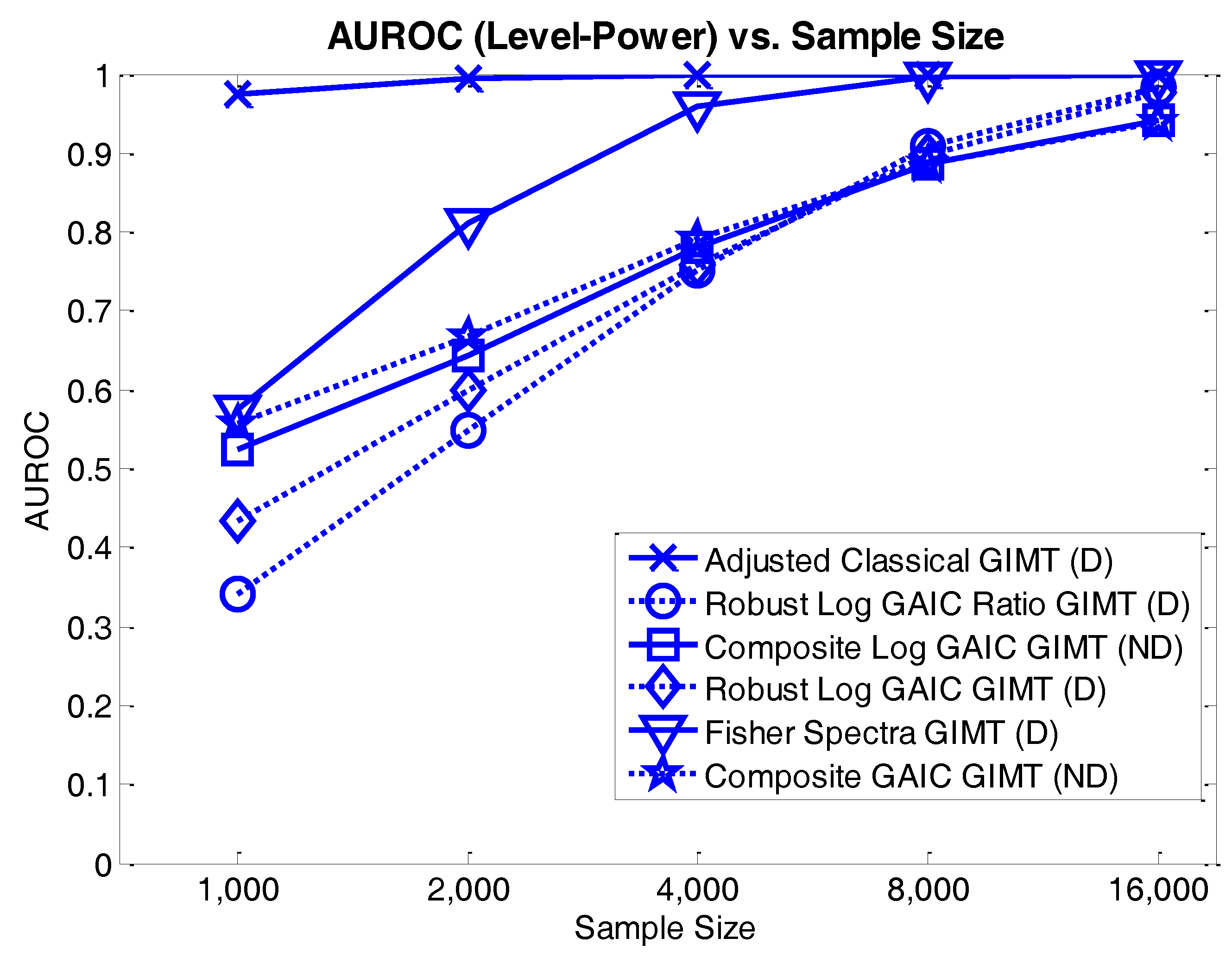
4.3.2. Level-Power Analyses
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Proofs of Theorems and Propositions
References
- H. White. “Maximum Likelihood Estimation of Misspecified Models.” Econometrica 50 (1982): 1–25. [Google Scholar] [CrossRef]
- H. White. Estimation, Inference, and Specification Analysis. New York, NY, USA: Cambridge University Press, 1994. [Google Scholar]
- T.M. Kashner, S.S. Henley, R.M. Golden, A.J. Rush, and R.B. Jarrett. “Assessing the preventive effects of cognitive therapy following relief of depression: A methodological innovation.” J. Affect. Disord. 104 (2007): 251–261. [Google Scholar] [CrossRef] [PubMed]
- T.M. Kashner, R. Rosenheck, A.B. Campinell, A. Suris, R. Crandall, N.J. Garfield, P. Lapuc, K. Pyrcz, T. Soyka, and A. Wicker. “Impact of work therapy on health status among homeless, substance-dependent veterans: A randomized controlled trial.” Arch. Gen. Psychiatry 59 (2002): 938–944. [Google Scholar] [CrossRef] [PubMed]
- T.M. Kashner, T.J. Carmody, T. Suppes, A.J. Rush, M.L. Crismon, A.L. Miller, M. Toprac, and T. Madhukar. “Catching up on health outcomes: The Texas Medication Algorithm Project.” Health Serv. Res. 38 (2003): 311–331. [Google Scholar] [CrossRef] [PubMed]
- T.M. Kashner, S.S. Henley, R.M. Golden, J.M. Byrne, S.A. Keitz, G.W. Cannon, B.K. Chang, G.J. Holland, D.C. Aron, E.A. Muchmore, and et al. “Studying the Effects of ACGME Duty Hours Limits on Resident Satisfaction: Results From VA Learners’ Perceptions Survey.” Acad. Med. 85 (2010): 1130–1139. [Google Scholar] [CrossRef] [PubMed]
- S.S. Henley, T.M. Kashner, R.M. Golden, and A.N. Westover. “Response to letter regarding “A systematic approach to subgroup analyses in a smoking cessation trial”.” Am. J. Drug Alcohol Abuse 42 (2016): 112–113. [Google Scholar] [CrossRef] [PubMed]
- A.N. Westover, T.M. Kashner, T.M. Winhusen, R.M. Golden, and S.S. Henley. “A Systematic Approach to Subgroup Analyses in a Smoking Cessation Trial.” Am. J. Drug Alcohol Abuse 41 (2015): 498–507. [Google Scholar] [CrossRef] [PubMed]
- S.C. Brakenridge, S.S. Henley, T.M. Kashner, R.M. Golden, D. Paik, H.A. Phelan, M. Cohen, J.L. Sperry, E.E. Moore, J.P. Minei, and et al. “Comparing Clinical Predictors of Deep Venous Thrombosis vs. Pulmonary Embolus After Severe Blunt Injury: A New Paradigm for Post-Traumatic Venous Thromboembolism? ” J. Trauma Acute Care Surg. 74 (2013): 1231–1238. [Google Scholar] [CrossRef] [PubMed]
- S.C. Brakenridge, H.A. Phelan, S.S. Henley, R.M. Golden, T.M. Kashner, A.E. Eastman, J.L. Sperry, B.G. Harbrecht, E.E. Moore, J. Cuschieri, and et al. “Early blood product and crystalloid volume resuscitation: Risk association with multiple organ dysfunction after severe blunt traumatic injury.” J. Trauma 71 (2011): 299–305. [Google Scholar] [CrossRef] [PubMed]
- A. Chesher. “The information matrix test: Simplified calculation via a score test interpretation.” Econ. Lett. 13 (1983): 45–48. [Google Scholar] [CrossRef]
- T. Lancaster. “The Covariance Matrix of the Information Matrix Test.” Econometrica 52 (1984): 1051–1054. [Google Scholar] [CrossRef]
- T. Aparicio, and I. Villanua. “The asymptotically efficient version of the information matrix test in binary choice models. A study of size and power.” J. Appl. Stat. 28 (2001): 167–182. [Google Scholar] [CrossRef]
- R. Davidson, and J.G. MacKinnon. “Graphical Methods for Investigating the Size and Power of Hypothesis Tests.” Manch. Sch. 66 (1998): 1–26. [Google Scholar] [CrossRef]
- R. Davidson, and J.G. MacKinnon. “A New Form of the Information Matrix Test.” Econometrica 60 (1992): 145–157. [Google Scholar] [CrossRef]
- G. Dhaene, and D. Hoorelbeke. “The information matrix test with bootstrap-based covariance matrix estimation.” Econ. Lett. 82 (2004): 341–347. [Google Scholar] [CrossRef]
- C. Stomberg, and H. White. Bootstrapping the Information Matrix Test. Discussion Paper; San Diego, CA, USA: Department of Economics, University of California, 2000. [Google Scholar]
- L.W. Taylor. “The Size Bias of White’s Information Matrix Test.” Econ. Lett. 24 (1987): 63–67. [Google Scholar] [CrossRef]
- B. Presnell, and D.D. Boos. “The IOS Test for Model Misspecification.” J. Am. Stat. Assoc. 99 (2004): 216–227. [Google Scholar] [CrossRef]
- M. Capanu, and B. Presnell. “Misspecification tests for binomial and beta-binomial models.” Stat. Med. 27 (2008): 2536–2554. [Google Scholar] [CrossRef] [PubMed]
- M. Capanu. “Tests of Misspecification for Parametric Models.” University of Florida, 2005. Available online: http://etd.fcla.edu/UF/UFE0010943/capanu_m.pdf (accessed on 1 June 2016).
- S. Zhang, P.X.K. Song, D. Shi, and Q.M. Zhou. “Information ratio test for model misspecification on parametric structures in stochastic diffusion models.” Comput. Stat. Data Anal. 56 (2012): 3975–3987. [Google Scholar] [CrossRef]
- R.M. Golden, S.S. Henley, H. White, and T.M. Kashner. “New Directions in Information Matrix Testing: Eigenspectrum Tests.” In Causality, Prediction, and Specification Analysis: Recent Advances and Future Directions: Essays in Honor of Halbert L. White, Jr. (Festschrift Hal White Conference). Edited by X. Chen and N.R. Swanson. New York, NY, USA: Springer, 2013, pp. 145–178. [Google Scholar]
- J.S. Cho, and H. White. “Testing the Equality of Two Positive-Definite Matrices with Application to Information Matrix Testing.” In Essays in Honor of Peter C. B. Phillips. Edited by Y. Chang, T.B. Fomby and J.Y. Park. Bingley, UK: Emerald Group Publishing Limited, 2014, pp. 491–556. [Google Scholar]
- Q.M. Zhou, P.X.K. Song, and M.E. Thompson. “Information Ratio Test for Model Misspecification in Quasi-Likelihood Inference.” J. Am. Stat. Assoc. 107 (2012): 205–213. [Google Scholar] [CrossRef]
- W. Huang, and A. Prokhorov. “A Goodness-of-Fit Test for Copulas.” Econom. Rev. 33 (2014): 751–771. [Google Scholar] [CrossRef] [Green Version]
- W.H. Marlow. Mathematics for Operations Research. Mineola, NY, USA: Dover Publications, 2012. [Google Scholar]
- J.R. Magnus. “On the concept of matrix derivative.” J. Multivar. Anal. 101 (2010): 2200–2206. [Google Scholar] [CrossRef]
- J.R. Magnus, and H. Neudecker. Matrix Differential Calculus with Applications in Statistics and Econometrics. New York, NY, USA: John Wiley & Sons, 1999. [Google Scholar]
- R.I. Jennrich. “Asymptotic Properties of Non-linear Least Squares Estimators.” Ann. Math. Stat. 40 (1969): 633–643. [Google Scholar] [CrossRef]
- H. White. “Consequences and detection of misspecified nonlinear regression models.” J. Am. Stat. Assoc. 76 (1981): 419–433. [Google Scholar] [CrossRef]
- P. Huber. “The Behavior of Maximum Likelihood Estimates under Non-Standard Conditions.” In Proceedings Fifth Berkeley Symposium on Mathematical Statistics and Probability, Vol. 1. Berkeley, CA, USA: University of California Press, 1967, pp. 221–233. [Google Scholar]
- A. Prokhorov, U. Schepsmeier, and Y. Zhu. Generalized Information Matrix Tests for Copulas, Working Paper. Sydney, Australia: University of Sydney Business School, Discipline of Business Analytics, 2015. [Google Scholar]
- H. Bozdogan. “Model selection and Akaike’s information criterion (AIC): The general theory and its analytical extensions.” Psychometrika 52 (1987): 345–370. [Google Scholar] [CrossRef]
- H. Linhart, and W. Zucchini. Model Selection. New York, NY, USA: Wiley, 1986. [Google Scholar]
- K. Takeuchi. “Distribution of information statistics and a criterion of model fitting for adequacy of models.” Math. Sci. 153 (1976): 12–18. [Google Scholar]
- J. Cho, and P. Phillips. “Testing Equality of Covariance Matrices via Pythagorean Means.” 2014. Available online: http://ssrn.com/abstract=2533002 (accessed on 1 June 2016).
- R.M. Golden. “Statistical tests for comparing possibly misspecified and nonnested models.” J. Math. Psychol. 44 (2000): 153–170. [Google Scholar] [CrossRef] [PubMed]
- R.M. Golden. “Discrepancy risk model selection test theory for comparing possibly misspecified or nonnested models.” Psychometrika 68 (2003): 229–249. [Google Scholar] [CrossRef]
- S.S. Henley, R.M. Golden, T.M. Kashner, and H. White. Exploiting Hidden Structures in Epidemiological Data: Phase II Project. Plano, TX, USA: NIH/NIAAA, 2000. [Google Scholar]
- S.S. Henley, R.M. Golden, T.M. Kashner, H. White, and D. Paik. Robust Classification Methods for Categorical Regression: Phase II Project. Plano, TX, USA: National Cancer Institute, 2008. [Google Scholar]
- S.S. Henley, R.M. Golden, T.M. Kashner, H. White, and R.D. Katz. Model Selection Methods for Categorical Regression: Phase I Project. Plano, TX, USA: NIH/NIAAA, 2003. [Google Scholar]
- Q.H. Vuong. “Likelihood ratio tests for model selection and non-nested hypotheses.” Econometrica 57 (1989): 307–333. [Google Scholar] [CrossRef]
- H. Bozdogan. “Akaike’s Information Criterion and Recent Developments in Information Complexity.” J. Math. Psychol. 44 (2000): 62–91. [Google Scholar] [CrossRef] [PubMed]
- T. Fawcett. “An introduction to ROC analysis.” Pattern Recogn. Lett. 27 (2006): 861–874. [Google Scholar] [CrossRef]
- M.S. Pepe. The Statistical Evaluation of Medical Tests for Classification and Prediction. Oxford, UK: Oxford University Press, 2004. [Google Scholar]
- T.D. Wickens. Elementary Signal Detection Theory. New York, NY, USA: Oxford University Press, 2002. [Google Scholar]
- T. Hastie, and R. Tibshirani. Generalized Additive Models. New York, NY, USA: Chapman and Hall, 1990. [Google Scholar]
- P. McCullagh, and J.A. Nelder. Generalized Linear Models. London, UK: New York, NY, USA: Chapman and Hall, 1989. [Google Scholar]
- B. Wei. Exponential Family Nonlinear Models. New York, NY, USA: Springer, 1998. [Google Scholar]
- D.W. Hosmer, and S. Lemeshow. Applied Logistic Regression. New York, NY, USA: Wiley, 1989. [Google Scholar]
- F.E. Harrell. Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis. New York, NY, USA: Springer, 2001. [Google Scholar]
- G. Arminger, and M.E. Sobel. “Pseudo-maximum likelihood estimation of mean and covariance structures with missing data.” J. Am. Stat. Assoc. 85 (1990): 195–203. [Google Scholar] [CrossRef]
- J. Gallini. “Misspecifications that can result in path analysis structures.” Appl. Psychol. Meas. 7 (1983): 125–137. [Google Scholar] [CrossRef]
- S.W. Raudenbush, and A.S. Bryk. Hierarchical Linear Models: Applications and Data Analysis Methods. Thousand Oaks, CA, USA: Sage Publications, Inc., 2002. [Google Scholar]
- D.W. Hosmer, and S. Lemeshow. “A goodness-of-fit test for the multiple logistic regression model.” Commun. Stat. A10 (1980): 1043–1069. [Google Scholar] [CrossRef]
- D.W. Hosmer, S. Lemeshow, and J. Klar. “Goodness-of-Fit Testing for Multiple Logistic Regression Analysis when the Estimated Probabilities are Small.” Biom. J. 30 (1988): 1–14. [Google Scholar] [CrossRef]
- D.W. Hosmer, S. Taber, and S. Lemeshow. “The importance of assessing the fit of logistic regression models: A case study.” Am. J. Public Health 81 (1991): 1630–1635. [Google Scholar] [CrossRef] [PubMed]
- R.J. Serfling. Approximation Theorems of Mathematical Statistics. New York, NY, USA: Wiley-Interscience, 1980. [Google Scholar]
- H. White. Asymptotic Theory for Econometricians, Revised Edition. New York, NY, USA: Academic Press, 2001. [Google Scholar]
- H. White. “Using least squares to approximate unknown regression functions.” Int. Econ. Rev. 21 (1980): 149–170. [Google Scholar] [CrossRef]
| Generalized Information Matrix Test (GIMT) | Test Type | p = 0.01 | p = 0.025 | p = 0.05 | p = 0.10 |
|---|---|---|---|---|---|
| Adjusted Classical (≤10 df) | Directional | 0.0136 | 0.0308 | 0.0550 | 0.1059 |
| (0.0012) | (0.0017) | (0.0023) | (0.0031) | ||
| Composite GAIC (2 df) | Non-Directional | 0.0830 | 0.1014 | 0.1225 | 0.1546 |
| (0.0027) | (0.0030) | (0.0032) | (0.0036) | ||
| Composite Log GAIC (2 df) | Non-Directional | 0.0564 | 0.0742 | 0.0930 | 0.1219 |
| (0.0023) | (0.0026) | (0.0029) | (0.0032) | ||
| Fisher Spectra (4 df) | Directional | 0.0205 | 0.0337 | 0.0584 | 0.1035 |
| (0.0014) | (0.0018) | (0.0023) | (0.0030) | ||
| Robust Log GAIC (1 df) | Directional | 0.0185 | 0.0360 | 0.0618 | 0.1144 |
| (0.0013) | (0.0018) | (0.0024) | (0.0031) | ||
| Robust Log GAIC Ratio (1 df) | Directional | 0.0158 | 0.0335 | 0.0590 | 0.1135 |
| (0.0012) | (0.0018) | (0.0023) | (0.0031) |
| Generalized Information Matrix Test (GIMT) | Test Type | p = 0.01 | p = 0.025 | p = 0.05 | p = 0.10 |
|---|---|---|---|---|---|
| Adjusted Classical (≤10 df) | Directional | 0.0085 | 0.0195 | 0.0409 | 0.0916 |
| (0.0009) | (0.0014) | (0.0020) | (0.0029) | ||
| Composite GAIC (2 df) | Non-Directional | 0.0662 | 0.0821 | 0.1006 | 0.1259 |
| (0.0024) | (0.0026) | (0.0029) | (0.0032) | ||
| Composite Log GAIC (2 df) | Non-Directional | 0.0403 | 0.0498 | 0.0646 | 0.0884 |
| (0.0019) | (0.0021) | (0.0023) | (0.0027) | ||
| Fisher Spectra (4 df) | Directional | 0.0071 | 0.0161 | 0.0264 | 0.0535 |
| (0.0008) | (0.0012) | (0.0015) | (0.0021) | ||
| Robust Log GAIC (1 df) | Directional | 0.0045 | 0.0138 | 0.0236 | 0.0622 |
| (0.0006) | (0.0011) | (0.0014) | (0.0023) | ||
| Robust Log GAIC Ratio (1 df) | Directional | 0.0032 | 0.0097 | 0.0285 | 0.0588 |
| (0.0005) | (0.0009) | (0.0016) | (0.0022) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Golden, R.M.; Henley, S.S.; White, H.; Kashner, T.M. Generalized Information Matrix Tests for Detecting Model Misspecification. Econometrics 2016, 4, 46. https://doi.org/10.3390/econometrics4040046
Golden RM, Henley SS, White H, Kashner TM. Generalized Information Matrix Tests for Detecting Model Misspecification. Econometrics. 2016; 4(4):46. https://doi.org/10.3390/econometrics4040046
Chicago/Turabian StyleGolden, Richard M., Steven S. Henley, Halbert White, and T. Michael Kashner. 2016. "Generalized Information Matrix Tests for Detecting Model Misspecification" Econometrics 4, no. 4: 46. https://doi.org/10.3390/econometrics4040046
APA StyleGolden, R. M., Henley, S. S., White, H., & Kashner, T. M. (2016). Generalized Information Matrix Tests for Detecting Model Misspecification. Econometrics, 4(4), 46. https://doi.org/10.3390/econometrics4040046





