Abstract
In this paper, we suggest an approach to recovering behavior-related, preference-choice network information from observational data. We model the process as a self-organized behavior based random exponential network-graph system. To address the unknown nature of the sampling model in recovering behavior related network information, we use the Cressie-Read (CR) family of divergence measures and the corresponding information theoretic entropy basis, for estimation, inference, model evaluation, and prediction. Examples are included to clarify how entropy based information theoretic methods are directly applicable to recovering the behavioral network probabilities in this fundamentally underdetermined ill posed inverse recovery problem.
Keywords:
random exponential networks; binary and weighed networks; inverse problem; adjacency matrix; Cressie-Read family of divergence measures; conditional moment conditions; self organized behavior systems JEL Classification:
C1; C10; C24
1. Introduction
By tradition, our ability to measure evidence and make predictions relative to economic behavioral systems has been linked to reductionist parametric econometric models and ad hoc sampling model designs. Using traditional estimation and inference methods with fragile static econometric models and dynamic sample data often leads to probability parameter estimation biases, incorrect inferences and obscures the intervention-treatment-causal path effects information that one hopes to measure. This traditional methodological focus has led to fragile economic theories and questionable inferences and has failed in terms of prediction and the extraction of quantitative information relative to the nature of underlying economic behavioral systems.
To go beyond traditional reductionist modeling and mathematical anomalies, a network paradigm is developing under the name of Network Science (for example, see [1,2,3]). This new paradigm recognizes that the network representation of economic processes arise quite naturally from microeconomic theory where markets and weighted and binary linked networks are equivalent and is based on observed adaptive behavior data sets that are by nature indirect, incomplete and noisy. There are several things that make this approach attractive for information recovery in economics and in other social sciences. First of all, in the economic behavioral sciences, everything seems to depend on everything else, and this fits the interconnectedness-simultaneity of the nonlinear dynamic network paradigm. There is also a close link in economic behavioral systems between information recovery and inference in random network models and adaptive intelligent behavior, causal entropy maximization and information theoretic methods.
A problem of great interest across the sciences in general and network recovery in particular, is how to infer, given noisy limited data, the mathematical form of the corresponding probability distribution function. In this context with information recovery and inference in mind, we propose an adaptive intelligent behavior framework that permits the interpretation of behavioral networks in terms of causal entropy maximization and entropy based inference methods. To address the unknown nature of the probability sampling model in recovering behavior related preference-choice network pathway information from limited noisy observational data, we use the Cressie-Read (CR)-information theoretic entropy family of divergence measures as a distributional basis for linking the data and the unknown and unobservable behavioral network edge-path probabilities. This permits the recovery of estimates of the unknown link parameters and pathway probabilities across the network ensemble that can be computed analytically without sampling the configuration space.
In the sections ahead, we consider econometrics as an exercise in inference and recognize that the observed samples of network data come from complex dynamic adaptive behavior systems that are non-deterministic in nature, involve information and uncertainty, and are driven toward a certain optimal stationary state. To recover econometric-network behavior related choice-preference information from samples of indirect, incomplete and noisy observational or quasi-controlled samples of behavioral data, we use random network models to demonstrate the nature of the entropy based information theoretic approach to recovering the unknown mathematical form of the underlying probability distribution and pathway probabilities of the behavioral network system. Finally, we note that the emergence of large data sets and recovery methods linked to causal entropy maximization and information theoretic methods appear to offer a promising new paradigm to the quantitative analysis of behavioral structural and network systems. In Appendices, we (i) illustrate the connection between a simple network and corresponding adjacency matrices; and (ii) discuss an information theoretic approach to statistical network models.
2. Modeling Notation and a Network Recovery Criterion
From a quantitative information recovery standpoint, a necessary next step is how to model the patterns of connections in the form of a behavioral network that is typically represented by a graph of nodes and edges-links. One basis for modeling this type of economic behavior is to use a network-graph, which consists of a set of nodes or agents and the ties connecting them called edges or links (see, for example, [4,5,6]). Nodes in the network may represent individual agents or some other unit of study and the path of a network is a walk over distinct nodes. Edges correspond to links or interactions between the units and may be directed or undirected. Building on this base, the network-graph of a behavioral network may be mathematically represented by an adjacency matrix Aij, which reflects its node and edge characteristics. In the simple case, this is an n × n symmetric matrix, where n is the number of vertices-nodes in the network. The adjacency matrix has elements Aij = 1, if the vertices I, and j, are connected, and, Aij = 0, otherwise. For a discussion of a particular network graph and its relation to the adjacency matrix, see Appendix A.
Given some of the basic notation involved in specifying the model structure in adaptive behavioral networks, our problem at this point and one of broad interest across the sciences, is the basis for inferring or identifying the corresponding mathematical form of the probability distribution function of the network ensemble pathways null model from limited data. How, for example, should we select the best set of network path probabilities? In making this choice, we note that often in theoretical and applied constrained network and matching economic-econometric models, the optimizing choice criterion has been based on utility, that essential but elusive concept in static and dynamic behavioral studies. Contrary to economic practice where a utility function is usually maximized, it is far from definitive that this is optimal with respect to any scalar functional that is known a priori. A problem with utility as the status measure is that it is only additive under the very restrictive assumption of a quasi-linear utility function. Consequently, from an econometric standpoint, the nonadditive nature of utility as a criterion-status measure may impose structure and yield probability distributions with biases that are not present in or warranted by the data (see [7,8]). In the section ahead, in choosing the optimizing criterion, we note the connection between adaptive behavior and causal entropy maximization, and use entropy that is convex and additive as the optimizing criterion-status measure. This permits the use of information theoretic methods as the basis for identifying the data based network pdf, and the basis for inference.
3. Optimizing Criterion-Status Measure
As an invariance objective for modeling behavior, we seek a causal model that works equally well in network environments and settings. In the search of such an optimizing criterion-status measure, we follow [9] and recognize the connection between adaptive intelligent behavior and causal entropy maximization (AIB-CEM). Under this optimizing criterion, each microstate can be seen as a causal consequence of the macro state to which it belongs. This permits us to recast a behavioral system in terms of path microstates, where entropy reflects the number of ways a macro state can evolve along a path of possible microstates. The more diverse the number of path microstates, the larger the causal path entropy. A uniform-unstructured distribution of the microstates corresponds to a macro state with maximum entropy and minimum information. The result of the AIB-CEM connection is a causal entropic approach that captures self-organized equilibrium seeking behavior. Thus, causal entropy maximization is a link that leads us to believe that a behavioral system with a large number of individuals, interacting locally and in finite time, is in fact optimizing itself. In this context, we recognize that network data comes from dynamic adaptive behavior systems that can be quantified by the notion of information (see [10]). In this setting, the unknown items of network choices are behavior related in the same sense that in an economic system, prices do not behave, people behave. As a framework for predicting choices and preferences, this permits us to consider self organized-equilibrium seeking market like types of behavioral systems in the form of weighted and binary networks. The AIB-CEM connection reflects the micro nature of behavioral network econometric models. From an information recovery standpoint, this usually means that there are more unknowns than data points and thus leads to a stochastic ill posed inverse problem. Traditionally, this has resulted in the use of regularization methods such as tuning parameters and penalized likelihoods. Given the unsatisfactory inferential performance of these methods, in this paper, we seek a unified theory and demonstrate the use of information theoretic entropy based methods to solve the resulting ill-posed stochastic inverse problem and recover estimates of the unknown behavioral network ensemble pathways.
4. The Information Theoretic Entropy Connection
The connection between adaptive intelligent behavior and causal entropy maximization as an optimizing criterion-status measure developed in Section 3, leads directly to information theoretic entropy based methods that provide a natural basis for establishing a causal influence-economic-econometric-inferential link to the data and solving the resulting stochastic inverse problem. Uncertainty regarding statistical models and associated estimating equations and the data sampling-probability distribution function create unsolved problems as they relate to information recovery. Although likelihood is a common loss function used in fitting statistical models, the optimality of a given likelihood method is fragile inference-wise under model uncertainty. In addition, the precise functional representation of the data sampling process cannot usually be justified from physical or behavioral theory. Given this situation, a natural solution is to use estimation and inference methods that are designed to deal with systems that are fundamentally ill posed and stochastic, and where uncertainty and random behavior are basic to information recovery. To identify estimation and inference measures that represent a way to link the model of the process to a family of possible likelihood functions associated with network data, we use the Cressie and Read [11] and Read and Cressie [12] entropy single parameter multi parametric convex CR family of entropic functional-power divergence measures:
In (1), is a parameter that indexes members of the CR-entropy family of distributions, represent the subject probabilities and the , are interpreted as reference probabilities. Being probabilities, the usual probability distribution characteristics of , , and are assumed to hold. In (1), as varies, the resulting CR-entropy family of estimators that minimize power divergence, exhibit qualitatively different sampling behavior that includes Shannon’s entropy, the Kullback-Leibler measure and, in general, includes a range of independent (additive) and correlated network systems (see [13,14,15,16]). In identifying the probability space, the CR family of power divergences is defined through a class of additive convex functions and the CR power divergence measure leads to a broad family of likelihood functions and test statistics. The CR measure exhibits proper convexity in p, for all values of and q, and embodies the required probability system characteristics, such as additivity and invariance with respect to a monotonic transformations of the divergence measures (see [13]). In the context of extremum metrics, the general CR family of power divergence statistics represents a flexible family of pseudo-distance measures from which to recover the joint distribution empirical path probabilities. Thus, the information theoretic entropy based CR family provides a basic information recovery framework for analyzing the joint distribution over possible behavioral network path ensembles. For example, CR γ→0 belongs to the class of exponential probability distributions, and given data underlying a fixed number of nodes and constraints, the resulting ensemble corresponds to the family of exponential random networks (see [17,18]).
If in the CR family of entropy functionals →0, the solution of the first-order condition leads to the logistic expression for the conditional probabilities: Alternatively, if in the family of CR entropy functionals →−1, the solution of the first-order condition leads to the maximum empirical likelihood distribution for the conditional probabilities. Thus, to obtain the probability distribution over the pathways, the principle is to maximize the entropy over pathways, subject to constraints. In general, these solutions do not have a closed-form expression and the optimal values of the unknown network parameters must be numerically determined.
An Optimal Choice of
In terms of an optimal choice of the entropy functional, as varies, the resulting entropy path estimation rules exhibit qualitatively different sampling behavior. In choosing a member of the CR family of entropy divergence functions, we follow [19,20] and consider a bounded parametric family of convex information divergences that satisfy additivity and trace conditions. Convex combinations of γ→0 and γ→−1 span an important part of the probability space and produce a remarkable family of distributions. This parametric family of divergence measures is essentially the linear convex combination of the cases where γ→0 and γ→−1. This family is tractable analytically and provides a basis for joining (combining) statistically independent subsystems. When the reference distribution q is taken to be a uniform noninformative probability density function, we arrive at a one-parameter family of additive convex dynamic functions (for example, see Section 4 of [13]). From the standpoint of extremum-minimization with respect to p, the generalized divergence family, under uniform q, reduces to
In the limit, as , the minimum power divergence entropy likelihood functional is recovered. As , the maximum empirical likelihood (MEL) functional is recovered. This generalized family of divergence measures permits a broadening of the canonical distribution functions and provides a framework for developing a quadratic loss-minimizing estimation rule (see [15]), and raises a question concerning solutions that are independent of a probability distribution and a loss function.
5. Network Information Recovery
Using the notation and network terminology of Section 2, the optimizing criteria of Section 3, and the information theoretic entropy family of Section 4, if we express the network protocol information in the form of an adjacency matrix Aij, the corresponding unknown pathway probabilities Pij must be estimated from data that is observational, noisy and limited in nature. Because the number of unknown pathway parameters of the unobserved and unobservable protocol matrix Aij, are usually much larger than the number of measured data points, the components of the matrix Aij cannot be solved directly. Consequently, while the observed data are directly influenced by the values of model components, the observations are not themselves the direct values of these components and only indirectly reflect their influence. The relationship characterizing the effect of unobservable components on the observed data must be inverted to recover information concerning the unobservable model components from the indirect observations. This means that this type of ill-posed pure or stochastic inverse regularization problem cannot be solved by traditional information recovery-econometric methods.
As we seek a systematic way to generate random networks-graphs that display desired properties, consider a finite discrete linear version of a network problem
where we are given data in the form of an R-dimensional vector y and the network linear operator A is a (R × (K > R) ) non invertible matrix, and we wish to determine the unknown and unobservable network ensemble frequency p = (p1, p2, …, pk). Thus, out of all the probability distributions that satisfy (3) and fulfill the non-negative and adding up probability conditions, we wish to recover the unknown pathway probabilities that cannot be justified by just random interaction.
y = Ap,
As noted earlier, in economics, the representation of a market as a behavioral network comes naturally from microeconomic theory with outcomes presented in the form of a micro canonical ensemble that represents a probability distribution of the microscopic states of the system and the probability of finding the micro system in a possible state. This provides a statistical justification of real networks where statistical means that the network connections Aij are viewed as the realization of a random variable defined over a discrete non negative domain. In this context, a market may then be represented as a random matrix A with statistically independent entries, where analytically we seek an expression for the unknown probabilities that are connected in the random-statistical ensemble A of pathways. The objective is to recover the unknown pathway probabilities across the ensemble without going through the traditional statistical sampling and inference process.
This type of pure-deterministic or stochastic pathway problem may be formulated as a maximization problem over the network pathways, subject to constraints. Thus, the nodes, edges-links properties of the network, act as constraints in the model. Pathway maximization problems of this type, may be formulated as H(pk), where pk is the probability that the process follows one particular path k. Constraints on the process may then be indexed by the Lagrange constraint parameter , Fλ(pk) = 0. The result provides (i) an exact expression for the probabilities over the ensemble of pathways and yields the preferred edge probabilities and (ii) a statistical justification of real networks where statistical means the network connections Aij are viewed in a static or dynamic way as the realization of a random variable defined over a discrete nonnegative domain. For example, a market may be represented as a random matrix A with statistically independent entries.
To indicate the nature and application of information theoretic entropy based inference methods to information recovery in behavioral networks, we use the CR family (1) of entropy functionals , network protocols in the form of a constraining adjacency matrix Aij, and the unknown ensemble of pathway probabilities, . This results in a nonlinear system of equations, where the corresponding Lagrange parameters provide the solution for the unknown pathway probabilities pj. If in the context of (3), we indicate by y the R-dimensional vector of observed fluxes-flows and by p the intermediate pathway measures, the activity of an origin-destination network may be expressed as
where A is a random R × K rectangular matrix that encodes node-specific information about the connections. If we then write the corresponding finite discrete linear inverse problem as
where, and are known, is unknown and we may use the CR family of entropic divergence measures (2) and write static and dynamic problems and define path entropy in the following constrained conditional optimization form:
Taking a derivative with respect to (6) yields a solution for the path probabilities, pj, in terms of the Lagrange multipliers and the underlying probability distribution. Since we work with random networks, the observables conditioned by constraints are formulated in terms of statistics computed over the network ensemble. In the solution process, we associate the ensemble average with an empirical estimate of such an average. Since observables depend on network realizations, we equate the ensemble average against the probability of observing such an average. The resulting constrained statistical ensemble acts as a null model for the observed network data. Thus, network inference and monitoring problems have a strong resemblance to inverse-regularization problems in which key aspects of a system are not directly observable.
y = Ap,
A Binary Network Example
The network recovery Equations (5) and (6) in Section 5 are formalistic. The objective in this section is to clarify how entropy maximization is directly applicable to computing the behavioral network probabilities. To demonstrate the nature and applicability of information theoretic methods in network information recovery, we consider a simple binary directed network example. In this type of network, edges point in a particular direction between two vertices to represent, the flow of information, goods or traffic and the direction the edge is pointing may be represented by an asymmetric adjacency matrix with Aij = 1. In an economic behavioral network, the efficiency of information flow is predicated on discovering or designing protocols that efficiently route information. In many ways, this is like a network where the emphasis is on design and efficiency in routing the flows (see for example, [21]). To carry the above behavioral routing information flow analogy a bit farther, consider the problem of determining least-time point-to-point flows between sub networks, when only the average origin-destination rate flow volume is known. Given information about the network protocol in the form of a matrix composed of binary elements that encode the information about the possible connections, the problem is to recover the origin-destination routing flows from the noisy network data. The preferred probability distribution of dynamical pathways is that obtained by maximizing route-flow entropy over the possible ensemble of possible networks, subject to the known value of an observable average flow-flux rate. Since the unknown path probabilities are much larger than the single average flow data point, this results in an ill-posed linear inverse problem of the type first discussed in Section 3.
To indicate the applicability and implications of the formulation and information recovery method, we follow [22] and use a transportation network problem with aggregate traffic volumes measured at T points in time, yit, where i denotes the sub network. The routing protocol matrix, A, encompasses the routing protocol, and Aij = 1, if the point-to-point traffic at sub network i is 1, and 0, otherwise. The network may at any one point in time, be expressed by the relationship:
If is the total traffic at each sub network, then
In this problem, there are m + 1 constraints that involve an additivity constraint, and m other constraints,
The problem is fundamentally underdetermined and indeterminate because there are more unknowns than data points on which to base a solution.
If we let and qi, be a uniform distribution, the resulting Lagrangean function for the constrained maximization problem is
The derivative of the Lagrangian function leads to,
and yields a solution for the probabilities, pj, in terms of the Lagrange multipliers. In general, the solution for this fundamentally underdetermined problem does not have a closed-form expression, and the optimum values of the unknown parameters must be numerically determined (see [22]). For details of the application of this type of information theoretic entropic methods to weighted and binary flow behavioral network information flow problems, see [8,22,23,24,25,26].
6. Other Network Modeling Alternatives
The formation of behavioral networks may be modeled by interactions among the choice-decision units involved. Like much of traditional theoretical and applied economics and econometrics, the joint determination of these types of behavioral network interactions-linkages are expressed in terms of functional analysis (for example, see [3,5,6,27,28,29]). Because of the nonlinear and often ordinal nature of network interactions, this functional approach poses problems when used in modeling and expressing behavioral network linkages. However, if one chooses to use traditional reductionist functional methods in static and dynamic networks, an alternative is to use information theoretic methods and an entropy basis for recovery and inference.
To put the information theoretic recovery methods of Section 4 and Section 5 in terms of traditional econometric static and dynamic network models, we start by using familiar notation and assuming a general stochastic econometric model of behavioral network equations that involve endogenous and exogenous variables Y and X. Data consistent with the econometric model, may be reflected in terms of general empirical sample moments-constraints such as , where Y, X, and Z are, respectively, a , , vector/matrix of dependent variables, explanatory variables, and instruments, and the parameter vector is the objective of the network recovery process. A solution to the stochastic inverse problem, in the context of the CR family of entropy functionals (1) and based on the optimized value of , is one basis for representing a range of data sampling processes-pdfs and likelihood functions. As γ varies, the resulting estimators that minimize power divergence exhibit qualitatively different sampling behavior. Using empirical sample moments, a solution to the stochastic inverse problem, for any given choice of the parameter, may be formulated as the following extremum-type estimator for :
where the reference distribution q is usually specified as a uniform distribution. This class of diditable versionestimation procedures is referred to as Minimum Power Divergence (MPD) estimation (see [13,15,16,30]).
Identifying the probability space the CR family of divergence measures (1) permits us to exploit the statistical machinery of information theory to gain an insight into the probability density function (PDF) underlying network behavior system or process. The likelihood functionals-PDFs-divergences have an intuitive interpretation in terms of uncertainty and measures of distance. To make use of the CR family of divergence measures to choose an optimal statistical behavioral network system, one might focus on minimizing a loss function in choosing CR () and follow [20] and consider a parametric family of convex information divergences that satisfy additivity and trace conditions. For example, convex combinations of CR (→0) and CR (→−1) span an important part of the probability space and produce a remarkable family of divergences-distributions. This generalized family of divergence measures permits a broadening of the canonical distribution functions and provides a framework for developing a loss-minimizing estimation rule. Given MPD-type convex estimation rules, one option is to use the well-known squared error-quadratic loss criterion and associated quadratic risk function in (14) to choose among a given set of discrete alternatives for the CR goodness-of-fit measures and associated estimators for . The method seeks to define the convex combination of a set of estimators for that minimizes QR, where each estimator is defined, in this case, by the solution to the extremum problem (12). The convex combination of estimators is defined by
The optimum use of the discrete alternatives under QR is then determined by choosing the particular convex combination of the estimators that minimizes
This loss-based convex combination rule represents one possible method of choosing the unknown parameter and permits us to gain insights into the probability distribution-pdf of behavioral networks and to make causal based predictions.
7. Conclusions
The objective of this paper was to provide a basis for extending the adaptive behavior causal entropy maximization concept and information theoretic method to a range of network-graph types of behavioral information recovery settings. To address the unknown nature of the probability sampling model in recovering behavior related preference-choice network pathway information from limited noisy observational data, we have used the Cressie-Read (CR) family of divergence measures and the corresponding information theoretic entropy basis for estimation, inference, model evaluation, and prediction. As a network system objective, this permits entropy, which is convex and additive, as the optimizing criterion and as a basis for inference. The information theoretic method leads to a broad family of entropic functionals that provide a solution to quantitative economic network information recovery under quadratic loss. Applications of binary and weighted networks have been referenced to make clear how entropy maximization is directly applicable to computing the probabilities of behavioral network pathways. We have also indicated in Section 6 how traditional behavioral network formation and interactions among the choice-decision units may be modeled by information theoretic methods. Future research involves extending this new paradigm to grasping the complexity of a range of theoretical and applied behavioral network and matching problems.
Acknowledgments
I would like to acknowledge the helpful comments of M. Ahmed, A. Annila, J. Lee, R. Mittelhammer, A. Nagurney, L. Robinson, S. Villas-Boas, A. Wissner-Gross, A. Zaman, and B. Ziebart.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Network Topology
To give a basis for network topology and the formation and analysis of the adjacency matrix, we use a network graph proposed by D’Souza [31], and depicted in Figure A1.
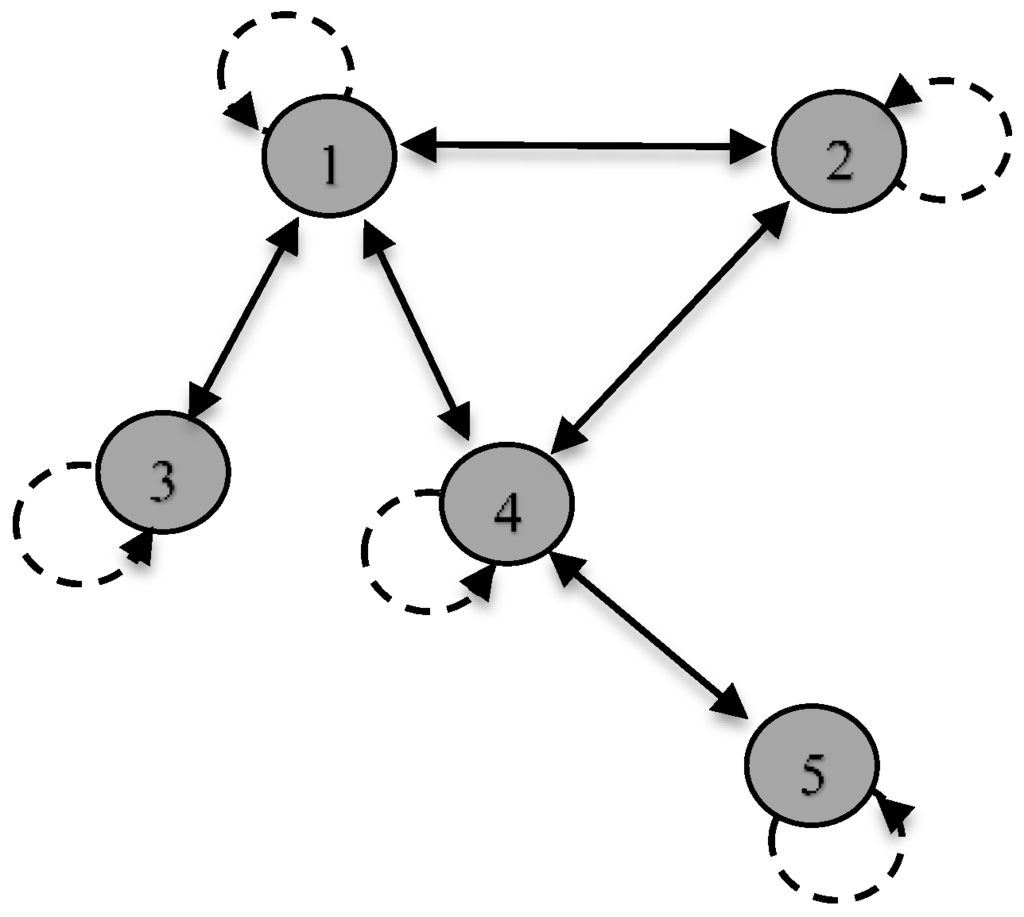

Figure A1.
Example of a simple network. Reproduced with permission.
For completeness we note if the adjacency matrix is symmetric, there is an edge between all i and j. When Aij is binary, then its network links may only take on binary values. In a directed network, edges point in a particular direction between two vertices to represent, the flow of information, goods or traffic and the direction the edge is pointing may be represented by an asymmetric adjacency matrix with Aij = 1. For undirected edges, the adjacency matrix is symmetric. Another useful measure is the concept of network paths that represent a sequence of vertices that follow edges from one to another across the network. In some networks, the edges may be weighted and this means some nonzero elements of the adjacency matrix Aij may be generalized to values other than 1 to represent stronger and weaker.
Appendix B. Statistical Network Models
The exponential family of probability distributions is perhaps the simplest instance of a statistical network model that is based on node degrees and a simple undirected version of statistical models for directed networks introduced by [32], and referred to in the literature as the model (see [33,34]). In this statistical model context, in line with an information theoretic approach, we consider a family of null models for network data. Following Perry and Wolfe [35], let A be an n × n binary symmetric adjacency matrix with zeroes its main diagonal and corresponding to an undirected network of n nodes. Let A be random and a = (a1 ,…, an) be a vector of node specific parameters. When A is composed of independent elements above the main diagonal, then the probability (Aij = 1) = pij(a). Data arising from such an experiment may be represented in the form of a contingency table with empty diagonal cells, where the (i,j)th cell contains the count ai,j, for i not equal to j. For modeling purposes, we need only consider the upper triangular part of the table. We now have the basis for specifying the following corresponding family of CR null models for A:
where a is a vector of node specific parameters, each parameterized by a. When γ→0, the logistic link function is specified, and when γ→−1, the empirical likelihood link function results. To choose among null models in search of an optimal probability system, one might consider a parametric family of convex information divergences and focus on minimizing a quadratic loss function in choosing CR () (see, for example, (2)).
References
- W. Willinger, D. Alderson, and J. Doyle. “Mathematics and the Internet: A Source of Enormous Confusion and Great Potential.” Not. Am. Math. Soc. 56 (2009): 586–599. [Google Scholar]
- A.-L. Barabasi. “The Network Takeover.” Nat. Phys. 8 (2012): 14–16. [Google Scholar] [CrossRef]
- A. Chandrasekhar. “Econometrics of Network Formation.” In The Oxford Handbook of Economic Networks. New York, NY, USA: Oxford University Press, 2016. [Google Scholar]
- M. Newman. “The Mathematics of Networks.” In The New Palgrave Dictionary of Economics, 2nd ed. Edited by S.N. Durlauf and L.E. Blume. Basingstoke, UK: Palgrave Macmillan, 2008. [Google Scholar]
- A. De Paula. “Econometrics of Network Models.” 2015. Available online: http://www.cemmap.ac.uk/uploads/cemmap/wps/cwp521515.pdf (accessed on 10 April 2014).
- B. Graham. “Methods of Identification in Social Networks.” Annu. Rev. Econ. 7 (2015): 465–485. [Google Scholar] [CrossRef]
- S. Presse, K. Ghosh, J. Lee, and K. Dill. “Nonadditive Entropies Yield Probability Distributions with Biases Not Warranted by the Data.” Phys. Rev. Lett. 111 (2013): 180604. [Google Scholar] [CrossRef] [PubMed]
- S. Presse, K. Ghosh, J. Lee, and K. Dill. “Principles of Maximum Entropy and Maximum Caliber in Statistical Physics.” Rev. Mod. Phys. 85 (2013): 1115–1141. [Google Scholar] [CrossRef]
- A. Wissner-Gross, and C.E. Freer. “Causal Entropic Forces.” Phys. Rev. Lett. 110 (2013): 168702. [Google Scholar] [CrossRef] [PubMed]
- N. Georgescu-Roegen. The Entropy Law and the Economic Process. Cambridge, MA, USA: Harvard University Press, 1971. [Google Scholar]
- N. Cressie, and T. Read. “Multinomial Goodness of Fit Tests.” J. R. Stat. Soc. Ser. B 46 (1984): 440–464. [Google Scholar]
- T.R. Read, and N.A. Cressie. Goodness of Fit Statistics for Discrete Multivariate Data. New York, NY, USA: Springer Verlag, 1988. [Google Scholar]
- A. Gorban, P. Gorban, and G. Judge. “Entropy: The Markov Ordering Approach.” Entropy 12 (2010): 1145–1193. [Google Scholar] [CrossRef]
- R. Mittelhammer, and G. Judge. “A family of empirical likelihood functions and estimators for the binary response model.” J. Econom. 164 (2011): 207–217. [Google Scholar] [CrossRef]
- G.G. Judge, and R.C. Mittelhammer. An Information Theoretic Approach to Econometrics. New York, NY, USA: Cambridge University Press, 2012. [Google Scholar]
- G.G. Judge, and R.C. Mittelhammer. “Implications of the Cressie-Read Family of Additive Divergences for Information Recovery.” Entropy 14 (2012): 2427–2438. [Google Scholar] [CrossRef]
- J. Park, and M. Newman. “Statistical Mechanics of Networks.” Phys. Rev. E 74 (2004): 036104. [Google Scholar] [CrossRef] [PubMed]
- L.S. Bargigli, A. Lionetta, and S. Viaggiu. “A Statistical Representation of Markets as Complex Networks.” 2013. Available online: https://arxiv.org/abs/1307.0817 (accessed on 10 April 2014).
- A. Gorban, and I. Karlin. Equilibrium Encirculing Equations of Chemical Kinetics and Their Thermodynamic Analysis. Novosibirsk, Russia: Nauka, 1984. [Google Scholar]
- A.N. Gorban, and I.V. Karlin. “Family of Additive Entropy Functions out of Thermodynamic Limit.” Phys. Rev. E 67 (2003): 016104. [Google Scholar] [CrossRef] [PubMed]
- R. Castro, M. Coates, G. Laing, R. Nowak, and B. Yu. “Network Tomography: Recent Developments.” Stat. Sci. 19 (2004): 499–517. [Google Scholar] [CrossRef]
- W. Cho, and G. Judge. “An Information Theoretic Approach to Network Tomography.” Appl. Econom. Lett. 22 (2014). [Google Scholar] [CrossRef]
- W. Cho, and G. Judge. “Information Theoretic Solutions for Correlated Bivariate Processes.” Econ. Lett. 7 (2006): 201–207. [Google Scholar] [CrossRef]
- T. Squartini, S.E. Ser-Giacomi, D. Garlaschelli, and G. Judge. “Information Recovery in Behavioral Networks.” PLoS ONE 10 (2015): e01277. [Google Scholar] [CrossRef] [PubMed]
- B. Ziebart, J. Bagnell, and A. Dey. “Modeling Interaction Via The Principles of Maximum Causal Entropy.” In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010.
- B. Ziebart, J. Bagnell, and A. Dey. “The Principle of Maximum Causal Entropy for Estimating Interacting Processes.” IEEE Trans. Inf. Theory 59 (2013): 1966–1980. [Google Scholar] [CrossRef]
- C. Manski. “Identification of Endogenous Social Effects: The Reflection Problem.” Rev. Econ. Stud. 60 (1993): 531–542. [Google Scholar] [CrossRef]
- S. Simpson, M. Moussa, and P. Laurenti. “An Exponential Random Graph Modeling Approach to Creating Group Based Representative Whole Brain Connectivity Networks.” 2011. Available online: https://arxiv.org/abs/1101.2592 (accessed on 10 April 2014).
- L.W. Blume, B.S. Durlauf, and R. Jayaraman. “Linear Social Interaction Models.” J. Political Econ. 123 (2015): 444–496. [Google Scholar] [CrossRef]
- D. Miller, and G. Judge. “Information Recovery in a dynamic Statistical Markov Model.” Econometrics 3 (2015): 187–198. [Google Scholar] [CrossRef]
- R. D’Souza. “Network Theory and Applications.” 2014. Available online: http://mae.engr.ucdavis.edu/dsouza/ecs289 (accessed on 11 April 2014).
- P. Holland, and S. Leinhardt. “An Exponential Family of probability Distributions for Directed Graphs.” J. Am. Stat. Assoc. 76 (1981): 33–51. [Google Scholar] [CrossRef]
- A. Goldenberg, X. Zheng, S.E. Fienberg, and E.M. Airoldi. “A Survey of Statistical Network Models.” Mach. Learn. 2 (2009): 129–233. [Google Scholar] [CrossRef]
- A. Rinaldo, S. Petrovic, and S. Fienberg. “Maximum Likelihood Estimation in the Beta-Mode.” Ann. Stat. 41 (2013): 1085–1110. [Google Scholar] [CrossRef]
- P. Perry, and P. Wolfe. “Null Models for Network Data.” 2012. Available online: https://arxiv.org/abs/1201.5871 (accessed on 11 April 2014).
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).