Building a Structural Model: Parameterization and Structurality †
Abstract
:1. Introduction
2. Structural Econometric Modeling: A Specific Approach
2.1. Econometric Models as Statistical Models
2.2. Recursive Decomposition
2.3. Recursive Decomposition: Explanation and Structurality
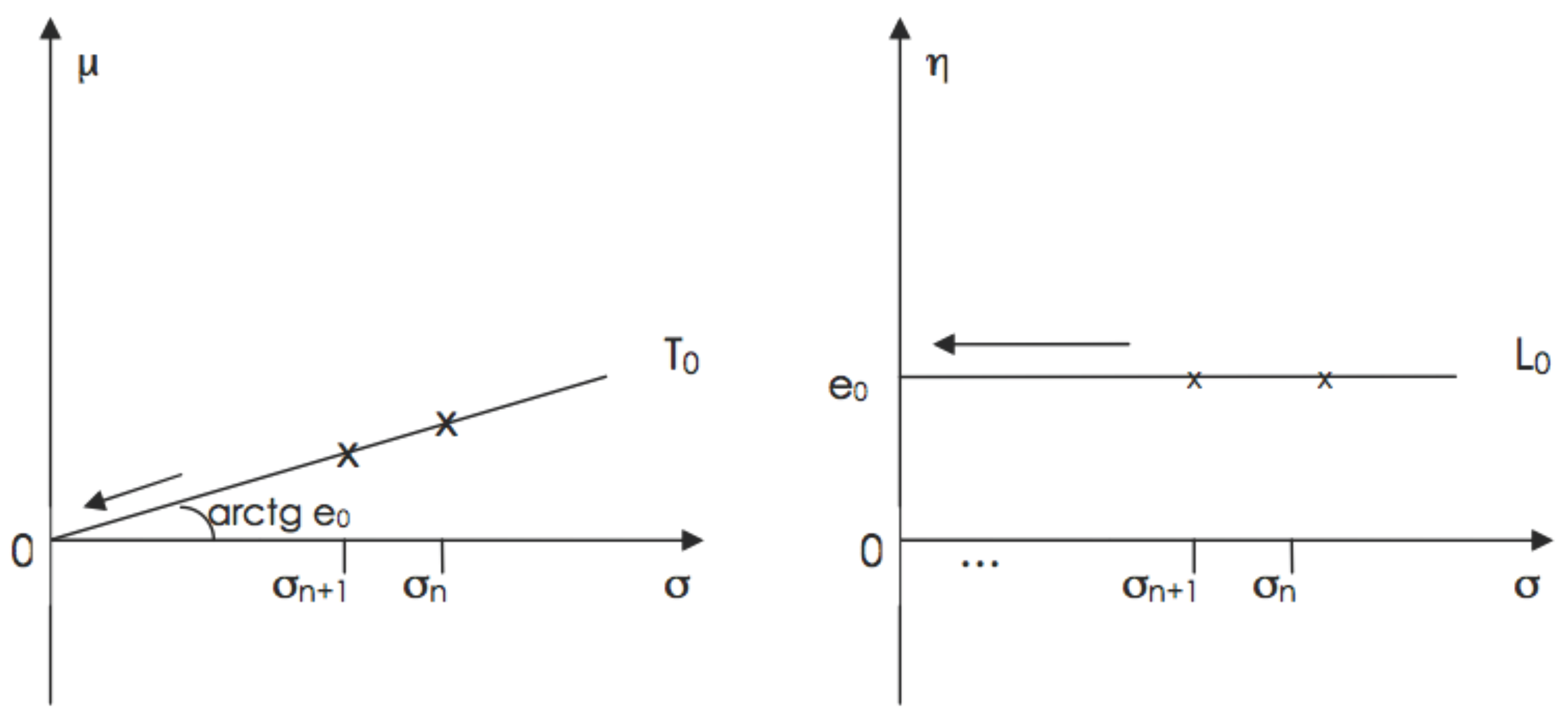
2.4. Parsimonious Modelling
2.5. Causal and Structural Models
3. Structural Model and Parameterization
4. Pitfalls with Alternative Parameterizations
4.1. Reparameterizations Suggesting Erroneous Constraints
4.1.1. A Simple Pedagogic Example
4.1.2. A Case in Simultaneous Equations
4.2. Reparameterizations Involving Different but Observationally Equivalent Sub-Mechanisms
5. Concluding Remarks
5.1. Summarizing: The Basic Framework
5.2. On the Use of Models for the Design of Economic Policy
Author Contributions
Conflicts of Interest
References
- P.M. Illari, and J. Williamson. “What is a mechanism? Thinking about mechanisms across the sciences.” Eur. J. Philos. Sci. 2 (2012): 119–135. [Google Scholar] [CrossRef]
- M. Mouchart, G. Wunsch, and F. Russo. “The issue of control in multivariate systems: A contribution of structural modelling.” Available online: http://dial.uclouvain.be/handle/boreal:162165?sit_ename=UCL (accessed on 7 April 2016).
- T.C. Koopmans. “When is an Equation System Complete for Statistical Purposes? ” In Statistical Inference in Dynamic Economic Models. Edited by T.C. Koopmans. Cowles Commission Monograph 10; New York, NY, USA: John Wiley & Sons, 1950. [Google Scholar]
- T. Haavelmo. “Methods of measuring the marginal propensity to consume.” J. Am. Stat. Assoc. 42 (1947): 105–122. [Google Scholar] [CrossRef]
- J.D. Sargan. “Wages and Prices in the United Kingdom: A Study in Econometric Methodology, (with Discussion).” In Econometric Analysis for National Economic Planning. Edited by P.E. Hart, G. Mills and J.K. Whitaker. London, UK: Butterworth, 1964, Volume 16, pp. 25–63. [Google Scholar] Reprinted in Econometrics and Quantitative Economics. D.F. Hendry, and K.F Wallis, eds. Oxford, UK: Blackwel, 1984. and in Contribution to Econometrics. J.D. Sargan, ed. Cambridge, UK: Cambridge Univesity Press, 1988, Volume 1.
- D.F. Hendry. “Econometric Methodology: A Personal Perspective.” In Advances in Econometrics. Edited by T.F. Bewley. Cambridge, UK: Cambridge Univesity Press, 1987. [Google Scholar]
- T. Haavelmo. “The Probability Approach in Econometrics.” Econometrica 12 (1944): 1–118. [Google Scholar] [CrossRef]
- A. Zellner. “Statistical Analysis of Econometric Models.” J. Am. Stat. Assoc. 74 (1979): 628–643. [Google Scholar] [CrossRef]
- D.F. Hendry. Dynamic Econometrics. Oxford, UK: Oxford University Press, 1995. [Google Scholar]
- G. Wunsch, M. Mouchart, and F. Russo. “Functions and mechanisms in structural-modelling explanations.” J. Gen. Philos. Sci. 45 (2014): 187–208. [Google Scholar] [CrossRef]
- J.-F. Richard. “Models with several regimes and changes in exogeneity.” Rev. Econ. Stud. 47 (1980): 1–20. [Google Scholar] [CrossRef]
- D.F. Hendry, and G.E. Mizon. “Exogoneity, causality, and co-breaking in economic policy analysis of a small econometric model of money in the UK.” Empir. Econ. 23 (1998): 267–294. [Google Scholar] [CrossRef]
- R. Lucas. “Econometric Policy Evaluation: A Critique.” In The Phillips Curve and Labour Markets. Edited by K. Bruner and A. Metzler. Carnegie-Rochester Conference Series on Public Policy; New York, NY, USA: American Elsevier, 1976, Volume 1, pp. 19–46. [Google Scholar]
- A.S. Deaton. “Model Selection Procedures, or, does the Consumption Function Exist? ” In Evaluating the Reliability of Macro-Economic Models. Edited by G.C. Chow and P. Corsi. New York, NY, USA: John Wiley and Sons, 1982, Chapter 5; pp. 43–69. [Google Scholar]
- J.J. Heckman, and E.J. Vytlacil. “Econometric evaluation of social programs, part I: Causal models, structural models and econometric policy evaluation.” In Handbook of Econometrics. Edited by J. Heckman and E. Leamer. Amsterdam, The Netherlands: Elsevier, 2007, Volume 6B, pp. 4779–4874. [Google Scholar]
- J.J. Heckman. “The scientific model of causality.” Sociol. Methodol. 35 (2005): 1–97. [Google Scholar] [CrossRef]
- J.J. Heckman. “Econometric causality.” Int. Stat. Rev. 76 (2008): 1–27. [Google Scholar] [CrossRef]
- M. Mouchart, and F. Russo. “Causal explanation: Recursive decompositions and mechanisms.” In Causality in the Sciences. Edited by P. McKay Illari, F. Russo and J. Williamson. Oxford, UK: Oxford University Press, 2011, Chapter 15; pp. 317–337. [Google Scholar]
- J. Pearl. Causality: Models, Reasoning, and Inference, Revised and Enlarged edition 2009. Cambridge, UK: Cambridge University Press, 2000. [Google Scholar]
- J.-F. Richard. “Exogeneity, causality and structural invariance in econometric modelling.” In Evaluating the Reliability of Macro-Economic Models. Edited by G.C. Chow and P. Corsi. New York, NY, USA: Wiley and Sons, 1982, Chapter 7; pp. 105–112. [Google Scholar]
- D.B. Rubin. “Statistics and causal inference, Comment: Which ifs have causal answers.” J. Am. Stat. Assoc. 81 (1986): 961–962. [Google Scholar] [CrossRef]
- G.W. Imbens, and D.B. Rubin. Causal Inference in Statistics, Social and Biomedical Sciences. Cambridge, UK: Cambridge University Press, 2015. [Google Scholar]
- J.J. Heckman, and R. Pinto. Causal Analysis after Haavelmo. Working Paper Series, No. 19453; Cambridge, MA, USA: The national bureau of economic research, 2013, pp. 1–51. [Google Scholar]
- O. Barndorff-Nielsen. Information and Exponential Families in Statistical Theory. New York, NY, USA: John Wiley & Sons, 1978. [Google Scholar]
- J.-P. Florens, M. Mouchart, and J.-M. Rolin. “Réductions dans les Expériences Bayésiennes Séquentielles, paper presented at the Colloque Processus Aléatoires et Problèmes de Prévision, Bruxelles, Belgium, 24–25 April 1980.” Cahiers du Centre d’Etudes de Recherche Opérationnelle 23 (1980): 353–362. [Google Scholar]
- J.-P. Florens, and M. Mouchart. “Conditioning in Dynamic Models.” J. Time Ser. Anal. 53 (1985): 15–35. [Google Scholar] [CrossRef]
- R. Engle, D. Hendry, and J.-F. Richard. “Exogeneity.” Econometrica 51 (1983): 277–304. [Google Scholar] [CrossRef]
- J.-P. Florens, M. Mouchart, and J.-M. Rolin. “Noncausality and marginalization of Markov processes.” Econom. Theory, 9 (1993): 241–262. [Google Scholar] [CrossRef]
- H. Genberg. “Constraints on the parameters in two simple simultaneous equation models.” Econometrica 40 (1972): 855–865. [Google Scholar] [CrossRef]
- A. Zellner. “Constraints often overlooked in analyses of simultaneous equation models.” Econometrica 40 (1972): 849–853. [Google Scholar] [CrossRef]
- A. Zellner. “Constraints often overlooked in analyses of simultaneous equation models: Reply.” Econometrica 44 (1976): 619–624. [Google Scholar] [CrossRef]
- A. Zellner. “Constraints often overlooked in analyses of simultaneous equation models: Further reply.” Econometrica 44 (1976): 627–628. [Google Scholar] [CrossRef]
- G.S. Maddala. “Constraints often overlooked in analyses of simultaneous equation models: Comment.” Econometrica 44 (1976): 615–616. [Google Scholar] [CrossRef]
- G.S. Maddala. “Constraints often overlooked in analyses of simultaneous equation models: Rejoinder.” Econometrica 44 (1976): 625. [Google Scholar] [CrossRef]
- R.J. Bowden. “Specification, estimation and inference for models in disequilibrium.” Int. Econ. Rev. 19 (1978): 711–726. [Google Scholar] [CrossRef]
- R.C. Fair, and D.M. Jaffee. “Methods of estimation for markets in disequilibrium.” Econometrica 40 (1972): 497–514. [Google Scholar] [CrossRef]
- S. An, and F. Schorfheide. “Bayesian analysis of DSGE Models.” Econom. Rev. 26 (2007): 113–172. [Google Scholar] [CrossRef]
- 1But if the estimation of introduces new data, then we have a case of mixed estimation, “à-la-Theil”, or of mixed Bayesian estimation and the constraints may have a role in the procedure of blending two sources of data but not for introducing new constraints on the parameter space.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mouchart, M.; Orsi, R. Building a Structural Model: Parameterization and Structurality. Econometrics 2016, 4, 23. https://doi.org/10.3390/econometrics4020023
Mouchart M, Orsi R. Building a Structural Model: Parameterization and Structurality. Econometrics. 2016; 4(2):23. https://doi.org/10.3390/econometrics4020023
Chicago/Turabian StyleMouchart, Michel, and Renzo Orsi. 2016. "Building a Structural Model: Parameterization and Structurality" Econometrics 4, no. 2: 23. https://doi.org/10.3390/econometrics4020023
APA StyleMouchart, M., & Orsi, R. (2016). Building a Structural Model: Parameterization and Structurality. Econometrics, 4(2), 23. https://doi.org/10.3390/econometrics4020023




