Bayesian Approach to Disentangling Technical and Environmental Productivity

Abstract

This paper models the firm’s production process as a system of simultaneous technologies for desirable and undesirable outputs. Desirable outputs are produced by transforming inputs via the conventional transformation function, whereas (consistent with the material balance condition) undesirable outputs are by-produced via the so-called “residual generation technology”. By separating the production of undesirable outputs from that of desirable outputs, not only do we ensure that undesirable outputs are not modeled as inputs and thus satisfy costly disposability, but we are also able to differentiate between the traditional (desirable-output-oriented) technical productivity and the undesirable-output-oriented environmental, or so-called “green”, productivity. To measure the latter, we derive a Solow-type Divisia environmental productivity index which, unlike conventional productivity indices, allows crediting the ceteris paribus reduction in undesirable outputs. Our index also provides a meaningful way to decompose environmental productivity into environmental technological and efficiency changes.

1. Introduction

The by-production of undesirable, or so-called “bad”, outputs is an inherent attribute of many production processes. Electric power generation is a classical example of such a process, where the production of electricity (desirable output) is accompanied by the emission of pollutant gases (undesirable outputs). It is therefore imperative to account for undesirable outputs when estimating the productivity growth for such processes (e.g., see [1,2]).

The estimation of productivity (and, potentially, its components) naturally requires the estimation of the firm’s production process, the modeling of which in the presence of undesirable outputs is however not a clear-cut issue. A standard approach is to condition the conventional transformation (production) function on undesirable outputs (e.g., [3,4,5]) which, effectively, treats these outputs as inputs. Such a treatment of undesirable outputs has since been heavily criticized due the implied strong disposability of undesirable outputs [6] and the violation of the “material balance condition” [7]. A popular alternative approach to tackling undesirable outputs is to specify a (single) directional output distance function [6,8] which accommodates both the expansion in desirable outputs and a simultaneous contraction in undesirable outputs. Feng and Serletis [9] have recently proposed a primal Divisia productivity index based on such a directional output distance function.

Both the directional output distance function and the productivity index based on the latter allow the identification of a “composite” measure of inefficiency and productivity (respectively) only. Specifically, when modeling the production technology via a (single) directional distance function (e.g., [6]), the inefficiency is defined over the entire vector of outputs, both desirable and undesirable. This produces a single measure of inefficiency which is a weighted combination of the technical and environmental inefficiencies, where the “weighting” is done on the basis of the prespecified directional vector. Similarly, the directional-output-distance-function-based productivity index identifies the “composite” productivity growth only. Thus, modeling undesirable outputs via the standard directional functions precludes researchers from disentangling the technical inefficiency/productivity, conventionally oriented along desirable outputs, from the environmental, or so-called “green”, inefficiency/productivity, oriented along undesirable outputs.1 Both can be of great interest from a policy perspective.

In this paper, we follow a different path to modeling the production process with undesirable outputs in the spirit of Fernández et al. [11,12, Forsund [13] and Murty et al. [7]. Specifically, we model the firm’s production process as a system of separate simultaneous production technologies for desirable and undesirable outputs. In this setup, desirable outputs are produced by transforming inputs via the conventional transformation function satisfying all standard assumptions. Consistent with the material balance condition, the by-production of undesirable outputs is however treated as the so-called “residual generation technology”. The above setup explicitly recognizes that the generation of undesirable outputs is not the intended production but rather the by-production process. By separating the generation of undesirable outputs from that of desirable outputs, we ensure that the former are not modeled as inputs as well as take into account their “costly disposability” (see [7]).

The by-production system approach that we employ in this paper permits us to not only distinguish between technical efficiency and (undesirable-output-specific) environmental efficiencies but to also differentiate between traditional technical productivity and environmental (“green”) productivity. Specifically, we derive a Solow [14] type primal (Divisia) environmental productivity index which, unlike a conventional desirable-output-oriented productivity index, is defined as the contraction rate in undesirable outputs unexplained by the contraction in desirable outputs. This allows us to credit the ceteris paribus reduction in undesirable outputs. Our environmental productivity index also provides a meaningful way to decompose productivity into environmental technological change and environmental efficiency change.

We apply our system approach as well as the environmental productivity index to study the efficiency and productivity trends among coal-fired electric power generating plants in the U.S. during the 1985–1995 period. The production of (desirable) electric power by these utilities is accompanied by the (undesirable) emission of SO₂ and NO_x gases.

We estimate the model subject to theoretical regularity conditions using (numerically) efficient Bayesian MCMC technique, where we also allow for unobserved plant-specific heterogeneity in addition to time-varying inefficiencies. We impose monotonicity and curvature regularity restrictions (at every data point) in order to ensure that our results are economically meaningful, as emphasized by Barnett et al. [15] and Barnett [16]. Among many things, we find that electric utilities in our sample tend to suffer from higher levels of environmental inefficiency in the emission of SO₂ than in the emission of NO_x gases. We also document a significant divergence between the electric-power-oriented technical productivity and the emission-oriented environmental productivity. Specifically, we find that, while the pooled posterior mean estimate of (annual) productivity growth is negative for electric power generation (–0.13%), it is non-negligibly positive for the SO₂ and NO_x emissions:2 2.25% and 3.31% per annum, respectively. The cumulative eleven-year growth is 23.26% for the SO₂-oriented environmental productivity, 37.98% for the NO_x-oriented environmental producitivity and a mere 5.33% for the electric-power-oriented technical productivity.

The rest of the paper proceeds as follows. Section 2 describes the by-production system approach to modeling production technology in the presence of undesirable outputs as well as provides the derivation of the environmental productivity index. Data are discussed in Section 3. We explain our econometric strategy in Section 4. Section 5 presents the results, and Section 6 concludes.

2. The By-Production Model

Building on Fernández et al. [11,12], the undesirable-output-generating production system (𝕋) with J inputs $\mathbf{X}\in {\mathbb{R}}_{+}^J$, M desirable outputs $\mathbf{Y}\in {\mathbb{R}}_{+}^M$ and P undesirable outputs $\mathbf{B}\in {\mathbb{R}}_{+}^P$ can be formalized as the intersection of the primary technology used in the production of desirable outputs (${\mathbb{T}}_0$) and P individual undesirable-output residual generation technologies (${\mathbb{T}}_p,p=1,\dots ,P$), i.e.,3

$$\begin{array}{c} \mathbb{T}={\mathbb{T}}_0\cap {\mathbb{T}}_1\cap \dots \cap {\mathbb{T}}_p\dots \cap {\mathbb{T}}_P,\text{where}\hfill \\ {\mathbb{T}}_0\stackrel{\text{def}}{=}\{(\mathbf{X},\mathbf{Y}):\mathbf{X}\text{can}\text{produce}\mathbf{Y}\}\hfill \\ {\mathbb{T}}_p\stackrel{\text{def}}{=}\{(B_p,\mathbf{Y}):\mathbf{Y}\text{generates}{B}_p\}\forall p=1,\dots ,P.\hfill \end{array}$$

(1)

Consider the case of $J=3$ inputs, $M=1$ desirable and $P=2$ undesirable outputs (as in our empirical application). Allowing for technical inefficiency in the production of a desirable output and environmental inefficiency in the by-production of undesirable outputs, we rewrite system 𝕋 in terms of the stochastic transformation function and two separate (environmental) residual generation functions for each undesirable output, i.e.,

$$\begin{array}{cc}\hfill F(\mathbf{X},{\theta }^{-1}Y)& =exp\left\{v_0\right\}\hfill \end{array}$$

(2a)

$$\begin{array}{cc}\hfill H_p\left(Y,{\lambda }_p{B}_p\right)& =exp\left\{v_p\right\}\forall p=1,2,\hfill \end{array}$$

(2b)

where $\theta \le 1$ and ${\lambda }_p\le 1$ are technical and environmental efficiencies, respectively; and $(v_0,v_p)$ are the white noise terms. The transformation function $F(·)$ is assumed to satisfy all standard properties such as continuity, positive (negative) monotonicity in Y (X), linear homogeneity in Y and concavity in X and Y. Similarly, the residual generation function $H_p(·)$ is continuous, positively (negatively) monotonic in $B_p$ (Y), linearly homogeneous in $B_p$ and convex in Y and $B_p$.

Thus, the production system (2) permits the identification of both the technical and environmental efficiencies: θ and ${\lambda }_p(p=1,\dots ,P)$. The latter is feasible due to the separability of the primary desirable-output generating production technology (2a) from the undesirable-output residual generating technologies (2b), which is motivated by the by-production approach satisfying the material balance condition. For instance, one would generally be unable to disentangle technical and environmental efficiencies (the way the above system approach allows us to) if following a popular alternative to the estimation of production processes in the presence of undesirable outputs based on the directional distance function [8].

Specifically, when modeling the production technology via a (single) directional distance function (e.g., [6]), the inefficiency is defined over the entire vector of outputs, both desirable and undesirable, using an a priori specified directional vector. The latter precludes researchers from disentangling the technical inefficiency conventionally oriented along desirable outputs from the environmental inefficiency oriented along undesirable outputs. The directional distance function rather produces a “composite” measure of inefficiency which is a weighted combination of the two, where the “weighting” is done on the basis of the prespecified direction. Further, unlike a system in (2), the directional distance function yields an additive, not a proportional, measure of inefficiency.

Technical and Environmental Productivity

The production system 𝕋 that we consider in this paper permits us to not only distinguish between technical efficiency θ (conventionally defined over the desirable output) and undesirable-output-specific environmental efficiencies $\{{\lambda }_p;p=1,\dots ,P\}$ but to also differentiate between traditional technical productivity and environmental, or the so-called “green”, productivity.

Letting time t enter the transformation and residual generation functions $F(·)$ and $H_p(·)$ explicitly and making use of their linear homogeneity properties, system (2) can be rewritten in the log form as

$$\begin{array}{cc}\hfill ln{Y}_t& =lnf({\mathbf{X}}_t,t)-u_{0,t}+v_{0,t}\hfill \end{array}$$

(3a)

$$\begin{array}{cc}\hfill ln{B}_{p,t}& =ln{h}_p(Y_t,t)+u_{p,t}+v_{p,t}\forall p=1,2,\hfill \end{array}$$

(3b)

where, for convenience, we define $f(·)\stackrel{\text{def}}{=}{\left[F(·,1)\right]}^{-1}$ and $h_p(·)\stackrel{\text{def}}{=}{\left[H_p(·,1)\right]}^{-1}$; and $u_{0,t}\stackrel{\text{def}}{=}-ln{\theta }_t\ge 0$ and $u_{p,t}\stackrel{\text{def}}{=}-ln{\lambda }_{p,t}\ge 0(p=1,2)$ are technical and environmental inefficiencies, respectively.

Total differentiation of (3) with respect to t yields

$$\begin{array}{cc}\hfill \frac{dln{Y}_t}{dt}& =\sum _{j=1}^J\frac{\partial lnf({\mathbf{X}}_t,t)}{\partial ln{X}_{j,t}}\frac{\partial ln{X}_{j,t}}{\partial t}+\frac{\partial lnf({\mathbf{X}}_t,t)}{\partial t}-\frac{\partial u_{0,t}}{\partial t}\hfill \end{array}$$

(4a)

$$\begin{array}{cc}\hfill \frac{dln{B}_{p,t}}{dt}& =\frac{\partial ln{h}_p(Y_t,t)}{\partial ln{Y}_t}\frac{\partial ln{Y}_t}{\partial t}+\frac{\partial ln{h}_p(Y,t)}{\partial t}+\frac{\partial u_{p,t}}{\partial t}\forall p=1,2,\hfill \end{array}$$

(4b)

where we have made use of $\partial v_{0,t}/\partial t=\partial v_{p,t}/\partial t=0$ since $(v_0,v_p)$ are the i.i.d. white noise. After some rearranging, from (4a) we get the following Solow [14] type (Divisia) technical productivity index:

$$TPG\stackrel{\text{def}}{=}\frac{dln{Y}_t}{dt}-\sum _{j=1}^J\frac{\partial lnf({\mathbf{X}}_t,t)}{\partial ln{X}_{j,t}}\frac{\partial ln{X}_{j,t}}{\partial t}=\underset{TTC}{\underbrace{\frac{\partial lnf({\mathbf{X}}_t,t)}{\partial t}}}\underset{TEC}{\underbrace{-\frac{\partial u_{0,t}}{\partial t}}},$$

(5)

along with the similarly defined environmental productivity index from (4b):

$$EP{G}_p\stackrel{\text{def}}{=}-\left(\frac{dln{B}_{p,t}}{dt}-\frac{\partial ln{h}_p(Y_t,t)}{\partial ln{Y}_t}\frac{\partial ln{Y}_t}{\partial t}\right)=\underset{ET{C}_p}{\underbrace{-\frac{\partial ln{h}_p(Y,t)}{\partial t}}}\underset{EE{C}_p}{\underbrace{-\frac{\partial u_{p,t}}{\partial t}}}\forall p=1,2.$$

(6)

The negative monotonicity of $F(·)$ and $H_p(·)$ in inputs and desirable outputs, respectively, imply that $\partial lnf({\mathbf{X}}_t,t)/\partial ln{X}_{j,t}\ge 0$ and $\partial ln{h}_p(Y_t,t)/\partial ln{Y}_t\ge 0$.4

Unlike $TPG$ which is conventionally defined as the expansion rate in a desirable output unexplained by the growth in inputs, the environmental productivity index $EPG$ is defined as the contraction rate in an undesirable output unexplained by the contraction in desirable outputs.5 This allows crediting the ceteris paribus reduction in undesirable outputs.

Further, Equations (5) and (6) provide a meaningful way to decompose respective productivity indices into technical/technological change and efficiency change. The conventional technical productivity index $TPG$ equals the sum of the technical change $TTC=\partial lnf({\mathbf{X}}_t,t)/\partial t$, which measures the temporal shift in the production frontier, and technical efficiency change $TEC=-\partial u_{0,t}/\partial t$, which measures the movement toward (away from) the frontier. Similarly, the $B_p$-oriented environmental productivity index $EP{G}_p$ is decomposed into similarly interpreted environmental technological change $ET{C}_p=-\partial ln{h}_p(Y_t,t)/\partial t$ and environmental efficiency change $EE{C}_p=-\partial u_{p,t}/\partial t$.

Note the conceptual difference between the definition of a “technological progress” for desirable outputs and that for undesirable outputs. Namely, for a desirable output Y the technological progress corresponds to the case of $TTC>0$, i.e., an outward shift in the production frontier over time, whereas for an undesirable output $B_p$ the technological progress corresponds to $ET{C}_p<0$, i.e., an inward shift in the residual generating frontier over time. Thus, the residual generating frontier $H_p(·)(p=1,\dots ,P)$ is defined as the minimum quantity of undesirable output generated when producing a given quantity of desirable outputs subject to the material balance condition.

We emphasize that the primary advantage of employing a system approach to model the production process with undesirable outputs, which we consider in this paper, is the opportunity to disentangle technical and environmental productivities. For instance, as in the case of inefficiency, one generally cannot do that when using the productivity index based on the directional distance function [9].

3. Data

The data we use come from Pasurka [17] and Murty et al. [7]. A balanced panel consists of 92 coal-fired electric power generating plants operating in the U.S. over the period from 1985 to 1995. We focus on coal-fired plants only in order to minimize heterogeneity among units. More specifically, we focus on utilities of which at least 95% of total fuel consumption (measured in Btu) come from coal. We also exclude utilities whose consumption of fuels other than coal, oil and natural gas exceeds ${10}^{-4}\%$ of total fuel consumption.

The specification of outputs and inputs is as follows. The desirable output is the net electric power generation Y, measured in kWh. The two undesirable outputs are (i) the SO₂ (sulfur dioxide) gas emissions $B_1$ and (ii) the NO_x (nitrogen oxides) gas emissions $B_2$, both measured in short-tons. The three inputs to the production are (i) the real stock of physical capital $X_1$, constructed from historical cost of plant data and deflated to constant dollars using the Handy-Whitman Index; (ii) labor $X_2$, measured in the number of employees; and (iii) energy $X_3$, i.e., the heat content of coal, oil and natural gas consumption, measured in Btu.

The data on the cost of plants and equipment (used in the construction of the capital stock) and the number of employees come from the U.S. Federal Energy Regulatory Commission Form 1 survey. The data on fuel consumption, net power generation and pollutant gas emissions come from the U.S. Department of Energy Form EIA-767 survey. For more details on the data, see Pasurka [17].

4. Econometric Strategy

Under the assumption of the translog functional form of $lnf(·)$ and $ln{h}_b(·)$, from system (3) we get the following system consisting of the production function for a desirable output $Y_{it}$:

$$\begin{array}{cc}\hfill y_{it}=& {\alpha }_{0,i}+\sum _{j=1}^J{\alpha }_j{x}_{j,it}+\frac{1}{2}\sum _{h=1}^J\sum _{j=1}^J{\alpha }_{hj}{x}_{h,it}{x}_{j,it}+\hfill \\ & \sum _{t^{\prime }=1}^T{\beta }_{t^{\prime }}{D}_{i{t}^{\prime }}+\sum _{t^{\prime }=1}^T\sum _{j=1}^J{\beta }_{t^{\prime }j}{D}_{i{t}^{\prime }}{x}_{j,i{t}^{\prime }}+v_{0,it}-u_{0,it},i=1,\dots ,n;t=1,\dots ,T,\hfill \end{array}$$

(7)

complemented by the (environmental) residual generation technologies for undesirable outputs $(B_{1,it},B_{2,it})$:

$$\begin{array}{cc}\hfill b_{1,it}& ={\gamma }_{0,i}+{\gamma }_1{y}_{it}+\frac{1}{2}{\gamma }_{11}{y}_{it}^2+\sum _{t^{\prime }=1}^T{\phi }_{t^{\prime }}{D}_{it}+\sum _{t^{\prime }=1}^T{\phi }_{t^{\prime }1}{D}_{it}{y}_{it}+v_{1,it}+u_{1,it}\hfill \end{array}$$

(8a)

$$\begin{array}{cc}\hfill b_{2,it}& ={\delta }_{0,i}+{\delta }_1{y}_{it}+\frac{1}{2}{\delta }_{11}{y}_{it}^2+\sum _{t^{\prime }=1}^T{\psi }_{t^{\prime }}{D}_{it}+\sum _{t^{\prime }=1}^T{\psi }_{t^{\prime }1}{D}_{it}{y}_{it}+v_{2,it}+u_{2,it},\hfill \end{array}$$

(8b)

where a lower-case variable denotes the log of its upper-case counterpart, and $D_{it}$ denotes the time dummy. For greater flexibility, we also allow for unobserved firm-specific heterogeneity which we model via “true” random effects $\{({\alpha }_{0,i},{\gamma }_{0,i},{\delta }_{0,i});i=1,\dots ,n\}$. The presence of these random effects (in addition to inefficiencies) captures additional technological heterogeneity among firms.

Since $y_{it}$ appears on the right-hand side of equations for undesirable outputs $b_{1,it}$ and $b_{2,it}$, it is imperative that all three equations in (7)–(8) be estimated as a system (of simultaneous equations) in order to control for the endogeneity of outputs. We estimate this production system subject to symmetry (${\alpha }_{hj}={\alpha }_{jh}$) as well as monotonicity and curvature restrictions. In this paper, we thus concur with Barnett [15] and Barnett [16] on the importance of maintaining the latter theoretical regularity conditions when modeling technology (especially, if allowing for inefficiency) in order to ensure that the results are economically meaningful.

Specifically, the monotonicity conditions are:

$$\begin{array}{cc}\hfill \frac{\partial y_{it}}{\partial x_{j,it}}& ={\alpha }_j+\sum _{h=1}^J{\alpha }_{hj}{x}_{h,it}+\sum _{t^{\prime }=1}^T{\beta }_{t^{\prime }j}{D}_{i{t}^{\prime }}\ge 0\forall j=1,\dots ,J\hfill \\ \hfill \frac{\partial b_{1,it}}{\partial y_{it}}& ={\gamma }_1+{\gamma }_{11}{y}_{it}+\sum _{t^{\prime }=1}^T{\phi }_{t^{\prime }1}{D}_{it}\ge 0\hfill \\ \hfill \frac{\partial b_{2,it}}{\partial y_{it}}& ={\delta }_1+{\delta }_{11}{y}_{it}+\sum _{t^{\prime }=1}^T{\psi }_{t^{\prime }1}{D}_{it}\ge 0.\hfill \end{array}$$

(9)

The curvature is imposed using restrictions on the eigenvalues of the Hessian matrices in levels (see [18]). We employ the following stochastic specification for system (7)–(8):

$$\begin{gathered} \begin{array}{cc}\hfill {\mathbf{v}}_{it}={[v_{0,it},v_{1,it},v_{2,it}]}^{\prime }& \sim \text{i.i.d.}𝒩(\mathbf{0},\Sigma )\hfill \end{array} \\ \begin{array}{cc}\hfill {\mathbf{u}}_{it}={[u_{0,it},u_{1,it},u_{2,it}]}^{\prime }& \sim {𝒩}_{+}({\mathbf{Z}}_{it}\tau ,{\Sigma }_u),\hfill \end{array} \end{gathered}$$

(10)

where ${𝒩}_{+}$ denotes the (multivariate) half-normal distribution;6 Σ and ${\Sigma }_u$ are the covariance matrices; ${\mathbf{Z}}_{it}={\mathbf{I}}_3\otimes \mathbf{D}$ where ${\mathbf{I}}_{\kappa }$ is an identity matrix of dimension κ and $\mathbf{D}={[D_{i1},\dots ,D_{iT}]}^{\prime }$; and $\tau =\mathrm{vec}\left\{{\tau }_{kt};k=0,1,2;t=1,\dots ,T\right\}$ is a set of $3T$ unknown parameters. The location parameters of each inefficiency term $u_{k,it}(k=0,1,2)$ is given by ${\sum }_{t=1}^T{\tau }_{kt}{D}_{it}$. Thus, for greater flexibility in modeling time effects, we allow inefficiency to be time-varying (i.e., a function of the time dummies). The error components $({\mathbf{v}}_{it},{\mathbf{u}}_{it})$ are assumed to be orthogonal as well as independent of $x_{j,it}(j=1,\dots ,J)$. Further, the random effects $({\alpha }_{0,i},{\gamma }_{0,i},{\delta }_{0,i})$ are assumed to be identically, independently distributed from the error components $({\mathbf{v}}_{it},{\mathbf{u}}_{it})$ as well as independent of $x_{j,it}(j=1,\dots ,J)$:

$${[{\alpha }_{0,i},{\gamma }_{0,i},{\delta }_{0,i}]}^{\prime }\sim \text{i.i.d.}𝒩\left(\mathbf{0},\Omega \right),$$

(11)

where $\Omega =\mathrm{diag}\{{\sigma }_{\alpha }^2,{\sigma }_{\gamma }^2,{\sigma }_{\delta }^2\}$.

4.1. Priors

For the parameters in system (7)–(8), which we collectively denote by ϑ, we assume a non-informative prior that imposes the regularity restrictions so that $p\left(\vartheta \right)\propto \mathrm{I}(\vartheta \in ℛ)$, where $ℛ$ denotes the set of acceptable parameters. For scale parameters $\left({\sigma }_{\alpha }^2,{\sigma }_{\gamma }^2,{\sigma }_{\delta }^2\right)$, we assume $p\left({\sigma }_k\right)\propto {\sigma }^{-(N^{\prime }+1)}exp\left\{-Q^{\prime }/\left(2{\sigma }_k^2\right)\right\}$$\forall k\in \{\alpha ,\gamma ,\delta \}$, where $N^{\prime }=1$ and $Q^{\prime }={10}^{-4}$. For τ, we assume a proper but relatively non-informative prior of the form $\tau \sim 𝒩(\mathbf{0},c{\mathbf{I}}_{3T})$ with $c={10}^4$. For Σ and ${\Sigma }_u$, we assume proper but relatively non-informative priors in the Wishart family. The results are not sensitive to c, $N^{\prime }$ or $Q^{\prime }$ unless c becomes approximately less than 0.1, in which case it approaches the domain of a dogmatic prior.

One may inquire if it would be possible to select objective priors such as in the case of Jeffreys’ prior. One way to proceed with objective priors would be along the lines of Berger and Mortera [20] and Mulder et al. [21]. For instance, the use of a constrained posterior prior along the lines of Berger and Mortera [20] is an option. The Jeffreys’ prior cannot be obtained analytically but can be computed using numerical or analytic derivatives. This computation is certainly heavy. Furthermore, the Jeffreys’ prior is not used as much in the present literature, and the emphasis is rather placed on the so-called intrinsic Bayes factor (see [22]). We leave the issue for future research, but we do not expect much change since our results were not sensitive to important aspects of the prior.

4.2. Posterior Distribution

For convenience, we let ${\sigma }^2\stackrel{\text{def}}{=}\left({\sigma }_{\alpha }^2,{\sigma }_{\gamma }^2,{\sigma }_{\delta }^2\right)$ and ${\alpha }_i\stackrel{\text{def}}{=}({\alpha }_{0,i},{\gamma }_{0,i},{\delta }_{0,i})$. The kernel posterior distribution of all parameters denoted by $\theta \in {\mathbb{R}}^d$ (a superset of ϑ), if conditioned on the latent inefficiencies and random effects, is given by

$$\begin{array}{cc}\hfill p\left(\theta |\Xi ,\alpha ,\mathbf{u}\right)\propto & {|\Sigma |}^{-nT/2}exp\left\{-\frac{1}{2}\sum _{i=1}^n\sum _{t=1}^T({\mathbf{r}}_{it}-{\mathbf{u}}_{it}){\Sigma }^{-1}({\mathbf{r}}_{it}-{\mathbf{u}}_{it})\right\}\times \hfill \\ & exp\left\{-\frac{1}{2}\sum _{i=1}^n\sum _{t=1}^T({\mathbf{u}}_{it}-{\mathbf{Z}}_{it}\tau ){\Sigma }_u^{-1}({\mathbf{u}}_{it}-{\mathbf{Z}}_{it}\tau )\right\}\times \hfill \\ & \prod _{i=1}^n\prod _{t=1}^T{\Phi }_3^{-1}\left({\mathbf{C}}_u\left({\mathbf{Z}}_{it}\tau \right)\right)\times p(\vartheta ,\tau ,\Sigma ,{\Sigma }_u,\sigma ),\hfill \end{array}$$

(12)

where $\alpha =\{{\alpha }_i;i=1,\dots ,n\}$ and $\mathbf{u}=\{{\mathbf{u}}_{it};i=1,\dots ,n;t=1,\dots ,T)$. Also:

$$r_{it}=\left[\begin{array}{c}-y_{it}+{\alpha }_{0,i}+{\Xi }_{0,it}{\vartheta }_0\\ b_{1,it}-{\gamma }_{0,i}-{\Xi }_{1,it}{\vartheta }_1\\ b_{2,it}-{\delta }_{0,i}-{\Xi }_{1,it}{\vartheta }_2\end{array}\right],$$

(13)

where ${\Xi }_{0,it}$ and ${\Xi }_{1,it}$ denote regressors in (7) and (8), respectively (some of which are endogenous); $\{{\vartheta }_k;k=0,1,2\}$ denotes vectors of parameters in the three equations of the system and $\vartheta ={\left[{\vartheta }_0^{\prime },{\vartheta }_1^{\prime },{\vartheta }_2^{\prime }\right]}^{\prime }$; and $\Xi =\{{\Xi }_{0,it},{\Xi }_{1,it},y_{it},b_{1,it},b_{2,it};i=1,\dots ,n;t=1,\dots ,T\}$ denotes the entire available data. Further, ${\Sigma }_u^{-1}={\mathbf{C}}_u^{\prime }{\mathbf{C}}_u$ (via the Cholesky decomposition) and ${\Phi }_k\left(\mathbf{w}\right)$ denotes the k-variate normal probability integral evaluated at some vector $\mathbf{w}\in {\mathbb{R}}^k$.

The first term in the third line of (12) owes to the constraint ${\mathbf{u}}_{it}\ge 0$. Specifically, our stochastic assumptions about ${\mathbf{u}}_{it}$ imply the density

$$\begin{array}{cc}\hfill p\left({\mathbf{u}}_{it}\right|{\mathbf{Z}}_{it},\tau ,{\Sigma }_u)=& {\left(2\pi \right)}^{-3/2}{\left|{\Sigma }_u\right|}^{-1/2}{\Phi }_3^{-1}\left({\mathbf{C}}_u\left({\mathbf{Z}}_{it}\tau \right)\right)\times \hfill \\ & exp\left\{-\frac{1}{2}({\mathbf{u}}_{it}-{\mathbf{Z}}_{it}\tau ){\Sigma }_u^{-1}({\mathbf{u}}_{it}-{\mathbf{Z}}_{it}\tau )\right\},\hfill \end{array}$$

(14)

which requires the evaluation of a tri-variate normal integral that can be performed using standard numerical algorithms. Before proceeding with MCMC methods for inference, note that the posterior is given by

$$p\left(\theta |\Xi \right)\propto {\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}_{+}^{nT}}p\left(\theta |\Xi ,\alpha ,\mathbf{u}\right)d\mathbf{u}d\alpha .$$

(15)

While the multivariate integration can be performed in the closed form with respect to inefficiencies u, the induced nonlinearity however precludes analytical integration with respect to random effects α. We are not aware of any efficient MCMC scheme that draws these random effects as a block from the posterior, especially when n is relatively large.

The posterior conditional distribution of latent inefficiencies is

$${\mathbf{u}}_{it}|·\sim {𝒩}_{+}\left(\mathbf{V}({\Sigma }^{-1}{\mathbf{r}}_{it}+{\Sigma }_u^{-1}{\mathbf{Z}}_{it}\tau ),\mathbf{V}\right),$$

(16)

where $\mathbf{V}={\left({\Sigma }^{-1}+{\Sigma }_u^{-1}\right)}^{-1}$. Draws from the above conditional distribution can be easily obtained. The same is true for the posterior conditional distribution of the random effects if we write ${\mathbf{r}}_{it}$ from (13) as ${\mathbf{r}}_{it}\equiv {\alpha }_i-{\mathbf{R}}_{it}$, where ${\mathbf{R}}_{it}$ is defined in an obvious way. We can then draw the random effects as a block for observation i as follows

$${\alpha }_i|·\sim 𝒩\left({\overline{\alpha }}_i,{\mathbf{V}}_{\alpha }\right),$$

(17)

where

$$\begin{array}{cc}\hfill {\overline{\alpha }}_i& ={\left(T\Sigma +{\Omega }^{-1}\right)}^{-1}\times T{\Sigma }^{-1}{\overline{\mathbf{R}}}_i,{\overline{\mathbf{R}}}_i=T^{-1}\sum _{t=1}^T{\mathbf{R}}_{it}\hfill \\ \hfill {\mathbf{V}}_{\alpha }& ={\left(T\Sigma +{\Omega }^{-1}\right)}^{-1}.\hfill \end{array}$$

(18)

If it were not for the regularity constraints and the non-standard form of the posterior conditional distribution of τ (due do the term involving the multivariate normal integral), we could easily derive the posterior conditional distribution of parameters of interest ϑ.

Collecting data for all observations over $i=1,\dots ,n$ and $t=1,\dots ,T$, we rewrite our model in an obvious matrix notation:

$$\left[\begin{array}{ccc}\hfill \mathbf{y}+{\mathbf{u}}_0& =& {\Xi }_0{\vartheta }_0+{\mathbf{v}}_0\hfill \\ \hfill {\mathbf{b}}_1-{\mathbf{u}}_1& =& {\Xi }_1{\vartheta }_1+{\mathbf{v}}_1\hfill \\ \hfill {\mathbf{b}}_2-{\mathbf{u}}_2& =& {\Xi }_1{\vartheta }_2+{\mathbf{v}}_2\hfill \\ \hfill {\mathbf{u}}_0& =& \mathbf{Z}{\tau }_0+{\zeta }_0\hfill \\ \hfill {\mathbf{u}}_1& =& \mathbf{Z}{\tau }_1+{\zeta }_1\hfill \\ \hfill {\mathbf{u}}_2& =& \mathbf{Z}{\tau }_2+{\zeta }_2\hfill \end{array}\right],$$

(19)

where we assume

$$\zeta ={\left[{\zeta }_0^{\prime },{\zeta }_1^{\prime },{\zeta }_2^{\prime }\right]}^{\prime }\sim 𝒩(\mathbf{0},{\Sigma }_u).$$

(20)

We rewrite the system of equations (19) compactly as

$$\mathbb{Y}=\mathbb{X}\varpi +\mathbb{E},$$

(21)

where 𝕐 is an $nT\times (2\times 3)$ vector of “data” appearing on the left-hand side of equalities in (19), $\mathbb{X}=\mathrm{diag}\{{\Xi }_0,{\Xi }_1,{\Xi }_2,\mathbf{Z},\mathbf{Z},\mathbf{Z}\}$, $\mathbb{E}={[{\mathbf{v}}_0^{\prime },{\mathbf{v}}_1^{\prime },{\mathbf{v}}_2^{\prime },{\zeta }_0^{\prime },{\zeta }_1^{\prime },{\zeta }_2^{\prime }]}^{\prime }$ and $\varpi ={[{\vartheta }^{\prime },{\tau }^{\prime }]}^{\prime }$ is a conformable vector of parameters.

System (21) takes the form of a multivariate regression model with

$$\mathrm{cov}\left\{\mathbb{E}\right\}=\mathbf{V}=\Phi \otimes {\mathbf{I}}_{nT},\text{where}\Phi =\left[\begin{array}{cc}\Sigma & \mathbf{0}\\ \mathbf{0}& {\Sigma }_u\end{array}\right].$$

(22)

The GLS estimator of Θ is given by

$$\widehat{\varpi }={\left({\mathbb{X}}^{\prime }{\mathbf{V}}^{-1}\mathbb{X}\right)}^{-1}{\mathbb{X}}^{\prime }{\mathbf{V}}^{-1}\mathbb{Y},$$

(23)

with the corresponding covariance matrix:

$$\mathrm{cov}\left\{\widehat{\varpi }\right\}={\left({\mathbb{X}}^{\prime }{\mathbf{V}}^{-1}\mathbb{X}\right)}^{-1}.$$

(24)

We note that the above approximation however ignores that ϑ included in ϖ needs to satisfy $\vartheta \in ℛ$ (the regularity conditions).

Let us define a multivariate normal distribution centered at $\widehat{\varpi }$ of which the covariance is $h\times \mathrm{cov}\left\{\widehat{\varpi }\right\}$ for some constant $h>0$. We denote this distribution by $f_{𝒩,\kappa }\left(\varpi ;\widehat{\varpi },h\times \mathrm{cov}\left\{\widehat{\varpi }\right\}\right)$, where κ is the dimensionality of ϖ, i.e., the number of parameters in the extended system (19). We use the GLS quantities to form a proposal density for generating candidate parameter draws as we describe below.

Next, we describe how to realize draws from the conditional posterior distributions of σ, Σ and ${\Sigma }_u$. Except for ${\Sigma }_u$, σ and Σ can be drawn from standard statistical distributions. Specifically, for the elements of σ we have:

$$\begin{array}{cc}\hfill \frac{Q^{\prime }+Q_{\alpha }}{{\sigma }_{\alpha }^2}|{\theta }_{-\alpha },\Xi & \sim {\chi }_{n+N^{\prime }}^2\hfill \\ \hfill \frac{Q^{\prime }+Q_{\gamma }}{{\sigma }_{\gamma }^2}|{\theta }_{-\gamma },\Xi & \sim {\chi }_{n+N^{\prime }}^2\hfill \\ \hfill \frac{Q^{\prime }+Q_{\delta }}{{\sigma }_{\delta }^2}|{\theta }_{-\delta },\Xi & \sim {\chi }_{n+N^{\prime }}^2,\hfill \end{array}$$

(25)

where $Q_{\alpha }={\sum }_{i=1}^n{\alpha }_{0,i}^2$, $Q_{\gamma }={\sum }_{i=1}^n{\gamma }_{0,i}^2$ and $Q_{\delta }={\sum }_{i=1}^n{\delta }_{0,i}^2$. Here, ${\theta }_{-k}$ denotes all elements of the entire parameter vector θ including all latent variables except the indicated subscripted parameter $k\in \{\alpha ,\gamma ,\delta \}$.

Our priors are conditionally conjugate, i.e.,

$$\begin{array}{cc}\hfill p\left(\Sigma \right)& \propto |{\Sigma }^{-1}{|}^{\overline{N}+nT-(3+1)/2}exp\left\{-\frac{1}{2}\overline{\mathbf{A}}{\Sigma }^{-1}\right\}\hfill \\ \hfill p\left({\Sigma }_u\right)& \propto |{\Sigma }_u^{-1}{|}^{\overline{N}-(3+1)/2}exp\left\{-\frac{1}{2}{\overline{\mathbf{A}}}_u{\Sigma }_u^{-1}\right\},\hfill \end{array}$$

(26)

where $\overline{N}$ is a scalar prior parameter and $\overline{\mathbf{A}},{\overline{\mathbf{A}}}_u$ are prior matrices. In our empirical work we take $\overline{N}=10$ and $\overline{A}={\overline{A}}_u={10}^{-3}\times {\mathbf{I}}_3$.

The posterior conditional of Σ is

$$p\left({\Sigma }^{-1}|{\theta }_{-\Sigma },\Xi \right)\propto {\left|{\Sigma }^{-1}\right|}^{\overline{N}+nT-(3+1)/2}exp\left\{-\frac{1}{2}\mathrm{tr}\{\overline{\mathbf{A}}+\mathbf{A}\}{\Sigma }^{-1}\right\},$$

(27)

where $\mathbf{A}=\left({\mathbb{Y}}_k-{\mathbb{X}}_k{\vartheta }_k\right){\left({\mathbb{Y}}_{k^{\prime }}-{\mathbb{X}}_{k^{\prime }}{\vartheta }_{k^{\prime }}\right)}^{\prime }$ for $k,k^{\prime }=0,1,2$.

The conditional posterior of ${\Sigma }_u$ is

$$\begin{array}{cc}\hfill p\left({\Sigma }_u^{-1}|{\theta }_{-{\Sigma }_u},\Xi \right)\propto & |{\Sigma }_u^{-1}{|}^{\overline{N}+nT-(3+1)/2}exp\left\{-\frac{1}{2}\mathrm{tr}\{{\overline{\mathbf{A}}}_u+{\mathbf{A}}_u\}{\Sigma }_u^{-1}\right\}\times \hfill \\ & \prod _{i=1}^n\prod _{t=1}^T{\Phi }_3^{-1}\left({\mathbf{C}}_u\left({\mathbf{Z}}_{it}\tau \right)\right),\hfill \end{array}$$

(28)

where ${\mathbf{A}}_u=\left({\mathbf{u}}_m-\mathbf{D}{\tau }_m\right){\left({\mathbf{u}}_m-\mathbf{D}{\tau }_m\right)}^{\prime }$ for $k,k^{\prime }=0,1,2$.

Clearly, ${\Sigma }^{-1}$ belongs to the Wishart family. The same would have been true for ${\Sigma }_u$ if it were not for the second line of (28) which involves the Cholesky factor of this matrix. Therefore, we use the Wishart distribution to draw a candidate matrix and we retain the candidate with probability

$$min\left\{1,\frac{{\prod }_{i=1}^n{\prod }_{t=1}^T{\Phi }_3^{-1}\left({\mathbf{C}}_u^{\left(c\right)}\left({\mathbf{Z}}_{it}\tau \right)\right)}{{\prod }_{i=1}^n{\prod }_{t=1}^T{\Phi }_3^{-1}\left({\mathbf{C}}_u^{\left(s\right)}\left({\mathbf{Z}}_{it}\tau \right)\right)}\right\},$$

(29)

where ${\mathbf{C}}_u^{\left(c\right)}$ denotes the candidate draw and ${\mathbf{C}}_u^{\left(s\right)}$ is the existing sth draw ($s=1,...,S$).

4.3. Imposition of Restrictions

Imposing restrictions is not trivial in our application. Since the restrictions depend on the data, we adopt the following strategy. We draw from the proposal density described in the previous subsection subject to the constraints $\vartheta \in ℛ$ using a special form of rejection to improve the efficiency of “naive rejection” which would keep drawing parameters until all constraints are satisfied. Specifically, we first use acceptance at a limited number of points to facilitate acceptance and then we keep drawing from the proposal distribution until all regularity constraints hold at all data points.

We first impose the restrictions at the means of variables (normalized to zero) and then at points $\pm r$ around the mean. We choose $r=\{0.5,1,2,3\}$, and the restrictions hold without much trouble in the positive direction. In the negative direction, the restrictions are first tested for $r=-0.1,-0.2,...,-2$ and then tested at the remaining points. This yields considerable improvement in the efficiency (i.e., timing) of acceptance rates from a density which we describe next.

Based on a current draw ${\varpi }^{\left(s\right)}$ such that ${\vartheta }^{\left(s\right)}\in ℛ$, a new candidate ${\varpi }^{\left(c\right)}\sim 𝒩(\widehat{\varpi },h\times \mathrm{cov}\left\{\widehat{\varpi }\right\})\times \mathrm{I}({\vartheta }^{\left(c\right)}\in ℛ)$ is generated until it satisfies the regularity restrictions. The candidate is accepted and we set ${\varpi }^{(s+1)}={\varpi }^{\left(c\right)}$ with the Metropolis-Hastings probability

$$min\left\{1,\frac{p\left({\varpi }^{\left(c\right)}\right|\alpha ,\mathbf{u},\Xi )/f_{𝒩,\kappa }\left({\varpi }^{\left(c\right)};\widehat{\varpi },h\times \mathrm{cov}\left\{\widehat{\varpi }\right\}\right)}{p\left({\varpi }^{\left(s\right)}\right|\alpha ,\mathbf{u},\Xi )/f_{𝒩,\kappa }\left({\varpi }^{\left(s\right)};\widehat{\varpi },h\times \mathrm{cov}\left\{\widehat{\varpi }\right\}\right)}\right\},$$

(30)

otherwise we repeat the current draw, that is ${\varpi }^{(s+1)}={\varpi }^{\left(s\right)};s=1,\dots ,S$. We adjust the scaling constant h so that the acceptance rate of the Metropolis-Hastings algorithm is between 20% and 30%. The Metropolis-Hastings algorithm also takes care of nonlinearity of the posterior in τ.

We generate the covariance matrix Σ and scale parameters σ from their respective posterior conditional distributions which are all in standard form (inverted Wishart and inverted Gamma). The latter however is not the case for ${\Sigma }_u$ (i.e., this matrix cannot be drawn using an inverted Wishart). We therefore take an extra Metropolis-Hastings step to accommodate the presence of the Cholesky factor of ${\Sigma }_u$ (i.e., ${\mathbf{C}}_u$) in the posterior inside the multivariate normal integral. Acceptance rates using a simple Metropolis-Hastings step were quite high (over 90%), and simple scaling has brought it down to the range of 20%–25%.

Our MCMC uses $S^{\prime }$ preliminary or transient passes until we obtain convergence using Geweke’s [23] relative numerical efficiency (RNE) diagnostic. Once convergence is achieved, we take another 100,000 passes. We do not use thinning. Instead, we report posterior standard deviations based on Newey-West HAC covariance matrices using 10 lags. For details, see Table 1.

Table 1. Computational Experience with the Data.

	(1)	(2)
median RNE	0.113	0.615
median NSE	0.0010	0.0012
draws to convergence	150,000	70,000
median ACF at lag 50	0.977	0.312

NOTES: (1) denotes MCMC using full MCMC, drawing random effects and inefficiencies through regular Gibbs sampling. In (2), MCMC is applied by marginalizing the random effects to draw inefficiencies. RNE—relative numerical efficiency; NSE—numerical standard error; ACF—autocorrelation function.

Table 1. Computational Experience with the Data.

	(1)	(2)
median RNE	0.113	0.615
median NSE	0.0010	0.0012
draws to convergence	150,000	70,000
median ACF at lag 50	0.977	0.312

NOTES: (1) denotes MCMC using full MCMC, drawing random effects and inefficiencies through regular Gibbs sampling. In (2), MCMC is applied by marginalizing the random effects to draw inefficiencies. RNE—relative numerical efficiency; NSE—numerical standard error; ACF—autocorrelation function.

4.4. Improving Performance of MCMC

We can explicitly integrate u out of (12) to obtain a kernel posterior of the following form:

$$p\left(\theta |\Xi ,\alpha \right)\propto {\int }_{{\mathbb{R}}_{+}^{nT}}p\left(\theta |\Xi ,\alpha ,\mathbf{u}\right)d\mathbf{u}.$$

(31)

Further, we can also derive the closed-form conditional posterior of random effects $p\left(\alpha \right|\Xi ,{\theta }_{-\alpha })$.

We can achieve a significant improvement of MCMC performance by recognizing that the random effects α can be explicitly integrated out of the posterior, when the parameters ϑ are drawn. Specifically, similar to (19), we consider the following system

$$\begin{array}{cc}\hfill y_{it}+u_{0,it}& ={\alpha }_{0,i}+{\Xi }_{0,it}{\vartheta }_0+v_{0,it}\hfill \\ \hfill b_{1,it}-u_{1,it}& ={\gamma }_{0,i}+{\Xi }_{1,it}{\vartheta }_1+v_{1,it}\hfill \\ \hfill b_{2,it}-u_{2,it}& ={\delta }_{0,i}+{\Xi }_{1,it}{\vartheta }_2+v_{2,it},\hfill \end{array}$$

(32)

which we can rewrite in compact notation as

$${\mathbb{Y}}_{it}={\alpha }_i+{\mathbb{X}}_{it}\vartheta +{\mathbf{v}}_{it},$$

(33)

where ${\mathbb{X}}_{it}=\mathrm{diag}\{{\Xi }_{0,it},{\Xi }_{1,it},{\Xi }_{2,it}\}$. Collecting all (time) observations for a given firm i together, we obtain:

$${\mathbb{Y}}_i={\mathbb{X}}_i\vartheta +{\mathbb{V}}_i,$$

(34)

where ${\mathbb{Y}}_i$, ${\mathbb{X}}_i$ and ${\mathbb{V}}_i$ are defined in an obvious way. Clearly:

$${\mathbb{V}}_i\sim 𝒩\left(\mathbf{0},\Omega \otimes {\mathbf{J}}_T+\Sigma \otimes {\mathbf{I}}_T\right)\forall i=1,\dots ,n,$$

(35)

where ${\mathbf{J}}_T$ is a $T\times T$ matrix of which all elements are equal to one.

Therefore, we can redefine the GLS quantities that are used to obtain a good proposal distribution for ϑ using the following as the covariance matrix V, i.e.,

$$\mathbf{V}=\left(\Omega \otimes {\mathbf{J}}_T+\Sigma \otimes {\mathbf{I}}_T\right)\otimes {\mathbf{I}}_n.$$

(36)

Using the modified proposal density, we effectively marginalize out the random firm-specific effects from the posterior and thus can draw latent inefficiencies ${\mathbf{u}}_{it}$ marginally on these effects hoping to reduce overall autocorrelation in MCMC due to the correlation between ${\alpha }_i$ and ${\mathbf{u}}_{it}$.7 This requires a trivial modification in the way we draw latent inefficiencies.

Since model (32) may be written as

$$\begin{array}{cc}\hfill -y_{it}& =-{\alpha }_{0,i}-{\Xi }_{0,it}{\vartheta }_0-v_{0,it}+u_{0,it}\hfill \\ \hfill b_{1,it}& ={\gamma }_{0,i}+{\Xi }_{1,it}{\vartheta }_1+v_{1,it}+u_{1,it}\hfill \\ \hfill b_{2,it}& ={\delta }_{0,i}+{\Xi }_{1,it}{\vartheta }_2+v_{2,it}+u_{2,it},\hfill \end{array}$$

(37)

after collecting all (time) observations for a given firm i, in obvious notation, we have

$${\Psi }_i={\mathbb{X}}_i\vartheta +{\mathbb{V}}_i+{\mathbb{U}}_i,$$

(38)

where ${\mathbb{X}}_i$ and ${\mathbb{V}}_i$ are naturally redefined to account for a change of sign in the first equation of (37) in order to accommodate a uniform sign in front of inefficiencies ${\mathbb{U}}_i$. Also recall that ${\mathbb{V}}_i$ and its stochastic properties have been defined before. Now we can draw $3T\times 1$ inefficiencies ${\mathbb{U}}_i$ as a block, after we couple system (38) with the following specification:

$${\mathbb{U}}_i=\left({\mathbf{I}}_T\otimes {\mathbf{Z}}_i\right)\tau +{\zeta }_i$$

(39)

subject to ${\mathbb{U}}_i\ge \mathbf{0}$ and ${\zeta }_i\sim 𝒩(\mathbf{0},{\Sigma }_u\otimes {\mathbf{I}}_T);i=1,\dots ,n$.

Since

$$\mathrm{cov}\{{\mathbb{U}}_i,{\zeta }_i\}=\left[\begin{array}{cc}\Omega \otimes {\mathbf{J}}_T+\Sigma \otimes {\mathbf{I}}_T& \mathbf{0}\\ \mathbf{0}& {\Sigma }_u\otimes {\mathbf{I}}_T\end{array}\right]\stackrel{\text{def}}{=}\left[\begin{array}{cc}\mathbb{H}& \mathbf{0}\\ \mathbf{0}& \mathbb{M}\end{array}\right],$$

(40)

we can draw latent inefficiencies, marginally on random effects, using the following multivariate truncated normal distributions, i.e.,

$${\mathbb{U}}_i\sim {𝒩}_{+}\left({\tilde{\mathbb{U}}}_i,\mathbb{W}\right),$$

(41)

the first two moments of which are

$$\begin{array}{cc}\hfill {\tilde{\mathbb{U}}}_i& ={\left({\mathbb{H}}^{-1}+{\mathbb{M}}^{-1}\right)}^{-1}\left\{{\mathbb{H}}^{-1}\left({\Psi }_i-{\mathbb{X}}_i\vartheta \right)+{\mathbb{M}}^{-1}\left({\mathbf{I}}_T\otimes {\mathbf{Z}}_i\right)\tau \right\}\hfill \\ \hfill \mathbb{W}& ={\left({\mathbb{H}}^{-1}+{\mathbb{M}}^{-1}\right)}^{-1}.\hfill \end{array}$$

(42)

We have found that drawing blocks of latent inefficiencies marginally on random effects ${\alpha }_i$ (and conditionally on various covariance matrices and $(\vartheta ,\tau )$) results in vast improvements in terms of computational efficiency. Table 1 summarizes our computational experience with the data.

4.5. Random Effects

Based on our discussion above, we note that given the way the variance parameters ${\sigma }^2$ enter the covariance matrix Ω, in principle, there is no problem in treating the random effects ${\alpha }_i$ as jointly normally distributed, i.e., ${\alpha }_i\sim 𝒩\left(\mathbf{0},\Omega \right)$, independently over $i=1,...,n$ as well as independent from all other random variables and regressors in the model. All our derivations, including the conditional posterior distribution of ${\alpha }_i$, hold true. The only difference is that, in a more general setting (when random effects are allowed to be correlated across equations) one has to draw Ω from its conditional posterior distribution as a general positive definite matrix, whereas, when the random effects are a priori independent, the problem boils down to drawing variances ${\sigma }^2$ only.

A general case of correlated random effects has an empirical implication of firm-specific effects in the production function being correlated with those in residual generation functions for undesirable outputs. The latter possibility is testable and is of interest on its own. Should Ω be found not to be diagonal, one should naturally focus on the sign of the correlation between the random effects.

Given a proper prior $p\left(\Omega \right)$ on the different elements of Ω and the marginal posterior $p\left(\Omega |\Xi \right)$, the Verdinelli and Wasserman [25] approach to computing the Bayes factor in favor of diagonality is given by

$$B{F}_{\mathrm{diag}}=\frac{p\left(\Omega =\mathrm{diagonal}|\Xi \right)}{p\left(\Omega =\mathrm{diagonal}\right)},$$

(43)

which, in the general case, involves testing $k\left(k-1\right)/2$ zero restrictions, where k is the dimension of Ω (in our case, $k=3$). By “$\Omega =\mathrm{diagonal}$”, we mean the zero restrictions ${\Omega }_{ij}=0,i>j,i,j=1,...,3$, where $\Omega \equiv \left[{\Omega }_{ij}\right]$.

While the denominator of $B{F}_{\mathrm{diag}}$ is easy to compute, the numerator is computed in a standard fashion as

$$p\left(\Omega =\mathrm{diagonal}|\Xi \right)=S^{-1}\sum _{s=1}^{S}p\left(\Omega =\mathrm{diagonal},{\theta }_{-\Omega }^{\left(\mathrm{s}\right)}|\Xi \right)$$

(44)

where ${\theta }_{-\Omega }^{\left(s\right)}$ is the sth (of S) MCMC draw of all parameters θ except those in Ω. Note that ${\theta }_{-\Omega }^{\left(s\right)}$ does include the diagonal elements of Ω in this computation.

It remains to show how draws from the conditional posterior distribution may be realized. Our prior is conditionally conjugate and has the following form:

$$p\left({\Omega }^{-1}\right)\propto {\left|{\Omega }^{-1}\right|}^{{\overline{N}}_o-(3+1)/2}exp\left\{-\frac{1}{2}\mathrm{tr}\left\{{\mathbf{A}}_o{\Omega }^{-1}\right\}\right\}.$$

(45)

The conditional posterior distribution is given by

$$p\left({\Omega }^{-1}|{\theta }_{-\Omega },\Xi \right)\propto {\left|{\Omega }^{-1}\right|}^{{\overline{N}}_o+nT-(3+1)/2}exp\left\{-\frac{1}{2}\mathrm{tr}\{{\mathbf{A}}_o+{\mathbf{A}}_{\Omega }\}{\Omega }^{-1}\right\},$$

(46)

where ${\mathbf{A}}_{\Omega }={\sum }_{i=1}^n{\mathbf{R}}_i{\mathbf{R}}_i^{\prime }$ and ${\mathbf{R}}_i\stackrel{\text{def}}{=}{\alpha }_i-{\mathbf{r}}_{it}$ as before. We define the baseline prior using ${\overline{N}}_o=10$ and ${\mathbf{A}}_o=c\times {\mathbf{I}}_3$ with $c={10}^{-3}$. Clearly, Ω belongs to the Wishart family.

The Bayes factor $B{F}_{\mathrm{diag}}$ using the baseline prior is $2.402\times {10}^{-3}$ with the corresponding range of $(1.015\times {10}^{-5};0.0893)$, which suggests that the diagonality of Ω can be definitely rejected. In order to compute the range of $B{F}_{\mathrm{diag}}$, we generate 1000 alternative priors and implement the approximated MCMC using the sampling-iterative-resampling (SIR) algorithm which re-weights the original MCMC sample without recomputing MCMC samples for a new prior. For each one of the SIR re-weighted samples, we implement the Verdinelli and Wasserman [25] approach, and the range is taken as the 95% confidence interval of the computed approximate Bayes factors in favor of diagonality. The 1000 alternative priors are generated by uniformly varying ${\overline{N}}_o$ in the interval $[1;100]$ and c in the interval $[{10}^{-7};10]$ without restricting them to integer values.

Table Table 2 reports the posterior means and standard deviations of the correlation coefficients between random effects ${\alpha }_i$ derived from Ω. We find that unobserved firm-specific effects are all positively correlated.

Table 2. Correlation between Random Effects.

	${\gamma }_{0,i}$	${\delta }_{0,i}$
${\alpha }_{0,i}$	0.831 (0.0011)	0.630 (0.0130)
${\gamma }_{0,i}$		0.601 (0.0102)

NOTES: The random effects $({\alpha }_{0,i},{\gamma }_{0,i},{\delta }_{0,i})$ are for $(y,b_1,b_2)$, respectively. Standard deviations are in parenthesis and are computed using a Newey-West HAC correction with 10 lags.

Table 2. Correlation between Random Effects.

	${\gamma }_{0,i}$	${\delta }_{0,i}$
${\alpha }_{0,i}$	0.831 (0.0011)	0.630 (0.0130)
${\gamma }_{0,i}$		0.601 (0.0102)

NOTES: The random effects $({\alpha }_{0,i},{\gamma }_{0,i},{\delta }_{0,i})$ are for $(y,b_1,b_2)$, respectively. Standard deviations are in parenthesis and are computed using a Newey-West HAC correction with 10 lags.

5. Results

Before proceeding to the discussion of technical and environmental inefficiencies as well as productivity and its components, we first focus on elasticities of the production process by electric utilities in our data sample. Table 3 reports the summary of posterior estimates of these elasticities, including input elasticities of the primary production function (i.e., electric power generation) as well as elasticities of SO₂ and NO_x emissions (undesirable outputs) with respect to the net generated electric power (desirable output).8 In particular, the reported input elasticity estimates imply a posterior mean estimate of the returns to scale, defined as the sum of input elasticities, of 0.90, which suggests that, on average, electric utilities operated at decreasing returns to scale during our sample period.

The estimates of $\partial b_{p,it}/\partial y_{it}(p=1,2)$ are of particular interest since they capture the cost of expanding the production of electric power in terms of the associated increase in the generation of the SO₂ and NO_x emissions. It is intuitive to interpret these estimates as “shadow prices” (in the elasticity form) of the power generation. The posterior mean estimates of the two shadow prices are 1.09 and 1.13. The latter implies that, on average, an increase in the net power generation by 1% requires a simultaneous increase in the SO₂ and NO_x emissions by at least 1.09% and 1.13%, respectively. Note that emissions may increase by even more if the firm is not on the residual generating frontier, i.e., environmentally inefficient.

We next proceed to the discussion of technical and environmental inefficiencies exhibited by the utilities in our sample. Figure 1 plots kernel densities of the posterior estimates of the three types of inefficiency. In order to construct the figure, we use a Gaussian kernel with the cross-validated bandwidth parameters. We find apparent differences between the distributions of technical and environmental inefficiencies. Specifically, while technical inefficiency is relatively symmetrically distributed around its mean of 0.09, the distribution of the NO_x-oriented environmental inefficiency is noticeably skewed to the right and the distribution of the SO₂-oriented environmental inefficiency exhibits apparent bi-modality. There may be many reasons for such a stark difference between the levels of technical and environmental inefficiencies across utilities. One plausible explanation is that technical inefficiency may also be capturing declines in the desirable output due to unforeseen fluctuations in the demand for electric power. Since inputs often cannot be immediately adjusted/reallocated and electric power is not easily storable, electric plants may be forced to under-utilize their facilities and labor, which our model would detect and classify as technical underperformance (inefficiency) relative to the frontier. However, such a demand uncertainty would not apply to the by-production of undesirable SO₂ and NO_x gases given the exact physical relationship between the power generation and the associated emission of pollutant gases. The latter is also capable of at least partly explaining why environmental inefficiency (in the emission of both SO₂ and NO_x gases) appears to be relatively more stable over time unlike the electric-power-oriented technical inefficiency, which we discuss in more detail later in the paper.

Table 3. Summary of Posterior Estimates.

	Mean	Median	St.Dev.	95% Credible Interval
Elasticity
Capital Elasticity	0.2985	0.2984	0.0505	(0.1992; 0.3959)
Labor Elasticity	0.4032	0.4043	0.0482	(0.3076; 0.4935)
Energy Elasticity	0.2002	0.1998	0.0103	(0.1801; 0.2205)
RTS	0.9018	0.9032	0.0726	(0.7608; 1.0370)
SO2 Shadow Price	1.0873	1.0664	0.1437	(0.8524; 1.4334)
NOx Shadow Price	1.1275	1.1163	0.1161	(0.9366; 1.3988)
Inefficiency
Tech. Ineff.	0.0905	0.0915	0.0257	(0.0361; 0.1390)
SO2 Env. Ineff.	0.0870	0.0875	0.0351	(0.0254; 0.1504)
NOx Env. Ineff.	0.0458	0.0438	0.0156	(0.0186; 0.0798)
Efficiency Change
TEC	0.0029	0.0022	0.0308	(–0.0575; 0.0647)
SO2 EEC	–0.0000	–0.0004	0.0099	(–0.0133; 0.0207)
NOx EEC	0.0000	–0.0004	0.0038	(–0.0050; 0.0107)
Technological Change
TTC	–0.0042	–0.0027	0.0104	(–0.0272; 0.0117)
SO2 ETC	0.0225	0.0224	0.0110	(0.0024; 0.0446)
NOx ETC	0.0331	0.0332	0.0052	(0.0229; 0.0431)
Productivity Growth
TPG	–0.0013	0.0009	0.0323	(–0.0663; 0.0626)
SO2 EPG	0.0225	0.0220	0.0149	(–0.0021; 0.0495)
NOx EPG	0.0331	0.0330	0.0064	(0.0211; 0.0453)

Table 3. Summary of Posterior Estimates.

	Mean	Median	St.Dev.	95% Credible Interval
Elasticity
Capital Elasticity	0.2985	0.2984	0.0505	(0.1992; 0.3959)
Labor Elasticity	0.4032	0.4043	0.0482	(0.3076; 0.4935)
Energy Elasticity	0.2002	0.1998	0.0103	(0.1801; 0.2205)
RTS	0.9018	0.9032	0.0726	(0.7608; 1.0370)
SO2 Shadow Price	1.0873	1.0664	0.1437	(0.8524; 1.4334)
NOx Shadow Price	1.1275	1.1163	0.1161	(0.9366; 1.3988)
Inefficiency
Tech. Ineff.	0.0905	0.0915	0.0257	(0.0361; 0.1390)
SO2 Env. Ineff.	0.0870	0.0875	0.0351	(0.0254; 0.1504)
NOx Env. Ineff.	0.0458	0.0438	0.0156	(0.0186; 0.0798)
Efficiency Change
TEC	0.0029	0.0022	0.0308	(–0.0575; 0.0647)
SO2 EEC	–0.0000	–0.0004	0.0099	(–0.0133; 0.0207)
NOx EEC	0.0000	–0.0004	0.0038	(–0.0050; 0.0107)
Technological Change
TTC	–0.0042	–0.0027	0.0104	(–0.0272; 0.0117)
SO2 ETC	0.0225	0.0224	0.0110	(0.0024; 0.0446)
NOx ETC	0.0331	0.0332	0.0052	(0.0229; 0.0431)
Productivity Growth
TPG	–0.0013	0.0009	0.0323	(–0.0663; 0.0626)
SO2 EPG	0.0225	0.0220	0.0149	(–0.0021; 0.0495)
NOx EPG	0.0331	0.0330	0.0064	(0.0211; 0.0453)

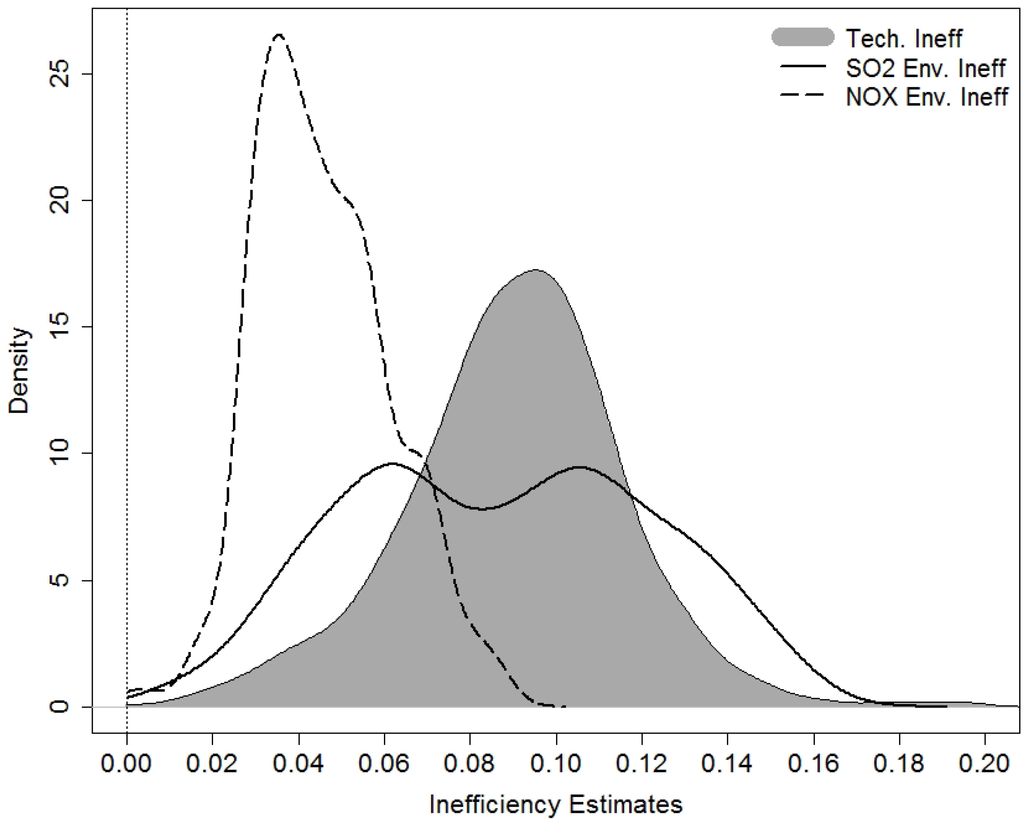
Figure 1. Kernel Densities of Technical and Environmental Inefficiency Estimates.

Figure 1. Kernel Densities of Technical and Environmental Inefficiency Estimates.

Further, we find that electric utilities tend to suffer from higher levels of inefficiency in the emission of SO₂ than in the emission of NO_x gases. These differences may be reflective of varying degree of strictness of environmental regulations (or the degree of their enforceability) for different pollutants across states. For instance, loose regulations for the SO₂ emissions could potentially explain why the SO₂-oriented environmental inefficiency is considerably higher on average and is more dispersedly distributed than the NO_x-oriented inefficiency. Lastly, we document little correlation between the two environmental inefficiencies as well as between the environmental inefficiencies and the technical inefficiency. Table 4 reports such Spearman rank correlation coefficients for the posterior inefficiency estimates. For instance, there appears to be virtually no relationship between the electric-power-oriented technical inefficiency and the SO₂-oriented environmental inefficiency exhibited by utilities.

Table 4. Rank Correlation Coefficients.

Inefficiency				Efficiency Change
Tech. Ineff	1.000			TEC	1.000
SO2 Env. Ineff	0.080	1.000		SO2 EEC	–0.059	1.000
NOx Env. Ineff	0.112	0.227	1.000	NOx EEC	0.080	0.139	1.000
Technological Change				Productivity Growth
TTC	1.000			TPG	1.000
SO2 ETC	–0.001	1.000		SO2 EPG	–0.024	1.000
NOx ETC	–0.020	0.045	1.000	NOx EPG	–0.049	0.065	1.000

Table 4. Rank Correlation Coefficients.

Inefficiency				Efficiency Change
Tech. Ineff	1.000			TEC	1.000
SO2 Env. Ineff	0.080	1.000		SO2 EEC	–0.059	1.000
NOx Env. Ineff	0.112	0.227	1.000	NOx EEC	0.080	0.139	1.000
Technological Change				Productivity Growth
TTC	1.000			TPG	1.000
SO2 ETC	–0.001	1.000		SO2 EPG	–0.024	1.000
NOx ETC	–0.020	0.045	1.000	NOx EPG	–0.049	0.065	1.000

We next proceed to the posterior estimates of the productivity growth components—technological change and efficiency change—as defined in (5) and (6). From Table 3, we see that the levels of both environmental efficiencies appear to be stable over time: posterior mean estimates of the SO₂ $EEC$ and the NO_x $EEC$ are virtually zero. The left panel of Figure 2, which depicts box-and-whiskers plots of the distributions of technical and environmental efficiency change estimates for each year in our sample, confirms the relative stability of environmental efficiency levels (see the left panel of the figure). The electric-power-oriented (i.e., desirable-output-oriented) technical efficiency is however less stable over the course of the years. The mean estimates of $TEC$ are predominantly positive across utilities in 1986, 1988 and 1995, whereas a significant decrease in efficiency is documented for 1987 and 1994. However, the mean posterior estimate of $TEC$ pooled over the entire sample is a mere 0.29% (also see Table 3).

We document several regularities in the estimates of the technological change. First, the technical change $TTC$ is primarily negative and is close to zero in the production of electric power (a desirable output). The posterior mean estimate of annual $TTC$ is –0.42%. This finding is in sharp contrast with what we observe for the environmental technological change $ETC$. The posterior mean estimates of $ETC$ for the SO₂ and NO_x emissions (undesirable outputs) are staggering 2.25% and 3.31% per annum, respectively. Second, we find that technological change is fairly stable across the years in all dimensions, be it the intended production of electric power or undesirable by-production of emission gases. The right panel of Figure 2 confirms this observation: the distributions of $TTC$ and the two $ETC$ do not change much over the course of the years.

The discussed differences in the temporal dynamics between technical and environmental efficiency change and technological change result in dramatic differences in the measures of productivity across desirable and undesirable outputs. We find that, while the pooled posterior mean estimate of (annual) productivity growth is negative for electric power generation (–0.13%), it is substantially positive for the SO₂ and NO_x emissions: annual 2.25% and 3.31%, respectively. In other words, keeping input quantities constant, the net electric power generation, on average, fell by 0.13% per year during our sample period. Utilities however did a significantly better job in terms of cutting the emission of SO₂ and NO_x gases for any fixed quantity of the net electric power generated: on average, emissions fell by respective 2.25% and 3.31% per year ceteris paribus. This disconnect between technical and environmental productivities of electric plants in our sample is also confirmed by virtually zero rank correlation coefficients between $TPG$ and $EPG$ for the SO₂ and NO_x emissions (see Table 4).

Figure 3 vividly illustrates the differences between technical and environmental productivities. It plots the productivity indices that are normalized to 100 in the year 1985 and are constructed using the (respective)-output-weighted average annual productivity growth rates (over all utilities in the sample). The figure shows that the industry enjoyed stable positive rates of $EPG$ during the 1985–1995 period, whereas $TPG$ was more sporadic and included periods of both positive and negative growth. The cumulative eleven-year growth is 23.26% for the SO₂-oriented $EPG$, 37.98% for the NO_x-oriented $EPG$ and a mere 5.33% for the electric-power-oriented $TPG$.

Figure 2. Technical and Environmental Efficiency Change and Technological Change.

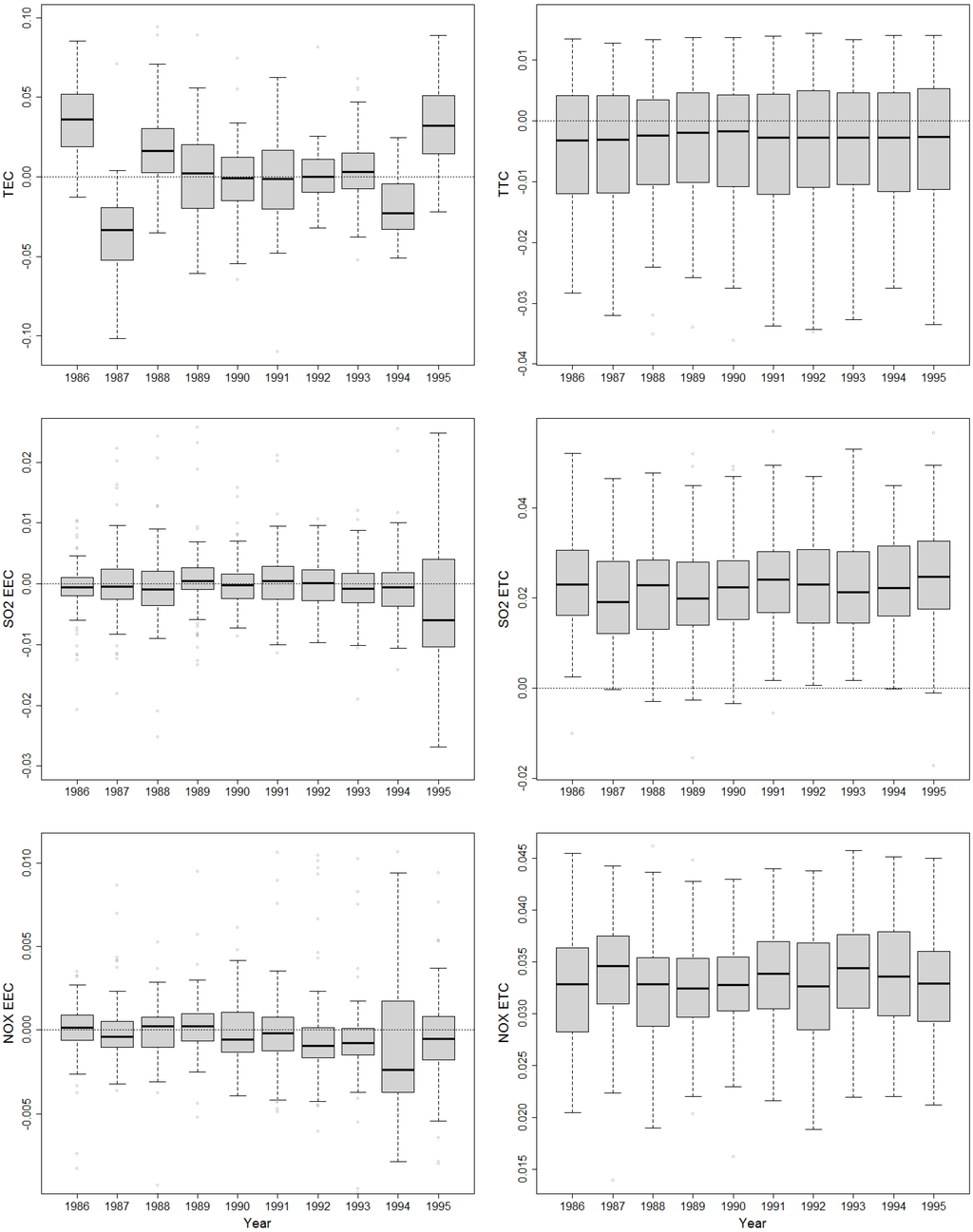
Figure 2. Technical and Environmental Efficiency Change and Technological Change.

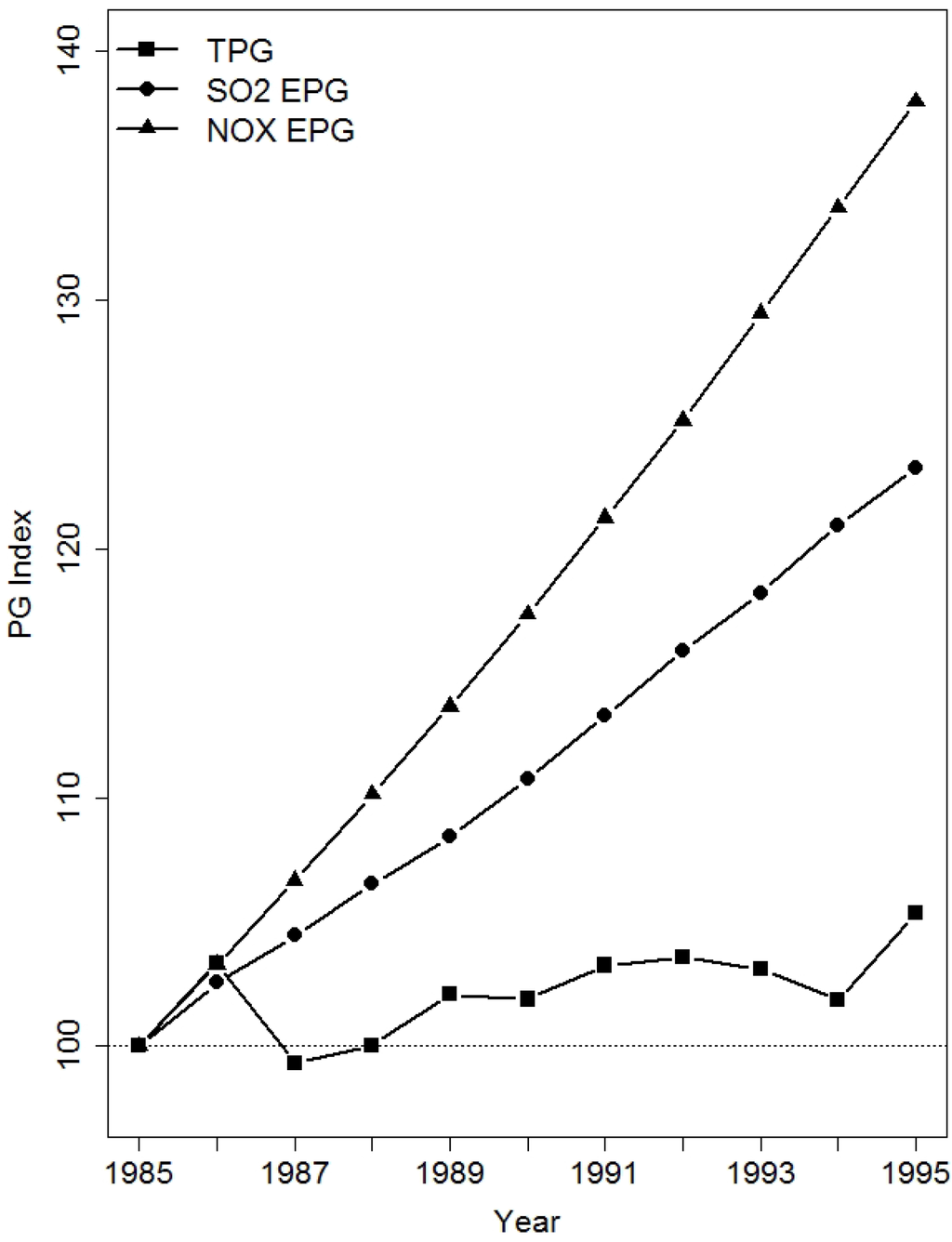
Figure 3. Technical and Environmental PG Indices.

Figure 3. Technical and Environmental PG Indices.

6. Conclusions

The prevalent approaches to modeling the firm’s production process in the presence of undesirable outputs either treat these outputs as inputs, which questionably implies their strong disposability as well as violates the “material balance condition”, or employ the directional distance function that, despite a sound theoretical foundation, allows the identification of a “composite” measure of inefficiency only. Similarly, the directional-output-distance-function-based productivity index identifies only the composite productivity which is a weighted combination of the technical and environmental productivities. This precludes researchers from disentangling the technical inefficiency/productivity, conventionally defined over desirable outputs, from the environmental (“green”) inefficiency/productivity, defined over undesirable outputs.

In this paper, we follow a different path to modeling the production process with undesirable outputs in the spirit of Fernández et al. [11,12, Forsund [13] and Murty et al. [7]. Specifically, we model the productive operations of the firm as a system of simultaneous production technologies for desirable and undesirable outputs. In this setup, desirable outputs are produced by transforming inputs via the conventional transformation function satisfying all standard assumptions. Consistent with the material balance condition, the by-production of undesirable outputs is however treated as the so-called “residual generation technology”. The above setup explicitly recognizes that the generation of undesirable outputs is not the intended production but rather the by-production process. By separating the generation of undesirable outputs from that of desirable outputs, we ensure that the former are not modeled as inputs as well as take into account their “costly disposability”.

The by-production system approach that we employ in this paper permits us to not only distinguish between technical efficiency and (undesirable-output-specific) environmental efficiencies but to also differentiate between traditional technical productivity and environmental productivity. Specifically, we derive a Solow [14] type primal (Divisia) environmental productivity index which, unlike a conventional desirable-output-oriented productivity index, is defined as the contraction rate in undesirable outputs unexplained by the contraction in desirable outputs. This allows us to credit the ceteris paribus reduction in undesirable outputs. Our environmental productivity index also provides a meaningful way to decompose productivity into environmental technological change and environmental efficiency change.