The SAR Model for Very Large Datasets: A Reduced Rank Approach
Abstract
:1. Introduction
2. SAR Model and SRE Model Specifications
2.1. SAR Model
2.2. SRE Model
3. Motivation for the Spatial Basis Functions
4. Specification of the SAR-Calibrated SRE Model
5. Parameter Estimation
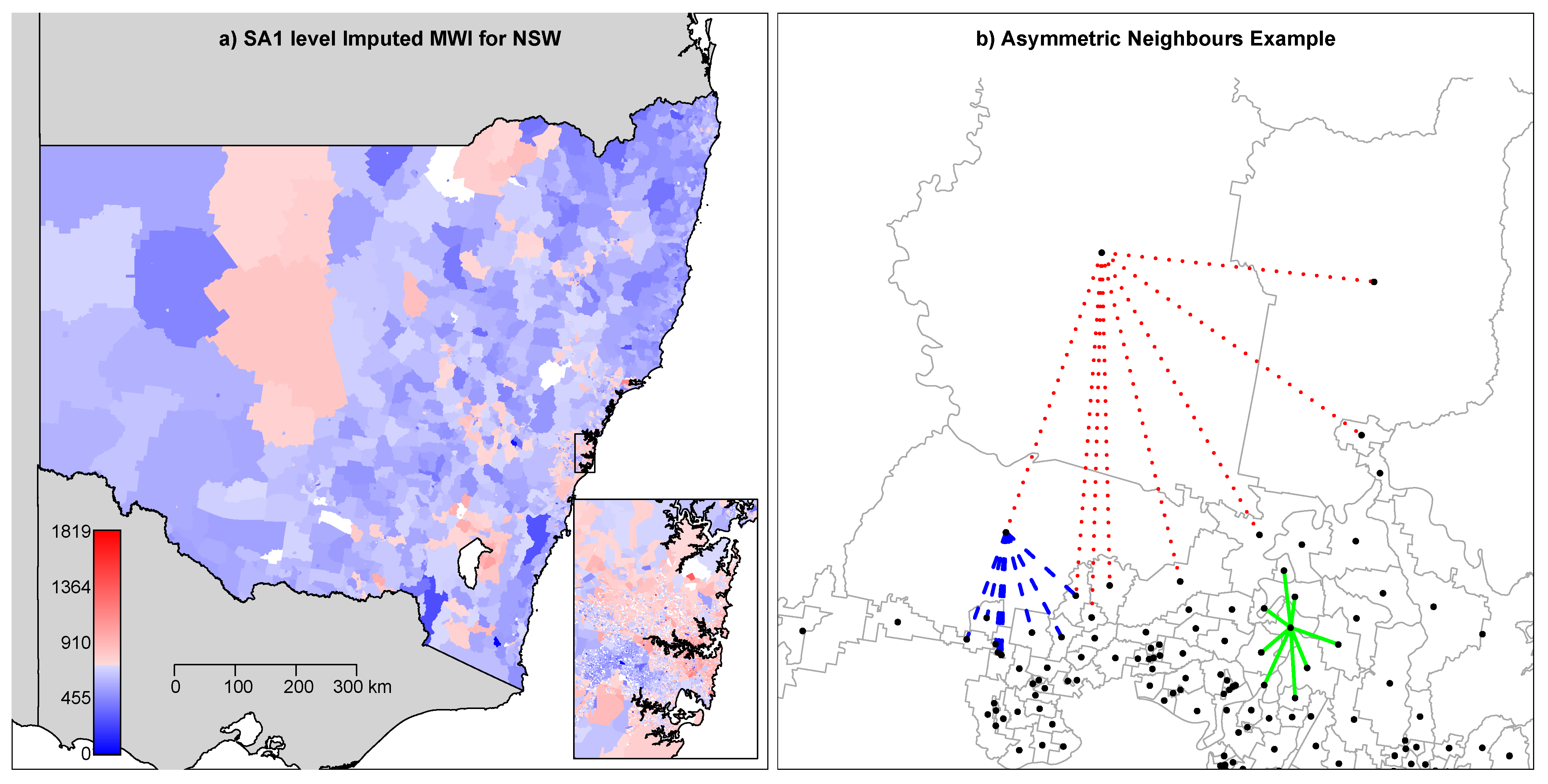
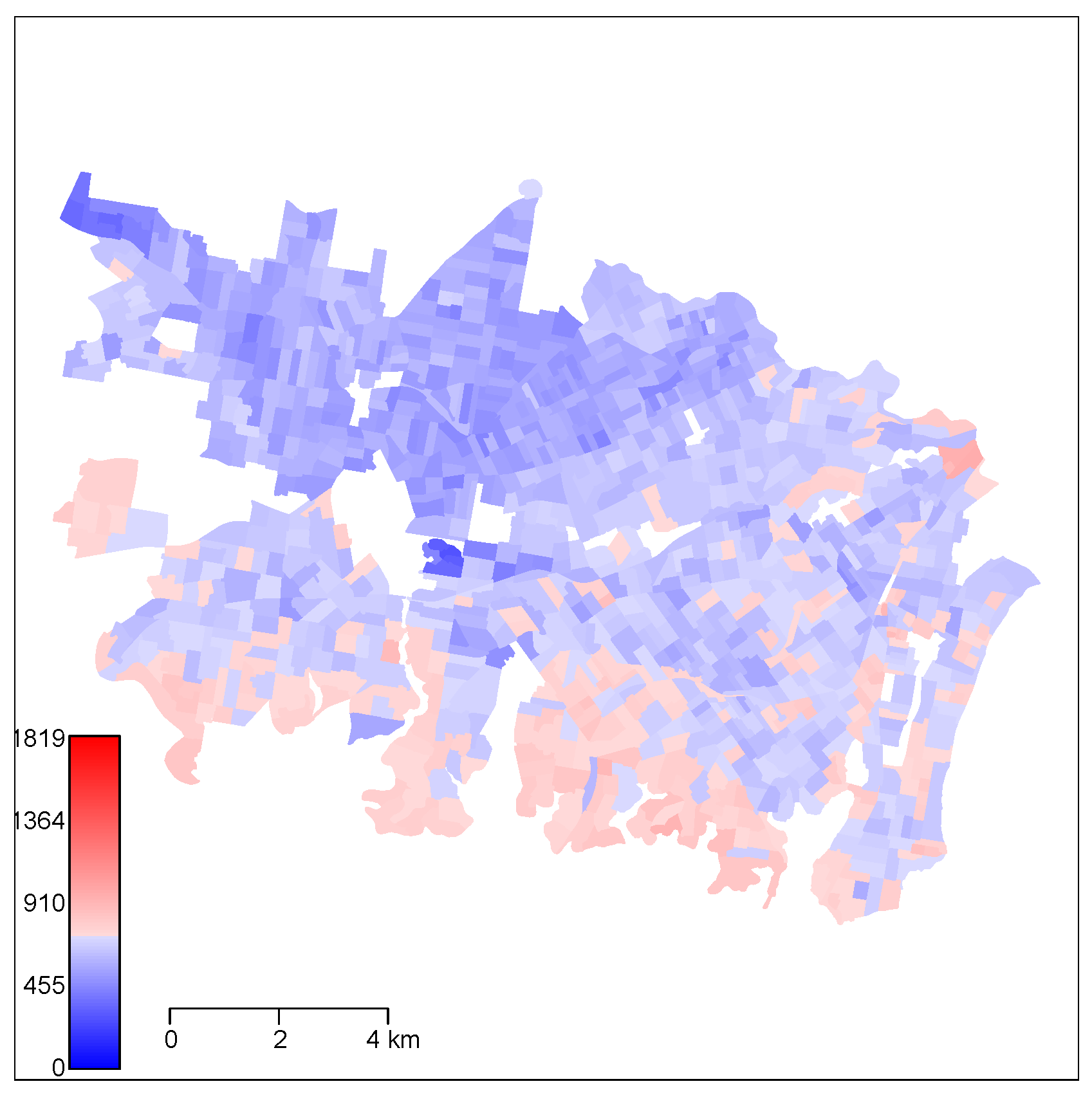
6. Fitting a Spatial Model to Mean Usual Weekly Income
6.1. Imputed MWI
6.2. A Simple Heteroskedastic Model for MWI
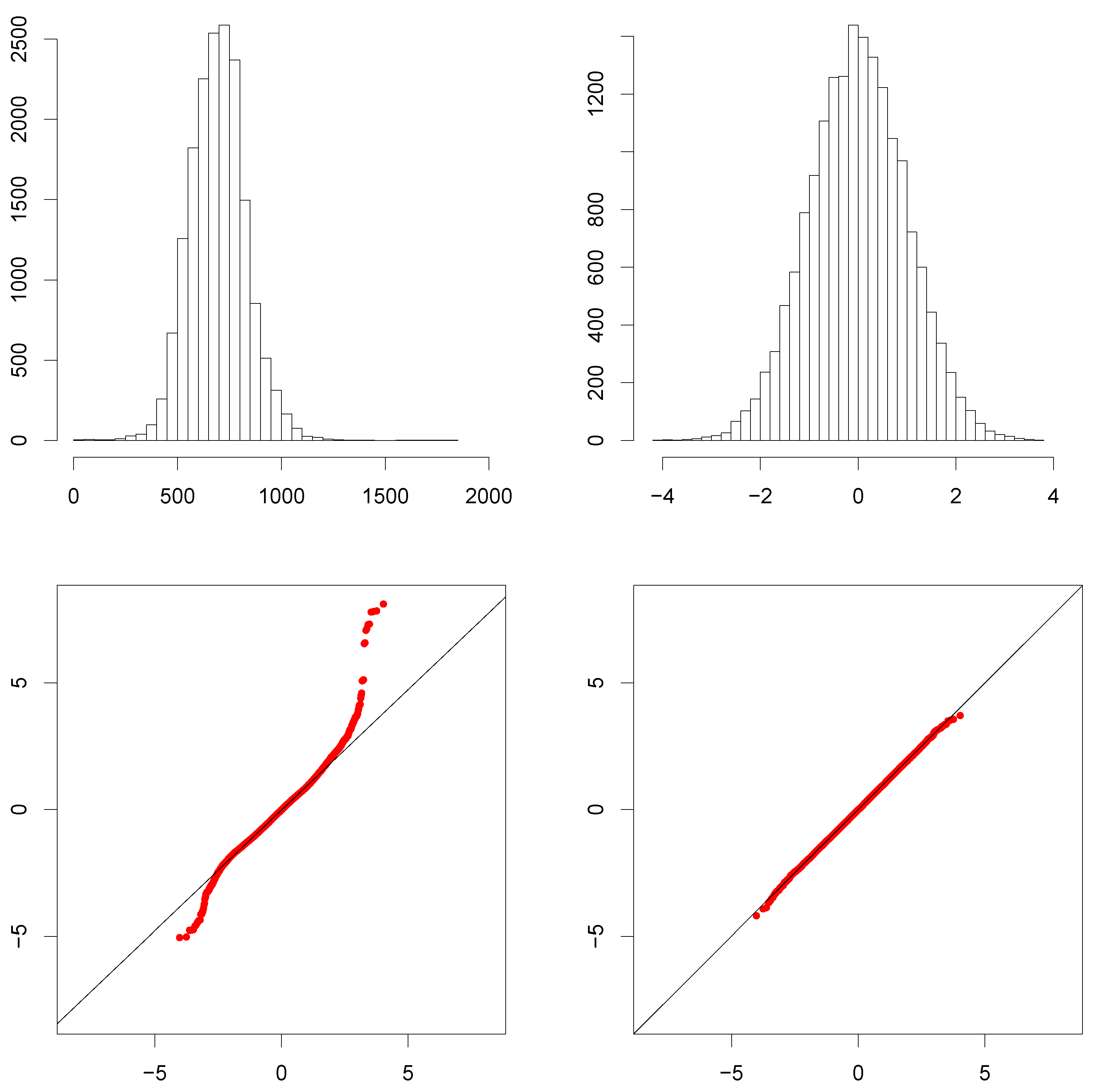
6.3. Measurement Error in MWI
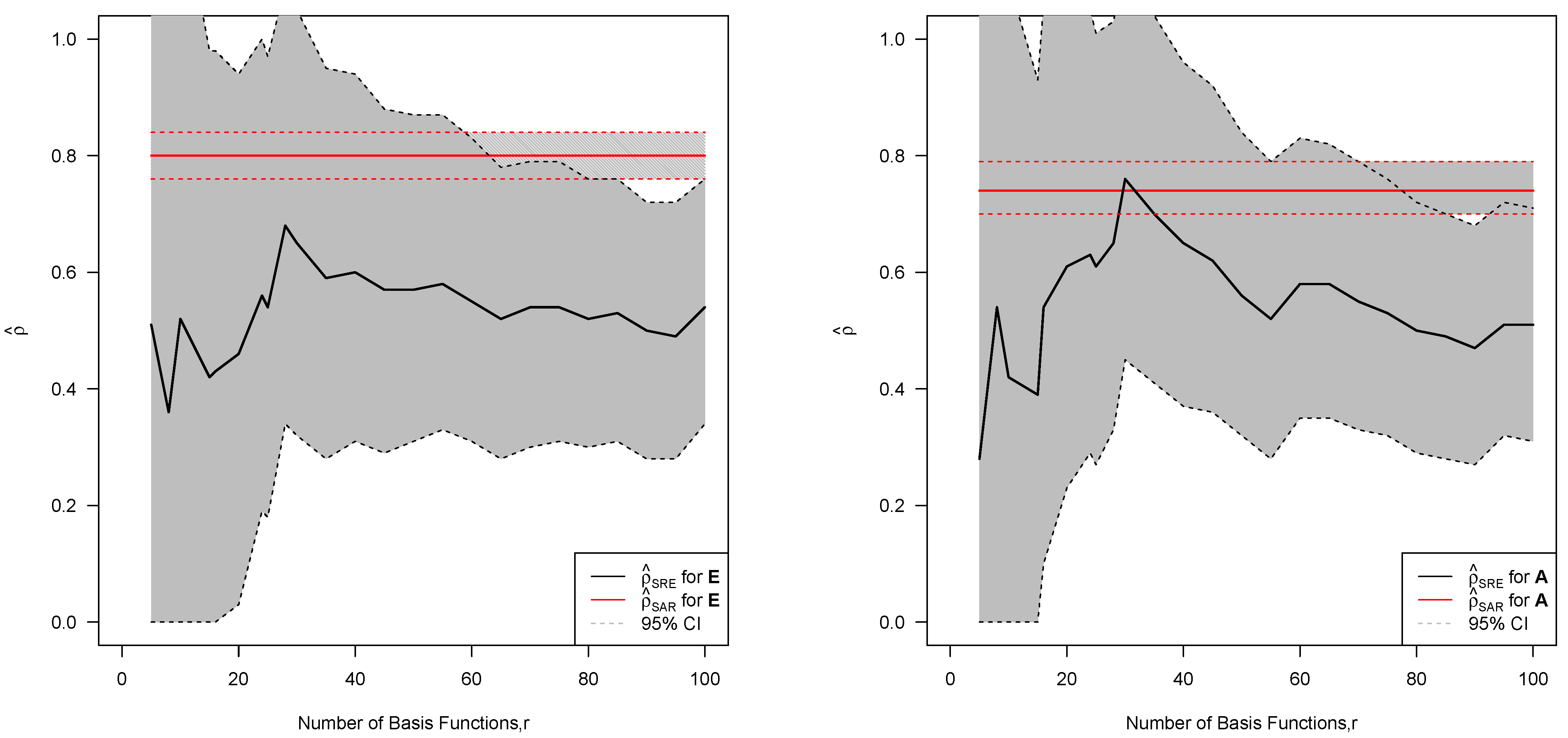
6.4. Specifying the Spatial Dependence Matrix
6.5. Statistical Inference
| 463 | 47.5 | 773 | −782 | −201 | 675 | |
| (432,494) | (−6.7,102) | (732,814) | (−836,−729) | (−256,−146) | (622,728) | |
| 481 | −95.6 | 719 | −695 | −177 | 789 | |
| 346 | 0.0443 | 0.298 | −234 | −15.1 | ||
| (302,390) | (0.042,0.0466) | (0.287,0.309) | (−244,−224) | (−18.7,−11.3) | ||
| 219 | 0.0472 | 0.197 | −245 | −7.84 |
7. Discussion and Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- P. Whittle. “On stationary processes in the plane.” Biometrika 41 (1954): 434–449. [Google Scholar]
- L. Anselin. Spatial Econometrics: Methods and Models. Dordrecht, The Netherlands; Boston, MA, USA: Kluwer Academic Publishers, 1988. [Google Scholar]
- R.K. Pace, and R. Barry. “Sparse spatial autoregressions.” Stat. Probab. Lett. 33 (1997): 291–297. [Google Scholar]
- O.A. Smirnov. “Computation of the information matrix for models with spatial interaction on a lattice.” J. Comput. Graph. Stat. 14 (2005): 910–927. [Google Scholar] [CrossRef]
- R.K. Pace, and J.P. Le Sage. “Chebyshev approximation of log-determinants of spatial weight matrices.” Comput. Stat. Data Anal. 45 (2004): 179–196. [Google Scholar]
- C.K. Wikle. “Low rank representations as models for spatial processes.” In Handbook of Spatial Statistics. Edited by A.E. Gelfand, P.J. Diggle, M. Fuentes and P. Guttorp. Boca Raton, FL, USA: Chapman and Hall/CRC Press, 2010, pp. 107–118. [Google Scholar]
- H.F. Lopes, D. Gamerman, and E. Salazar. “Generalized spatial dynamic factor models.” Comput. Stat. Data Anal. 55 (2011): 1319–1330. [Google Scholar] [CrossRef]
- S. Banerjee, A.E. Gelfand, A.O. Finley, and H. Sang. “Gaussian predictive process models for large spatial data sets.” J. R. Stat. Soc. Ser. B 70 (2008): 825–848. [Google Scholar]
- A.O. Finley, H. Sang, S. Banerjee, and A.E. Gelfand. “Improving the performance of predictive process modelling for large datasets.” Comput. Stat. Data Anal. 53 (2009): 2873–2884. [Google Scholar] [CrossRef] [PubMed]
- J. Eidsvik, A.O. Finley, S. Banerjee, and H. Rue. “Approximate Bayesian inference for large spatial datasets using predictive process models.” Comput. Stat. Data Anal. 56 (2012): 1362–1380. [Google Scholar] [CrossRef]
- N. Cressie, and G. Johannesson. “Spatial prediction for massive data sets.” In Proceedings of the Australian Academy of Science Elizabeth and Frederick White Conference: Mastering the data explosion in the earth and environmental sciences, Shine Dome, Canberra, Australia, 19–21 April 2006; pp. 1–11.
- N. Cressie, and G. Johannesson. “Fixed rank kriging for very large spatial data sets.” J. R. Stat. Soc. Ser. B 70 (2008): 209–226. [Google Scholar]
- H.H. Kelejian, and I.R. Prucha. “A generalized moments estimator for the autoregressive parameter in a spatial model.” Int. Econ. Rev. 40 (1999): 509–533. [Google Scholar] [CrossRef]
- J. Hughes, and M. Haran. “Dimension reduction and alleviation of confounding for spatial generalized linear mixed models.” J. R. Stat. Soc. Ser. B 75 (2013): 139–159. [Google Scholar] [CrossRef]
- A. Sengupta, and N. Cressie. “Hierarchical statistical modeling of big spatial datasets using the exponential family of distributions.” Spat. Stat. 4 (2013): 14–44. [Google Scholar] [CrossRef]
- T. Shi, and N. Cressie. “Global statistical analysis of MISR aerosol data: A massive data product from NASA’s Terra satellite.” Environmetrics 18 (2007): 665–680. [Google Scholar] [CrossRef]
- N. Cressie, and C.K. Wikle. Statistics for Spatio-Temporal Data. Hoboken, NJ, USA: Wiley, 2011. [Google Scholar]
- J.A. Royle, and C.K. Wikle. “Efficient statistical mapping of avian count data.” Environ. Ecol. Stat. 12 (2005): 225–243. [Google Scholar] [CrossRef]
- M.D. Buhmann. Radial Basis Functions: Theory and Implementations. Cambridge, UK; New York, NY, USA: Cambridge University Press, 2003. [Google Scholar]
- T. Hastie, R. Tibshirani, and J.H. Friedman. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed. New York, NY, USA: Springer, 2001. [Google Scholar]
- M. Katzfuss, and N. Cressie. “Bayesian hierarchical spatio-temporal smoothing for very large datasets.” Environmetrics 23 (2012): 94–107. [Google Scholar] [CrossRef]
- D. Nychka, C.K. Wikle, and J.A. Royle. “Multiresolution models for non-stationary spatial covariance functions.” Stat. Model. 2 (2002): 315–331. [Google Scholar] [CrossRef]
- J.R. Bradley, N. Cressie, and T. Shi. “Selection of rank and basis functions in the spatial random effects mode.” In 2011 Proceedings of the Joint Statistical Meetings. Alexandria, VA, USA: American Statistical Association, 2011, pp. 3393–3406. [Google Scholar]
- D.A. Griffith. “Eigenfunction properties and approximations of selected incidence matrices employed in spatial analyses.” Linear Algebra Appl. 321 (2000): 95–112. [Google Scholar] [CrossRef]
- D.A. Griffith. “Spatial-filtering-based contributions to a critique of geographically weighted regression (GWR).” Environ. Plan. A 40 (2008): 2751–2769. [Google Scholar] [CrossRef]
- M. Tiefelsdorf, and D.A. Griffith. “Semiparametric filtering of spatial autocorrelation: The eigenvector approach.” Environ. Plan. A 39 (2007): 1193–1221. [Google Scholar] [CrossRef]
- B.J. Reich, J.S. Hodges, and V. Zadnik. “Effects of residual smoothing on the posterior of the fixed effects in disease-mapping models.” Biometrics 62 (2006): 1197–1206. [Google Scholar] [CrossRef] [PubMed]
- J.R. Bradley, S.H. Holan, and C.K. Wikle. “Mixed effects modelling for areal data that exhibit multivariate spatio-temporal dependencies.” 2014. arXiv:1407.7479v2 [stat.ME]. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1407.7479 (accessed on 7 October 2014).
- J. Besag, J. York, and A. Mollié. “Bayesian image restoration, with two applications in spatial statistics.” Ann. Inst. Stat. Math. 43 (1991): 1–20. [Google Scholar] [CrossRef]
- A.D. Cliff, and J.K. Ord. Spatial Processes: Models and Applications. London, UK: Pion, 1981. [Google Scholar]
- N. Cressie. Statistics for Spatial Data, 2nd ed. New York, NY, USA: John Wiley and Sons, Inc, 1993. [Google Scholar]
- J.P. Le Sage. “Bayesian estimation of spatial autoregressive models.” Int. Reg. Sci. Rev. 20 (1997): 113–129. [Google Scholar] [CrossRef]
- L. Anselin. “Under the hood.” Agric. Econ. 27 (2002): 247–267. [Google Scholar]
- J.P. LeSage, and R.K. Pace. Introduction to Spatial Econometrics. Boca Raton, FL, USA: CRC Press, 2009. [Google Scholar]
- A. Sengupta, and N. Cressie. “Empirical hierarchical modelling for count data using the spatial random effects model.” Spat. Econ. Anal. 8 (2013): 389–418. [Google Scholar] [CrossRef]
- H. Li, C.A. Calder, and N. Cressie. “One-step estimation of spatial dependence parameters: Properties and extensions of the APLE statistic.” J. Multivar. Anal. 105 (2011): 68–84. [Google Scholar] [CrossRef]
- N. Cressie, and S.N. Lahiri. “The asymptotic distribution of REML estimators.” J. Multivar. Anal. 45 (1993): 217–233. [Google Scholar] [CrossRef]
- O. Schabenberger, and C.A. Gotway. Statistical Methods for Spatial Data Analysis. Boca Raton, FL, USA: Chapman & Hall/CRC, 2005. [Google Scholar]
- M. Tiefelsdorf. Modelling Spatial Processes: The Identification and Analysis Of Spatial Relationships in Regression Residuals by Means Of Moran’s I. Berlin, Germany; New York, NY, USA: Springer-Verlag, 2000, Volume 87, Lecture Notes in Earth Sciences. [Google Scholar]
- M. Tiefelsdorf, and B. Boots. “The exact distribution of Moran’s I.” Environ. Plan. A 27 (1995): 985–999. [Google Scholar] [CrossRef]
- D.A. Griffith. “Spatial autocorrelation and eigenfunctions of the geographic weights matrix accompanying geo-referenced data.” Can. Geogr. 40 (1996): 351–367. [Google Scholar] [CrossRef]
- N.J. Higham. “Computing a nearest symmetric positive semidefinite matrix.” Linear Algebra Appl. 103 (1988): 103–118. [Google Scholar] [CrossRef]
- H.V. Henderson, and S.R. Searle. “On deriving the inverse of a sum of matrices.” SIAM Rev. 23 (1981): 53–60. [Google Scholar] [CrossRef]
- Australian Bureau of Statistics. 2011 Australian Census of Population and Housing: New South Wales (SA1 and SA2 Level areas), Basic Community Profile, Table 17; Canberra, Australia: Australian Bureau Statistics, 2011.
- Australian Bureau of Statistics. Survey of Income and Housing 2011-12, Confidentialised Unit Record File; Canberra, Australia: Australian Bureau Statistics, 2012.
- Australian Bureau of Statistics. Socio-Economic Indexes for Areas (SEIFA) 2011—Technical Paper: ABS Catalogue no. 2033.0.55.001; Canberra, Australia: Australian Bureau Statistics, 2013.
- Australian Bureau of Statistics. 2011 Australian Census of Population and Housing: Data Quality Statement for Total Personal Income (weekly) (INCP); Canberra, Australia: Australian Bureau Statistics, 2011.
- H. Rue, and H. Tjelmeland. “Fitting Gaussian Markov random fields to Gaussian fields.” Scand. J. Stat. 29 (2002): 31–49. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burden, S.; Cressie, N.; Steel, D.G. The SAR Model for Very Large Datasets: A Reduced Rank Approach. Econometrics 2015, 3, 317-338. https://doi.org/10.3390/econometrics3020317
Burden S, Cressie N, Steel DG. The SAR Model for Very Large Datasets: A Reduced Rank Approach. Econometrics. 2015; 3(2):317-338. https://doi.org/10.3390/econometrics3020317
Chicago/Turabian StyleBurden, Sandy, Noel Cressie, and David G. Steel. 2015. "The SAR Model for Very Large Datasets: A Reduced Rank Approach" Econometrics 3, no. 2: 317-338. https://doi.org/10.3390/econometrics3020317
APA StyleBurden, S., Cressie, N., & Steel, D. G. (2015). The SAR Model for Very Large Datasets: A Reduced Rank Approach. Econometrics, 3(2), 317-338. https://doi.org/10.3390/econometrics3020317






