Abstract
The SAR model is widely used in spatial econometrics to model Gaussian processes on a discrete spatial lattice, but for large datasets, fitting it becomes computationally prohibitive, and hence, its usefulness can be limited. A computationally-efficient spatial model is the spatial random effects (SRE) model, and in this article, we calibrate it to the SAR model of interest using a generalisation of the Moran operator that allows for heteroskedasticity and an asymmetric SAR spatial dependence matrix. In general, spatial data have a measurement-error component, which we model, and we use restricted maximum likelihood to estimate the SRE model covariance parameters; its required computational time is only the order of the size of the dataset. Our implementation is demonstrated using mean usual weekly income data from the 2011 Australian Census.
Keywords:
asymmetric spatial dependence matrix; Australian census; heteroskedasticity; Moran operator; spatial autoregressive model; spatial basis functions; spatial random effects model JEL classifications:
C21
1. Introduction
The spatial autoregressive (SAR) model, originally proposed by Whittle [1] (see also, [2]), is widely used in spatial econometrics to model Gaussian processes on a discrete spatial lattice (which may be irregular). It has an autoregressive structure that models the spatial dependence of the attributes through a precision matrix that is typically a function of the proximity between elements of the lattice. This spatial dependence matrix is generally sparse. An important application of the SAR model is when the lattice is made up of n spatially-contiguous areas, such that for two areas that are “far apart”, the corresponding entry in the spatial dependence matrix is zero.
Despite its popularity, the SAR model has some limitations for the analysis of large datasets, because maximum likelihood estimation of its parameters is not scalable in the size of the spatial dataset. This limits the size of the problems for which SAR models can be effectively used. Algorithmic approaches to reduce the computational burden include sparse-matrix techniques [3,4] and approximate methods, such as Taylor series and Chebyshev approximations [4,5].
Rather than modelling spatial dependence through a precision matrix that is a function of the spatial proximity of areas, it could be modelled directly through a covariance matrix; a reduced-rank covariance model could then be used to lower the order of computations (e.g., [6]) to . Reduced-rank approaches include latent-factor-analysis models [7], predictive-process models for Gaussian data [8,9] and non-Gaussian data [10], spatial random effects (SRE) models [11,12] and spatial generalised linear mixed models (SGLMMs) [13,14,15]. The advantage of the SRE approach is a substantial improvement in computational efficiency for a broad class of flexible, spatial, non-stationary covariance functions [12,16]. The spatial dependence is captured through the choice of basis functions and through an covariance matrix of the coefficients of the basis functions. By reducing the rank of the spatial covariance function from n to r through the use of r spatial basis functions, the SRE model has a computational cost of , which is for [12]. Our challenge in this paper is to calibrate and fit a computationally-efficient SRE model so that its parameters are directly interpretable in terms of the familiar SAR model.
An important aspect of model definition is specifying appropriate basis functions. Several classes of basis functions have previously been used for SRE models, including empirical orthogonal functions (EOFs) (summarised in, e.g., [6,17]), Fourier basis functions [18], smoothing splines [6], radial basis functions (e.g., [19,20], pp. 186–187), and multi-resolutional basis functions (i.e., basis functions obtained from functions defined at multiple resolutions), such as bisquare spatial basis functions [12,21] and wavelets [16,22], that capture the spatial dependence at multiple scales. Selecting an appropriate class of basis functions is generally problem dependent, although the use of the conditional Akaike information criterion and the generalised-degrees-of-freedom criterion have been considered [23]. The spatial basis functions selected for the model need not be orthogonal, but they are recommended to be multi-resolutional and fast to evaluate [12]. More recently, a spectral decomposition of the matrix in the numerator of Moran’s I statistic, called the Moran operator [14], has been used to identify a set of orthogonal eigenvectors associated with dominant patterns of positive spatial dependence (e.g., [24,25,26]). These eigenvectors have been used to obtain spatial basis functions for SGLMMs [27], and substantial computational efficiency has been achieved for both SGLMMs [14] and SRE models [28] by including only the first basis functions in the model.
Moran’s I can be motivated from a simple SAR model with homoskedastic errors and a symmetric spatial dependence matrix given by nearest-neighbour adjacencies. In this article, we consider a heteroskedastic SAR model with an asymmetric spatial dependence matrix and define a generalised Moran operator (GMO) whose eigenvectors define our spatial basis functions. In particular, we propose to model spatial data for small areas using an SRE model with these spatial basis functions calibrated from the proposed SAR model. The SAR-calibrated SRE model, for which computational efficiencies are readily available, is well suited to very large datasets, and its parameters are interpretable in terms of the original SAR parameters.
The plan for the rest of the article is as follows. Section 2 outlines the main features of the SAR and SRE models. A motivation is given in Section 3 for spatial basis functions obtained from a generalised Moran operator. Dimension reduction using these basis functions is developed in Section 4. Parameter estimation under the SAR-calibrated SRE model is presented in Section 5. An example of their use for Australian Census data is presented in Section 6, and the paper concludes with a discussion and conclusions in Section 7.
2. SAR Model and SRE Model Specifications
Consider a set of n geographic areas in a spatial domain, and identify the location of a well-defined feature in each area, denoted , respectively. Define an irregular, finite spatial lattice over the region of interest, , and consider the attributes associated with the areas.
We are interested in making inference on a spatial process , which we henceforth assume is Gaussian. However, is a latent process: rather than observing , we observe data , which offer an imperfect view of the latent process due to limitations in the measurement process (including averaging, the use of proxy measures rather than direct measurement and observation error).
In this section, we specify hierarchical models that allow us to make inference on the latent process using the observed data . We first define a SAR model for and then a measurement-error model for given . Subsequently, we consider an SRE model for and discuss the implications of equating the SAR and SRE models’ respective means, variances and covariances.
2.1. SAR Model
A SAR model for over the lattice , which includes a spatially-varying mean, is defined as:
where is an n-dimensional vector representing the mean of and is a measure of the spatial dependence between the locations and with the convention that ; . We define the SAR’s spatial dependence matrix as . In general, ; that is, is an asymmetric square matrix. The elements of the error vector are independent Gaussian random variables with mean zero and variance , . Their joint distribution can be written as , where . For many applications, is parametrised as , where , and is a known function of location. We write , where the diagonal matrix may be the identity or may model heteroskedasticity (e.g., the inverse of the population size in each area; see Section 6).
Here, we model the mean as a linear function of p known covariates; that is , where , for , and is the associated p-dimensional vector of regression coefficients. In this case, (1) can be written equivalently as,
The spatial dependence matrix has zeros down the diagonal; generally it is asymmetric, and it is often defined in terms of the proximity of the lattice elements. For (2) to be well defined, we consider only those for which is invertible. Generally, (and hence, ) is sparse. In many applications, is parametrised as , where is a known, in general asymmetric, spatial-weights matrix with zeros down the diagonal, and ρ is a spatially-dependent parameter. The case of corresponds to “no spatial dependence,” since .
Henceforth, we parametrise our model as and , where and are known. Consequently, there are two covariance parameters, ρ and . From (2), the mean vector and the covariance matrix of are, respectively, given by,
A statistical model for the observations, , is defined in terms of the latent process, , by assuming a conditional Gaussian distribution for the observed data. The resulting data model can be written in terms of additive measurement error, as follows:
The term in (4) represents an uncorrelated Gaussian process with mean zero and individual variances given by , for , where , and is a known function of location; is also independent of . Hence,
where “Gau” is the Gaussian (or normal) distribution, and may be the identity matrix or it may represent heterogeneous conditions associated with the measurement process. Together, (2) and (4) yield the following model for ,
where , independent of . Traditional spatial econometrics has fitted a SAR model directly to the spatial data, , as follows (e.g., [2]): . We believe that (5) presents the three components of variability, namely trend, SAR spatial dependence and measurement error, in an unambiguous and interpretable manner.
Motivated by Besag et al. [29], we have assumed a SAR model for the spatial errors, , to avoid confounding with β. Furthermore, to recognise that the measurement is never perfect, we have added measurement error to the latent process . Details regarding these models and their estimation can be found in, for example, Anselin [2] Cliff and Ord [30], Cressie [31], Le Sage [32], Anselin [33], as well as LeSage and Pace [34].
2.2. SRE Model
The SRE model is a reduced-rank spatial statistical model that can be written as follows:
where is a known vector of spatial basis functions and is its corresponding r-dimensional vector of random effects. The random effects are assumed to have a multivariate Gaussian distribution with mean and covariance matrix , so that . The last term in (6), , represents fine-scale variation, independent of , which is assumed here to follow,
where , and is a known function of location. Hence, , where , and the diagonal matrix may be the identity matrix or may represent heterogeneity, for example through in each area; see Section 6. Using vector notation, (6) can also be written as,
where . The mean vector and the covariance matrix of for the SRE model are, respectively, given by,
As was done for the SAR model, we define in terms of the latent process through the data model, (4). Together, (7) and (4) yield the following model for :
We calibrate the specification of , and in the SRE model to the spatial dependence in the SAR model, by initially matching their first two moments. Now, the mean of the SRE model (7) is the same as the mean of the SAR model (2). Then, after setting the measurement-error terms in (5) and (9) to be the same, we set (e.g., [35]). That is, we set:
Notice that in the SRE model (left-hand side), the contribution to spatial dependence is from the reduced-rank matrix , whilst in the SAR model (right-hand side), the contribution to spatial dependence comes from the full-rank matrix, . When , we respectively obtain an SRE model and an SAR model with no spatial dependence. In this case, the SRE model and the SAR model are equivalent if:
This says that heteroskedasticity in the SRE’s fine-scale variation component ξ should reflect the heteroskedasticity in the SAR model’s ν, when there is no spatial dependence.
When spatial dependence is present in the SAR model, the spatial dependence component of the SRE model should, according to (10), be equal to:
Critically, (12) should also be positive-definite with rank . Ensuring that these restrictions hold leads to our new methodology, which is presented in Section 4.
3. Motivation for the Spatial Basis Functions
We use this section to motivate the construction of our SAR-calibrated spatial basis functions for use in the SRE model. The motivation is clearest for the case where , and hence, in this section, we temporarily assume . The SAR model parameters are . Minus twice the log-likelihood function for the SAR model is:
Consider the transformation . The spatial process is distributed as , where , and (e.g., see [36], for details). Hence (13) can be written as,
The SAR model maximum likelihood estimates, , are those values that minimise or, equivalently, they are those values that minimise .
Maximum likelihood estimates for the covariance parameters ρ and are well known to exhibit negative bias (e.g., [37]). To reduce the bias, estimation commonly proceeds using restricted (or residual) maximum likelihood (REML) (e.g., see [38], for a summary of its use for spatial data). REML estimation is carried out by performing maximum likelihood estimation on , where is chosen, such that , rank, and p is the rank of the matrix of covariates, . Suppose we choose . Note that is symmetric (i.e., ) and idempotent (i.e., ). Effectively, we are substituting an ordinary-least-squares estimator of β (based on and ) into (14), and then, we minimise this empirical version of the likelihood to obtain REML estimates. The “data” are now , with and . Hence, we minimise the restricted likelihood,
resulting in the REML estimates. From (15), these estimates depend critically on the non-negative-definite matrix,
Expanding (16) gives the equivalent expression,
In (17), the dominant term in ρ is proportional to:
Notice that Moran’s I statistic for data and covariates is,
where is the adjacency matrix whose entries are one (when two entries are “adjacent”) and zero (otherwise); see [24]. When an asymmetric matrix is used in place of , Tiefelsdorf ([39], p. 29) has suggested that be “symmetrised” by replacing in (19) with the symmetric matrix .
We have seen that (18) plays an important role in the restricted likelihood (15), and it takes the form of the numerator of Tiefelsdorf’s modification to the Moran statistic for an asymmetric spatial dependence matrix. Hence, we use it to define a generalised Moran operator. Recall that captures heterogeneity and captures asymmetric spatial dependence in the SAR model. We can write and, since ,
where:
Hence, we define the generalized Moran operator (GMO),
where is defined by (20).
Notice that for and (the symmetric adjacency matrix), we obtain , and hence, (21) is equal to . This is the Moran operator given by Griffith [24] and Hughes and Haran [14]. Spectral decomposition of the Moran operator has been shown to yield natural spatial basis functions for spatial modelling (e.g., see [24,27,40,41] and, more recently, [14,28]), and we propose the same for the GMO given by (21). For spatial generalised linear models where heteroskedasticity appears through a mean-variance relationship, Reich et al. [27] suggest modifying the Moran operator using weights obtained from iteratively reweighted least squares. This bears a formal resemblance to and lends support to our proposed generalisation. Notice that the GMO allows for both heteroskedasticity (through ) and asymmetry (through ) simultaneously.
4. Specification of the SAR-Calibrated SRE Model
In this section, we define an SAR-calibrated SRE model for the latent process , using the SRE model that is defined in Section 2.2. Our approach is to use eigenvectors from the spectral decomposition of given by (21), to define the r basis functions for the SRE model, (8). Now, the spectral decomposition of (21) yields,
where the eigenvectors of satisfy ; and is an diagonal matrix with elements in the diagonal matrix ordered so that , for , the eigenvalues of . Define the matrix , which corresponds to the r largest absolute eigenvalues of , namely the diagonal elements in . Similarly, and correspond to the smallest absolute eigenvectors. Then,
Notice that eigenvectors corresponding to large positive and negative eigenvalues may be chosen; Hughes and Haran [14] only choose eigenvectors that correspond to large positive eigenvalues, which limits their approach to capturing only positive spatial dependence. In the application given in Section 6, several large absolute eigenvectors that corresponded to negative dependence were chosen.
From (3), using a second-order Taylor-series expansion for ρ around zero, the SAR model covariance matrix for is:
Hence, a candidate for the matrix in the SRE model (8) is obtained by pre- and post-multiplying (24) by , where :
The candidate given by (25) is fast to evaluate for given values of ρ and . However, while the matrix in (25) is symmetric, it is not necessarily positive-definite. Higham [42] shows how to obtain the nearest symmetric positive approximant to any real square matrix . Call this positive-definite matrix , and hence, define,
Then, since , the matrix (),
is positive-definite. In conclusion, we shall use the positive-definite matrix given by (27) to define our SAR-calibrated SRE model. What remains in the calibration is specification of in (8). Since is assumed known, we only need to specify , which will generally be a function of ρ and . We use the closeness of the inverses of the SAR and SRE covariance matrices to achieve this, which is concomitant with the eigenvectors in coming from large absolute eigenvalues.
Recall that the SAR model’s inverse covariance matrix is easy to evaluate as is the SRE model’s inverse covariance matrix using the Sherman–Morrison–Woodbury identity (e.g., [43]): for generic matrices , , and of appropriate order,
where the inverses on the right-hand side are fast to evaluate. Consequently, for an SRE model for with the form of (8) and with , diagonal and positive-definite , the inverse covariance matrix is,
where . Consider the Frobenius norm between the inverse of the SAR covariance matrix of and (28); this is proportional to:
as a function of ζ. The final step in the calibration is to minimise (29) with respect to , for all ρ in its parameter space; call the minimised value .
Hence, the SAR-calibrated SRE covariance matrix of is,
where is a positive-definite matrix, , by construction, and recall that is known. Notice that all parameters in the SRE model’s covariance matrix (30) are expressed as functions of the SAR model’s parameters and ρ. Furthermore, notice that, while we have made close (in the Frobenius-norm sense) to , they are not equal; this difference is the only source of approximation in this article. The dominant (positive and negative) spatial dependencies in the SAR model are included in the calibrated model in a reduced-rank form, and residual variability is captured by setting (which is a function of ρ). In the next section, we fit the model,
using likelihood-based methods, where is given by (30).
5. Parameter Estimation
We use likelihood-based estimators of the parameters of the SAR-calibrated SRE model (31), because they have asymptotic optimality properties, and they are preserved under transformation. The SAR model’s parameters are β, ρ and , which appear in the SRE likelihood defined by (30) and (31); we assume that the measurement-error component, , is known, which is often the case (Section 6.3).
We estimate the SAR covariance parameters ρ and using the log-restricted-likelihood function given by:
where and . We solve for (ρ, ) by minimising in terms of ρ and in two stages. First, for each value of ρ, we minimise with respect to , to obtain . Then, we minimise the profile, , with respect to ρ. The resulting and are the REML estimates. When making likelihood calculations, we use the Sherman–Morrison–Woodbury formulas [43] for both the inverse and the determinant of the SRE model’s covariance function.
This estimation technique requires a starting value for for each value of ρ; we use method-of-moments estimation to obtain the starting values. Specifically, define , and hence:
where and . Consequently,
where is any symmetric, matrix. For example, in Section 6, we choose , where , is the number of people in area i. The resulting method-of-moments estimator is,
which we use as a starting value for solving:
for each ρ in its parameter space. The profile restricted log-likelihood for ρ is given by,
for ρ in its parameter space. The minimum of is found using a univariate grid-search algorithm.
A likelihood-based confidence interval (CI) for a model parameter, with a significance level of α, can be obtained by inverting the (restricted) likelihood-ratio test. Hence, an approximate % CI for ρ is given by:
where is the percentile of the chi-squared distribution on one degree of freedom.
Finally, the empirical generalised-least-squares estimate for β is,
and an estimate of its covariance matrix is .
6. Fitting a Spatial Model to Mean Usual Weekly Income
We illustrate the methodology developed in Section 2, Section 3, Section 4 and Section 5 using Australian Census data [44] from the 2011 Census conducted by the Australian Bureau of Statistics (ABS). Our interest lies in modelling the spatial distribution of mean usual weekly income (MWI) for small geographic areas in the state of New South Wales (NSW), Australia, and then fitting the spatial model by estimating its parameters. In the following sections, we describe the data, the fitting of an SAR-calibrated SRE model, our assumptions regarding measurement error and the statistical inferences that follow.
6.1. Imputed MWI
In NSW, 2011 Census summaries are available for four nested sets of geographic areas, called Statistical Areas (SA), where the most disaggregated level consists of SA1 areas. We fit a spatial model to MWI for the SA1 areas (Figure 1) with a population >100 persons, which is 97% of the total SA1 areas; populations ≤100 are too granular for the statistical analysis that we shall undertake. SA1 areas in NSW exhibit a wide range in both population and area, since the state’s population is concentrated along the coastline (in the east of the state). For the SA1 areas we consider, their populations range from 100 to 13,000 (with a median of 395).
In the Census, each person ≥15 years specifies their usual mean weekly income by selecting from 11 possible income ranges {≤$0, $1 to $199, $200 to $299, $300 to $399, $400 to $599, $600 to $799, $800 to $999, $1,000 to $1,249, $1,250 to $1,499, $1,500 to $1,999, ≥$2,000}. For the SA1 areas, the Census data are the number of persons, , in the j-th income range. Thus, the 2011 Census does not directly measure MWI for SA1s; denote the true MWI process as . However, in the 2011 to 2012 Australian Survey of Income and Housing (SIH) [45], the mean usual weekly income of a large sample of individuals was measured, but with limited spatial information. Hence, we use the SIH microdata to impute an MWI value, , for the 2011 Census SA1 area , where the “bar” on is added to emphasise that MWI refers to mean income. In this analysis, we use only the SIH data and Census counts from the Census income ranges corresponding to $0 < MWI < $2,000, which includes most (approximately 94%) of the incomes in the Census. Negative, zero and very large incomes are set aside. These incomes, along with SA1 areas with populations less than 100, need special attention that is beyond the goal of this section.
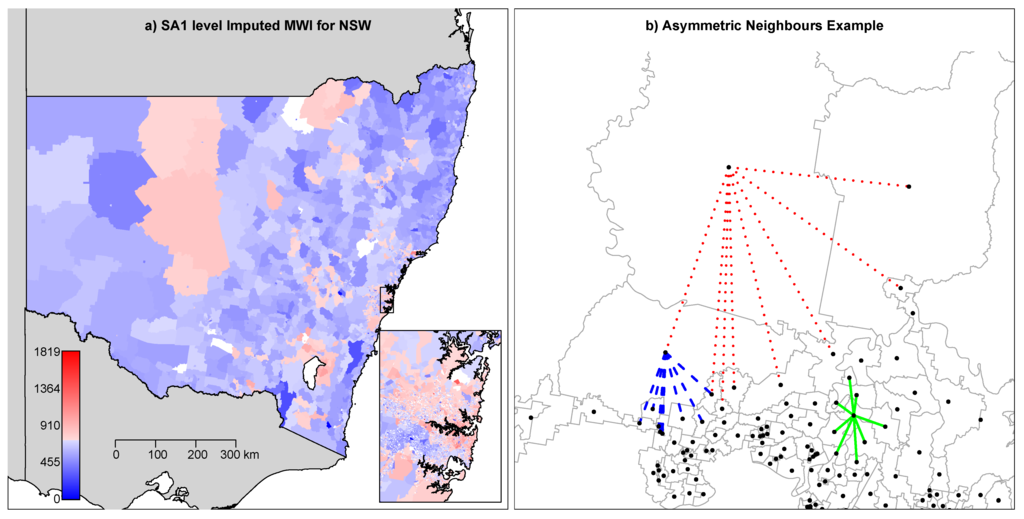
Figure 1.
(a) Chloropleth map of imputed mean usual weekly income (MWI) ($0 < MWI < $2,000) for Statistical Area 1 (SA1) areas in NSW, Australia; the resolution around Sydney is enhanced. (b) An excerpt of SA1 areas from (a) showing how asymmetry can occur in the spatial dependence matrix. The lines join the centroids of neighbouring areas, which are obtained using a K-nearest-neighbour algorithm, where here .
To impute the MWI values, we first stratify the Australia-wide SIH data using the Census income ranges, resulting in SIH records for the income ranges. The SIH data include weights that are used to account for unequal selection probabilities when calculating population estimates. We use them to impute MWI values, , by sampling SIH records, with replacement, from , for each of , . As mentioned above, the MWI values in the samples are selected using the same probability distribution that was used to select individuals in the SIH survey. We average the imputed values for each area, to obtain an imputed MWI value:
where . Hence, the spatial data that we shall analyse in this section are,
6.2. A Simple Heteroskedastic Model for MWI
A basic heteroskedastic model for MWI was explored and found to fit reasonably well: assume that for each area i and stratum j, income values are a random sample from a distribution with mean and variance . From (38) and for given ,
Contrast this with an overly simple model that assumes a constant mean and variance for the elements of .
In Figure 2, the left panel gives a histogram and Q-Q plot of unstandardised motivated by the overly simple model that assumes constant mean and variance over the SA1 areas. The right panel gives a histogram and Q-Q plot of the standardised values from the basic heteroskedastic model:
where and in (40) are estimated straightforwardly from the SIH data. The fit of the histogram in the right panel to a distribution is striking and indicates that any spatial model we fit should aim to capture the same types of heteroskedastic behaviour given by (40). Of course, is an important part of the randomness in defined by (38) and (39), and in a formal (spatial) model, we cannot have them describing the first two moments (as we do informally in (40)).
To capture the heteroskedasticity in (40) and illustrated in Figure 2, recall from (5) that . We estimate using the centiles of the Socio-Economic Indicator For Areas Index of Economic Resources (IER), a well-established socio-economic indicator produced for SA1 areas in Australia by the ABS [46]. There are 35 SA1 areas out of 16,850 that do not have an IER. For each of these, we obtained a value for the IER based on a regression of the 16,815 IER values that we do have, regressed on the covariates included in our model (see Section 6.5). Finally, then, we have 16,850 IER values whose centiles define 100 groups of SA1 areas, as follows:
Define , , , and hence, we set:
That is, in (42), we replace the random weights given in (40) with centile-smoothed weights. This leaves a single variance, , to be estimated.
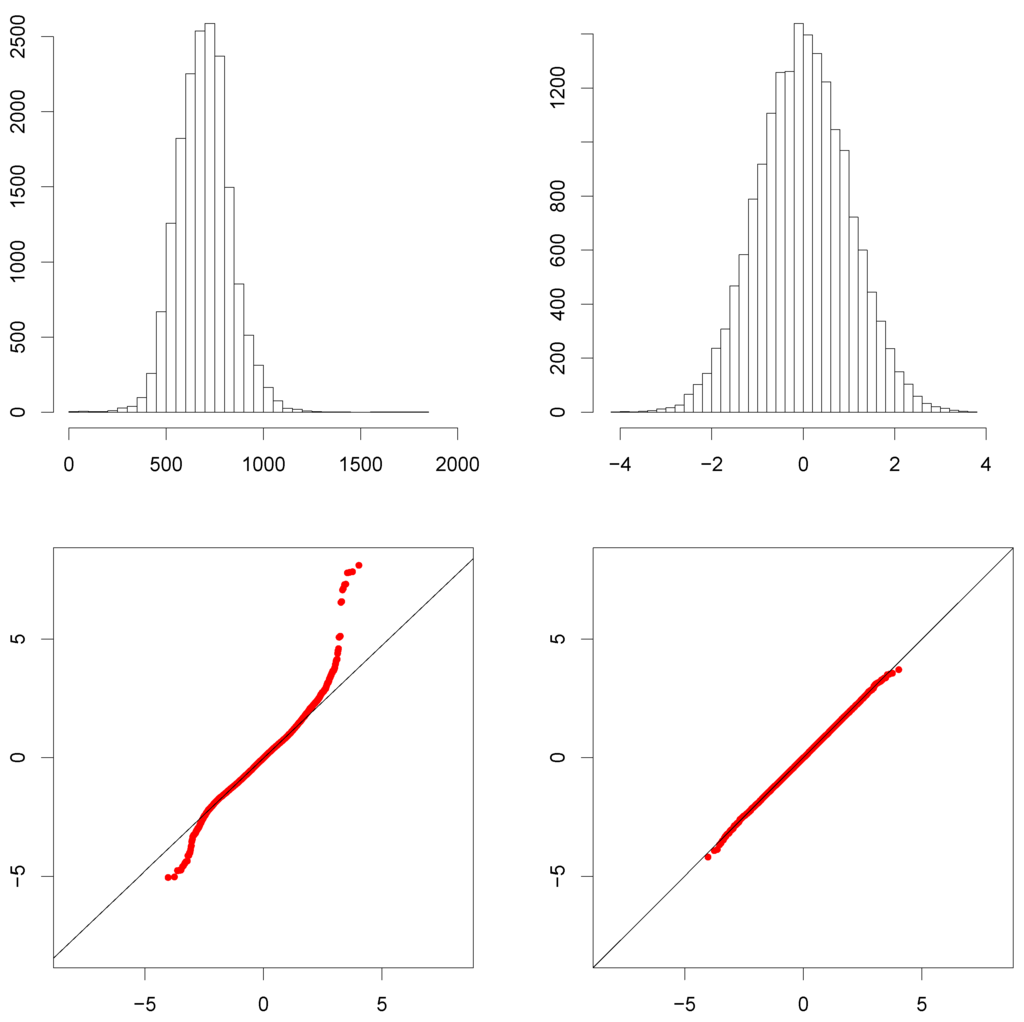
Figure 2.
Histogram and Q-Q plot of for 16,850 SA1 areas (left panels). Histogram and Q-Q plot of standardised values (41) for the same SA1 areas (right panels).
6.3. Measurement Error in MWI
Known sources of measurement error in the Census are due to non-response, invalid responses and random error purposely applied to the SA1 areas that have small populations (for confidentiality reasons; see [44] for further details). In the 2011 Census, item non-response for mean usual weekly income at the person level was approximately 7.9% [47].
Here, we model the non-response as “missing completely at random.” Then, for the i-th area, the observed is the sum of Bernoulli random variables, , where is an indicator variable with , obtained from the item non-response, and is the true number of people. From the randomness associated with , we calculate using the delta method. That is,
Recall that is the fully enumerated population total for area i and stratum j, and we define . To estimate (43), we use for and for . Because the measurement-error calculations come from a separate study of item non-response, the values given by (43) are considered as known, and hence, is known.
A summary statistic giving the measurement-error component of variability as a fraction of the total variability is:
where . In our case, this is equal to 0.01%, which is very small.
6.4. Specifying the Spatial Dependence Matrix
The simple exploratory model we proposed in Section 6.2 does not account for spatial dependence between the SA1 areas. Now that we have captured the heteroskedasticity (Section 6.2) and measurement error (Section 6.3), we can build a SAR model (see Section 2.1) for the MWI values, , defined for a fully enumerated population. That is, assume that has a covariance matrix given by (3), which is parametrised in terms of ρ and .
Because there are small areas, fitting the SAR model is numerically challenging, so we turn to estimating the SAR parameters ρ and by fitting the SAR-calibrated SRE model given in Section 4. Recall that we choose , to be the matrix containing the n-dimensional eigenvectors corresponding to the r largest absolute eigenvalues in (23), which are obtained from a spectral decomposition of the GMO (21) for a heteroskedastic SAR model.
The basis functions and the SRE model parameters and all depend on the spatial dependence matrix in (3). In NSW, there is substantial variation in the physical areas of the SA1s and in the spatial proximity of neighbouring areas. Along the eastern coastline and in the major urban centres, SA1s are reasonably uniformly distributed, whereas in other parts of the state, there is much greater asymmetry in the number and proximity of neighbouring areas.
A common choice for is the symmetric adjacency matrix:
where if the i-th area shares a common boundary with the -th area; and , otherwise. However, an asymmetric is more reasonable in this instance where distance or the shortest travel time between areas is more important than sharing a boundary. On a regular spatial lattice, the eight nearest neighbours are also the adjacent neighbours, but on an irregular lattice, they can be very different (see Figure 1b). Here, we model based on the eight nearest neighbours of the irregular SA1 spatial lattice; that is,
where , for:
and is the distance between the respective centroids of the i-th and -th areas,
Clearly, from Figure 1b, if , it may not be true that , and hence, will generally be asymmetric. In our analysis, we fitted the SAR-calibrated SRE model using equal to both (row-standardised) and (row-standardised) , and we compared them.
6.5. Statistical Inference
In this section, we obtain parameter estimates for ρ, , and β from the SAR-calibrated SRE model, using the methodology outlined in Section 5. Initially, we estimate the parameters for a small subset of the SA1 data obtained from the 1,230 SA1 areas that are located within the 2011 Census SA4 region of southwestern (SW) Sydney (Figure 3). We use these results to help select the number of basis functions, r, to use when modelling the full NSW dataset. With , the SAR model estimate for ρ can be computed, and hence, r is chosen so that (which depends on r) is close to the target value .
We subsequently analyse the full NSW dataset using this selected value of r in a SAR-calibrated SRE model. Clearly, direct likelihood-based parameter estimates based on the SAR model are no longer possible for all of NSW, due to the size of the dataset ().
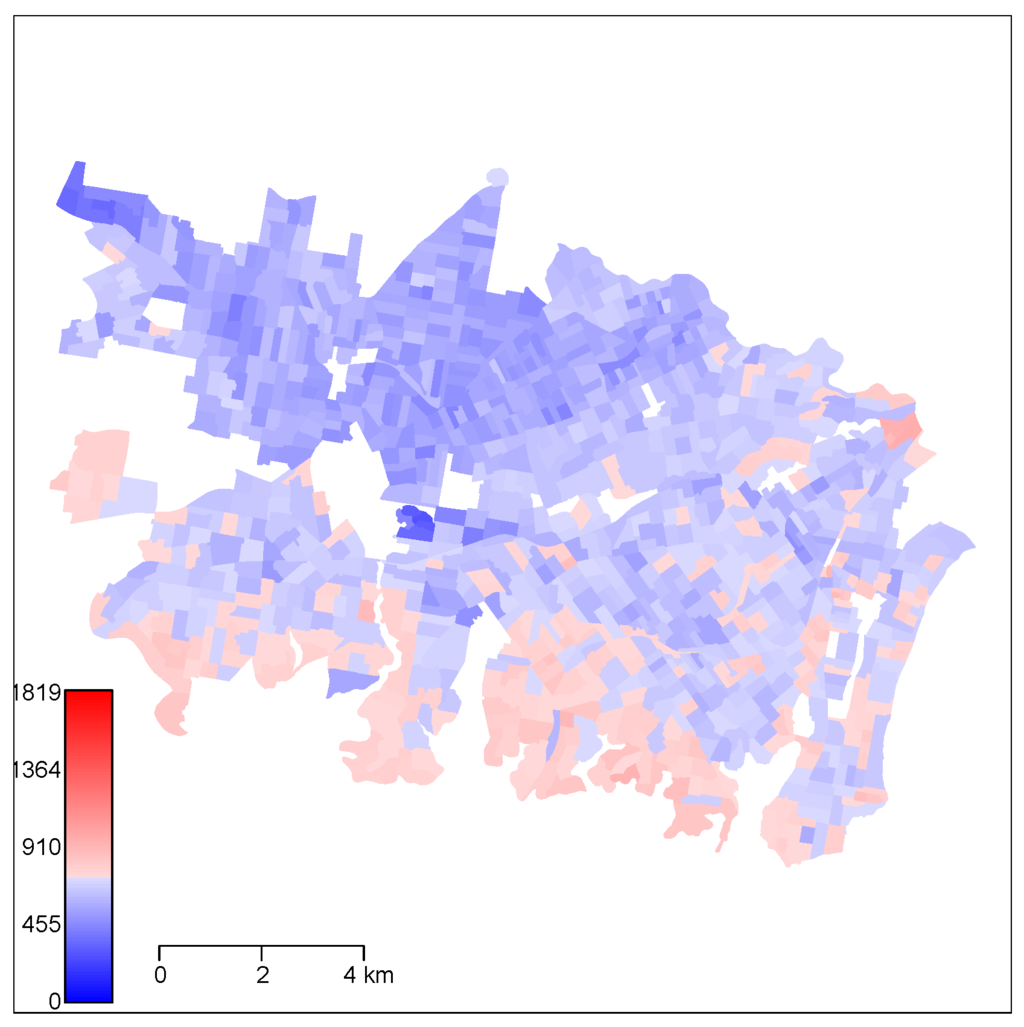
Figure 3.
SA1 level imputed MWI for SW Sydney.
While the basic heteroskedastic model for MWI in Section 6.2 fitted well, we cannot use it for inference, because its mean depends on the random counts used to impute the data. Socio-economic and demographic covariates are generally used in an attempt to explain the variability in MWI. Using various selection criteria, we settled on the following explanatory variables: the proportion of males, out of the total population, in the age groups 15 to 24, 25 to 64 and ≥65 (three covariates), the proportion of females, out of the total population, in the same age groups (three covariates), the median mortgage repayment, the median rent, the average household size and the average number of persons per bedroom (four covariates) and the overall mean effect (one covariate). That is, we fitted a regression, , for the mean of the spatial model, where the number of regression parameters was . The estimate of β is important and interpretable, and it may even be used by governments to make policy.
We specify the matrices that we use to represent heteroskedasticity, measurement error and spatial dependence in the model using (42), (43) and (44) or (45) from Section 6.2, Section 6.3 and Section 6.4, respectively. To complete our specification of the model, we use the term to capture the additional variance not captured by the spatial basis functions included in the model. We expect the variance to depend on the number of observations in each area, and hence, we set , where is a scaling constant that makes comparable to .
We use the restricted-maximum-likelihood-estimation method described in Section 5 to obtain REML estimates, and , for the SW Sydney and the NSW datasets, for the spatial dependence matrices and defined by (44) and (45), respectively. In each case, we used a grid-search algorithm to obtain . For each value of ρ, we obtained a starting value, using (34) with , and then, we iteratively estimated . We calculated the profile restricted log-likelihood for each value of (ρ,), from which we obtained , and hence, . Finally, we used (37) to obtain generalised least-squares parameter estimates, .
For the SW Sydney dataset, we compared and with the target SAR model estimates. Hence, we use restricted maximum likelihood estimation and account for the measurement error to obtain SAR model parameter estimates, and .
Based on Figure 4 for SW Sydney, we see that for spatial basis functions, the SAR-calibrated SRE model yields a 95% confidence interval for ρ that contains for and for . From this and plots of SAR-calibrated estimates of ρ and versusr for all of NSW, we chose basis functions for our dimension-reduced analysis of MWI in the 16,850 SA1 areas of NSW shown in Figure 1. To choose which spatial dependence matrix to use for the NSW dataset, we compared the magnitude of the restricted log-likelihood functions for SW Sydney obtained using and using , since the number of parameters is the same in both models. The asymmetric spatial dependence matrix resulted in a smaller value for the negative restricted log-likelihood, so we used to fit the model for NSW.
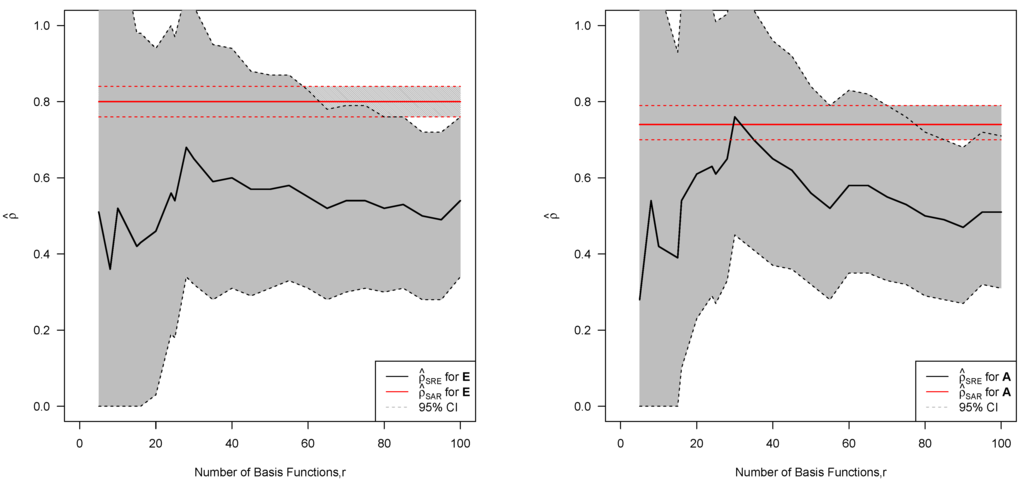
Figure 4.
SAR-calibrated spatial random effects (SRE) model restricted (or residual) maximum likelihood (REML) estimates for and for SW Sydney as a function of r for (left-hand panel) and for (right-hand panel); the SAR model estimate and 95% profile log-likelihood confidence intervals (CI) for ρ are included for comparison (36).
We fit the resulting SAR-calibrated SRE model given by (31) and (30) to the full NSW dataset, to obtain SAR-calibrated SRE model REML estimates, and . We also obtain , and hence, . From these results, we conclude that MWI exhibits substantial spatial dependence in NSW, after allowing for the covariates included in the regression model.
Table 1 compares the SAR-calibrated SRE model estimates of β given by (37) with the ordinary least-squares (OLS) regression parameter estimates, ; the latter estimates ignore heteroskedasticity and spatial dependence. For all of the covariates except the intercept and “Female, 15 to 24 years”, the OLS estimates do not fall within the 95% CI for their respective β’s obtained using the SAR-calibrated SRE model. The OLS estimate is based on the overly simple model, , and for this dataset, it is inadequate. This demonstrates the importance of capturing small-scale heteroskedastic spatial variation in our analysis of MWI.

Table 1.
MWI for NSW. Ordinary least-squares regression-parameter estimates, generalised least-squares regression-parameter estimates obtained from fitting an SAR-calibrated SRE model and 95% confidence intervals (CIs). The SRE model is based on 25 basis functions and given by (45).
| 463 | 47.5 | 773 | −782 | −201 | 675 | |
| (432,494) | (−6.7,102) | (732,814) | (−836,−729) | (−256,−146) | (622,728) | |
| 481 | −95.6 | 719 | −695 | −177 | 789 | |
| 346 | 0.0443 | 0.298 | −234 | −15.1 | ||
| (302,390) | (0.042,0.0466) | (0.287,0.309) | (−244,−224) | (−18.7,−11.3) | ||
| 219 | 0.0472 | 0.197 | −245 | −7.84 |
7. Discussion and Conclusions
This paper has considered the specification and estimation of a hierarchical model that includes a computationally-efficient spatial random effects (SRE) model for a latent spatial process and an additive measurement error model for the observed data. Using the generalised Moran operator, we calibrate this model to an SAR model, a model that is widely used in spatial econometrics, but that is computationally prohibitive for large datasets. We use restricted maximum likelihood on a computationally-efficient SRE model to estimate the SAR model’s covariance parameters.
Implementation of our model is demonstrated using Australian Census data for mean income. It is clear from the SAR-calibrated SRE model fitted to NSW’s 16,850 SA1 areas that a regression model with the 11 covariates and independent residuals does not properly capture the small-scale variability. This (heteroskedastic) spatial variability is important, which is reflected in the estimate for ρ, namely for 25 basis functions. It is also reflected in the change of regression coefficient estimates when the spatial variability is used to improve both the estimates and their estimation variance.
Notice the role of model calibration here, which is different from model fitting. The SRE model is calibrated to be close to the SAR model of interest, and then, the computationally-efficient SAR-calibrated SRE model is fitted. Importantly, the parameters that are fitted are those of the original, interpretable SAR model. This enables SAR model parameters to be estimated for much larger datasets than is currently possible.
It is easy to see that our SAR-calibrated SRE model can be adapted to obtain a CAR-calibrated SRE model. In some sense, this represents the converse of the calibration undertaken by Rue and Tjelmeland [48], who find the Gaussian–Markov random field (GMRF) that comes closest to a geostatistical model; note that the CAR model is a GMRF and that the SRE model is a geostatistical model.
Besides the advantages of the SAR-calibrated SRE model in producing parameter estimates, the r spatial basis functions in could be used to identify hidden, possibly overlapping, regions or classes of areas. The associated random effects can be easily predicted, and hence, regions or classes having higher or lower values of MWI could also be predicted. Moreover, as the covariance matrix of the random effects is not constrained to be diagonal, the SRE model captures additional dependence associated with these classes.
Acknowledgements
We would like to express our appreciation to the reviewers for their helpful comments. This research was partially supported by the U.S. National Science Foundation (NSF) and the U.S. Census Bureau under NSF Grant SES-1132031, funded through the NSF-Census Research Network (NCRN) program; and it was partially supported by a 2015 to 2017 Australian Research Council Discovery Project.
Author Contributions
David G. Steel suggested the problem. Noel Cressie suggested the methodology to use. Sandy Burden implemented these suggestions to solve the problem. All three authors contributed to the final paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- P. Whittle. “On stationary processes in the plane.” Biometrika 41 (1954): 434–449. [Google Scholar]
- L. Anselin. Spatial Econometrics: Methods and Models. Dordrecht, The Netherlands; Boston, MA, USA: Kluwer Academic Publishers, 1988. [Google Scholar]
- R.K. Pace, and R. Barry. “Sparse spatial autoregressions.” Stat. Probab. Lett. 33 (1997): 291–297. [Google Scholar]
- O.A. Smirnov. “Computation of the information matrix for models with spatial interaction on a lattice.” J. Comput. Graph. Stat. 14 (2005): 910–927. [Google Scholar] [CrossRef]
- R.K. Pace, and J.P. Le Sage. “Chebyshev approximation of log-determinants of spatial weight matrices.” Comput. Stat. Data Anal. 45 (2004): 179–196. [Google Scholar]
- C.K. Wikle. “Low rank representations as models for spatial processes.” In Handbook of Spatial Statistics. Edited by A.E. Gelfand, P.J. Diggle, M. Fuentes and P. Guttorp. Boca Raton, FL, USA: Chapman and Hall/CRC Press, 2010, pp. 107–118. [Google Scholar]
- H.F. Lopes, D. Gamerman, and E. Salazar. “Generalized spatial dynamic factor models.” Comput. Stat. Data Anal. 55 (2011): 1319–1330. [Google Scholar] [CrossRef]
- S. Banerjee, A.E. Gelfand, A.O. Finley, and H. Sang. “Gaussian predictive process models for large spatial data sets.” J. R. Stat. Soc. Ser. B 70 (2008): 825–848. [Google Scholar]
- A.O. Finley, H. Sang, S. Banerjee, and A.E. Gelfand. “Improving the performance of predictive process modelling for large datasets.” Comput. Stat. Data Anal. 53 (2009): 2873–2884. [Google Scholar] [CrossRef] [PubMed]
- J. Eidsvik, A.O. Finley, S. Banerjee, and H. Rue. “Approximate Bayesian inference for large spatial datasets using predictive process models.” Comput. Stat. Data Anal. 56 (2012): 1362–1380. [Google Scholar] [CrossRef]
- N. Cressie, and G. Johannesson. “Spatial prediction for massive data sets.” In Proceedings of the Australian Academy of Science Elizabeth and Frederick White Conference: Mastering the data explosion in the earth and environmental sciences, Shine Dome, Canberra, Australia, 19–21 April 2006; pp. 1–11.
- N. Cressie, and G. Johannesson. “Fixed rank kriging for very large spatial data sets.” J. R. Stat. Soc. Ser. B 70 (2008): 209–226. [Google Scholar]
- H.H. Kelejian, and I.R. Prucha. “A generalized moments estimator for the autoregressive parameter in a spatial model.” Int. Econ. Rev. 40 (1999): 509–533. [Google Scholar] [CrossRef]
- J. Hughes, and M. Haran. “Dimension reduction and alleviation of confounding for spatial generalized linear mixed models.” J. R. Stat. Soc. Ser. B 75 (2013): 139–159. [Google Scholar] [CrossRef]
- A. Sengupta, and N. Cressie. “Hierarchical statistical modeling of big spatial datasets using the exponential family of distributions.” Spat. Stat. 4 (2013): 14–44. [Google Scholar] [CrossRef]
- T. Shi, and N. Cressie. “Global statistical analysis of MISR aerosol data: A massive data product from NASA’s Terra satellite.” Environmetrics 18 (2007): 665–680. [Google Scholar] [CrossRef]
- N. Cressie, and C.K. Wikle. Statistics for Spatio-Temporal Data. Hoboken, NJ, USA: Wiley, 2011. [Google Scholar]
- J.A. Royle, and C.K. Wikle. “Efficient statistical mapping of avian count data.” Environ. Ecol. Stat. 12 (2005): 225–243. [Google Scholar] [CrossRef]
- M.D. Buhmann. Radial Basis Functions: Theory and Implementations. Cambridge, UK; New York, NY, USA: Cambridge University Press, 2003. [Google Scholar]
- T. Hastie, R. Tibshirani, and J.H. Friedman. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed. New York, NY, USA: Springer, 2001. [Google Scholar]
- M. Katzfuss, and N. Cressie. “Bayesian hierarchical spatio-temporal smoothing for very large datasets.” Environmetrics 23 (2012): 94–107. [Google Scholar] [CrossRef]
- D. Nychka, C.K. Wikle, and J.A. Royle. “Multiresolution models for non-stationary spatial covariance functions.” Stat. Model. 2 (2002): 315–331. [Google Scholar] [CrossRef]
- J.R. Bradley, N. Cressie, and T. Shi. “Selection of rank and basis functions in the spatial random effects mode.” In 2011 Proceedings of the Joint Statistical Meetings. Alexandria, VA, USA: American Statistical Association, 2011, pp. 3393–3406. [Google Scholar]
- D.A. Griffith. “Eigenfunction properties and approximations of selected incidence matrices employed in spatial analyses.” Linear Algebra Appl. 321 (2000): 95–112. [Google Scholar] [CrossRef]
- D.A. Griffith. “Spatial-filtering-based contributions to a critique of geographically weighted regression (GWR).” Environ. Plan. A 40 (2008): 2751–2769. [Google Scholar] [CrossRef]
- M. Tiefelsdorf, and D.A. Griffith. “Semiparametric filtering of spatial autocorrelation: The eigenvector approach.” Environ. Plan. A 39 (2007): 1193–1221. [Google Scholar] [CrossRef]
- B.J. Reich, J.S. Hodges, and V. Zadnik. “Effects of residual smoothing on the posterior of the fixed effects in disease-mapping models.” Biometrics 62 (2006): 1197–1206. [Google Scholar] [CrossRef] [PubMed]
- J.R. Bradley, S.H. Holan, and C.K. Wikle. “Mixed effects modelling for areal data that exhibit multivariate spatio-temporal dependencies.” 2014. arXiv:1407.7479v2 [stat.ME]. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1407.7479 (accessed on 7 October 2014).
- J. Besag, J. York, and A. Mollié. “Bayesian image restoration, with two applications in spatial statistics.” Ann. Inst. Stat. Math. 43 (1991): 1–20. [Google Scholar] [CrossRef]
- A.D. Cliff, and J.K. Ord. Spatial Processes: Models and Applications. London, UK: Pion, 1981. [Google Scholar]
- N. Cressie. Statistics for Spatial Data, 2nd ed. New York, NY, USA: John Wiley and Sons, Inc, 1993. [Google Scholar]
- J.P. Le Sage. “Bayesian estimation of spatial autoregressive models.” Int. Reg. Sci. Rev. 20 (1997): 113–129. [Google Scholar] [CrossRef]
- L. Anselin. “Under the hood.” Agric. Econ. 27 (2002): 247–267. [Google Scholar]
- J.P. LeSage, and R.K. Pace. Introduction to Spatial Econometrics. Boca Raton, FL, USA: CRC Press, 2009. [Google Scholar]
- A. Sengupta, and N. Cressie. “Empirical hierarchical modelling for count data using the spatial random effects model.” Spat. Econ. Anal. 8 (2013): 389–418. [Google Scholar] [CrossRef]
- H. Li, C.A. Calder, and N. Cressie. “One-step estimation of spatial dependence parameters: Properties and extensions of the APLE statistic.” J. Multivar. Anal. 105 (2011): 68–84. [Google Scholar] [CrossRef]
- N. Cressie, and S.N. Lahiri. “The asymptotic distribution of REML estimators.” J. Multivar. Anal. 45 (1993): 217–233. [Google Scholar] [CrossRef]
- O. Schabenberger, and C.A. Gotway. Statistical Methods for Spatial Data Analysis. Boca Raton, FL, USA: Chapman & Hall/CRC, 2005. [Google Scholar]
- M. Tiefelsdorf. Modelling Spatial Processes: The Identification and Analysis Of Spatial Relationships in Regression Residuals by Means Of Moran’s I. Berlin, Germany; New York, NY, USA: Springer-Verlag, 2000, Volume 87, Lecture Notes in Earth Sciences. [Google Scholar]
- M. Tiefelsdorf, and B. Boots. “The exact distribution of Moran’s I.” Environ. Plan. A 27 (1995): 985–999. [Google Scholar] [CrossRef]
- D.A. Griffith. “Spatial autocorrelation and eigenfunctions of the geographic weights matrix accompanying geo-referenced data.” Can. Geogr. 40 (1996): 351–367. [Google Scholar] [CrossRef]
- N.J. Higham. “Computing a nearest symmetric positive semidefinite matrix.” Linear Algebra Appl. 103 (1988): 103–118. [Google Scholar] [CrossRef]
- H.V. Henderson, and S.R. Searle. “On deriving the inverse of a sum of matrices.” SIAM Rev. 23 (1981): 53–60. [Google Scholar] [CrossRef]
- Australian Bureau of Statistics. 2011 Australian Census of Population and Housing: New South Wales (SA1 and SA2 Level areas), Basic Community Profile, Table 17; Canberra, Australia: Australian Bureau Statistics, 2011.
- Australian Bureau of Statistics. Survey of Income and Housing 2011-12, Confidentialised Unit Record File; Canberra, Australia: Australian Bureau Statistics, 2012.
- Australian Bureau of Statistics. Socio-Economic Indexes for Areas (SEIFA) 2011—Technical Paper: ABS Catalogue no. 2033.0.55.001; Canberra, Australia: Australian Bureau Statistics, 2013.
- Australian Bureau of Statistics. 2011 Australian Census of Population and Housing: Data Quality Statement for Total Personal Income (weekly) (INCP); Canberra, Australia: Australian Bureau Statistics, 2011.
- H. Rue, and H. Tjelmeland. “Fitting Gaussian Markov random fields to Gaussian fields.” Scand. J. Stat. 29 (2002): 31–49. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).