We now develop the basic analytical tools for a shift that can be matched by a single step indicator in
Subsection 5.1 and check the outcomes by simulation in
Subsection 5.2.
Subsection 5.3 considers the effects of misspecifying the timing of an indicator. The basic setting is generalized in
Subsection 5.4 to an unknown shift period requiring a two-step indicator.
Subsection 5.5 and
Subsection 5.6 consider the occurrence of two shifts where one lies in each half, first when opposite-signed, then when they are equal magnitudes, signs and durations.
Subsection 5.7 then considers an unknown shift spanning both halves where multi-path search across several splits is likely to outperform split-half one-cut; see [
33] for more detailed simulation evidence and comparisons with IIS.
5.1. Unknown Shift Period Matched by a Single Step Indicator
We first show that detection of a single location shift falling entirely within a half-sample of the data (
) as in Equation (6) is feasible using the split-half one-cut analysis of step-indicator saturation. In matrix notation, let
denote a
vector with elements of unity till
and zeroes thereafter, so the DGP is:
As before, add the first half of the step indicators, assuming
T is even, so the model becomes:
We assume an intercept of zero in Equation (12) to highlight the main aspects of the algebra, written in matrix form as:
where
and
.
Theorem 2. The distribution of the least-squares estimator of in Equation (13) is:
where r is a vector with unity in the -th position, and zeroes elsewhere.
Proof. From Equation (11):
where
is:
The inverse of
is the ‘double difference’ matrix:
Therefore:
which is the forward-difference matrix. Consequently, letting
, from Equation (15):
where
r is a
vector with unity in the
-th position and zeroes elsewhere, so:
where the (
vector
. All the elements of
up to the
-th should be near zero and only the
-th reflects
, corresponding to the location shift, with the others being distributed around zero as
. Thus:
Furthermore:
Therefore:
☐
Effectively, (
18) shows that only the value of
at the shift is being picked up, so the incremental information is equivalent to an impulse indicator for
. Further, letting
, so:
as
and
, then for
:
Thus, the estimated error variance, adjusted for degrees of freedom, based on the second half:
will be an unbiased estimator of
.
Consequently, estimating (
12) leads to the test statistic:
where
is the non-centrality. In IIS, one-cut selection was feasible given the orthogonality of the impulse indicators. The high collinearity between the step indicators entails that there is little information accrual at the level of Equation (24), so sequential selection eliminating the least significant indicators, or multi-path search, is essential for SIS. At 1%,
, so normalizing on
requires
for even a 50% chance of being significant before simplification. It is unlikely that the smallest
occurs at
, and when the least significant indicators are deleted from the model,
will fall rapidly from Equation (23). For irrelevant step indicators:
Therefore, on average, of the irrelevant step indicators will be adventitiously significant during selection, as found under the null. If all irrelevant step indicators were eliminated correctly, just would remain, and the non-centrality would become , which is larger than the non-centrality before selection. We assume sequential simplification or multi-path search will be used, so it will approximate that outcome, as the simulations below confirm.
Having completed the selection of indicators from the first half, these are eliminated, and the second half of the step indicators,
are added, noting that
is the intercept. Now, the model becomes:
written as:
where
and
.
Theorem 3. The distribution of the least-squares estimator of in Equation (27) is:
where c is a vector of ones, and is a vector of zeroes other than unity in its first position, so only the first element of depends on .
Proof. From (11), estimation yields:
where
is:
which is:
Therefore:
as:
since:
Next:
so that:
and as:
then:
☐
Thus, the indicator nearest to the shift is most likely to be retained when the relevant indicator is not ‘carried forward’, as simulations confirm. If the shift is in the second half, the last indicator in the first-half will be kept.
Finally, combine the selected step indicators in a model and reselect. When all irrelevant indicators are removed and the relevant one retained:
The distribution resulting in the case of a perfect selection must coincide with Equation (9); any irrelevant indicators retained by chance would reduce the degrees of freedom and increase variances from collinearity.
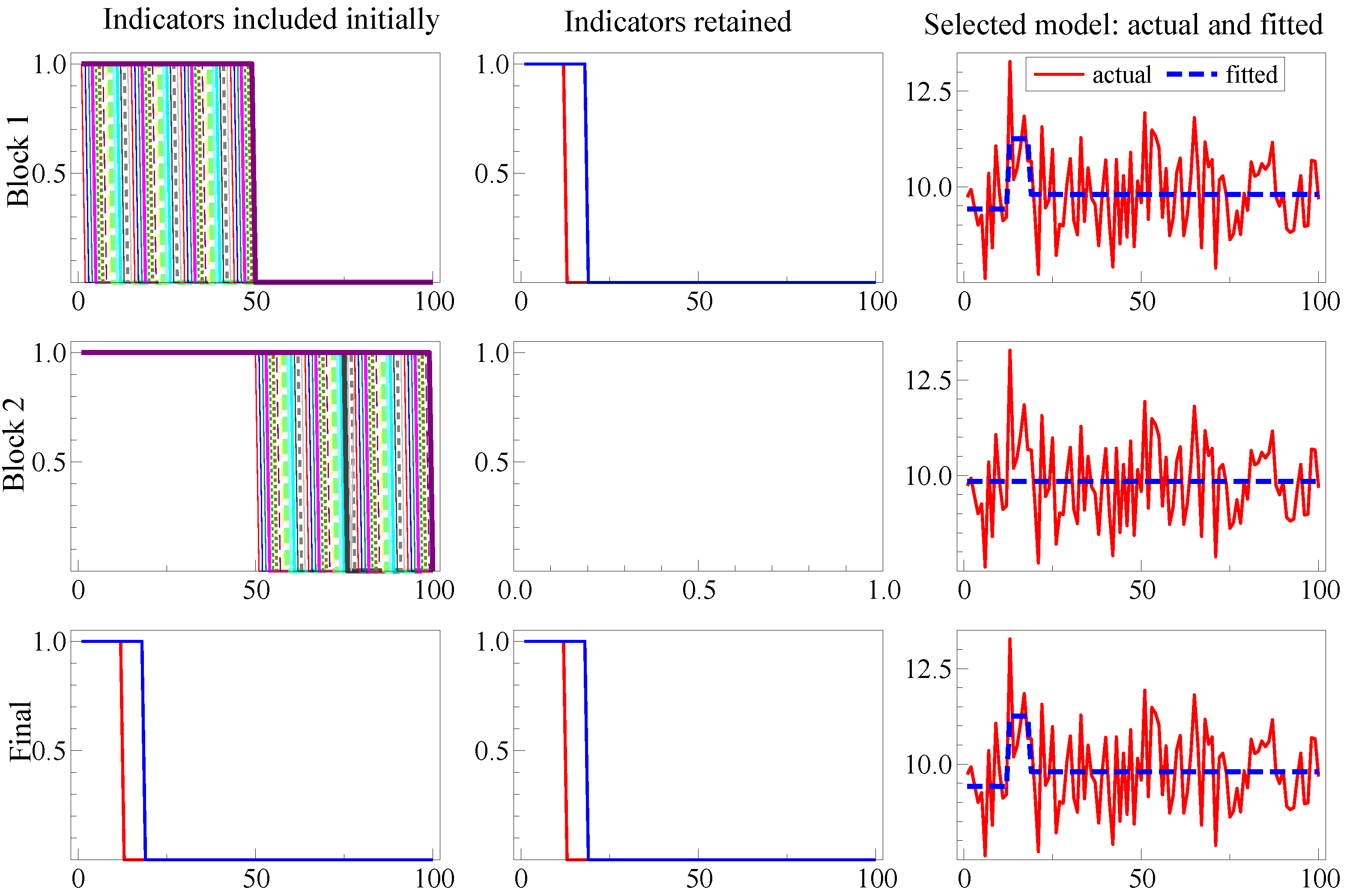
Figure 2 illustrates SIS for a location shift over the last 25 observations in the DGP:
where
. Initially, the last step indicator captures the mean shift drop (Row 1) matching the above analysis, then the location shift is found in Row 2, so the now redundant indicator is eliminated in Row 3. Thus, the outcome here coincides with the optimal test for a known location shift, namely a
t-test in Equation (34) at
onwards, without requiring knowledge: (1) that it was a location shift; (2) of the shift timing; (3) that it was the only shift; and (4) that the same magnitude of shift continued thereafter.
Figure 2.
Illustrating split-half one-cut SIS for the shift in Equation (34).
Figure 2.
Illustrating split-half one-cut SIS for the shift in Equation (34).
5.2. Simulating an Unknown Shift Period Matched by a Single Indicator
We now simulate the properties of SIS for a single location shift during the first half of the sample, using the DGP in Equation (11), where the timing of the location shift is set to
: varying shift lengths are investigated in
Table 2. The shift magnitude
is set equal to
and
, with selection at
.
For the split-half one-cut approach outlined in
Subsection 5.1, the open histograms and their densities in
Figure 3b show that, while the density of
is centred around the true value of
, in the case of
errors, the variance of the estimator is twice that of the error (d), in line with Equation (23) below. The associated
t-statistic density overlaps zero (c).
The retention frequencies of the step indicator
for varying lengths of shift and two levels of
without and with sequential selection of indicators are provided in
Table 2. Given the relatively low retention frequency in the simple split-half one-cut approach, sequential selection of step indicators is essential. Iterative elimination of the least significant indicators leads to a rapid fall in the variance of the estimator
(
Figure 3b, d), an increase in the retention frequency of the correct step indicators in (c) and a reduction in the number of incorrectly retained indicators. As the shaded histograms and their densities in
Figure 3 and the lower section of
Table 2 both show sequential selection or multi-path search as in Autometrics, this dramatically improves the outcomes of SIS in the single-shift experiment. For a step shift of
, sequential selection increases the retention frequency on average to 0.93 from 0.59 with split-half one-cut.
Table 2.
Retention frequency of for varying shift lengths l and magnitudes, , at .
Table 2.
Retention frequency of for varying shift lengths l and magnitudes, , at .
| Algorithm | | | | | | |
|---|
| Known shift: | | 0.56 (2.77) | 0.98 (4.72) | 0.99 (6.27) | 1.00 (8.17) | 1.00 (9.65) |
| 0.99 (5.59) | 1.00 (9.50) | 1.00 (12.57) | 1.00 (16.36) | 1.00 (19.31) |
| Split-half one-cut | | 0.15 (1.43) | 0.12 (1.42) | 0.13 (1.47) | 0.14 (1.44) | 0.16 (1.47) |
| 0.61 (2.88) | 0.61 (2.88) | 0.63 (2.92) | 0.59 (2.88) | 0.60 (2.92) |
| Split-half sequential: | | 0.17 (3.01) | 0.50 (3.68) | 0.57 (4.63) | 0.56 (5.86) | 0.56 (6.92) |
| 0.89 (4.10) | 0.93 (6.81) | 0.93 (8.96) | 0.92 (11.62) | 0.93 (13.70) |
| Multi-path | | 0.41 (3.89) | 0.57 (5.24) | 0.57 (6.33) | 0.58 (7.78) | 0.55 (8.65) |
| 0.95 (5.89) | 0.93 (9.45) | 0.95 (11.73) | 0.93 (14.79) | 0.92 (16.57) |
Figure 3.
Comparing SIS on a single shift without (open) and with (shaded) sequential selection. (a) shows the time series with a location shift; (b) and (c) the simulated estimator and test-statistic densities for split-half and sequential selection; and (d) their simulated variances.
Figure 3.
Comparing SIS on a single shift without (open) and with (shaded) sequential selection. (a) shows the time series with a location shift; (b) and (c) the simulated estimator and test-statistic densities for split-half and sequential selection; and (d) their simulated variances.
Varying the shift length at the start of the sample appears to have little impact on the retention frequencies of the shift indicator, except in the case of a single impulse. Using split-half sequential selection, a shift of is retained on average around 50% of the time, with an increase to around 90% for a shift of (at , ).
These simulations are consistent with the analysis in
Subsection 5.1: the
t-statistics for split-half one cut
in SIS are close to half those from IIS at the equivalent
, but, with sequential simplification or multi-path search, converge to those for a known indicator. There is only a slight drop in retention frequency of the correct step at
despite searching over
T indicators, though a rather larger drop at
. Although the
t-values of retained indicators increase with the shift length
l, the retention probability remains relatively constant in all cases for
, possibly because we only record the retention of
, although a neighbouring indicator may have been found instead. Since the predictive failure test of [
26] is based on IIS, as shown by [
34], SIS should dominate the Chow test, yet not require knowledge of the shift point. IIS can already dominate [
18], as shown in [
10], so SIS multi-path should be a useful method for detecting and modelling location shifts.
5.3. Misspecified Indicator Timing
A step indicator selected in the marginal process may not exactly match the period characterizing a location shift because: (1) it ends after (or starts before); (2) it is a subset (so it starts after and ends before); and (3) it starts after and ends after (or starts before and ends before). Setting (1) is representative of the likely costs of misspecification, so we consider it in the special case just involving a shift and no other parameters. Let
denote the indicator where
, so that the marginal DGP is:
but now approximated by the incorrect model:
with
. Autometrics selects congruent representations, so its step-indicator saturation algorithm will be directed away from non-overlapping indicators, like
, when shifts are large or
is long. Moreover, the costs of not matching dates precisely decline rapidly for small shifts. Similar analyses apply to Cases (2) and (3), with additional costs when parts of a shift are also not captured.
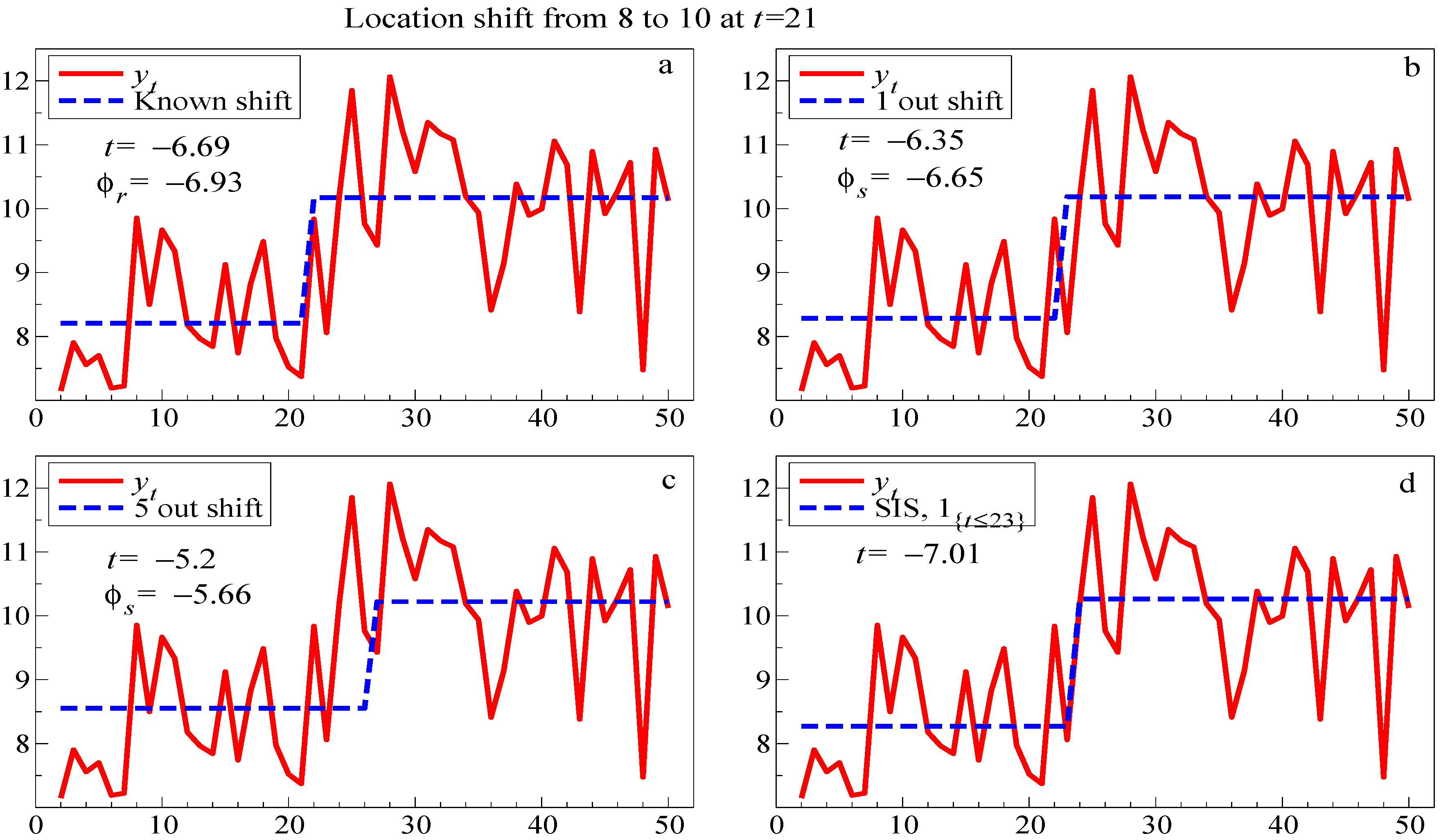
The choice of the period selected by SIS for a step indicator is because it has the largest
t-statistic, so serious mismatches that leave large residuals are unlikely. To illustrate this, consider
where
, estimated for a known indicator as:
The four panels in
Figure 4 show the match to the data in one replication when the indicator is: (a) correct; (b) too long by one, (so
); (c) too long by five; and (d) selected by SIS, which picked
, but had the most significant outcome. The
t-values are close to the theoretical non-centralities,
ϕ as recorded in the figure. Moreover, although the SIS selection ‘misses’ by two periods, that is precisely because that is when the shift is shown most clearly, and the residuals for
are not unusually large.
Figure 4.
Fitted and actual values for four step-indicator specifications to a location shift at . (a): known shift with t value and non-centrality ; (b): shift approximated by a step one period late and (c): shift approximated by a step 5 periods late, both with non-centralities ; and (d): SIS selection.
Figure 4.
Fitted and actual values for four step-indicator specifications to a location shift at . (a): known shift with t value and non-centrality ; (b): shift approximated by a step one period late and (c): shift approximated by a step 5 periods late, both with non-centralities ; and (d): SIS selection.
That the slow increase in potency shown in
Table 2 is primarily due to slight mistiming rather than not detecting the shift is shown in
Table 3. Potency increases monotonically down all columns, and even for
and relatively short breaks, is 0.9 or higher by
. However, unlike the
-test non-centrality of
from analytic power calculations for a known break point exactly matched by the correct step function in a static regression, where
r is the break-length fraction, potency does not increase much with
. The results for
are similar, but are not reported, as potency is near unity for all break lengths using
.
Overall, SIS has relatively high potency for detecting a single location shift, albeit within a few periods on either side of its ending.
Table 3.
Potency of for varying break lengths and accuracy of timing using Autometrics.
Table 3.
Potency of for varying break lengths and accuracy of timing using Autometrics.
| | | | | |
|---|
| 0.58 | 0.55 | 0.59 | 0.59 | 0.59 |
| 0.76 | 0.77 | 0.79 | 0.83 | 0.81 |
| 0.84 | 0.87 | 0.86 | 0.90 | 0.89 |
| 0.89 | 0.91 | 0.92 | 0.93 | 0.92 |
5.4. Unknown Shift Requiring a Two-Step Indicator in One-Half Sample
An unknown location shift may require a two-step indicator, as in the following DGP:
where
, and
, so as in
Subsection 5.1, the shift is entirely within one-half of the sample. The model for the first-half split is:
where
and
. For Equation (36) estimated on data from Equation (35):
where
s is a
selection vector with unity in the
-th position,
in the
-th position and zeroes elsewhere. Thus, a similar analysis to
Subsection 5.1 holds for two relevant indicators, with
r replaced by
s, so selecting indicators in the latter half of the sample should remain as before.
To simulate an unknown shift period requiring a two-step indicator in the first-half, we set
and
, and only consider sequentially selected indicators here, retaining the selected indicators from
and
at
.
Table 4 shows the simulation results for sequential selection from the split-half for two shifts, so retention frequencies are close to the case of a single shift.
Table 4.
Split-half sequential selection: gauge and retention frequencies for a shift with two indicators.
Table 4.
Split-half sequential selection: gauge and retention frequencies for a shift with two indicators.
| | Gauge | Retention frequency |
|---|
| | | step | step |
| 0.020 | 0.011 | 0.52 | 0.55 |
| 0.004 | 0.017 | 0.91 | 0.94 |
5.5. Unknown Opposite-Signed Shifts in Each Split Half
If shifts in each half of the sample have opposite signs, or perhaps very different magnitudes, then both can be detected even in a split-half sequential selection approach. Consider the DGP:
where
as before, and
, whereas
with
. To remove the mean effect of the other location shift, since:
the intercept must be retained without selection.
The formula in (37) still applies, with appropriate adjustments for estimating the intercepts, but even if the first shift is correctly modelled, the equation in (22) for the residuals becomes:
which has a larger estimated error variance than in the previous cases, because:
To compensate for the equivalent effect of Equation (40), when searching for a second shift, step indicators found in the first half should be be included in the second-half selection.
To simulate unknown opposite-signed shifts in each half,
and
are chosen, such that
, where the shift timing is given by
to
and
to
.
Table 5 shows that even with shifts falling in the middle of each half, SIS can be successful in identifying the shift points.
Table 5.
Split-half sequential selection: opposite-signed shifts in each half, .
Table 5.
Split-half sequential selection: opposite-signed shifts in each half, .
| | Gauge | Retention frequency |
|---|
| | | step | step | step | step |
| 0.021 | 0.045 | 0.52 | 0.55 | 0.57 | 0.56 |
| 0.004 | 0.030 | 0.91 | 0.94 | 0.93 | 0.93 |
5.6. Unknown Equal Shifts in Each Split Half
Shifts with relatively equal magnitudes, durations and the same signs in each half, so they are roughly evenly distributed between the two halves, could well appear as just a larger error variance, rendering the simplest split-half one-cut approach ineffective. Nevertheless, when
T is sufficiently large, both shifts can be detected using a modified split-half approach. First, saturate the second half by impulse indicators, then the first half can be tackled by a split-half approach, so quarters are examined, without any additional cost under the null. That procedure is then reversed for the first half. This is a variant of super saturation, where IIS is also undertaken with SIS as in [
15], but here limiting IIS to the alternate half and not using the information it reveals about outliers and shifts.
Under the alternative, by eliminating the shift in the second half, the first half comes under the above analysis for a single shift, which is then detectable provided it is not evenly split between the quarters. In practice, Autometrics uses multiple block searches, and this has proven effective for IIS in detecting multiple shifts. Blocks would need to span most of the length of a location shift to detect it using SIS, but that may be less essential for super saturation.
Unknown shifts of equal magnitude are assessed by setting
, with
to
and
to
, so there are two same-sign step shifts of equal magnitude and length in each half. We consider both the split-half sequential selection approach and multi-path selection using Autometrics (where a single gauge value is reported for
and
).
Table 6 provides summary results showing little difference in retention frequencies.
Table 6.
Split-half sequential selection and multi-path: unknown equal shifts in each half, .
Table 6.
Split-half sequential selection and multi-path: unknown equal shifts in each half, .
| Algorithm | Gauge | Retention Frequency |
|---|
| | | | step | step | step | step |
| Sequential: | 0.021 | 0.044 | 0.52 | 0.55 | 0.59 | 0.60 |
| | 0.005 | 0.030 | 0.91 | 0.94 | 0.94 | 0.94 |
| & | | step | step | step | step |
| Multi-path: | 0.038 | | 0.53 | 0.48 | 0.55 | 0.55 |
| | 0.018 | | 0.87 | 0.91 | 0.94 | 0.92 |
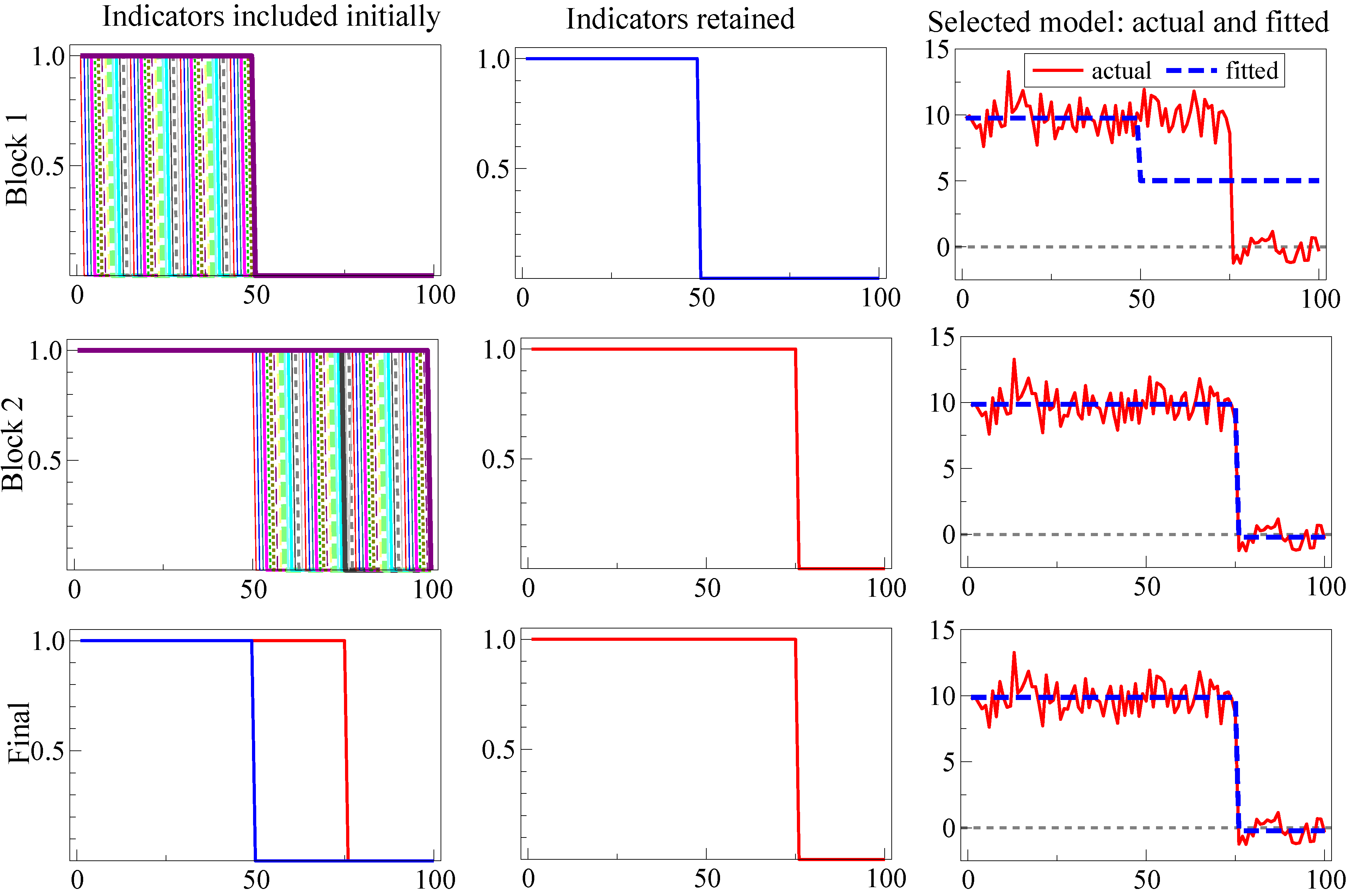
5.7. Unknown Shift Period Spanning Both Splits
The analysis in
Subsection 5.6 may be effective in capturing a location shift spanning the initial halves, as then the shift will almost always lie entirely within a quarter of the sample. This follows, since within the first half of
where the shift lies towards the end by necessity of spanning into the second half, if it were longer than
, SIS would find the shorter as if it were the shift and similarly for the second half.
To simulate a shift period spanning both splits, the shift timing is set such that the end of the first shift occurs just as the second shift starts,
i.e.,
and
with
and
, leading to a single step shift of a length of 30 periods spanning both halves.
Table 7 presents the results when using split-half sequential selection, as well as multi-path. Both correctly show the absence of shifts at
and
(as the shift spans the two halves), and as before, there is little difference between these, exhibiting retention frequencies at
and
of around 0.9 for a step shift of
.
Table 7.
Split-half sequential sequential and multi-path: shift spanning both splits, .
Table 7.
Split-half sequential sequential and multi-path: shift spanning both splits, .
| Algorithm | Gauge | Retention frequency |
|---|
| | | Step | Step | Step | Step |
| Sequential: | 0.011 | 0.039 | 0.58 | 0.001 | 0.0 | 0.56 |
| 0.002 | 0.02 | 0.94 | 0.0 | 0.0 | 0.93 |
| & | | Step | Step | Step | Step |
| Multi-path: | 0.029 | | 0.57 | 0.01 | 0.01 | 0.55 |
| 0.019 | | 0.94 | 0.02 | 0.02 | 0.96 |