Locationally Varying Production Technology and Productivity: The Case of Norwegian Farming
Abstract
:1. Introduction
“Spatial dimensions of input groupings may be particularly important in agriculture because the inputs must be tailored to the heterogeneity of firm resources, which differ substantially by climate and land quality (location).”
2. Locational Heterogeneity in Production
3. Methodology
3.1. Proxy Variable Identification
3.2. Semiparametric Estimation
4. Data
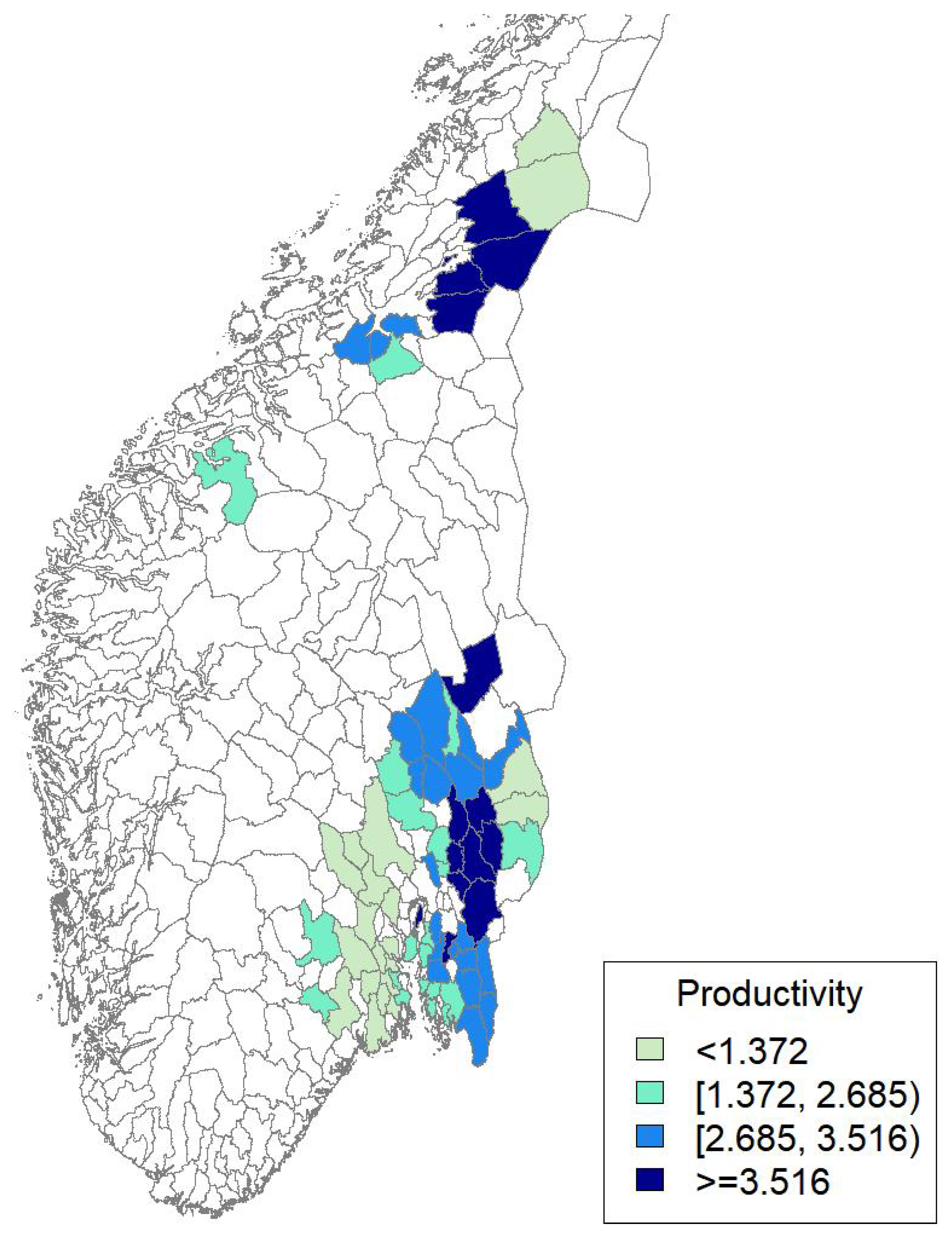
5. Results
5.1. Production Function
5.2. Productivity Process
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | As noted by Just and Pope (2001), while the agricultural marketing literature frequently considers temporal and spatial distinctions, these aspects are often disregarded in the agricultural production economics literature. |
| 2 | The firm’s location is suppressed in the list of state variables because of its time-invariance. |
| 3 | The asymptotic property of the estimator is well-documented in the literature. For example, Li et al. (2002) proposed a local least squares method with a kernel weight function to estimate the smooth coefficient function (similar to what we do in the paper) and established the consistency of the estimator and its asymptotic normality. |
| 4 | Malikov et al. (2022) investigated the performance of the proposed bootstrap procedure in Monte Carlo simulations. Their simulations show satisfactory performance of the bootstrap confidence intervals in finite samples. |
| 5 | In this paper, we used a data-driven leave-one-location-out cross-validation method to choose the optimal bandwidth. These selected optimal bandwidths are capable of adapting to the local distribution of the data and yield the smallest sum of squared residuals. We also tried using fixed bandwidths, but the results remained robust. These additional results are available upon request. |
| 6 | The standard deviations of longitude and latitude in our sample are 0.6941 and 1.5162 decimal degrees, respectively. |
| 7 | As examples of exceptions that include spatial heterogeneity in their analysis of agricultural production, we mention Billé et al. (2018), Canello and Vidoli (2020), and Bai et al. (2021). Recently, several efficiency studies dealing with spatial aspects of agricultural production have also emerged, e.g., Fusco and Vidoli (2013) and Vidoli et al. (2016). |
References
- Ackerberg, Daniel A., Kevin Caves, and Garth Frazer. 2015. Identification properties of recent production function estimators. Econometrica 83: 2411–51. [Google Scholar] [CrossRef]
- Aida, Takeshi. 2018. Neighbourhood effects in pesticide use: Evidence from the rural philippines. Journal of Agricultural Economics 69: 163–81. [Google Scholar] [CrossRef]
- Álvarez, Antonio, Julio Del Corral, Daniel Solís, and José A. Pérez. 2008. Does intensification improve the economic efficiency of dairy farms? Journal of Dairy Science 91: 3693–98. [Google Scholar] [CrossRef]
- Anselin, Luc. 2010. Thirty years of spatial econometrics. Papers in Regional Science 89: 3–25. [Google Scholar] [CrossRef]
- Bai, Xiuguang, Tianwen Zhang, Shujuan Tian, and Yanan Wang. 2021. Spatial analysis of factors affecting fertilizer use efficiency in China: An empirical study based on geographical weighted regression model. Environmental Science and Pollution Research 28: 16663–681. [Google Scholar] [CrossRef]
- Billé, Anna Gloria, Cristina Salvioni, and Roberto Benedetti. 2018. Modelling spatial regimes in farms technologies. Journal of Productivity Analysis 49: 173–85. [Google Scholar] [CrossRef]
- Blundell, Richard, and Stephen Bond. 2000. GMM estimation with persistent panel data: An application to production functions. Econometric Reviews 19: 321–40. [Google Scholar] [CrossRef]
- Brunsdon, Chris, A. Stewart Fotheringham, and Martin E. Charlton. 1996. Geographically weighted regression: A method for exploring spatial nonstationarity. Geographical Analysis 28: 281–98. [Google Scholar] [CrossRef]
- Canello, Jacopo, and Francesco Vidoli. 2020. Investigating space-time patterns of regional industrial resilience through a micro-level approach: An application to the italian wine industry. Journal of Regional Science 60: 653–76. [Google Scholar] [CrossRef]
- Capello, Roberta. 2009. Space, growth and development. In Handbook of Regional Growth and Development Theories. Cheltenham: Edward Elgar Publishing. [Google Scholar]
- Chen, Xiaohong. 2007. Large sample sieve estimation of semi-nonparametric models. In Handbook of Econometrics. Amsterdam: Elsevier, vol. 6, pp. 5549–632. [Google Scholar]
- Collard-Wexler, Allan, and Jan De Loecker. 2015. Reallocation and technology: Evidence from the US steel industry. American Economic Review 105: 131–71. [Google Scholar] [CrossRef]
- De Loecker, Jan. 2013. Detecting learning by exporting. American Economic Journal: Microeconomics 5: 1–21. [Google Scholar] [CrossRef]
- Doraszelski, Ulrich, and Jordi Jaumandreu. 2013. R&D and productivity: Estimating endogenous productivity. Review of Economic Studies 80: 1338–83. [Google Scholar]
- Doraszelski, Ulrich, and Jordi Jaumandreu. 2018. Measuring the bias of technological chance. Journal of Political Economy 126: 1027–84. [Google Scholar] [CrossRef]
- Dosi, Giovanni, and Richard R. Nelson. 2010. Technical change and industrial dynamics as evolutionary processes. In Handbook of the Economics of Innovation. Amsterdam: Elsevier, vol. 1, pp. 51–127. [Google Scholar]
- Eberhardt, Markus, and Francis Teal. 2013. No mangoes in the Tundra: Spatial heterogeneity in agricultural productivity analysis. Oxford Bulletin of Economics and Statistics 75: 914–39. [Google Scholar] [CrossRef]
- Efron, Bradley. 1987. Better bootstrap confidence intervals. Journal of the American Statistical Association 82: 171–85. [Google Scholar] [CrossRef]
- Fusco, Elisa, and Francesco Vidoli. 2013. Spatial stochastic frontier models: Controlling spatial global and local heterogeneity. International Review of Applied Economics 27: 679–94. [Google Scholar] [CrossRef]
- Gandhi, Amit, Salvador Navarro, and David A. Rivers. 2020. On the identification of gross output production functions. Journal of Political Economy 128: 2973–3016. [Google Scholar] [CrossRef]
- Goodwin, Barry K., and Ashok K. Mishra. 2004. Farming efficiency and the determinants of multiple job holding by farm operators. American Journal of Agricultural Economics 86: 722–29. [Google Scholar] [CrossRef]
- Greene, William. 2005. Reconsidering heterogeneity in panel data estimators of the stochastic frontier model. Journal of Econometrics 126: 269–303. [Google Scholar] [CrossRef]
- Holmes, Thomas J., and Sanghoon Lee. 2012. Economies of density versus natural advantage: Crop choice on the back forty. Review of Economics and Statistics 94: 1–19. [Google Scholar] [CrossRef]
- Isard, Walter. 1954. Location theory and trade theory: Short-run analysis. The Quarterly Journal of Economics 68: 305–20. [Google Scholar] [CrossRef]
- Just, Richard E., and Rulon D. Pope. 2001. The agricultural producer: Theory and statistical measurement. In Handbook of Agricultural Economics. Amsterdam: Elsevier, vol. 1, pp. 629–741. [Google Scholar]
- Knutsen, Heidi. 2020 Norwegian Agriculture Status and Trends 2019. NIBIO POP. 6. Available online: http://hdl.handle.net/11250/2643268 (accessed on 13 February 2023).
- Konings, Jozef, and Stijn Vanormelingen. 2015. The impact of training on productivity and wages: Firm-level evidence. Review of Economics and Statistics 97: 485–97. [Google Scholar] [CrossRef]
- Kumbhakar, Subal C., and Efthymios G. Tsionas. 2010. Estimation of production risk and risk preference function: A nonparametric approach. Annals of Operations Research 176: 369–78. [Google Scholar] [CrossRef]
- Kumbhakar, Subal C., and Gudbrand Lien. 2010. Impact of subsidies on farm productivity and efficiency. In The Economic Impact of Public Support to Agriculture. Edited by V. Eldon Ball, Roberto Fanfani and Luciano Gutierrez. Berlin/Heidelberg: Springer, pp. 109–24. [Google Scholar]
- Läpple, Doris, and Hugh Kelley. 2015. Spatial dependence in the adoption of organic drystock farming in ireland. European Review of Agricultural Economics 42: 315–37. [Google Scholar] [CrossRef]
- Läpple, Doris, Garth Holloway, Donald J. Lacombe, and Cathal O’Donoghue. 2017. Sustainable technology adoption: A spatial analysis of the irish dairy sector. European Review of Agricultural Economics 44: 810–35. [Google Scholar]
- Levinsohn, James, and Amil Petrin. 2003. Estimating production functions using inputs to control for unobservables. Review of Economic Studies 70: 317–41. [Google Scholar] [CrossRef]
- Li, Qi, Cliff J. Huang, Dong Li, and Tsu-Tan Fu. 2002. Semiparametric smooth coefficient models. Journal of Business & Economic Statistics 20: 412–22. [Google Scholar]
- Lien, Gudbrand, Subal C. Kumbhakar, and J. Brian Hardaker. 2010. Determinants of off-farm work and its effects on farm performance: The case of norwegian grain farmers. Agricultural Economics 41: 577–86. [Google Scholar] [CrossRef]
- Malikov, Emir, and Gudbrand Lien. 2021. Proxy variable estimation of multiproduct production functions. American Journal of Agricultural Economics 103: 1878–902. [Google Scholar] [CrossRef]
- Malikov, Emir, and Shunan Zhao. 2021. On the estimation of cross-firm productivity spillovers with an application to fdi. Review of Economics and Statistics. forthcoming. [Google Scholar] [CrossRef]
- Malikov, Emir, Jingfang Zhang, Shunan Zhao, and Subal C. Kumbhakar. 2022. Accounting for cross-location technological heterogeneity in the measurement of operations efficiency and productivity. Journal of Operations Management 68: 153–84. [Google Scholar] [CrossRef]
- Malikov, Emir, Shunan Zhao, and Subal C. Kumbhakar. 2020. Estimation of firm-level productivity in the presence of exports: Evidence from China’s manufacturing. Journal of Applied Econometrics 35: 457–80. [Google Scholar] [CrossRef]
- McMillen, Daniel P., and Christian L. Redfearn. 2010. Estimation and hypothesis testing for nonparametric hedonic house price functions. Journal of Regional Science 50: 712–33. [Google Scholar] [CrossRef]
- Mundlak, Yair. 2001. Production and supply. In Handbook of Agricultural Economics. Amsterdam: Elsevier, vol. 1, pp. 3–85. [Google Scholar]
- O’Donnell, Christopher John, and William E. Griffiths. 2006. Estimating state-contingent production frontiers. American Journal of Agricultural Economics 88: 249–66. [Google Scholar] [CrossRef]
- Olley, G. Steven, and Ariel Pakes. 1996. The dynamics of productivity in the telecommunications equipment industry. Econometrica 64: 1263–97. [Google Scholar] [CrossRef]
- Orea, Luis, and Subal C. Kumbhakar. 2004. Efficiency measurement using a latent class stochastic frontier model. Empirical Economics 29: 169–83. [Google Scholar] [CrossRef]
- Pfeiffer, Lisa, Alejandro López-Feldman, and J. Edward Taylor. 2009. Is off-farm income reforming the farm? Evidence from Mexico. Agricultural Economics 40: 125–38. [Google Scholar] [CrossRef]
- Postiglione, Paolo, Roberto Benedetti, and Federica Piersimoni. 2022. Spatial Econometric Methods in Agricultural Economics Using R. Boca Raton: CRC Press. [Google Scholar]
- Rizov, Marian, Jan Pokrivcak, and Pavel Ciaian. 2013. CAP subsidies and productivity of the EU farms. Journal of Agricultural Economics 64: 537–57. [Google Scholar] [CrossRef]
- Saint-Cyr, Legrand D. F., Hugo Storm, Thomas Heckelei, and Laurent Piet. 2019. Heterogeneous impacts of neighbouring farm size on the decision to exit: Evidence from brittany. European Review of Agricultural Economics 46: 237–66. [Google Scholar] [CrossRef]
- Sauer, Johannes, and Catherine J. Morrison Paul. 2013. The empirical identification of heterogeneous technologies and technical change. Applied Economics 45: 1461–79. [Google Scholar] [CrossRef]
- Schmidtner, Eva, Christian Lippert, Barbara Engler, Anna Maria Häring, Jaochim Aurbacher, and Stephan Dabbert. 2012. Spatial distribution of organic farming in germany: Does neighbourhood matter? European Review of Agricultural Economics 39: 661–83. [Google Scholar] [CrossRef]
- Skevas, Theodoros, Ioannis Skevas, and Scott M. Swinton. 2018. Does spatial dependence affect the intention to make land available for bioenergy crops? Journal of Agricultural Economics 69: 393–412. [Google Scholar] [CrossRef]
- Storm, Hugo, Klaus Mittenzwei, and Thomas Heckelei. 2015. Direct payments, spatial competition, and farm survival in norway. American Journal of Agricultural Economics 97: 1192–205. [Google Scholar] [CrossRef]
- Syverson, Chad. 2011. What determines productivity? Journal of Economic Literature 49: 326–65. [Google Scholar] [CrossRef]
- Ullah, Amman. 1985. Specification analysis of econometric models. Journal of Quantitative Economics 1: 187–209. [Google Scholar]
- Van Biesebroeck, Johannes. 2005. Exporting raises productivity in sub-Saharan African manufacturing firms. Journal of International Economics 67: 373–91. [Google Scholar] [CrossRef]
- Vidoli, Francesco, Concetta Cardillo, Elisa Fusco, and Jacopo Canello. 2016. Spatial nonstationarity in the stochastic frontier model: An application to the Italian wine industry. Regional Science and Urban Economics 61: 153–64. [Google Scholar] [CrossRef]
- Wang, Haoying. 2018. The spatial structure of farmland values: A semiparametric approach. Agricultural and Resource Economics Review 47: 568–91. [Google Scholar] [CrossRef]
- Zhengfei, Guan, and Alfons Oude Lansink. 2006. The source of productivity growth in dutch agriculture: A perspective from finance. American Journal of Agricultural Economics 88: 644–56. [Google Scholar] [CrossRef]




| Variable Name | Var. | Mean | First Quartile | Median | Third Quartile |
|---|---|---|---|---|---|
| Production function variables | |||||
| Output | Y | 468,669.14 | 218,259.31 | 340,533.00 | 588,818.06 |
| Capital | K | 1,957,916.73 | 901,384.75 | 1,545,676.80 | 2,586,060.80 |
| Labor | L | 853.70 | 400.00 | 700.00 | 1100.00 |
| Land | N | 35.23 | 19.20 | 29.00 | 41.00 |
| Materials | M | 188,155.60 | 92,480.62 | 145,776.42 | 228,719.84 |
| Productivity determinants | |||||
| Subsidy/return ratio | 0.30 | 0.22 | 0.28 | 0.36 | |
| Off-farm income share | 0.80 | 0.74 | 0.86 | 0.92 | |
| Debt/asset ratio | 0.46 | 0.30 | 0.50 | 0.64 | |
| Location variables | |||||
| Longitude | 10.77 | 10.22 | 10.89 | 11.33 | |
| Latitude | 60.55 | 59.51 | 60.01 | 60.81 | |
| Locationally Varying | Location-Invariant | ||||
|---|---|---|---|---|---|
| Mean | 1st Qu. | Median | 3rd Qu. | Point Estimate | |
| Capital | 0.183 | 0.119 | 0.201 | 0.237 | 0.139 |
| (0.109, 0.291) | (0.020, 0.246) | (0.125, 0.320) | (0.140, 0.390) | (0.095, 0.185) | |
| Labor | 0.079 | 0.062 | 0.090 | 0.130 | 0.110 |
| (0.041, 0.140) | (0.020, 0.140) | (0.026, 0.166) | (0.070, 0.231) | (0.051, 0.173) | |
| Land | 0.263 | 0.214 | 0.243 | 0.264 | 0.447 |
| (0.036, 0.373) | (0.021, 0.396) | (0.009, 0.359) | (0.031, 0.316) | (0.364, 0.521) | |
| Materials | 0.38 | 0.367 | 0.38 | 0.398 | 0.378 |
| (0.371, 0.395) | (0.35, 0.386) | (0.367, 0.399) | (0.392, 0.416) | (0.360, 0.398) | |
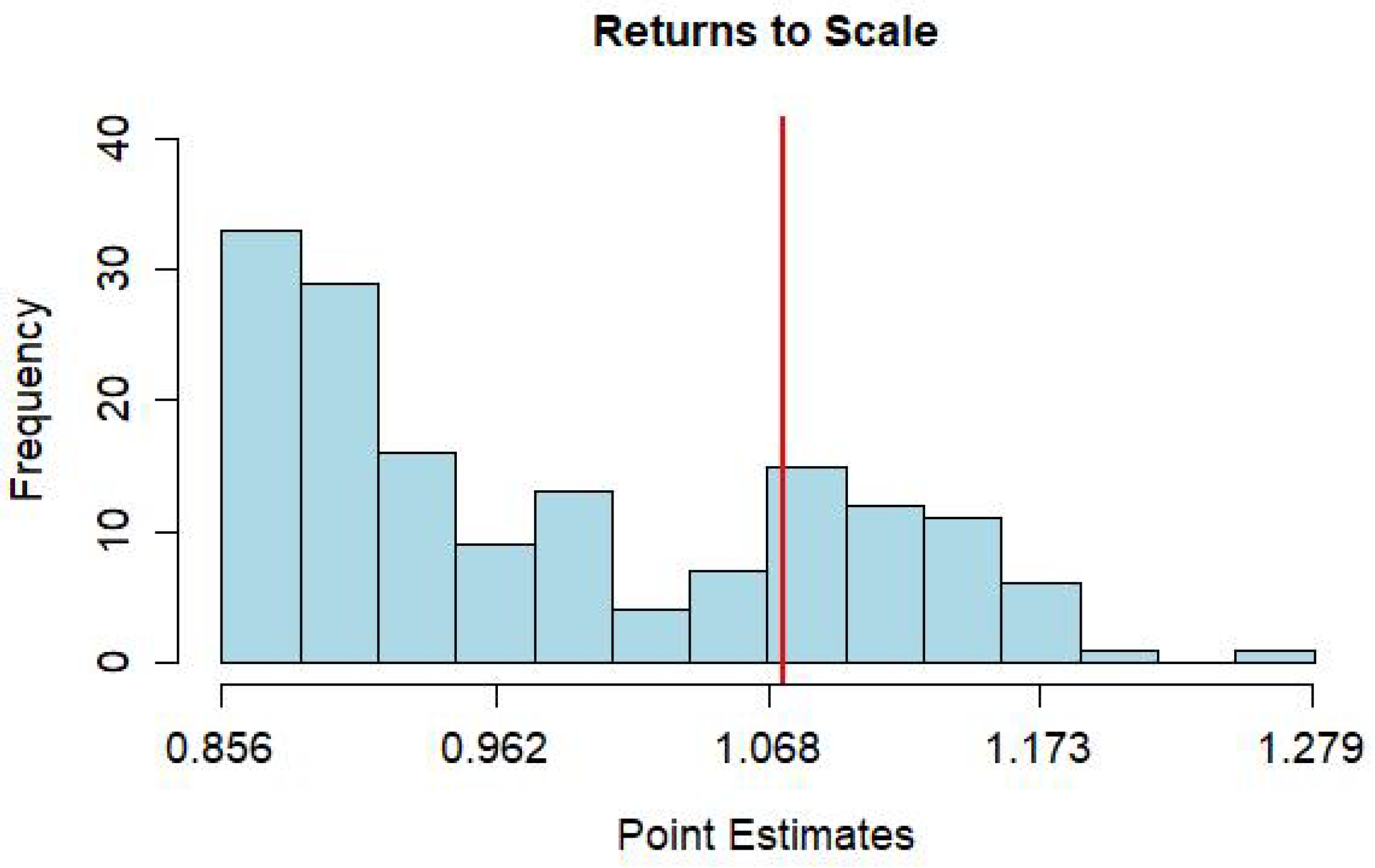
| Mean | 1st Qu. | Median | 3rd Qu. | <1 | =1 | >1 | |
|---|---|---|---|---|---|---|---|
| RTS | 0.926 | 0.833 | 0.911 | 1.011 | 26.29 | 74.86 | 4.57 |
| (0.762, 1.110) | (0.655, 0.995) | (0.700, 1.079) | (0.830, 1.206) |
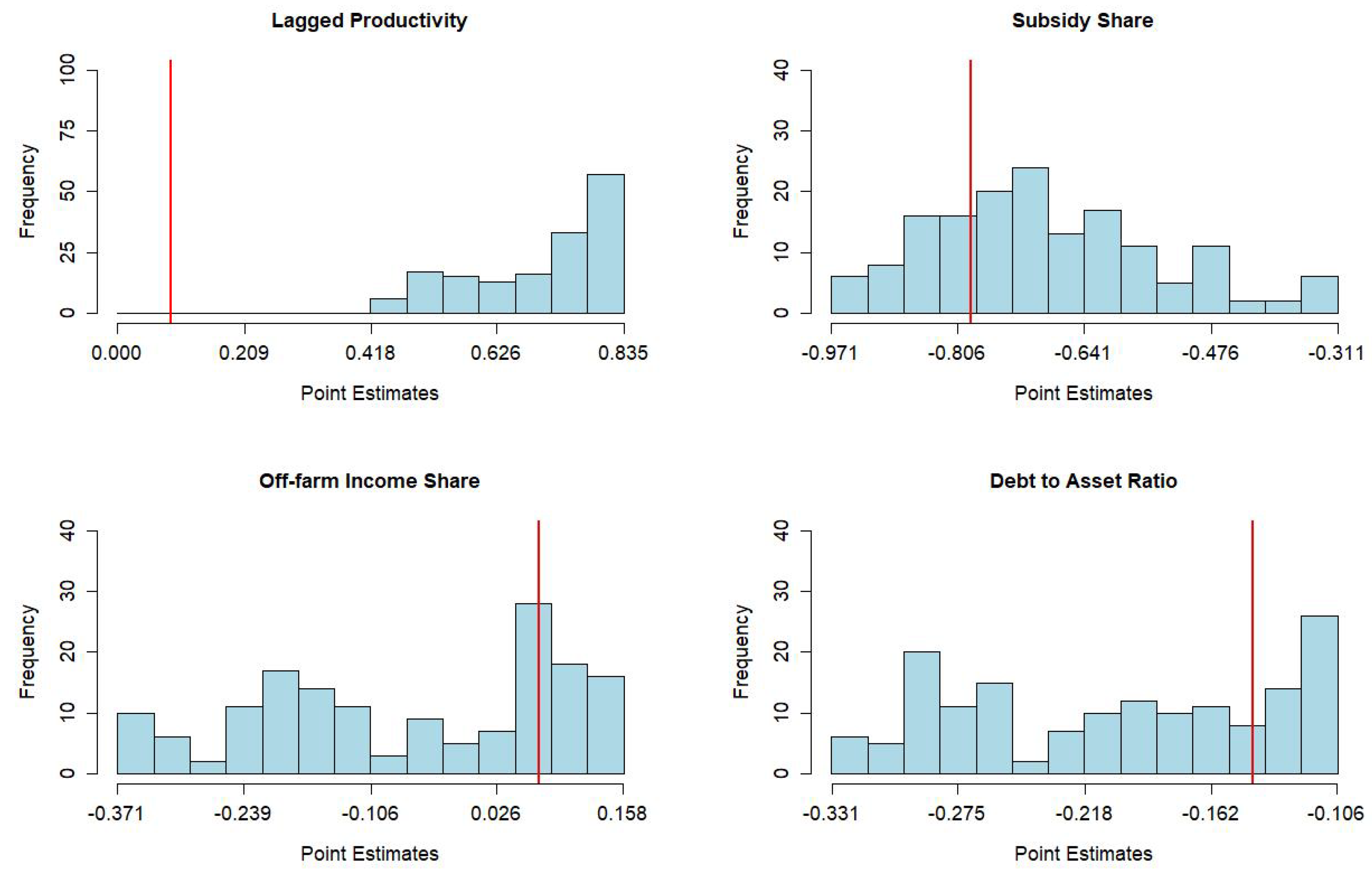
| Locationally Varying | Location-Invariant | ||||||
|---|---|---|---|---|---|---|---|
| Variables | Mean | 1st Qu. | Median | 3rd Qu. | >0 | <0 | Point Estimate |
| Lagged | 0.789 | 0.734 | 0.835 | 0.877 | 100 | 0 | 0.088 |
| productivity | (0.522, 0.976) | (0.609, 0.983) | (0.592, 1.057) | (0.471, 1.078) | (−0.037, 0.200) | ||
| Subsidy/return | −0.640 | −0.803 | −0.688 | −0.475 | 0 | 73.71 | −0.789 |
| ratio | (−0.714, −0.301) | (−0.886, −0.502) | (−0.775, −0.411) | (−0.593, −0.043) | (–1.086, −0.517) | ||
| Off-farm | −0.098 | −0.217 | −0.085 | 0.057 | 1.14 | 32 | 0.070 |
| income share | (−0.307, 0.012) | (−0.431, −0.022) | (−0.296, 0.000) | (−0.198, 0.150) | (−0.089, 0.303) | ||
| Debt/asset | −0.222 | −0.292 | −0.216 | −0.104 | 0 | 63.43 | −0.143 |
| ratio | (−0.334, −0.072) | (−0.403, −0.109) | (−0.342, −0.079) | (−0.264, 0.019) | (−0.264, −0.013) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumbhakar, S.C.; Zhang, J.; Lien, G. Locationally Varying Production Technology and Productivity: The Case of Norwegian Farming. Econometrics 2023, 11, 20. https://doi.org/10.3390/econometrics11030020
Kumbhakar SC, Zhang J, Lien G. Locationally Varying Production Technology and Productivity: The Case of Norwegian Farming. Econometrics. 2023; 11(3):20. https://doi.org/10.3390/econometrics11030020
Chicago/Turabian StyleKumbhakar, Subal C., Jingfang Zhang, and Gudbrand Lien. 2023. "Locationally Varying Production Technology and Productivity: The Case of Norwegian Farming" Econometrics 11, no. 3: 20. https://doi.org/10.3390/econometrics11030020
APA StyleKumbhakar, S. C., Zhang, J., & Lien, G. (2023). Locationally Varying Production Technology and Productivity: The Case of Norwegian Farming. Econometrics, 11(3), 20. https://doi.org/10.3390/econometrics11030020







