Algorithmic Modelling of Financial Conditions for Macro Predictive Purposes: Pilot Application to USA Data
Abstract
:1. Introduction
2. Algorithmic Model Design
2.1. Macro Model Setting and Model Training
2.2. Algorithm for FCI Construction
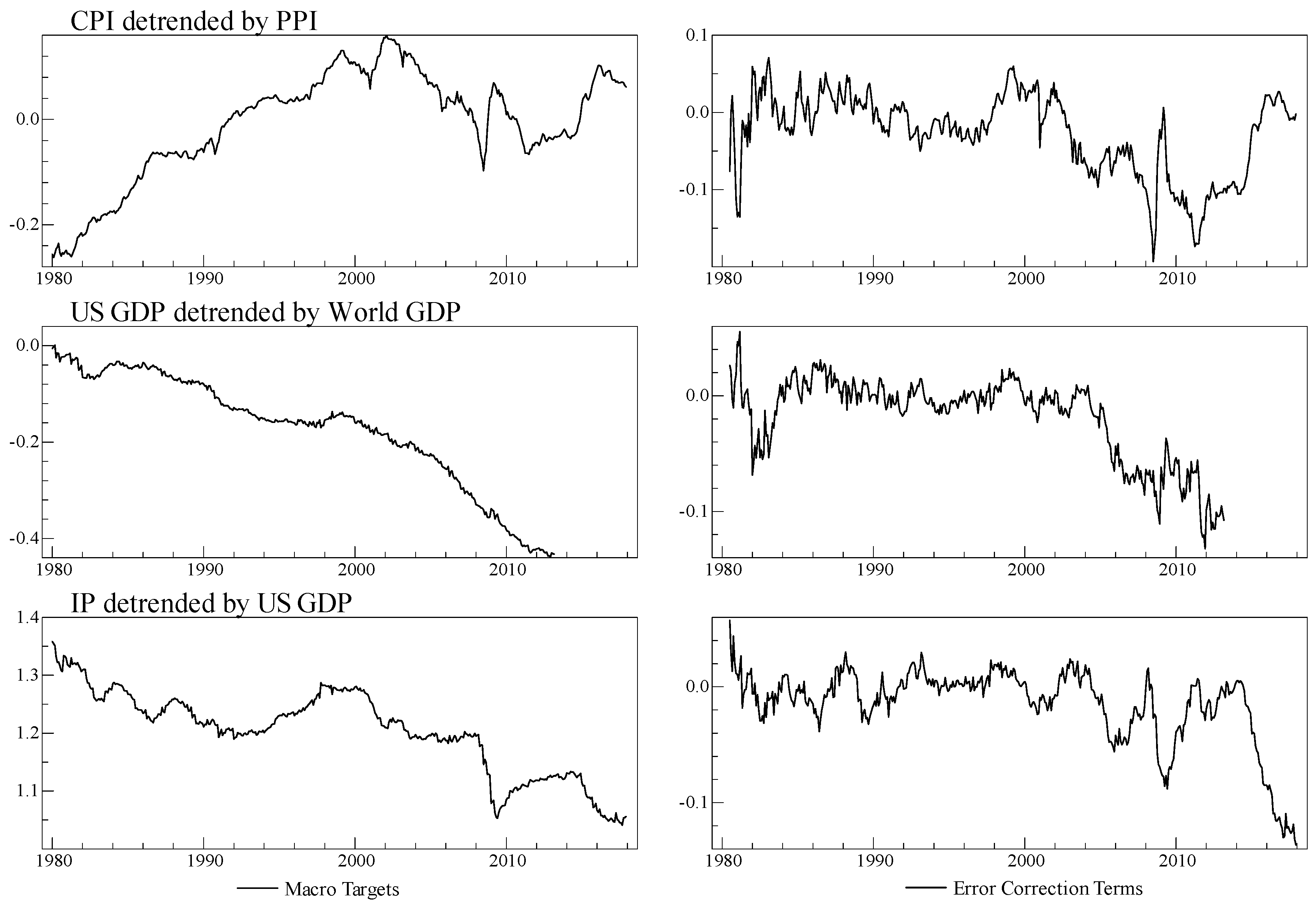
3. Data
4. Empirical Results
4.1. Input Indicator Selection
4.2. Aggregation
4.3. Prediction
5. Concluding Discussion
- On model conceptualisation: Essentially, the model-based FCIs are pooled and partial predictors. However, it can be challenging to reach a consensus on the interpretation of these predictors, in view of the intense debates and discussions on the nature of latent variables or composite variates in PLS regression modelling and formative measurement modelling.15 From the stance of statistical modelling, the question of interpretability touches on the crux of under what conditions a theoretical identity has a one-to-one mapping from a statistical identity, see Markus (2016). Aside from epistemological concerns, the discussion highlights the primary importance of the algorithm design to ensure consistency between math/statistical aggregation rules and desired properties of the theoretical constructs, e.g., see Munda (2012).
- On model design: Improvements can be made from two sides. From the input side, more elaborate aggregation rules should be introduced with help from dimensionality reduction techniques in machine learning. For instance, multi-path or classification models should be experimented with to replace the man-made filtering step of redundant indicators. The possibility of interactive dynamics among indicators should also be considered to search for more effective and parsimonious ways to formulate dynamic input features. From the target side, more attention should be focused on how to exploit the target selection capacity of this modelling approach to better serve policy purposes.16
- On model testing: Improvements of methods of model evaluation are desired at various stages. Here, active research is worth tracking in two areas. One is concerned with the quality of composite indicators and tackled by sensitivity analysis, see Saisana et al. (2005), and Dobbie and Dail (2013). The other is on evaluation of various aspects of formative PLS path models, such as content, construct, convergent and discriminant validity, see Andreev et al. (2009), and Bentler and Huang (2014).
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Algorithm A1 Long-Run FCI Construction | |
| 1: | for each increasing update interval to do |
| 2: | standardise each column of matrix by its mean and sd |
| 3: | compute the weight vector |
| 4: | set |
| 5: | for to do |
| 6: | for to do |
| 7: | if then |
| 8: | |
| 9: | else |
| 10: | |
| 11: | end if |
| 12: | end for |
| 13: | end for |
| 14: | compute the first factor |
| 15: | compute LRFCI |
| 16: | end for |
| Notes: Matrixes are bold and in capital letters and vectors are bold and in lower case. is the vector of the long-run target as specified in (3). is a by matrix of financial indicators and their respective lagged versions. The selected in step 8 is in (4). indicates the standard deviation of vector and its mean. | |
| Algorithm A2 Short-Run FCI Construction | |
| 1: | for each increasing update interval to do |
| 2: | standardise each column of matrix by its mean and sd |
| 3: | set and |
| 4: | for to do |
| 5: | regress on |
| 6: | extract 3 coefficients with smallest p-value (including intercept) |
| 7: | regress on 3 selected variables |
| 8: | drop insignificant coefficients with p-value larger than threshold |
| 9: | if there is at least one remaining variable then |
| 10: | |
| 11: | save the remaining coefficient estimates as |
| 12: | set the other insignificant coefficient estimates to zero |
| 13: | if intercept is significant then |
| 14: | |
| 15: | end if |
| 16: | else |
| 17: | set |
| 18: | end if |
| 19: | end for |
| 20: | compute SRFCI |
| 21: | end for |
| Notes: Matrixes are bold and in capital letters and vectors are bold and in lower case. is the vector of the short-run target as specified in (5). is a by matrix of financial indicators and their respective lagged versions. indicates the standard deviation of vector and its mean. | |
Appendix B
| Variable | Description | Source | Series Title |
|---|---|---|---|
| O1 | 3-month market interest rate of US | Reuters | US INTERBANK RATE–3 MONTH |
| O2 | 3-month market interest rate of UK | Bank of England | UK BOE LIBID/LIBOR–3 MONTH |
| O3 | 3-month market interest rate of Canada | IMF, International Financial Statistics | CN interest rates: money market rate NADJ |
| O4 | 3-month market interest rate of Sweden | Sveriges Riksbank | SD interbank money rate: 3 months (EP) NADJ |
| O5 | Exchange rate of UK | Bank of England | GBP to USD (BOE)–Exchange rate |
| O6 | Exchange rate of Canada | Reuters | Canadian $ to US $ (WMR)–Exchange Rate |
| O7 | Exchange rate of Sweden | Bank of England | SEK to USD (BOE)–Exchange Rate |
| O8 | Forward exchange rate of UK | Reuters | UK £ to US $ 3M FWD (WMR)–Exchange Rate |
| O9 | Forward exchange rate of Canada | Barclays Bank PLC | Canadian $ to US $ 3M FWD (BBI)–Exchange Rate |
| O10 | Forward exchange rate of Sweden | Barclays Bank PLC | Swedish Krona TO US $ 3M FWD (BBI)–Exchange Rate |
| O11 | Stock market index of US | Standard and Poors (S&P) | S&P 500 Composite–Price index |
| O12 | Stock market index of Canada | IMF, International Financial Statistics | CN Share prices, total NADJ |
| O13 | Stock market index of Germany | Reuters | BD DAX Share Price Index, EP NADJ |
| O14 | Stock market index of Japan | Tokyo Stock Exchange | TOPIX–Price Index |
| O15 | Stock market index of UK | IMF, International Financial Statistics | UK Share Prices, TOTAL NADJ |
| O16 | 1-year government bond | Thomson Reuters Datastream | United States GVT BMK Bid Yield 1 Year |
| O17 | 10-year government bond | OECD, Main economic indicators | US Yield 10-Year FED GVT SECS NADJ |
| O18 | 30-year government bond | Thomson Reuters Datastream | TR US GVT BMK BID YLD 30Y (U$)–RED. YIELD |
| O19 | 3-month T bill | Federal Reserve | US T-BILL 3 Month (W) |
| O20 | 6-month T bill | Federal Reserve | US T-BILL 6 Month (W) |
| O26 | Lending rate | Federal Reserve | US Prime rate charged by banks (Month avg) NADJ |
| O27 | Mortgage rate | Freddie Mac | Mortgage Lending Rates, Conforming 30-Year Fixed Rate Mortgage, Total, Average Interest Rate |
| O28 | Mortgage volume of the banking sector | Federal Reserve | US Commercial Bank Assets–Real estate loans |
| O29 | Loan volume of the banking sector | Federal Reserve | US Commercial Bank Assets–Loans & Leases in Bank credit |
| O30 | Total liabilities of the banking sector | Federal Reserve | US Commercial Bank Liabilities–Total |
| O31 | Equity of the banking sector | Federal Reserve | US Commercial Bank Residual (Assets less Liabilities) |
| O32 | Deposit volume of the banking sector | Federal Reserve | US Commercial Bank Liabilities–Deposits |
| O33 | M1 | Federal Reserve | US Money Supply M1 |
| O34 | Real effective exchange rate | IMF, International Financial Statistics | US Real Effective FX Rate (REER) Based on Consumer price index |
| O35 | Consumer Price Index | OECD, Main economic indicators | US CPI All items NADJ |
| O36 | Producer Price Index | Bureau of Labor Statistics, U.S. Department of Labor | US PPI–All Commodities |
| O37 | Industrial Production Index | Federal Reserve | US Industrial Production–Total Index VOLA |
| O38 | GDP (quarterly) | OECD, Main economic indicators | US Gross Domestic Product (at COnstant PPP) |
| O39 | Global output (quarterly) | From Di Mauro and Pesaran (2013) |
| 1. | The inadequacy of capturing the financial sector impact in macro modelling has been highlighted recently from a broader angle in a special issue of Oxford Review of Economic Policy vol. 34, i.e., see Stiglitz (2018), and Vines and Wills (2018). |
| 2. | The PLS method was proposed by H. Wold (1966, 1975, 1980); for more background information, see Wegelin (2000), Sanchez (2013) and McIntosh et al. (2014). It has been extended into the causal interpretation of PLS path modelling in relation to measurement theory, see Vinzi et al. (2010), Howell et al. (2013) and Howell (2014). A few trial applications of PLS can be found in the econometric literature: e.g., Lin and Tsay (2005), Eickmeier and Ng (2011), Lannsjö (2014), Kelly and Pruitt (2015), Fuentes et al. (2015), Groen and Kapetanios (2016), and Kapetanios et al. (2018), but none has adopted the causal model basis of the method. |
| 3. | |
| 4. | Historically, the reflective model is referred to as ‘mode A’ and the formative model ‘mode B’, see Wold (1980) and also Vinzi et al. (2010). In a reflective model, weights are identified by the assumption of conditional independence, i.e., all the manifest indicators are effects of one common cause. In contrast, this assumption does not apply to the formative model. Hence, the weights of the indicators in a formative model cannot be identified by a single criterion, such as the common variance criterion of PCA. An additional criterion is needed for the identification (Markus and Borsboom 2013, p. 113). |
| 5. | Although the concept of supervised versus unsupervised data reduction is unfamiliar to economists, the idea of targeting the index construction process at dependent variables has been around since early warning systems research, e.g., Gramlich et al. (2010). The method of selecting indicators based on their ability to signal turning points in Levanon et al. (2015) effectively follows the supervised learning approach. |
| 6. | This incorrect formalization of problems falls into what is referred to as ‘Type III error’ by Hand (1994, p. 317). |
| 7. | |
| 8. | Evidence of lack of volatility synchronization among financial indicators has been discussed in the literature, e.g., Cesa-Bianchi et al. (2014). |
| 9. | When this long-run combination of the ECM fits the description of cointegration, our formulation can be interpreted as exploiting the Granger-Engle two-step procedure. |
| 10. | |
| 11. | See Di Mauro and Pesaran (2013) for the data source and definition. |
| 12. | Selection of the unprocessed series is carried out with reference to Alessi and Detken (2011), Hatzius et al. (2010), Bisias et al. (2012), and Moccero et al. (2014). Particular attention is paid to the coverage of credit and property price information, see Borio (2014b). The processed data series are downloaded from: https://sethpruitt.net/2016/03/31/systemic-risk-and-the-macroeconomy-an-empirical-evaluation/ (accessed on 11 April 2022); see Giglio et al. (2016) Table 1 Systemic Risk Measures. |
| 13. | |
| 14. | Estimating the unrestricted ECM showed that the imposition agrees with data information. A natural extension of this imposition is calibration, a commonly used method in macro DSGE modelling practice, i.e., experimenting with small variation of the imposed values to choose the best possible one by certain modelling criteria, see van Huellen et al. (2022). |
| 15. | For the recent literature, see Rigdon (2012), Rönkkö and Evermann (2013), Henseler et al. (2014), Bentler and Huang (2014), Hair et al. (2017) and also the November issue, vol. 44 (2013) of the DATABASE for Advances in Information Systems, Aguirre-Urreta et al. (2016) and all its commentaries in vol. 14 (3–4) of Measurement: Interdisciplinary Research and Perspectives. |
| 16. | Experiments in a subsequent research project have already yielded some encouraging results on this point, see van Huellen et al. (2022). |
References
- Aguirre-Urreta, Miguel I., Mikko Rönkkö, and George M. Marakas. 2016. Omission of Causal Indicators: Consequences and Implications for Measurement—A Rejoinder. Measurement: Interdisciplinary Research and Perspectives 14: 170–75. [Google Scholar] [CrossRef]
- Alessi, Lucia, and Carsten Detken. 2011. Quasi Real Time Early Warning Indicators for Costly Asset Price Boom/Bust Cycles: A Role for Global Liquidity. European Journal of Political Economy 27: 520–33. [Google Scholar] [CrossRef]
- Andreev, Pavel, Tsipi Heart, Hanan Maoz, and Nava Pliskin. 2009. Validating Formative Partial Least Squares (PLS) Models: Methodological Review and Empirical Illustration. ICIS 2009 Proceedings 193. Available online: https://aisel.aisnet.org/icis2009/193/ (accessed on 11 April 2022).
- Aramonte, Sirio, Samuel Rosen, and John W. Schindler. 2017. Assessing and Combining Financial Conditions Indexes. International Journal of Central Banking 13: 1–52. [Google Scholar]
- Barnett, William A. 2012. Getting It Wrong: How Faulty Monetary Statistics Undermine the Fed, the Financial System, and the Economy. Cambridge: The MIT Press. [Google Scholar]
- BCBS. 2011. The Transmission Channels between the Financial and Real Sectors: A Critical Survey of the Literature, February. Available online: https://www.bis.org/publ/bcbs_wp18.htm (accessed on 11 April 2022).
- Bentler, Peter M., and Wenjing Huang. 2014. On Components, Latent Variables, PLS and Simple Methods: Reactions to Rigdon’s Rethinking of PLS. Long Range Planning, Rethinking Partial Least Squares Path Modeling: Looking Back and Moving Forward 47: 138–45. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bisias, Dimitrios, Mark Flood, Andrew W. Lo, and Stavros Valavanis. 2012. A Survey of Systemic Risk Analytics. Annual Review of Financial Economics 4: 255–96. [Google Scholar] [CrossRef] [Green Version]
- Borio, Claudio. 2011. Rediscovering the Macroeconomic Roots of Financial Stability Policy: Journey, Challenges, and a Way Forward. Annual Review of Financial Economics 3: 87–117. [Google Scholar] [CrossRef] [Green Version]
- Borio, Claudio. 2013. The Great Financial Crisis: Setting Priorities for New Statistics. Journal of Banking Regulations 14: 306–17. [Google Scholar] [CrossRef]
- Borio, Claudio. 2014a. The Financial Cycle and Macroeconomics: What Have We Learnt? Journal of Banking & Finance 45: 182–98. [Google Scholar] [CrossRef] [Green Version]
- Borio, Claudio. 2014b. The International Monetary and Financial System: Its Achilles Heel and What to Do about It. International Political Economy: Investment & Finance eJournal, 1–27. [Google Scholar] [CrossRef]
- Borio, Claudio, and Philip Lowe. 2002. Asset Prices, Financial and Monetary Stability: Exploring the Nexus. BIS Working Paper No. 114. Basel: Bank for International Settlements. [Google Scholar] [CrossRef] [Green Version]
- Brave, Scott, and R. Andrew Butters. 2011. Monitoring Financial Stability: A Financial Conditions Index Approach. Economic Perspectives 35: 22–43. [Google Scholar]
- Breiman, Leo. 2001. Statistical Modeling: The Two Cultures (with Comments and a Rejoinder by the Author). Statistical Science 16: 199–231. [Google Scholar] [CrossRef]
- Cesa-Bianchi, Ambrogio, M. Hashem Pesaran, and Alessandro Rebucci. 2014. Uncertainty and Economic Activity: A Global Perspective. 4736. CESifo Working Paper Series. CESifo Group Munich. Available online: https://ideas.repec.org/p/ces/ceswps/_4736.html (accessed on 11 April 2022).
- Chauvet, Marcelle, Zeynep Senyuz, and Emre Yoldas. 2015. What Does Financial Volatility Tell Us about Macroeconomic Fluctuations? Journal of Economic Dynamics and Control 52: 340–60. [Google Scholar] [CrossRef] [Green Version]
- Clements, Michael P., and David F. Hendry. 1993. On the Limitations of Comparing Mean Square Forecast Errors. Journal of Forecasting 12: 617–37. [Google Scholar] [CrossRef]
- Cox, David, R. Fitzpatrick, Astrid Fletcher, Sheila Gore, D. J. Spiegelhalter, and D. R. Jones. 1992. Quality-of-Life Assessment: Can We Keep It Simple? Journal of the Royal Statistical Society: Series A (Statistics in Society) 155: 353. [Google Scholar] [CrossRef] [Green Version]
- Cunningham, John P., and Zoubin Ghahramani. 2015. Linear Dimensionality Reduction: Survey, Insights, and Generalizations. Journal of Machine Learning Research 16: 2859–900. [Google Scholar]
- Di Mauro, Filippo, and M. Hashem Pesaran. 2013. The GVAR Handbook: Structure and Applications of a Macro Model of the Global Economy for Policy Analysis. Oxford: Oxford University Press. [Google Scholar]
- Dobbie, Melissa J., and David Dail. 2013. Robustness and Sensitivity of Weighting and Aggregation in Constructing Composite Indices. Ecological Indicators 29: 270–77. [Google Scholar] [CrossRef]
- Drehmann, Mathias, Claudio Borio, and Kostas Tsatsaronis. 2012. Characterising the Financial Cycle: Don’t Lose Sight of the Medium Term! BIS Working Paper No. 380. Available online: https://ssrn.com/abstract=2084835 (accessed on 11 April 2022).
- Eickmeier, Sandra, and Tim Ng. 2011. Forecasting National Activity Using Lots of International Predictors: An Application to New Zealand. International Journal of Forecasting 27: 496–511. [Google Scholar] [CrossRef] [Green Version]
- Ericsson, Neil R. 1992. Parameter Constancy, Mean Square Forecast Errors, and Measuring Forecast Performance: An Exposition, Extensions, and Illustration. Journal of Policy Modeling 14: 465–95. [Google Scholar] [CrossRef] [Green Version]
- Ericsson, Neil R. 1993. On the Limitations of Comparing Mean Square Forecast Errors: Clarifications and Extensions. Journal of Forecasting 12: 644–51. [Google Scholar] [CrossRef]
- Fuentes, Julieta, Pilar Poncela, and Julio Rodríguez. 2015. Sparse Partial Least Squares in Time Series for Macroeconomic Forecasting. Journal of Applied Econometrics 30: 576–95. [Google Scholar] [CrossRef] [Green Version]
- Gadanecz, Blaise, and Kaushik Jayaram. 2009. Measures of Financial Stability—A Review. IFC Bulletins Chapters. Bank for International Settlements. Available online: https://econpapers.repec.org/bookchap/bisbisifc/31-26.htm (accessed on 11 April 2022).
- Giglio, Stefano, Bryan Kelly, and Seth Pruitt. 2016. Systemic Risk and the Macroeconomy: An Empirical Evaluation. Journal of Financial Economics 119: 457–71. [Google Scholar] [CrossRef]
- Gramlich, Dieter, Gavin Miller, Mikhail V. Oet, and Stephen J. Ong. 2010. Early Warning Systems for Systemic Banking Risk: Critical Review and Modeling Implications. Bank and Bank Systems 5: 199–211. [Google Scholar]
- Groen, Jan J. J., and George Kapetanios. 2016. Revisiting Useful Approaches to Data-Rich Macroeconomic Forecasting. Computational Statistics & Data Analysis 100: 221–39. [Google Scholar] [CrossRef] [Green Version]
- Hair, Joe, Carole L. Hollingsworth, Adriane B. Randolph, and Alain Yee Loong Chong. 2017. An Updated and Expanded Assessment of PLS-SEM in Information Systems Research. Industrial Management & Data Systems 117: 442–58. [Google Scholar] [CrossRef]
- Hand, David J. 1994. Deconstructing Statistical Questions. Journal of the Royal Statistical Society. Series A (Statistics in Society) 157: 317–56. [Google Scholar] [CrossRef]
- Harvey, David, Stephen J. Leybourne, and Paul Newbold. 1997. Testing the Equality of Prediction Mean Squared Errors. International Journal of Forecasting 13: 281–91. [Google Scholar] [CrossRef]
- Harvey, David, Stephen J. Leybourne, and Paul Newbold. 1998. Tests for Forecast Encompassing. Journal of Business & Economic Statistics 16: 254–59. [Google Scholar] [CrossRef]
- Hastie, Trevor, Robert Tibshirani, and Jerome Friedman. 2009. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed. Springer Series in Statistics; New York: Springer, Available online: https://www.springer.com/la/book/9780387848570 (accessed on 11 April 2022).
- Hatzius, Jan, Peter Hooper, Frederic S Mishkin, Kermit L Schoenholtz, and Mark W. Watson. 2010. Financial Conditions Indexes: A Fresh Look after the Financial Crisis. NBER Working Paper 16150. Cambridge: National Bureau of Economic Research. [Google Scholar] [CrossRef]
- Hayduk, Leslie A., Hannah Pazderka Robinson, Greta G. Cummings, Kwame Boadu, Eric L. Verbeek, and Thomas A. Perks. 2007. The Weird World, and Equally Weird Measurement Models: Reactive Indicators and the Validity Revolution. Structural Equation Modeling: A Multidisciplinary Journal 14: 280–310. [Google Scholar] [CrossRef]
- Hendry, David F. 1995. Dynamic Econometrics. Oxford: Oxford University Press. [Google Scholar]
- Henseler, Jörg, Theo K. Dijkstra, Marko Sarstedt, Christian M. Ringle, Adamantios Diamantopoulos, Detmar W. Straub, David J. Ketchen, Joseph F. Hair, G. Tomas M. Hult, and Roger J. Calantone. 2014. Common Beliefs and Reality About PLS: Comments on Rönkkö and Evermann (2013). Organizational Research Methods 17: 182–209. [Google Scholar] [CrossRef] [Green Version]
- Howell, Roy D. 2014. What Is the Latent Variable in Causal Indicator Models? Measurement: Interdisciplinary Research and Perspectives 12: 141–45. [Google Scholar] [CrossRef]
- Howell, Roy D., Einar Breivik, and James Wilcox. 2013. Formative Measurement: A Critical Perspective. ACM SIGMIS Database 44: 44–55. [Google Scholar] [CrossRef]
- Kapetanios, George, Simon Price, and Garry Younge. 2018. A UK Financial Conditions Index Using Targeted Data Reduction: Forecasting and Structural Identification. Econometrics and Statistics 7: 1–17. [Google Scholar] [CrossRef] [Green Version]
- Kelly, Bryan T., and Seth Pruitt. 2015. The Three-Pass Regression Filter: A New Approach to Forecasting Using Many Predictors. Journal of Econometrics 186: 294–316. [Google Scholar] [CrossRef]
- Kotchoni, Rachidi, Maxime Leroux, and Dalibor Stevanovic. 2019. Macroeconomic Forecast Accuracy in a Data-Rich Environment. Journal of Applied Econometrics 34: 1050–72. [Google Scholar] [CrossRef]
- Lannsjö, Fredrik. 2014. Forecasting the Business Cycle Using Partial Least Squares. Available online: http://urn.kb.se/resolve?urn=urn:nbn:se:kth:diva-151378 (accessed on 11 April 2022).
- Levanon, Gad, Jean-Claude Manini, Ataman Ozyildirim, Brian Schaitkin, and Jennelyn Tanchua. 2015. Using Financial Indicators to Predict Turning Points in the Business Cycle: The Case of the Leading Economic Index for the United States. International Journal of Forecasting 31: 426–45. [Google Scholar] [CrossRef]
- Lin, Jin-lung, and Ruey S. Tsay. 2005. Comparisons of Forecasting Methods with Many Predictors. Working Paper. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.489.1401&rep=rep1&type=pdf (accessed on 11 April 2022).
- Marcellino, Massimiliano. 2006. Leading Indicators. In Handbook of Economic Forecasting, Vol. 1. Amsterdam: North Holland. [Google Scholar] [CrossRef]
- Markus, Keith A. 2016. Causal Measurement Models: Can Criticism Stimulate Clarification? Measurement: Interdisciplinary Research and Perspectives 14: 110–13. [Google Scholar] [CrossRef]
- Markus, Keith A., and Denny Borsboom. 2013. Frontiers of Test Validity Theory: Measurement, Causation, and Meaning, 1st ed. New York: Routledge. [Google Scholar]
- McIntosh, Cameron N., Jeffrey R. Edwards, and John Antonakis. 2014. Reflections on Partial Least Squares Path Modeling. Organizational Research Methods 17: 210–51. [Google Scholar] [CrossRef] [Green Version]
- Moccero, Diego Nicolas, Matthieu Darracq Pariès, and Laurent Maurin. 2014. Financial Conditions Index and Credit Supply Shocks for the Euro Area. International Finance 17: 297–321. [Google Scholar] [CrossRef]
- Morley, James. 2016. Macro-Finance Linkages. Journal of Economic Surveys 30: 698–711. [Google Scholar] [CrossRef]
- Munda, Giuseppe. 2012. Choosing Aggregation Rules for Composite Indicators. Social Indicators Research 109: 337–54. [Google Scholar] [CrossRef]
- Ng, Tim. 2011. The Predictive Content of Financial Cycle Measures for Output Fluctuations. Risk Management Journal, 1–13. Available online: https://www.bis.org/publ/qtrpdf/r_qt1106g.htm (accessed on 11 April 2022).
- OECD. 2008. Handbook on Constructing Composite Indicators: Methodology and User Guide. Paris: OECD Publishing. [Google Scholar] [CrossRef]
- Qin, Duo, and Qing Chao Wang. 2016. Predictive Macro-Impacts of PLS-based Financial Conditions Indices: An Application to the USA. SOAS Department of Economics Working Paper Series No. 201. Available online: https://ideas.repec.org/p/soa/wpaper/201.html (accessed on 11 April 2022).
- Qin, Duo, and Xinhua He. 2012. Modelling the Impact of Aggregate Financial Shocks External to the Chinese Economy. BOFIT Discussion Paper No. 25/2012. Available online: https://papers.ssrn.com/abstract=2163531 (accessed on 11 April 2022).
- Rigdon, Edward E. 2012. Rethinking Partial Least Squares Path Modeling: In Praise of Simple Methods. Long Range Planning, Analytical Approaches to Strategic Management: Partial Least Squares Modeling in Strategy Research 45: 341–58. [Google Scholar] [CrossRef]
- Rönkkö, Mikko, and Joerg Evermann. 2013. A Critical Examination of Common Beliefs About Partial Least Squares Path Modeling. Organizational Research Methods 16: 425–48. [Google Scholar] [CrossRef]
- Saisana, Michaela, Andrea Saltelli, and Stefano Tarantola. 2005. Uncertainty and Sensitivity Analysis Techniques as Tools for the Quality Assessment of Composite Indicators. Journal of the Royal Statistical Society: Series A (Statistics in Society) 168: 307–23. [Google Scholar] [CrossRef]
- Sanchez, G. 2013. PLS Path Modeling with R. Berkeley: Trowchez Editions 383: 551. [Google Scholar]
- Shalev-Shwartz, Shai, and Shai Ben-David. 2014. Understanding Machine Learning: From Theory to Algorithms. New York: Cambridge University Press. [Google Scholar]
- Stiglitz, Joseph E. 2018. Where Modern Macroeconomics Went Wrong. Oxford Review of Economic Policy 34: 70–106. [Google Scholar] [CrossRef]
- Stock, James H., and Mark W. Watson. 1989. New Indexes of Coincident and Leading Economic Indicators. Working Paper 1380. NBER Macroeconomics Annual 4: 351–409. [Google Scholar] [CrossRef]
- Stock, James H., and Mark W. Watson. 2002. Macroeconomic Forecasting Using Diffusion Indexes. Journal of Business & Economic Statistics 20: 147–62. [Google Scholar] [CrossRef] [Green Version]
- Stock, James H., and Mark W. Watson. 2009. The Methodology and Practice of Econometrics: Festschrift in Honour of David F. Hendry. Oxford: Oxford University Press. [Google Scholar]
- Stock, James H., and Mark W. Watson. 2011. Dynamic Factor Models. Oxford: The Oxford Handbook of Economic Forecasting. [Google Scholar] [CrossRef]
- Terry, Leann, and Ken Kelley. 2012. Sample Size Planning for Composite Reliability Coefficients: Accuracy in Parameter Estimation via Narrow Confidence Intervals. The British Journal of Mathematical and Statistical Psychology 65: 371–401. [Google Scholar] [CrossRef]
- van Huellen, Sophie, Duo Qin, Shan Lu, Huiwen Wang, Qing Chao Wang, and Thanos Moraitis. 2022. Modelling Opportunity Cost Effects in Money Demand Due to Openness. International Journal of Finance & Economics 27: 697–744. [Google Scholar] [CrossRef]
- Vines, David, and Samuel Wills. 2018. The Financial System and the Natural Real Interest Rate: Towards a ‘New Benchmark Theory Model’. Oxford Review of Economic Policy 34: 252–68. [Google Scholar] [CrossRef]
- Vinzi, Vincenzo Esposito, Laura Trinchera, and Silvano Amato. 2010. PLS Path Modeling: From Foundations to Recent Developments and Open Issues for Model Assessment and Improvement. In Handbook of Partial Least Squares: Concepts, Methods and Applications. Edited by Vincenzo Esposito Vinzi, Wynne W. Chin, Jörg Henseler and Huiwen Wang. Springer Handbooks of Computational Statistics. Berlin/Heidelberg: Springer, pp. 47–82. [Google Scholar] [CrossRef]
- Wang, Qing Chao. 2017. Testing a New Approach to Construct International Financial Market Indices: An Application to Asian-Pacific Economies. Ph.D. Thesis, SOAS University of London, London, UK. [Google Scholar]
- Wegelin, Jacob A. 2000. A Survey of Partial Least Squares (PLS) Methods, with Emphasis on the Two-Block Case. Technical Report. Seattle: Department of Statistics, University of Washington. [Google Scholar]
- Wold, Herman. 1966. Estimation of principal component and related models by iterative least squares. In Multivariate Analysis. New York: Academic Press, pp. 391–420. [Google Scholar]
- Wold, Herman. 1975. PLS path models with latent variables: The NIPALS approach. In Quantitative Sociology: International Perspectives on Mathematical and Statistical Modeling. Edited by Hubert M. Blalock, Abel Aganbegian, Fridrich M. Borodkin, Raymond Boudon and Vittorio Cappecchi. New York: Academic Press. [Google Scholar]
- Wold, Herman. 1980. Model Construction and Evaluation When Theoretical Knowledge Is Scarce. In Evaluation of Econometric Models. New York: Academic Press, pp. 47–74. [Google Scholar] [CrossRef] [Green Version]






| Group | Ind. | Indicator Description | Construction |
|---|---|---|---|
| Forex Market | I1 | CIP vis-à-vis UK sterling | ln(O2)−ln(O1)−(ln(O8)−ln(O5)) |
| I2 | CIP vis-à-vis Canadian dollar | ln(O3)−ln(O1)−(ln(O9)−ln(O6)) | |
| I3 | CIP vis-à-vis Sweden krona | ln(O4)−ln(O1)−(ln(O10)−ln(O7)) | |
| I4 | Real effective rate of US dollar | O29 | |
| Equity Market | I5 | Ratio of SMI: Canada/USA | O12/O11 |
| I6 | Ratio of SMI: Germany/USA | O13/O11 | |
| I7 | Ratio of SMI: Japan/USA | O13/O11 | |
| I8 | Ratio of SMI: UK/USA | O14/O11 | |
| Fixed Income Market | I9 | TB spread: 10-to-1 years | O17−O16 |
| I10 | TB spread: 30-to-10 years | O18−O17 | |
| I11 | TB spread: 30-to-1 years | O18−O16 | |
| I12 | TB spread: 6-to-3 months | O20−O19 | |
| I13 | TED spread: interbank loan to TB rates | O19−O1 | |
| Banking Sector | I14 | Total liability to equity ratio of the banking sector | O25/O26 |
| I15 | Total lending to deposit ratio of the banking sector | O24/O27 | |
| I16 | IR spread: lending-to-deposit rates | O21/O1 | |
| I17 | Debt to liquidity ratio: M1 to liquidity | O28/O25 | |
| I18 | IR spread: mortgage-to-bond rates | O22−O18 | |
| I19 | Bank lending: mortgage to loan ratio | O23/O24 | |
| Systemic Risk Measures | I22 | CatFin: Institution specific value-at-risk measure | Giglio et al. (2016) |
| I23 | CoVar: Value-at-risk measure | Giglio et al. (2016) | |
| I24 | Mes: Institution specific exposure to shocks measure | Giglio et al. (2016) | |
| I25 | Mes_be: Variation of Mes | Giglio et al. (2016) | |
| I26 | Dci: Interconnectedness of financial institutions | Giglio et al. (2016) | |
| I27 | Size_conc: Size concentration of financial institutions | Giglio et al. (2016) |
| Target | CPI | GDP | IP | ||||
|---|---|---|---|---|---|---|---|
| Indicator | Lag | Loading | Lag | Loading | Lag | Loading | |
| Forex | I1 | 0 | 0.0537 | 0, 6 | −0.0448 | 0, 6 | −0.1395 |
| I2 | 3, 5 | −0.0117 | 0, 2, 6 | 0.0144 | 6, 5 | −0.1122 | |
| I3 | 2, 6, 0 | −0.0017 | 2, 6, 0 | 0.0065 | 0, 3, 6 | −0.1252 | |
| I4 | 0 | −0.0544 | 6, 0 | 0.0655 | 0 | 0.0664 | |
| Equity | I5 | 2, 4, 6 | −0.1534 | 0, 4, 6 | 0.1403 | 5, 6 | 0.0817 |
| I6 | 0, 4 | 0.0612 | 6, 0 | −0.0493 | 0 | −0.0855 | |
| I7 | 0 | −0.0488 | 0 | 0.0685 | 6 | −0.0535 | |
| I8 | 0, 1 | −0.0783 | 0, 6 | 0.0815 | 6, 0 | −0.0158 | |
| Fixed Income | I9 | 6 | 0.0450 | 0, 6 | −0.0387 | 0, 6 | −0.1185 |
| I10 | 0, 5 | 0.0850 | 0, 6 | −0.0854 | 0 | −0.1047 | |
| I11 | 6 | 0.0596 | 0, 6 | −0.0554 | 0, 6 | −0.1266 | |
| I12 | 2 | −0.0189 | 1, 2 | 0.0114 | 2, 6 | 0.0071 | |
| I13 | 4, 2 | 0.1150 | 0, 1 | −0.1022 | 0 | −0.1240 | |
| Banking Sector | I14 | 0 | −0.1236 | 0 | 0.1274 | 0 | 0.0379 |
| I15 | 1, 6 | 0.1331 | 3, 6, 0 | −0.1252 | 6 | −0.0325 | |
| I16 | 0 | 0.1202 | 0 | −0.1299 | 0 | −0.0680 | |
| I17 | 0 | −0.0684 | 0 | 0.0733 | 0, 6 | −0.0153 | |
| I18 | 4 | −0.0909 | 4, 0, 6 | 0.0839 | 0 | 0.1004 | |
| I19 | 0 | 0.1407 | 6 | −0.1546 | 0 | −0.1150 | |
| Target | CPI | GDP | IP | ||||
|---|---|---|---|---|---|---|---|
| Indicator | Lag | Loading | Lag | Loading | Lag | Loading | |
| Forex | I1 | NA | −0.0058 | D12|L1 | −0.0093|−0.0037 | D16|L1 | −0.0143|−0.0053 |
| I2 | - | 0.0000 | L1 | −0.0058 | L1 | −0.0099 | |
| I3 | NA | −0.0027 | D16|L1 | −0.0095|−0.0027 | D16|L1 | −0.0260|−0.0031 | |
| I4 | D16|L6 | 0.0099|−0.0026 | - | 0.0000 | - | 0.0000 | |
| Equity | I5 | L4 | 0.0145 | D26|L6 | 0.0295|−0.0006 | D36|L6 | 0.0413|−0.0069 |
| I6 | NA | −0.0028|−0.0021 | NA | 0.0033|−0.0020 | L1 | 0.0055 | |
| I7 | - | 0.0000 | D16|L6 | 0.0106|−0.0006 | D16|L1 | 0.0144|0.0017 | |
| I8 | L1 | 0.0074 | - | 0.0000 | - | 0.0000 | |
| Fixed Income | I9 | L16 | −0.0131 | D16|L6 | −0.0103|0.0013 | D16|L6 | −0.0156|0.0031 |
| I10 | L12 | −0.0128 | L6 | 0.0042 | L6 | 0.0121 | |
| I11 | L16 | −0.0136 | D16|L6 | −0.0117|0.0018 | D16|L6 | −0.0183|0.0045 | |
| I12 | NA | −0.0065 | - | 0.0000 | - | 0.0000 | |
| I13 | L12 | −0.0192 | L2 | 0.0073 | L6 | 0.0147 | |
| Banking Sector | I14 | D16|L1 | 0.0107|0.0062 | D16|L1 | −0.0271|−0.0003 | D16|L1 | −0.0403|−0.0039 |
| I15 | L1 | −0.0120 | D14|L1 | 0.0501|0.0001 | D15|L1 | 0.1033|0.0052 | |
| I16 | L46 | −0.0120 | L1 | −0.0045 | NA | −0.0009|−0.0055 | |
| I17 | NA | 0.0145 | NA | −0.0366|0.0018 | D16|L6 | −0.0546|0.0079 | |
| I18 | L26 | 0.0121 | NA | −0.0078 | L26 | −0.0208 | |
| I19 | - | 0.0000 | NA | −0.0467|−0.0015 | NA | −0.1197|0.0040 | |
| (A) Long-Run Macro Targets | |||||||||||||
| Target | CPI | IP | |||||||||||
| Lag Cha. | Loadings | Lag Cha. | Loadings | ||||||||||
| Ind. | Pre | Post | Pre | Post | Diff. | Pre | Post | Pre | Post | Diff. | |||
| Forex | I1 | 0 | 3 | 0.0537 | 0.0583 | 0.01 | 1 | 3 | −0.1395 | −0.0799 | 0.06 | ||
| I2 | 2 | 3 | −0.0117 | −0.0150 | 0.00 | 2 | 4 | −0.1122 | −0.0525 | 0.06 | |||
| I3 | 2 | 0 | −0.0017 | −0.0147 | 0.01 | 2 | 4 | −0.1252 | −0.0607 | 0.07 | |||
| I4 | 0 | 0 | −0.0544 | −0.0512 | 0.00 | 0 | 0 | 0.0664 | 0.0858 | 0.02 | |||
| Equity | I5 | 2 | 0 | −0.1534 | −0.1674 | 0.01 | 1 | 0 | 0.0817 | 0.0356 | 0.05 | ||
| I6 | 2 | 0 | 0.0612 | 0.0385 | 0.03 | 0 | 0 | −0.0855 | −0.1302 | 0.05 | |||
| I7 | 0 | 0 | −0.0488 | −0.0602 | 0.01 | 0 | 2 | −0.0535 | 0.0342 | 0.09 | |||
| I8 | 1 | 1 | −0.0783 | −0.0895 | 0.01 | 2 | 3 | −0.0158 | 0.0487 | 0.07 | |||
| Fixed Income | I9 | 0 | 0 | 0.0450 | 0.0484 | 0.00 | 1 | 2 | −0.1185 | −0.1030 | 0.02 | ||
| I10 | 1 | 2 | 0.0850 | 0.0792 | 0.01 | 0 | 0 | −0.1047 | −0.1218 | 0.02 | |||
| I11 | 0 | 0 | 0.0596 | 0.0611 | 0.00 | 1 | 0 | −0.1266 | −0.1178 | 0.01 | |||
| I12 | 0 | 0 | −0.0189 | −0.0185 | 0.00 | 2 | 3 | 0.0071 | 0.0012 | 0.01 | |||
| I13 | 1 | 1 | 0.1150 | 0.1227 | 0.01 | 0 | 2 | −0.1240 | −0.0995 | 0.03 | |||
| Banking Sector | I14 | 0 | 0 | −0.1236 | −0.1126 | 0.01 | 0 | 0 | 0.0379 | 0.1093 | 0.07 | ||
| I15 | 1 | 0 | 0.1331 | 0.1315 | 0.00 | 0 | 1 | −0.0325 | −0.0231 | 0.01 | |||
| I16 | 0 | 0 | 0.1202 | 0.1279 | 0.01 | 0 | 2 | −0.0680 | −0.0805 | 0.01 | |||
| I17 | 0 | 0 | −0.0684 | −0.0684 | 0.00 | 1 | 0 | −0.0153 | 0.1007 | 0.12 | |||
| I18 | 0 | 0 | −0.0909 | −0.0933 | 0.00 | 0 | 2 | 0.1004 | 0.0991 | 0.00 | |||
| I19 | 0 | 0 | 0.1407 | 0.1233 | 0.02 | 0 | 1 | −0.1150 | −0.1425 | 0.03 | |||
| (B) Short-Run Macro Targets | |||||||||||||
| CPI | IP | ||||||||||||
| Lag Cha. | Loadings | Lag Cha. | Loadings | ||||||||||
| Ind. | Pre | Po | Pre | Post | Pre | Po | Pre | Post | |||||
| Forex | I1 | 1 | 3 | −0.0058 | −0.0019 | 0 | 1 | −0.0143|−0.0053 | −0.0026|−0.0098 | ||||
| I2 | 0 | 0 | 0.0000 | 0.0000 | 0 | 1 | −0.0099 | −0.0017 | |||||
| I3 | 2 | 3 | −0.0027 | 0.0015|−0.0035 | 0 | 2 | −0.0260|−0.0031 | −0.0166|−0.0009 | |||||
| I4 | 0 | 1 | 0.0099|−0.0026 | 0.0078|0.0005 | 0 | 0 | 0.0000 | 0.0000 | |||||
| Equity | I5 | 0 | 4 | 0.0145 | 0.0077 | 0 | 2 | 0.0413|−0.0069 | 0.0245|−0.0081 | ||||
| I6 | 1 | 1 | −0.0028|−0.0021 | −0.0009|−0.0086 | 1 | 3 | 0.0055 | 0.0008|−0.0110 | |||||
| I7 | 0 | 0 | 0.0000 | 0.0000 | 0 | 1 | 0.0144|0.0017 | 0.0028|0.0126 | |||||
| I8 | 0 | 0 | 0.0074 | 0.0072 | 0 | 6 | 0.0000 | 0.0009|0.0097 | |||||
| Fixed Income | I9 | 0 | 1 | −0.0131 | −0.0118 | 0 | 0 | −0.0156|0.0031 | −0.0194|−0.0019 | ||||
| I10 | 0 | 0 | −0.0128 | −0.0123 | 0 | 2 | 0.0121 | −0.0071|0.0020 | |||||
| I11 | 0 | 0 | −0.0136 | −0.0125 | 0 | 0 | −0.0183|0.0045 | −0.0239|−0.0013 | |||||
| I12 | 1 | 2 | −0.0065 | −0.0042 | 0 | 0 | 0.0000 | 0.0000 | |||||
| I13 | 0 | 2 | −0.0192 | −0.0170 | 0 | 1 | 0.0147 | 0.0174 | |||||
| Banking Sector | I14 | 0 | 3 | 0.0107|0.0062 | 0.0189|0.0080 | 0 | 0 | −0.0403|−0.0039 | −0.0475|0.0027 | ||||
| I15 | 0 | 3 | −0.0120 | 0.0027|−0.0089 | 0 | 2 | 0.1033|0.0052 | 0.0875|−0.0021 | |||||
| I16 | 0 | 2 | −0.0120 | −0.0110 | 1 | 3 | −0.0009|−0.0055 | −0.0052|−0.0001 | |||||
| I17 | 1 | 4 | 0.0145 | −0.0231|0.0081 | 0 | 2 | −0.0546|0.0079 | −0.1116|0.0127 | |||||
| I18 | 0 | 1 | 0.0121 | 0.0121 | 0 | 2 | −0.0208 | −0.0148 | |||||
| I19 | 0 | 6 | 0.0000 | −0.0218|−0.0175 | 1 | 4 | −0.1197|0.0040 | −0.2585|−0.0038 | |||||
| (A) CPI-Based Annual Inflation Is CPI. Is PPI. | |||
| Model (1)–Baseline | Model (2)–FCI-Based | ||
| 0.0019 [0.0005] ** | 0.0021 [0.0005] ** | ||
| 1.1278 [0.0567] ** | 1.1362 [0.0566] ** | ||
| −0.2065 [0.0516] ** | −0.2233 [0.0513] ** | ||
| 0.2074 [0.0214] ** | 0.2114 [0.0214] ** | ||
| −0.1797 [0.0226] ** | −0.1790 [0.0226] ** | ||
| −0.0049 [0.0019] * | −0.0047 [0.0019] * | ||
| 0.1011 [0.0277] ** | −0.0130 [0.0034] ** | ||
| (B) Annual GDP Growth Is US GDP. Is GDP World. | |||
| Model (1)–Baseline | Model (2)–FCI-Based | ||
| −0.0200 [0.0051] ** | −0.0022 [0.0014] | ||
| 0.8632 [0.0281] ** | 0.8227 [0.0296] ** | ||
| 1.0090 [0.0528] ** | 0.9854 [0.9854] ** | ||
| −0.8279 [0.0590] ** | −0.7831 [0.0584] ** | ||
| −0.0643 [0.0151] ** | −0.1464 [0.0261] ** | ||
| −0.2394 [0.0754] ** | 0.8527 [0.3809] * | ||
| (C) Annual IP Growth Is US Industrial Production. is US GDP. | |||
| Model (1)–Baseline | Model (2)–FCI-Based | ||
| 0.1361 [0.0221] ** | 0.0607 [0.0102] ** | ||
| 0.8471 [0.0239] ** | 0.8741 [0.0217] ** | ||
| 0.6300 [0.0420] ** | 0.6068 [0.0408] ** | ||
| −0.3308 [0.0470] ** | −0.4186 [0.0456] ** | ||
| −0.1124 [0.0179] ** | −0.1688 [0.0275] ** | ||
| 0.1659 [0.0519] ** | 0.7402 [0.2152] ** | ||
| Forecast Encompassing Tests † | ||||||
|---|---|---|---|---|---|---|
| MSFE Baseline (1) | MSFE FCI-Based (2) | Harvey et al. (1997) | Ericsson (1992) | |||
| H1 | H2 | H1 | H2 | |||
| 2001M1–2006M12 | ||||||
| CPI | 0.0027 | 0.0027 | 0.4082 | 0.5500 | 0.2754 | 0.0443 * |
| GDP | 0.0066 | 0.0068 | 0.4147 | 0.4762 | 0.9357 | 0.0028 ** |
| IP | 0.0065 | 0.0064 | 0.4336 | 0.4200 | 0.7381 | 0.0029 ** |
| 2001M1–2010M12 | ||||||
| CPI | 0.0028 | 0.0028 | 0.4239 | 0.5161 | 0.6715 | 0.0526 |
| IP | 0.0096 | 0.0095 | 0.4760 | 0.4361 | 0.4272 | 0.0221 * |
| 2001M1–2017M12 | ||||||
| CPI | 0.0024 | 0.0024 | 0.4431 | 0.5072 | 0.7815 | 0.0341 * |
| IP | 0.0087 | 0.0085 | 0.4809 | 0.4199 | 0.0424* | 0.0092 ** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, D.; van Huellen, S.; Wang, Q.C.; Moraitis, T. Algorithmic Modelling of Financial Conditions for Macro Predictive Purposes: Pilot Application to USA Data. Econometrics 2022, 10, 22. https://doi.org/10.3390/econometrics10020022
Qin D, van Huellen S, Wang QC, Moraitis T. Algorithmic Modelling of Financial Conditions for Macro Predictive Purposes: Pilot Application to USA Data. Econometrics. 2022; 10(2):22. https://doi.org/10.3390/econometrics10020022
Chicago/Turabian StyleQin, Duo, Sophie van Huellen, Qing Chao Wang, and Thanos Moraitis. 2022. "Algorithmic Modelling of Financial Conditions for Macro Predictive Purposes: Pilot Application to USA Data" Econometrics 10, no. 2: 22. https://doi.org/10.3390/econometrics10020022
APA StyleQin, D., van Huellen, S., Wang, Q. C., & Moraitis, T. (2022). Algorithmic Modelling of Financial Conditions for Macro Predictive Purposes: Pilot Application to USA Data. Econometrics, 10(2), 22. https://doi.org/10.3390/econometrics10020022







