Adaptive Probabilistic Flooding for Information Hovering in VANETs
Abstract
1. Introduction
- It includes a more extensive literature review, reporting recent works pertinent to the considered problem.
- It demonstrates the effectiveness of the proposed estimation algorithm by comparing the performance of the proposed protocol (which uses the estimation algorithm) with that of a modified version which assumes a known density.
- The effectiveness of the proposed methodology is demonstrated by designing a density adaptive extended area scheme which adaptively regulates an area beyond the hovering in which message exchange is allowed. This scheme is an adaptive version of the scheme proposed in Reference [28] and has not been presented in any previous work.
2. Related Work
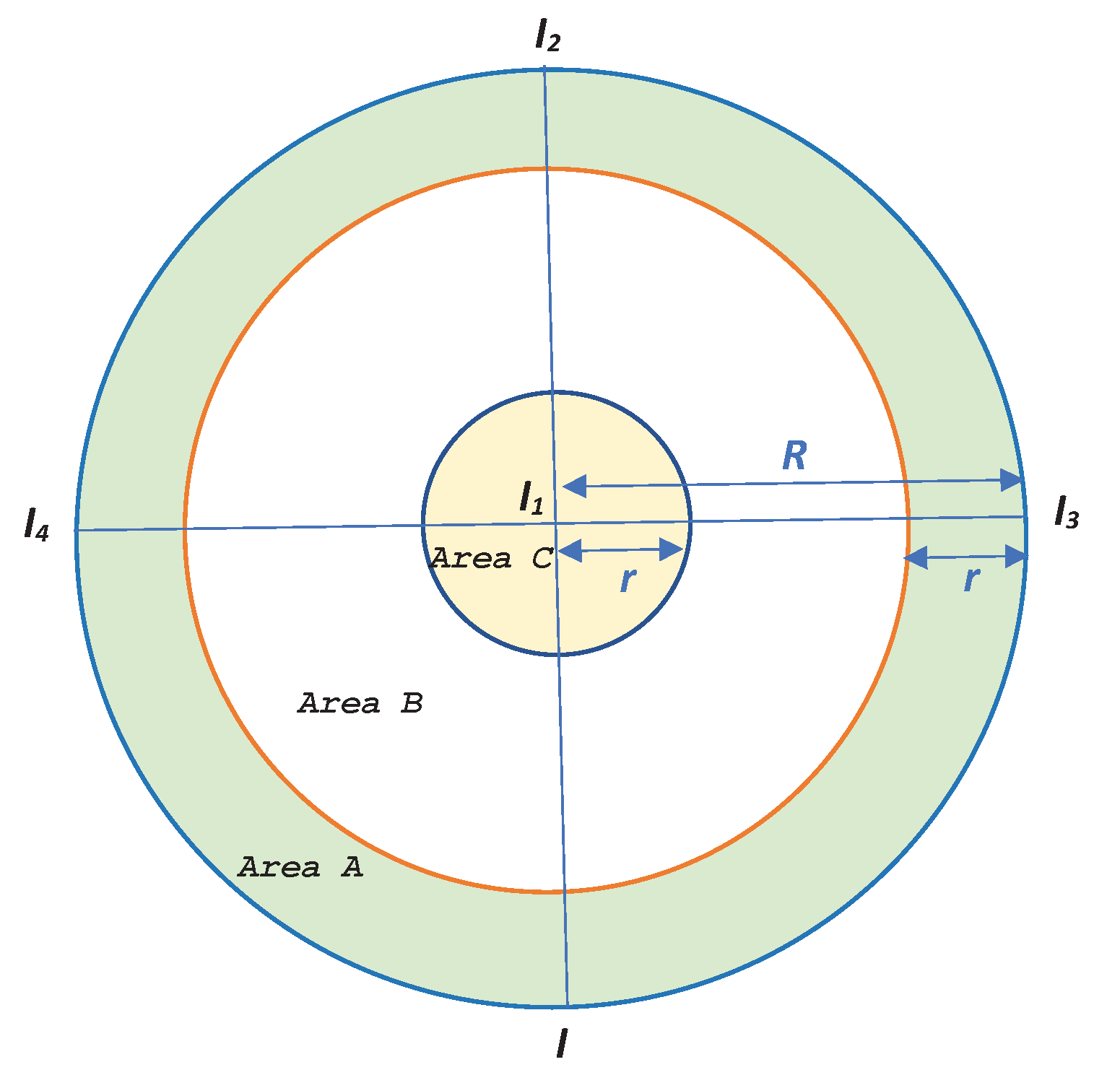
3. Problem Description
4. Proposed Traffic Adaptive Information Hovering Protocol
5. Estimation of the Vehicle Density
- (i)
- estimation of the average number of neighbors in the anchor area ();
- (ii)
- number of neighbors n;
- (iii)
- number of neighbors of each of its neighbors ( for j neighbor);
- (iv)
- estimates of the average number of neighbors of each of its neighbors( for the neighbor j).
6. Performance Evaluation
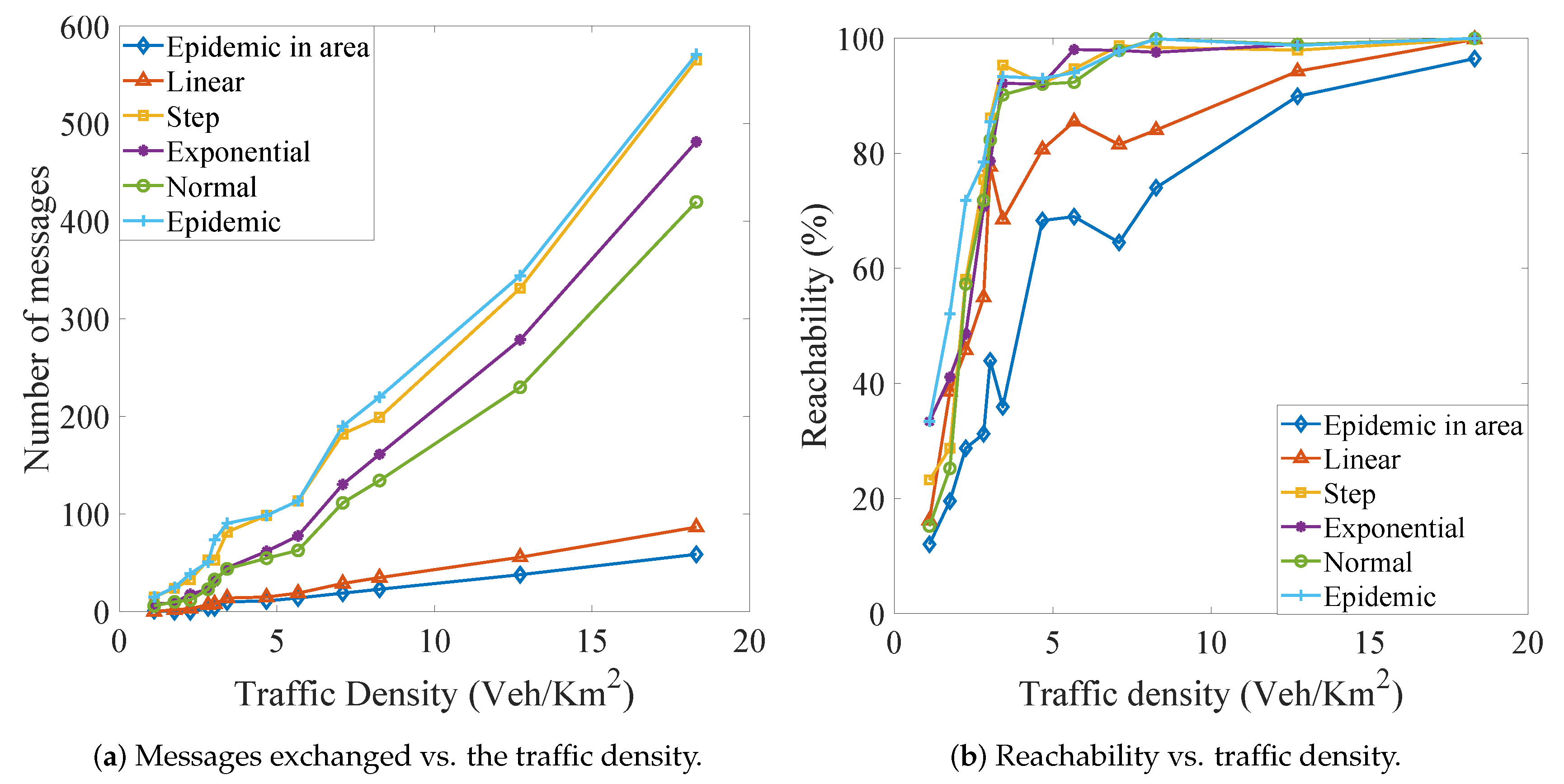
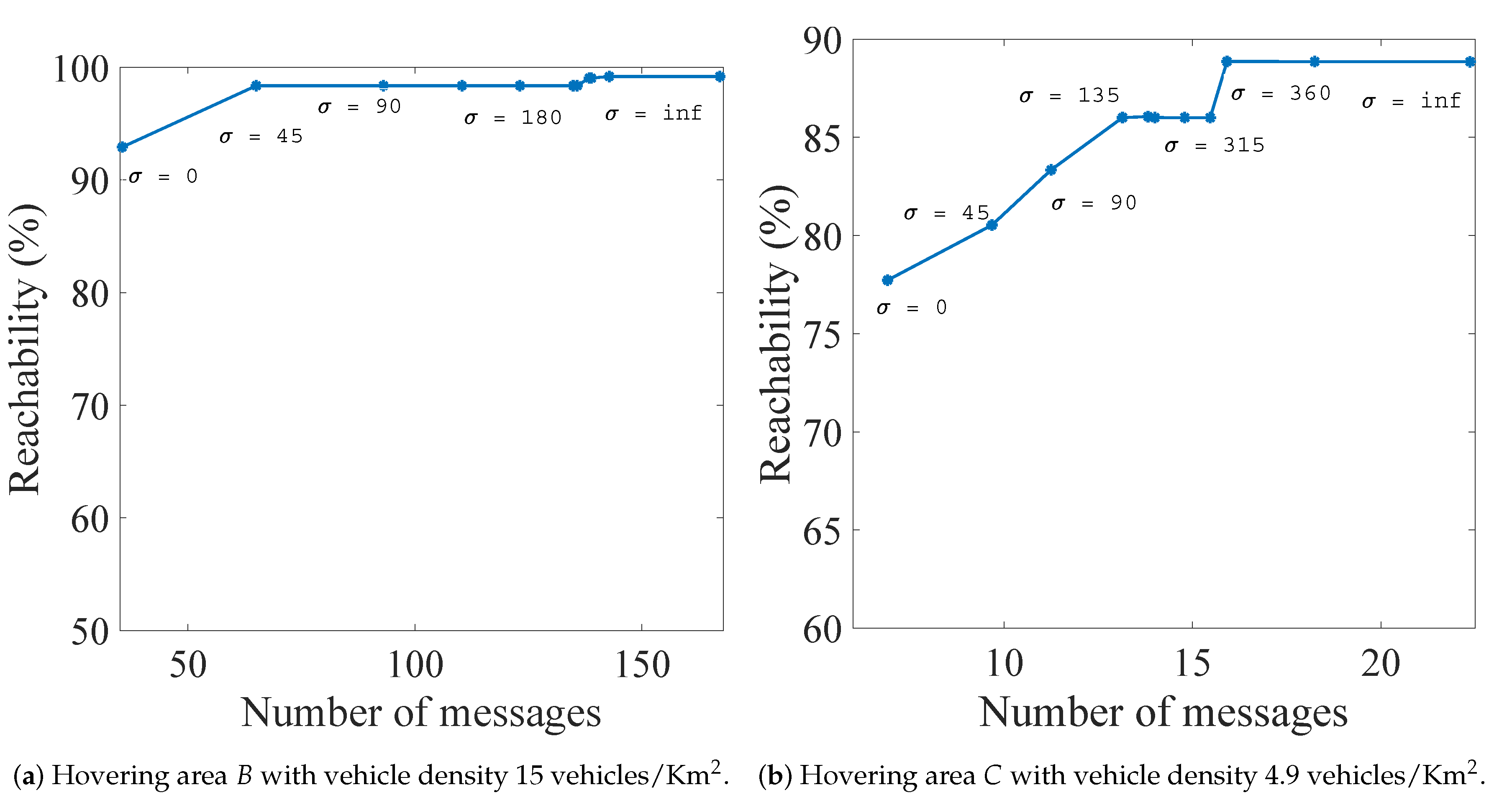
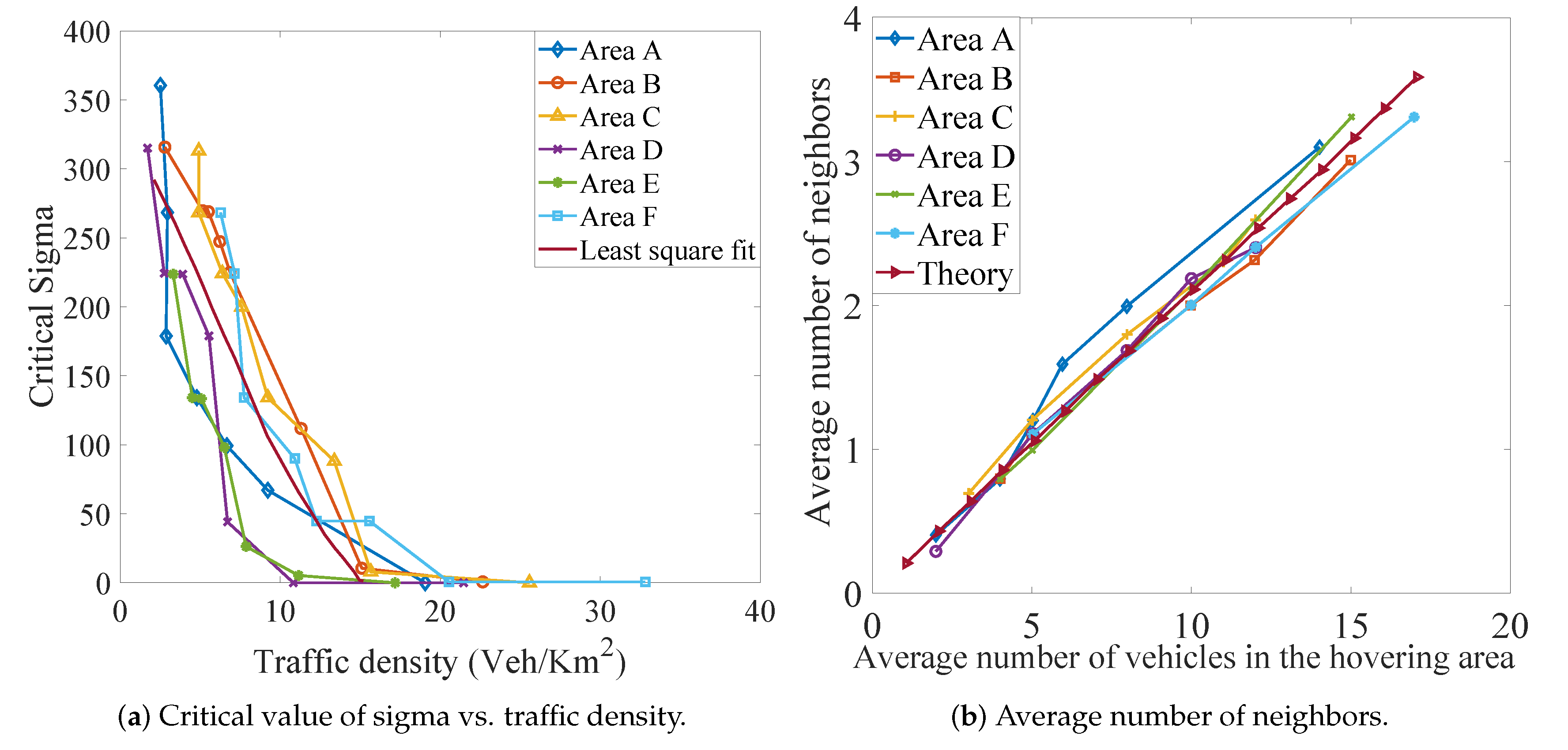
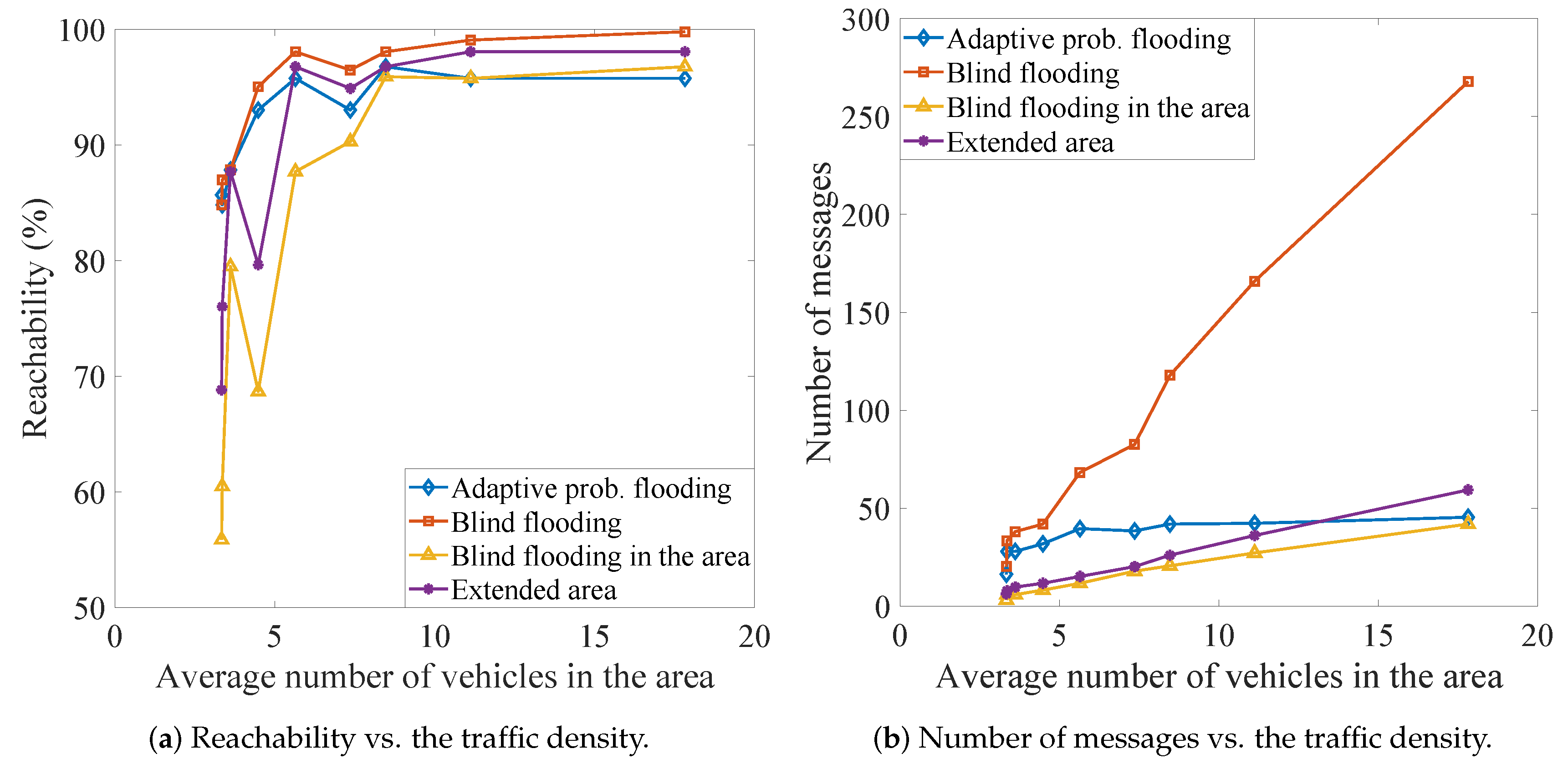
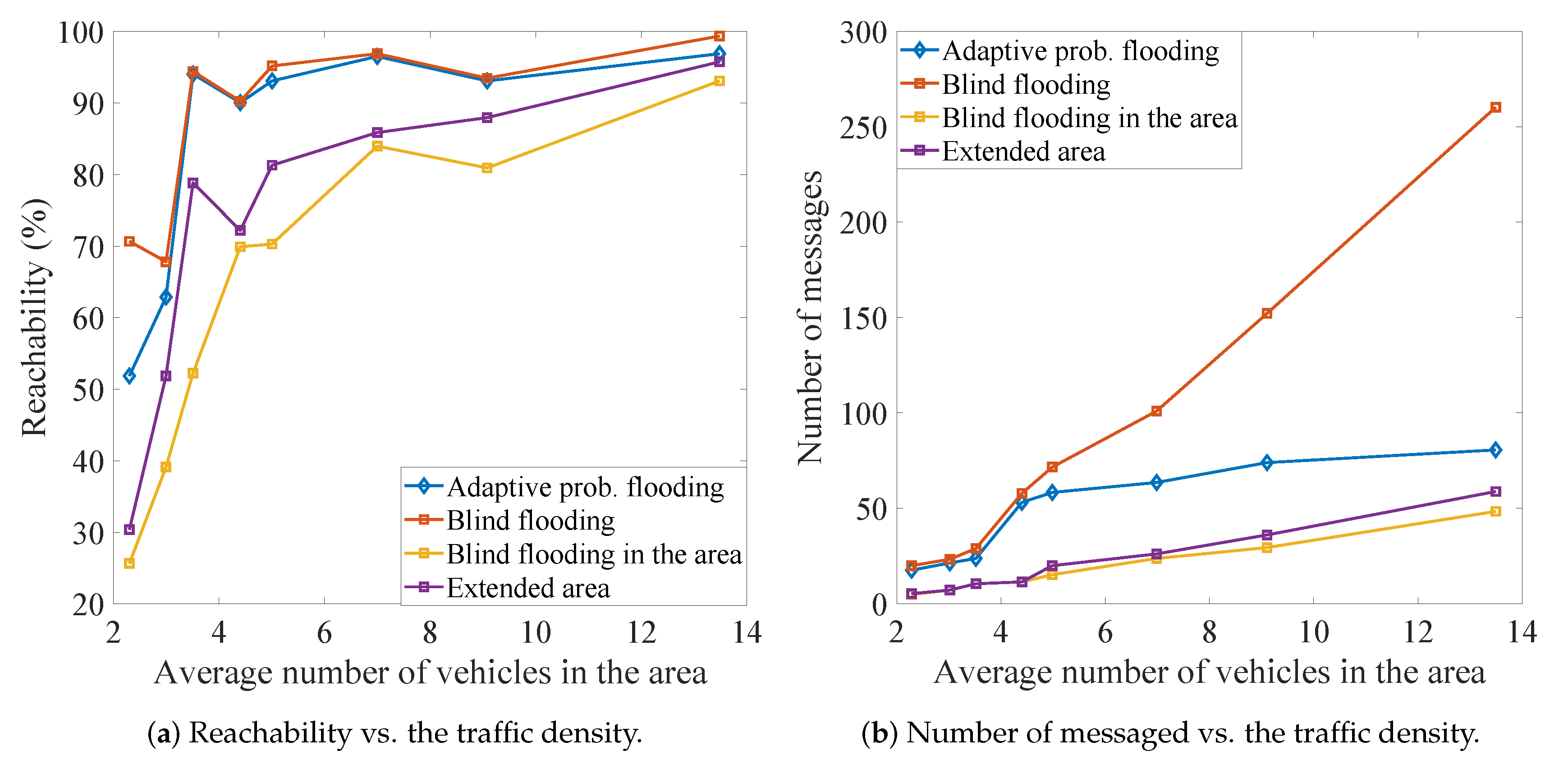
6.1. Effectiveness of Adaptive Probabilistic Flooding
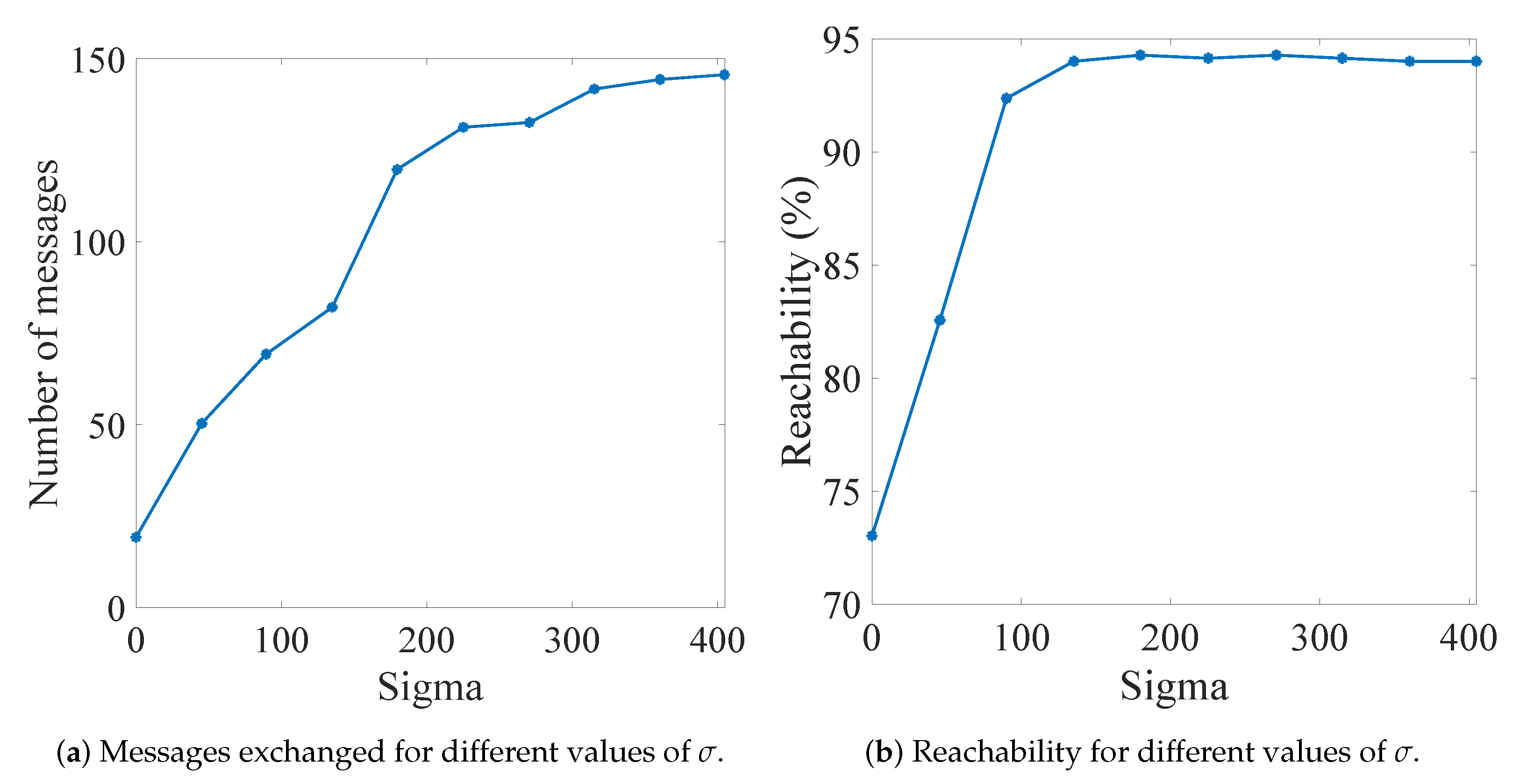
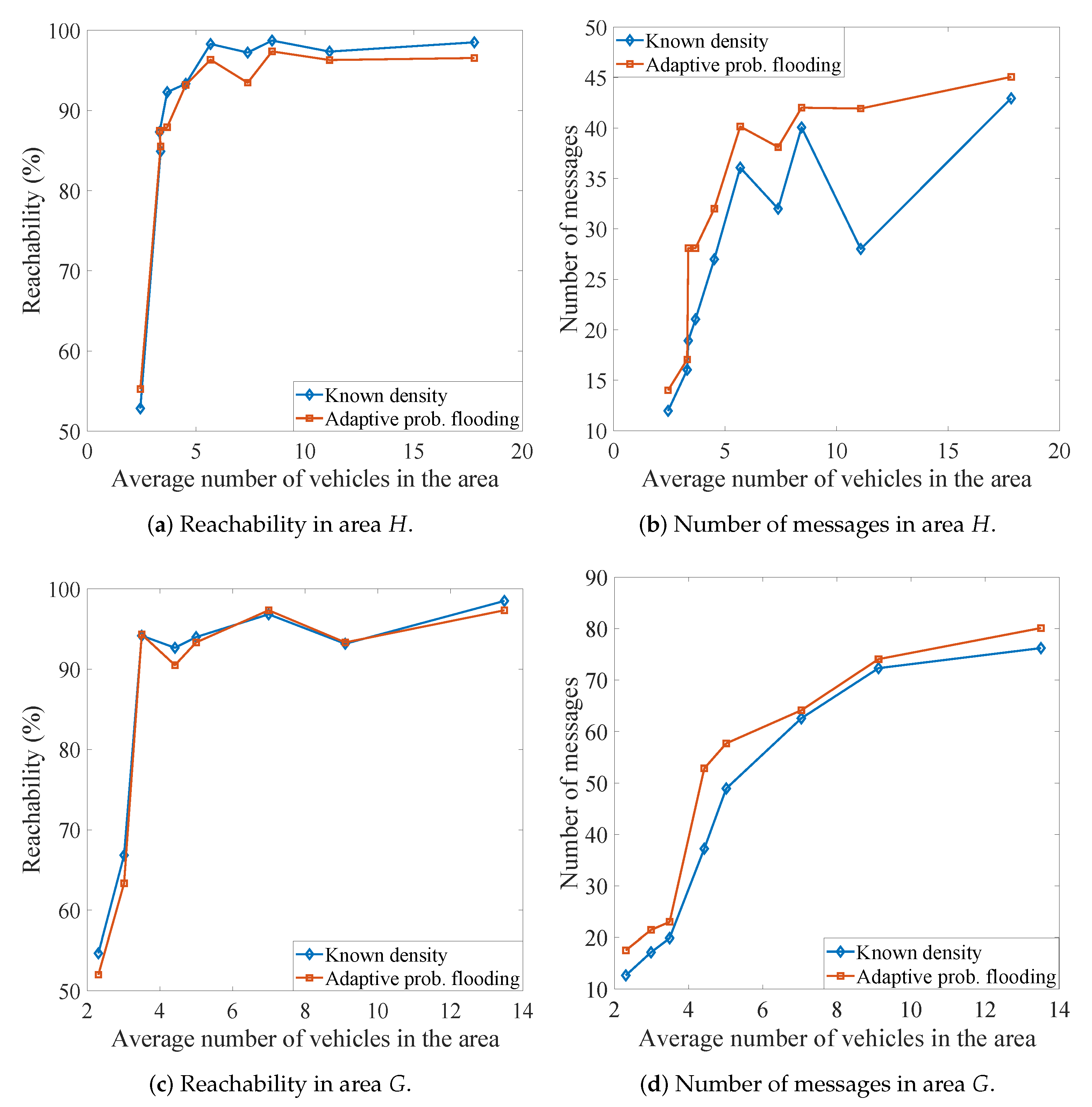
6.2. Effectiveness of the Estimation Algorithm
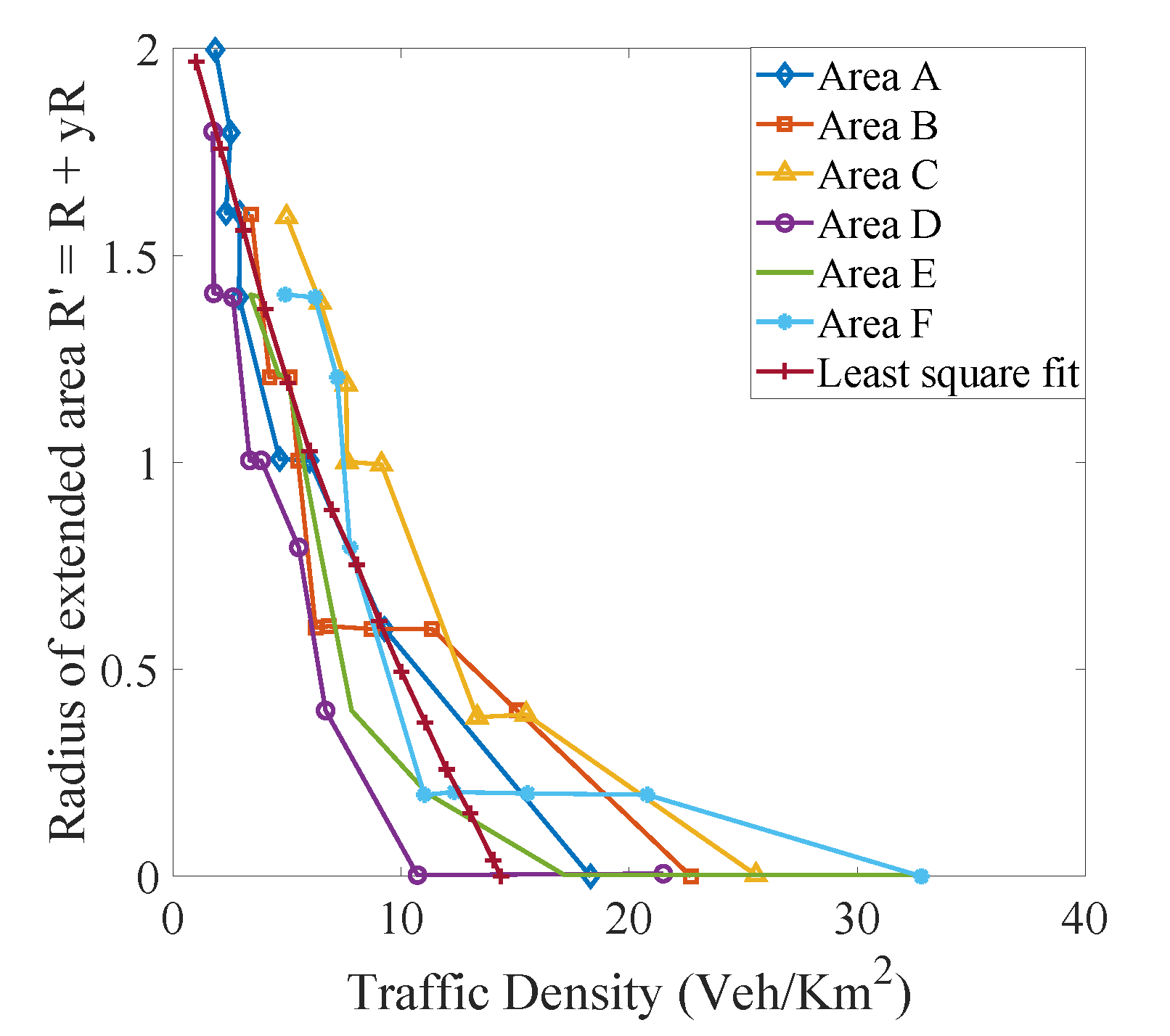
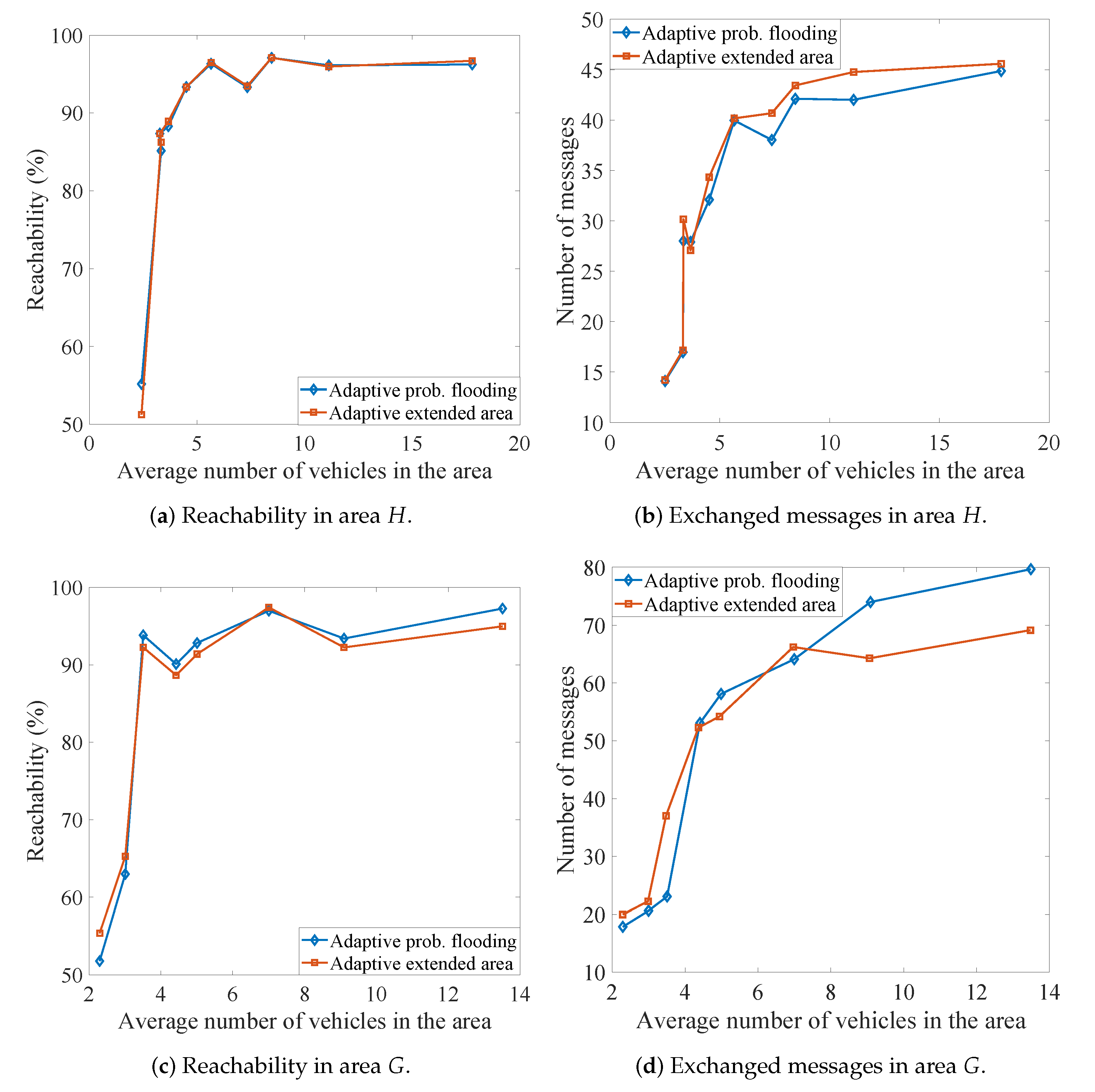
6.3. Comparison with Adaptive Area Regulation
7. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DTN | Delay Tolerant Networks |
| MFC | Message Frequency Control |
| RTT | Round Trip Times |
| RSUs | Roadside Units |
| VANETs | Vehicular Adhoc Networks |
| TPC | Transmit Power Control |
| VDTNs | vehicular Delay Tolerant Networks |
| V2V | Vehicle-to-Vehicle |
| V2I | Vehicle-to-Infrastructure |
References
- Silva, C.M.; Masini, B.M.; Ferrari, G.; Thibault, I. A Survey on Infrastructure-Based Vehicular Networks. Mob. Inf. Syst. 2017, 2017, 28–56. [Google Scholar] [CrossRef]
- Swain, P.; Christophorou, C.; Bhattacharjee, U.; Silva, C.M.; Pitsillides, A. Selection of UE-based Virtual Small Cell Base Stations using Affinity Propagation Clustering. In Proceedings of the 2018 14th International Wireless Communications Mobile Computing Conference (IWCMC), Limassol, Cyprus, 25–29 June 2018; pp. 1104–1109. [Google Scholar] [CrossRef]
- Silva, C.M.; Meira, W., Jr. Managing Infrastructure-Based Vehicular Networks. In Proceedings of the 2015 16th IEEE International Conference on Mobile Data Management (MDM), Pittsburgh, PA, USA, 15–18 June 2015; Volume 2, pp. 19–22. [Google Scholar] [CrossRef]
- Eriksson, J.; Girod, L.; Hull, B.; Newton, R.; Madden, S.; Balakrishnan, H. The pothole patrol: Using a mobile sensor network for road surface monitoring. In Proceedings of the 6th International Conference on Mobile Systems, Applications, and Services, ACM MobiSys, Breckenridge, CO, USA, 17–20 June 2008. [Google Scholar]
- Mukhtar, A.; Xia, L.; Tang, T.B. Vehicle Detection Techniques for Collision Avoidance Systems: A Review. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2318–2338. [Google Scholar] [CrossRef]
- Silva, C.M.; Aquino, A.L.L.; Meira, W., Jr. Smart Traffic Light for Low Traffic Conditions. Mob. Netw. Appl. 2015, 20, 285–293. [Google Scholar] [CrossRef]
- Johnson, D.A.; Trivedi, M.M. Driving style recognition using a smartphone as a sensor platform. In Proceedings of the 2011 14th International IEEE Conference on Intelligent Transportation Systems (ITSC), Washington, DC, USA, 5–7 October 2011; pp. 1609–1615. [Google Scholar]
- Oliveira, T.R.; Silva, C.M.; Macedo, D.F.; Nogueira, J.M.S. SNVC: Social networks for vehicular certification. Comput. Netw. 2016, 111, 129–140. [Google Scholar] [CrossRef]
- Silva, C.M.; Silva, F.A.; Sarubbi, J.F.; Oliveira, T.R.; Meira, W., Jr.; Nogueira, J.M.S. Designing mobile content delivery networks for the Internet of vehicles. Veh. Commun. 2017, 8, 45–55. [Google Scholar] [CrossRef]
- Khelifi, H.; Luo, S.; Nour, B.; Moungla, H.; Faheem, Y.; Hussain, R.; Ksentini, A. Named data networking in vehicular ad hoc networks: State-of-the-art and challenges. IEEE Commun. Surv. Tutor. 2019, 22, 320–351. [Google Scholar] [CrossRef]
- Sharma, A.; Awasthi, L.K. A Comparative Survey on Information Dissemination in Heterogeneous Vehicular Communication Networks. In Proceedings of the 2018 First International Conference on Secure Cyber Computing and Communication (ICSCCC), Jalandhar, India, 15–17 December 2018; pp. 556–560. [Google Scholar]
- Toor, Y.; Muhlethaler, P.; Laouiti, A. Vehicle ad hoc networks: Applications and related technical issues. IEEE Commun. Surv. Tutor. 2008, 10, 74–88. [Google Scholar] [CrossRef]
- Zeadally, S.; Hunt, R.; Chen, Y.S.; Irwin, A.; Hassan, A. Vehicular ad hoc networks (VANETS): Status, results, and challenges. Telecommun. Syst. 2012, 50, 217–241. [Google Scholar] [CrossRef]
- Silva, C.M.; Silva, L.D.; Santos, L.A.L.; Sarubbi, J.F.M.; Pitsillides, A. Broadening Understanding on Managing the Communication Infrastructure in Vehicular Networks: Customizing the Coverage Using the Delta Network. Future Internet 2018, 11, 1. [Google Scholar] [CrossRef]
- Silva, C.M.; Meira, W., Jr. Design of roadside communication infrastructure with QoS guarantees. In Proceedings of the 2015 IEEE Symposium on Computers and Communication (ISCC), Larnaca, Cyprus, 6–9 July 2015; pp. 439–444. [Google Scholar] [CrossRef]
- Silva, C.M.; Guidoni, D.L.; Souza, F.S.H.; Pitangui, C.G.; Sarubbi, J.F.M.; Pitsillides, A. Gamma Deployment: Designing the Communication Infrastructure in Vehicular Networks Assuring Guarantees on the V2I Inter-Contact Time. In Proceedings of the 2016 IEEE 13th International Conference on Mobile Ad Hoc and Sensor Systems (MASS), Brasilia, Brazil, 10–13 October 2016; pp. 263–271. [Google Scholar] [CrossRef]
- Villalba, A.; Konstantas, D. Towards hovering information. In Smart Sensing and Context; Springer: Berlin/Heidelberg, Germany, 2006; pp. 250–254. [Google Scholar]
- Castro, A.A.V.; Serugendo, G.D.M.; Konstantas, D. Hovering information–self-organizing information that finds its own storage. In Autonomic Communication; Springer: Berlin/Heidelberg, Germany, 2009; pp. 111–145. [Google Scholar]
- Di, G.; Serugendo, M. Dependable requirements for hovering information. In Supplemental Volume—The 37th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN’07); IEEE Computer Society Press: Edinburgh, UK, 2007. [Google Scholar]
- Shoaib, M.; Song, W.C. Hovering information based vanet applications. In International Conference on Networked Digital Technologies; Springer: Berlin/Heidelberg, Germany, 2012; pp. 551–564. [Google Scholar]
- Nikolovski, T. Design and Performance Evaluation of Data Dissemination and Hovering Information Protocols for Vehicular Ad Hoc Networks (VANETs). Master’s Thesis, University of Ontario Institute of Technology, Oshawa, ON, Canada, 2017. [Google Scholar]
- Ciocan, M.; Dobre, C.; Cristea, V.; Mavromoustakis, C.X.; Mastorakis, G. Analysis of vehicular storage and dissemination services based on floating content. In International Conference on Mobile Networks and Management; Springer: Berlin/Heidelberg, Germany, 2014; pp. 387–400. [Google Scholar]
- Nikolovski, T.; Pazzi, R.W. A Lightweight and Efficient Approach (LEA) for Hovering Information protocols. In Proceedings of the 6th ACM Symposium on Development and Analysis of Intelligent Vehicular Networks and Applications, Valletta, Malta, 13–17 November 2016; pp. 31–38. [Google Scholar]
- Xeros, A.; Lestas, M.; Andreou, M.; Pitsillides, A. Adaptive probabilistic flooding for Information Hovering in VANETs. In Proceedings of the Vehicular Networking Conference (VNC), Jersey City, NJ, USA, 13–15 December 2010; pp. 239–246. [Google Scholar]
- Ott, J.; Hyytiá, E.; Lassila, P.; Vaegs, T.; Kangasharju, J. Floating content: Information sharing in urban areas. In Proceedings of the 2011 IEEE International Conference on Pervasive Computing and Communications (PerCom), Kyoto, Japan, 11–15 March 2011; pp. 136–146. [Google Scholar]
- Konstantas, D.; Villalba, A. Hovering Information: A paradigm for sharing location-bound information. In Proceedings of the European Conference on Smart Sensing and Context; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Liaskos, C.; Xeros, A.; Papadimitriou, G.I.; Lestas, M.; Pitsillides, A. Balancing wireless data broadcasting and information hovering for efficient information dissemination. IEEE Trans. Broadcast. 2012, 58, 66–76. [Google Scholar] [CrossRef]
- Hermann, S.D.; Michl, C.; Wolisz, A. Time-stable geocast in intermittently connected ieee 802.11 manets. In Proceedings of the 2007 IEEE 66th Vehicular Technology Conference, Baltimore, MD, USA, 30 September–3 October 2007; pp. 1922–1926. [Google Scholar]
- Bhaskar, K.; Stephen, B.W.; Ramon, B. Phase Transition Phenomena in Wireless Ad-Hoc Networks. In Proceedings of the GLOBECOM, San Antonio, TX, USA, 25–29 November 2001. [Google Scholar]
- Xeros, A.; Lestas, M.; Andreou, M.; Pitsillides, A.; Ioannou, P. Information hovering in vehicular ad-hoc networks. In Proceedings of the 2009 IEEE GLOBECOM Workshops, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6. [Google Scholar]
- Tseng, Y.C.; Ni, S.Y.; Chen, Y.S.; Sheu, J.P. The broadcast storm problem in a mobile ad hoc network. Wirel. Netw. 2002, 8, 153–167. [Google Scholar] [CrossRef]
- Williams, B.; Camp, T. Comparison of broadcasting techniques for mobile ad hoc networks. In Proceedings of the 3rd ACM International Symposium on Mobile Ad Hoc Networking & Computing; ACM: New York, NY, USA, 2002; pp. 194–205. [Google Scholar]
- Silva, C.M.; Meira, W., Jr. An architecture integrating stationary and mobile roadside units for providing communication on Intelligent Transportation Systems. In Proceedings of the NOMS 2016—2016 IEEE/IFIP Network Operations and Management Symposium, Istanbul, Turkey, 25–29 April 2016; pp. 358–365. [Google Scholar] [CrossRef]
- Boussoufa-Lahlah, S.; Semchedine, F.; Bouallouche-Medjkoune, L. Geographic routing protocols for Vehicular Ad hoc NETworks (VANETs): A survey. Veh. Commun. 2018, 11, 20–31. [Google Scholar] [CrossRef]
- Tian, D.; Liu, C.; Duan, X.; Sheng, Z.; Ni, Q.; Chen, M.; Leung, V.C. A distributed position-based protocol for emergency messages broadcasting in vehicular ad hoc networks. IEEE Internet Things J. 2018, 5, 1218–1227. [Google Scholar] [CrossRef]
- Sung, Y.; Lee, M. A road layout based broadcast mechanism for urban vehicular ad hoc networks. Wirel. Commun. Mob. Comput. 2018, 2018, 1565363. [Google Scholar] [CrossRef]
- Maia, G.; Villas, L.A.; Viana, A.C.; Aquino, A.L.; Boukerche, A.; Loureiro, A.A. A rate control video dissemination solution for extremely dynamic vehicular ad hoc networks. Perform. Eval. 2015, 87, 3–18. [Google Scholar] [CrossRef]
- Oliveira, R.; Montez, C.; Boukerche, A.; Wangham, M.S. Reliable data dissemination protocol for VANET traffic safety applications. Ad Hoc Netw. 2017, 63, 30–44. [Google Scholar] [CrossRef]
- Rayeni, M.S.; Hafid, A.; Sahu, P.K. Dynamic spatial partition density-based emergency message dissemination in VANETs. Veh. Commun. 2015, 2, 208–222. [Google Scholar] [CrossRef]
- Woon, W.; Yeung, K.L. Self-pruning broadcasting for mobile ad hoc networks. In Proceedings of the Global Telecommunications Conference, GLOBECOM 2009, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6. [Google Scholar]
- Peng, W.; Lu, X.C. On the reduction of broadcast redundancy in mobile ad hoc networks. In Proceedings of the 1st ACM International Symposium on Mobile ad Hoc Networking & Computing; IEEE Press: Piscataway, NJ, USA, 2000; pp. 129–130. [Google Scholar]
- Bakhouya, M.; Gaber, J.; Lorenz, P. An adaptive approach for information dissemination in vehicular ad hoc networks. J. Netw. Comput. Appl. 2011, 34, 1971–1978. [Google Scholar] [CrossRef]
- Yassein, M.B.; Nimer, S.F.; Al-Dubai, A.Y. A new dynamic counter-based broadcasting scheme for mobile ad hoc networks. Simul. Model. Pract. Theory 2011, 19, 553–563. [Google Scholar] [CrossRef]
- Reina, D.; Toral, S.; Johnson, P.; Barrero, F. A survey on probabilistic broadcast schemes for wireless ad hoc networks. Ad Hoc Netw. 2015, 25, 263–292. [Google Scholar] [CrossRef]
- Liu, W.; Nakauchi, K.; Shoji, Y. A neighbor-based probabilistic broadcast protocol for data dissemination in mobile iot networks. IEEE Access 2018, 6, 12260–12268. [Google Scholar] [CrossRef]
- Cunha, F.; Boukerche, A.; Villas, L.; Viana, A.; Loureiro, A. Data Communication in VANETs: A Survey, Challenges and Applications. Ad Hoc Netw. 2016, 44, 90–103. [Google Scholar] [CrossRef]
- Kaiwartya, O.; Kumar, S. Guaranteed geocast routing protocol for vehicular adhoc networks in highway traffic environment. Wirel. Pers. Commun. 2015, 83, 2657–2682. [Google Scholar] [CrossRef]
- Kaiwartya, O.; Kumar, S. Enhanced caching for geocast routing in vehicular Ad Hoc network. In Intelligent Computing, Networking, and Informatics; Springer: Berlin/Heidelberg, Germany, 2014; pp. 213–220. [Google Scholar]
- Allani, S.; Yeferny, T.; Chbeir, R. A scalable data dissemination protocol based on vehicles trajectories analysis. Ad Hoc Netw. 2018, 71, 31–44. [Google Scholar] [CrossRef]
- Ko, Y.B.; Vaidya, N.H. Geocasting in mobile ad hoc networks: Location-based multicast algorithms. In Proceedings of the WMCSA’99. Second IEEE Workshop on Mobile Computing Systems and Applications, New Orleans, LA, USA, 25–26 February 1999; pp. 101–110. [Google Scholar]
- Allal, S.; Boudjit, S. Geocast routing protocols for vanets: Survey and guidelines. In Proceedings of the 2012 Sixth International Conference on Innovative Mobile and Internet Services in Ubiquitous Computing (IMIS), Palermo, Italy, 4–6 July 2012; pp. 323–328. [Google Scholar]
- Maihöfer, C.; Leinmüller, T.; Schoch, E. Abiding geocast: Time–stable geocast for ad hoc networks. In Proceedings of the 2nd ACM International Workshop on Vehicular ad Hoc Networks, Cologne, Germany, 2 September 2005; pp. 20–29. [Google Scholar]
- Yu, Q.; Heijenk, G. Abiding geocast for warning message dissemination in vehicular ad hoc networks. In Proceedings of the IEEE International Conference on Communications Workshops, 2008. ICC Workshops’ 08, Beijing, China, 19–23 May 2008; pp. 400–404. [Google Scholar]
- Soares, V.N.; Rodrigues, J.J.; Farahmand, F. GeoSpray: A geographic routing protocol for vehicular delay-tolerant networks. Inf. Fusion 2014, 15, 102–113. [Google Scholar] [CrossRef]
- Pereira, P.R.; Casaca, A.; Rodrigues, J.J.; Soares, V.N.; Triay, J.; Cervelló-Pastor, C. From delay-tolerant networks to vehicular delay-tolerant networks. IEEE Commun. Surv. Tutor. 2012, 14, 1166–1182. [Google Scholar] [CrossRef]
- Kloiber, B.; Strang, T.; Spijker, H.; Heijenk, G. Improving information dissemination in sparse vehicular networks by adding satellite communication. In Proceedings of the 2012 IEEE Intelligent Vehicles Symposium (IV), Madrid, Spain, 3–7 June 2012; pp. 611–617. [Google Scholar]
- Mittag, J.; Thomas, F.; Härri, J.; Hartenstein, H. A comparison of single-and multi-hop beaconing in VANETs. In Proceedings of the Sixth ACM International Workshop on Vehicular Internetworking; ACM: New York, NY, USA, 2009; pp. 69–78. [Google Scholar]
- Shah, S.A.A.; Ahmed, E.; Xia, F.; Karim, A.; Shiraz, M.; Noor, R.M. Adaptive beaconing approaches for vehicular ad hoc networks: A survey. IEEE Syst. J. 2016, 12, 1263–1277. [Google Scholar] [CrossRef]
- Boukerche, A.; Rezende, C.; Pazzi, R.W. Improving neighbor localization in vehicular ad hoc networks to avoid overhead from periodic messages. In Proceedings of the Global Telecommunications Conference, GLOBECOM 2009, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6. [Google Scholar]
- Schmidt, R.K.; Leinmuller, T.; Schoch, E.; Kargl, F.; Schafer, G. Exploration of adaptive beaconing for efficient intervehicle safety communication. IEEE Netw. 2010, 24, 14–19. [Google Scholar] [CrossRef]
- Tielert, T.; Jiang, D.; Chen, Q.; Delgrossi, L.; Hartenstein, H. Design methodology and evaluation of rate adaptation based congestion control for vehicle safety communications. In Proceedings of the 2011 IEEE Vehicular Networking Conference (VNC), Amsterdam, The Netherlands, 14–16 November 2011; pp. 116–123. [Google Scholar]
- Kloiber, B.; Harri, J.; Strang, T. Dice the TX power—Improving Awareness Quality in VANETs by random transmit power selection. In Proceedings of the 2012 IEEE Vehicular Networking Conference (VNC), Seoul, Korea, 14–16 November 2012; pp. 56–63. [Google Scholar]
- Torrent-Moreno, M.; Mittag, J.; Santi, P.; Hartenstein, H. Vehicle-to-vehicle communication: Fair transmit power control for safety-critical information. IEEE Trans. Veh. Technol. 2009, 58, 3684–3703. [Google Scholar] [CrossRef]
- Burleigh, S.; Hooke, A.; Torgerson, L.; Fall, K.; Cerf, V.; Durst, B.; Scott, K.; Weiss, H. Delay-tolerant networking: An approach to interplanetary internet. IEEE Commun. Mag. 2003, 41, 128–136. [Google Scholar] [CrossRef]
- Fall, K.; Scott, K.L.; Burleigh, S.C.; Torgerson, L.; Hooke, A.J.; Weiss, H.S.; Durst, R.C.; Cerf, V. Delay-Tolerant Networking Architecture RFC 4838. April 2007. Available online: https://tools.ietf.org/html/rfc4838 (accessed on 10 June 2020).
- Scott, K.; Burleigh, S. Bundle Protocol Specification, IETF RFC 5050, Experimental. November 2007. Available online: https://tools.ietf.org/html/rfc5050 (accessed on 10 June 2020).
- Soares, V.N.; Farahmand, F.; Rodrigues, J.J. A layered architecture for vehicular delay-tolerant networks. In Proceedings of the IEEE Symposium on Computers and Communications, ISCC 2009, Sousse, Tunisia, 5–8 July 2009; pp. 122–127. [Google Scholar]
- Benamar, N.; Singh, K.D.; Benamar, M.; El Ouadghiri, D.; Bonnin, J.M. Routing protocols in vehicular delay tolerant networks: A comprehensive survey. Comput. Commun. 2014, 48, 141–158. [Google Scholar] [CrossRef]
- Mangrulkar, R.; Atique, M. Routing protocol for delay tolerant network: A survey and comparison. In Proceedings of the 2010 IEEE International Conference on Communication Control and Computing Technologies (ICCCCT), Ramanathapuram, India, 7–9 October 2010; pp. 210–215. [Google Scholar]
- Spyropoulos, T.; Psounis, K.; Raghavendra, C.S. Spray and wait: An efficient routing scheme for intermittently connected mobile networks. In Proceedings of the 2005 ACM SIGCOMM Workshop on Delay-Tolerant Networking; ACM: New York, NY, USA, 2005; pp. 252–259. [Google Scholar]
- Jain, S.; Fall, K.; Patra, R. Routing in a delay tolerant network. In Proceedings of the 2004 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications, Portland, OR, USA, 30 August–3 September 2004; Volume 34. [Google Scholar]
- Leontiadis, I.; Mascolo, C. GeOpps: Geographical opportunistic routing for vehicular networks. In Proceedings of the 2007 IEEE International Symposium on a World of Wireless, Mobile and Multimedia Networks, Helsinki, Finland, 18–21 June 2007; pp. 1–6. [Google Scholar]
- Zhu, X.; Chen, C.; Pan, Z.; Guan, X. Fast and Reliable Warning Message Dissemination Mechanism in Urban Expressway VANETs. In Proceedings of the IEEE/CIC International Conference on Communications in China, Chengdu, China, 27–29 July 2016; pp. 1–6. [Google Scholar]
- Liu, Y.; Chen, C.; Guan, X. A hovering-based warning information dissemination approach in highway entrances. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 16–20 June 2014; pp. 2719–2724. [Google Scholar]
- Shuai, X. Neighbor Trigger for Hovering Information. J. Phys. Conf. Ser. 2018, 1060, 012039. [Google Scholar] [CrossRef]
- Amjad, Z.; Song, W.C.; Ahn, K.J. Context-Aware Routing for hovering information in Vehicular Ad-Hoc Networks. In Proceedings of the 2016 18th Asia-Pacific Network Operations and Management Symposium (APNOMS), Kanazawa, Japan, 5–7 October 2016; pp. 1–6. [Google Scholar]
- Song, W.C.; Ur Rehman, S.; Awan, M.B. Road Aware Information Sharing in VANETs. KSII Trans. Internet Inf. Syst. 2015, 9. [Google Scholar] [CrossRef]
- PTV Traffic Mobility Logistics. Available online: http://www.ptvamerica.com/vissim.htm (accessed on 10 June 2020).
- Silva, C.M.; Meira, W.; Sarubbi, J.F.M. Non-Intrusive Planning the Roadside Infrastructure for Vehicular Networks. IEEE Trans. Intell. Transp. Syst. 2016, 17, 938–947. [Google Scholar] [CrossRef]
- Mylonas, Y.; Lestas, M.; Pitsillides, A.; Ioannou, P.; Papadopoulou, V. Speed Adaptive Probabilistic Flooding for Vehicular Ad Hoc Networks. IEEE Trans. Veh. Technol. 2015, 64, 1973–1990. [Google Scholar] [CrossRef]

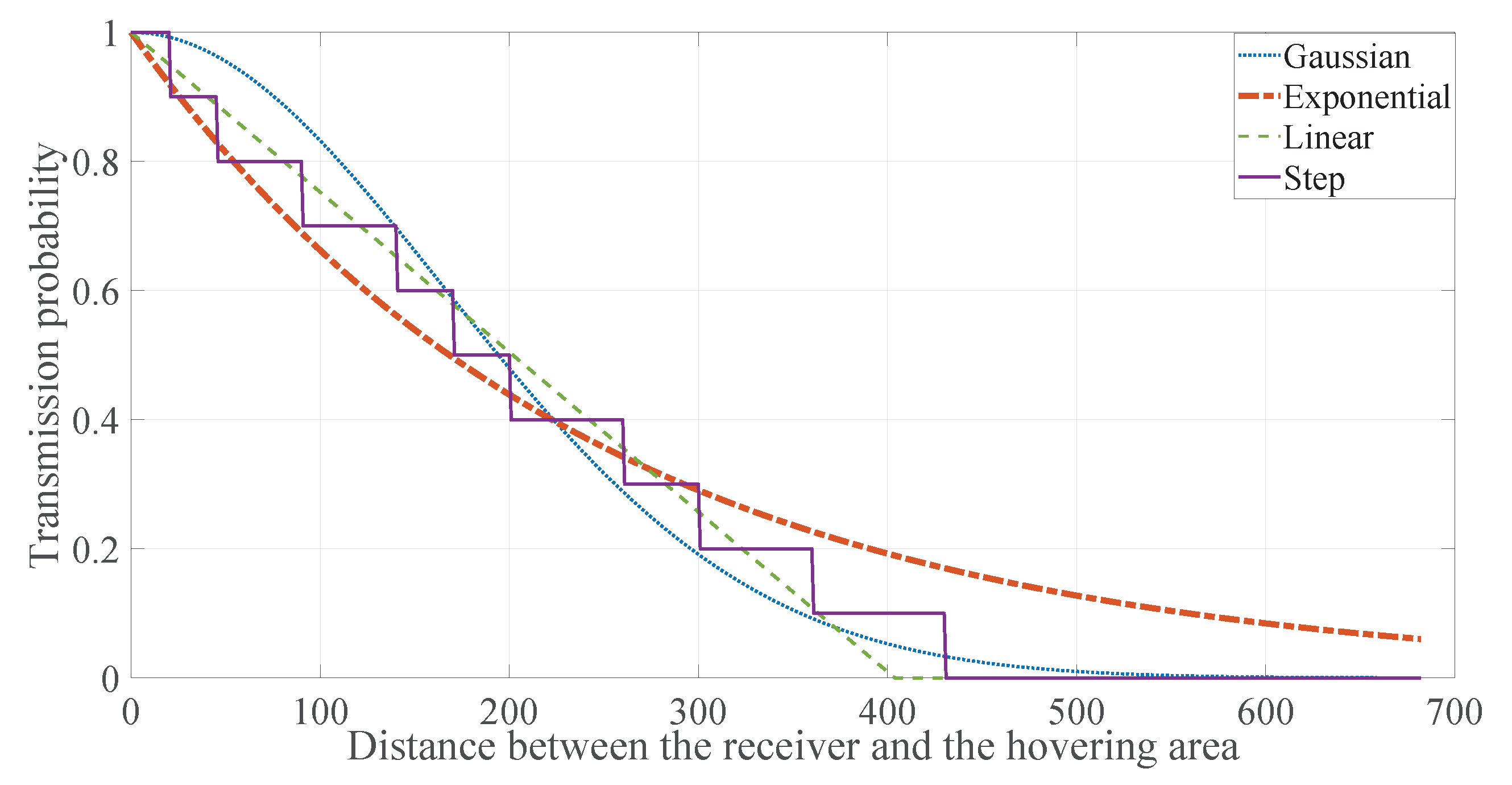
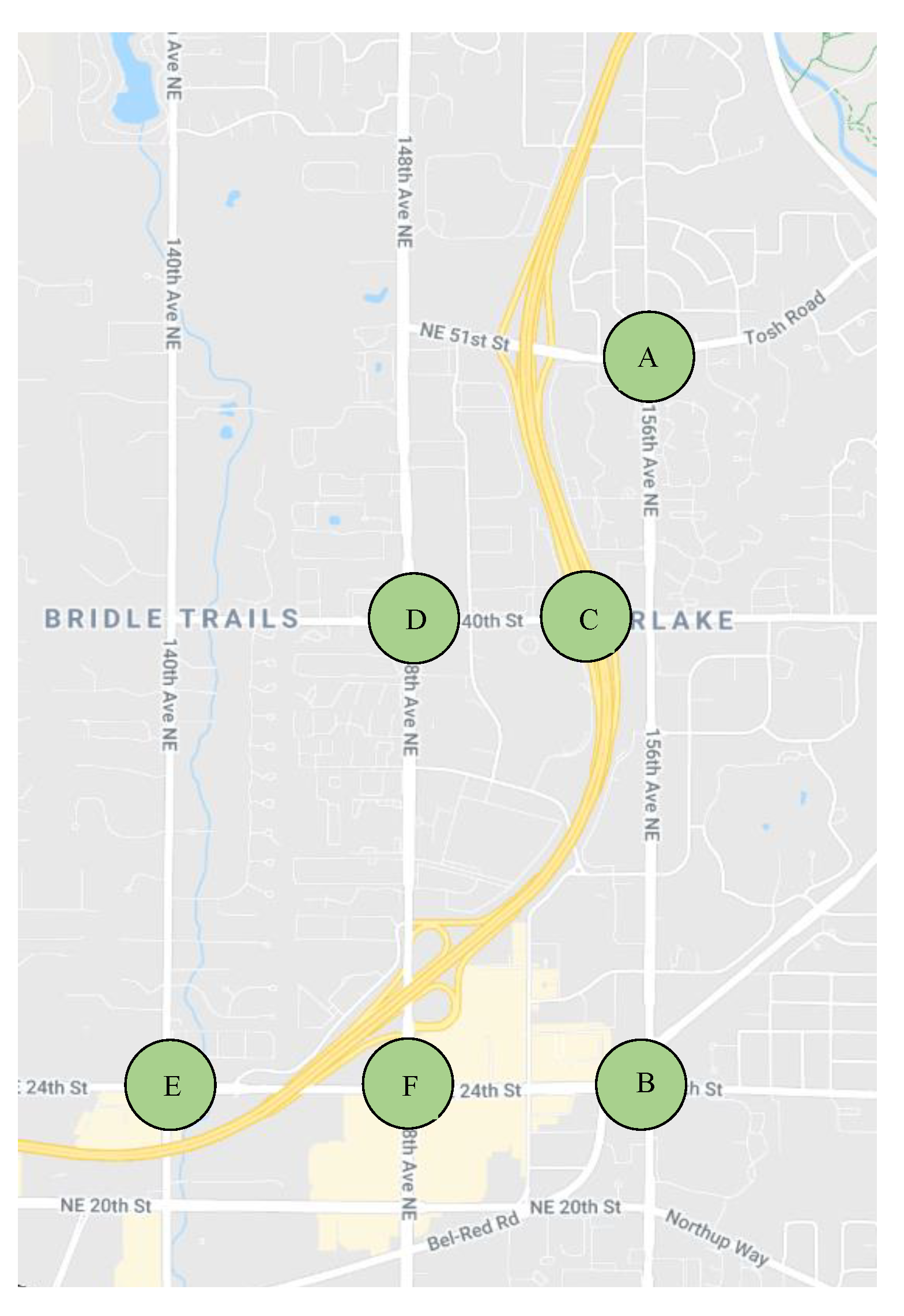
| p | Rebroadcast Probability |
| : rebroadcast probability function | |
| d | distance from the hovering area |
| r | vehicle transmission range |
| R | radius of the hovering area |
| number of vehicles residing in the hovering area | |
| roadway edges | |
| directional roadway link between and | |
| vehicle i | |
| R | radius of the anchor area |
| probability that vehicle i resides in hovering area h | |
| probability that is neighbor of given that the latter is in hovering area h | |
| average number of neighbors | |
| number of neighbors of the jth neighbor |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xeros, A.; Saeed, T.; Lestas, M.; Andreou, M.; Silva, C.M.; Pitsillides, A. Adaptive Probabilistic Flooding for Information Hovering in VANETs. J. Sens. Actuator Netw. 2020, 9, 29. https://doi.org/10.3390/jsan9020029
Xeros A, Saeed T, Lestas M, Andreou M, Silva CM, Pitsillides A. Adaptive Probabilistic Flooding for Information Hovering in VANETs. Journal of Sensor and Actuator Networks. 2020; 9(2):29. https://doi.org/10.3390/jsan9020029
Chicago/Turabian StyleXeros, Andreas, Taqwa Saeed, Marios Lestas, Maria Andreou, Cristiano M. Silva, and Andreas Pitsillides. 2020. "Adaptive Probabilistic Flooding for Information Hovering in VANETs" Journal of Sensor and Actuator Networks 9, no. 2: 29. https://doi.org/10.3390/jsan9020029
APA StyleXeros, A., Saeed, T., Lestas, M., Andreou, M., Silva, C. M., & Pitsillides, A. (2020). Adaptive Probabilistic Flooding for Information Hovering in VANETs. Journal of Sensor and Actuator Networks, 9(2), 29. https://doi.org/10.3390/jsan9020029







