Data Imputation in Wireless Sensor Networks Using a Machine Learning-Based Virtual Sensor
Abstract
:1. Introduction
2. Background
2.1. Learning Systems
2.2. Virtual Sensor
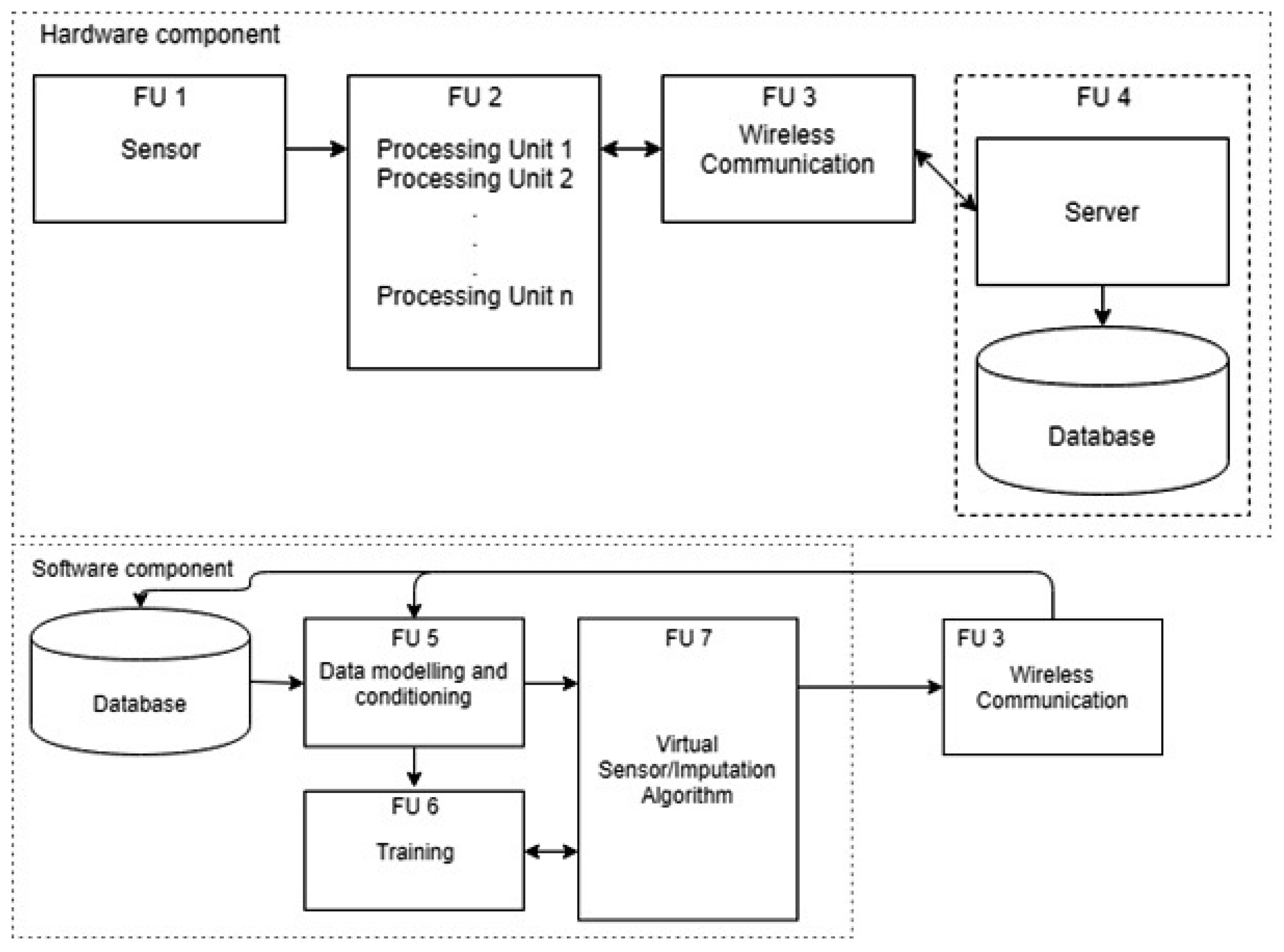
3. System Overview
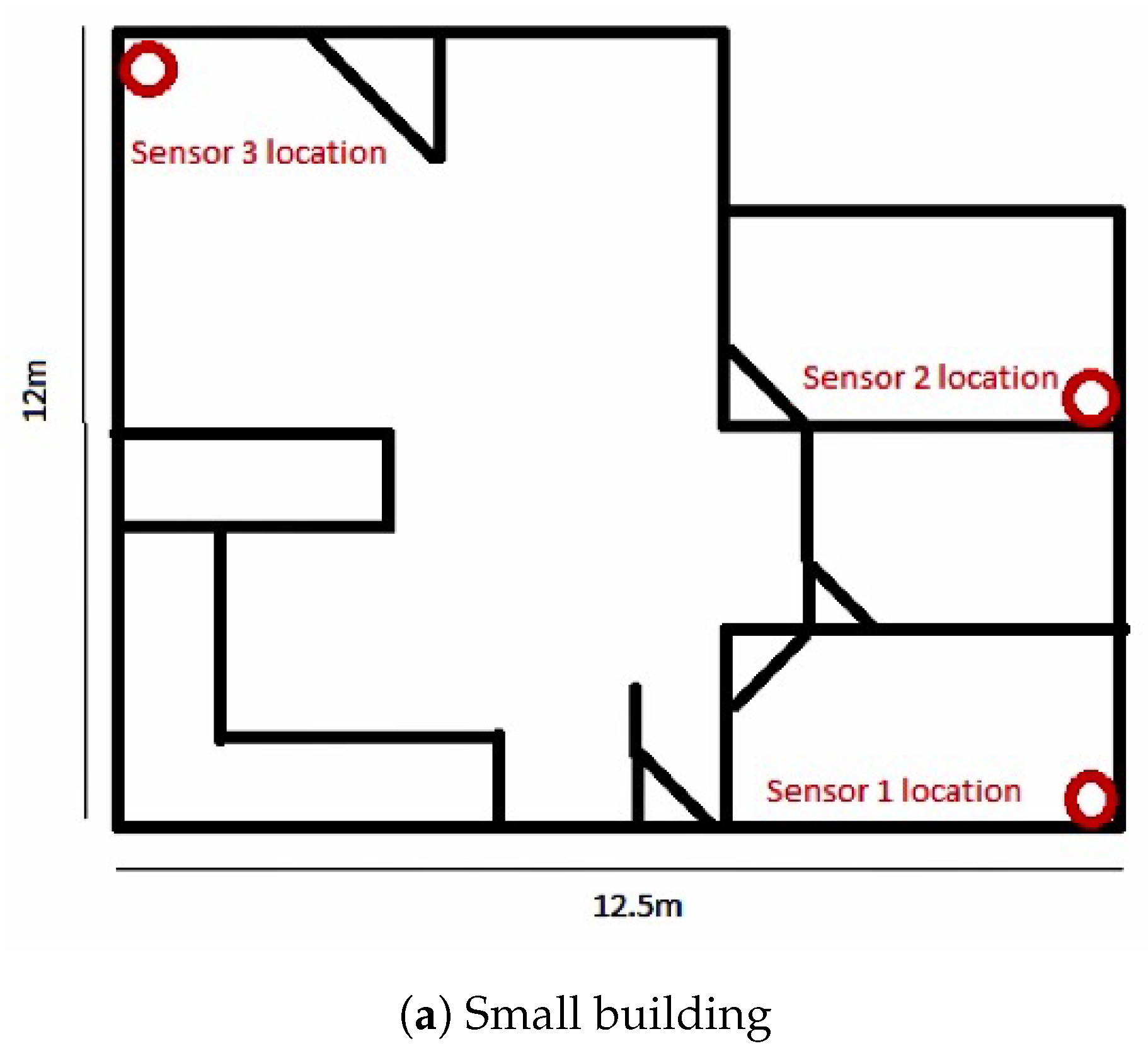
3.1. PhysicalSensor Nodes
3.2. Virtual Sensor
4. System Design
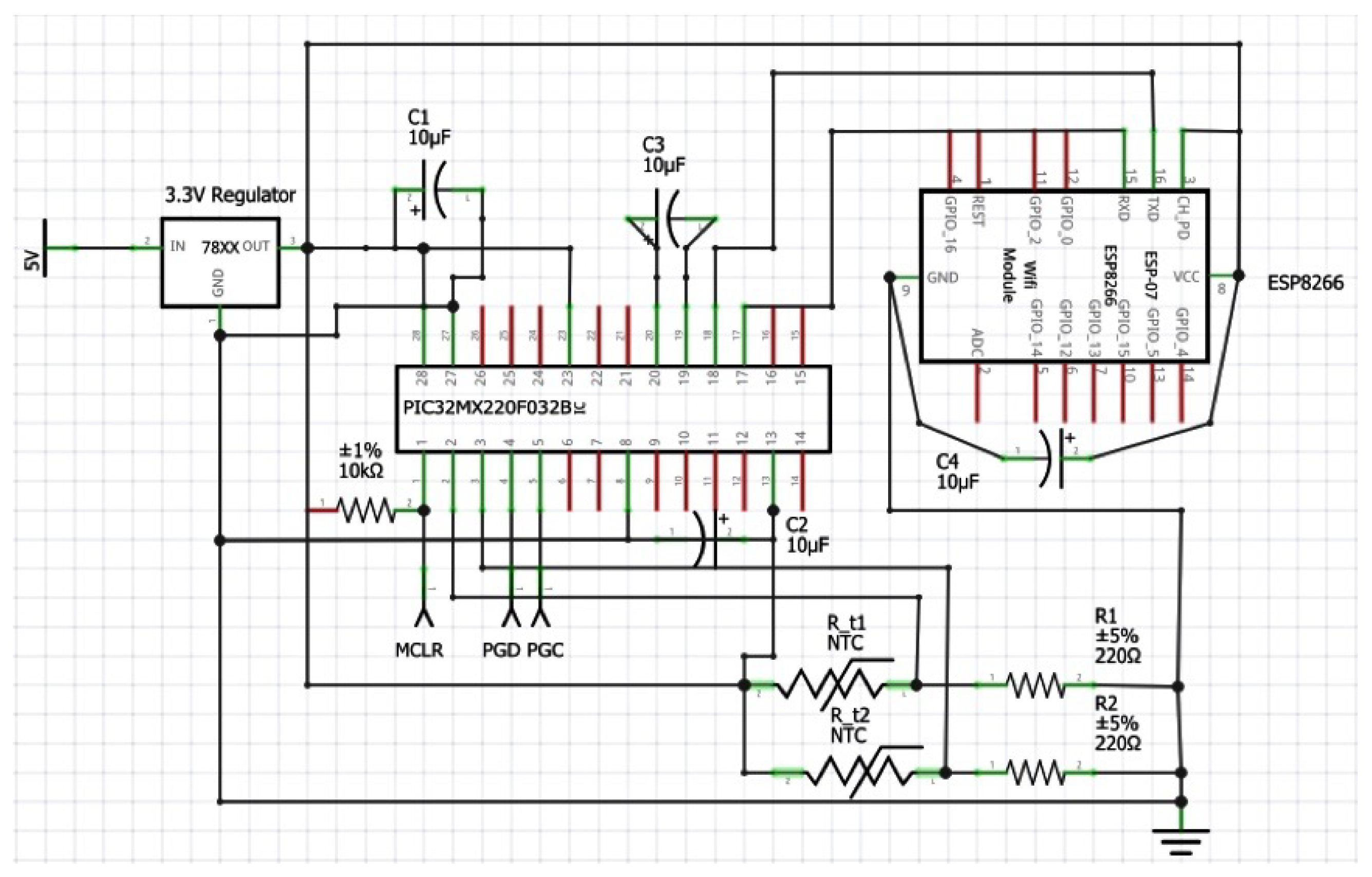
4.1. Sensor Node
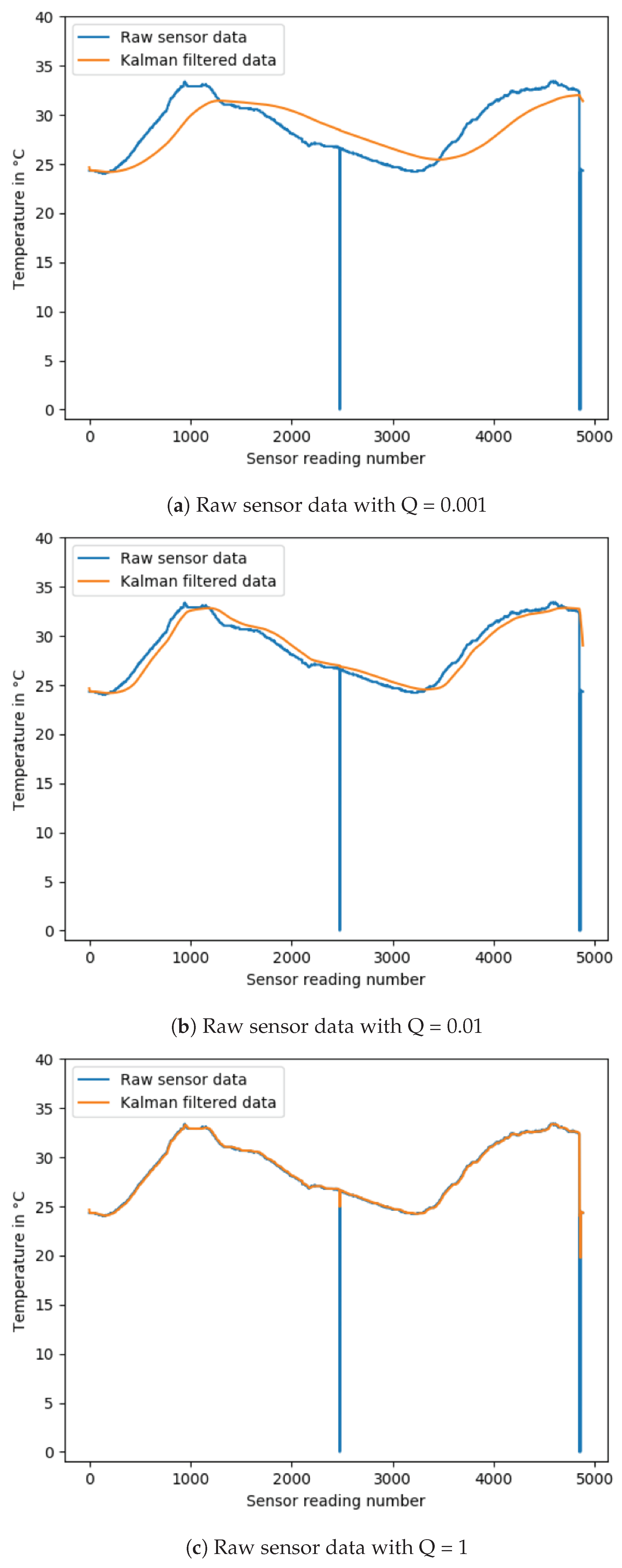
4.2. Scalar Kalman Filter
4.3. Data Imputation
4.3.1. Neural Network Structure
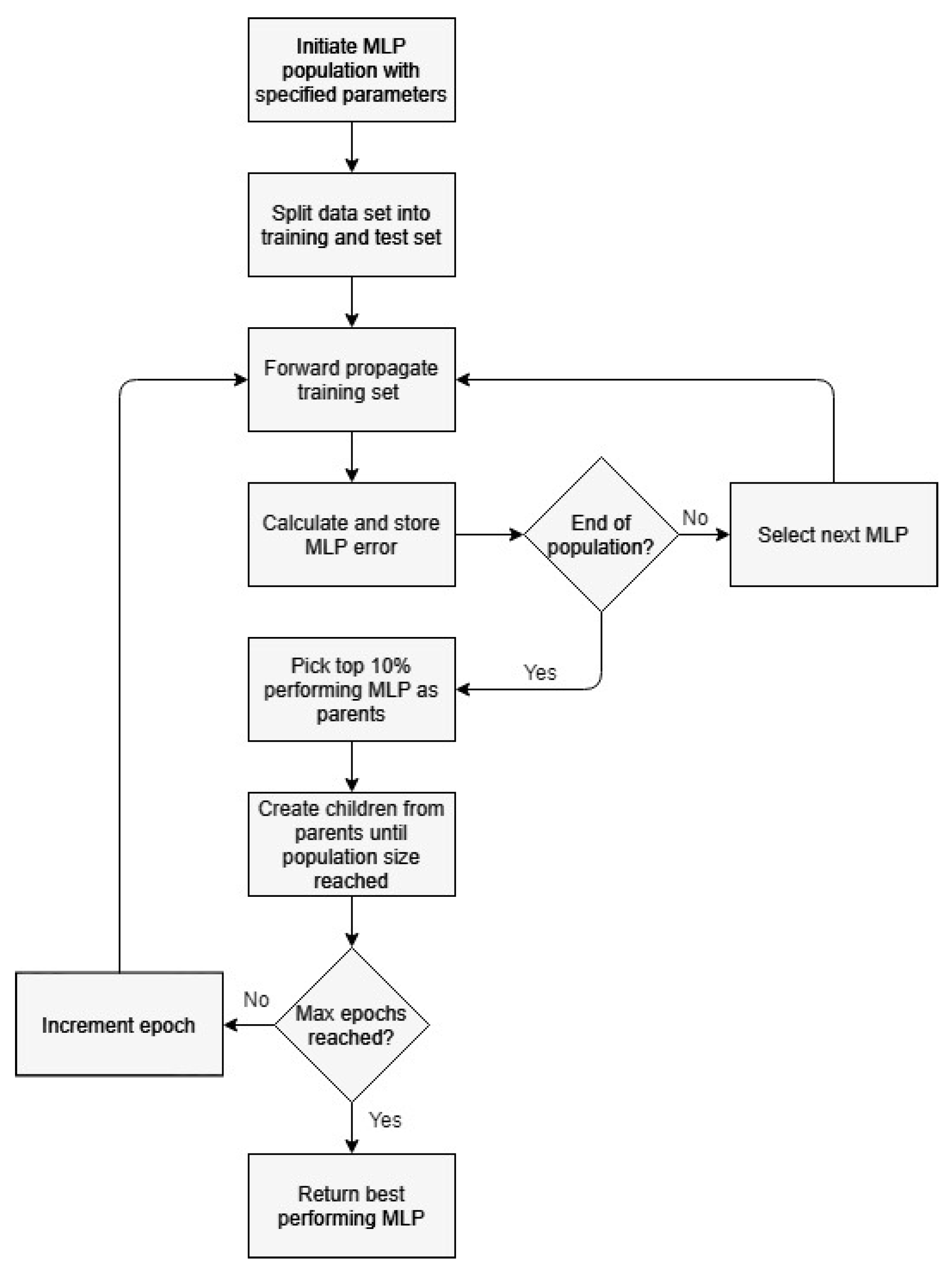
4.3.2. Genetic Algorithm
5. Results
5.1. Virtual Sensor Accuracy
Comparison with State-of-the-Art
5.2. Standard Deviation
5.3. Imputation Time
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kocakulak, M.; Butun, I. An overview of Wireless Sensor Networks towards internet of things. In Proceedings of the IEEE 7th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 9–11 January 2017; pp. 1–6. [Google Scholar]
- Yaqoob, I.; Ahmed, E.; Hashem, I.A.T.; Ahmed, A.I.A.; Gani, A.; Imran, M.; Guizani, M. Internet of things architecture: Recent advances, taxonomy, requirements, and open challenges. IEEE Wirel. Commun. 2017, 24, 10–16. [Google Scholar] [CrossRef]
- Sibanyoni, S.V.; Ramotsoela, D.T.; Silva, B.J.; Hancke, G.P. A 2-D Acoustic Source Localization System for Drones in Search and Rescue Missions. IEEE Sens. J. 2019, 19, 332–341. [Google Scholar] [CrossRef]
- Nkomo, M.; Hancke, G.; Abu-Mahfouz, A.; Sinha, S.; Onumanyi, A. Overlay virtualized wireless sensor networks for application in industrial internet of things: A review. Sensors 2018, 18, 3215. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, W.; Gong, Y.; Liu, X.; Wu, J.; Peng, H. Collaborative energy and information transfer in green wireless sensor networks for smart cities. IEEE Trans. Ind. Inform. 2018, 14, 1585–1593. [Google Scholar] [CrossRef]
- Peng, Y.; Qiao, W.; Qu, L.; Wang, J. Sensor fault detection and isolation for a wireless sensor network-based remote wind turbine condition monitoring system. IEEE Trans. Ind. Appl. 2018, 54, 1072–1079. [Google Scholar] [CrossRef]
- Ramotsoela, D.T.; Hancke, G.P.; Abu-Mahfouz, A.M. A Survey of Anomaly Detection in Industrial Wireless Sensor Networks with Critical Water System Infrastructure as a Case Study. Sensors 2018, 18, 2491. [Google Scholar] [CrossRef] [Green Version]
- Bhushan, B.; Sahoo, G. Recent advances in attacks, technical challenges, vulnerabilities and their countermeasures in wireless sensor networks. Wirel. Pers. Commun. 2018, 98, 2037–2077. [Google Scholar] [CrossRef]
- Ramotsoela, D.T.; Hancke, G.P.; Abu-Mahfouz, A.M. Attack detection in water distribution systems using machine learning. Hum.-Centric Comput. Inf. Sci. 2019, 9, 13. [Google Scholar] [CrossRef]
- Anwar, S.; Mohamad Zain, J.; Zolkipli, M.F.; Inayat, Z.; Khan, S.; Anthony, B.; Chang, V. From intrusion detection to an intrusion response system: Fundamentals, requirements, and future directions. Algorithms 2017, 10, 39. [Google Scholar] [CrossRef] [Green Version]
- Inayat, Z.; Gani, A.; Anuar, N.B.; Anwar, S.; Khan, M.K. Cloud-based intrusion detection and response system: Open research issues, and solutions. Arab. J. Sci. Eng. 2017, 42, 399–423. [Google Scholar] [CrossRef]
- Oke, J.T.; Agajo, J.; Nuhu, B.K.; Kolo, J.G.; Ajao, L. Two Layers Trust-Based Intrusion Prevention System for Wireless Sensor Networks. Adv. Electr. Electron. Eng. 2018, 1, 23–29. [Google Scholar]
- Liu, X.; Liu, A.; Wang, T.; Ota, K.; Dong, M.; Liu, Y.; Cai, Z. Adaptive data and verified message disjoint security routing for gathering big data in energy harvesting networks. J. Parallel Distrib. Comput. 2020, 135, 140–155. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, A.; He, S. A novel joint logging and migrating traceback scheme for achieving low storage requirement and long lifetime in WSNs. AEU-Int. J. Electron. Commun. 2015, 69, 1464–1482. [Google Scholar] [CrossRef]
- Liu, X.; Dong, M.; Ota, K.; Yang, L.T.; Liu, A. Trace malicious source to guarantee cyber security for mass monitor critical infrastructure. J. Comput. Syst. Sci. 2018, 98, 1–26. [Google Scholar] [CrossRef]
- Jerez, J.M.; Molina, I.; García-Laencina, P.J.; Alba, E.; Ribelles, N.; Martín, M.; Franco, L. Missing data imputation using statistical and machine learning methods in a real breast cancer problem. Artif. Intell. Med. 2010, 50, 105–115. [Google Scholar] [CrossRef]
- Sovilj, D.; Eirola, E.; Miche, Y.; Björk, K.M.; Nian, R.; Akusok, A.; Lendasse, A. Extreme learning machine for missing data using multiple imputations. Neurocomputing 2016, 174, 220–231. [Google Scholar] [CrossRef]
- Duan, Y.; Lv, Y.; Liu, Y.L.; Wang, F.Y. An efficient realization of deep learning for traffic data imputation. Transp. Res. Part C Emerg. Technol. 2016, 72, 168–181. [Google Scholar] [CrossRef]
- Liu, Y.; Gopalakrishnan, V. An overview and evaluation of recent machine learning imputation methods using cardiac imaging data. Data 2017, 2, 8. [Google Scholar] [CrossRef] [Green Version]
- Dong, X.; Lin, L.; Zhang, R.; Zhao, Y.; Christiani, D.C.; Wei, Y.; Chen, F. TOBMI: Trans-omics block missing data imputation using a k-nearest neighbor weighted approach. Bioinformatics 2018, 35, 1278–1283. [Google Scholar] [CrossRef]
- Verpoort, P.; MacDonald, P.; Conduit, G.J. Materials data validation and imputation with an artificial neural network. Comput. Mater. Sci. 2018, 147, 176–185. [Google Scholar] [CrossRef] [Green Version]
- Wang, S. Application of self-organising maps for data mining with incomplete data sets. Neural Comput. Appl. 2003, 12, 42–48. [Google Scholar] [CrossRef]
- Sen, J. A Survey on Wireless Sensor Network Security. Int. J. Commun. Netw. Inf. Secur. (IJCNIS) 2009, 1, 55–78. [Google Scholar]
- Ramotsoela, T.D.; Hancke, G.P. Data aggregation using homomorphic encryption in wireless sensor networks. In Proceedings of the Information Security for South Africa (ISSA), Johannesburg, South Africa, 12–13 August 2015; pp. 1–8. [Google Scholar]
- Oehmcke, S.; Zielinski, O.; Kramer, O. Input quality aware convolutional LSTM networks for virtual marine sensors. Neurocomputing 2018, 275, 2603–2615. [Google Scholar] [CrossRef]
- Osman, M.S.; Abu-Mahfouz, A.M.; Page, P.R. A survey on data imputation techniques: Water distribution system as a use case. IEEE Access 2018, 6, 63279–63291. [Google Scholar] [CrossRef]
- Salehi, H.; Das, S.; Chakrabartty, S.; Biswas, S.; Burgueño, R. A machine-learning approach for damage detection in aircraft structures using self-powered sensor data. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Portland, OR, USA, 25–29 March 2017; Volume 10168. [Google Scholar]
- Zhang, S. Nearest neighbor selection for iteratively kNN imputation. J. Syst. Softw. 2012, 85, 2541–2552. [Google Scholar] [CrossRef]
- Song, G.; Rochas, J.; Huet, F.; Magoules, F. Solutions for processing k nearest neighbor joins for massive data on mapreduce. In Proceedings of the 23rd Euromicro International Conference on Parallel, Distributed, and Network-Based Processing, Turku, Finland, 4–6 March 2015; pp. 279–287. [Google Scholar]
- Walters-Williams, J.; Li, Y. Comparative study of distance functions for nearest neighbors. In Advanced Techniques in Computing Sciences and Software Engineering; Springer: Berlin/Heidelberg, Germany, 2010; pp. 79–84. [Google Scholar]
- Sheng, Z.; Wang, H.; Yin, C.; Hu, X.; Yang, S.; Leung, V.C. Lightweight management of resource-constrained sensor devices in internet of things. IEEE Internet Things J. 2015, 2, 402–411. [Google Scholar] [CrossRef]
- Tkáč, M.; Verner, R. Artificial neural networks in business: Two decades of research. Appl. Soft Comput. 2016, 38, 788–804. [Google Scholar] [CrossRef]
- Ramchoun, H.; Idrissi, M.A.J.; Ghanou, Y.; Ettaouil, M. Multilayer Perceptron: Architecture Optimization and Training. Int. J. Interact. Multimed. Artif. Intell. 2016, 4, 26–30. [Google Scholar] [CrossRef]
- Iwashita, Y.; Stoica, A.; Nakashima, K.; Kurazume, R.; Torresen, J. Virtual sensors determined through machine learning. In Proceedings of the World Automation Congress (WAC), Stevenson, WA, USA, 3–6 June 2018; pp. 1–5. [Google Scholar]
- Singh, N.; Javeed, A.; Chhabra, S.; Kumar, P. Missing value imputation with unsupervised kohonen self organizing map. In Emerging Research in Computing, Information, Communication and Applications; Springer: Berlin/Heidelberg, Germany, 2015; pp. 61–76. [Google Scholar]
- Folguera, L.; Zupan, J.; Cicerone, D.; Magallanes, J.F. Self-organizing maps for imputation of missing data in incomplete data matrices. Chemom. Intell. Lab. Syst. 2015, 143, 146–151. [Google Scholar] [CrossRef]
- Madria, S.; Kumar, V.; Dalvi, R. Sensor cloud: A cloud of virtual sensors. IEEE Softw. 2014, 31, 70–77. [Google Scholar] [CrossRef]
- Rallo, R.; Ferré-Giné, J.; Giralt, F. Best feature selection and data completion for the design of soft neural sensors. In Proceedings of the AIChE 2003, 2nd Topical Conference on Sensors, San Francisco, CA, USA, 16–21 November 2003. [Google Scholar]
- Oehmcke, S.; Zielinski, O.; Kramer, O. Recurrent neural networks and exponential PAA for virtual marine sensors. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 4459–4466. [Google Scholar]
- D’Aniello, G.; Gaeta, M.; Hong, T.P. Effective quality-aware sensor data management. IEEE Trans. Emerg. Top. Comput. Intell. 2018, 2, 65–77. [Google Scholar] [CrossRef]
- Siddique, M.; Tokhi, M. Training neural networks: Backpropagation vs. genetic algorithms. In Proceedings of the International Joint Conference on Neural Networks, Washington, DC, USA, 15–19 July 2001; pp. 2673–2678. [Google Scholar]
- Chen, C. Evaluation of resistance–temperature calibration equations for NTC thermistors. Measurement 2009, 42, 1103–1111. [Google Scholar] [CrossRef]
- Mitchell, M. Genetic Algorithms: An Overview. In An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998; pp. 2–26. [Google Scholar]

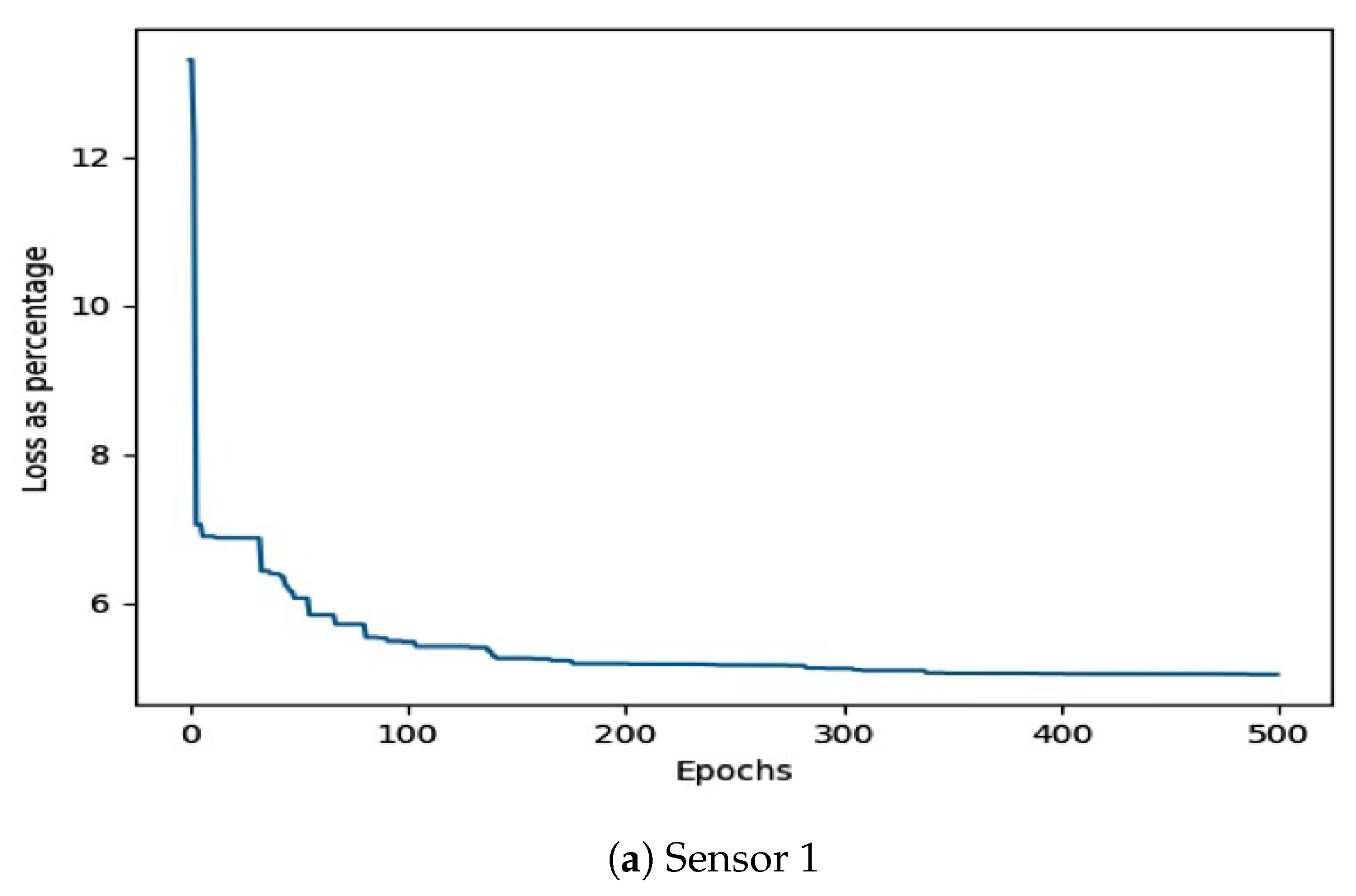
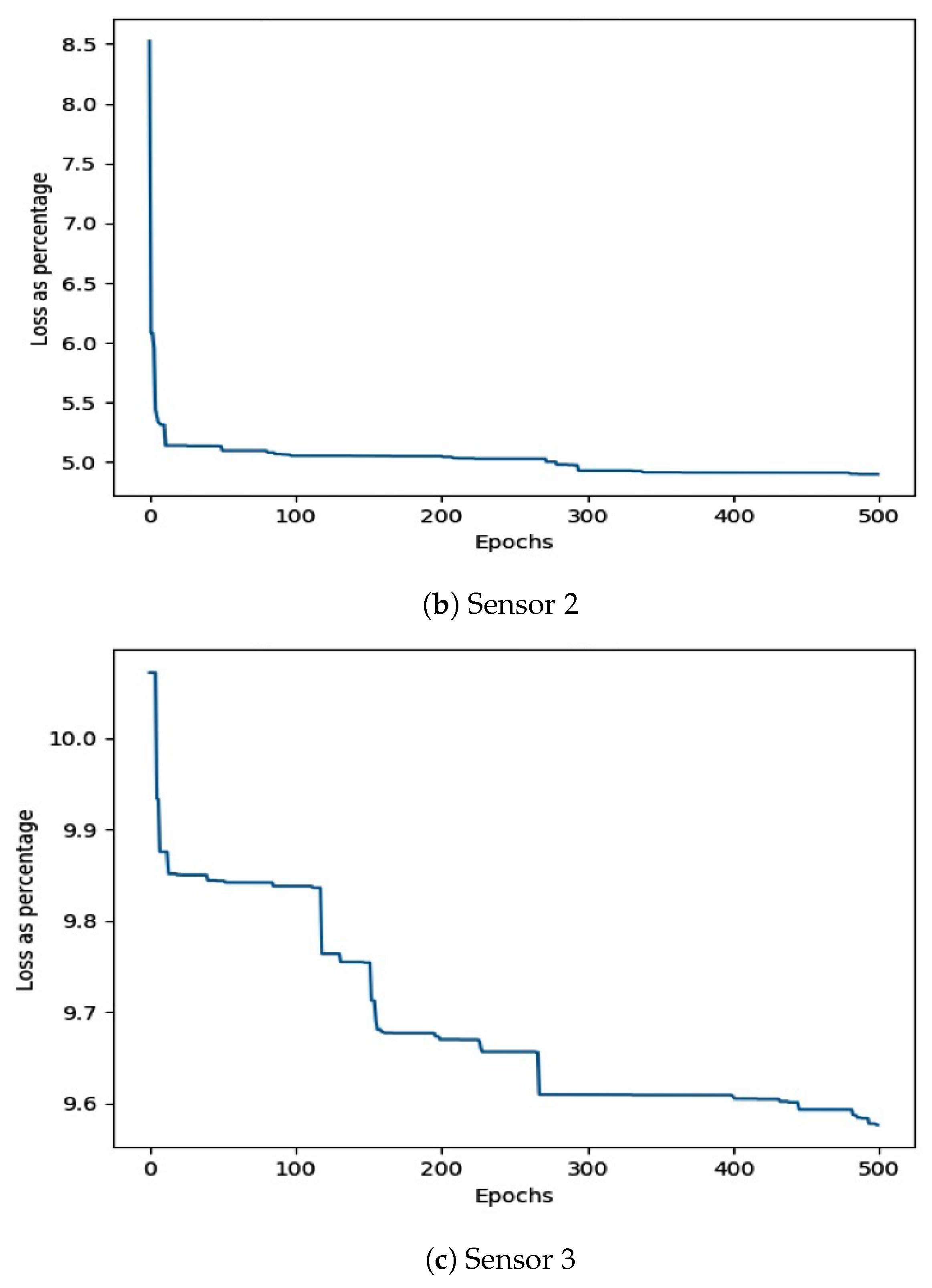



| Building | VS # | Min acc % | Max acc % | Avg acc % |
|---|---|---|---|---|
| VS 1 | 78.96847 | 99.99847 | 94.03248 | |
| Small | VS 2 | 92.47204 | 99.99996 | 97.07589 |
| VS 3 | 86.52291 | 99.99825 | 95.15422 | |
| VS 1 | 85.52389 | 99.99967 | 94.70205 | |
| Large | VS 2 | 88.34544 | 99.99998 | 96.54874 |
| VS 3 | 87.90576 | 99.99992 | 96.28131 |
| Building | VS # | MLP % | kNN % | LinReg % |
|---|---|---|---|---|
| VS 1 | 94.03248 | 91.34519 | 91.80413 | |
| Small | VS 2 | 97.07589 | 92.55777 | 93.88260 |
| VS 3 | 95.15422 | 81.60299 | 79.39729 | |
| VS 1 | 94.70205 | 78.94263 | 71.84740 | |
| Large | VS 2 | 96.54874 | 85.37011 | 86.25564 |
| VS 3 | 96.28131 | 81.38311 | 81.31372 |
| Building | VS # | STD DEV (°C) |
|---|---|---|
| VS 1 | 1.226344 | |
| Small | VS 2 | 0.518652 |
| VS 3 | 0.721729 | |
| VS 1 | 0.964535 | |
| Large | VS 2 | 0.784815 |
| VS 3 | 0.692576 |
| Location | VS # | min (ms) | max (ms) | avg (ms) |
|---|---|---|---|---|
| VS 1 | 382 | 588 | 413 | |
| Node | VS 2 | 391 | 547 | 412 |
| VS 3 | 378 | 550 | 412 | |
| VS 1 | 9.322 | 9.366 | 9.379 | |
| Server | VS 2 | 9.343 | 9.392 | 9.379 |
| VS 3 | 9.327 | 9.374 | 9.379 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matusowsky, M.; Ramotsoela, D.T.; Abu-Mahfouz, A.M. Data Imputation in Wireless Sensor Networks Using a Machine Learning-Based Virtual Sensor. J. Sens. Actuator Netw. 2020, 9, 25. https://doi.org/10.3390/jsan9020025
Matusowsky M, Ramotsoela DT, Abu-Mahfouz AM. Data Imputation in Wireless Sensor Networks Using a Machine Learning-Based Virtual Sensor. Journal of Sensor and Actuator Networks. 2020; 9(2):25. https://doi.org/10.3390/jsan9020025
Chicago/Turabian StyleMatusowsky, Michael, Daniel T. Ramotsoela, and Adnan M. Abu-Mahfouz. 2020. "Data Imputation in Wireless Sensor Networks Using a Machine Learning-Based Virtual Sensor" Journal of Sensor and Actuator Networks 9, no. 2: 25. https://doi.org/10.3390/jsan9020025
APA StyleMatusowsky, M., Ramotsoela, D. T., & Abu-Mahfouz, A. M. (2020). Data Imputation in Wireless Sensor Networks Using a Machine Learning-Based Virtual Sensor. Journal of Sensor and Actuator Networks, 9(2), 25. https://doi.org/10.3390/jsan9020025






