1. Introduction
In the modern era of Industry 4.0 and Smart Manufacturing, concepts and paradigms such as Cloud Computing and Internet of Things (IoT) are becoming more important by enabling innovations and advances in many domains [
1,
2,
3]. As one of the recent examples, the cloud computing as a promising technological paradigm, plays a significant role in developing future large-scale complex smart cities applications [
4].
By utilizing the cloud computing concept, distributed, scalable and elastic computing resources are provided to the end-users over high speed computer networks, such as the Internet. Resources in cloud environments can be anything, from central processing units (CPUs), memory and storage to development platforms and applications. A cloud computing paradigm enables efficient utilization of available physical resources through the virtualization technology, where different clients share the same underlying physical hardware infrastructure.
Scheduling is one of the most important challenges and topics in the cloud computing domain. In order to provide and to maintain guaranteed quality of service (QoS) to the end-users, cloud systems should utilize algorithms that map tasks (cloudlets) submitted by the clients to the available resources in an efficient manner. With the increasing number of resources and submitted tasks, many potential mapping combinations exist and, in large-scale cloud environments, the cloudlet scheduling problem belongs to the category of NP (nondeterministic polynomial time) hard optimization. No algorithms that are able to generate optimal solutions within the polynomial time exist for such kind of problems.
For solving a task scheduling problem in cloud environments, exhaustive search methods and deterministic algorithms are not able to generate optimal or suboptimal results within a reasonable computational time, and, for this reason, these approaches can not be applied efficiently in this domain. The best way to tackle cloudlet scheduling problem is by utilizing heuristic and metaheuristic based techniques that do not guarantee finding the optimal solution, but are able to obtain satisfying (near optimal) solutions within the polynomial time.
Since the metaheuristics can efficiently handle massive search space, and, since they proved to be robust NP-hard problem solvers [
5,
6], in the area of tasks cloud scheduling, metaheuristic methods like swarm intelligence may obtain better results than other proposed approaches. Moreover, due to the fact that many real-life problems such as wireless sensor networks (WSNs) node localization, transportation problems, portfolio optimization, etc., can be modeled as optimization tasks, metaheuristic algorithms are widely implemented for addressing many practical NP-hard challenges, as can be seen from the literature.
1.1. Cloud Computing Definitions and Concept
In the era of advancement of networking and communication, cloud computing technology, as an emerging paradigm demonstrates how the utilization of the right resources and the available processing power can lead to the infrastructure that facilitates delivery of hardware and software resources over the network that satisfies end-users’ requirements. Due to its efficiency in providing computing resources, as well as for a variety of delivered services, the cloud computing has been widely adopted by the information technology (IT) industry and by the academic and research communities around the world.
Many definitions that portray the significance of cloud computing paradigm exist, and one of them states that the cloud computing presents an elastic and distributed system in which computing resources such as processing power and storage space, information and software, are propagated through the network and delivered in the distributed location in the cloud where it can be shared and obtained [
7]. Another definition states that the cloud represents a collection of heterogeneous hardware and software resources that enables services to the cloud users, hence the fact that is not necessary the cloud users to have their own hardware and software infrastructure [
8]. One of the most important definitions of cloud computing that is accepted by many major global cloud vendors is provided by the National Institute of Standards and Technology (NIST). According to this definition, cloud computing can be described as a model for enabling ubiquitous and convenient on-demand network access to a shared pool of configurable computing resources (e.g., networks, servers, storage, applications, and services) that can be rapidly provisioned and released with minimal management effort or service provider interaction [
9].
Two state-of-the-art technologies that enabled the concept of cloud computing and proper availability and resource management are virtualization and hyper-converged infrastructure (HCL). Virtualization is technology that enables simultaneous execution of different tasks by the virtual machines (VMs) that are decoupled from the underlying physical hardware infrastructure. The hypervisor, or virtual machine monitor (VMM), is a software component that performs management and control operations of the virtual environment by creating, managing and terminating VMs. The HCL is computing infrastructure that virtualizes components of the traditional physical hardware infrastructure by utilizing the “defined by the software” concept. This platform at a bare minimum includes hypervisor, software-defined networks (SDNs) and software-defined storage (SDS).
The cloud service provider (CSP) is able to deliver software and hardware computing services and resources to the end-users in an efficient and cost-effective way via the communication network by exploiting the HCL and virtualization technologies. Some of the most important features of cloud computing include: scalability of tasks and available resources, dynamic provisioning, load balancing, fault tolerance, on time resource execution, and resources interoperability [
10].
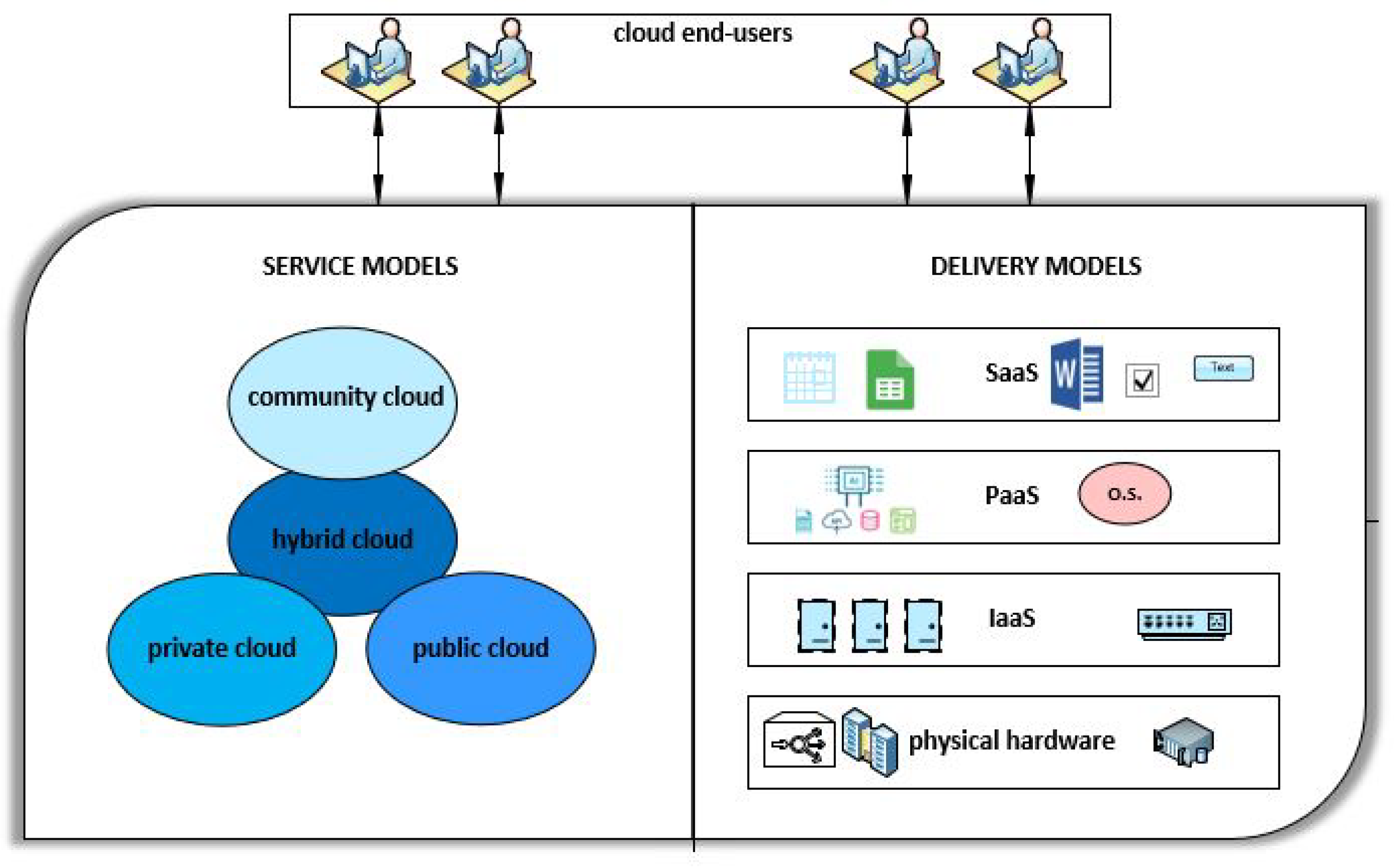
When overviewing a cloud computing concept, two most significant taxonomies of cloud computing models should be mentioned. First, categorization uses the criteria of service models and divides cloud computing into three base groups: software as a service (SaaS), platform as a service (PaaS) and infrastructure as a service (IaaS). The SaaS delivers a software that is available in a form of hosted service, to the end-users. The PaaS provides platform (operating systems and development environments), where cloud users are able to develop, install and configure their own applications, while the PaaS distributes the whole computing infrastructure, such as processing power, networking and storage, to the cloud system users.
The second taxonomy makes a distinction between public, private, community and hybrid clouds, by utilizing the criteria of delivery models. The accent here is not on the ownership over cloud resources, rather on a party who exploits them. As an example, in private cloud environments, the whole cloud system is being exploited by one single entity (individual or corporate user), while the owner of the infrastructure may be the party who utilizes it, or the CSP. On the contrary, the public cloud is shared among many parties. The most prominent examples of public cloud include Amazon Web Services Elastic Compute Cloud - AWS EC3 (Amazon.com, Inc, Seattle, Washington, USA), Microsoft Azure (Microsoft Corporation, Redmond, Washington, USA) and Oracle Cloud (Oracle Corporation, Redwood Shores, California, USA).
Cloud service and delivery models are depicted in
Figure 1.
1.2. Management and Economy Perspectives of Cloud Computing
Considering the fact that the research that was presented in this paper has both theoretical and practical (management) contributions (please refer to
Section 1.3) from the domain of cloud computing, in this subsection, we provide some more details regarding management and economic cloud computing perspectives.
First, we provide data considering the size of cloud computing market, and then we try to identify the main driving factors that have influence on the rapid growth in popularity, as well as in the usage of cloud computing services globally.
Since this is very short overview of management and economical cloud computing aspects, we encourage readers to find additional information in [
11,
12,
13,
14,
15].
The cloud computing market, as well as the adoption of this model by small and medium-sized enterprises (SMEs), is rapidly growing. According to the Gartner, the public cloud world-wide revenue was 182.4 billions of U.S. dollars in 2018, with the prediction that its value will reach 214.3 billions of U.S. dollars by the end of 2019 [
16].
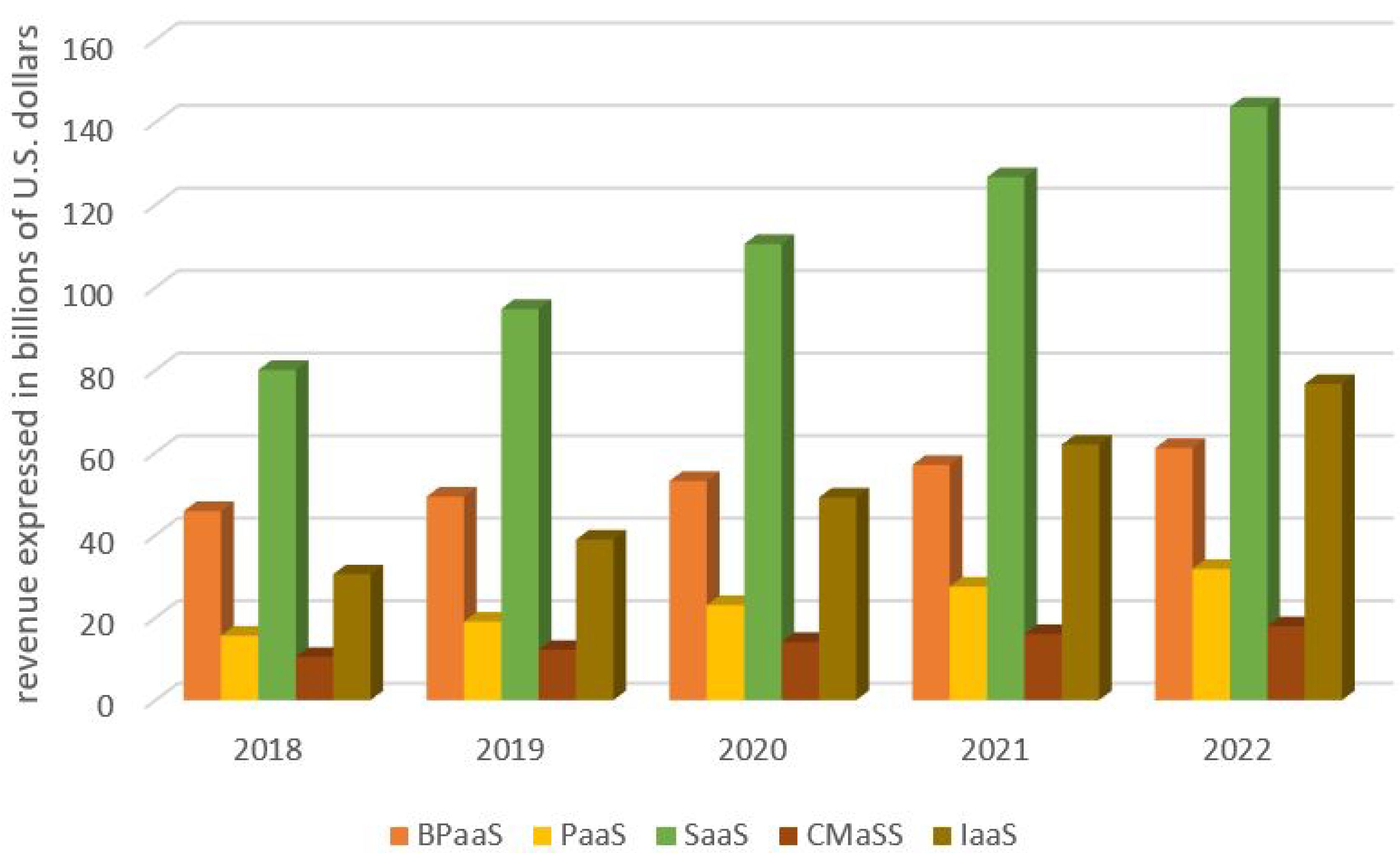
Predictions of the company Gartner about the size of world-wide public cloud market up to the year 2022, by categories of public cloud services, expressed in billions of U.S. dollars, are shown in
Figure 2.
In addition, the cloud computing market and the adoption of this concept by the enterprises is rapidly growing in the European Union (EU) countries. According to the most recent study conducted by the Eurostat, in year 2018, 26% of the EU enterprises used cloud computing for email services and for storing e-documents, while 55% of them utilized some of the advanced cloud services, such as financial and accounting applications and customer relationship management (CRM) systems. In addition, according to the Eurostat, more enterprises used public cloud services (18%) compared to the private cloud (11%) [
17].
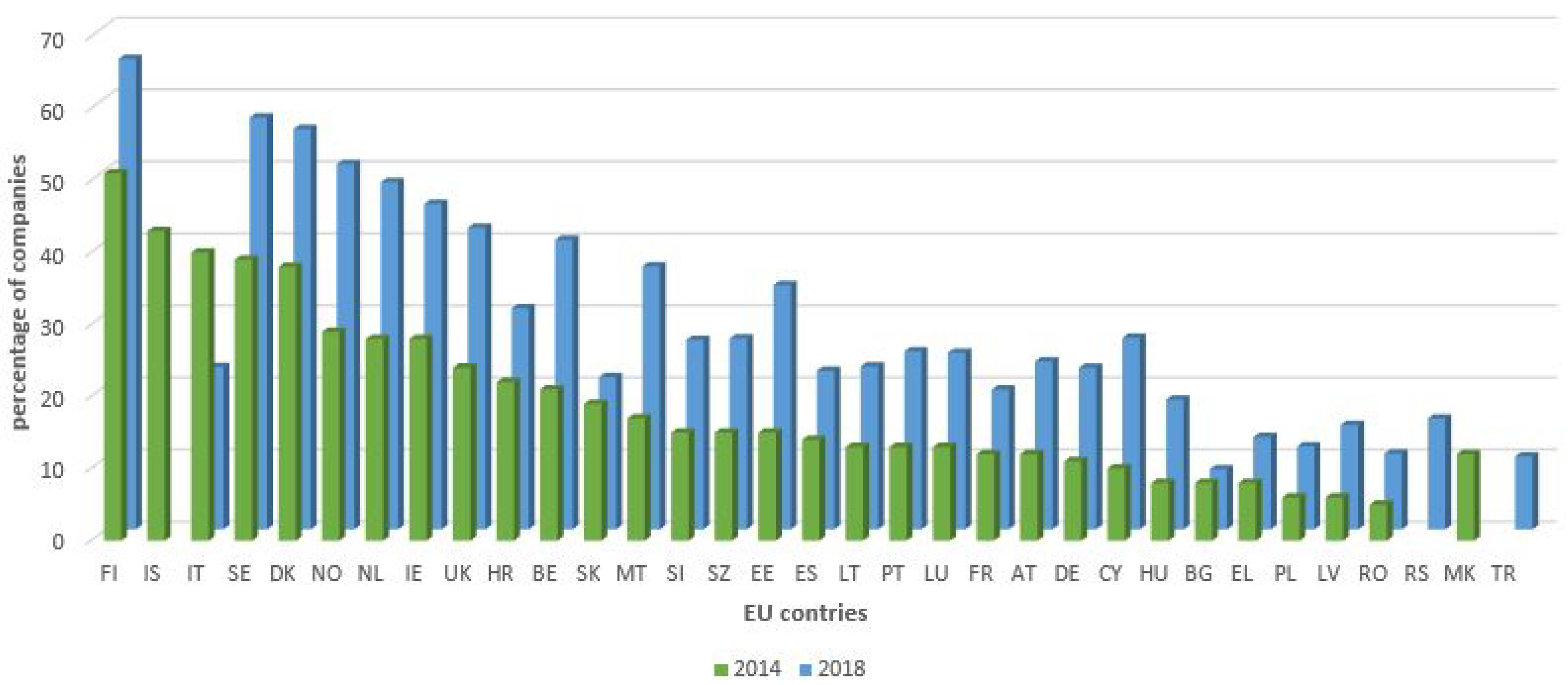
It is important to mention that, in the year 2018, the use of cloud computing, particular by large enterprises, increased by 21%, when compared to the year 2014. In
Figure 3, we show graph that visualizes the usage of cloud computing in the year 2014 vs. the year 2018 by EU countries, expressed in the percentage of companies that utilize this model. We note that, since the data for some countries were not available for both years, some metrics are omitted.
For the sake of better understanding cloud computing, it is important to realize reasons that drove its popularity and factors that have influenced the intention to use this relatively new model of delivering computing resources. An excellent research study of the drivers and barriers of the cloud computing in SMEs, from the position of the EU may be found in [
18]. According to this study, cost savings and simplifications of the technological infrastructure represent two of the most decisive factors for the increasing use of cloud computing concept. In addition, according to the same study, the lack of standardization and the need for new professionals and the emergence of distrust are some of the barriers to its adoption [
18].
The main motivation behind rapid growth in utilization and popularity of cloud computing concept are generated benefits, particularly for business and economy. According to [
19], some of the most important benefits that cloud computing accomplishes for business may be defined as: software and hardware cost reductions, maintenance and operational costs reduction, access to services from any place in the world, market-oriented architecture, potential to transform business process, ability to establish competitive advantage, easy-to-use cloud-based solutions, etc.
Based on the viewpoint of this paper’s authors, key benefits that an enterprise may acquire when adopting cloud infrastructure can be summarized as: cost reduction and efficiency, scalability, data security, disaster recovery (DR), mobility and competitive advantage.
By using the cloud infrastructure, enterprises do not suffer from large initial capital investments when buying hardware, software and other equipment. In addition, costs related facilities, utilities, buildings and IT staff are drastically reduced. Due to the benefits of virtualization technology, efficiency and the degree of utilization of available computing resources is significantly enhanced, which leads to the further decrease in costs. Another cost related aspect of using the cloud are costs related to downtime. In the standard IT environments, downtime happens from time to time, and companies waste large amounts of money on fixing potential issues. On the contrary, downtime is rare in cloud computing environments.
Traditional IT infrastructure is organized in so-called “IT silos”, which function as separate units. This may lead to the redundant hardware and under optimal computing resources utilization. In such environments, it is very difficult to scale up/down computing infrastructure. The cloud environment enables enterprises to efficiently and quickly scale up or down their IT departments according to business needs and demands.
In the modern era of cyber attacks, security of the data and systems is one of the major issues. The SMEs in most cases can not afford to buy sophisticated security appliances, and their systems and the data are most of the time under great risk. However, since CSPs offer state-of-the-art security appliances to their users, the SMEs are in a position to obtain sophisticated security devices with relatively low costs.
Many CSP offer to their clients advanced DR systems with low costs. Many organization that use traditional IT infrastructure can not afford to implement DR mechanisms and frequently suffer data outages. Cloud-based services provide quick data recovery for all kinds of emergency scenarios—from natural disasters to power outages.
Another great benefit of cloud computing is mobile access to enterprise services via smartphones and other portable devices. In this way, the enterprise is more flexible and can easily adapt to new tasks and objectives.
Finally, by employing cloud computing concept and models, and by combining together all above-mentioned cloud computing benefits, an enterprise may accomplish and maintain competitive edge on the market. Many companies have already realized this, and the adoption of cloud services rapidly increases every year.
1.3. Research Question, Objectives, Contributions and Paper’s Structure
By reviewing modern literature, it can be concluded that the swarm intelligence metaheuristics have been successfully applied for tackling different kinds of job (cloudlet) scheduling problems in cloud computing environments [
20,
21]. The basic objective, as well as the focus, of the research that is presented in this paper is to establish further improvements in solving cloud task scheduling problems by utilization of swarm algorithms.
With the goal of achieving further improvements and efficiencies in cloudlet scheduling in terms of the makespan objective, we have implemented two versions of the monarch butterfly optimization (MBO) swarm metaheuristics, one original and one hybridized. The MBO algorithm was recently proposed by Wang, Deb and Cui [
22], and no implementations for cloud computing task scheduling of the MBO algorithm exist in the literature. By applying a hybridized MBO approach, we have improved the results that have previously been obtained by other metaheuristics that were tested on the same problem instance.
The hybridized monarch butterfly optimization approach, as well as adaptations of any monarch butterfly optimization version for cloudlet scheduling problem, could not be found in the literature survey.
It should be noted that the authors have been analyzing and performing experiments with the MBO algorithm before, and the research presented in this paper is the result of authors’ previous experience in this domain. For example, in ref. [
23], the authors have shown an adapted version of the basic MBO algorithm for radio frequency identification (RFID) network planning problem and, in ref. [
24], adaptations of the MBO for WSNs localization problem were proposed.
The research question addressed in the conducted research can be formulated as follows: “Is it possible to achieve further enhancements in tackling cloudlet scheduling problem by employing swarm intelligence metaheuristics”?
Research that is presented in this paper is oriented towards two basic objectives: enhancements by hybridization of the original MBO algorithm, and improvements in solving cloudlet scheduling problem by adapting and applying a hybridized MBO implementation to this problem.
Research methodology that was utilized is simulation in the standard environment and with the typical benchmark instances. Only by using standardized methodology could we establish and compare performance of our methods with other approaches in a realistic way.
In order to test robustness of the enhanced algorithm, we first performed tests on standard unconstrained benchmarks and presented comparative analysis with the original implementation. Later, in the second simulation suite, we conducted experiments for the practical cloudlet scheduling problem by utilizing artificial and real data sets.
Simulation and practical experiments are conducted in a robust and scalable environment of the CloudSim framework. All of the details, including the settings of the algorithms’ control parameters, simulation framework settings and employed data sets are fully provided in this paper, so the researcher who wants to implement proposed approaches and to run simulations has more than enough information to do this on her/his own.
In general, a contribution of this paper is threefold: improvements in solving task scheduling problems in cloud environments by minimizing the makespan objective, implementations of the original and hybridized MBO algorithm for cloudlet scheduling and improvements by hybridization of the original MBO approach.
More precisely, contributions of this paper fall into the domain of algorithm improvements and in the domain of cloud management enhancements. By hybridizing the original MBO, we enhanced solutions’ quality and convergence, as it was proved in
Section 5. Contributions in the area of cloud management encompass better utilization of cloud infrastructure by establishing lower values of the makespan objective and the degree of imbalance metric than other methods that were tested on the same instance of cloudlet scheduling problem. Better utilization of cloud hardware and lower makespan value in turn have a positive influence on the overall cloud infrastructure and maintenance costs, QoS and end-users’ satisfaction.
Limitations of the presented research refer to the following: first, only a few data sets from the real-world cloud environments are available and, secondly, performance could be evaluated only in simulated environments, since the experiments in real conditions would require large financial investments.
2. Review of Swarm Intelligence Metaheuristics and Its Applications in Cloud Computing
Metaheuristics can be in general divided into two basic groups: those that are inspired by the nature, and those that are not inspired by the nature. Nature-inspired (bio-inspired) metaheuristics can be further categorized as evolutionary algorithms (EA) and swarm intelligence. One of the most representative examples of EA is a genetic algorithm (GA). The applications of the GA for cloud computing can be found in the literature survey [
25,
26,
27].
Swarm intelligence is population-based, stochastic and iterative approaches that try to improve potential problem solutions in a predefined number of cycles (iterations). The swarm is composed of relatively simple and unsophisticated agents that collectively exhibit intelligent behavior and characteristics. According to the survey of modern literature sources, swarm algorithms have many implementations for the cloud computing domain [
28,
29].
The particle swarm optimization (PSO) is one of the best known swarm intelligence representatives [
30]. This algorithm was modified/improved and adapted for tackling many real-world optimization problems [
31,
32,
33]. The PSO metaheuristics has also implementations for various problems from cloud computing. For example, in [
25], the authors proposed a new model to optimize virtual machines selection in cloud-IoT health services applications and adapted original PSO and parallel PSO (PPSO) for tackling this kind of problem. In addition, in [
8], by utilizing the PSO-based scheduling (PSO-COGENT) algorithm, makespan, execution cost and the energy consumption of cloud data centers, considering deadline as a constraint, were successfully optimized.
Another well-known swarm intelligence metaheuristics is artificial bee colony (ABC) that performs the search process by simulating honey bee swarms [
34]. The ABC approach was successfully tested on a wider set of benchmark functions [
35,
36] and it also has many implementations for practical NP-hard tasks [
37,
38,
39,
40]. Moreover, the ABC algorithm has been applied to problems from the cloud computing field [
41]. As one representative example, in [
42], the authors developed a state-of-the-art hybrid ABC approach that managed to substantially reduce energy consumption while performing VM migration.
A firefly algorithm (FA), which was devised by Yang in 2009 [
43], was inspired by the flashing behavior of the firefly insects. By examining available literature sources, it can be seen that the FA could be successfully adapted for different types of practical NP-hard challenges [
6,
44,
45,
46,
47]. This approach was also tested on standard benchmark problems in modified [
48] and hybridized versions [
49]. The FA algorithm was also applied to cloud computing problems, such as load balancing [
50] and workflow scheduling [
51].
Another two widely employed swarm intelligence metaheuristics are cuckoo search (CS), devised by Yang and Deb [
52], and the bat algorithm (BA), created by Yang [
53]. Both metaheuristics have various applications for practical NP-hard challenges, RFID network planning problem [
54], training feed-forward neural networks [
55] and constrained portfolio optimization [
56], and were also tested for benchmark functions [
57,
58]. Some of the BA and CS implementations for cloud computing challenges include scheduling workflow applications [
59,
60], cloud service composition [
61], task scheduling [
62] and load balancing [
63].
The moth search (MS) approach is a relatively recent swarm intelligence algorithm that emulates the phototaxis and Lévy flights of the moths [
64]. The MS was tested on a wider set of bound-constrained and constrained benchmarks [
64,
65], and also has some implementations for practical tasks, for example in the domains of wireless sensor networks (WSNs) localization [
66] and drone placement [
67]. Only a few implementations of the MS for cloud computing tasks can be found in the literature [
68].
The elephant herding optimization (EHO) also belongs to the group of novel swarm algorithms [
69]. According to the literature survey, many practical EHO implementations can be found [
5,
70,
71,
72]. In addition, modified versions of the EHO that were tested on standard benchmark functions exist [
73]. By examining the available literature, we concluded that no EHO’s implementations for the cloud computing domain exist.
The fireworks algorithm (FWA), which has many versions, was devised by Tan in 2010 [
74]. This metaheuristics proved to be state-of-the-art NP-hard tasks optimizer for various types of practical problems [
75,
76,
77,
78,
79,
80]. In addition, some hybridized FWA versions can be found in the modern literature [
81]. The FWA was successfully adapted for cloud computing problems [
82].
Besides all mentioned above, there are also other state-of-the-art swarm intelligence algorithms that showed outstanding performance for tackling various kinds of practical problems, for example ant colony optimization (ACO) [
83], brain storm optimization (BSO) [
84,
85,
86], krill herd (KH) [
87] algorithm, tree growth algorithm (TGA) [
5,
88,
89], and many others [
90,
91,
92,
93].
Some of the other swarm algorithms’ implementations for cloud computing challenges that should be mentioned are presented in refs. [
94,
95], while a comprehensive review of swarm algorithms’ applications in a cloud computing domain can be found in refs. [
20,
21].
3. Cloud Task Scheduling Problem Formulation
In this section of the paper, we briefly describe a model for a cloudlet scheduling problem that was used for testing purposes of the research presented in this paper, along with the most important terminology and performance metrics.
The cloud hardware infrastructure is organized within the cloud data centers. The cloud data centers are composed of a limited number of homogeneous and/or heterogeneous physical servers, which are frequently referred to as hosts in the modern literature. Hosts are the state-of-the-art computing hardware, usually HCLs. Each host in the cloud data center has at least the following set of attributes: host unique identifier (hostID), number of processing elements (processing elements may be CPUs or CPU cores), performance of each processing element expressed in MIPS (million instructions per second) units, the size of system RAM memory, available network throughput, etc.
Each physical server (host) in the cloud data center hosts one or more VMs that execute in a pseudo-parallel manner using time-shared or space-shared VM scheduling policy. The VMs in turn serve as a platform for a different number of heterogeneous applications and services that represent the basic unit of execution of submitted user requests [
20]. In the context of cloud environment simulators, end-user requests (tasks) are usually referred as cloudlets. Since the terminology used in this paper is consistent with the cloud simulators terminology, the terms’ requests, tasks and cloudlets will be used interchangeably. The VMs have the same properties as the physical server that hosts them.
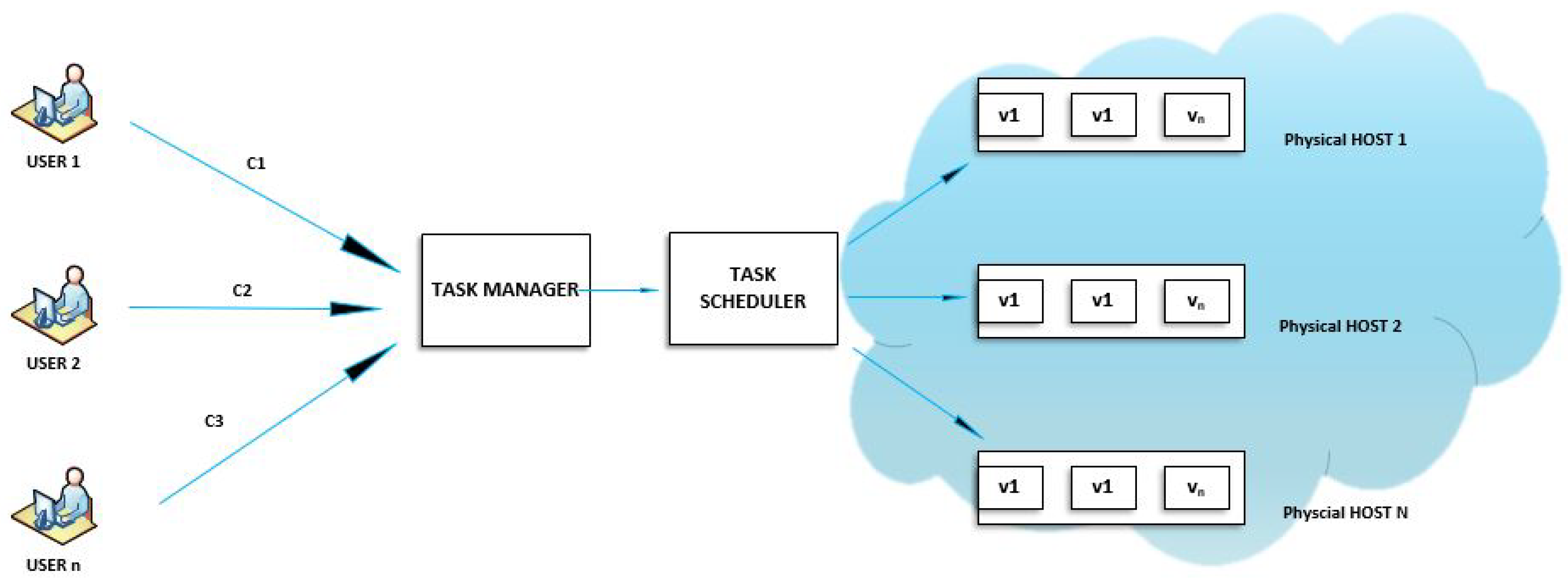
When end-users submit cloudlets to the cloud system, the cloudlets first come to the task manager component that performs organization of incoming requests, and provides the status of each task to the user that submitted it. The task manager then forwards task requests to the task scheduler, which assigns incoming tasks to the available and appropriate VMs by utilizing a scheduling algorithm. In the case, if no VMs are available for processing, the task will wait in the queue. When VM finishes the processing of a current task, VM becomes available for another task, and so on. Each VM executes a single task at each time step. A system model for task scheduling in cloud environments is depicted in
Figure 4.
Many definitions of the scheduling exist in the literature. According to the definition provided by Pinedo in [
96], the scheduling is a decision-making process that is regularly used in many services and manufacturing industries. With the goal to optimize one or more objectives, it deals with the allocation of available system resources to tasks (jobs) over a given time periods. In distributed environments, such as cloud computing, the basic role of a scheduler component is to choose the computational resource in which each cloudlet will be executed. This decision is based on the objective function. One of the most employed objective functions in modern cloud systems is task completion time, or makespan [
97] that should be minimized. Some of the other objective functions that are usually taken for research, as well as for the practical purposes include: minimization of the transfer and communication time, maximization of the throughput, maximization of the load balancing and resource utilization, and minimization of the computing costs and energy consumption.
For the sake of more realistic comparative analysis with other approaches and, due to its effectiveness in research, we used similar cloud scheduling mathematical formulation as in [
68]. In order to present the mathematical formulation of the cloudlet scheduling problem that is used in the research presented in this paper, let
denote the cloud infrastructure that consists of
physical hosts (
), where in turn each host is comprised of the
virtual machines (
):
where each
can be denoted as:
where
represents the
j-th VM that is allocated within the particular physical host. Each
is defined with the following set of properties (attributes):
where
and
denote the unique identifier (serial number) and processing performance in terms of MIPS units of
, respectively.
As already mentioned above, end-users submit set of cloudlets (
) that should be mapped and processes on a available and appropriate VM by using the scheduling algorithm:
where the
denote the total number of cloudlets (tasks) submitted by the end-users, and cloudlet
represents the
k-th cloudlet in the sequence, which is more precisely defined as:
where
and
denote the unique identifier and the length expressed in million instruction (MI) units of the cloudlet
k. The
represents the priority of the task
k, while the
denotes the expected time to complete for a task
k.
The allocation (mapping) of cloudlets to VMs has a great impact on the overall cloud system performance.
The ETC of a
k-th task (cloudlet) on the
j-th VM can be calculated as follows:
where
and
.
The ETC matrix can be used as a task model for a cloud environment with heterogeneous resources [
20].
The ETC matrix of a size
denote the execution time required to complete each cloudlet on a each VM machine [
68]:
As mentioned above, in this research, we utilized the makespan (MS) objective, as in [
68]. In order to establish the MS objective, first the execution time (ET) of all VMs has to be calculated. The ET of the
j-th VM (
) for the cloudlet
k depends on the decision variable
[
20]:
Then, the
, where
j is in the range [
], can be calculated as:
The MS objective is the maximum of
for all VMs:
Moreover, in addition to the MS objective, to better assess the performance of the proposed metaheuristics, we have also used the degree of imbalance (
) that can be calculated as:
where
,
and
denote maximum, minimum and average execution time of all VMs, respectively. The degree of imbalance was also employed in [
68].
The model described is one of the most widely utilized cloudlet (task) scheduling models for research purposes, due to its clear formulation and easy-to-track performance metrics [
68,
98]. It is a single-objective model, with the goal of minimizing the MS objective.
By utilizing this model, the performance of metaheuristics can be clearly defined. Moreover, since the same model formulation and its variations have been widely adopted in the modern literature, simulation results of different methods are available. In this way, by performing comparative analysis with other approaches, we could better establish performance improvements of our approach over other methods applied to the same model. This represents our main motivation for employing this model for testing the performance of the hybrid algorithm proposed in this paper.
Besides the cloud computing task scheduling model presented in this paper, many other cloudlet scheduling models exist for both single-objective and multi-objective optimization. For example, in [
99], a multi-objective task scheduling model, where the makespan and the budget cost objectives were taken into account, was presented. In this research, the fitness is calculated by combining the makespan and the budget cost objective values. Another example of multi-objective model was utilized in [
100], with the goals of simultaneously minimizing the execution time and maximizing the energy efficiency.
When testing algorithms for some more complicated cloudlet scheduling models, the results may be ambiguous and the performance metrics may be obscured. For this reason, according to our opinion, when adapting and testing new metaheuristics for cloudlet scheduling, it is better to utilize a more straightforward model with clearly defined performance metrics and objectives.
4. Original and Hybridized Monarch Butterfly Optimization Algorithm
The monarch butterfly optimization (MBO) was proposed in 2015 by Wang and Deb [
22]. The researchers who devised MBO in the very first published paper that describes this metaheuristics presented testing results on a wider set of standard bound-constrained benchmarks [
22]. Early testing results proved to have great potential of the MBO algorithm in the area of NP-hard optimization. Since the MBO proved its potential, later the MBO was adapted for some practical NP-hard problems, such as RFID network planning [
23] and node localization in WSNs [
24]. In addition, some hybridized versions of the MBO algorithm were devised [
101,
102].
In this section of the paper, we first describe the original MBO approach, and later we present devised hybrid MBO implementation, along with the adaptations for the practical cloudlet scheduling problem.
4.1. Original Monarch Butterfly Optimization Approach
Monarch butterflies’ spices inhabit regions of North America, and one of the most distinguishable characteristics that differentiate them from other groups of butterflies is long distance migration. Every year, monarch butterflies fly thousands of miles from the USA and southern Canada to Mexico. The migration behavior of monarch butterflies inspired research to simulate such behavior. More information about the biological background of the MBO algorithm can be obtained from [
22].
For the purpose of successful implementation of the MBO, the following simplifications of the real biological system were applied [
22]:
monarch butterfly population is situated only in two areas—Land 1 and Land 2;
by applying migration and adjusting operator on butterfly in Land 1 or Land 2, an offspring monarch butterfly is generated;
if the fitness of the offspring butterfly is greater than the fitness of its parent, the offspring is preserved, and it is transferred to the next iteration. On the contrary, the offspring is discarded from the population, and the parent is left intact;
on the solutions (butterflies) from the population with the best fitness, operators are not applied and they are transferred to the next iteration in the present form. In this way, by utilizing elitist selection, the performance of the algorithm will not be degraded from one iteration to another.
In order to be consistent with the optimization algorithms’ terminology, instead of the butterfly, a term solution will be used, and Land 1 and Land 2 will be denoted as subpopulation1 and subpopulation2.
As in the case of every other swarm intelligence algorithm, two basic methods that guide the search process are exploitation (intensification) and exploration (diversification). The MBO algorithm performs the exploration and exploitation by utilizing solutions migration and adjusting operators.
4.1.1. Solutions Migration Operator
At the initialization phase of the MBO, the number of solutions in subpopulation1 (
) and subpopulation2 (
) should be determined. For this purpose, Equations (
12) and (
13) [
22] are used:
where
represents the number of solutions in the whole population (subpopulation1 plus subpopulation2), function
rounds the argument
x to the nearest integer that is greater than or equal to
x, while the ratio of the number of solutions in subpopulation1 (
) to the total number of solutions (
) is denoted as
p.
The parameter p play an important role in the MBO’s search process. By adjusting the value of this parameter, a relative influence of subpopulation1 to the subpoplation2 is established. If the value of p is large, then most of the total population will be comprised of solutions from subpopulation1, and vice versa. In the original implementation, the value of p is set to 5/12.
By applying a solutions migration operator, a novel solution in iteration
is created by applying one the following equations [
22]:
where
stands for the
j-th parameter of the novel
solution at iteration
,
and
denote the
j-th component of the
and
solutions at the current iteration
t, respectively. The solutions
and
represent a pseudo-random solution from subpopulation1 and subpopulation2.
Whether the novel solution will be directed towards the solution in subpopulation1 or subpopulation2 is determined by taking into account the value of the parameter
r that is calculated according to the following expression:
where
that indicates a migration period, represents another MBO control parameter, and
is a number drawn from the uniform distribution. In our implementations, as well as in the original MBO’s implementation [
22], the value for the
is set to 1.2.
Finally, when the
condition is true, then the
j-th component of the solution
in generation
is created by using Equation (
14). In the opposite case for generating the
j-th component of the solution
in generation
, Equation (
15) is employed.
The solutions migration operator is applied only to solutions from subpoplation1.
4.1.2. Solutions Adjusting Operator
The second procedure that guides the MBO’s search process is a solutions adjusting operator. This operator performs both processes—exploration and exploitation. A direction of the search process depends on the value of the generated pseudo-random number , where two cases can be distinguished.
In the first case, if the condition
is satisfied, then the new solution is generated by applying the following equation to all parameters (components) of the current solution [
22]:
where
denotes the
j-th parameter of the new solution
i, and
is the
j-th parameter of the current best solution in the whole population.
In the second case, if
, then the new solution in the iteration
is generated by applying Equation (
18) to all parameters of the solution in the iteration
t:
where
represents the
j-th parameter of the randomly selected solution
from subpopulation2.
Moreover, if the condition
is established, newly generated solutions are further updated by applying [
22]:
where
represents solution adjusting rate, and
is the walk step of the solution
i that can be determined by using Lévy flights:
The weighting factor
that is utilized in Equation (
19) is given as [
22]:
where
is the maximum walk step in which an individual (solution) is able to move in one time step, while
t indicates the current iteration number.
The value of parameter establishes the balance between the exploitation and exploration. When is increased, the search step is longer, and the process of exploration has greater influence on the algorithm’s execution. In the opposite case, with the decrease of , the intensification has a more significant influence on the whole search process.
Solutions adjusting operator is applied only to solutions from subpoplation2.
4.2. Hybridized Monarch Butterfly Optimization Approach
In this subsection, we first emphasize the shortcomings of the original MBO implementation, and then we show implementation of our proposed hybridized MBO approach that overcomes observed deficiencies.
4.2.1. Drawbacks of the Original MBO
By performing practical simulations on standard bound-constrained benchmarks, we noticed some deficiencies in the original MBO’s implementation. In the following few paragraphs, observed deficiencies will be briefly described.
First, deficiency refers to the insufficient power of the exploration process.
In the basic MBO’s version, solutions migration operator performs the process of exploitation by moving solutions to the direction of existing solutions in subpopulation1 and subpopulation2. The second operator, solutions adjusting operator, conducts both processes—exploitation and exploration. By applying this operator, exploitation is performed by moving solutions in the direction of the current best solution in the whole population, or in the direction of a randomly selected solution from the subpopulation2 (please refer to Equations (
17) and (
18)). Only in the case when the condition
holds is the process of exploration conducted. However, even in this case, the intensity of exploration depends on the weighting factor
and the maximum walk step (
) that dynamically decreases during the algorithm’s run (please refer to Equation (
21)).
The observed lack of exploration power in early iterations of the algorithm’s execution has significant influence. In some runs of empirical testing, due to the insufficient exploration power, the MBO could not find the right part of the search space, which led to the worse mean values.
The second deficiency of the original MBO implementation refers to the inadequate trade-off between the exploitation and exploration that is set in favor of exploitation. The balance adjustment between these two processes is crucial for the performance of any swarm algorithm. In early stages of algorithms’ execution, with the assumption that the right part of the search domain is not found, this balance should be adjusted in favor of exploration. However, in the later stages, when the promising domain of the search space is hit, the balance should be shifted towards exploitation. By testing the MBO on standard benchmark functions, we noticed that, even when the value of parameter is high, an appropriate balance could not be established.
4.2.2. Details of the Hybrid MBO Approach
With the goal of overcoming observed shortcoming of the original MBO, we devised a hybrid MBO approach. Hybridization, as a method that combines strengths of two or more metaheursitcs (algorithms) and at the same time eliminates weaknesses, proved to be an efficient way to improve original implementations of swarm algorithms. Prior to the research conducted for the purpose of this paper, the authors have already implemented and tested some hybridized MBO versions [
101,
102].
Guided by the goal of enhancing the process of exploration, we adopted the mechanism of discarding exhausted solutions from the population from the ABC metaheuristics. For every solution in the population, we included an additional attribute
. In every iteration, in which the current solution could be improved, a
parameter is incremented by one. When a value of the
reaches a predetermined exhaustiveness value (
), it is said that this solution is exhausted and it is being replaced with the randomly generated solution within the lower and upper boundaries of the search space by utilizing Equation (
22). The parameter
represents an additional control parameter of the hybrid MBO metaheuristics:
where
and
denote lower and upper bounds of parameter
j, respectively, and
is pseudo-random number from the range
. We should note that this equation is also used in the initialization phase of the algorithm.
However, by conducting empirical simulation, if the mechanism of discarding exhausted solutions is being applied during the whole course of algorithm’s execution, then, in later iterations, with the assumption that the search process has converged to the domain where an optimum resides, too many solutions are “wasted” on the exploration.
To overcome this, we introduce another parameter, discarding mechanism trigger () that controls for how many iterations the mechanism of discarding exhausted solutions from the population is going to be executed. In most tests, we established the optimum value of this parameter to , where denotes the maximum number of iterations in one execution (run) of the algorithm, and function rounds argument x to the closest integer value. Thus, after iterations, discarding the mechanism trigger is not being executed.
We have also noticed that the search process in the original MBO’s implementation in early iterations may converge too fast to the suboptimal region of the search domain, and the algorithm frequently gets stuck in one of the local optima. This is a consequence of an inadequately established balance between the intensification and diversification, particularly in the search mechanism encapsulated within the solutions migration operator. This operator is applied to every solutions’ component. To overcome this, we have adapted another control parameter from the ABC metaheuristics, the modification rate
. In the method that models solutions migration operator, for each component of every solution from subpopulation1, we generate pseudo-random number
, and only if the condition that the
is satisfied, then the particular solutions’ components will be altered according to Equations (
14) or (
15). Otherwise, the components will be left intact.
By introducing three additional control parameters and the notion of solutions’ exhaustiveness from the ABC metaheuristics, we enhanced the exploration power of the original MBO approach and established better exploitation–exploration trade-off. Since modifications of the original MBO were inspired by the ABC algorithm, new metaheuristics is called MBO-ABC.
Pseudo-code of the MBO-ABC metaheuristics is given in Algorithm 1.
| Algorithm 1 Pseudo code of the MBO-ABC metaheuristics |
Initialization. Set the iteration counter t to 1, set the maximum iteration value, set the values for p, , , , and parameters; generate random initial population of size by using Equation ( 22); calculate and sizes of subopopulation1 and subpopulation2 with Equations ( 12) and ( 13); initialize property for solutions in the whole population to 0. Fitness calculation. Evaluate fitness of all solutions whiledo Sort all solutions according to their fitness value Divide the whole population into subpoplation1 of size and subpopulation2 of size for all solutions in subpopulation1 do for all components in the solution do Generate pseudo-random number if then Generate new component by employing Equations ( 14) or ( 15) end if end for Choose between old and new solutions according to their fitness value If the old solution is chosen, increment the value of the parameter end for for all solutions in subpopulation2 do for all components in the solution do Generate new component by utilizing Equations ( 17)–( 20) end for Choose between old and new solutions according to their fitness value If the old solution is chosen, increment the value of the parameter end for for all solutions in the whole population do if then Discard solutions for which the condition is satisfied and replace them with randomly created solutions (Equation ( 22)) end if end for Merge newly generated subpopulation1 and subpopulation2 into new population of size Calculate fitness and evaluate new population Adjust the value of parameter according to Equation ( 21) end while return The best solution from the population
|
4.3. Solution Encoding and Algorithms’ Adaptations
One of the greatest challenges in the process of adaptation of any metaheuristics for specific problem is how to encode candidate problem solutions. According to the problem formulation given in
Section 3, if there are
cloudlets and
VMs, the size of the search space and the number of possible allocations of cloudlets to VMs are
. In our adaptations of both MBOs’ implementations, the potential solution is represented as a set of cloudlets that should be executed, where each cloudlet is mapped to the appropriate VMs.
Every individual in the population is encoded as an array of size
, where every element of the array has the value in the range [1,
]. An example of a candidate solution with
number of cloudlets and
is given in
Figure 5. In this example, cloudlet
is scheduled for execution on the VM with
D
, cloudlet
will be executed on the VM with
D
, while cloudlets
and
will be both processed on the VM with
of 4.
If, as another example, we consider 10 tasks and four VMs, the potential solution can be represented as [3 2 3 1 4 2 4 2 2 1].
In the initialization phase of each run, the
number of individuals are randomly generated, where each individual
is represented as an array of size
(
=
,
,
, ...,
). Solutions are generated by using the following expression:
where for all solution components
, upper bound (
) and lower bound (
) were set to
and 1, respectively. The
is pseudo-random number from the interval
.
Since the search space is relatively large, there was no need to adapt metaheuristics for integer programming problems. In Equation (
23), as well as in Equations (
19) and (
20), results are rounded to the closest integer value using simple
function.
5. Practical Simulations
When a new metaheuristics is devised, or existing is improved/modified/upgraded/hybridized, it first should be tested on a wider range of benchmark problems. Due to this reason, in this section of the paper, we first show simulation (testing) results of the MBO-ABC on some of the well-known bound-constrained benchmarks, along with the comparative analysis with the basic MBO implementation. In this way, the improvements, in the terms of convergence speed and solutions’ quality, of the MBO-ABC over the original MBO can be established.
In the second suite of conducted simulations, we tested MBO-ABC on a practical cloudlet scheduling problem by utilizing two sets of data: artificial data generated in the CloudSim simulation environment and the real data taken from the real log-traces of the real-world cloud infrastructure. In both cases, we performed comparative analysis with other state-of-the-art approaches for task scheduling in cloud environments.
5.1. Experimental Suite 1: Bound-Constrained Benchmarks
In the following subsections, we show benchmark functions, algorithms’ parameters adjustments and comparative analysis between the MBO-ABC and the basic MBO.
5.1.1. Benchmark Functions and Parameter Settings
As stated above, in the first set of simulations, we tested the MBO-ABC metaheuristics on a group of eight standard bound-constrained (unconstrained) benchmarks. Details of the benchmarks are shown in
Table 1.
Metaheuristics parameters’ adjustments are summarized in
Table 2. For the sake of better distinction between parameters, parameters are categorized into three groups: basic initialization parameters, MBO and MBO-ABC common control parameters and MBO-ABC specific control parameters.
The group of basic initialization parameters includes settings that are used in all population-based metaheuristics, while the other two groups further separate control parameters that are common for both algorithms, MBO and MBO-ABC, from the parameters that are specific for the MBO-ABC implementation.
One of the greatest challenges when adapting and testing any swarm intelligence algorithm is how to choose optimal values of control parameters. The optimal control parameters’ values of swarm intelligence algorithms depend on the particular problem, and in most cases they are determined empirically, by conducting practical simulations.
We used the same values for the basic initialization parameters and for the parameters that are in common for MBO and MBO-ABC as in the paper [
22], where the MBO was firstly proposed. The authors of the MBO have been performing extensive empirical simulations and they have determined optimal MBO parameters’ values for the bound-constrained benchmarks. On the other hand, in the case of the
and
MBO-ABC specific control parameters, we established optimal values by performing practical simulations. Since the
parameter was adopted from the ABC algorithm, we set the value of this parameter as suggested in ref. [
35].
As stated in
Table 2, the values of
and
parameters were set to 4 and 33, respectively. By performing practical simulations, we found that the optimal or near optimal value for the
parameter can be calculated by using the following simple expression:
The value of the
parameter is calculated by using the formula
, as it was already mentioned in
Section 4.2.2. Finally, the optimum value for the
parameter was chosen empirically.
5.1.2. Testing Results and Analysis
We performed tests with the MBO and the MBO-ABC on eight benchmarks in 30 independent executions (runs), where, for each run, a different pseudo-random number seed is used. Moreover, we utilized two tests, one with 30-dimensional (D = 30) and the second with 60-dimensional (D = 60) solution spaces. In all conducted experiments, we tracked best value, as well as the mean and standard deviation values that are averaged over 30 independent runs.
Comparative analysis between the MBO-ABC and the basic MBO for benchmarks with 30 dimensions (
D = 30) is shown in
Table 3. In the presented table, the best results for each indicator are marked in bold.
From the results shown in
Table 3, it is evident that the MBO-ABC on average obtains better results than the original MBO approach. In addition, the exploitation–exploration balance, as well as the convergence speed is better in the case of the hybrid MBO metaheuristics.
For example, in the case of the test for benchmark, original MBO in early iterations performed exploitation in the wrong part of the search space. However, in some runs, it hits the right part of the search space, but, in later iterations, and as a consequence the optimum value can not be achieved. In the same test, the MBO-ABC manages to find the promising region of the search space in early iterations, and by performing fine-tuned search in this region in later iterations, an optimum can be obtained. This can be also concluded from observing the mean values for the same benchmark, in which case the mean value obtained by the MBO-ABC is more than two times better than the mean value, which is accomplished by the basic MBO.
Significant performance difference between MBO-ABC and the MBO can also be observed when comparing results for the benchmark. In this case, all three indicators, best, mean and standard deviation are substantially better in MBO-ABC simulations. For example, the best value obtained by the MBO-ABC is almost 30 times lower than the best accomplished by the original MBO. In addition, when making an overall observation for all eight benchmarks, it can be noticed that the MBO-ABC managed to obtain better mean value for every conducted simulation. This proves that the MBO-ABC establishes much better convergence speed than the original MBO.
However, there are few instances where the basic MBO performs better than the MBO-ABC. Such examples include the following: best indicator for and tests, and the standard deviation indicators for and benchmarks. In all these cases, the MBO obtained slightly (not significantly) better results than the MBO-ABC.
Despite of the fact that the basic MBO in few cases performed better than the MBO-ABC, based on overall simulation results, a conclusion that the MBO-ABC overcomes deficiencies in terms of the exploration power and exploitation–exploration trade-off of the original MBO approach, can be drawn.
A similar conclusion regarding the performance of the MBO-ABC and the MBO can be deduced from the results obtained in simulations performed over 60-dimensional search space for the same benchmark functions. These results are presented in
Table 4. In the table shown, the best results for each indicator are marked in bold.
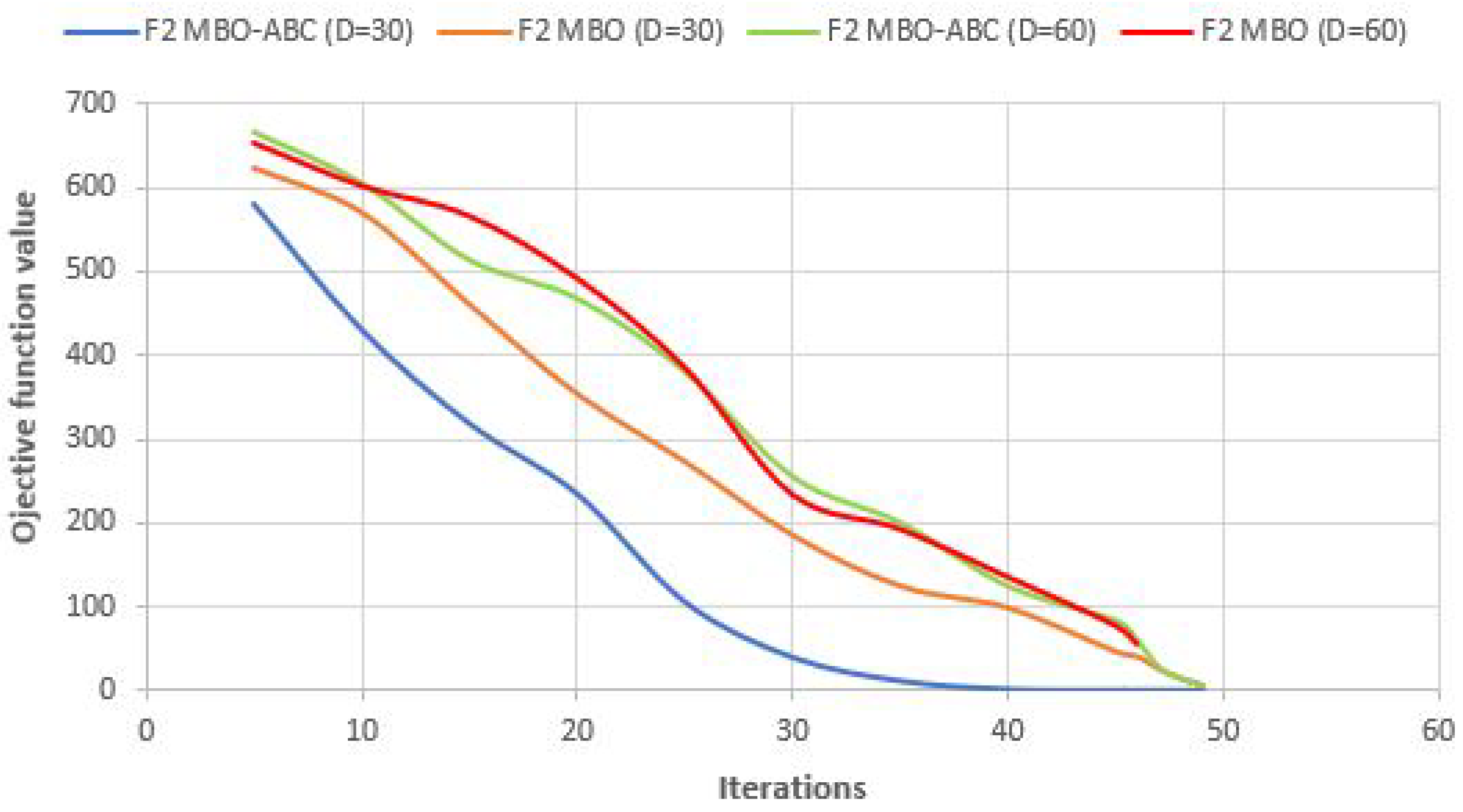
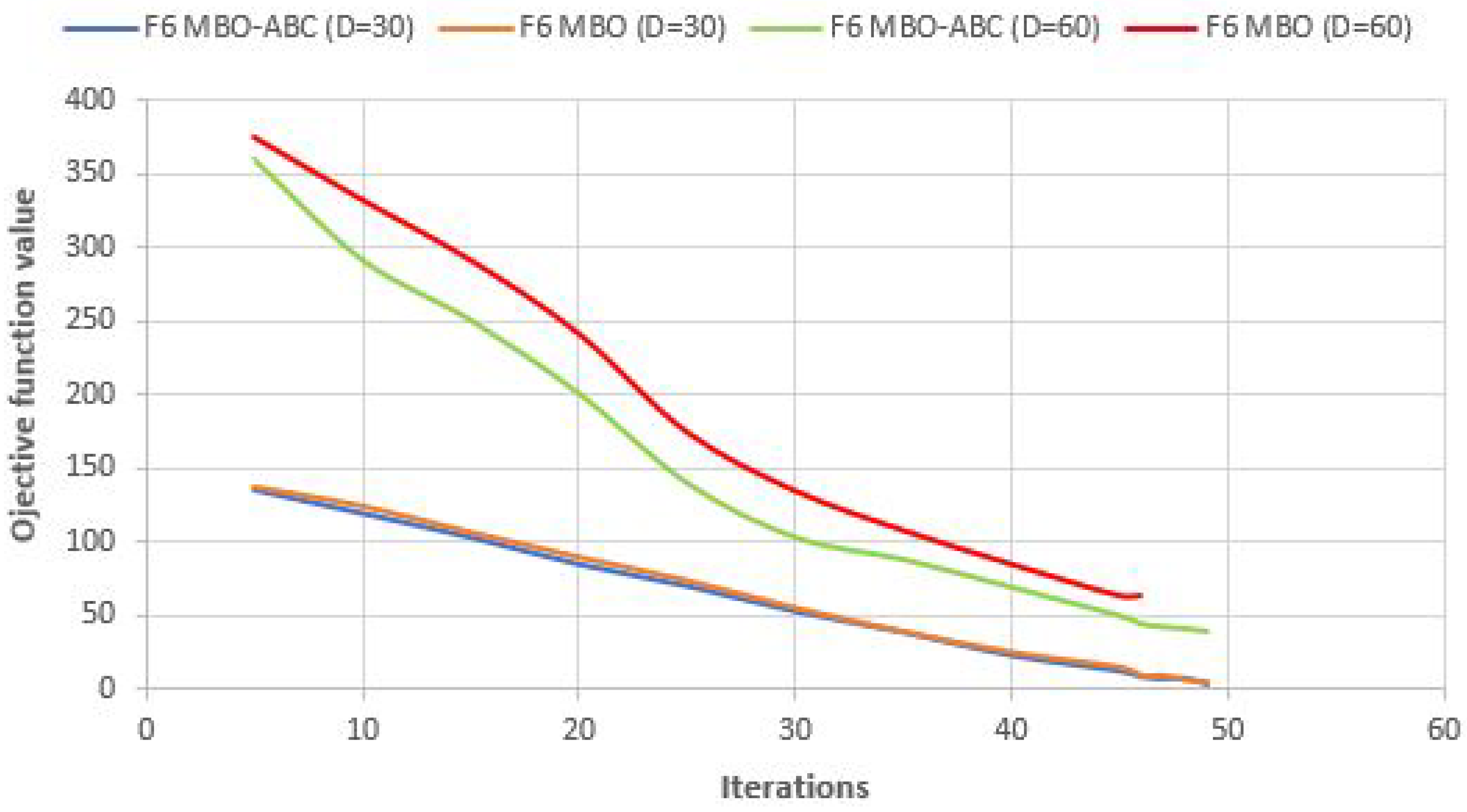
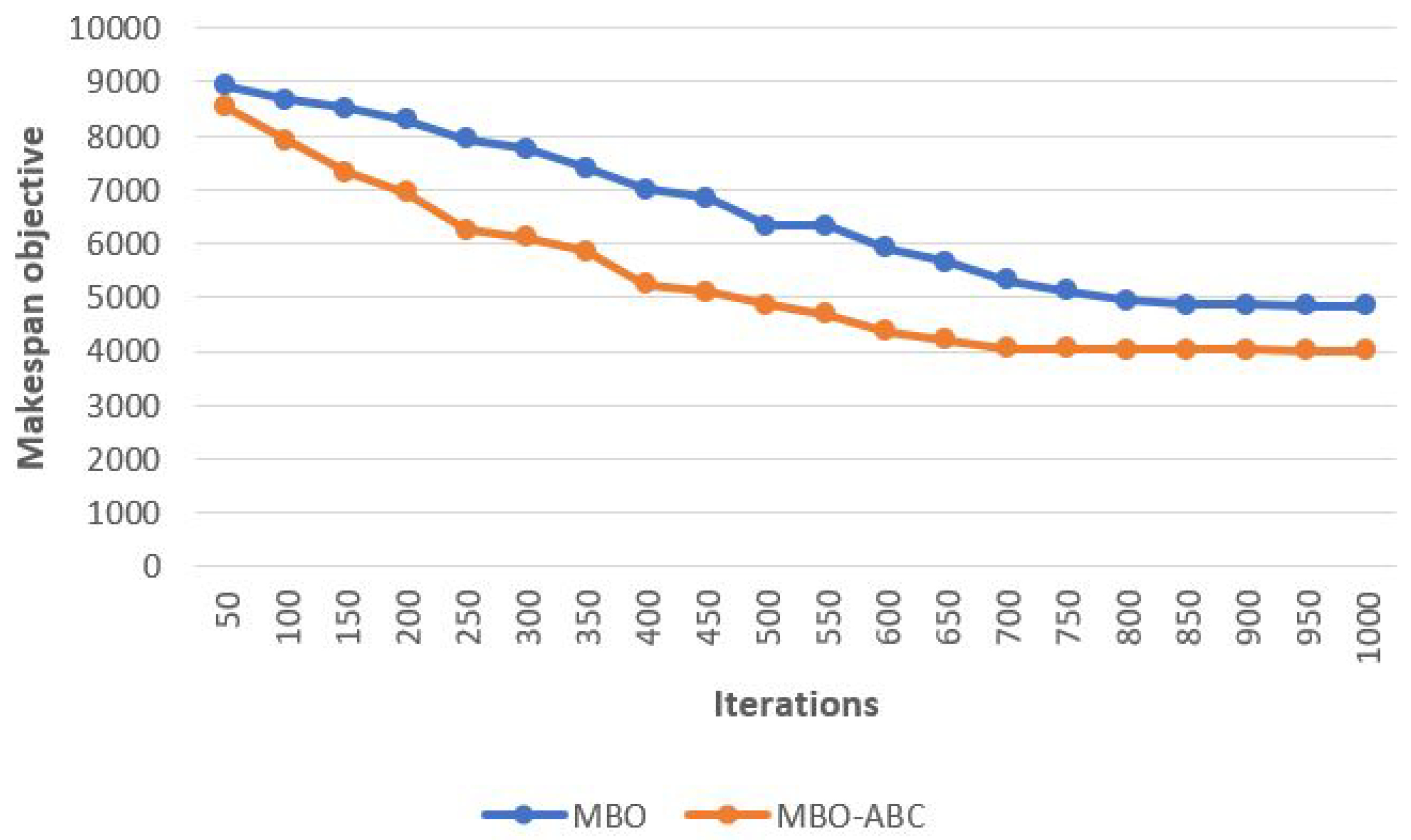
Convergence speed graphs of the best run for
and
benchmarks with
and
of MBO-ABC and MBO metaheuristics are shown in
Figure 6 and
Figure 7, respectively.
From
Figure 6, slightly better performance in the convergence speed for the
test of the MBO-ABC, compared to the basic MBO, can be observed. On the contrary, in the case of
60-dimensional benchmark (
Figure 7), the MBO-ABC obtains substantially better convergence than the original MBO. In the 30-dimensional
benchmark, both approaches establish almost the same convergence speed.
Finally, with the goal of providing empirical proofs for the theoretical background of proposed MBO-ABC algorithm, especially regarding the exploitation–exploration balance (please refer to
Section 4.2.1 and
Section 4.2.2), we have conducted simulations with varying values of the
and
parameters, while all other MBO-ABC parameters were set as in
Table 2. Despite of the fact that the value of
parameter also has influence on the exploitation–exploration trade-off, we did not change its value, since it was adopted from the ABC algorithm and set as suggested in [
35].
With the increase of the
parameter value, the power of exploitation increases, while at the same time the intensity of exploration decreases, and vice versa. As stated above, we found that the optimal value of the
parameter, with all other parameters set as in
Table 2, is 4.
Similarly, as in the case of the
control parameter, when the value of
parameter is increasing, the diversification power is decreasing, while the intensification capability of the search process is enhancing. As stated above, we found that the optimal value of the
parameter, with all other parameters set as in the
Table 2, is 33. With these settings, optimal balance between the exploitation and exploration of the MBO-ABC search process can be established.
In
Table 5, we show testing results of the MBO-ABC for unconstrained benchmarks with 30 dimensions in size, with
parameter set to 3, 4 and 5.
Similarly, in
Table 6, we show simulation results of the MBO-ABC for unconstrained benchmarks with 30 dimensions in size, with a
parameter set to 32, 33 and 34.
From presented tables, it is clear that the MBO-ABC establishes the best performance regarding the solutions quality (best values) and convergence speed, when the
and
values are set as shown in
Table 2. With these settings, the balance between exploitation and exploration is appropriate and the MBO-ABC obtains the best performance.
5.2. Experimental Suite 2: Cloudlet Scheduling Simulations
Cloudlet (task) scheduling simulations were performed in the environment of the CloudSim toolkit. As noted above, we conducted two types of tests (simulations).
In the first test, an artificial data set that is randomly generated within the simulation platform is utilized. However, in the second experiment, we used a realistic data set taken from the log-traces of one production cloud infrastructure.
5.2.1. CloudSim Simulation Environment and Computing Platform
CloudSim is a self-contained framework which provides an extensible simulation toolkit that enables modeling and simulation of cloud computing systems and application provisioning environments [
103]. The CloudSim Toolkit software, that was released as Open Source under the Apache Version 2.0 license, has been developed in Java technology by the Cloud Computing and Distributed Systems (CLOUDS) Laboratory, and it is widely used by the research and academic community for modeling and testing cloud systems and applications. The CloudSim can be freely downloaded from the URL:
https://github.com/Cloudslab/cloudsim/releases.
The following characteristics of the CloudSim make it a state-of-the-art toolkit for cloud simulations [
103]: it provides repeatable and controlled experimental environment for creating and modeling cloud entities; it can be easily extended to include user-defined scheduling and allocation policies; it provides network architecture and infrastructure that can be easily modified; and it enables VM, host, network and application provisioning.
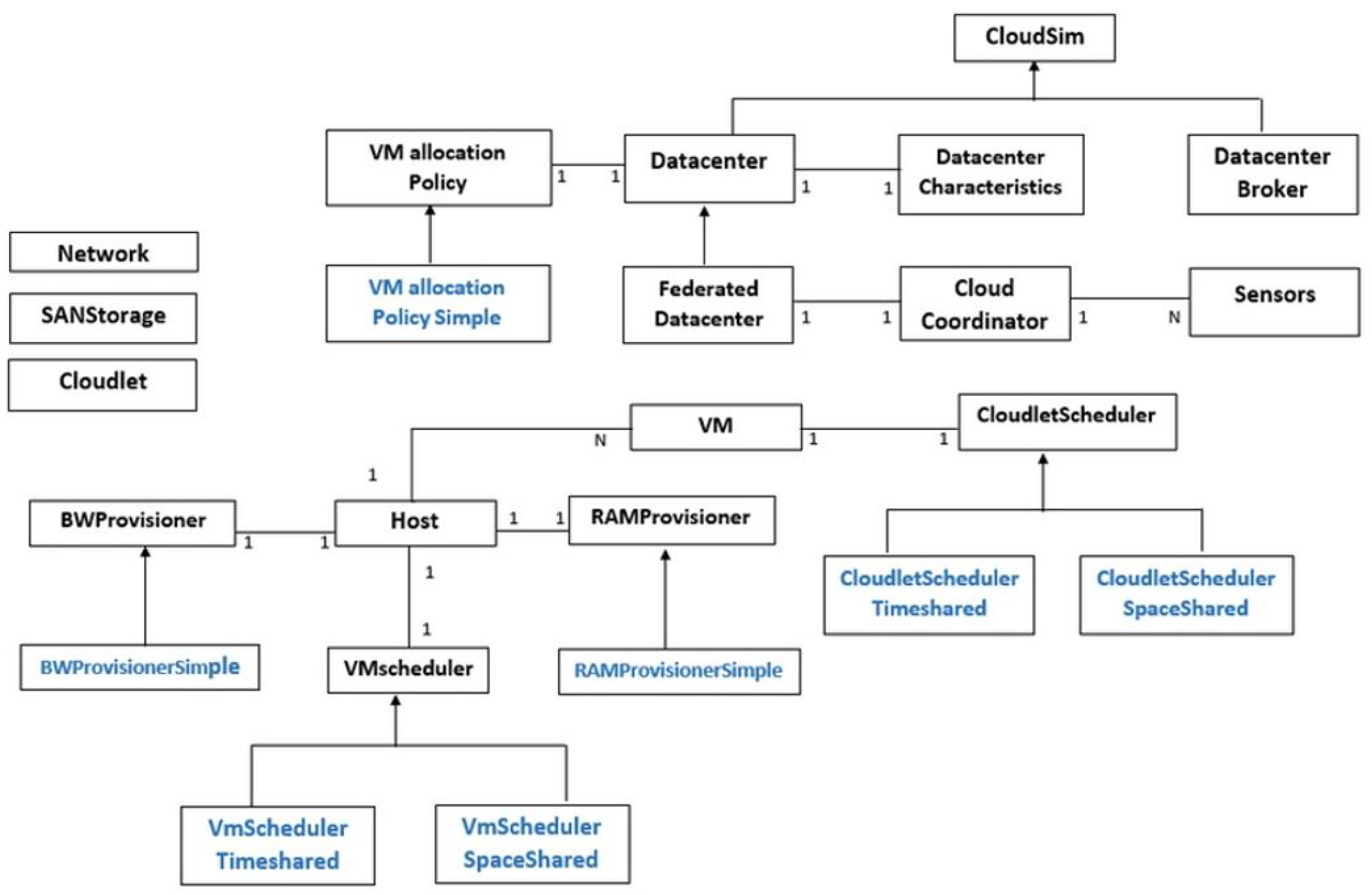
The whole CloudSim library consists of 12 packages that are used for simulating different kinds of cloud computing scenarios. The most important package is CloudSim, and it contains classes for modeling various cloud entities like Datacenter, Cloudlet, Host, VM and DatacenterBroker.
An overview of the CloudSim class design diagram and architecture is shown in
Figure 8. In the following few paragraphs, we briefly describe some of the most important components of the CloudSim architecture.
Cloudlet represents a class that models application services that are cloud-oriented, such as delivery of a content and business workflow, and also all other tasks that are submitted by the end-users for processing to the cloud system. For every application service, before starting the simulation, instruction length and data transfer overhead need to be defined. The cloudlet class can be easily extended to model various types of application services.
CloudletScheduler is an abstract class that is used for implementing different policies that define the way the processing power of VMs is shared between the cloudlets. In the basic CloudSim library, two types of these policies are available: space-shared (CloudletSchedulerSpaceShared) and time-shared (CloudletSchedulerTimeShared). Researchers are able to easily extend this class for modeling other policies, according to the research requirements and the utilized model.
Datacenter class models the underlying hardware architecture, on top of which the VMs execute. It is used for defining characteristics of host platforms that can be either homogeneous or heterogeneous. The homogeneous hosts are hosts that share the same hardware configurations (number and type of CPUs and CPUs cores, memory and storage capacity). In the heterogeneous hosts environment, different hosts have different physical hardware characteristics. It also should be mentioned that each Datacenter class instantiates a generalized application provisioning component that implements a group of policies for bandwidth, memory and storage allocation to hosts and VMs.
DatacenterBroker models a broker entity that acts as an intermediate between the SaaS and CSPs. The broker performs on behalf of the SaaS providers. When a request submitted by the end-users arrives, the broker discovers suitable CSPs by querying the cloud information service (CIS) and undertakes online negotiations for allocation of resources and/or services that can meet the application’s quality of service (QoS) needs [
103]. This class may be extended with the goals of developing and testing custom broker policies.
The class DatacenterCharacteristics encapsulates information regarding the configuration of various data center resources. Host is an important CloudSim component that models a physical resource. This class contains various important data about physical resource characteristics, such as the amount of available RAM memory and storage capacity, list and type of processing elements (cores), information about the policy used for sharing processing power between the VMs, and provisioning policies of bandwidth and memory to the VMs. The VmScheduler class is an abstract class that the Host component implements, which is used for modeling space-shared and time-shared policies for allocating processor cores of the physical host to the VMs.
Each
Host component of the CloudSim manages and hosts one or many VMs. The
Vm class is used for modeling the VMs. Attributes of the
Vm class represent following VM characteristics: processing speed, accessible memory, size of the storage, and the VM’s internal provisioning policy that is extended from an abstract
CloudletScheduler component [
103]. The
VmmAllocationPolicy is an abstract class that models the provisioning policy that a VMM employs for allocating VMs to hosts. The most important role of this class is to select an available host in the data center that meets the minimum requirements for deploying the VMs, in terms of the required memory, processing power and storage.
In the basic CloudSim installation package, some examples of generating and executing CloudSim simulations are included. Provided example instances are divided into following categories: basic, network, power and container examples. These examples provide more than enough information for the researcher to be able to generate and to perform CloudSim experiments on his/her own.
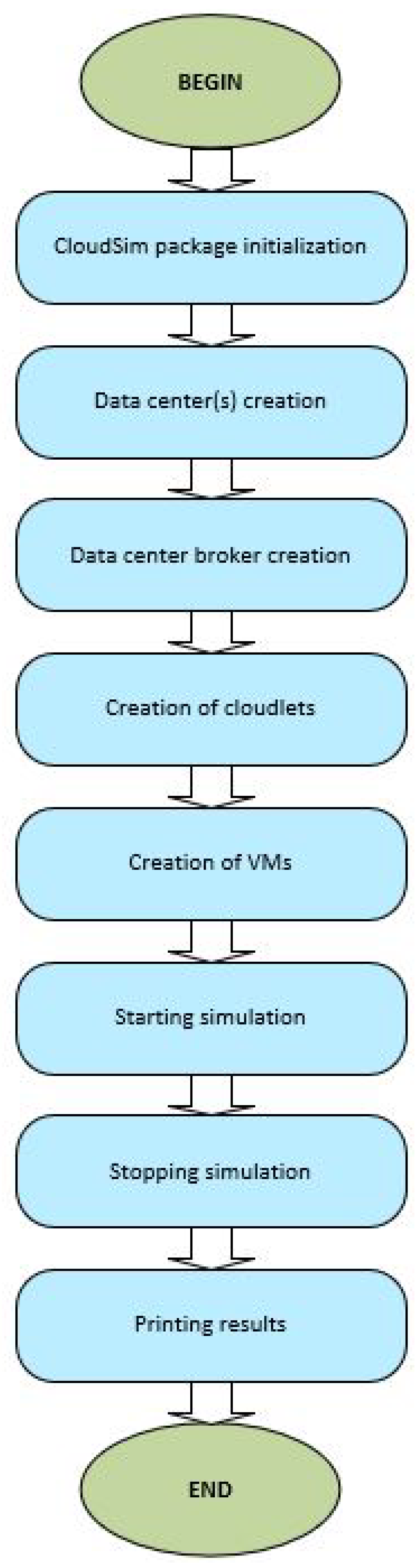
The process of generating CloudSim simulations (simulation life cycle) may be summarized into the following eight steps: initialization of the CloudSim package, creation of the data center(s), broker creation, generating cloudlets (defining the workloads), the VM creation, starting simulation (automated process, handled through discrete events simulation), stopping simulation and printing results (outputs visualization). In each of these steps, which are visualized in
Figure 9, various components of the CloudSim architecture (data centers, VMs, cloudlets, RAM, processing elements, provisioning and scheduling policies, etc.) are being implemented.
For more information about the CloudSim toolkit, please refer to [
103].
In conducted experimental simulations, we used CloudSim version 3.0.3. For the purposes of modeling cloud environment and implementing swarm algorithms, we modified some of the base classes provided in the CloudSim. In all tests, the computing platform with following characteristics was utilized: Intel® CoreTM i7-8700K CPU with 32 GB of RAM memory, Windows 10 operating system and Java SE Development Kit 12.0.1.
5.2.2. Simulations with Artificial Data Set
In the first cloudlet scheduling experiment, we used the same experimental conditions as in [
98] because we wanted to evaluate the performance of our hybridized metaheuristics against other approaches presented in this paper.
We took makespan for an objective function, as stated in
Section 3. For more details about the problem formulation, please refer to
Section 3.
We conducted tests with a different number of tasks (cloudlets), ranging from 100 to 600, as in [
98]. Every test instance is conducted in 100 independent algorithms’ runs, and, as the final result, we took the average of makespan values obtained in all runs. In this way, we wanted to decrease the influence of the randomization to the obtained results, and, overall, to make more precise evaluation of the performance of the proposed metaheuristics.
For every run of each test instance, a randomized cloud environment with characteristics shown in
Table 7 is generated.
As can be seen from
Table 7, for every independent run, a randomized cloud environment is created with CPU MIPS for VMs varying in the range between [1860,2660], Cloudlets’ task length varying within the range of [400–1000], etc. For the cost metrics provided within the DatacenterCharacteristics CloudSim entity, we took default values.
In performed simulations, we set the arrival rate of cloudlets to 10 tasks per second, as in [
98]. To simulate this behavior, we modified
DatacenterBroker CloudSim entity class, particulary
submitCloudlet() method.
In ref. [
98], an improved version of the ACO metaheuristics, performance budget ACO (PBACO), for job scheduling in cloud computing is presented and tested against the same data set that we used in our simulations. In order to make comparative analysis with other heuristics and metaheuristics, shown in ref. [
98], more realistic, we set the value of
to 20 and
to 50, yielding the total number of 1000 objective function evaluations (
). The PBACO was tested with 10 ants in the population and 100 iterations, establishing, as in our case, 1000 objective function evaluations.
The value of the
parameter was calculated according to Equation (
24), and was set to 10, while the value of the
was set to 33, by using the same expression as in simulations with bound-constrained benchmarks (please refer to
Section 5.1.1). The other MBO and MBO-ABC parameters were adjusted as shown in
Table 2.
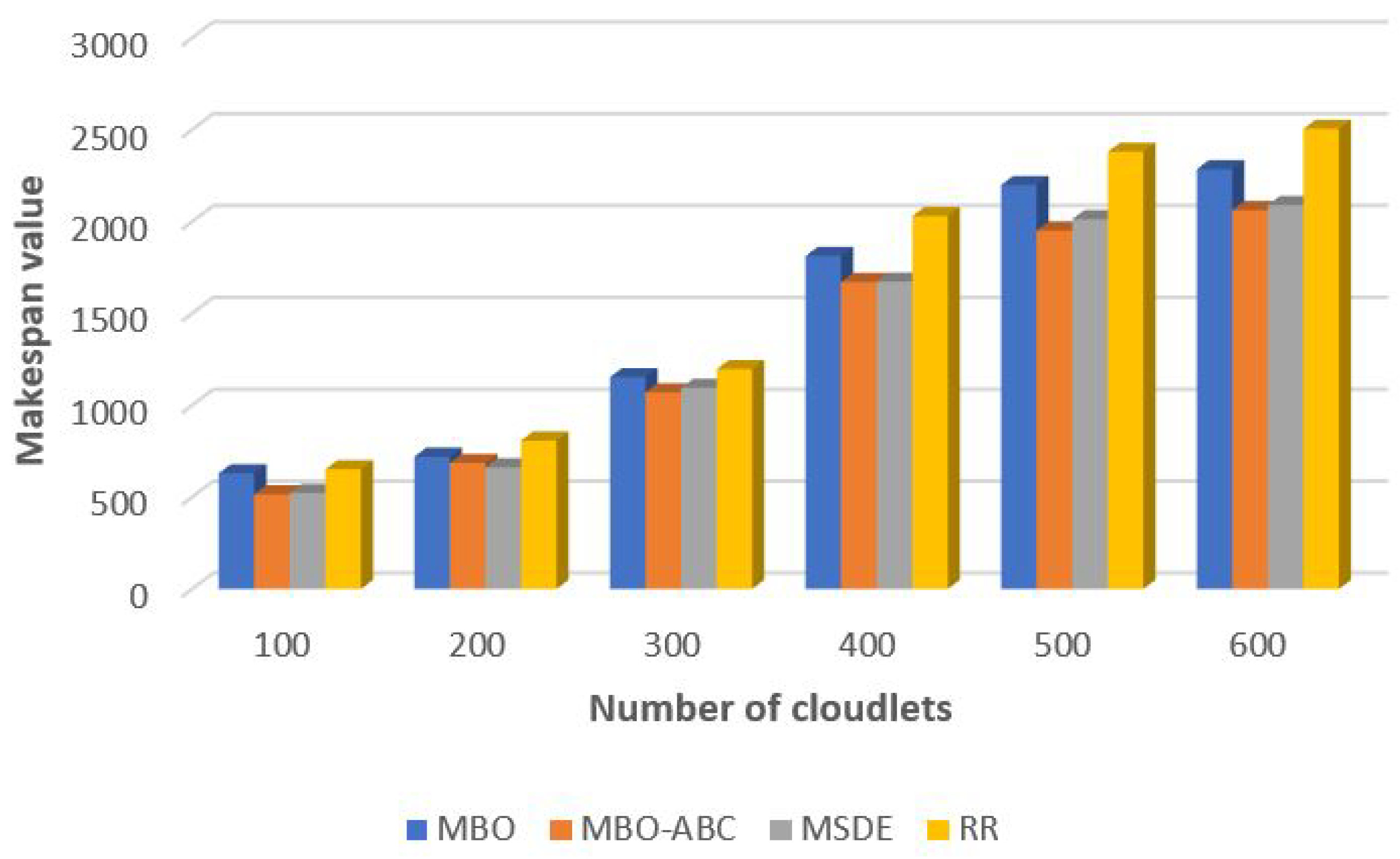
First, we wanted to perform comparison between the MBO-ABC and the MBO to measure improvements of our hybrid algorithm over original MBO implementation for this instance of cloudlet scheduling problem. Simulation results are visualized in
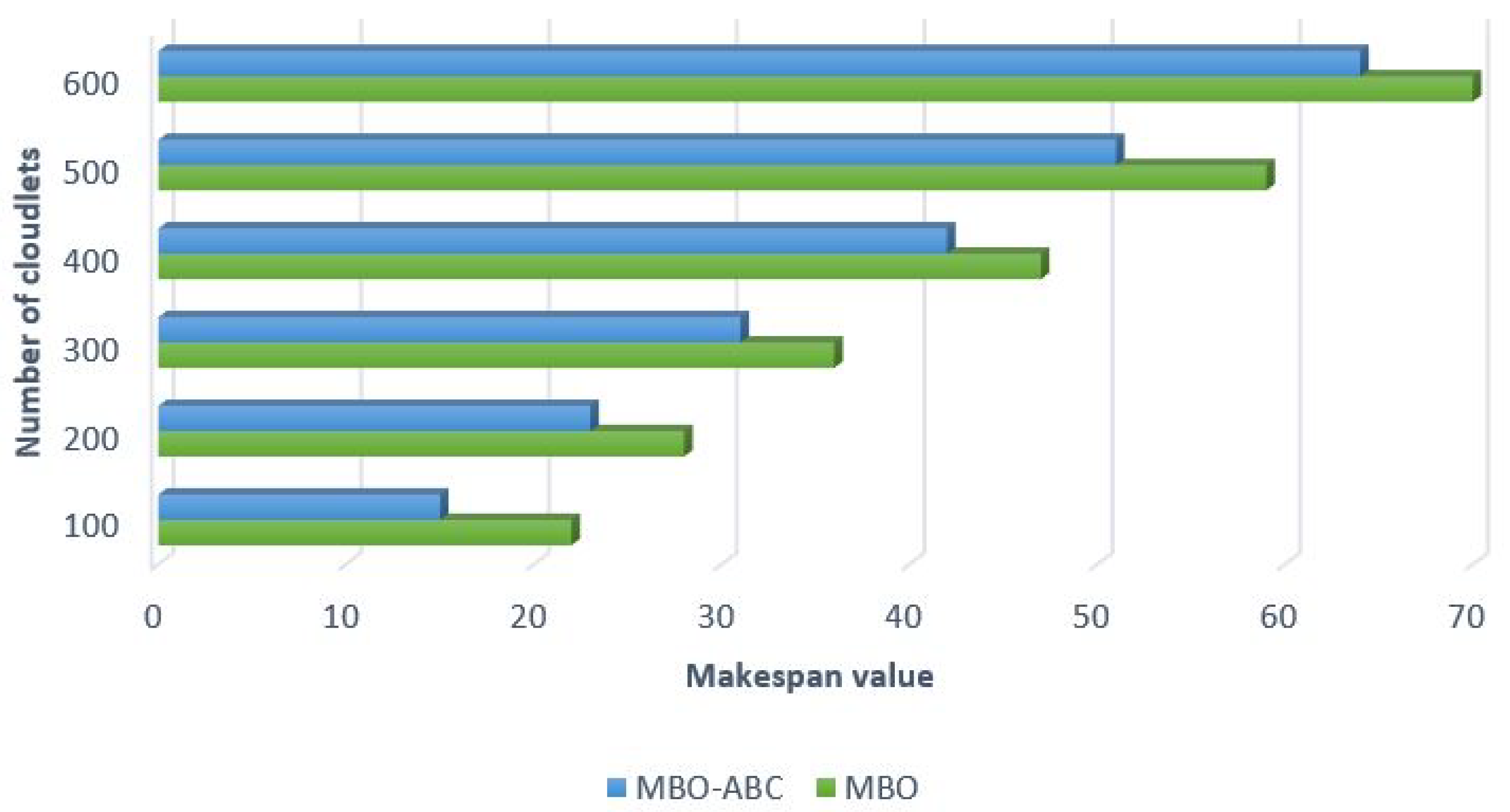
Figure 10.
From the results visualized in
Figure 10, it is evident that the MBO-ABC obtains better makespan value than the original MBO in all test instances. For example, in the case of the test with 100 cloudlets, the MBO-ABC establishes a decrease of 31.81% in the makespan value compared to the original MBO. Performance improvements in tests with 600 cloudlets is 8.57%, while the same metric for 300 and 400 cloudlets simulations is around 13%.
Improvements over the original MBO for all test instances with the artificial data set are summarized in
Table 8.
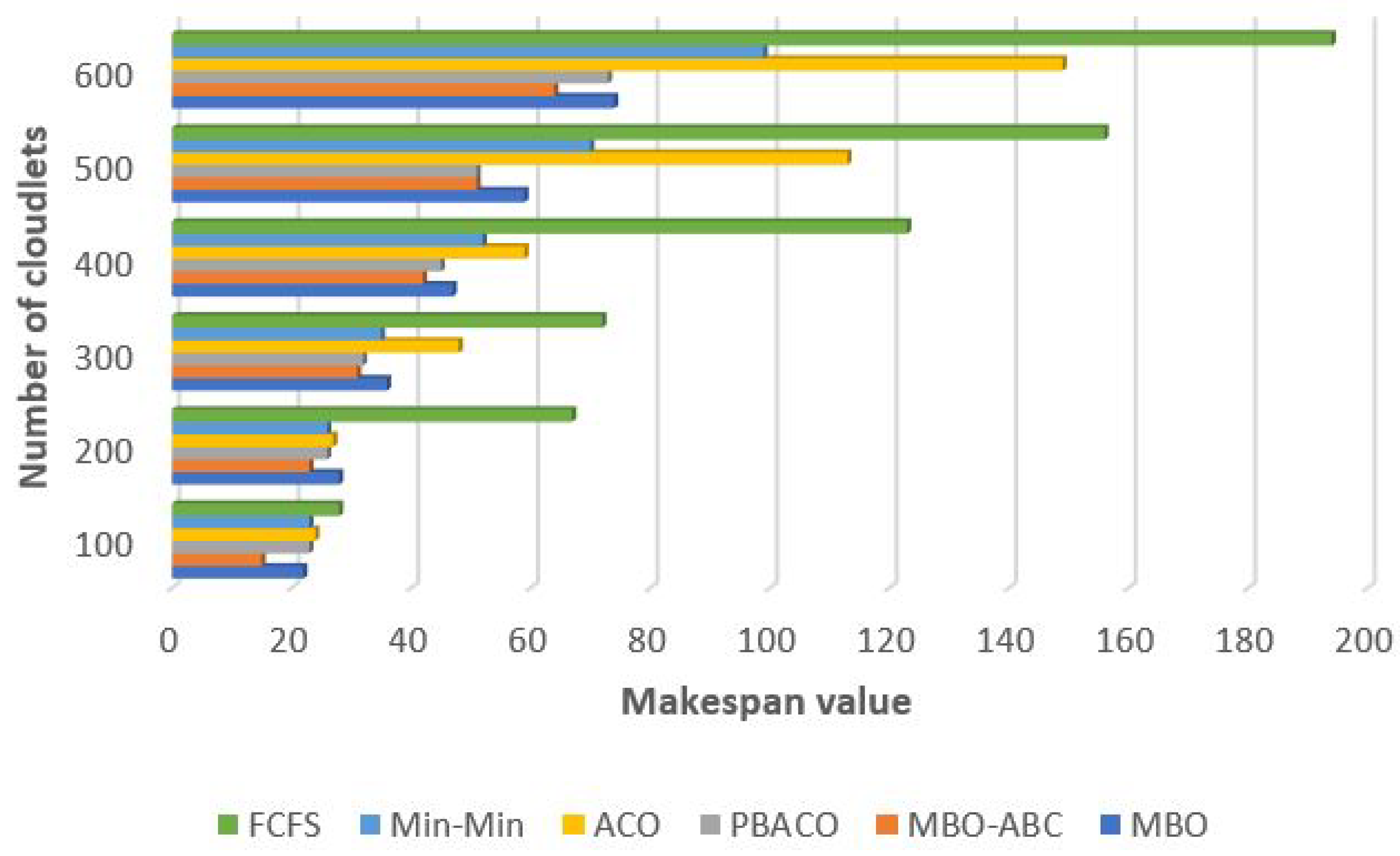
Comparative analysis between MBO-ABC and Min-Min, first come first serve (FCSF) heuristics and ACO and PBACO metaheuristics are depicted in
Figure 11. Results for Min-Min, FCFS, ACO and PBACO are taken from [
98]. The original MBO was also included in comparative analysis.
From the comparative analysis shown in
Figure 11, it is interesting to notice that the best performing metaheuristics is MBO-ABC, the second best is the PBACO, while the third best is the original MBO. Only in the case of the test with 500 cloudlets, the PBACO establishes the same makespan value as the MBO-ABC. Original MBO metaheuristics in average (when all test instances are taken into account) obtains slightly better performance than the original ACO and the Min-Min heuristics. The FCFS heuristics shows the worst performance among all tested approaches.
Performance increase (makespan value objective decrease) of the MBO-ABC over other heuristics and metaheuristics included in comparative analysis is summarized in
Table 9.
5.2.3. Simulations with a Real Data Set
In order to further test the robustness, solution quality and scalability of the proposed MBO-ABC metaheuristics, we simulated homogeneous cloud environment, where all VMs have the same characteristics, with varying number of tasks (from 100 to 2000). However, this time, we took the data set for the cloudlets parameters from the real-world computing environment.
The cloudlets used in performed simulations were generated from the Sweden standard formatted workload trace log of high performance computing—HPC2N. This log contains information for 527,371 cloudlets and 240 CPU resources collected in the period, from year 2002 to year 2006. We retrieved the workload trace log file
HPC2N-2002-2.2-cln.swf from the following URL:
http://www.cs.huji.ac.il/labs/parallel/workload/l_hpc2n/. Each row in the workload file represents characteristics of one cloudlet.
From the first column of the retrieved file, we extracted the cloudlet ID, while the length of each cloudlet (expressed in million instructions unit), and requested processing element (PE) are extracted from the columns four and eight, respectively.
In conducted simulations, we used ten VMs with the same configurations, one data center with the default CloudSim characteristics and two physical hosts. The same simulation environment, as well as the dataset, was utilized in [
68]. In [
68], a moth search algorithm hybridized with differential evolution (MSDE) was adapted and tested for a cloudlet scheduling problem.
For the sake of more objective comparative analysis with MSDE, population size of the MBO-ABC and MBO metaheuristics
were set to 30 with the maximum 1000 iterations in one run. The same control parameters were used in [
68].
As in the simulations with the artificial data set, the value of the
parameter was calculated according to Equation (
24), and was set to 133, while the value of the
was set to 667, by using the same expression as in simulations with bound-constrained benchmarks (please refer to
Section 5.1.1). Other MBO-ABC and MBO parameters were adjusted as shown in
Table 2.
The characteristics of VMs and hosts utilized in simulations are summarized in
Table 10.
Like in the previous test (
Section 5.2.2), for each test instance (the number of cloudlets), we executed metaheuristics in 100 independent runs and calculated the averages of the makespan objective and of the degree of imbalance (DI) indicator (Equation (
11)). Unlike in the previous test, we did not alter the arrival rate of cloudlets in the
DatacenterBroker class of the CloudSim environment.
In addition, it should be noted that, since there are 527,371 cloudlets in the data set, in each run, we have chosen random cloudlets (in test instance with 100 cloudlets, 100 cloudlets were randomly chosen, etc.). The effect of randomization to the algorithms’ performance is neutralized with 100 runs for every test instance.
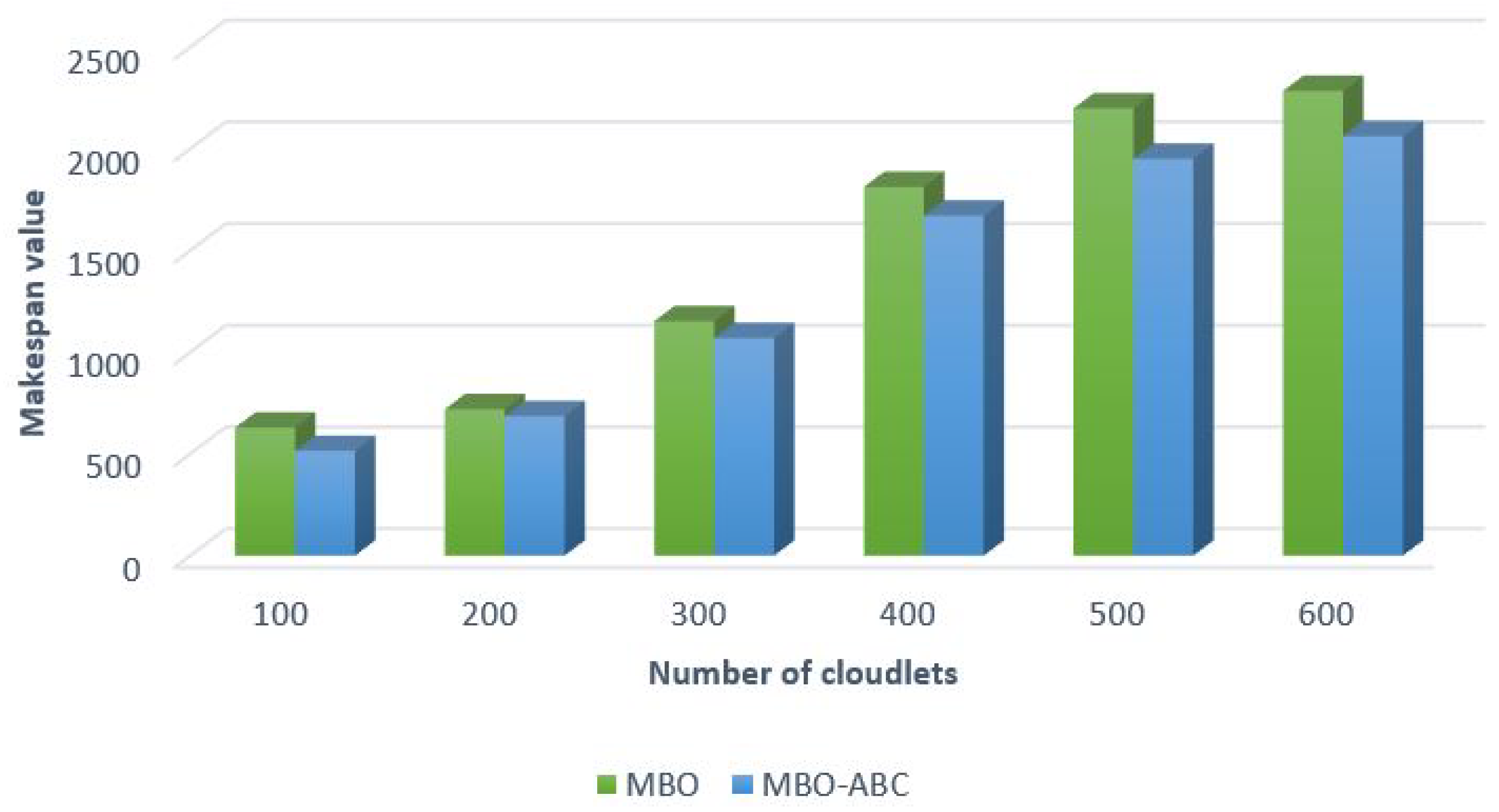
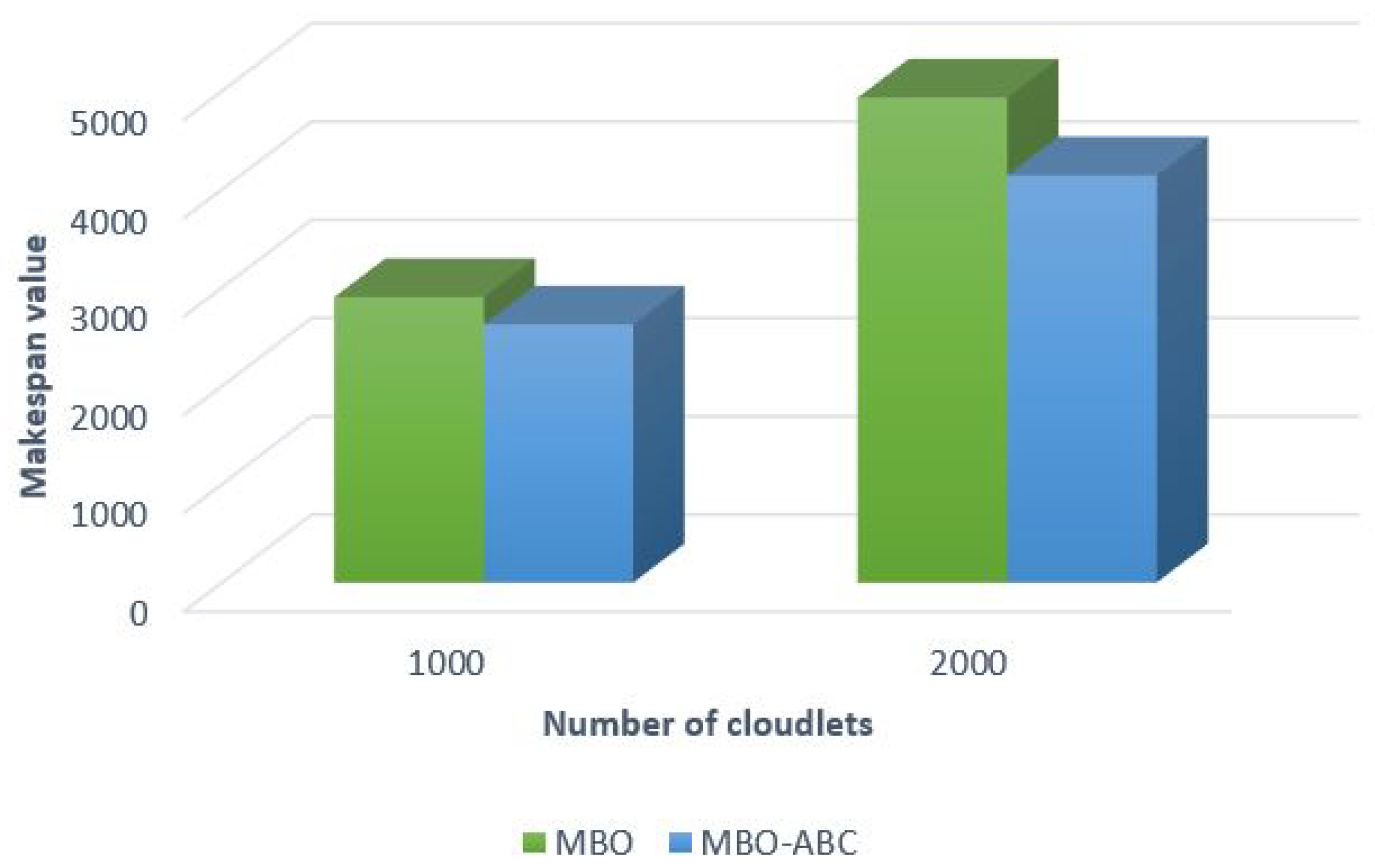
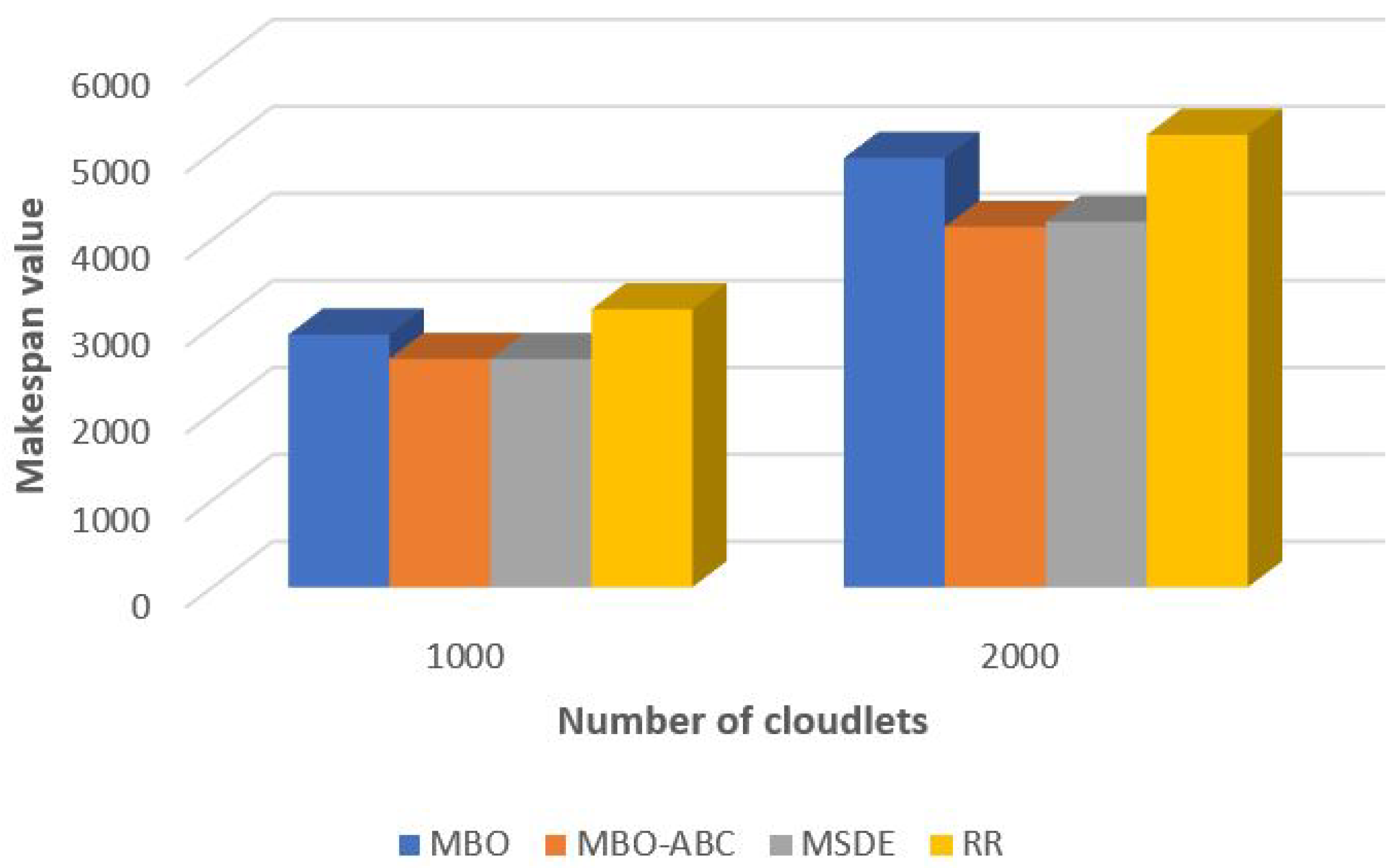
Comparative analysis between the MBO-ABC and the original MBO on a small number of cloudlets (100–600) and a large number of cloudlets (1000 and 2000) are shown in
Figure 12 and
Figure 13, respectively.
From the presented figures, it is evident that the MBO-ABC obtains better performance by establishing better value for the make span objective, for both test sets, with a smaller number and larger number of cloudlets. Improvements of the MBO-ABC over to the original MBO expressed in percents are summarized in
Table 11.
A convergence speed graph of the MBO-ABC and the MBO on problem instance with 2000 cloudlets in some of the better runs is given in
Figure 14.
From the presented figure, it is interesting to notice that, in early iterations, the MBO-ABC converges faster than the original MBO metaheuristics. This means that the solutions’ exhaustiveness mechanism adapted from the ABC algorithm improved the exploitation–exploration balance of the original MBO, and, in early iterations, MBO-ABC does not get stuck in some of the suboptimal search space domains. Moreover, by performing careful analysis, it can be observed that the MBO-ABC already in iterations between 650 and 700 started to perform a fine search in the promising region of the search space.
As stated above, we compared performance of the MBO-ABC with the MSDE, which was introduced in [
68]. By analyzing [
68], we noticed that, in this paper, the results for costs per user plus makespan were reported, as in [
99]. In our analysis, we show only the values of the makespan (not costs).
In the comparative analysis for small and large number of tasks, which are visualized in
Figure 15 and
Figure 16, respectively, we included the original MBO, as well as the round robin (RR) heuristics. The RR heuristics is used by default within the CloudSim platform.
According to presented results, the performance of the original MBO is significantly below the performance of the MSDE metaheuristics, but better than the results obtained by the RR method. On the contrary, hybridized MBO-ABC on average establishes slightly better solution quality than the MSDE metaheuristics. In simulations with 100, 300, 400, 500, 600 and 2000 cloudlets, MBO-ABC proved to be better than MSDE, while the MSDE outperformed MBO-ABC in experiments with 200 and 1000 cloudlets. The RR heuristics are included in analysis for proving the superiority of metaheuristics over heuristics approaches for tackling these kinds of problems.
Improvements of the MBO-ABC compared to the MSDE and RR in percentage are given in
Table 12.
Moreover, in simulations with the data set taken from production cloud environment, we have also included the DI indicator that is formulated according to Equation (
11). Comparative analysis with the DI is shown in
Table 13. The best results from each category are marked in bold.
Similarly, as in the case of the MS objective, the DI value is averaged over 100 independent algorithms’ runs is taken. We note that the DI was not taken as an optimization objective.
Results of the DI indicator comparison are as expected. The RR heuristics obtained the worst values for the DI. The MBO metaheuristics generated higher DI values than the MSDE and MBO-ABC. Finally, MSDE and MBO-ABC accomplish nearly the same performance for this indicator.
As a general conclusion, it can be stated that the MBO-ABC hybrid metaheuristics are able to accomplish better solution quality, robustness and scalability than other algorithms that are included in comparative analysis. Moreover, by applying the MBO-ABC, improvements in solving cloudlet scheduling problem in cloud computing can be established.
6. Conclusions and Future Work
The basic goal of the research that was presented in this paper is focused towards establishing further enhancements in tackling cloudlet (task) scheduling problem in cloud computing environments by utilizing swarm intelligence. This problem belongs to the category of NP-hard tasks and it is being addressed as one of the most important challenges and topics in the domain of cloud computing.
To achieve a defined goal, we have implemented a cloudlet scheduling model with the makespan objective, and for this purpose we have adapted two versions of the MBO swarm metaheuristics, one original and one hybridized with the ABC algorithm (MBO-ABC). Prior to this research, no adaptations of the MBO approach for the cloud computing challenges could be found in the literature. By applying a hybridized MBO approach, we have improved the results that have previously been obtained by other metaheuristics and heuristics that were tested on the same problem instances.
Simulation and practical experiments were conducted in a robust and scalable environment of the CloudSim framework that is accepted by many researchers world-wide. All of the details, including the settings of the algorithms’ control parameters, simulation framework setup, and the data sets that were used in experiments are fully provided in this paper, so the researcher who wants to implement the proposed approaches and to run simulations has more than enough information to do that.
For the purpose of this research, we have conducted two types of experiments. In the first experimental suite, we have tested original and the hybridized MBO metaheuristics on a wider set of bound-constrained (unconstrained) benchmarks, where we performed side-by-side comparison between these two approaches. We assumed that if the MBO-ABC exhibits better performance than the original MBO for standard benchmark tests, then it will also establish better solutions’ quality for practical NP-hard challenges, such as the task scheduling in cloud computing.
In the second experiments suite, we have tested MBO and MBO-ABC on a practical cloudlet scheduling task, when we also performed two types of tests. In the first test, we utilized a synthetic data set that was generated in a pseudo-random manner within the CloudSim platform, while, in the second test, we employed a data set from the real-world computing environment.
According to obtained experimental results and comparative analysis with other heuristics and metaheuristics that were tested on the same problem instances, and, under the same experimental conditions, we concluded that the further enhancements in solving task scheduling problems in cloud environments can be established by employing swarm intelligence methods.
6.1. Theoretical Implications of the Research
According to the contributions of this paper that are shown in
Section 1, presented research has theoretical and management implications.
Theoretical implications refer to the improvements by hybridization of the original MBO algorithm. The devised MBO-ABC hybrid obtains significantly better results in terms of the solutions’ quality and the convergence than the original MBO approach. Performance of the MBO-ABC was validated on a various benchmark tests, as was shown in
Section 5.
6.2. Management Implications of the Research
Besides improvements of the original MBO algorithm, we adapted basic and hybridized MBO for the cloudlet scheduling problem and obtained better results in terms of the makespan and the degree of imbalance than other methods. Improvements in solving a cloud scheduling problem have clearly defined implications in the area of cloud management.
By decreasing the makespan value and the degree of imbalance, the cloud infrastructure is better utilized, and the enterprise may obtain financial gains in a way in which the capital investments and maintenance costs are lowered. For example, if an enterprise may satisfy all business needs by better hardware utilization, there would be no need for buying additional hardware units. In addition, better hardware utilization and lower makespan value have an important influence on the QoS, which in turn may have a positive influence on the end-users’ satisfaction. Besides all mentioned, the money the company would invest into buying new equipment may be distributed to core business operations.
6.3. Future Research
As part of the future research in this domain, we will adapt and test proposed metaheuristics on other problems and challenges from the domain of cloud computing, such as workflow scheduling, load balancing, reduction of energy consumption, VMs migration, etc. Since swarm intelligence shows great potential in tackling cloud computing challenges, we assume that further improvements and enhancements in this area can be accomplished.
In accordance with this, as part of our future research, we also plan to implement and to adapt other swarm intelligence approaches for cloud computing problems and challenges. Moreover, we will definitely try to improve existing swarm algorithms by performing small changes (modifications in search equations, control parameters’ adjustments, etc.) and large modification by introducing hybridization with other heuristics and metaheuristics.