Estimating Directional Data From Network Topology for Improving Tracking Performance
Abstract
:1. Introduction
2. Problem Formulation
- Initialization: The marginal posterior PDF at is set to the prior PDF of .
- Prediction: By following the state transition model in Equation (6), the predictive PDF of the state at t is given by
- Update: According to Bayes’ rule [42,53], one has thatwhere is the likelihood and is just a normalizing constant that does not depend on , required to assure that integrates to 1 [39]. Generally, the marginal PDF at cannot be calculated in analytic form. Moreover, the integral in Equation (8) cannot be obtained in closed-form, unless the state model is linear. Hence, certain approximations are necessary to get .
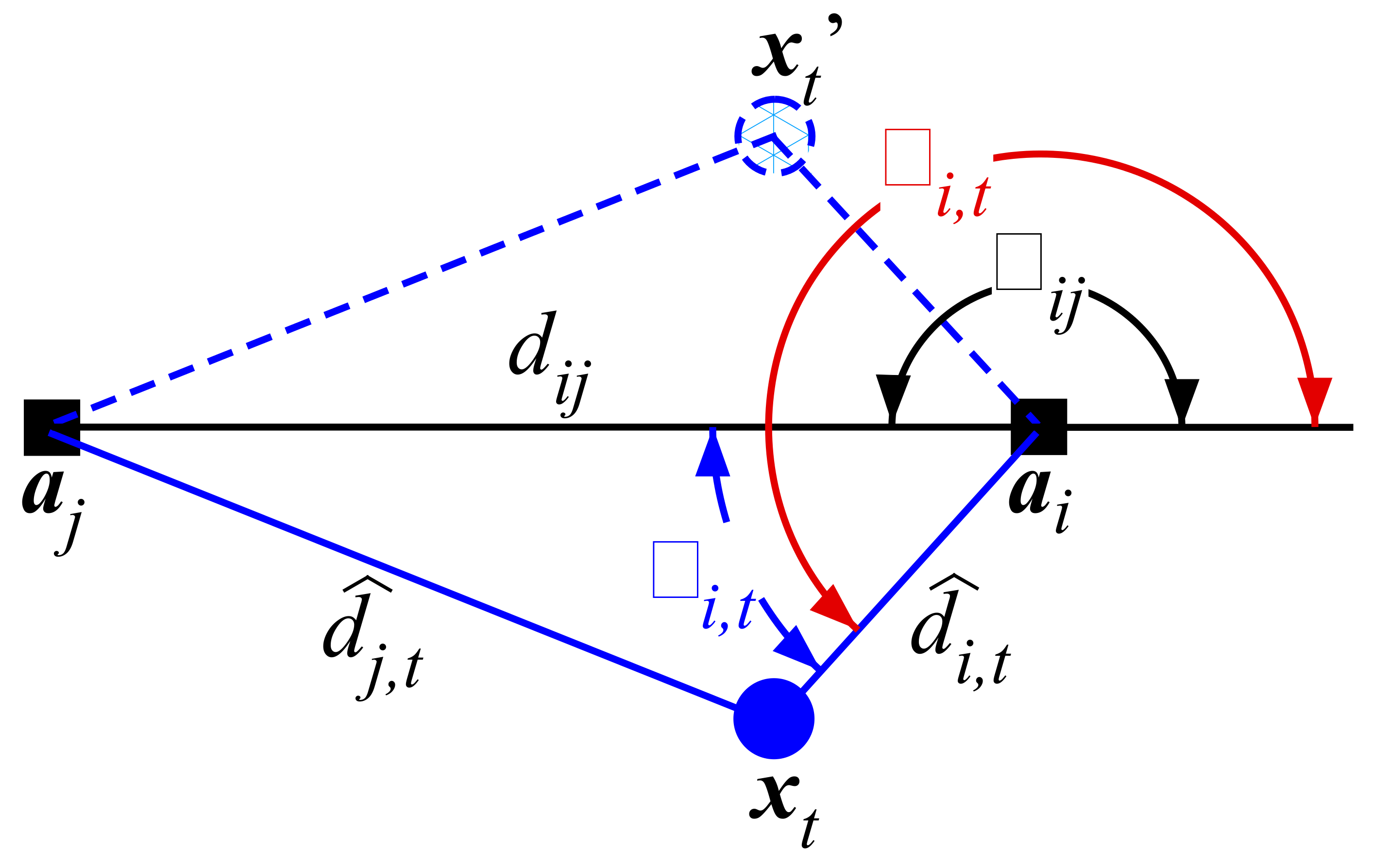
3. Angle of Arrival Estimation
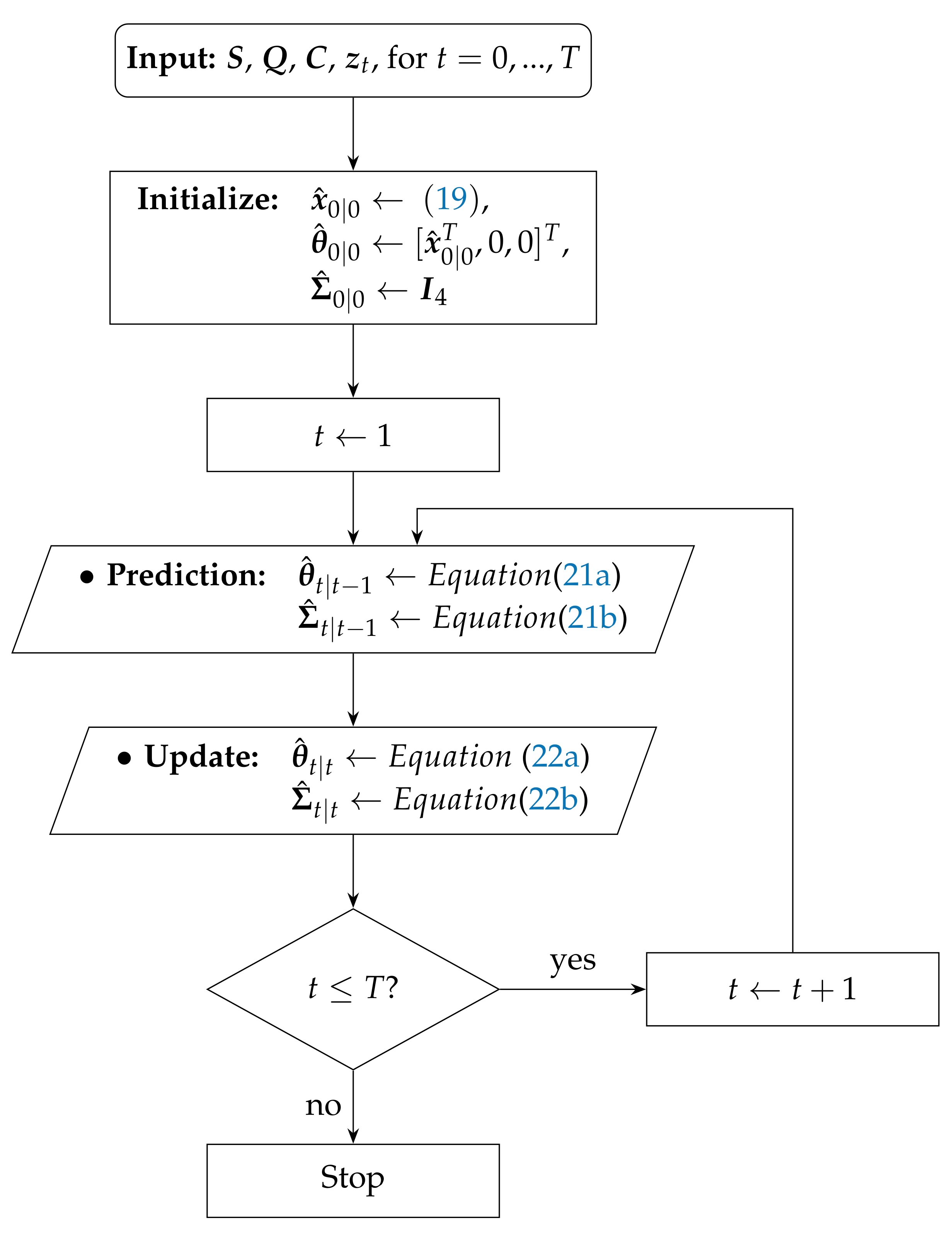
4. Target Tracking
| Algorithm 1 KF algorithm description. |
Require:, , , , for
|
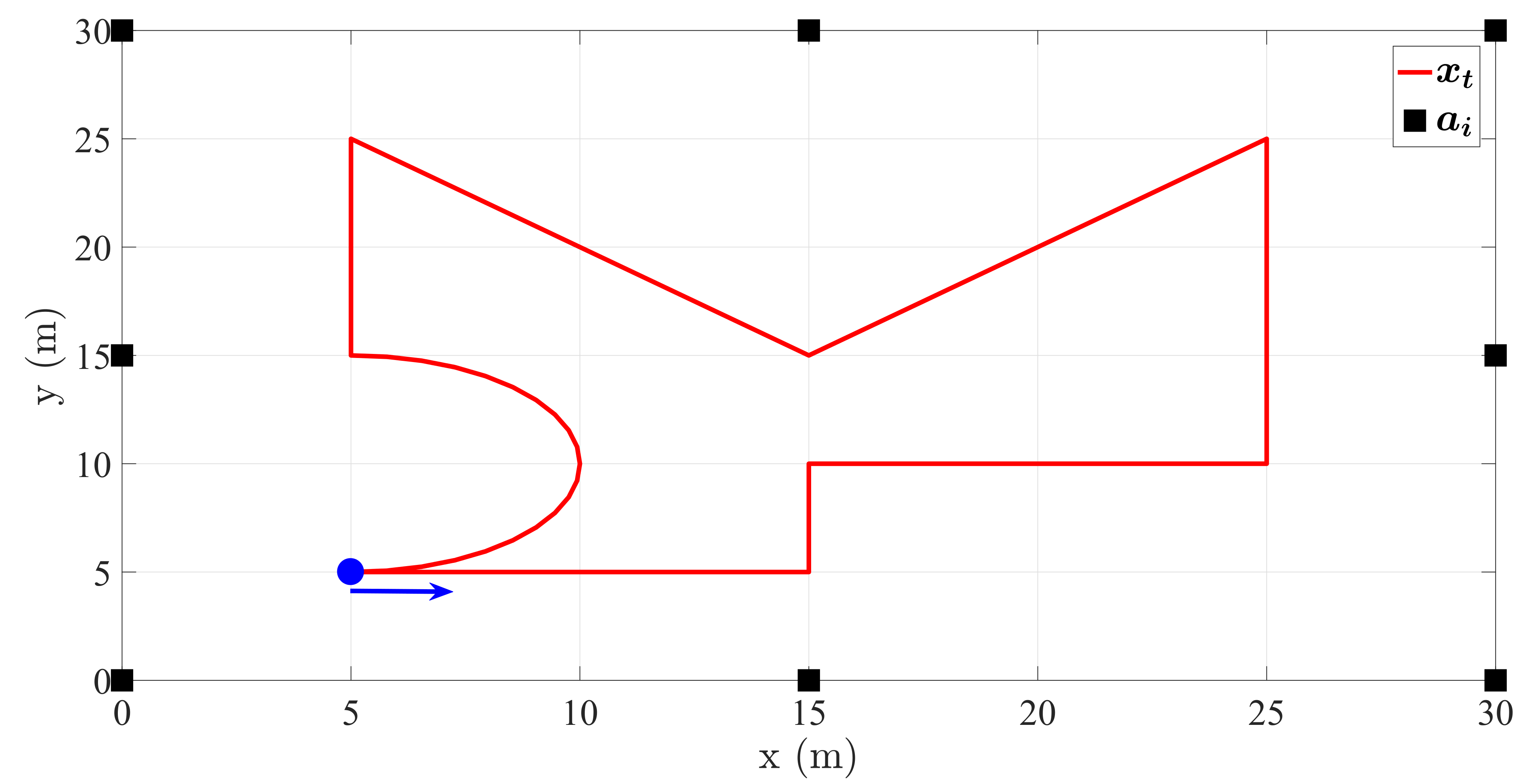
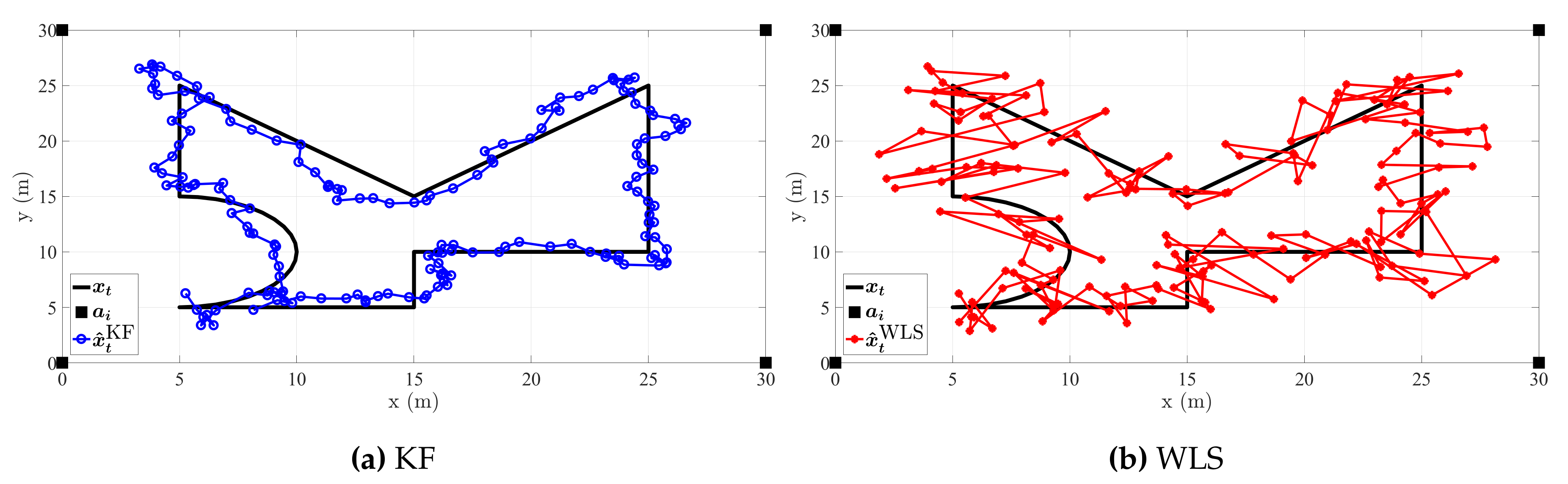
5. Performance Results
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A. Derivation of the State Transition Model
References
- Xu, E.; Ding, Z.; Dasgupta, S. Target Tracking and Mobile Sensor Navigation in Wireless Sensor Networks. IEEE Trans. Mob. Comput. 2013, 12, 177–186. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R.; Tuba, M.; Bacanin, N. RSS-AoA-Based Target Localization and Tracking in Wireless Sensor Networks, 1st ed.; River Publishers: Delft, The Netherlands, 2017. [Google Scholar]
- Correia, S.; Beko, M.; Cruz, L.; Tomic, S. Elephant Herding Optimization for Energy-Based Localization. Sensors 2019, 18, 2849. [Google Scholar]
- Chalisea, B.K.; Zhanga, Y.D.; Amina, M.G.; Himed, B. Target Localization in a Multi-static Passive Radar System Through Convex Optimization. Signal Process. 2014, 102, 207–215. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M. Target Localization via Integrated and Segregated Ranging Based on RSS and TOA Measurements. Sensors 2019, 19, 230. [Google Scholar]
- Martínez, S.; Bullo, F. Optimal Sensor Placement and Motion Coordination for Target Tracking. Automatica 2006, 42, 661–668. [Google Scholar] [CrossRef]
- Beko, M. Energy-based Localization in Wireless Sensor Networks Using Second-order Cone Programming Relaxation. Wirel. Pers. Commun. 2014, 77, 1847–1857. [Google Scholar]
- Pedro, D.; Tomic, S.; Bernardo, L.; Beko, M.; Oliveira, R.; Dinis, R.; Pinto, P.; Amaral, P. Algorithms for Estimating the Location of Remote Nodes Using Smartphones. IEEE Access 2019. [Google Scholar] [CrossRef]
- Paz, L.M.; Tardós, J.D.; Neira, J. Divide and Conquer: EKF SLAM in (n). IEEE Trans. Robot. 2008, 24, 1107–1120. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R.; Bernardo, L. On Target Localization Using Combined RSS and AoA Measurements. Sensors 2018, 18, 1266. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, M.; He, Y.; Jiang, J. P-cmommt Algorithm for the Cooperative Multi-robot Observation of Multiple Moving Targets. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; pp. 661–668. [Google Scholar]
- Tomic, S.; Beko, M. Exact Robust Solution to TW-ToA-based Target Localization Problem with Clock Imperfections. IEEE Sign. Process. Lett. 2018, 25, 531–535. [Google Scholar] [CrossRef]
- Patwari, N.; Ash, J.N.; Kyperountas, S.; Moses, R.L.; Correal, N.S. Locating the Nodes: Cooperative Localization in Wireless Sensor Networks. IEEE Sign. Process. Mag. 2005, 22, 54–69. [Google Scholar] [CrossRef]
- Khan, M.W.; Kemp, A.H.; Salman, N.; Mihaylova, L.S. Tracking of Wireless Mobile Nodes in the Presence of Unknown Path-loss Characteristics. In Proceedings of the 2015 18th International Conference on Information Fusion (Fusion), Washington, DC, USA, 6–9 July 2015; pp. 104–111. [Google Scholar]
- Tomic, S.; Beko, M.; Dinis, R. Distributed RSS-Based Localization in Wireless Sensor Networks Based on Second-Order Cone Programming. Sensors 2014, 14, 18410–18432. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.W.; Salman, N.; Ali, A.; Khan, A.M.; Kemp, A.H. A Comparative Study of Target Tracking With Kalman Filter, Extended Kalman Filter and Particle Filter Using Received Signal Strength Measurements. In Proceedings of the 2015 International Conference on Emerging Technologies (ICET), Peshawar, Pakistan, 19–20 December 2015; pp. 1–6. [Google Scholar]
- Tomic, S.; Beko, M.; Dinis, R. RSS-based Localization in Wireless Sensor Networks Using Convex Relaxation: Noncooperative and Cooperative Schemes. IEEE Trans. Veh. Technol. 2015, 64, 2037–2050. [Google Scholar] [CrossRef]
- Qua, X.; Xie, L. An Efficient Convex Constrained Weighted Least Squares Source Localization Algorithm Based on TDOA Measurements. Signal Process. 2016, 119, 142–152. [Google Scholar] [CrossRef]
- Wang, G.; Chen, H.; Li, Y.; Ansari, N. NLOS Error Mitigation for TOA-Based Localization via Convex Relaxation. IEEE Trans. Wirel. Commun. 2014, 13, 4119–4131. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R.; Montezuma, P. A Robust Bisection-based Estimator for TOA-based Target Localization in NLOS Environments. IEEE Commun. Lett. 2017, 21, 2488–2491. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, S.; Wang, G.; Li, Y. Robust NLOS Error Mitigation Method for TOA-Based Localization via Second-Order Cone Relaxation. IEEE Commun. Lett. 2015, 19, 2210–2213. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M. A Bisection-based Approach for Exact Target Localization in NLOS Environments. Sign. Process. 2018, 143, 328–335. [Google Scholar] [CrossRef]
- Niculescu, D.; Nath, B. Ad Hoc Positioning System (APS) Using AoA. In Proceedings of the Twenty-second Annual Joint Conference of the IEEE Computer and Communications Societies, San Francisco, CA, USA, 30 March–3 April 2003. [Google Scholar]
- Yu, K. 3-D Localization Error Analysis in Wireless Networks. IEEE Trans. Wirel. Commun. 2007, 6, 3473–3481. [Google Scholar]
- Biswas, P.; Aghajan, H.; Ye, Y. Semidefinite Programming Algorithms for Sensor Network Localization Using Angle of Arrival Information. In Proceedings of the Thirty-Ninth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 30 October–2 November 2005; pp. 220–224. [Google Scholar]
- Tomic, S.; Beko, M.; Dinis, R. 3-D Target Localization in Wireless Sensor Network Using RSS and AoA Measurement. IEEE Trans. Vehic. Technol. 2017, 66, 3197–3210. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, L.; Wang, Y.; Hu, L. Measurement-based Indoor NLOS TOA/RSS Range Error Modelling. Electron. Lett. 2016, 52, 165–167. [Google Scholar] [CrossRef]
- Coluccia, A.; Fascista, A. On the Hybrid TOA/RSS Range Estimation in Wireless Sensor Networks. IEEE Trans. Wirel. Commun. 2018, 17, 361–371. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R. Distributed RSS-AoA Based Localization with Unknown Transmit Powers. IEEE Wirel. Commun. Lett. 2016, 5, 392–395. [Google Scholar] [CrossRef]
- Yin, J.; Wan, Q.; Yang, S.; Ho, K.C. A Simple and Accurate TDOA-AOA Localization Method Using Two Stations. IEEE Sign. Process. Lett. 2016, 23, 144–148. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R.; Montezuma, P. Distributed Algorithm for Target Localization in Wireless Sensor Networks Using RSS and AoA Measurements. Pervasive Mob. Comput. 2017, 37, 63–77. [Google Scholar] [CrossRef]
- Macii, D.; Colombo, A.; Pivato, P.; Fontanelli, D. A Data Fusion Technique for Wireless Ranging Performance Improvement. IEEE Trans. Indstr. Meas. 2013, 62, 27–37. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R.; Montezuma, P. A Closed-form Solution for RSS/AoA Target Localization by Spherical Coordinates Conversion. IEEE Wirel. Commun. Lett. 2016, 5, 680–683. [Google Scholar] [CrossRef]
- Tiwari, S.; Wang, D.; Fattouche, M.; Ghannouchi, F. A Hybrid RSS/TOA Method for 3D Positioning in an Indoor Environment. ISRN Sign. Process. 2012, 2012, 503707. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Tuba, M.; Correia, V.M.F. Target Localization in NLOS Environments Using RSS and TOA Measurements. IEEE Wirel. Commun. Lett. 2018, 7, 1062–1065. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Tuba, M.; Correia, V.M.F. Target Localization in NLOS Environments Using RSS and TOA Measurements. IEEE Sign. Process. Lett. 2019, 26, 64–68. [Google Scholar] [CrossRef]
- Beaudeau, J.P.; Bugallo, M.F.; Djuric, P.M. RSSI-based Multi-target Tracking by Cooperative Agents Using Fusion of Cross-target Information. IEEE Trans. Sign. Process. 2015, 63, 5033–5044. [Google Scholar] [CrossRef]
- Masazade, E.; Niu, R.; Varshney, P.K. Dynamic Bit Allocation for Object Tracking in Wireless Sensor Networks. IEEE Trans. Sign. Process. 2012, 60, 5048–5063. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice-Hall: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Tomic, S.; Beko, M.; Dinis, R.; Tuba, M.; Bacanin, N. Bayesian Methodology for Target Tracking Using RSS and AoA Measurements. Phys. Commun. 2017, 25, 158–166. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Fortmann, T.E. Tracking and Data Association; Academic Press Professional, Inc.: San Diego, CA, USA, 1987. [Google Scholar]
- Dardari, D.; Closas, P.; Djuric, P.M. Indoor Tracking: Theory, Methods, and Technologies. IEEE Trans. Vehic. Technol. 2016, 64, 1263–1278. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R.; Gomes, J.P. Target Tracking with Sensor Navigation Using Coupled RSS and AoA Measurements. Sensors 2017, 17, 2690. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, H.; Chen, G.; Kwan, C.; Li, X.R. Comparison of Several Ballistic Target Tracking Filters. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 2197–2202. [Google Scholar]
- Farina, A.; Ristic, B.; Benvenuti, D. Tracking a Ballistic Target: Comparison of Several Nonlinear Filters. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 854–867. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. Unscented Filtering and Nonlinear Estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Wan, E.A.; van der Merwe, R. The Unscented Kalman Filter for Nonlinear Estimation. In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing ommunications, and Control Symposium, Lake Louise, AB, Canada, 4 October 2000; pp. 1–6. [Google Scholar]
- Chatzi, E.N.; Smyth, A.W. The Unscented Kalman Filter and Particle Filter Methods for Nonlinear Structural System Identification with Non-collocated Heterogeneous Sensing. Struct. Control Health Monit. 2009, 16, 99–123. [Google Scholar] [CrossRef]
- Chen, Z. Bayesian Filtering: From Kalman Filters to Particle Filters, and Beyond. Statistics 2003, 182, 1–69. [Google Scholar] [CrossRef]
- Zou, Y.; Chakrabarty, K. Distributed Mobility Management for Target Tracking in Mobile Sensor Networks. IEEE Trans. Mob. Comput. 2007, 6, 872–887. [Google Scholar] [CrossRef]
- Song, Y.; Yu, H. A New Hybrid TOA/RSS Location Tracking Algorithm for Wireless Sensor Network. In Proceedings of the 2008 9th International Conference on Signal Processing, Beijing, China, 26–29 December 2008; pp. 2645–2648. [Google Scholar]
- Khan, R.; Sottile, F.; Spirito, M.A. Hybrid Positioning through Extended Kalman Filter with Inertial Data Fusion. IJIEE 2013, 3, 127–131. [Google Scholar]
- Wang, G.; Li, Y.; Jin, M. On MAP-based Target Tracking Using Range-only Measurements. In Proceedings of the 2013 8th International Conference on Communications and Networking in China (CHINACOM), Guilin, China, 14–16 August 2013; pp. 1–6. [Google Scholar]
- Rappaport, T.S. Wireless Communications: Principles and Practice; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Kannan, A.A.; Fidan, B.; Mao, G.; Anderson, B.D.O. Analysis of Flip Ambiguities in Distributed Network Localization. In Proceedings of the 2007 Information, Decision and Control, Adelaide, Australia, 12–14 February 2017; pp. 193–198. [Google Scholar]
- Mardia, K.V. Statistics of Directional Data; Academic Press, Inc.: London, UK, 1972. [Google Scholar]
- Tomic, S.; Beko, M.; Tuba, M. A Linear Estimator for Network Localization Using Integrated RSS and AOA Measurements. IEEE Sign. Process. Lett. 2019, 26, 405–409. [Google Scholar] [CrossRef]
- Gomes, J.B.B. An Overview on Target Tracking Using Multiple Model Methods. M.Sc. Thesis, Universidade Técnica de Lisboa, Lisbon, Portugal, 2008. [Google Scholar]
- Brown, R.G.; Hwang, P.Y.C. Introduction to Random Signals and Applied Kalman Filtering, 3rd ed.; Wiley: Hoboken, NJ, USA, 1997. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R. Estimation with Applications to Tracking and Navigation, 1st ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2001. [Google Scholar]
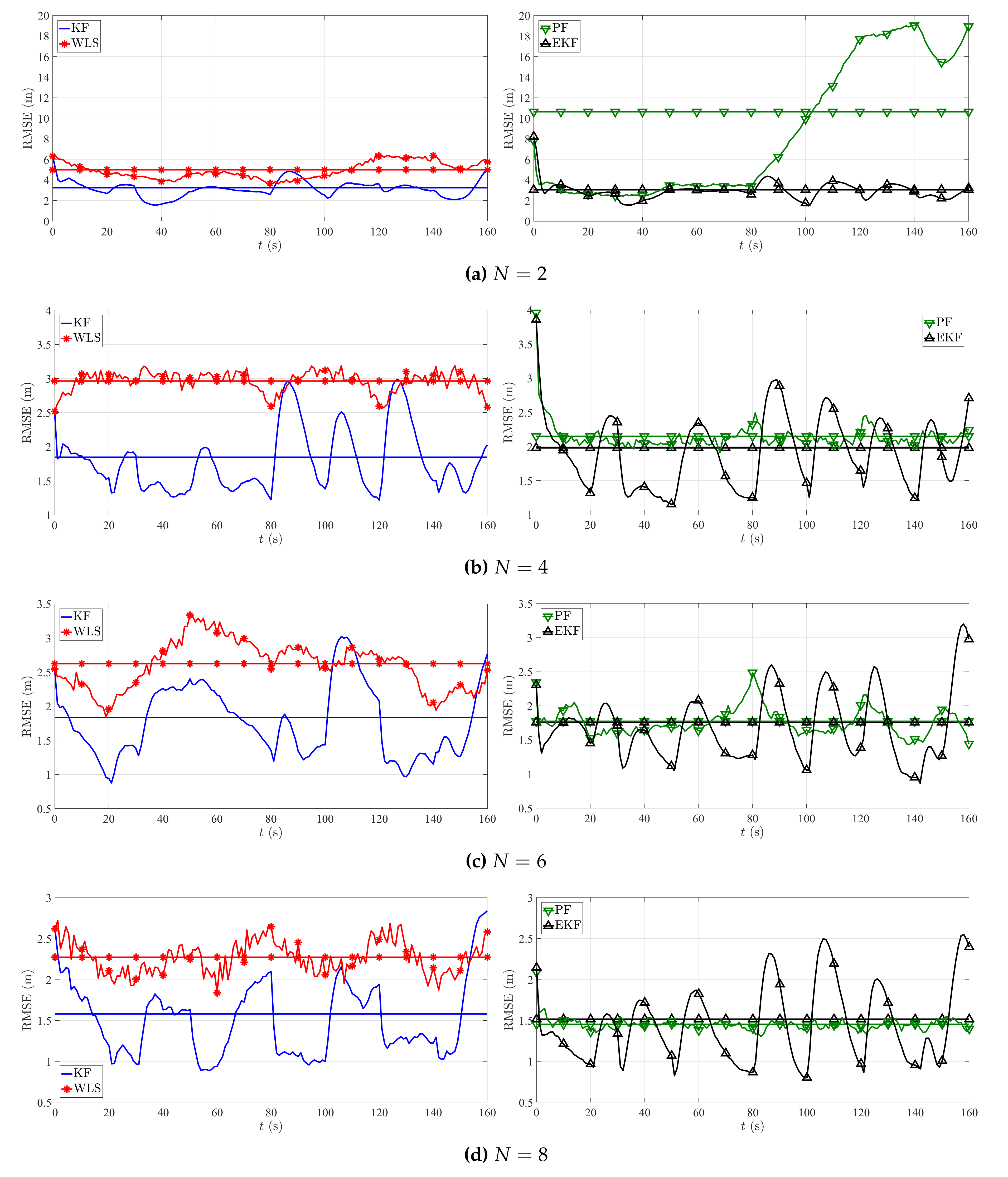
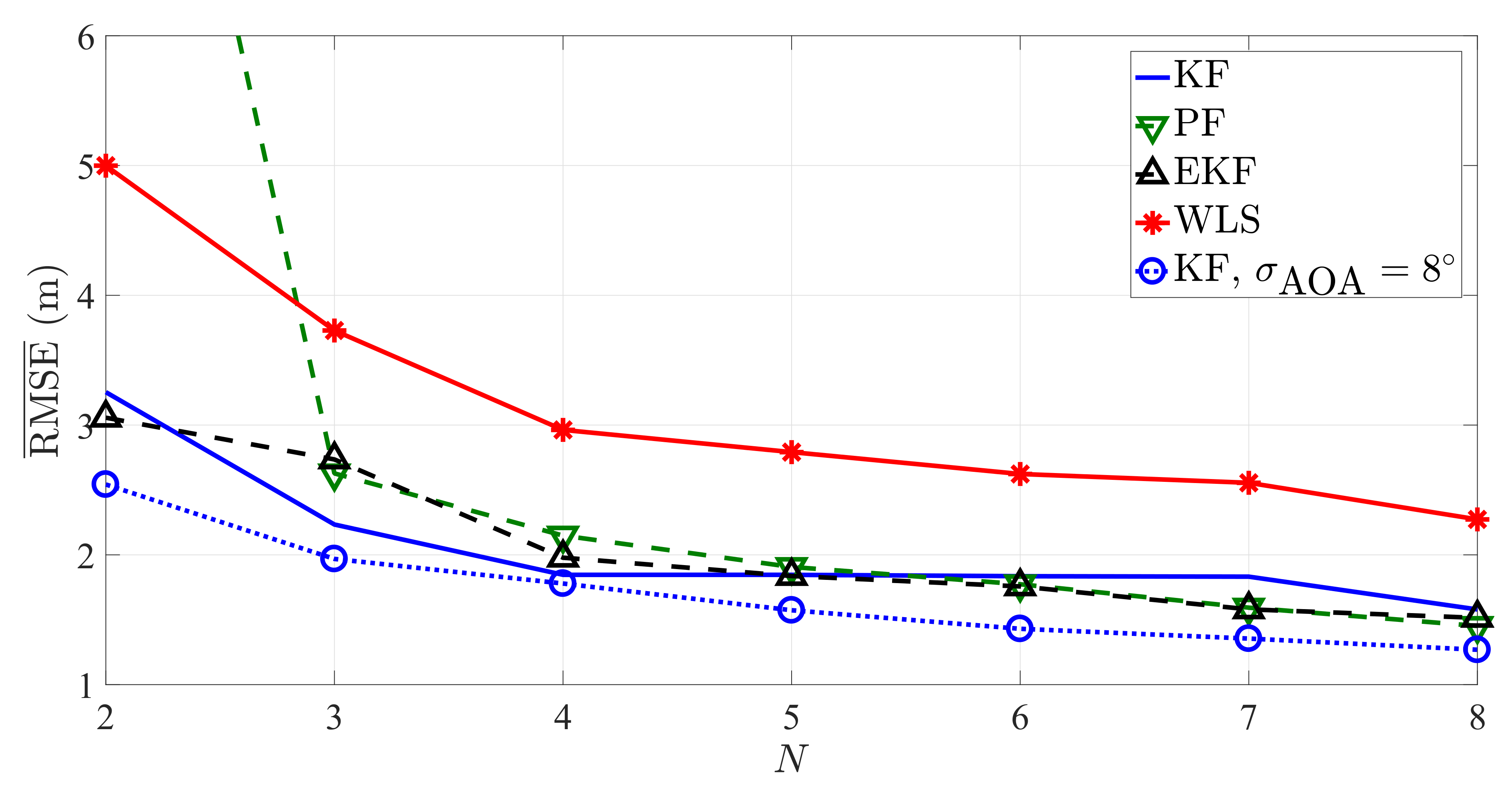
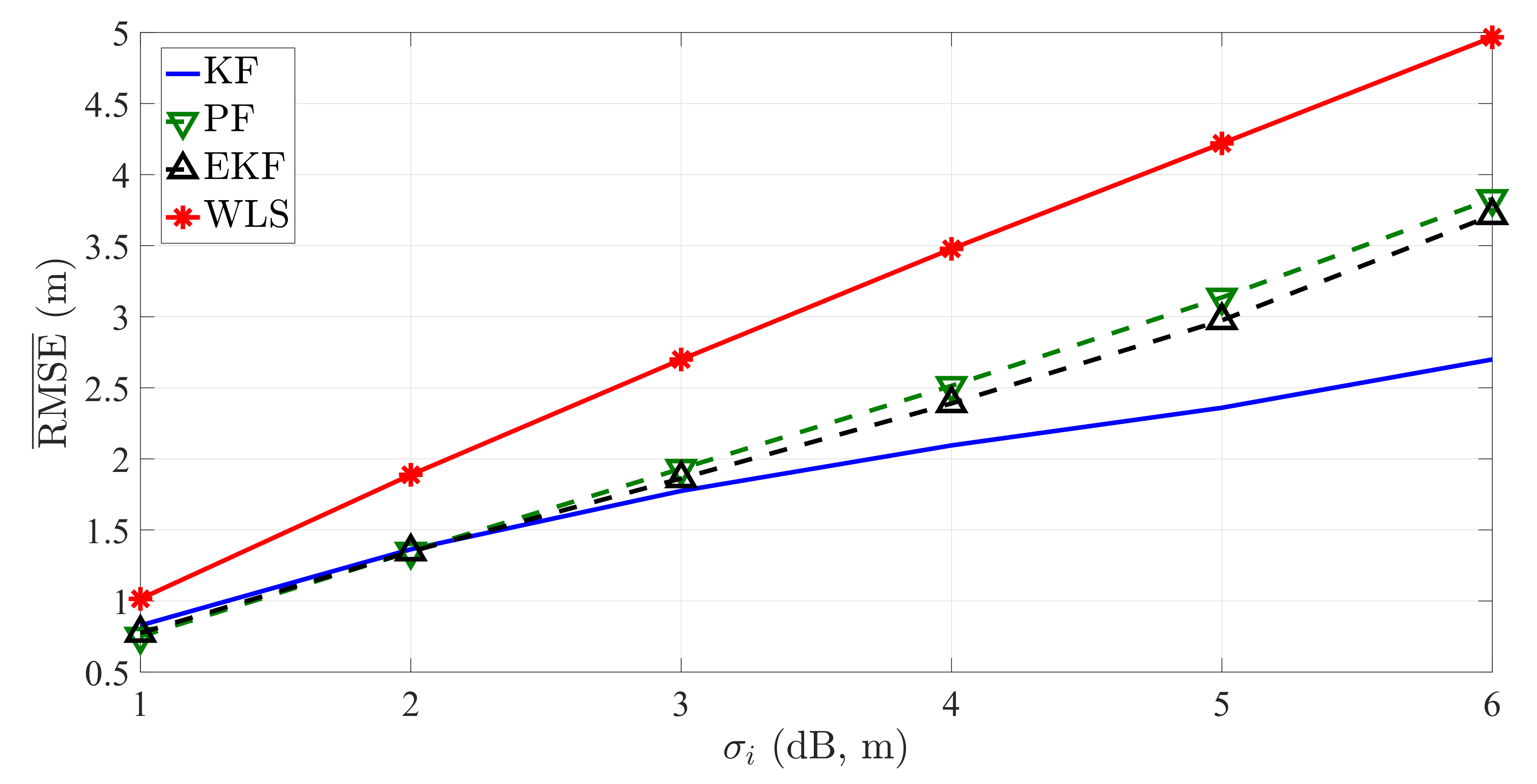

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| (m) | 0 | 0 | B | B | 0 | B | ||
| 0 | B | 0 | B | 0 | B |
| Parameter | Description | Value |
|---|---|---|
| N | The number of sensors | ≤8 |
| The number of NLOS links | N | |
| B | The length of the area border | 30 |
| The true anchor locations | See Table 1 | |
| The reference power | 20 (dBm) | |
| The reference distance | 1 (m) | |
| The PLE | 3 | |
| The noise power (RSS and TOA) | ≤6 (dB, m) | |
| The magnitude the NLOS bias (RSS and TOA) | ≤6 (dB, m) | |
| The NLOS bias (RSS and TOA) | (dB, m) | |
| Speed of the target | (m/s) | |
| The sampling interval | 1 (s) | |
| T | Trajectory duration | 160 (s) |
| q | The state process noise | () |
| The number of Monte Carlo runs | 500 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomic, S.; Beko, M.; Dinis, R.; Montezuma, P. Estimating Directional Data From Network Topology for Improving Tracking Performance. J. Sens. Actuator Netw. 2019, 8, 30. https://doi.org/10.3390/jsan8020030
Tomic S, Beko M, Dinis R, Montezuma P. Estimating Directional Data From Network Topology for Improving Tracking Performance. Journal of Sensor and Actuator Networks. 2019; 8(2):30. https://doi.org/10.3390/jsan8020030
Chicago/Turabian StyleTomic, Slavisa, Marko Beko, Rui Dinis, and Paulo Montezuma. 2019. "Estimating Directional Data From Network Topology for Improving Tracking Performance" Journal of Sensor and Actuator Networks 8, no. 2: 30. https://doi.org/10.3390/jsan8020030
APA StyleTomic, S., Beko, M., Dinis, R., & Montezuma, P. (2019). Estimating Directional Data From Network Topology for Improving Tracking Performance. Journal of Sensor and Actuator Networks, 8(2), 30. https://doi.org/10.3390/jsan8020030








